Distributed Optimization for Active Distribution Network Considering the Balance of Multi-Stakeholder
Abstract
1. Introduction
2. Considering the Benefits of Multi-Stakeholder Dispatching Strategy of ADN
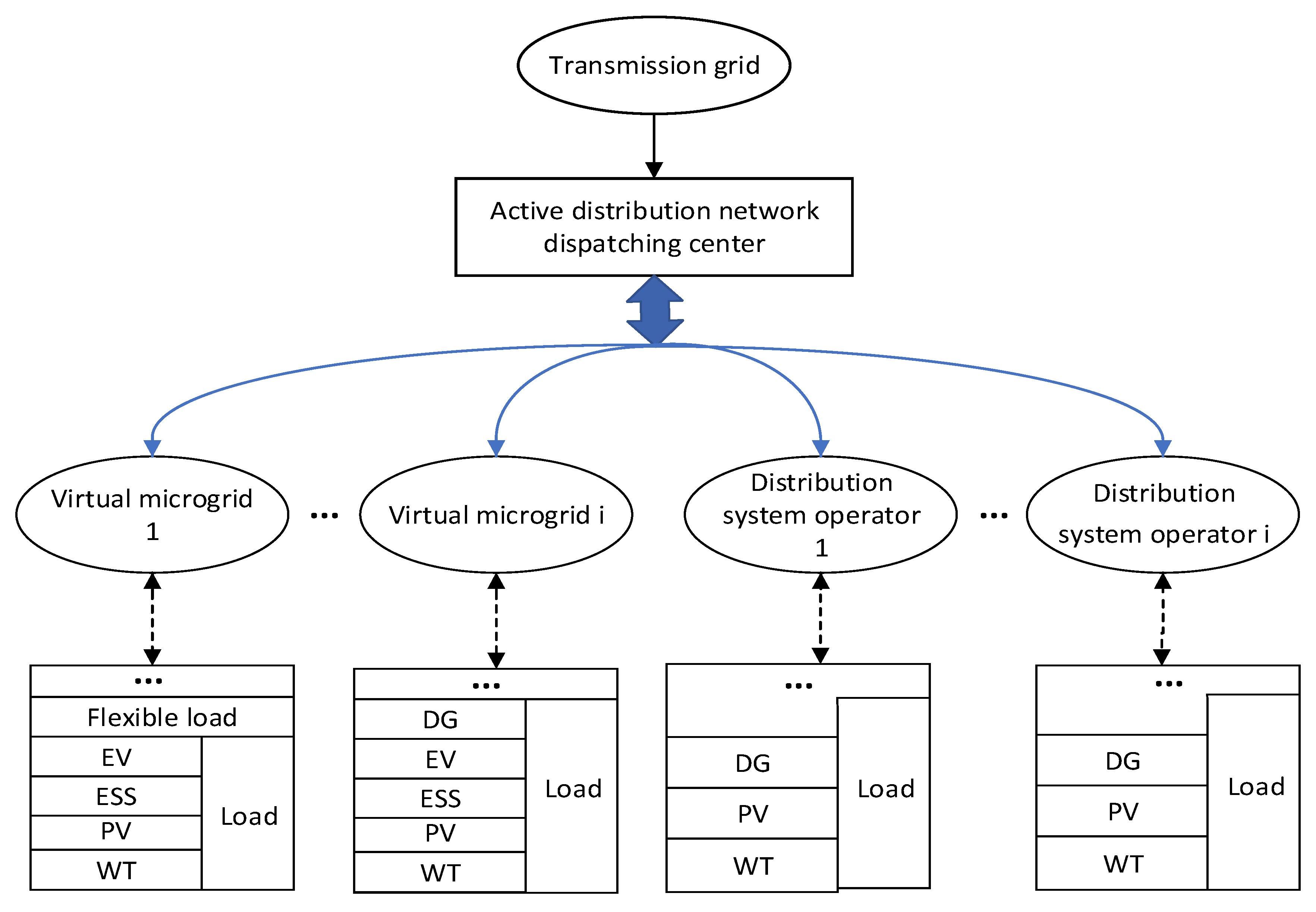
2.1. Electric System and Virtual Micro-Grid
2.2. Dispatching Overall Framework of Active Distribution Networks
3. Active Dispatching Distribution Network Bi-Level Optimization Dispatching Model
3.1. The Upper-Level Model
3.1.1. The Objective Function of Upper-Level Model
3.1.2. The Constraints of Upper-Level Model
3.2. The Lower-Level Model
3.2.1. The Objective Function of Upper-Level Model
3.2.2. The Constraints of Lower-Level Model
4. Distributed Solution Strategy of ADN Bi-Level Dispatching Model
4.1. Method Based on ADMM
4.2. The Distributed Solution Process for Active Distribution Network Bi-Level Dispatching Model
5. Discussion
5.1. Introduction to the System
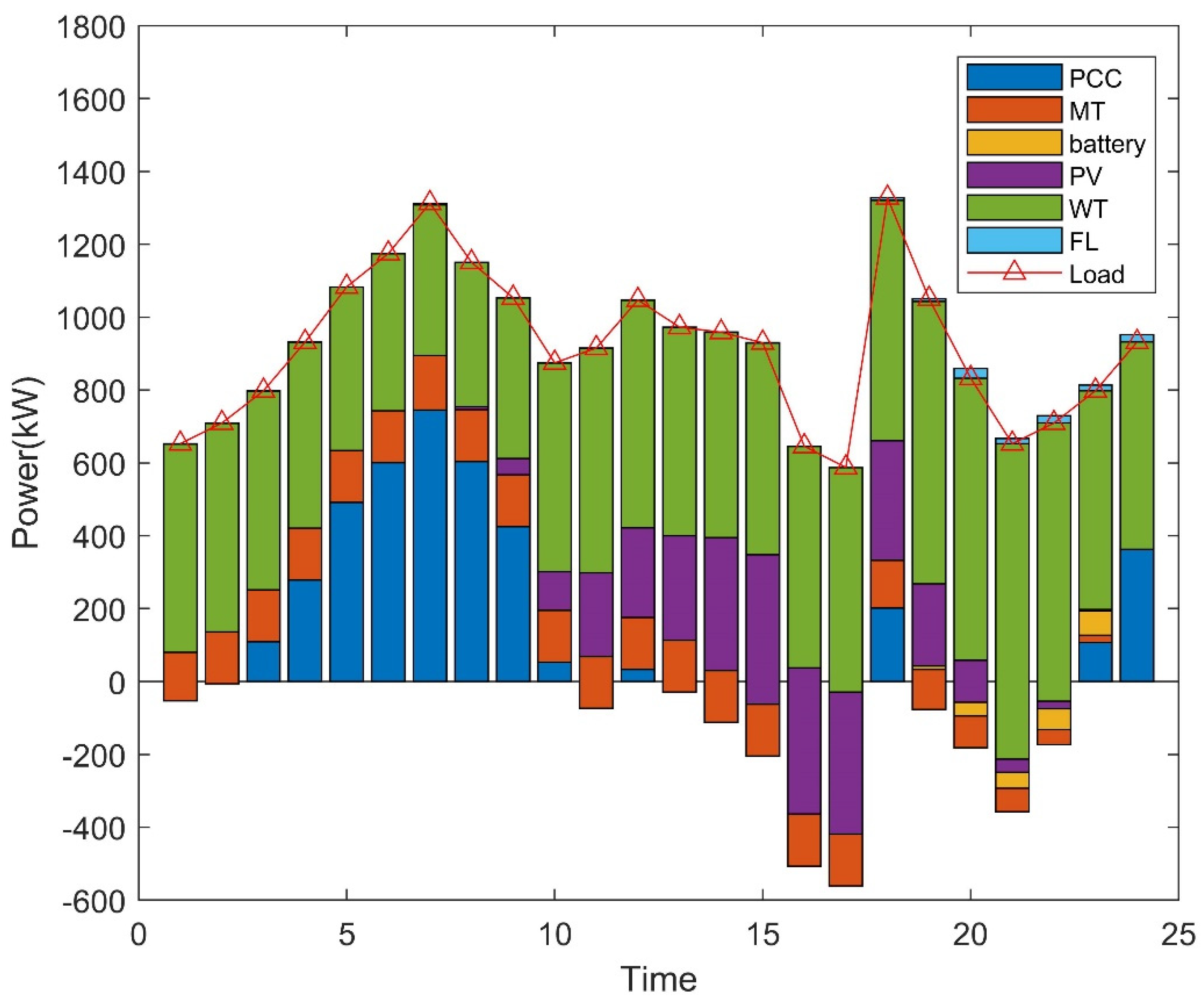
5.2. Dispatching Results and Analysis
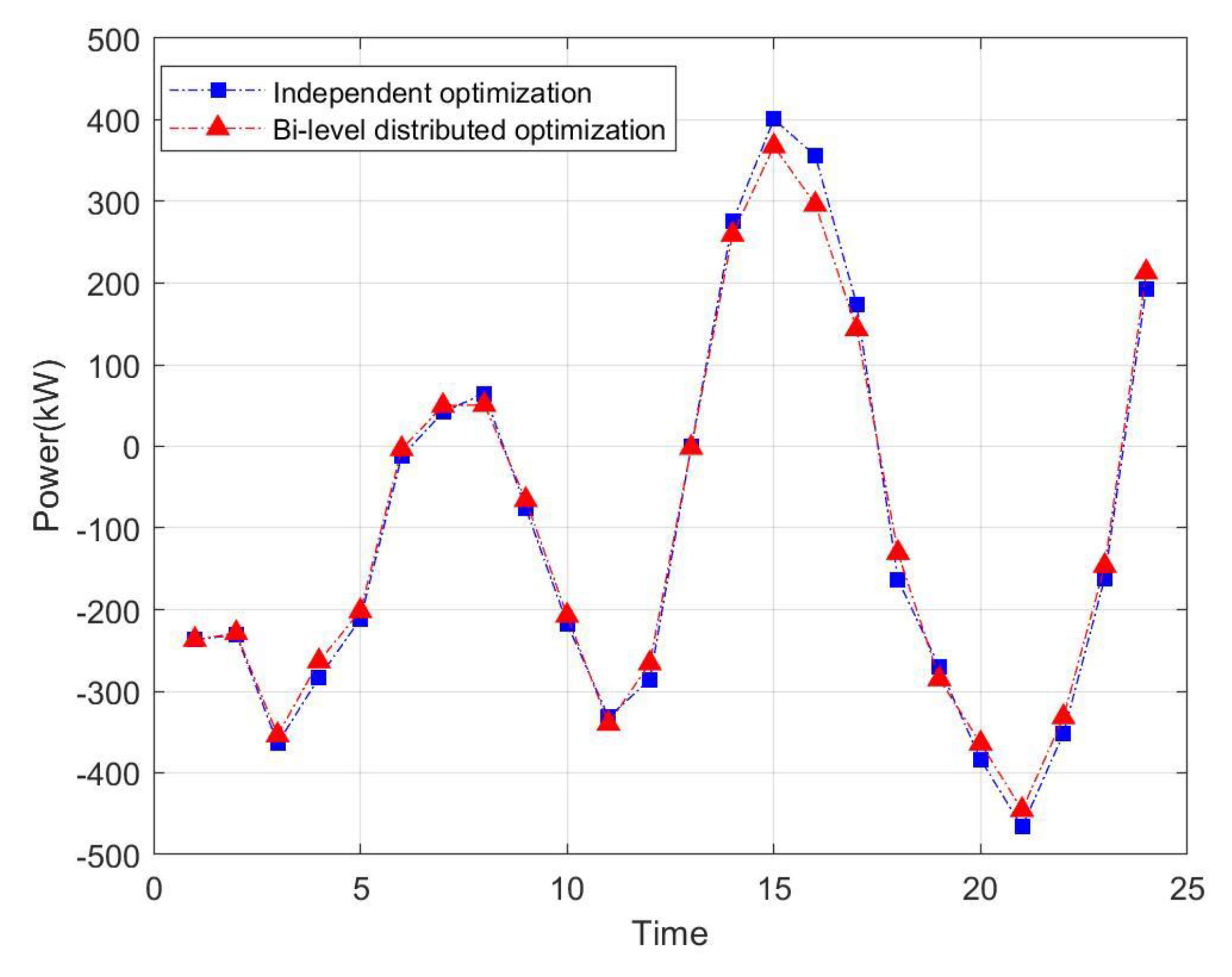
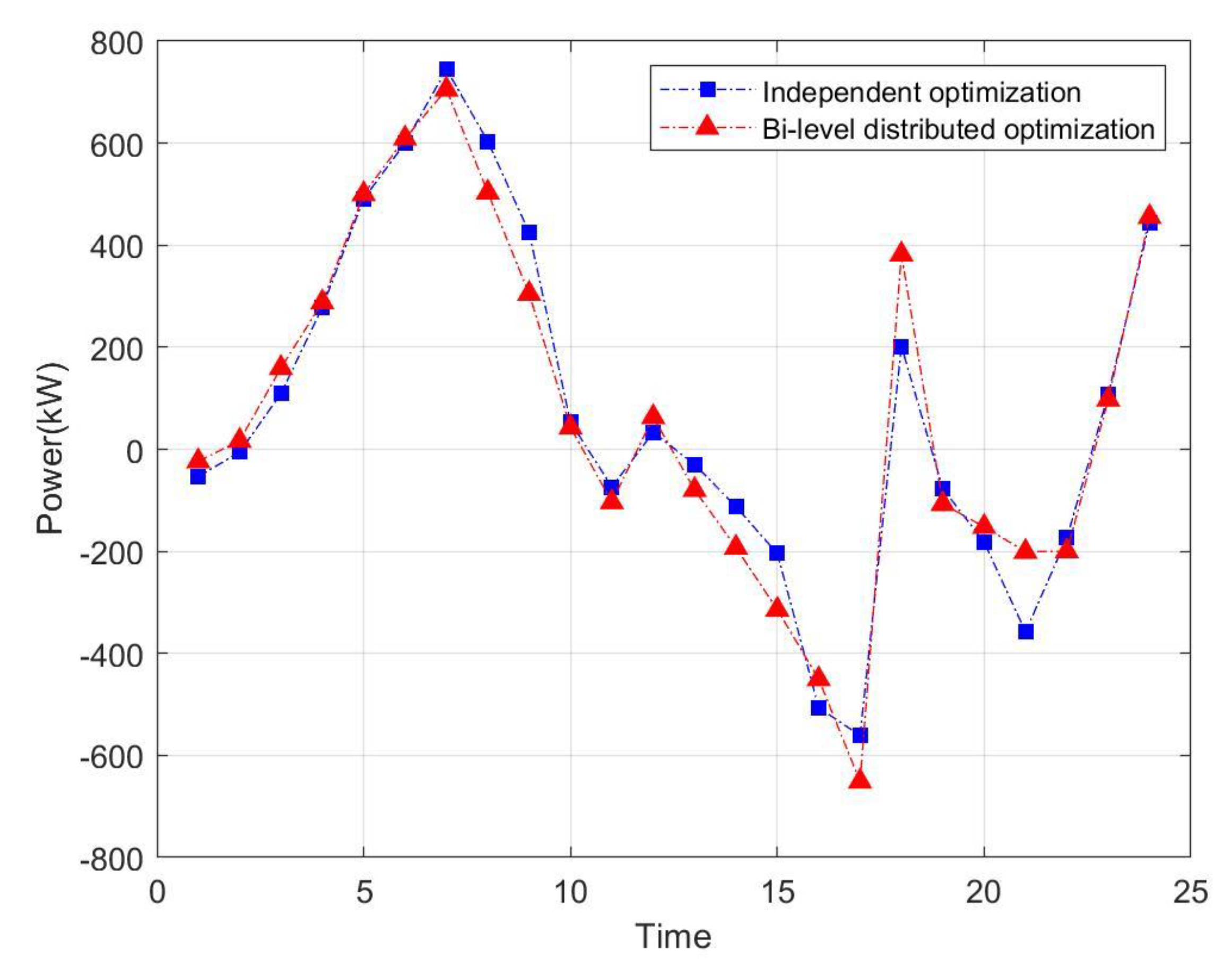
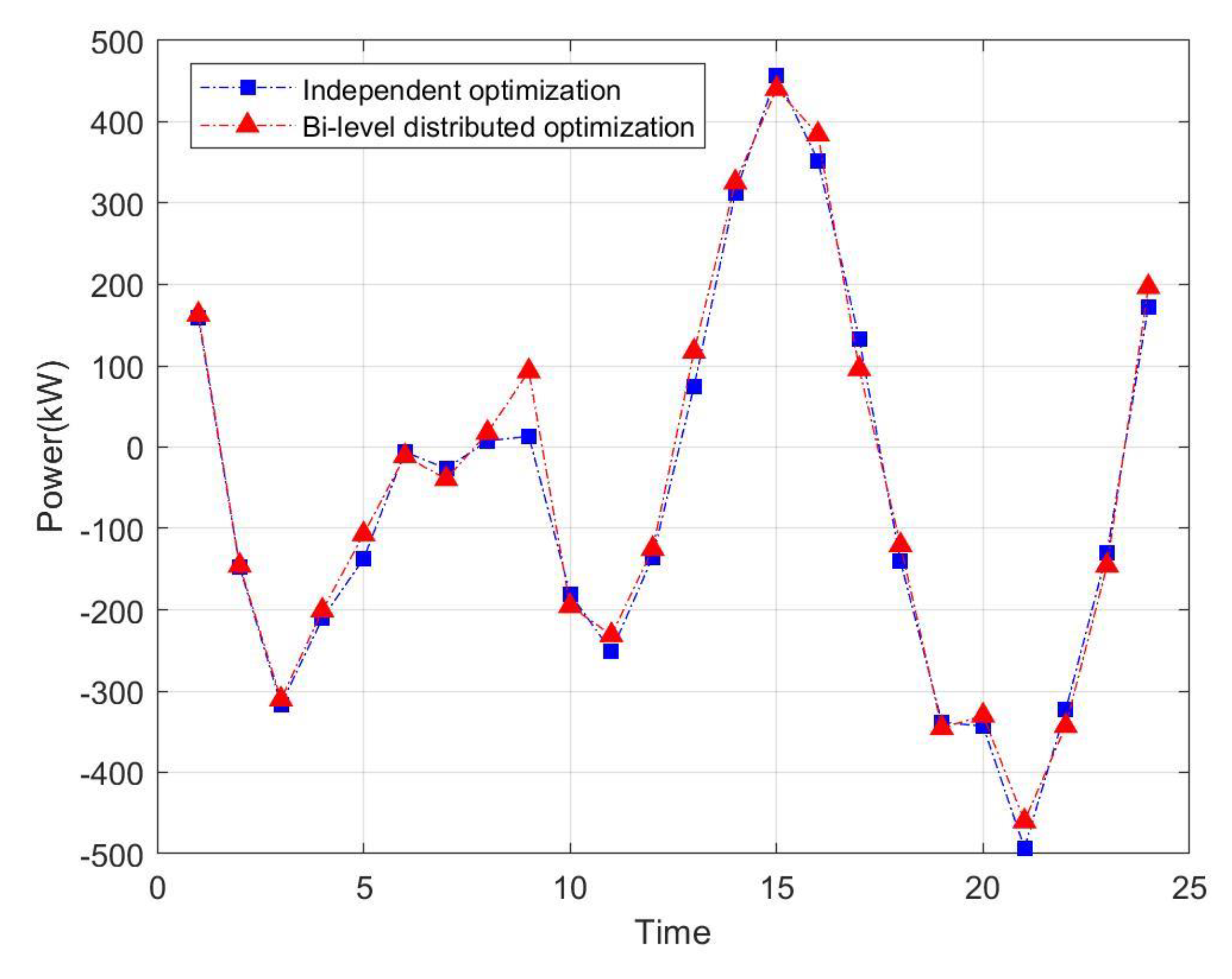
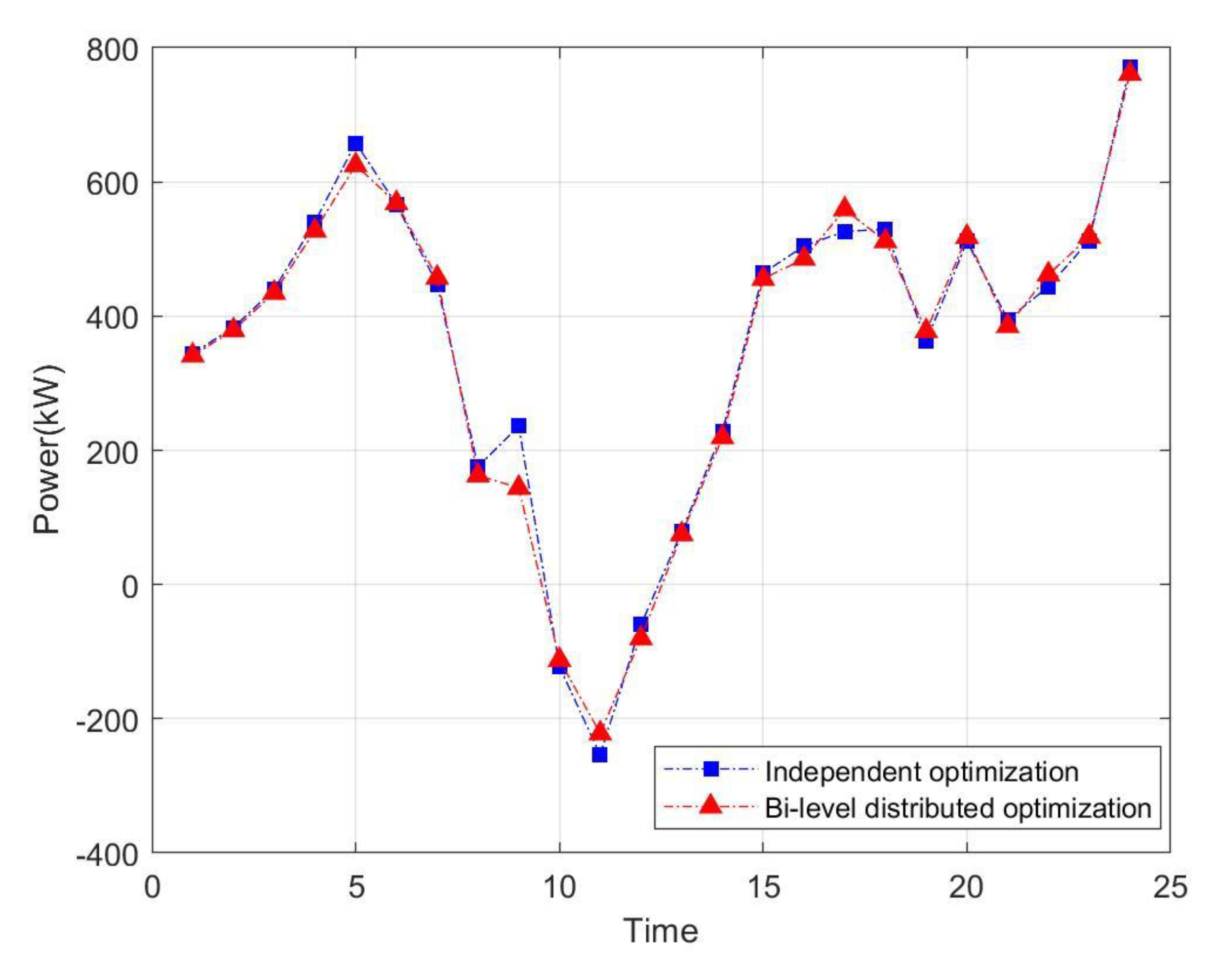
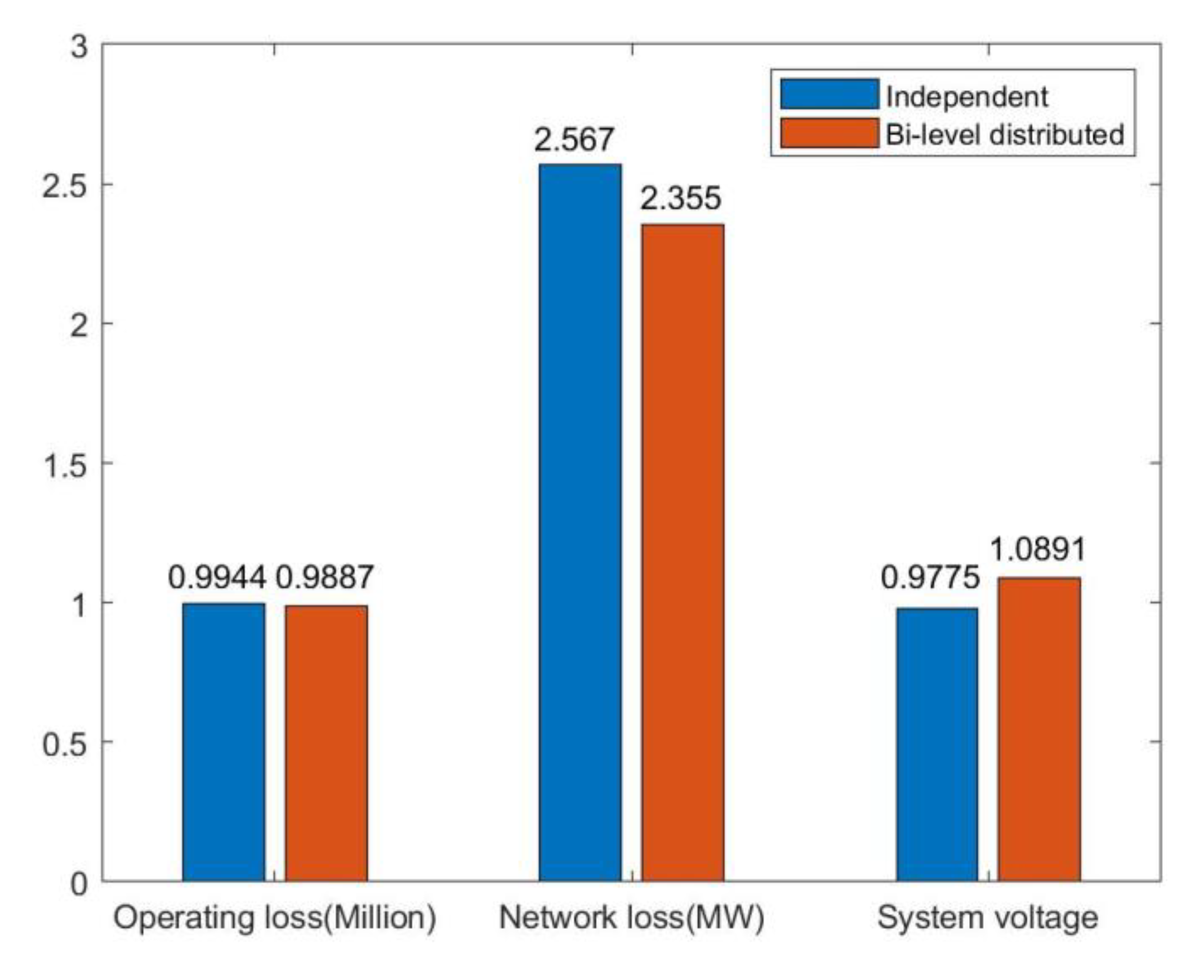
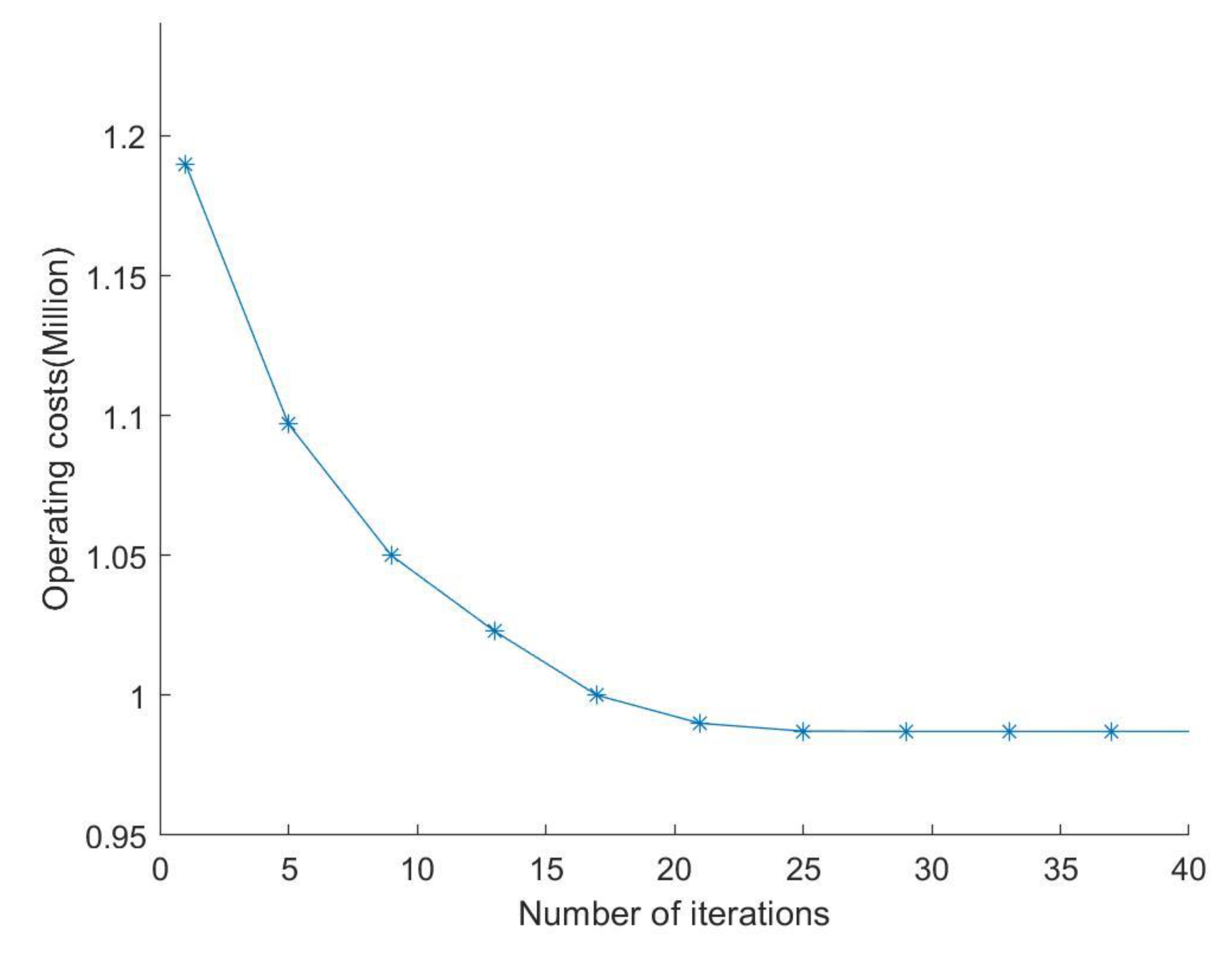
5.3. Analysis of Bi-Level Distributed Dispatching Optimization Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Branch Number | Starting Bus | Arrival Bus | R/pu | X/pu | Branch Bumber | Starting Bus | Arrival Bus | R/pu | X/pu |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0 | 1 | 0.0922 | 0.047 | 17 | 23 | 24 | 0.786 | 0.564 |
| 2 | 1 | 13 | 0.493 | 0.2511 | 18 | 5 | 6 | 1.509 | 0.9337 |
| 3 | 13 | 14 | 0.164 | 0.1565 | 19 | 6 | 7 | 1.03 | 0.74 |
| 4 | 14 | 15 | 0.4521 | 0.3083 | 20 | 7 | 8 | 0.8042 | 0.7006 |
| 5 | 15 | 16 | 0.366 | 0.1864 | 21 | 8 | 9 | 1.044 | 0.74 |
| 6 | 16 | 17 | 1.504 | 1.3554 | 22 | 9 | 10 | 0.5075 | 0.2585 |
| 7 | 17 | 18 | 0.3811 | 0.1941 | 23 | 10 | 11 | 0.1966 | 0.065 |
| 8 | 18 | 19 | 0.4095 | 0.4784 | 24 | 11 | 12 | 0.9744 | 0.963 |
| 9 | 1 | 2 | 0.896 | 0.7011 | 25 | 5 | 25 | 0.3744 | 0.1238 |
| 10 | 2 | 3 | 0.819 | 0.707 | 26 | 25 | 26 | 0.3105 | 0.3619 |
| 11 | 3 | 4 | 0.7089 | 0.9373 | 27 | 26 | 27 | 1.468 | 1.115 |
| 12 | 4 | 5 | 0.203 | 0.1034 | 28 | 25 | 28 | 0.341 | 0.5320 |
| 13 | 2 | 20 | 0.1872 | 0.6188 | 29 | 28 | 29 | 0.5412 | 0.7129 |
| 14 | 20 | 21 | 0.2842 | 0.1477 | 30 | 28 | 30 | 0.591 | 0.526 |
| 15 | 21 | 22 | 0.7144 | 0.2351 | 31 | 30 | 31 | 0.7463 | 0.545 |
| 16 | 22 | 23 | 0.732 | 0.574 | 32 | 31 | 32 | 1.289 | 1.721 |
References
- Ochoa, L.F.; Dent, C.J.; Harrison, G.P. Distribution network capacity assessment: Variable DG and active networks. IEEE Trans. Power Syst. 2010, 25, 87–95. [Google Scholar] [CrossRef]
- Yang, T.; Zhai, F.; Zhao, Y.; Pen, H. Explanation and Prospect of Ubiquitous Electric Power Internet of Things. Autom. Electr. Power Syst. 2019, 43, 9–20, In Chinese. [Google Scholar]
- Venkatesh, B.; Chandramohan, S.; Kayalvizhi, N.; Kumudini-Devi, R.P. Optimal reconfiguration of radial distribution systems using artificial intelligence methods. In Proceedings of the 2009 IEEE Toronto International Conference Science and Technology for Humanity (TIC-STH), Toronto, ON, Canada, 26–27 September 2009; pp. 660–665. [Google Scholar]
- Juang, C.; Hsiao, C.; Hsu, C. Hierarchical cluster based multispecies particle swarm optimization for fuzzy system optimization. IEEE Trans. Fuzzy Syst. 2010, 18, 14–26. [Google Scholar] [CrossRef]
- Shaaban, M.F.; Atwa, Y.M.; El-Saadany, E.F. DG allocation for benefit maximization in distribution networks. IEEE Trans. Power Syst. 2013, 28, 639–649. [Google Scholar] [CrossRef]
- El-Khattam, W.; Bhattacharya, K.; Hegazy, Y.; Salama, M.M.A. Optimal investment planning for distributed generation in a competitive electricity market. IEEE Trans. Power Syst. 2004, 19, 1674–1684. [Google Scholar] [CrossRef]
- Zia, M.F.; Benbouzid, M.; Elbouchikhi, E.; Muyeen, S.M.; Techato, K.; Guerrero, J.M. Microgrid Transactive Energy: Review, Architectures, Distributed Ledger Technologies, and Market Analysis. IEEE Access 2020, 8, 19410–19432. [Google Scholar] [CrossRef]
- Du, P.; Chen, Z.; Chen, Y.; Ma, Z.; Ding, H. Bi-level linearized dispatching model of active distribution network with multi-stakeholder participation based on analytical target cascading. IEEE Access 2019, 7, 154844–154858. [Google Scholar] [CrossRef]
- Farrokhifar, M.; Aghdam, F.H.; Alahyari, A.; Monavari, A.; Safari, A. Optimal energy management and sizing of renewable energy and battery systems in residential sectors via a stochastic MILP model. Electr. Power Syst. Res. 2020, 187, 106483. [Google Scholar] [CrossRef]
- Lu, J.; Chu, W.; Ren, H.; He, T.; Wang, F. Coordinated optimal dispatch of multi-stakeholder game based on demand response for active distribution network. IET Renew. Power Gener. 2019, 13, 898–904. [Google Scholar] [CrossRef]
- Ma, W.-J.; Wang, J.; Gupta, V.; Chen, C. Distributed energy management for networked microgrids using online ADMM with regret. IEEE Trans. Smart Grid 2018, 9, 847–856. [Google Scholar] [CrossRef]
- Zheng, W.; Wu, W.; Zhang, B.; Sun, H.; Liu, Y. A fully distributed reactive power optimization and control method for active distribution net-works. IEEE Trans. Smart Grid 2016, 7, 1021–1033. [Google Scholar]
- Nie, Y.; Farrokhifar, M.; Pozo, D. Electricity and Gas Network Expansion Planning: An ADMM-based Decomposition Approach. In Proceedings of the 2019 IEEE Milan PowerTech, Milan, Italy, 23–27 June 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhao, Y.; Yu, J.; Ban, M. Privacy-Preserving Economic Dispatch for An Active Distribution Network with Multiple Networked Microgrids. IEEE Access 2018, 6, 38802–38819. [Google Scholar] [CrossRef]
- Yang, X.; Chen, W.; Wu, L. Voltage Quality Control Method for Microgrid. Proc. CSU-EPSA 2018, 30, 63–69. [Google Scholar]
- Farag, H.E.Z.; El-Saadany, E.F. A novel cooperative protocol for distributed voltage control in active distribution systems. IEEE Trans. Power Syst. 2013, 28, 1645–1656. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Zaman, F.; Guerrero, J.M. Energy scheduling of community microgrid with battery cost using particle swarm optimization. Appl. Energy 2019, 254, 113723. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.R.; Squartini, S.; Zaman, F.; Muttaqi, K.M. Energy management of community microgrids considering degradation cost of battery. J. Energy Storage 2019, 22, 257–269. [Google Scholar] [CrossRef]
- Khodabakhsh, R.; Sirouspour, S. Optimal control of energy storage in a microgrid by minimizing conditional value-at-risk. IEEE Trans. Sustain. Energy 2016, 7, 1264–1273. [Google Scholar] [CrossRef]
- Dallinger, D.; Krampe, D.; Wietschel, D. Vehicle-to-grid regulation reserves based on a dynamic simulation of mobility behavior. IEEE Trans. Smart Grid 2011, 2, 302–303. [Google Scholar] [CrossRef]
- Vidoni, R.; Gasparetto, A.; Giovagnoni, M. A method for modeling three-dimensional flexible mechanisms based on an equivalent rigid-link system. J. Vib. Control 2014, 20, 483–500. [Google Scholar] [CrossRef]
- Shi, L.; Luo, Y.; Tu, G.Y. Bidding strategy of microgrid with consideration of uncertainty for participating in power market. Elect. Power Energy Syst. 2014, 59, 1–13. [Google Scholar] [CrossRef]
- Molzahn, D.K.; Dörfler, F.; Sandberg, H. A survey of distributed optimization and control algorithms for electric power systems. IEEE Trans. Smart Grid 2017, 8, 2941–2962. [Google Scholar] [CrossRef]
- Chang, T.H.; Liao, W.C.; Hong, M.; Wang, X. Asynchronous distributed admm for large-scale optimizationLinear convergence analysis and numerical performance. IEEE Trans. Signal Process. 2016, 64, 3131–3144. [Google Scholar] [CrossRef]
- Mota, J.; Xavier, J.; Aguiar, P.; Pschel, M. A proof of convergence for the alternating direction method of multipliers applied to polyhedral constrained functions. Mathematics 2011. [Google Scholar]
- Boyd, S.; Parikh, N.; Chu, E. Distributed optimization and statistical learning via the alternating direction method of multipliers. Found. Trends Mach. Learn. 2011, 3, 1–122. [Google Scholar] [CrossRef]
- Real, A.J.D.; Arce, A.; Bordons, C. Combined environmental and economic dispatch of smart grids using distributed model predictive control. Int. J. Electr. Power Energy Syst. 2014, 54, 65–76. [Google Scholar] [CrossRef]





| Period | Price/(kW·h) | ||
|---|---|---|---|
| Purchase Electricity | Sale of Electricity | ||
| Peak time | 18:00–21:00 | 0.83 | 0.65 |
| Usual time | 7:00–18:00 22:00–0:00 | 0.49 | 0.38 |
| Valley time | 0:00–7:00 | 0.17 | 0.13 |
| Type of Pollutant | Dust | ||||
|---|---|---|---|---|---|
| Levy fee/USD· | 1 | 1.95 | 0.00975 | 0.16 | 0.125 |
| Stakeholder | MT | WT | PV | ESS | EVS | FD |
|---|---|---|---|---|---|---|
| VMG1 | √ | √ | √ | √ | √ | √ |
| VMG2 | √ | √ | √ | √ | × | √ |
| DSO1 | √ | √ | √ | √ | × | × |
| DSO2 | √ | × | √ | √ | × | × |
| Stakeholder | Profit(Ten Thousand USD) |
|---|---|
| VMG1 | 0.9830 |
| VMG2 | 1.2211 |
| DSO1 | 1.1054 |
| DSO2 | 1.0494 |
| Region | Profit (Ten Thousand USD) | Acceptance |
|---|---|---|
| VMG1 | 0.9354 | 0.952 |
| VMG2 | 1.1270 | 0.931 |
| DSO1 | 0.9974 | 0.903 |
| DSO2 | 0.9452 | 0.901 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Liu, S.; Niu, Z. Distributed Optimization for Active Distribution Network Considering the Balance of Multi-Stakeholder. Processes 2020, 8, 987. https://doi.org/10.3390/pr8080987
Liu Y, Liu S, Niu Z. Distributed Optimization for Active Distribution Network Considering the Balance of Multi-Stakeholder. Processes. 2020; 8(8):987. https://doi.org/10.3390/pr8080987
Chicago/Turabian StyleLiu, Yang, Sanming Liu, and Zhuangzhuang Niu. 2020. "Distributed Optimization for Active Distribution Network Considering the Balance of Multi-Stakeholder" Processes 8, no. 8: 987. https://doi.org/10.3390/pr8080987
APA StyleLiu, Y., Liu, S., & Niu, Z. (2020). Distributed Optimization for Active Distribution Network Considering the Balance of Multi-Stakeholder. Processes, 8(8), 987. https://doi.org/10.3390/pr8080987





