The Liquid–Liquid Dispersion Homogeneity in a Vessel Agitated by a High-Shear Sawtooth Impeller
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
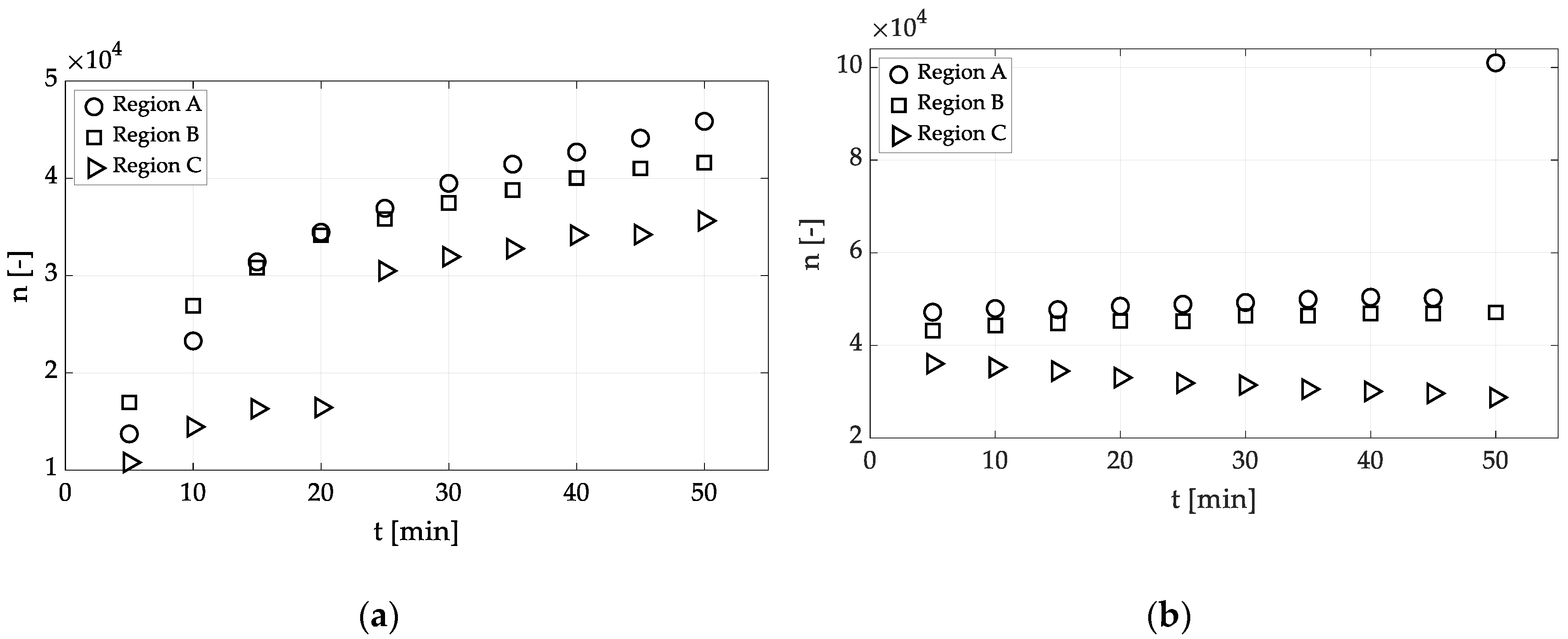
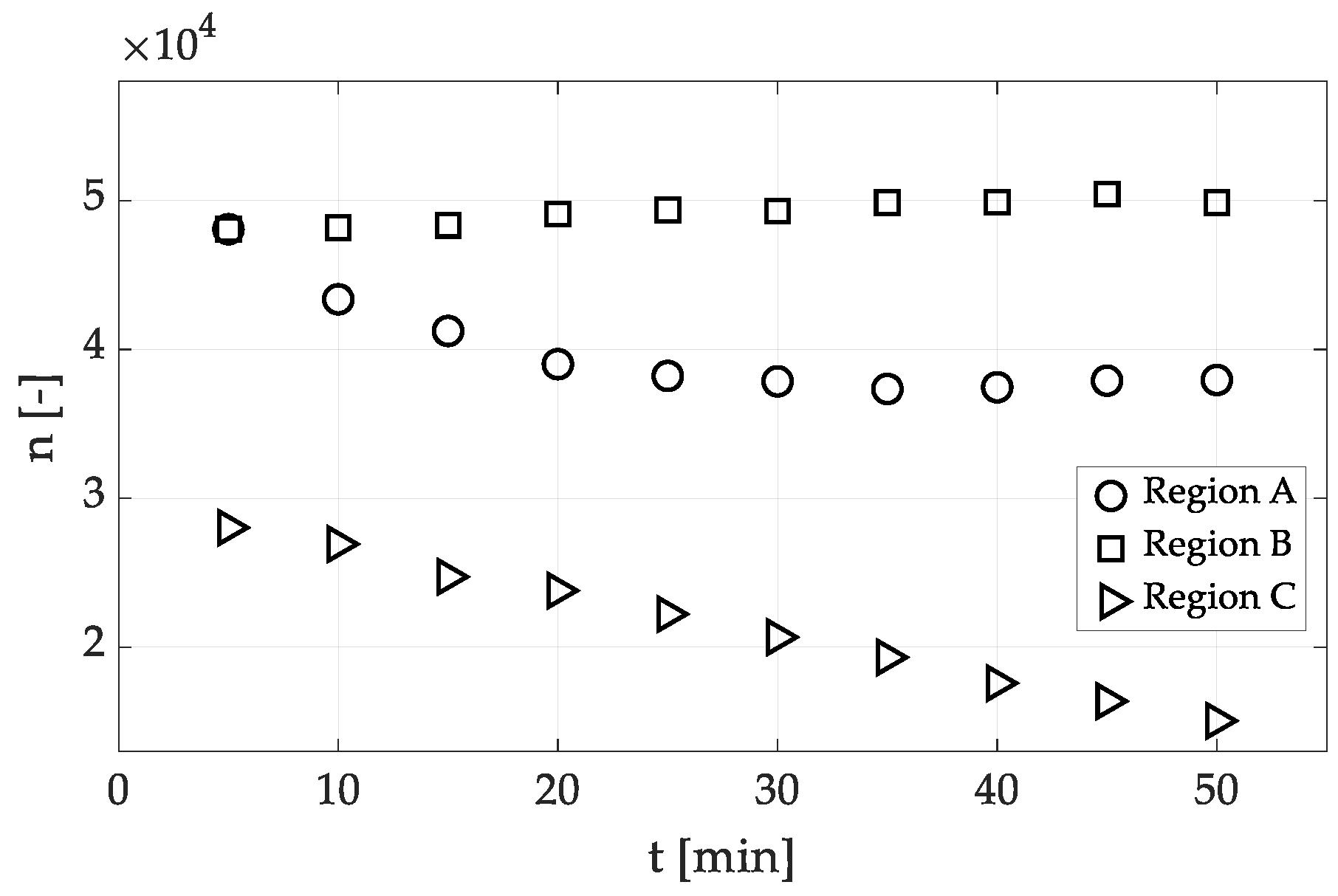
3.1. Number of Evaluated Drops, NoED
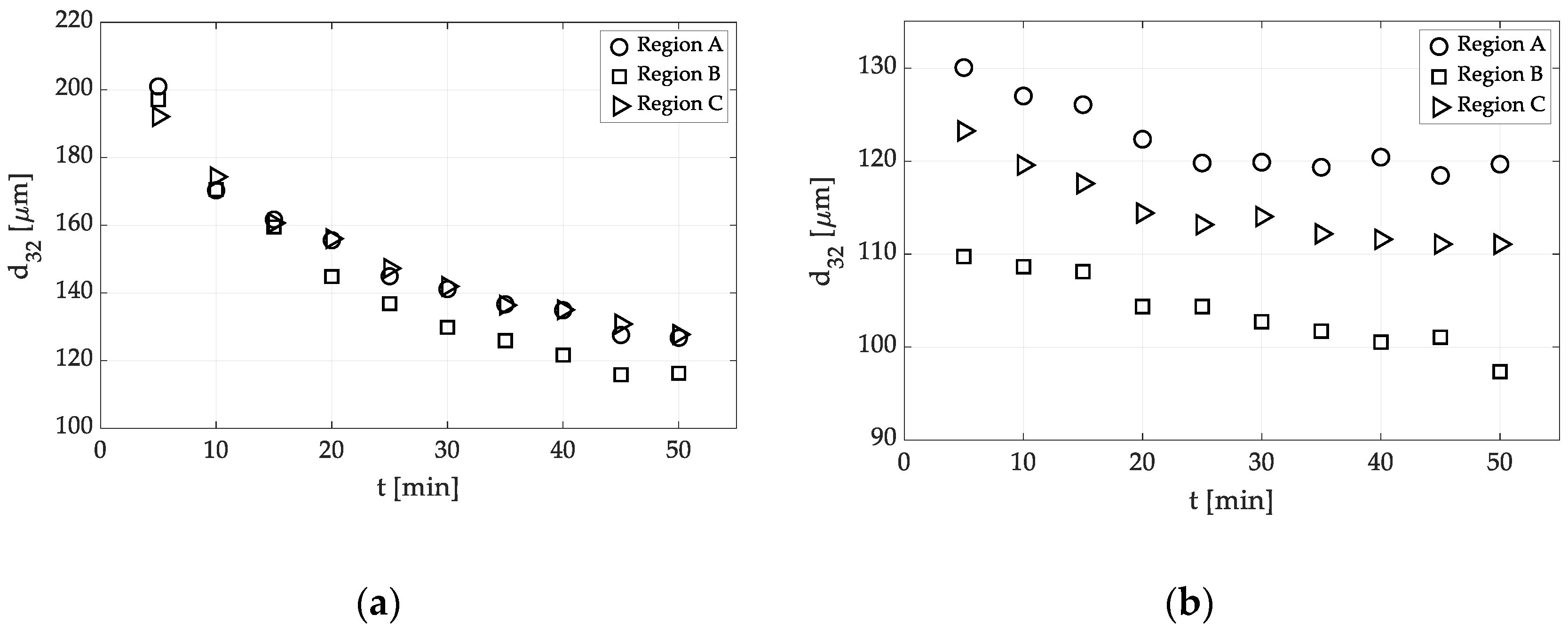
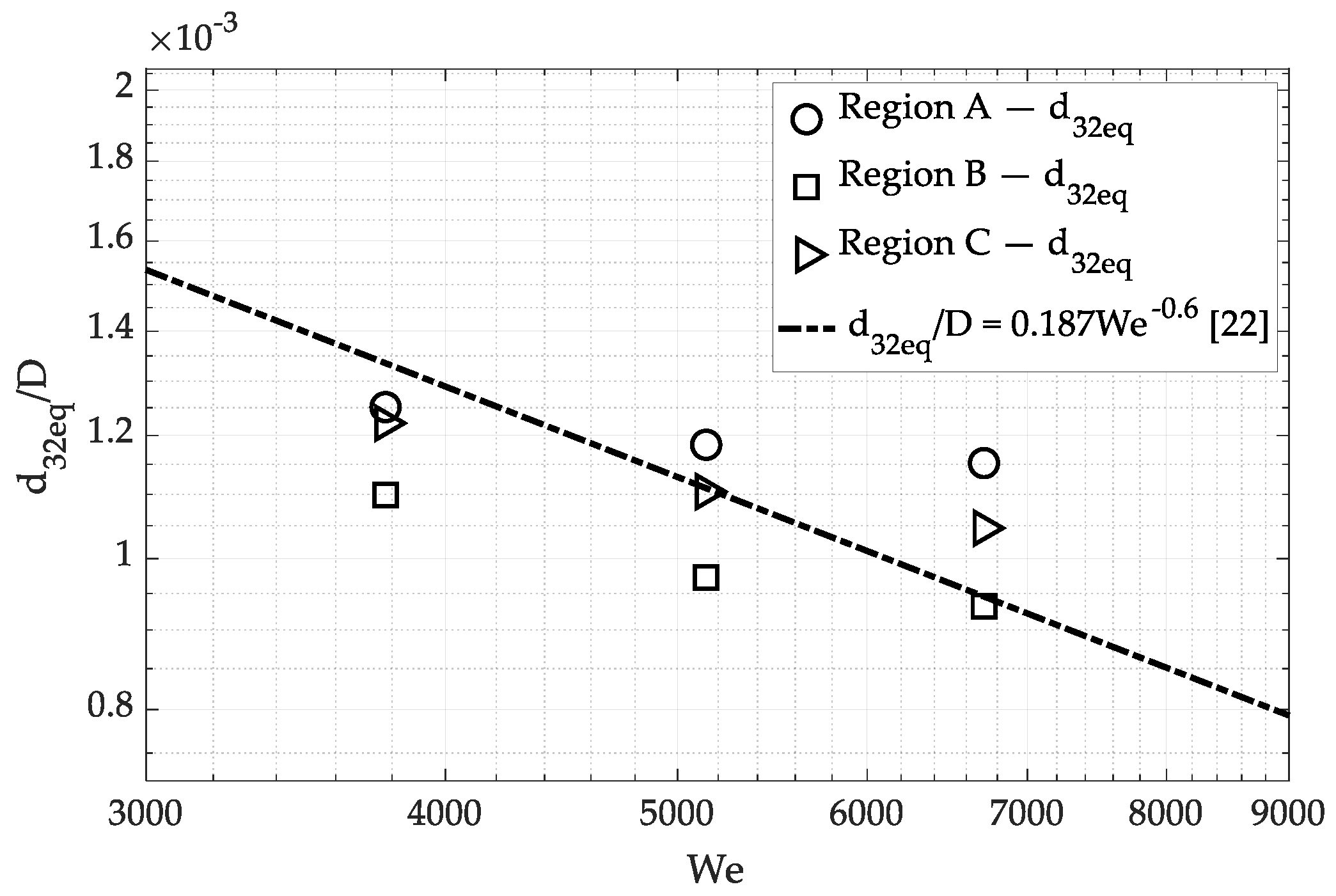
3.2. Sauter Mean Diameter, d32
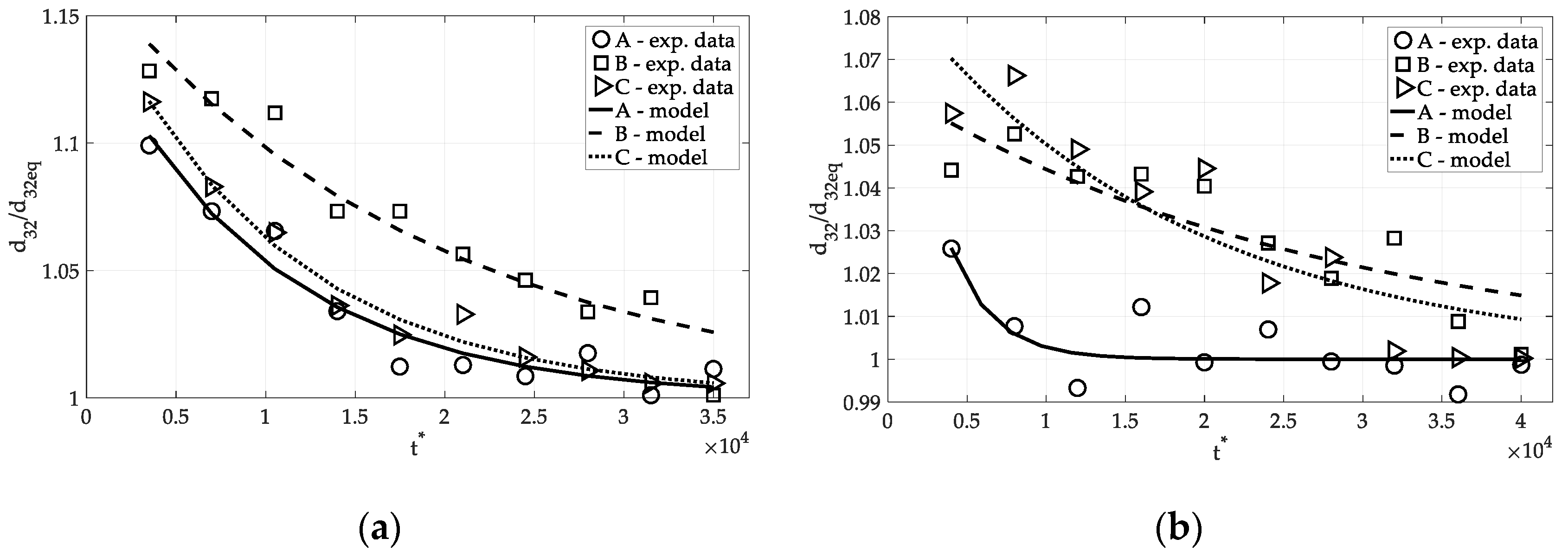
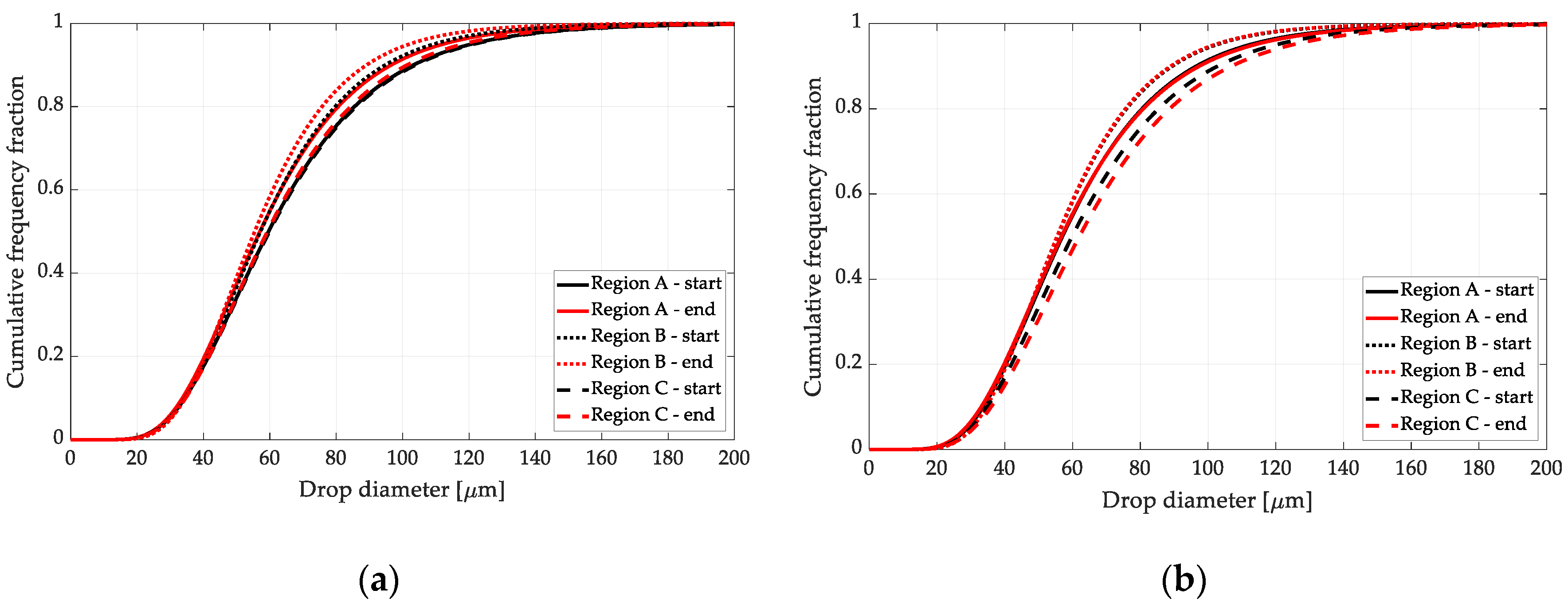
3.3. DSD Time Evolution
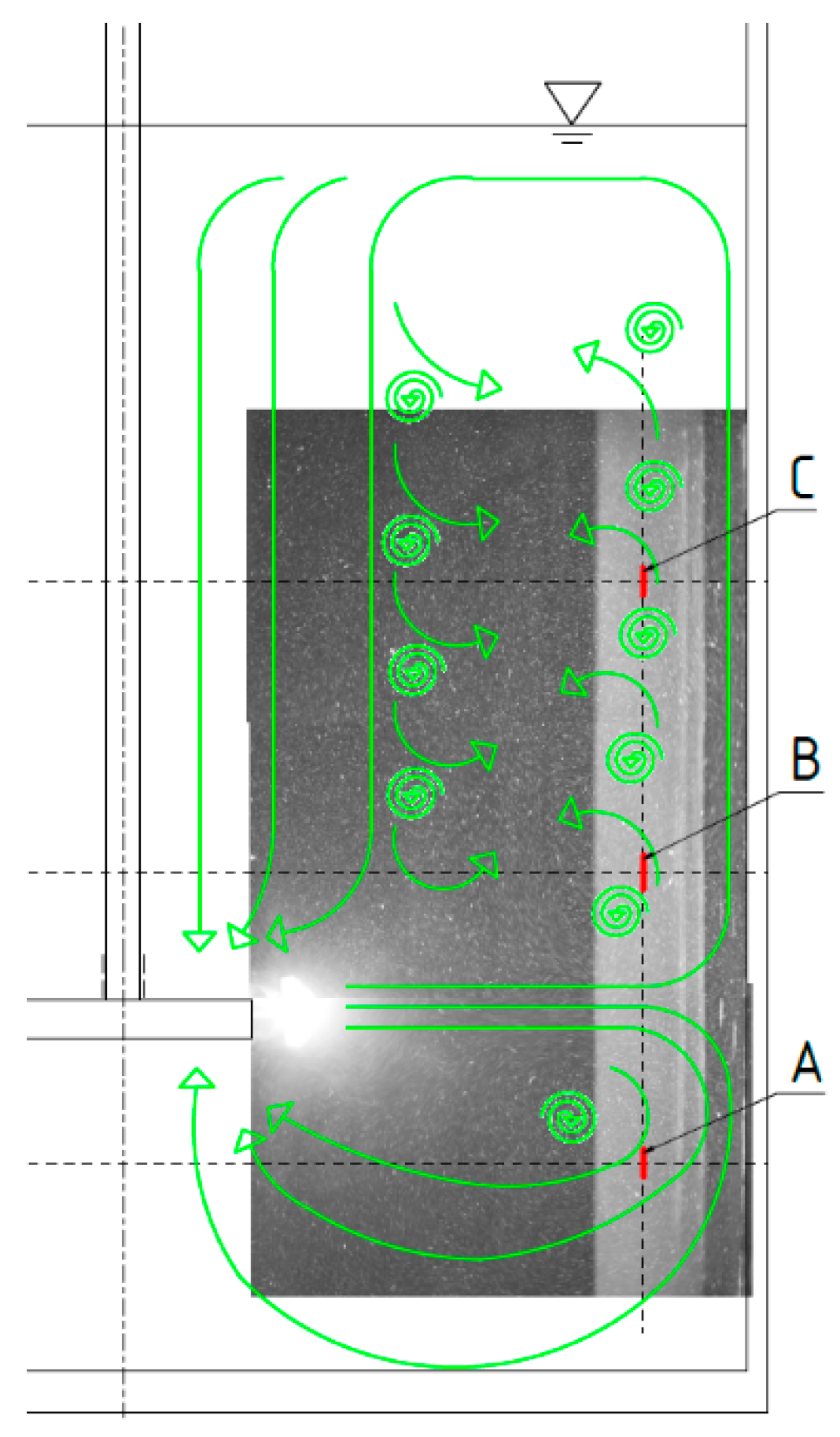
3.4. Flow Field
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| a | The distance of the region A from the vessel bottom (m) |
| b | Baffle width (m) |
| c | Distance between regions (m) |
| C1 | Constant of proportionality (-) |
| D | Impeller diameter (m) |
| d | Drop diameter (m) |
| d32 | Sauter mean diameter (m) |
| d32eq | Equilibrium Sauter mean diameter (m) |
| ds | Calibration sphere diameter (m) |
| e | Region distance from the vessel axis (m) |
| H | Liquid level (m) |
| K | Impeller clearance (m) |
| N | Impeller speed (s-1) |
| n | Number of evaluated drops (-) |
| p | Region distance from the vessel wall (m) |
| t | Time of measurement (s) |
| T | Vessel diameter (m) |
| teq | The time necessary to reach equilibrium state (s) |
| Greek letters | |
| α | Model parameter (-) |
| β | Model parameter (-) |
| δ | Focus depth (m) |
| μc | Dynamic viscosity of continuous phase (Pa s) |
| μd | Dynamic viscosity of dispersed phase (Pa s) |
| ρc | Density of continuous phase (kg m−3) |
| ρd | Density of dispersed phase (kg m−3) |
| σ | Interfacial tension (N m−1) |
| σc | Surface tension of continuous phase (N m−1) |
| σd | Surface tension of dispersed phase (N m−1) |
| φc | Volume fraction of continuous phase (-) |
| φd | Volume fraction of dispersed phase (-) |
References
- Ghotli, R.A.; Aziz, A.R.A.; Ibrahim, S. Liquid-liquid mass transfer studies in various stirred vessel designs. Rev. Chem. Eng. 2014, 31, 329–343. [Google Scholar] [CrossRef]
- Khalil, A.; Puel, F.; Chevalier, Y.; Galvan, J.-M.; Rivoire, A.; Klein, J.-P. Study of droplet size distribution during an emulsification process using in situ video probe coupled with an automatic image analysis. Chem. Eng. J. 2010, 165, 946–957. [Google Scholar] [CrossRef]
- Maaß, S.; Kraume, M. Determination of breakage rates using single drop experiments. Chem. Eng. Sci. 2012, 70, 146–164. [Google Scholar] [CrossRef]
- Hasan, B.O. Experimental study on the bubble breakage in a stirred tank. Part 1. Mechanism and effect of operating parameters. Int. J. Multiph. Flow 2017, 97, 94–108. [Google Scholar] [CrossRef]
- Ghotli, R.A.; Abbasi, M.R.; Bagheri, A.; Raman, A.A.A.; Ibrahim, S.; Bostanci, H. Experimental and modeling evaluation of droplet size in immiscible liquid-liquid stirred vessel using various impeller designs. J. Taiwan Inst. Chem. Eng. 2019, 100, 26–36. [Google Scholar] [CrossRef]
- Tang, Q.; Zhang, J.; Wu, Y.; Wang, Y.-D.; Liu, Z. An experimental study of immiscible liquid–liquid dispersions in a pump-mixer of mixer-settler. Chin. J. Chem. Eng. 2020, 28, 33–45. [Google Scholar] [CrossRef]
- Kraume, M.; Gabler, A.; Schulze, K. Influence of Physical Properties on Drop Size Distribution of Stirred Liquid-Liquid Dispersions. Chem. Eng. Technol. 2004, 27, 330–334. [Google Scholar] [CrossRef]
- Maluta, F.; Montante, G.; Paglianti, A. Analysis of immiscible liquid-liquid mixing in stirred tanks by Electrical Resistance Tomography. Chem. Eng. Sci. 2020, 227, 115898. [Google Scholar] [CrossRef]
- Malík, M.; Primas, J.; Kotek, M.; Jašíková, D.; Kopecký, V. Mixing of two immiscible phases measured by industrial electrical impedance tomography system. Mech. Ind. 2019, 20, 707. [Google Scholar] [CrossRef]
- Hinze, J.O. Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1955, 1, 289–295. [Google Scholar] [CrossRef]
- Kolmogorov, A.N. The breakage of drops in a turbulent current. Dokl. Akad. Nauk SSSR 1949, 66, 825–828. [Google Scholar]
- Rodgers, T.L.; Cooke, M. Correlation of drop size with sheat tip speed. In Proceedings of the 14th European Conference on Mixing, Warszawa, Poland, 10–13 September 2012; p. B17. [Google Scholar]
- Chen, H.T.; Middleman, S. Drop size distribution in agitated liquid-liquid systems. AIChE J. 1967, 13, 989–995. [Google Scholar] [CrossRef]
- Zhou, G.; Kresta, S.M. Evolution of drop size distribution in liquid-liquid dispersions for various impellers. Chem. Eng. Sci. 1998, 53, 2099–2113. [Google Scholar] [CrossRef]
- Bałdyga, J.; Bourne, J.; Pacek, A.; Amanullah, A.; Nienow, A. Effects of agitation and scale-up on drop size in turbulent dispersions: Allowance for intermittency. Chem. Eng. Sci. 2001, 56, 3377–3385. [Google Scholar] [CrossRef]
- Hong, P.O.; Lee, J.M. Unsteady-state liquid-liquid dispersions in agitated vessels. Ind. Eng. Chem. Process. Des. Dev. 1983, 22, 130–135. [Google Scholar] [CrossRef]
- Tang, H.; Wrobel, L.C. Modelling the interfacial flow of two immiscible liquids in mixing processes. Int. J. Eng. Sci. 2005, 43, 1234–1256. [Google Scholar] [CrossRef]
- Šulc, R.; Kysela, B.; Ditl, P. Time evolution of the drop size distribution for liquid–liquid dispersion in an agitated tank. Chem. Pap. 2018, 72, 543–553. [Google Scholar] [CrossRef]
- Kysela, B.; Konfršt, J.; Chára, Z.; Šulc, R.; Ditl, P. In-situ measurement of particle size distribution in an agitated vessel. In Proceedings of the 18th International Conference Transport & Sedimentation of solid particles, Prague, Czech Republic, 11–15 September 2017; pp. 177–183. [Google Scholar]
- Podgórska, W. The Influence of Internal Intermittency, Large Scale Inhomogeneity, and Impeller Type on Drop Size Distribution in Turbulent Liquid-Liquid Dispersions. Entropy 2019, 21, 340. [Google Scholar] [CrossRef]
- Sprow, F.B. Drop size distributions in strongly coalescing agitated liquid-liquid systems. AIChE J. 1967, 13, 995–998. [Google Scholar] [CrossRef]
- El-Hamouz, A.; Cooke, M.; Kowalski, A.; Sharratt, P. Dispersion of silicone oil in water surfactant solution: Effect of impeller speed, oil viscosity and addition point on drop size distribution. Chem. Eng. Process. Process Intensif. 2009, 48, 633–642. [Google Scholar] [CrossRef]
- Formánek, R.; Šulc, R. Dispersion of immiscible liquid-liquid system in a vessel agitated by a Sawtooth impeller: Drop size time evolution. In Proceedings of the International Conference Experimental Fluid Mechanics 2019, Franzensbad, Czech Republic, 19–22 November 2019; pp. 136–139. [Google Scholar]
- Formánek, R.; Kysela, B.; Šulc, R. Drop Size Evolution Kinetics in a Liquid-Liquid Dispersions System in a Vessel Agitated by a Rushton Turbine. Chem. Eng. Trans. 2019, 74, 1039–1044. [Google Scholar]
- Formánek, R.; Kysela, B.; Šulc, R. Image analysis of particle size: Effect of light source type. EPJ Web Conf. 2019, 213, 02021. [Google Scholar] [CrossRef]
- Hong, P.O.; Lee, J.M. Changes of the average drop sizes during the initial period of liquid-liquid dispersions in agitated vessels. Ind. Eng. Chem. Process. Des. Dev. 1985, 24, 868–872. [Google Scholar] [CrossRef]
- Bucciarelli, E.; Formánek, R.; Kysela, B.; Fořt, I.; Šulc, R. Dispersion kinetics in mechanically agitated vessel. EPJ Web Conf. 2019, 213, 02008. [Google Scholar] [CrossRef]




| Phase | Density ρ (kg m−3) | Viscosity μ (mPa s) | Surface Tension σ (mN m−1) | Volume Fraction φ (-) |
|---|---|---|---|---|
| Continuous | 997.66 | 0.94 | 71.97 | 0.99953 |
| Dispersed | 1075.58 | 223 | 26.42 | 0.00047 |
| Region | Area (mm × mm) | Image Resolution (mm Pixel−1) | NoED 1 (-) |
|---|---|---|---|
| A | 7.827 × 6.262 | 0.006115 | 1,292,901 |
| B | 7.834 × 6.267 | 0.00612 | 1,292,279 |
| C | 7.823 × 6.259 | 0.006112 | 793,029 |
| Impeller Speed (rpm) | Region | d32eq1 (μm) | α | β × 10−5 |
|---|---|---|---|---|
| 600 | A | 125.13 | 0.799 | 10.881 |
| B | 109.85 | 1.048 | 9.777 | |
| C | 122.19 | 0.727 | 8.555 | |
| 700 | A | 118.35 | 0.147 | 10.114 |
| B | 97.24 | 0.168 | 5.346 | |
| C | 110.42 | 0.162 | 9.517 | |
| 800 | A | 115.19 | 0.116 | 37.410 |
| B | 93.17 | 0.064 | 3.633 | |
| C | 104.62 | 0.088 | 5.606 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Formánek, R.; Šulc, R. The Liquid–Liquid Dispersion Homogeneity in a Vessel Agitated by a High-Shear Sawtooth Impeller. Processes 2020, 8, 1012. https://doi.org/10.3390/pr8091012
Formánek R, Šulc R. The Liquid–Liquid Dispersion Homogeneity in a Vessel Agitated by a High-Shear Sawtooth Impeller. Processes. 2020; 8(9):1012. https://doi.org/10.3390/pr8091012
Chicago/Turabian StyleFormánek, Roman, and Radek Šulc. 2020. "The Liquid–Liquid Dispersion Homogeneity in a Vessel Agitated by a High-Shear Sawtooth Impeller" Processes 8, no. 9: 1012. https://doi.org/10.3390/pr8091012
APA StyleFormánek, R., & Šulc, R. (2020). The Liquid–Liquid Dispersion Homogeneity in a Vessel Agitated by a High-Shear Sawtooth Impeller. Processes, 8(9), 1012. https://doi.org/10.3390/pr8091012





