Numerical Study of the Filling Process of a Liquid Hydrogen Storage Tank under Different Sloshing Conditions

Abstract

Cryogenic vessels are widely used in many areas, such as liquefied natural gas (LNG), aerospace, and medical fields. A suitable filling method is one of the prerequisites for the effective use of cryogenic containers. In this study, the filling process for the sloshing condition of a liquid hydrogen storage tank is numerically simulated and analyzed by coupling the sloshing model and the phase-change model. The effects of different sloshing conditions during the filling process are investigated by changing the amplitude and frequency of the sloshing. Within the scope of this study, there is a critical value for the effect of sloshing conditions on the pressure curve during the filling process. The critical value corresponds to a frequency f equal to 3 Hz and an amplitude A equal to 0.03 m. According to the simulation results, when the sloshing exceeds the critical value, the internal pressure curve of the storage tank increases significantly. Under microgravity conditions, within the scope of this study, the pressure curve changes less than the normal gravity, even if the amplitude and frequency increase. The sloshing makes it easier for the liquid to spread along the wall during the filling process. This also further weakens the temperature stratification in the storage tank.

1. Introduction

Cryogenic containers have been widely used in aerospace, transportation, medical treatment, household energy, and other fields. However, small vibrations can cause huge liquid movement inside a cryogenic storage tank due to the low viscosity of the cryogenic fluid, which is called liquid sloshing. Since refrigerants are usually stored at low temperatures, a small amount of heat leakage can cause severe fluid thermal stratification. This will inevitably have a certain impact on the filling process when liquid sloshing occurs. In order to ensure the normal operation of cryogenic liquid filling, special attention should be paid to the liquid sloshing phenomenon.

In studies involving fluid sloshing, National Aeronautics and Space Administration (NASA) [1] is a pioneer in studying the dynamic behavior of fluid sloshing in aerospace missions. In the late 1950s, NASA developed a strong interest in fluid sloshing dynamics because it involved spacecraft and rockets. NASA researchers conducted a large amount of theoretical analysis and experimental research. The lateral sloshing force and the moment were studied in detail. Subsequently, research studies on fluid sloshing were carried out extensively with experimental and numerical simulation methods. Experimental research was mainly carried out on the ground. For example, to reflect the difference in the severity of sloshing, Moran et al. [2] combined the amplitude and the frequency to obtain different sloshing conditions. They found that the pressure response of a tank was different under different sloshing conditions. For instance, sloshing near the natural frequency of the tank-liquid system (i.e., in the unstable region) could lead to severe ullage collapse, but sloshing in the stable regions generally had little effect on the pressure response of the tank. It was also shown by E. J. Hopfinger and S. P. Das that large–amplitude capillary waves at the liquid–vapor interface substantially enhanced the interfacial heat and mass transfer [3]. To study the relationship between the internal pressure of a container and the sloshing condition, liquid nitrogen was used as a working medium in the research carried out by Arndt et al. [4] and Ludwig et al. [5]. In addition, the relationship between the heat and mass transfer at the phase interface and the sloshing condition was also studied through a ground sloshing experiment. It was found that in the presence of sloshing, the pressure drop could be large but it came rapidly to a stop. Similarly, the effectiveness of different baffles in suppressing the pressure was also experimentally investigated by Xue et al. [6] for different sloshing frequencies. The results showed that changing the flow field with baffles and altering the natural frequency might reduce the impact pressure effectively. In addition to experiments, fluid sloshing was also studied through numerical simulation. In addition, noise may be generated when the liquid sloshes. To understand the dynamics of liquid sloshing and the noise generation mechanism, Agawane et al. [7] performed an experimental study in a partially filled rectangular tank. The sloshing phenomenon inside the tank was classified as non-linear and linear flow regimes. Dynamic activities in the non–linear regime were the source of sloshing noise generation. Different from the work of Agawane et al. [7], in order to reduce the noise impact caused by liquid fuel sloshing inside the tank, He et al. [8] carried out related numerical simulation work. They chose to install anti-wave boards in the fuel tank and monitor the vibration acceleration in the fuel tank. The results indicated that the selected anti-wave board inhibited fuel from sloshing greatly. To simulate the free surface shape and the wave height change, Ming and Duan [9] used the volume of fluid (VOF) method to study the breakage, mixing, and other changes of the free liquid surface of the working liquid that were caused by the sloshing inside the container. The numerical results agreed well with the experimental data. The accurate prediction of the thermodynamic behavior of the cryogenic liquids in the tanks of liquid-propelled rockets was critical for the design of the pressurization system and the control algorithm. To analyze the behavior of the cryogenic liquids in the tanks before and during flight, Martin Konopka et al. [10] simulated the effect of sloshing on the nitrogen inside the cryogenic liquid storage tank. Both the experiments and the simulations showed that due to the sloshing, the cooling of the tank wall and the vapor condensation at the gas-liquid interface intensified, which ultimately caused a further pressure drop. On some occasions, such as earthquakes, this could also bring about the violent sloshing of cryogenic containers. Sanapala et al. [11] used LNG as the working fluid to simulate the effects of sloshing caused by earthquakes on the free surface of a liquid, pressure, and the sloshing force inside a container. It was found that baffles could effectively suppress the free surface fluctuations and the slosh forces. In order to systematically study the effect of sloshing on different types of cryogenic liquids, Liu et al. [12,13,14,15,16,17] used numerical simulation methods to systematically study the thermodynamic behavior of different liquids in liquid hydrogen storage tanks and liquid oxygen storage tanks under different sloshing conditions. This included changes in the thermal stress on the wall, the internal pressure of the storage tank, and the temperatures of the gas and liquid phases. The tank pressure decrease rate could be adjusted with proper intermittent excitation. In addition to using the VOF method to calculate the free surface, some scholars also used other methods to track the change of the free surface during sloshing. For example, a method for simulating fluid dynamics by potential flow theory and trigonometric function was developed by Dai et al. [18]. They used this method to study the dynamics of the fluid inside a truck during braking, and found that the wheels were subject to significant oscillatory forces under vehicle braking due to the liquid sloshing motion. In order to analyze the three-dimensional liquid slosh in a partially–filled tank under simultaneous longitudinal and lateral acceleration excitations, Kolaei et al. [19] developed a coupled multimodal and boundary–element method that is based on linear slosh theory. The result showed that this multimodal model could be easily integrated into the multi-body vehicle dynamics models for efficient analyses of liquid cargo–vehicle interactions because the hydrodynamic loads are functions of generalized coordinates and hydrodynamic coefficients. In summary, when studying the effect of sloshing on cryogenic tanks, the research objects are closed containers. However, during the process of filling or discharging a cryogenic container, the effect of sloshing may be different from the above research.

Aside from the study of closed containers, research on opening system is also of great significance for filling and discharge processes. Generally speaking, there are three main filling configurations, bottom injection, upward injection, and spray bar injection [20,21]. Moran et al. [20] conducted experiments using liquid hydrogen as a working liquid to study these three methods. The results showed that the top spray was the most efficient no-vent fill method out of the three configurations examined. In contrast to Moran, Kim et al. [22,23] used LNG as the working fluid to study the effects of bottom filling, top spray, and upward pipe discharge on the no-vent filling process. In addition to the experiment, they also proposed a numerical calculation method for predicting the filling process, and the method was in good agreement with the experiment. Similarly, Kim et al. [24] selected carbon tetrafluoride (CF4) as the working liquid and studied the effect of initial filling conditions on the entire filling process. The experimental results showed that the initial receiver tank wall temperature and the incoming liquid temperature were the primary factors that characterized the thermodynamic state at the start of a no-vent filling transfer. They also proposed a method for calculating the best filling condition based on the final filling state. The stress changes of the tank during the filling process were still worthy of study, except for the fluid itself. Zhu et al. [25] studied the effects of different filling rates on the thermal stress distribution and cooling characteristics of cryogenic storage tanks. It was found that the tank wall suffered from a remarkable temperature gradient at the liquid level due to the change of the cool–down pattern. The overall cooling rate of the tank and the thermal stress level within the tank wall increased with the liquid nitrogen filling rate. Overall, although there have been many studies on the filling process of cryogenic containers, these studies did not fully account for the effect of the sloshing condition.

With the development of the aerospace industry, on–orbit refueling has increasingly attracted people’s attention. Refueling concepts are potentially attractive because they reduce the maximum individual payload that must be placed in Earth’s orbit [26]. In order to investigate no-vent filling performance under microgravity, Ma et al. [21] analyzed the pressure, phase distribution, and temperature distribution of liquid hydrogen in a tank during the filling process via numerical simulation. The results showed that the no-vent filling under microgravity experienced more complete liquid evaporation and mixing than that during normal gravity, resulting in a more stable pressure response and a better filling performance. To control the diffusion of the liquid phase in a tank, adding blades is an effective method [27]. A vane–type tank is a type of receiving container during the on–orbit refueling process and it has good fluid orbital management ability. In addition to a cryogenic tank, the pipe connecting a supply tank and a receiving tank is also an indispensable part of the on–orbit refueling process. The distribution of cryogenic propellant in a spiral pipe in microgravity has been studied by Cui et al. [28]. The results showed that the liquid volume fraction after being separated could exceed 96% in a spiral pipe. During propellant transfer, the equivalent mass redistribution between the supplying tank and the receiving tank inevitably leads to an internal disturbance torque in the system [29], and it might cause sloshing of the tank. Therefore, sloshing under microgravity is also an important issue.

As mentioned above, research on cryogenic containers can be divided into two categories, with and without sloshing. For sloshing, many research studies have focused on the sloshing process of a closed container, but there has been little research on combining sloshing conditions with dynamic processes such as discharge and filling. With respect to the absence of sloshing, there have been many studies on the thermodynamic behavior of the liquid inside a container during the filling and discharging processes. However, little research has been done on the study of the changes in the state of the working fluid inside a cryogenic container due to sloshing during the filling process. Furthermore, on–orbit refueling has been ubiquitous in spacecraft applications. Therefore, if sloshing occurs when filling a cryogenic container under microgravity, it will have a certain effect on a cryogenic storage tank. Due to changes in gravity on the ground and in space, it is also of practical significance to study the effect of sloshing under microgravity on the filling process.

In this study, the effect of sloshing under normal gravity on the filling process of cryogenic storage tanks is studied via numerical simulation. Different sloshing conditions are obtained by combining different amplitudes and frequencies. Considering the fact that the on–orbit filling operation would be carried out in space, its gravity would be different from that on the ground. The effect of sloshing under microgravity on the filling process is also studied.

2. Model Description and Numerical Method

2.1. Physical and Computational Models

In order to study the effect of sloshing on the filling process of cryogenic containers, the liquid hydrogen storage tank used in Moran’s paper [20] is selected as the physical model. Figure 1a shows the structure of the liquid hydrogen storage tank. Figure 1b shows the three-dimensional computational domain, including the tank wall and the fluid domain. The y-axis is upward in the vertical direction. The x-axis and the z-axis are on the horizontal plane. In the calculation, the horizontal z-axis is used as the rotation axis of sloshing.

The interface between the two domains is set as a fluid-structure coupling surface. The working fluid used in the storage tank is liquid hydrogen, which is filled from the bottom. The inner volume of the storage tank is 34 L, the height is 0.508 m, the inner diameter is 0.318 m, the inner wall thickness is 3 mm, and the material used is SUS304 stainless steel. Because sloshing is a physical problem in three-dimensional space, a three-dimensional physical model is selected for numerical simulation research in this study. Furthermore, different combinations of the vibration frequency and amplitude are selected in order to analyze the effects of different sloshing conditions on the state of the working fluid during the filling process of the liquid hydrogen storage tank.

2.2. Mathematical Description

In this study, the ANSYS Fluent solver is used to solve the governing equations. The VOF model is chosen to simulate the two–phase flow for the filling process and the tracking of the complex gas-liquid interfaces [30,31,32,33,34]. The continuity equation, momentum equation, and energy equation are as follows:

$$\mathrm{gas}\mathrm{phase}\frac{\partial }{\partial t}({\theta }_{\mathrm{g}}{\rho }_{\mathrm{g}})+\nabla \cdot ({\theta }_{\mathrm{g}}{\rho }_{\mathrm{g}}\overrightarrow{v_{\mathrm{g}}})=S_{\mathrm{g}}$$

(1)

$$\mathrm{liquid}\mathrm{phase}\frac{\partial }{\partial t}({\theta }_{\mathrm{l}}{\rho }_{\mathrm{l}})+\nabla \cdot ({\theta }_{\mathrm{l}}{\rho }_{\mathrm{l}}\overrightarrow{v_{\mathrm{l}}})=S_{\mathrm{l}}$$

(2)

$$\frac{\partial }{\partial t}(\rho \overrightarrow{v})+\nabla \cdot (\rho \overrightarrow{v}\overrightarrow{v})=-\nabla p+\nabla \cdot [\eta (\nabla \overrightarrow{v}+\nabla {\overrightarrow{v}}^T)+\rho \overrightarrow{g}+\overrightarrow{F_v}$$

(3)

$$\frac{\partial }{\partial t}(\rho E)+\nabla \cdot (\overrightarrow{v}(\rho E+p))=\nabla \cdot ({\lambda }_{\mathrm{eff}}\nabla T)+S$$

(4)

where the subscripts g and l represent the gas and liquid phases, respectively.

To capture the movement of the liquid–vapor interface accurately, the VOF method is used. For each phase, a variable called the volume fraction (θ) of the phase in the computational cell, is introduced. In any control volume, the volume fractions of all phases add up to unity. Each phase shares a set of conservation equations, and the volume fractions of different phases are tracked in each computational cell of the entire domain. In the computational cell, the change of the interface can be tracked by solving the continuity equation of the liquid or gas volume fraction.

The volume fractions of the gas phase and the liquid phase have the following relationship [15]:

$${\theta }_{\mathrm{g}}+{\theta }_{\mathrm{l}}=1$$

(5)

The physical properties (density $\rho$, thermal conductivity $\lambda$, viscosity $\eta$) are related to the volume fraction θ:

$$\rho ={\rho }_{\mathrm{l}}{\theta }_{\mathrm{l}}+{\rho }_{\mathrm{g}}{\theta }_{\mathrm{g}}$$

(6)

$$\lambda ={\lambda }_{\mathrm{l}}{\theta }_{\mathrm{l}}+{\lambda }_{\mathrm{g}}{\theta }_{\mathrm{g}}$$

(7)

$$\eta ={\eta }_{\mathrm{l}}{\theta }_{\mathrm{l}}+{\eta }_{\mathrm{g}}{\theta }_{\mathrm{g}}$$

(8)

The energy term E (energy per unit mass) in the energy equation and the volume force $\overrightarrow{F_v}$ (the variation of surface tension force) in the momentum equation can be calculated by Equations (9) and (10):

$$E=\frac{{\rho }_{\mathrm{l}}{\theta }_{\mathrm{l}}{E}_{\mathrm{l}}+{\rho }_{\mathrm{g}}{\theta }_{\mathrm{g}}{E}_{\mathrm{g}}}{{\rho }_{\mathrm{l}}{\theta }_{\mathrm{l}}+{\rho }_{\mathrm{g}}{\theta }_{\mathrm{g}}}$$

(9)

$$\overrightarrow{F_v}={\sigma }_{\lg }\frac{{\rho }_{\mathrm{l}}{\theta }_{\mathrm{l}}{\kappa }_{\mathrm{g}}\nabla {\theta }_{\mathrm{g}}+{\rho }_{\mathrm{g}}{\theta }_{\mathrm{g}}{\kappa }_{\mathrm{l}}\nabla {\theta }_{\mathrm{l}}}{({\rho }_{\mathrm{l}}+{\rho }_{\mathrm{g}})/2}$$

(10)

where ${\sigma }_{\lg }$ is the surface tension of the gas-liquid interface /$\mathrm{N}\cdot {\mathrm{m}}^{-1}$; $\kappa$ is the surface curvature /m⁻¹; subscripts g and l represent the gas phase and liquid phase, respectively.

2.3. Interfacial Phase Change Model

The Lee model [35] is used to calculate the conversion of two phases of liquid hydrogen and hydrogen. The interfacial phase change is assumed to occur at constant pressure and in a quasi-thermal equilibrium state. The mass transfer is mainly dependent on the saturated temperature. The control equations are shown in Equations (11) and (12).

$$\begin{array}{c}{S}_{\mathrm{l}}=-S_{\mathrm{g}}=C_{\mathrm{l}}{\theta }_{\mathrm{l}}{\rho }_{\mathrm{l}}\left|(T_{\mathrm{l}}-T_{\mathrm{sat}})/T_{\mathrm{sat}}\right|\\ S_{\mathrm{g}}=-S_{\mathrm{l}}=C_{\mathrm{g}}{\theta }_{{}_{\mathrm{g}}}{\rho }_{{}_{\mathrm{g}}}\left|(T_{\mathrm{g}}-T_{\mathrm{sat}})/T_{\mathrm{sat}}\right|\end{array}\}$$

(11)

$$S=S_{\mathrm{l}}\cdot h_{\lg }$$

(12)

where S is the source term in Equations (1)–(4), h_lg is the enthalpy of vaporization, and the subscript sat represents the saturation state. C_l and C_g are positive mass-transfer coefficients, which are used to calculate the mass transfer rate in the cell. Many scholars have conducted extensive research on C_l and C_g values. The values of C_l and C_g not only depend on the flow geometry and flow conditions, but also on the grid size and time step [35]. In this study, the values of C_l and C_g are determined with reference to Ref. [21].

2.4. Numerical Method and Boundary Condition

In this study, Fluent 17.0 (ANSYS Inc., Pittsburgh, PA, USA) is used to solve the fluid-flow and heat-transfer processes. The solution method is based on the PISO algorithm, and the second-order upwind scheme is adopted to discretize the convection term. The gradient, pressure, and volume fraction are discretized using the Green-Gauss Cell Based, PREssure STaggering Option (PRESTO) and Geo-Reconstruct schemes. The convergence criterion is that the residuals of the energy equation and the other equations are less than 10⁻⁸ and 10⁻⁶, respectively. The standard $k-\epsilon$ model is used as the turbulence model [36].

In the calculation, the density of the gaseous hydrogen is calculated from the ideal gas law with a specific gas constant of 4124.3 J·kg⁻¹·K⁻¹ [21]. The outer wall surface is regarded as a thermal insulation surface, and the initial temperature is set to 44.3 K. The other thermos–physical properties of the gas and liquid phases that are involved can be set variably by inserting a polynomial function with reference to the temperature. All these properties for hydrogen can be obtained from the NIST Reference Fluid Properties Database (REFPROP) [37] and Material Properties DataBase (MPDB) [38]. The details for the physical property parameters are given in

Table 1. Thermo-physical properties of the fluid and solid.

Properties	Vapor	Liquid	Solid
cp/J·kg−1·K−1	14274.27 − 0.366T + 0.00161T2 − 4.630 × 10−7T3 + 4.103 × 10−11T4	5.657 × 105 + 1.459 × 105T − 1.471 × 104T2 + 7.322 × 102T3 − 17.98T4 + 0.175T5	−4.7335 + 0.848T
$\lambda$/W·m−1·K−1	0.0827 + 0.000356T + 1.072 × 10−8T2 − 4.405 × 10−12T3 + 3.263 × 10−16T4	7.267 × 10−2 − 1.294 × 10-3T + 5.948 × 10−4T2 − 3.969 × 10-5T3 + 1.081 × 10−6T4 − 1.147 × 10−8T5	2.839 − 0.1952T + 0.007T2
$\mu$/Pa·s	3.773 × 10−6 + 1.932 × 10−8T − 3.231 × 10−12T2 + 4.917 × 10−16T3 − 3.024 × 10−20T4	1.537 × 10−4 − 1.868 × 10−5T + 9.596 × 10−7T2 − 2.290 × 10−8T3 + 2.071 × 10−10T4
$\rho$/kg·m−3		50.137 + 6.9105T − 0.5756T2 + 0.0191T3 − 0.0002T4	8300

.

In the initial state, the interior of the liquid hydrogen storage tank is filled with gaseous hydrogen. The initial pressure is still lower than the saturation pressure. Since the cryogenic storage container has good thermal insulation performance, external heat leakage is ignored during the calculation. There is no outlet in the boundary conditions because it is a no-vent filling process. The thermal boundary conditions are set according to the experimental conditions in Moran’s research [20], as shown in

Table 2. Thermal boundary in Moran’s research [20].

	Temperature/K	Absolute Pressure/Pa	Vapor Volume Fraction
Wall	T = 44.3 K, τ = 0,
Inlet	T = Tsat, τ > 0,	P = psat, τ > 0,	0, τ > 0,
Fluid	T = Tsat, τ = 0,	P = 27,597 Pa, τ = 0,	1, τ = 0,

. Before the reloading started, the absolute pressure in the tank is 27,597 Pa, which is lower than the saturation pressure of liquid hydrogen. The wall temperature is 44.3 K, and the hydrogen temperature in the tank is consistent with the wall temperature. The filling method adopts bottom injection, and the flow direction of liquid hydrogen is the direction of the black arrow in Figure 2. During the filling process, the liquid hydrogen is kept at the saturation temperature, and the mass flow rate of the liquid hydrogen is 0.0113 kg/s. The pressure in the tank is recorded by a pressure sensor in the tank. In Table 2, T_sat represents the saturation temperature, and τ is the time for the filling process. The states of τ = 0 and τ > 0 indicate the state before and after the start of filling, respectively.

In order to simulate the effect of sloshing on the filling process, a dynamic boundary condition of sinusoidal sloshing is combined with the filling process of the liquid hydrogen storage tank. The z-axis is selected as the sloshing axis, which is perpendicular to the paper direction, as shown in Figure 2. In order to implement the coupling of the dynamic boundary conditions and the Fluent solver, the boundary conditions are compiled in Fluent using a user-defined function (UDF), which allows us to customize Fluent and can significantly enhance its capabilities. The sinusoidal sloshing excitation is adopted, as shown in the following expression [15].

$$y=A\sin (2\pi ft)$$

(13)

where A represents the amplitudes of the sinusoidal excitation with the values of 0.01 m, 0.02 m,0.03 m, and 0.04 m, f represents the sinusoidal excitation frequencies with the values of 1.0 Hz, 2.0 Hz, and 3.0 Hz, and t is the sloshing time, with the time step offset to 0.001 s.

The related sloshing velocity and acceleration are given as:

$$v=y^{\prime }=2\pi fA\cos (2\pi ft)$$

(14)

$$a=y^{″}=-4{\pi }^2{f}^{2}A\sin (2\pi ft)$$

(15)

3. Model Validation

Due to the use of dynamic boundary conditions, in order to effectively verify the accuracy of the model, the model verification is divided into two parts: the phase–change model verification and the vibration model verification.

3.1. Grid Independence

In this study, a three-dimensional grid system is established using the commercial software ICEM, and both the solid and fluid domains use structured meshes, as shown in Figure 3. Four sets of grid systems with 121,373, 221,369, 359,393, and 544,436 cells are selected for the grid independence test. The pressure changes in the liquid hydrogen storage tank that are calculated based on the different gird systems are shown in Figure 4. It can be seen in the figure that the difference in the pressure change between the last two grid systems is less than 1%. Thus, with consideration of the computational time cost and accuracy, the third grid system is selected for the subsequent calculations.

3.2. Verification of the Sloshing Model

3.2.1. Rectangle Tank without Phase Change

The results of the rectangular water tank in Manuel’s study [39] are selected as the basis for the verification of the vibration model. In Manuel’s study [39], a rectangular tank is partially filled with water stained with a color. In this experiment, a lateral sloshing wave impact in a 3D rectangular tank of width W = 900 mm, depth D = 62 mm, and height H = 508 mm is performed. The fluid is (colored) water of density ρ = 998 kg/m³ at 19 °C, and the tank is filled with it up to a height of h = 93 mm. A pressure sensor is located on the left tank wall at a height of 93 mm, as can be seen in Figure 5. Subsequently, a forced roll motion is established in about the center of the bottom line of the tank with a rotation frequency of f ≈ 0.6 Hz, and the values of the pressure sensor as well as the roll angles are recorded.

The water tank is placed in an atmospheric environment, and the dynamic boundary conditions of sinusoidal sloshing are applied to the bottom of the rectangular water tank, as shown in Figure 5. In this study, the pressure is used as an indicator to evaluate the sloshing model. The comparison results are shown in Figure 6. It can be seen in the figure that the average relative error between the simulation results in this study and the experimental results from Manuel’s study [39] is 14.4%, which proves the reliability of the numerical method. The error bars of the simulation results are shown in Figure 6. It can be seen from Figure 6 that at the time when the pressure peak appears, the simulation result is consistent with the experimental value, but there are still errors in the value, and the simulation result is too small. The appearance of the pressure peak has a certain relationship with the pressure sensor used in the experiment and the change of environmental conditions, which leads to the deviation of the simulation result and the experimental value. Under experimental conditions, the pressure even shows a negative value. The reason for this phenomenon may be that some of the gas in the experiment is involved in the liquid phase, which causes the pressure of the gas phase to decrease, or it is related to the accuracy of pressure sensor used. These factors cannot be predicted well during the simulation process, thus causing errors in experimental values.

3.2.2. Cylindrical Tank with Phase Change

In order to further verify the accuracy of the numerical method when both sloshing and phase changes to the evaporation existed, the research work for a cylindrical container in Grotle’s paper [40] is selected as another validation case. In Grotle’s paper [40], the experimental container is composed of a cylinder and two semicircles. The diameter and length of the cylinder are 0.35 m and 0.89 m, respectively. The container is placed horizontally, inside which temperature and pressure sensors are arranged. Water (50%) is poured into the container before the start of the experiment. During the experiment, the vibration frequency is 0.57 Hz, and the motion amplitude is kept constant and equal to 3 degrees in all tests. The verification results are shown in Figure 7. It can be seen in the figure that when there was sloshing, the pressure in the container is significantly reduced and the error between the calculated value and the experimental value is within 5%. It could be considered that the sloshing and phase change evaporation model in this study is reliable. It can be found in Figure 7 that the pressure in the container shows a downward trend over time during the sloshing process. The reason for this phenomenon can be explained as the sloshing caused the gas in the container to liquefy, causing the pressure to drop. Compared with the experimental value, the pressure simulation value in this paper is higher. This may be because the numerical simulation only considers the main environmental factors in the experimental test. For example, the estimated value of the heat transfer of the container to the outside during the sloshing process may not be consistent with the actual value.

3.2.3. Verification of the Phase Change Model in the Filling Process

With respect to the accuracy of the phase-change model in the filling process, the change of the internal pressure of the liquid hydrogen storage tank in Liu’s research [16] is selected as the evaluation index. The comparison results in Figure 8 show the good agreement between the numerical results and the experimental values in Liu’s research [16], with an average relative error of 12.05%. The error bars of the simulation results are also shown in Figure 8. It can be concluded that the numerical method in this study shows good reliability in the calculation of the phase change in the filling process of the storage tank. It can be seen that the pressure gradually increases due to the vaporization of liquid hydrogen during the closed filling process. Compared with the experimental value, the simulated value of pressure in the initial stage rises faster, and the rising speed gradually decreases after about 10 s, and it is consistent with the experimental value. The literature value increases slowly in the initial stage, which may be caused by the wall surface being sufficiently pre-cooled. The deviation between the two curves is mainly generated by the accumulation and transfer of the initial deviation in the beginning.

4. Results

Since the degree of sinusoidal sloshing is determined by both the amplitude and the frequency, three sloshing frequencies and four amplitudes are adopted to investigate the effect of sloshing on the filling process.

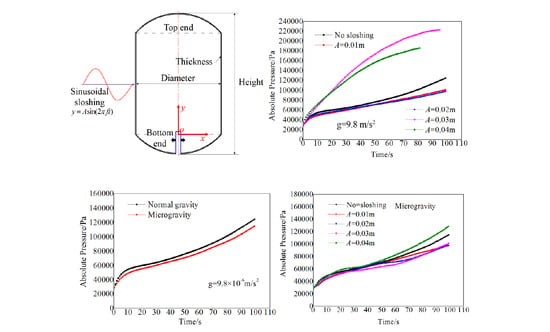
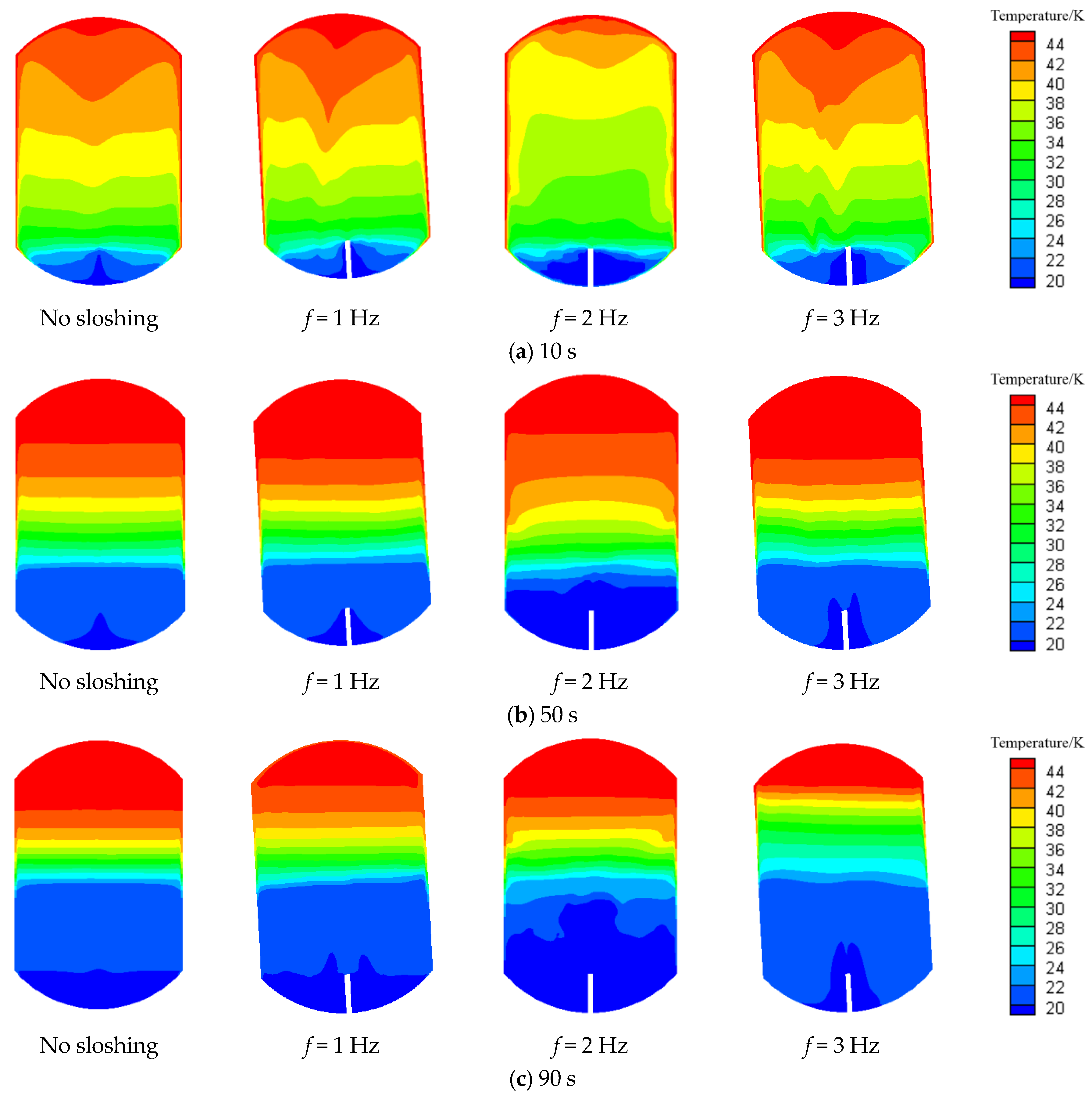
4.1. Effects of Frequency on the Pressure Curve During the Filling Process

The calculation results of the dynamic response of the sloshing at different frequencies to the internal pressure of the liquid hydrogen storage tank are shown in Figure 9. According to the results shown in Figure 9, regardless of the presence or absence of sloshing, the pressure in the tank increases continuously during the filling process of the liquid hydrogen storage tank. This phenomenon can be explained by the fact that, first, the gas phase space continues to shrink as the filling process progresses. Second, there are both vaporization and liquefaction processes in the storage tank, but vaporization plays a dominant role because the initial wall temperature of the storage tank is higher than the liquid hydrogen temperature. In addition, the saturation temperature of liquid hydrogen decreases with the decrease of pressure. Since the pressure in the cryogenic tank is lower in the initial stage, the liquid hydrogen inside the tank is in a boiling state due to heat leakage. This also means that a large amount of liquid hydrogen vaporizes, causing the pressure to rise sharply. These three effects led to an increase in pressure with time. Moreover, the pressure curve of the liquid hydrogen storage tank for sloshing conditions is clearly separated from the pressure curve without sloshing. As the sloshing frequency increases, the pressure curve with sloshing becomes lower compared to the condition without sloshing when the amplitude is low, as shown in Figure 9a,b. The reason for this appears to be that when there is a small sloshing condition, the presence of sloshing increases the liquefaction of gas, which eventually causes the liquefaction process to gradually dominate and further reduces the pressure.

As the sloshing amplitude further increases, the pressure curve gradually increases with the sloshing frequency, as shown in Figure 9c,d. At the same time, the pressure of the tank under high-frequency sloshing rises to a higher level. This is because the higher sloshing amplitude and frequency result in more disturbances in the storage tank, which in turn leads to more liquid vaporization. Therefore, the vaporization process dominates and leads to an increase in pressure.

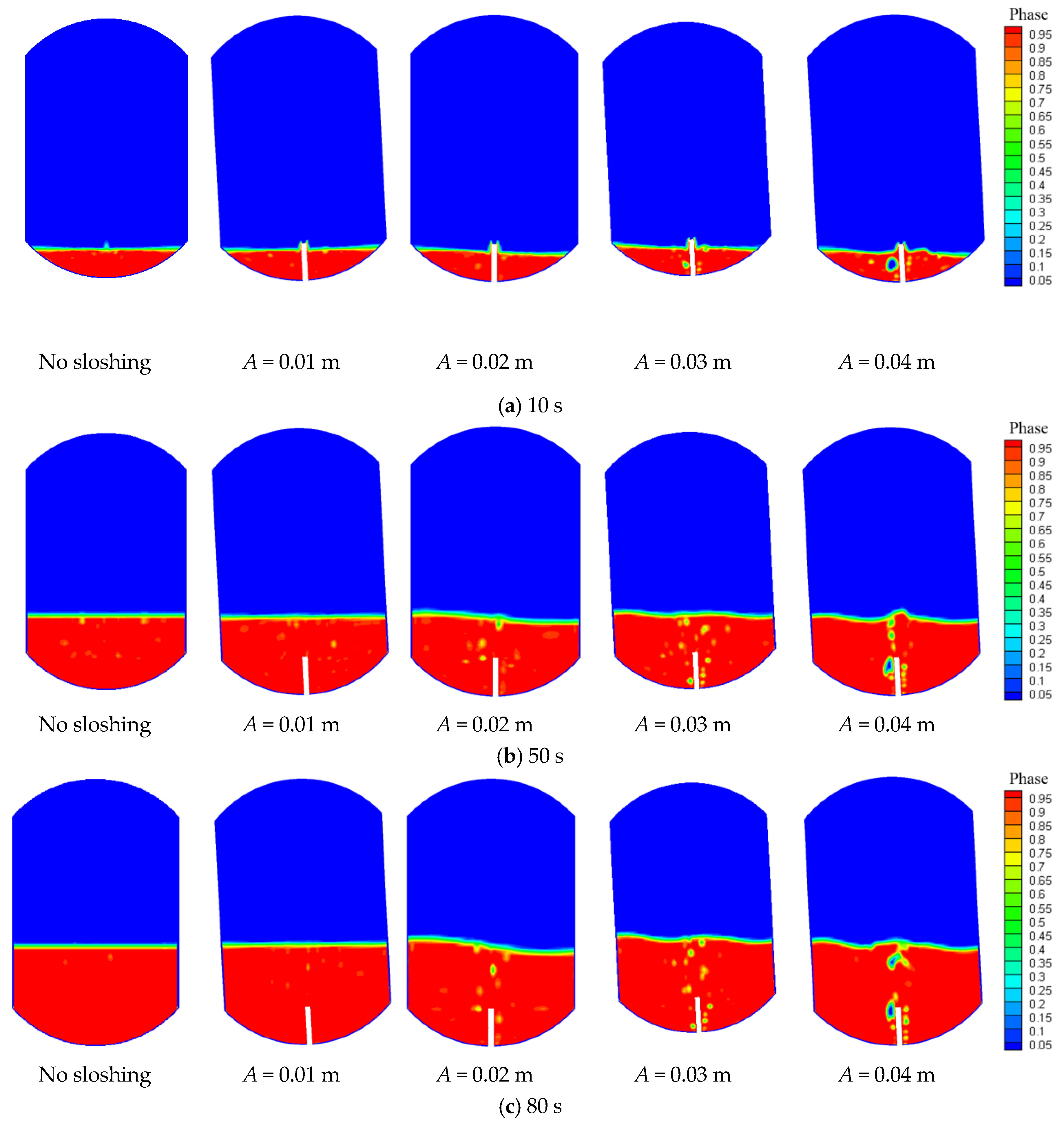
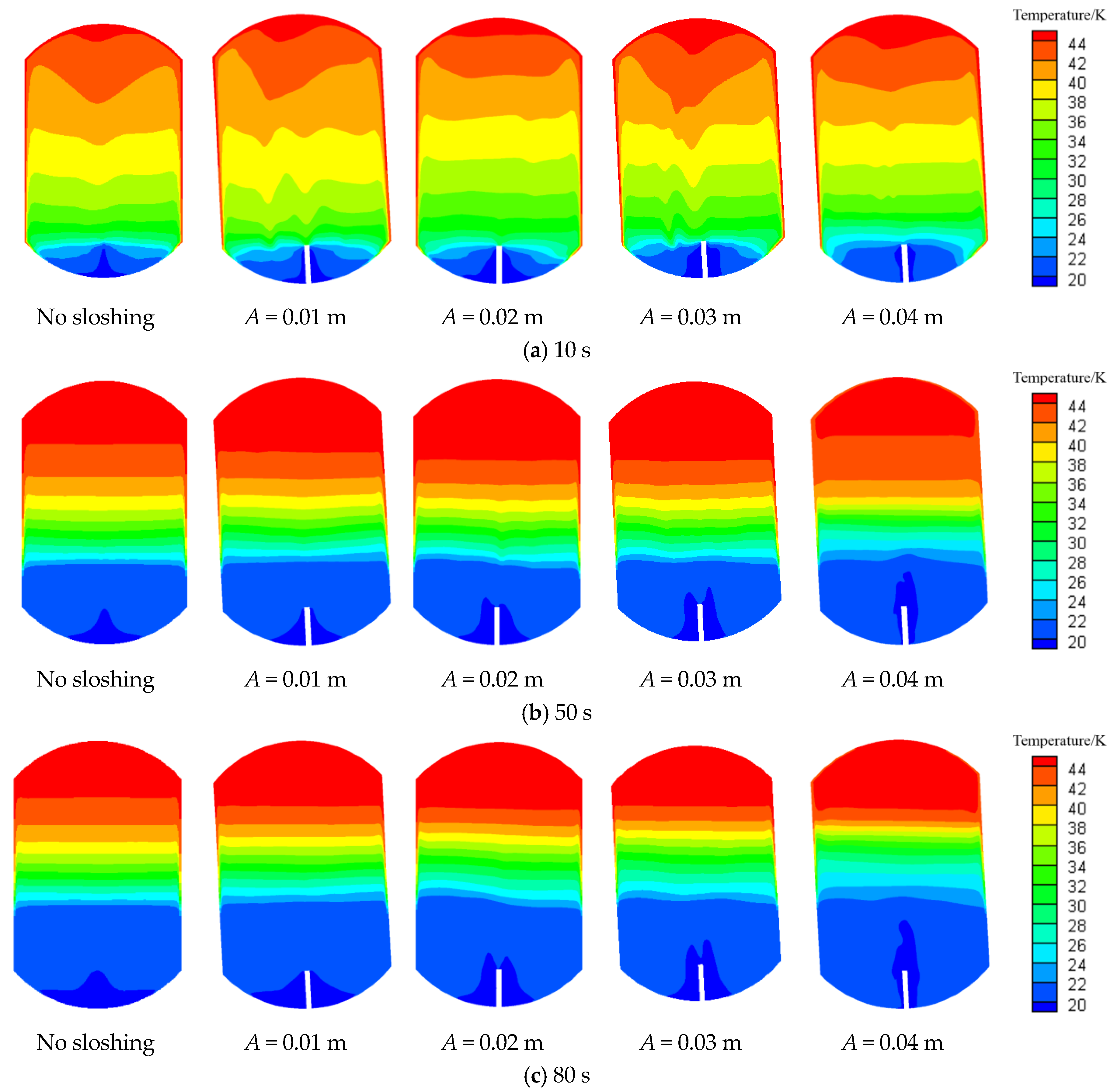
4.2. Effects of Amplitude on the Pressure Curve during the Filling Process

Figure 10 shows the pressure response of the liquid hydrogen storage tank at different amplitudes. It can be seen in Figure 10 that when the sloshing frequency f equals 1 Hz, as shown in Figure 10a, four different amplitudes have little effect on the pressure curve inside the liquid hydrogen storage tank. However, the pressure curve undergoes a process of first decreasing and then increasing when the amplitude gradually increases as shown in Figure 10c, which indicates that there should be a critical amplitude. Within this critical amplitude range, small sloshing causes the pressure curve to decrease. After exceeding the critical value, the increase in amplitude makes the pressure curve increase significantly. When the sloshing frequency f is equal to 2 Hz, the frequency and the amplitude have the same degree of influence, so there is no obvious regularity of the pressure curve with the amplitude, as shown in Figure 10b. It is speculated that when the frequency f is equal to 2 Hz, the effect of the amplitudes on the pressure curve is in a transition region. In other words, in this transition region, the increase in the amplitude does not necessarily cause the pressure curve to increase. When the frequency increases to 3 Hz, as shown in Figure 10c, the smaller amplitude conditions (A = 0.01 m and A = 0.02 m) lead to a slight decrease in pressure. However, the sloshing causes a greater change in pressure as the amplitude continues to increase. For example, when the amplitudes A are equal to 0.03 m and 0.04 m, the pressure curve of the liquid hydrogen storage tank increases significantly. It can also be noted from Figure 10c that the pressure curve is slightly lower at the amplitude of 0.04 m than at the amplitude of 0.03 m. The reason for this phenomenon is discussed in Section 4.3, below.

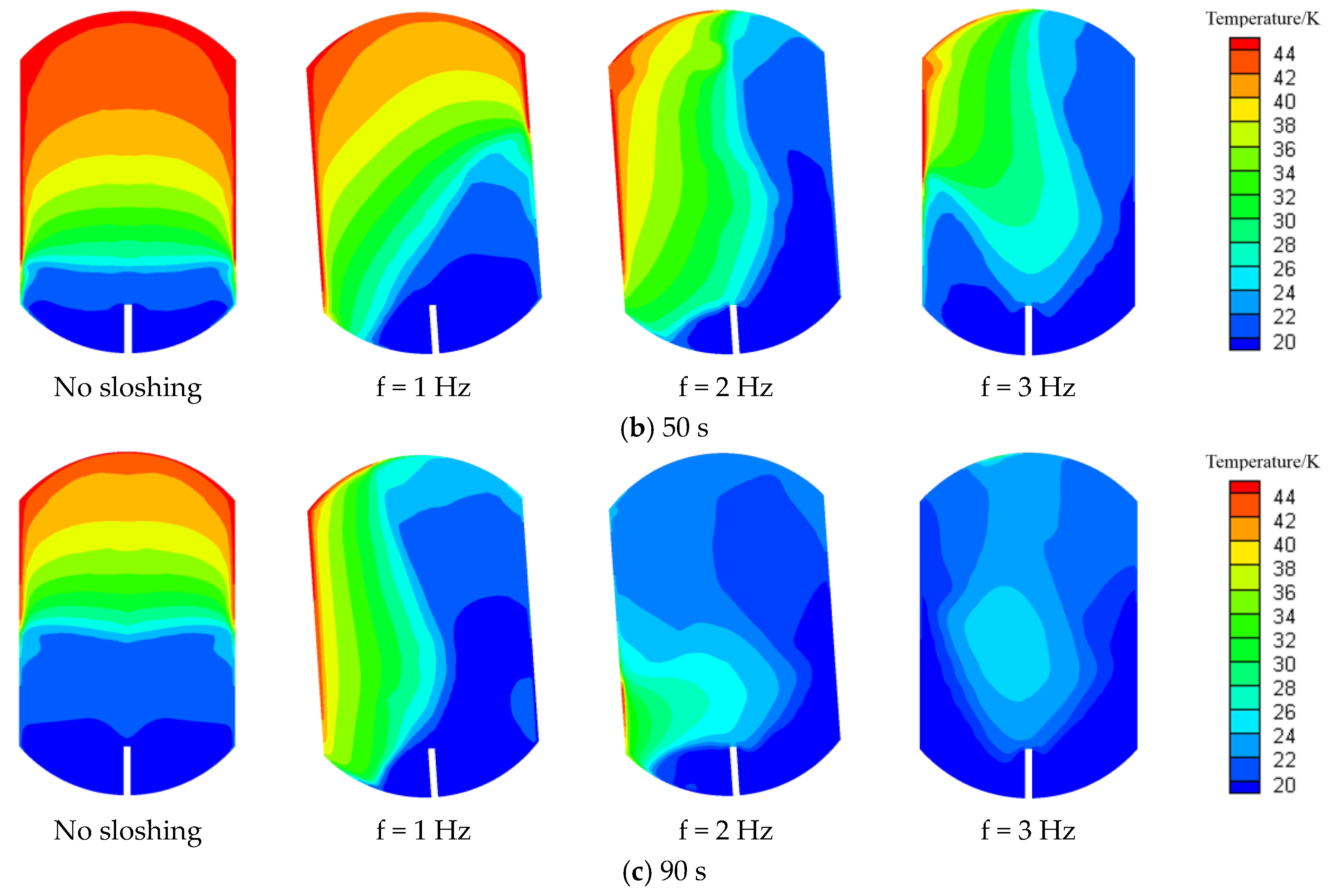
4.3. Effect of Sloshing on Phase Change and Temperature Distribution

In order to further explain the effects of sloshing, Figure 11 and Figure 12 show the intercept of the liquid phase distribution and the temperature distribution of the liquid in the hydrogen storage tank at different times and different sloshing frequencies with a fixed sloshing amplitude (A = 0.03 m). When the sloshing frequency is fixed (f = 0.03 Hz), the changes of the liquid phase distribution and the temperature distribution of the liquid in the hydrogen storage tank with the amplitude at different times are as shown in Figure 13 and Figure 14. It can be seen from Figure 11 that the gas-liquid free interface inside the liquid hydrogen storage tank is in a horizontal state and the liquid level rises steadily with time when there is no sloshing condition. After the sloshing conditions are applied, the liquid level fluctuations in the liquid phase are still relatively stable when sloshing at low frequencies. When the sloshing frequency continues to increase, there are obvious bubbles in the liquid phase and the gas-liquid interface is no longer stable. The liquid phase distribution at f equal to 3 Hz confirms this statement as shown in Figure 11. The liquid volume gradually increases and the fluctuation of the gas-liquid interface becomes more and more obvious as the filling process progresses. The appearance of bubbles indicates that the evaporation process of liquid hydrogen in the container is violent. A large amount of hydrogen is produced at the gas-liquid interface, but due to its low temperature, the phenomenon of squeezing the high–temperature hydrogen to the top of the container occurs during the heat absorption process as shown in Figure 12 (f = 3 Hz). It can be concluded that the sloshing brings extra energy into the storage tank, which eventually leads to the increased vaporization of the liquid and increased pressure.

The initial temperature of the solid domain is 44.3 K and it is higher than the liquid temperature. The temperature difference between the upper wall and the liquid phase eventually leads to temperature stratification. Figure 12 and Figure 14 demonstrate that the thermal stratification in the gas phase is also more obvious when there is no sloshing in the filling process of the liquid hydrogen storage tank. The gas-liquid interface begins to fluctuate significantly with the increasing sloshing frequency. When the frequency increases to the maximum value, bubbles even appear at the inlet. At the same time, the temperature distribution also fluctuates significantly, especially at the initial stage. Obviously, with the increase in the liquid volume, the thermal stratification tends to be stable, and it is generally parallel to the gas-liquid free interface. It can also be found that the thermal distribution near the gas-liquid interface shows the same fluctuation behavior as the gas-liquid interface. Furthermore, it can be seen that in the later stage of the filling process, the increase of the sloshing frequency causes the thickness of the temperature stratification area (the green areas in Figure 12 and Figure 14) of the gas phase to increase.

The variations of the pressure curve in Figure 10 could be further explained with Figure 13 and Figure 14. It can be seen in Figure 13 that when the frequency f is equal to 3 Hz, the gas-liquid interface fluctuates significantly as the amplitude increases, and bubbles appear in the liquid phase. When the amplitude reaches the maximum value (A = 0.04 m), it even appears that the hydrogen in the gas phase zone is involved in the liquid phase (Figure 13, A = 0.04 m). This is different from the bubbles generated from the bottom. Due to the limitation of heat, the bubbles produced by the evaporation of liquid hydrogen cannot readily develop into large pure gas bubbles, mostly in the gas-liquid mixed state in Figure 11 (f = 3 Hz). The entrapped gas is cooled by the liquid, and the temperature drops to the same temperature as the liquid phase. Figure 14 illustrates this phenomenon. This further causes the gas to be liquefied, thereby reducing the pressure in the gas phase space. This also explains the phenomenon shown in Figure 10c; even when the amplitude exceeds 0.03 m, the pressure curve at the amplitude A equal to 0.04 m still drops slightly.

4.4. Pressure Response under Microgravity and Sloshing Conditions

When sloshing occurs under microgravity conditions, the pressure response of the storage tank is different from that for normal gravity conditions. Figure 15 shows the pressure curve inside the tank for different gravities. It can be seen from the figure that the pressure curve of the liquid hydrogen storage tank under microgravity (g = 9.8 × 10⁻⁶ m/s²) is slightly lower than that for normal gravity (g = 9.8 m/s²). This shows that in the initial stage of filling under microgravity, the entry of cold fluid causes the hydrogen in the storage tank to liquefy, which ultimately causes a pressure drop.

According to Figure 16 and Figure 17, it can be determined that the pressure curve in the storage tank is lower when there is sloshing under microgravity. Compared to normal gravity, the critical conditions that are affected by sloshing conditions are not obvious at this time. At low frequencies and small amplitudes, the pressure curve caused by sloshing does not change much. As the amplitude and frequency increase further, the pressure curve shows an increasing trend, as shown in Figure 16d and Figure 17c. In general, within the scope of this study, the effect of sloshing under microgravity on the pressure is smaller than that of normal gravity. The critical condition for the effect of sloshing on the pressure curve shifts to higher amplitudes and frequencies. To explain this, in this study, the phase distribution and the temperature distribution contours are intercepted at different times, as shown in Figure 18 and Figure 19.

It can be seen in Figure 18 and Figure 19 that under microgravity conditions, the liquid is distributed along the storage tank wall due to surface tension, and the liquid gradually expands toward the center. When the sloshing condition is more severe, bubbles appear in the liquid and the wall surface. The gas-liquid interface also shows an irregular state. The sloshing of the liquid in the storage tank also causes the internal temperature stratification of the storage tank to weaken to a certain extent, which has a beneficial effect on controlling the pressure in the storage tank. In a microgravity environment, the liquid phase diffuses along the wall surface, at which time the wall surface is cooled. After the liquid completely wets the wall surface, the wall temperature tends to be consistent, and the temperature stratification in the storage tank is significantly weakened. The effect of this phenomenon is equivalent to that of the pre-cooling process, so that the pressure of the cryogenic liquid hydrogen storage tank does not rise particularly quickly during the filling process. It can be seen in Figure 18 that the sloshing makes it easier for the liquid to spread along the wall of the tank, so the temperature stratification during sloshing is also weakened. The weakening of the temperature stratification effectively reduces the heat and the mass transfer caused by the temperature difference in the storage tank. Therefore, under microgravity, the pressure curve inside the storage tank decreases when there is sloshing. When the amplitude and the frequency reach the maximum values, the pressure curve starts to be higher than the value for the no sloshing condition. This shows that the additional energy that is input in the storage tank with sloshing at that moment causes more liquid in the tank to evaporate, resulting in a pressure increase.

5. Discussion

There are essentially two ways to fill a cryogenic container. One is open filling; that is, the filling valve and the vent valve are opened at the same time. The opening of the vent valve is conducive to the discharge of other gases in the container. In addition, this method ensures that the pressure in a container does not rise too high in a short time. The other type is no-vent filling: only the filling valve is opened and the remaining valves are closed in this method. This filling method is generally used for flammable and explosive gas. However, compared to open filling, closed filling cannot release the pressure of a cryogenic container, so it is necessary to pre-cool a cryogenic container in advance. It is generally expected that a cryogenic liquid will be used to fill a cryogenic container as much as possible in a short period of time. Therefore, the slower the pressure increase process, the more favorable it is for the filling process. The results of the simulation analysis in this study show that when the sloshing amplitude is not too large and the sloshing frequency is not too high, the sloshing condition causes the pressure curve inside the liquid hydrogen storage tank to decrease during the filling process. In contrast, when the sloshing amplitude and the frequency increase, the sloshing conditions cause the pressure curve in the liquid hydrogen storage tank to increase significantly during the filling process.

Based on the above analysis, it is proposed in this study that there is a critical condition (amplitude A = 0.03 m and frequency f = 3 Hz) for the effect of sloshing on the pressure response of the liquid hydrogen storage tank during the filling process on the ground. For this critical condition, the effect of sloshing can be ignored. If the critical condition is exceeded, the effect of sloshing has to receive corresponding attention. Generally, the effect of slight sloshing on the filling process of the cryogenic containers is essentially negligible, and under suitable conditions, slight sloshing has a positive effect on the filling process. However, the impact of external sloshing must be considered for cryogenic containers under violent sloshing conditions, especially when storing flammable and explosive hazardous cryogenic liquids.

Finally, it should be pointed out that although there is more than one method to calculate the flow of fluid, they all have the disadvantage of a long calculation time. Taking this article as an example, 20 CPU nodes are selected for calculation, and the calculation time of each case of a 3D model takes about one week. In order to shorten the calculation time, Krzysztof Kosowski et al. [41] used artificial neural networks to calculate the flows in steam turbine cascades. The calculation result is equivalent to the CFD result, but the calculation time has been greatly shortened. In future work, in order to shorten the calculation time, the use of artificial neural networks to calculate the flow of fluid under more sloshing conditions is a method worth considering.

6. Conclusions

In this study, a numerical model is established for calculating the phase-change process in a liquid hydrogen storage tank under sloshing and filling conditions. The effect of sloshing on the filling process of the liquid hydrogen storage tank is studied using the proposed numerical model. Thus far, the experimental research in this area is mainly about sloshing in a closed system, while experimental study which couples the filling process of the cryogenic container with sloshing is limited. Therefore, relevant research has been implemented using numerical simulation methods in this paper. Based on this work, the following conclusions can be drawn.

(1)

Under normal gravity, the increase of frequency reduces the pressure curve and weakens the evaporation process of the liquid when the amplitude is low. However, at high amplitude, the pressure curve increases significantly with the increase in frequency.

(2)

Within the scope of this study, there is a critical condition (amplitude A = 0.03 m and frequency f = 3 Hz) for the effect of the sloshing conditions on the pressure curve under normal gravity. When sloshing exceeds the critical condition, the pressure curve of the liquid hydrogen storage tank during the filling process increases. That is, the pressure is higher and increases more quickly during the same time compared to the condition without sloshing. By contrast, when the sloshing is within the critical condition, properly increasing the sloshing causes the storage tank pressure curve to decrease.

(3)

Within the scope of this study, the pressure curve under microgravity changes less than normal gravity, even if the amplitude and frequency increase. The sloshing makes it easier for the liquid to spread along the wall during the filling process. This also further weakens the temperature stratification in the storage tank.