Gain-Scheduled Equivalent-Cascade IMC Tuning Method for Water Level Control System of Nuclear Steam Generator
Abstract
:1. Introduction
2. Problem Formulation
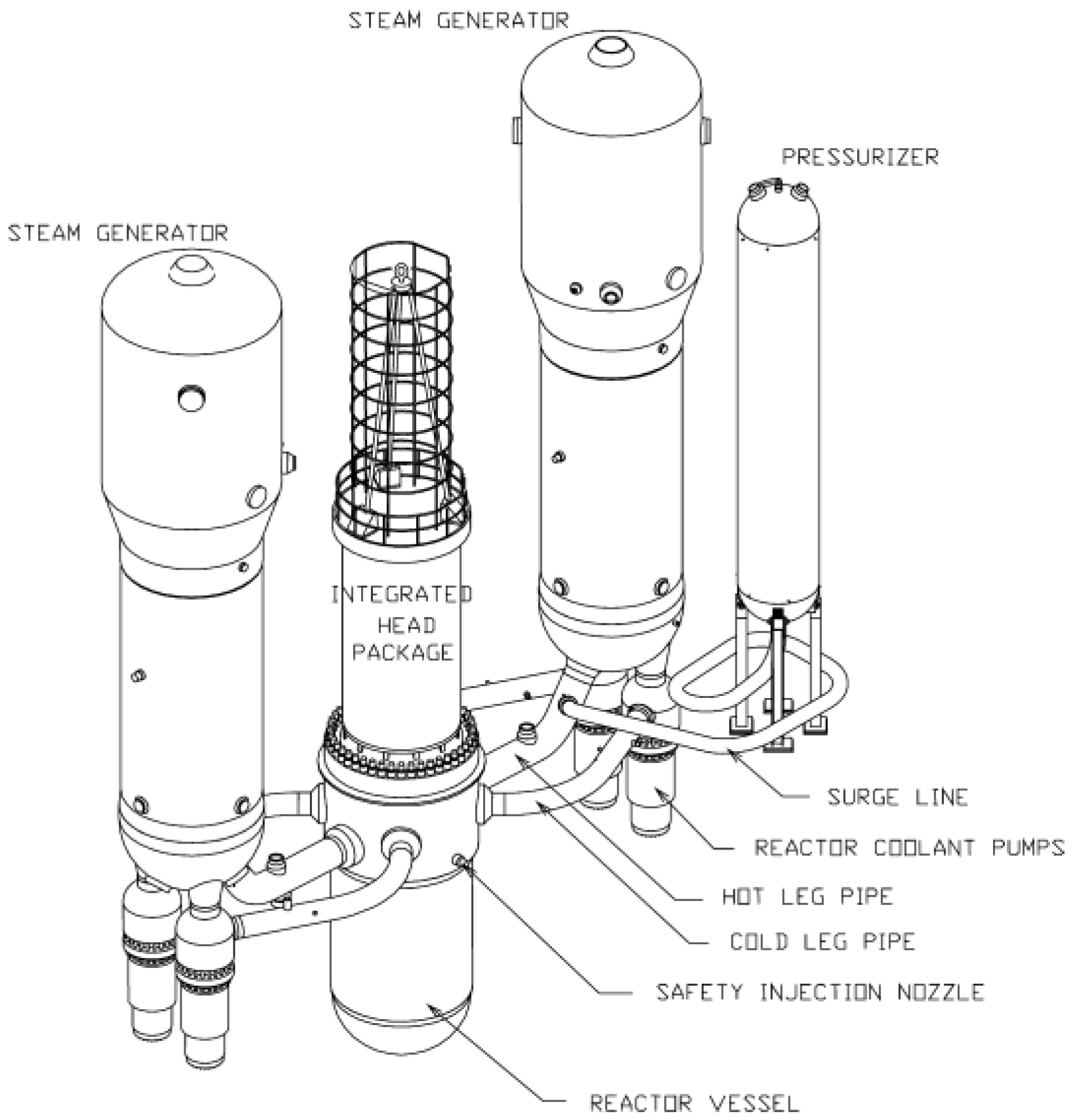
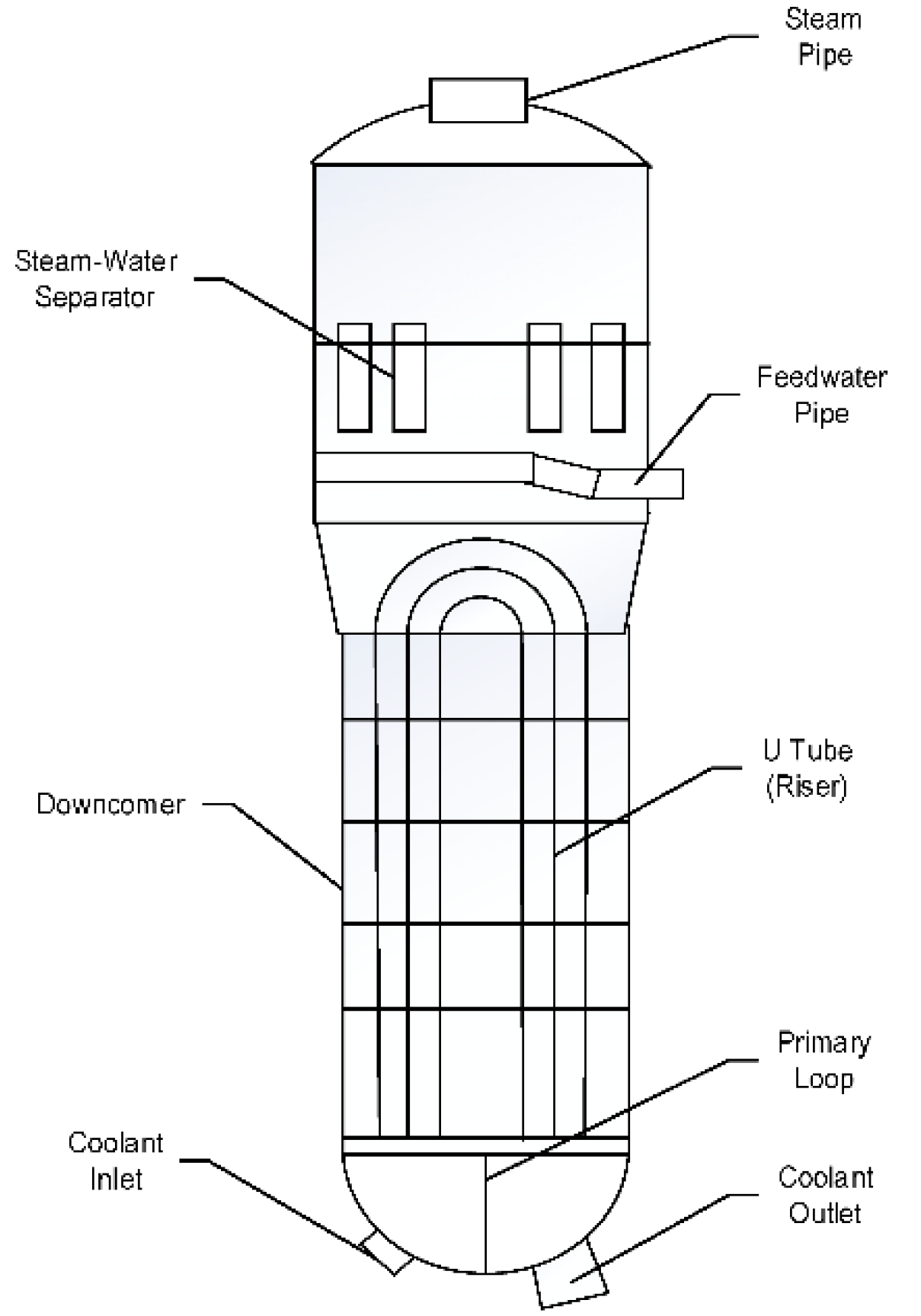
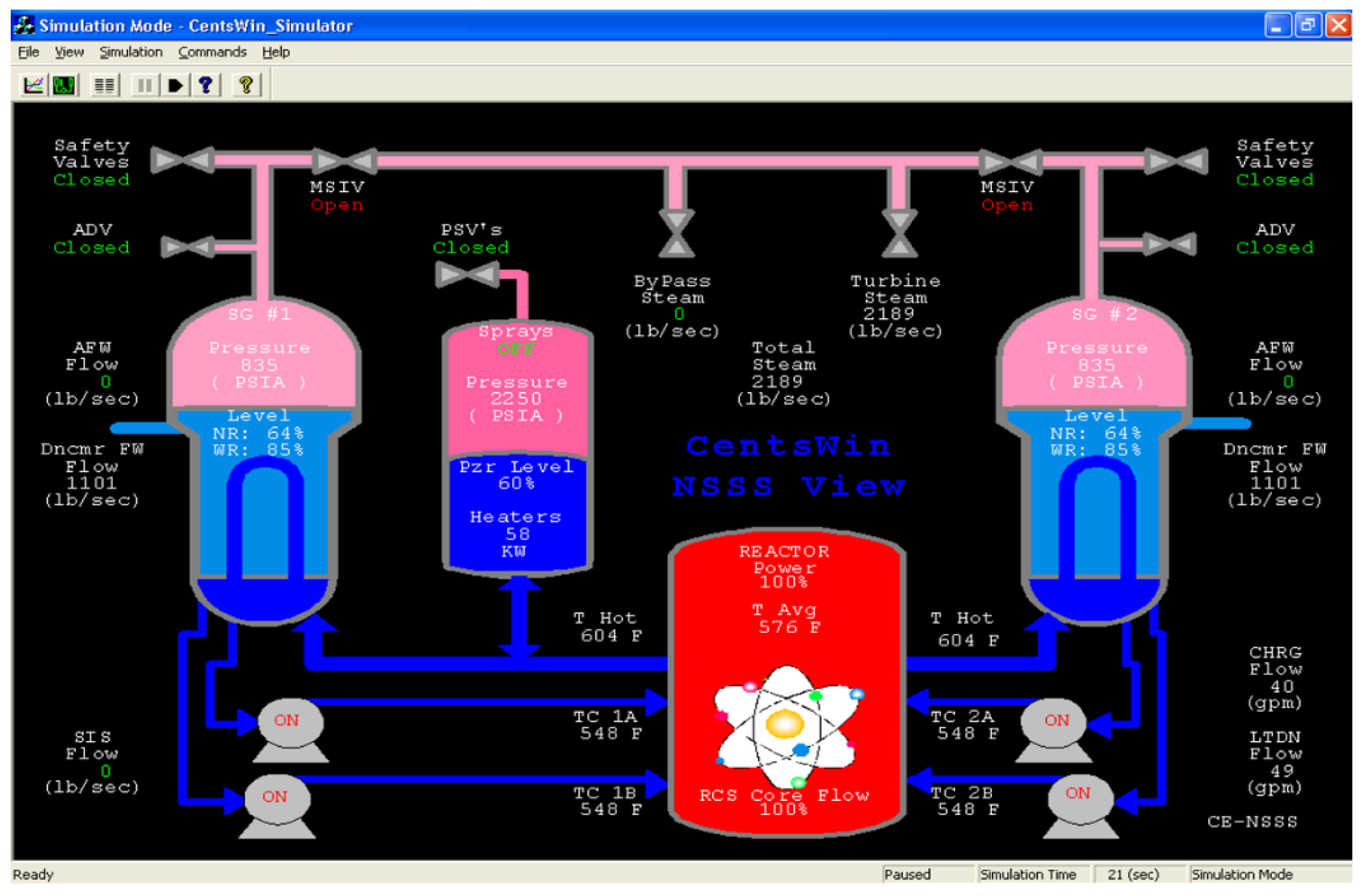
2.1. AP1000 Steam Generator
2.2. Control Problems of Steam Generator Water Level
- The open-loop dynamics of SG exhibit unstable behavior;
- The shrink and swell effects lead to strong inverse response behavior, which is remarkable at low power;
- Highly nonlinear characteristics, i.e., the dynamics of the process, vary with changes in operating power.
2.3. AP1000 Water Level Control System
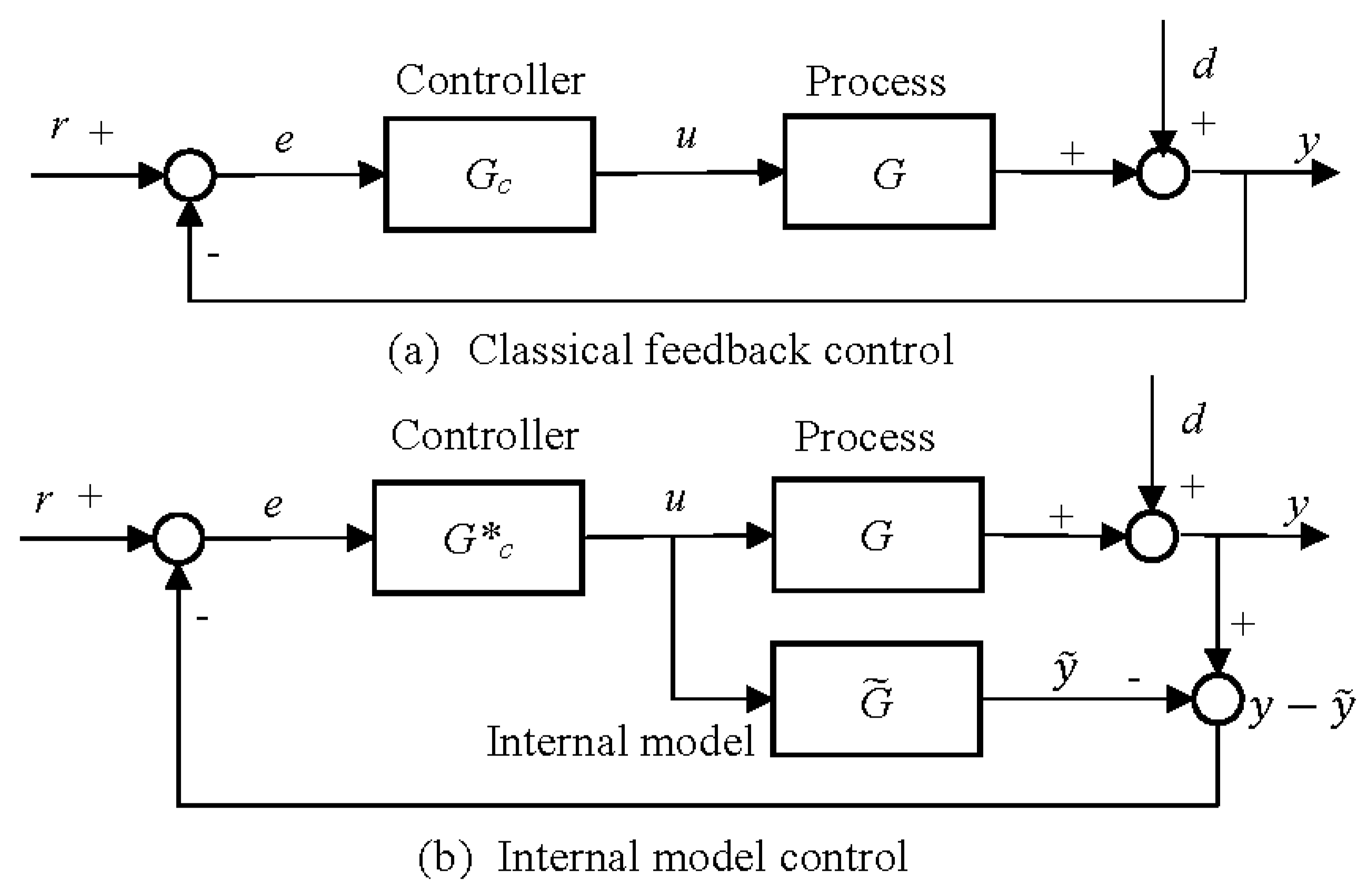
3. Equivalent-Cascade IMC Tuning Method
3.1. IMC-PID Tuning Theory
- Step 1.
- The process model can be expressed as , where contains any time delays and the right-half plane zeros with a steady-state gain of 1, and is the rest of .
- Step 2.
- The IMC controller is specified as , where f represents a low pass filter with a gain of 1. The filter f typically has the form , where r is sufficiently large to guarantee that the IMC controller is a proper transfer function. The parameter is the desired closed-loop time constant, which determines the speed of the response. The closed-loop transfer function for set-point changes is .
- Step 3.
- The equivalent feedback controller can be derived from Equation (1) and rearranged into the PID controller form.
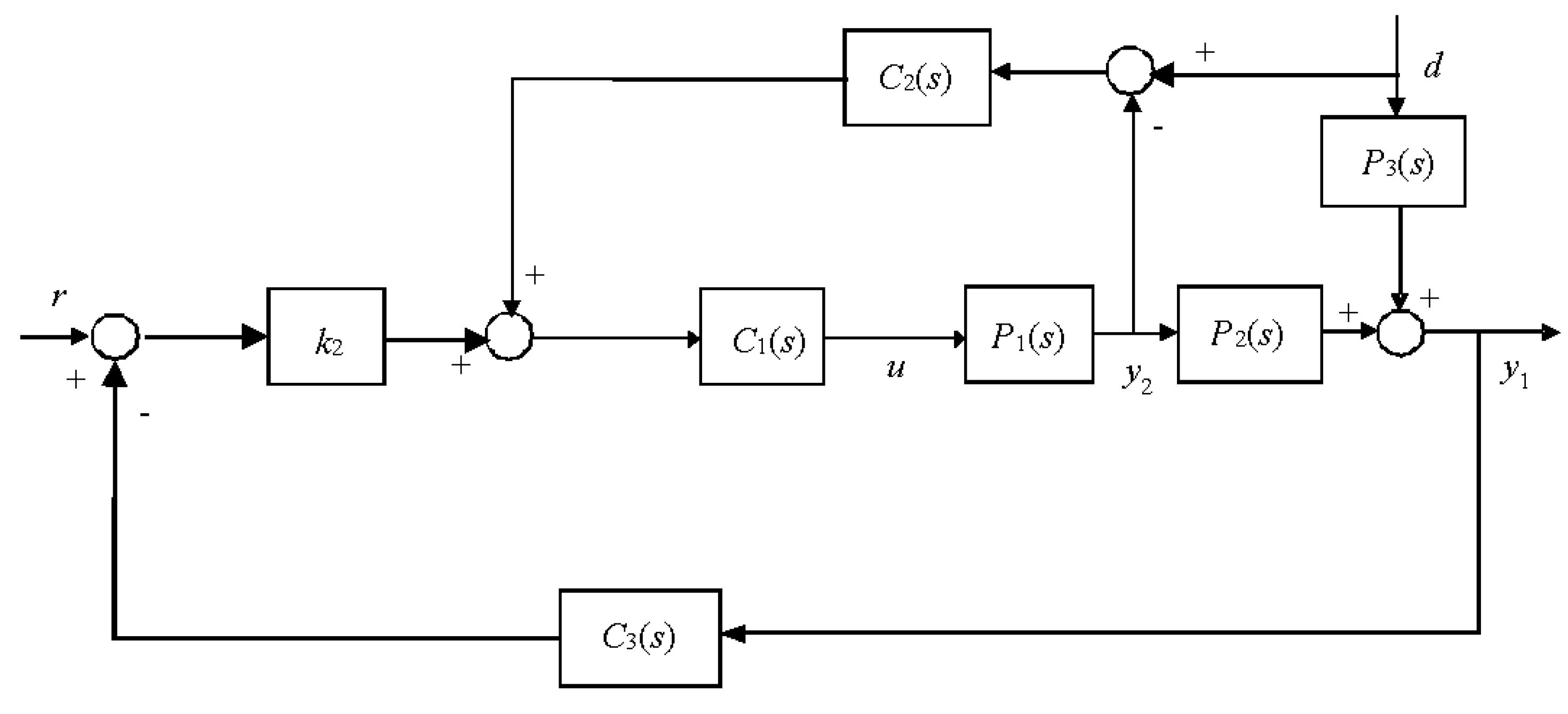
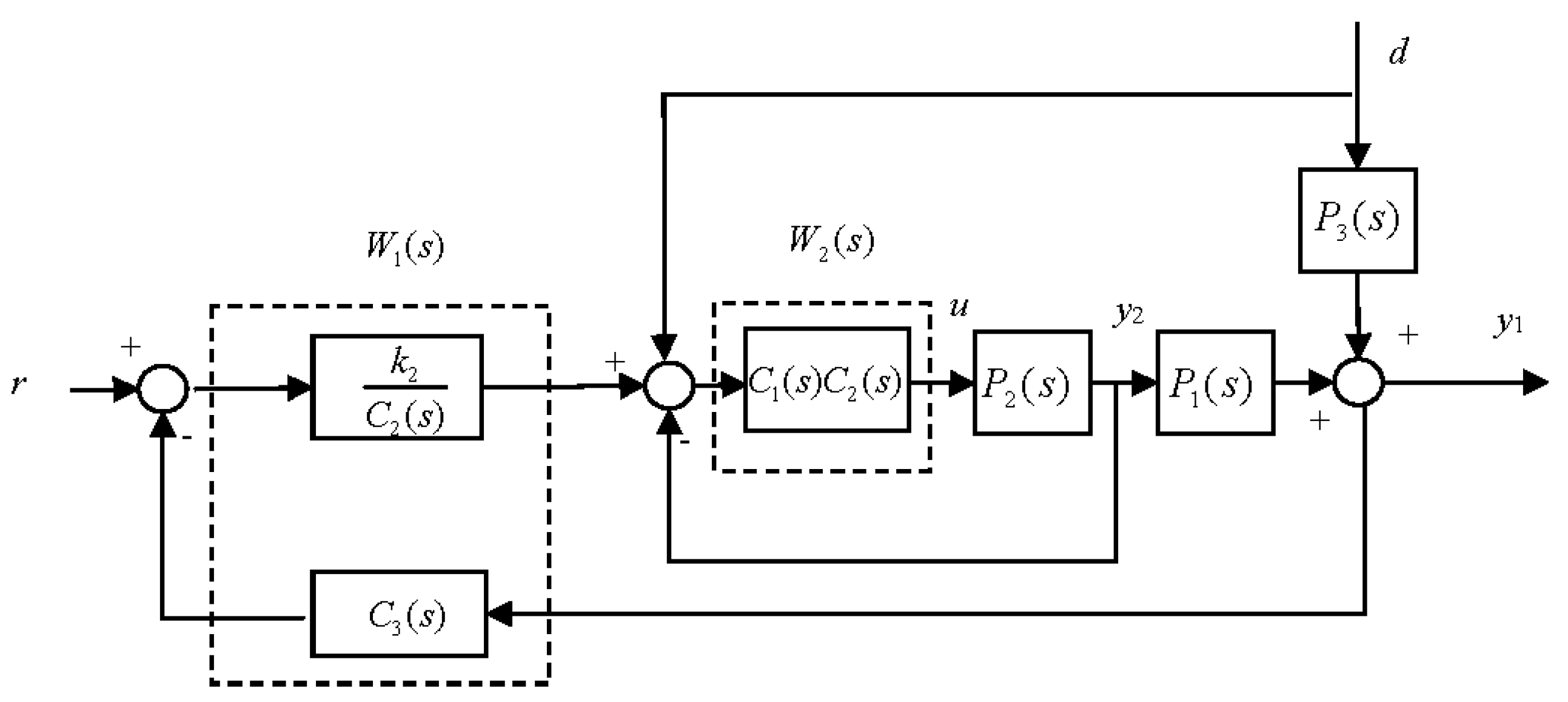
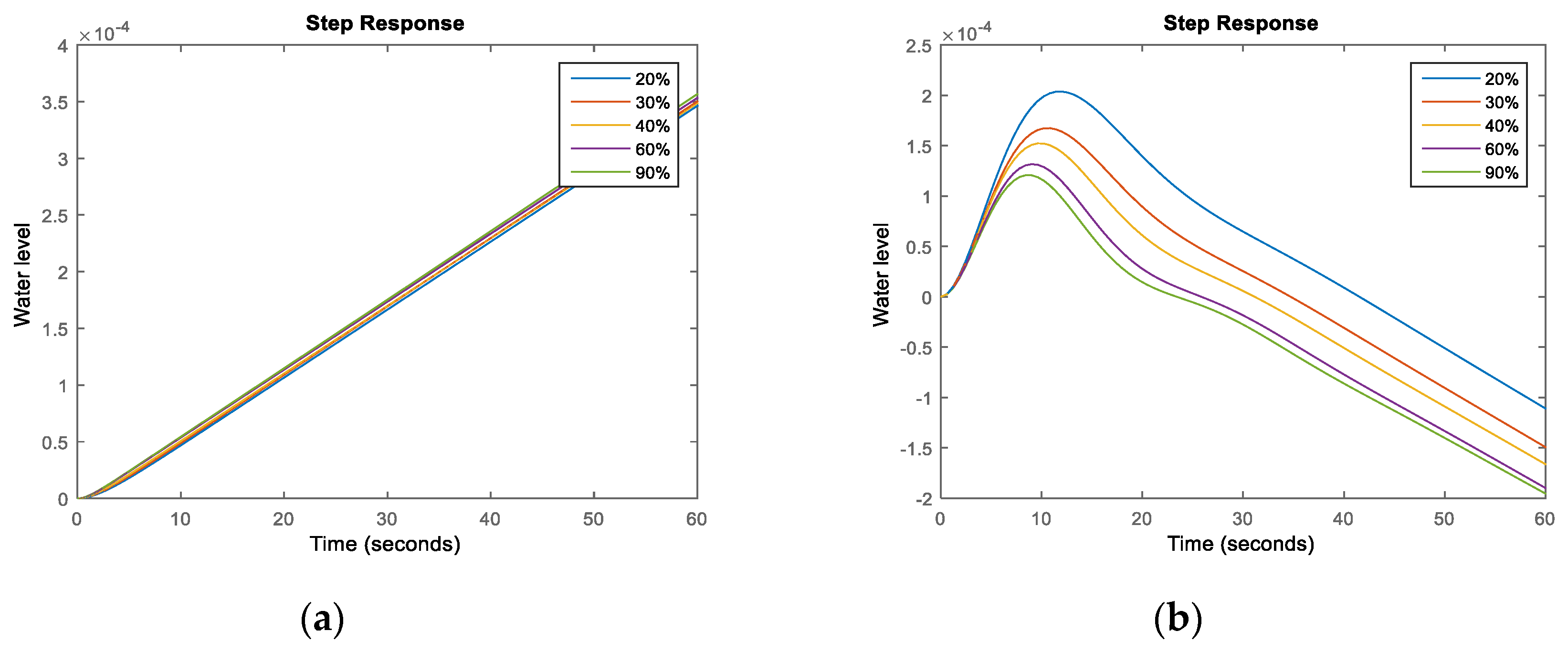
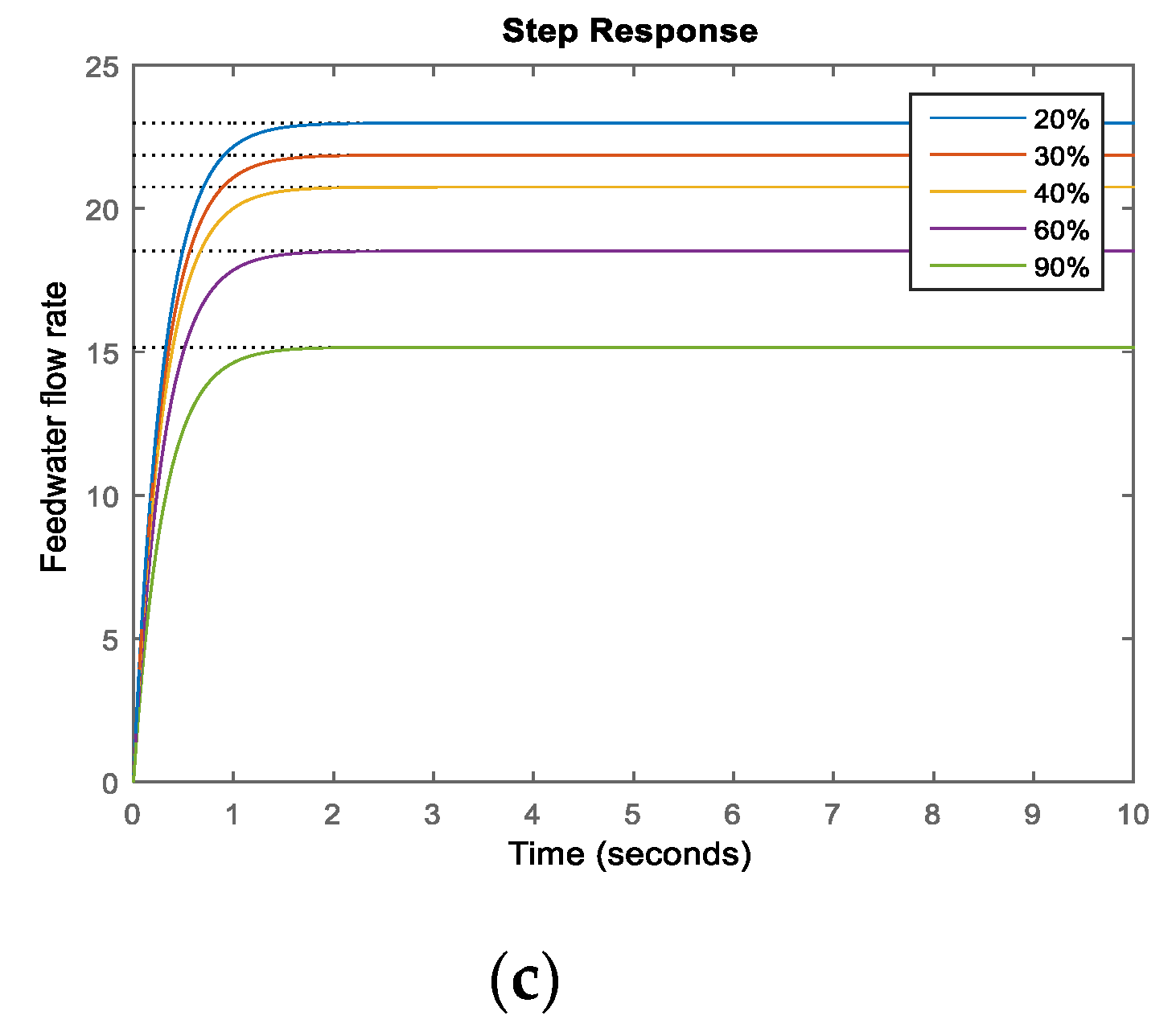
3.2. Structure Analysis of Water Level Control System
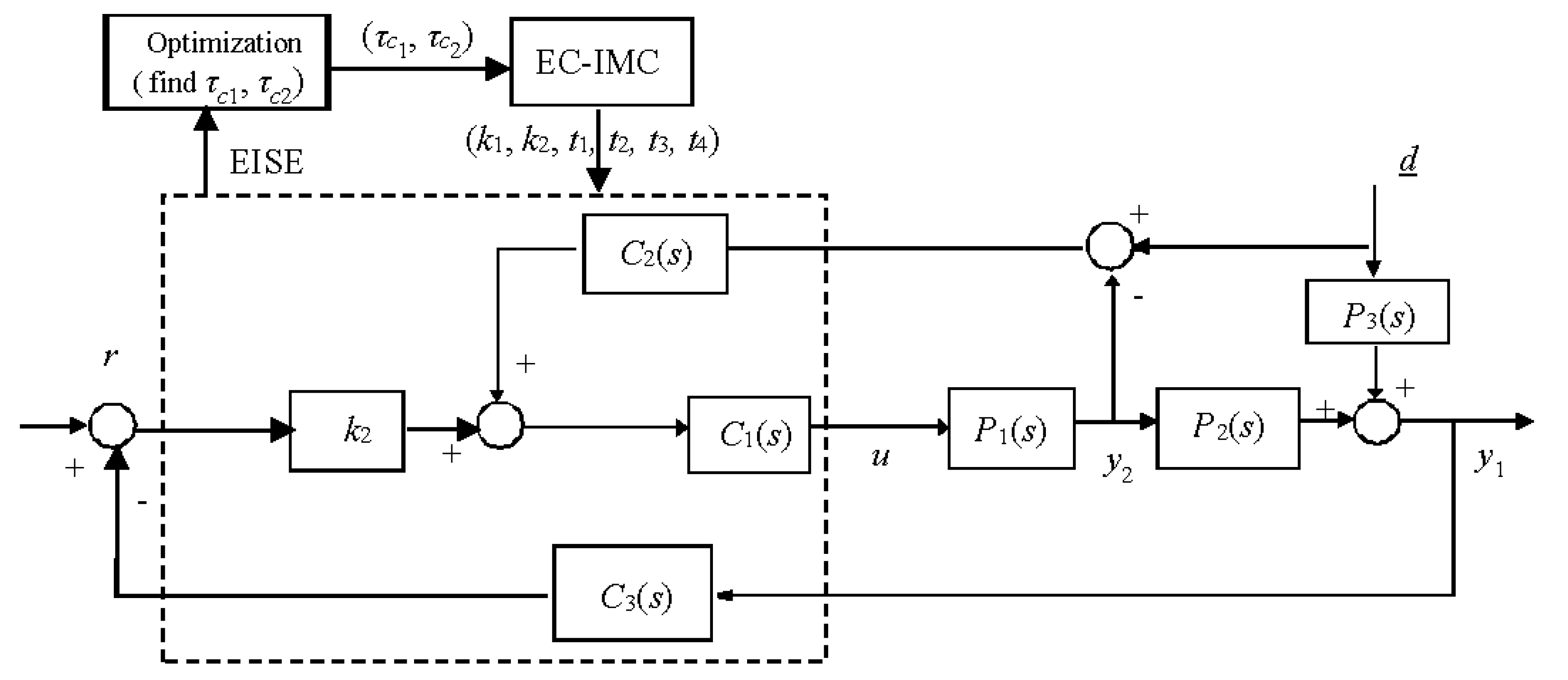
3.3. Equivalent-Cascade IMC-PID Tuning Method
- Step 1.
- Designing an equivalent secondary controller
- Step 2.
- Designing of an equivalent primary controller
- Step 3.
- By using Equation (5), controller parameters of the AP1000 water level control system are obtained as follows:
3.4. Summary
- Step 1.
- The operating power level is discretized by 10% from 20% to 100% and the linearized model of nuclear SG at each power level is identified;
- Step 2.
- Using the equivalent-cascade IMC-PID tuning method, local controller parameters at each power level are obtained based on the linearized model;
- Step 3.
- Piecewise linear function is utilized to construct a gain-scheduling module of controller parameters, in which the scheduling variable is the operating power level.
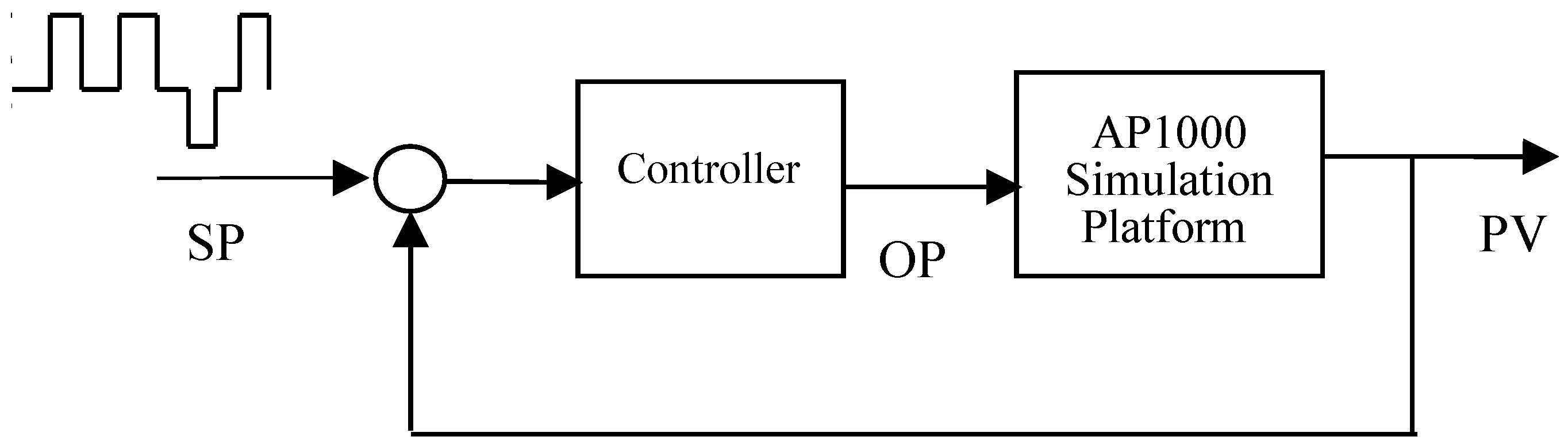
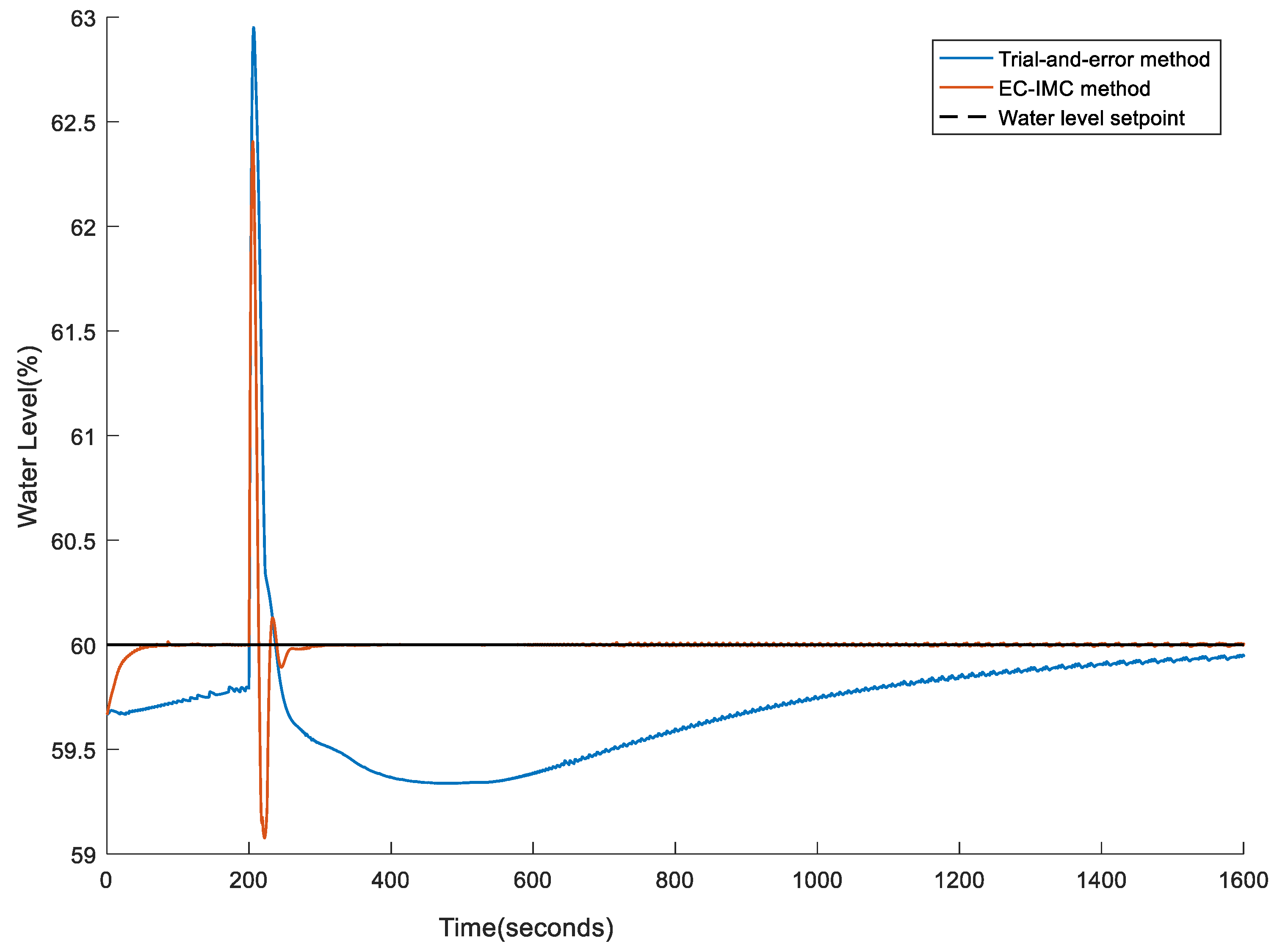
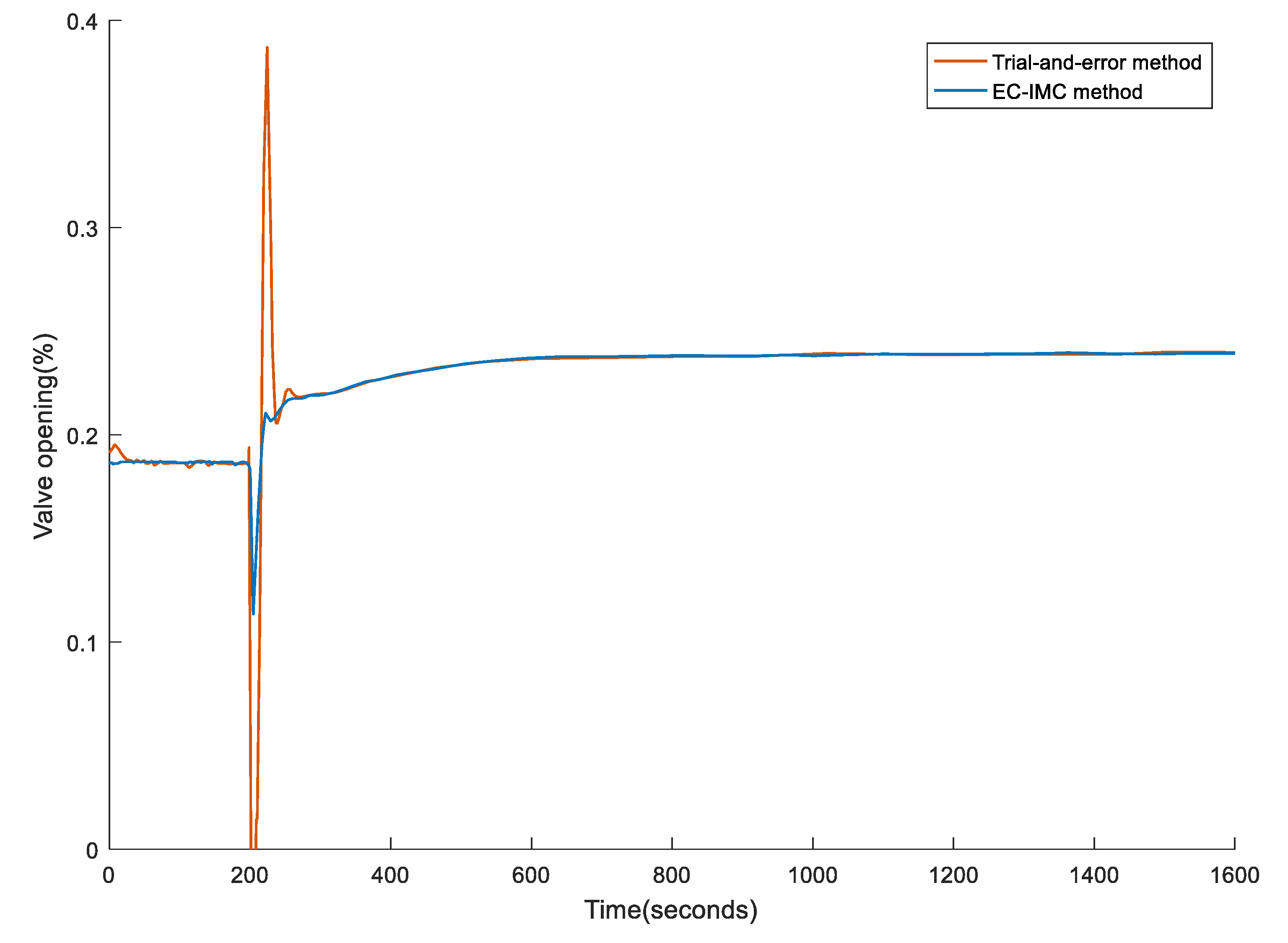
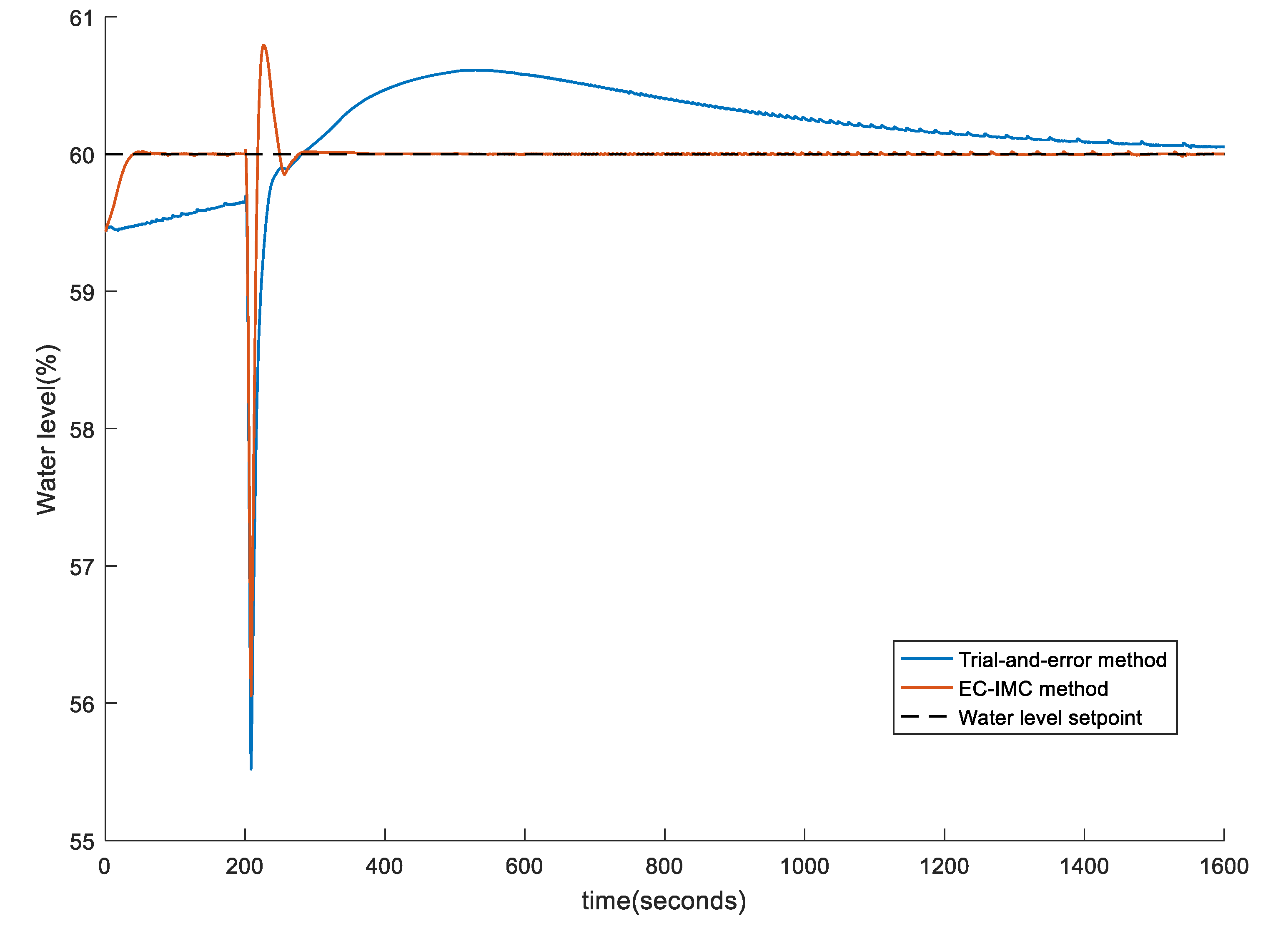
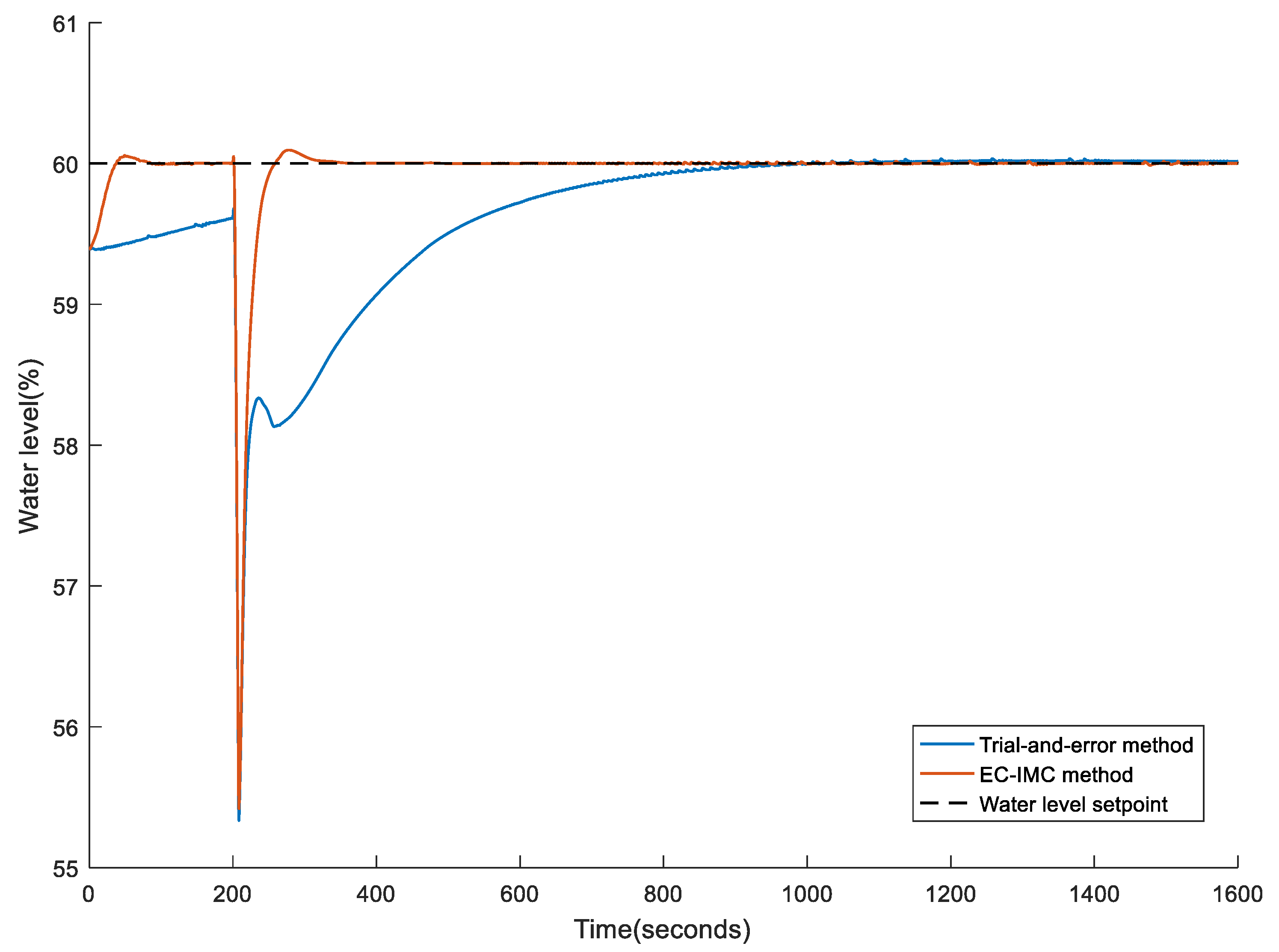
4. Experiment Result
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, J.S.; Song, H.B.; Yan, S.J.; Sun, J.; Zhao, F.Y. Development of a simulation platform for dynamic simulation and control studies of AP1000 nuclear steam supply system. Ann. Nucl. Energy 2015, 85, 704–716. [Google Scholar]
- Kothare, M.V.; Mettler, B.; Morari, M.; Bendotti, P. Level control in the steam generator of a nuclear power plant. IEEE Trans. Control Syst. Technol. 2000, 8, 55–69. [Google Scholar] [CrossRef]
- Fang, F.; Xiong, Y. Event-driven-based water level control for nuclear steam generators. IEEE Trans. Ind. Electron. 2014, 61, 5480–5489. [Google Scholar] [CrossRef]
- Akkawi, M.; Jiang, J. An inverse control-based set-point function for steam generator level in nuclear power plants. IEEE Trans. Nucl. Sci. 2011, 58, 3291–3304. [Google Scholar] [CrossRef]
- Parlos, A.G.; Rais, O.T. Nonlinear control of U-tube steam generators via H∞ control. Control Eng. Pract. 2000, 8, 921–936. [Google Scholar] [CrossRef]
- Na, M.G.; Sim, Y.R. Design of an adaptive predictive controller for Steam Generators. IEEE Trans. Nucl. Sci. 2003, 50, 186–193. [Google Scholar]
- Amin, F.; Mehrdad, B. Adaptive critic-based neurofuzzy controller for the steam generator water level. IEEE Trans. Nucl. Sci. 2008, 55, 1678–1685. [Google Scholar]
- Ansarifar, G.R.; Davilu, H.; Talebi, H.A. Gain scheduled dynamic sliding mode control for nuclear steam generators. Prog. Nucl. Energy 2011, 53, 651–663. [Google Scholar] [CrossRef]
- Safarzadeh, O.; Khaki-Sedigh, A.; Shirani, A.S. Identification and robust water level control of horizontal steam generators using quantitative feedback theory. Energy Convers. Manag. 2011, 52, 3103–3111. [Google Scholar] [CrossRef]
- Wei, L.; Fang, F.; Shi, Y. Adaptive backstepping-based composite nonlinear feedback water level control for the nuclear U-tube steam generator. IEEE Trans. Control Syst. Technol. 2014, 22, 369–377. [Google Scholar] [CrossRef]
- Carli, R.; Dotoli, M.A. A distributed control algorithm for waterfilling of networked control systems via consensus. IEEE Contr. Syst. Mag. 2017, 1, 334–339. [Google Scholar] [CrossRef]
- He, P.; Li, M.S.; Zhao, L.; Venkatesh, B.; Li, H.W. Water-filling exact solutions for load balancing of smart power grid systems. IEEE Trans. Smart Grid 2018, 9, 1397–1407. [Google Scholar] [CrossRef]
- Liu, X.; Jiang, D.; Lee, K.Y. Quasi-min-max fuzzy MPC of UTSG water level based on off-line invariant set. IEEE Trans. Nucl. Sci. 2015, 62, 2266–2272. [Google Scholar] [CrossRef]
- Ansarifar, G.R. Control of the nuclear steam generators using adaptive dynamic sliding mode method based on the nonlinear model. Ann. Nucl. Energy 2016, 88, 280–300. [Google Scholar] [CrossRef]
- Astrom, K.J.; Hagglund, T. PID Controllers: Theory, Design and Tuning; Instrument Society of America: Research Triangle Park, NC, USA, 1995. [Google Scholar]
- Schulz, T.L. Westinghouse AP1000 advanced passive plant. Nucl. Eng. Des. 2006, 236, 1547–1557. [Google Scholar] [CrossRef] [Green Version]
- Matzie, R.A. AP1000 will meet the challenges of near-term deployment. Nucl. Eng. Des. 2008, 238, 1856–1862. [Google Scholar] [CrossRef]
- Irving, E.; Miossec, C.; Tassart, J. Towards efficient full automatic operation of the PWR steam generator with water level adaptive control. In Boiler Dynamics and Control in Nuclear Power Stations; Thomas Telford Publishing: London, UK, 1980. [Google Scholar]
- Sun, H.H. Generation III Nuclear Power Technology AP1000; China Electric Power Press: Beijing, China, 2010. [Google Scholar]
- Rivera, D.E.; Morari, M.; Skogestad, S. Internal model control. 4. PID controller design. Ind. Eng. Chem. Res. 1986, 25, 252–265. [Google Scholar] [CrossRef]
- Morari, M.; Zafiriou, E. Robust Process Control; Prentice-Hall: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Chien, I.-L.; Fruehauf, P.S. Consider IMC tuning to improve controller performance. Chem. Eng. Prog. 1990, 86, 33–41. [Google Scholar]
- Seborg, D.E.; Edgar, T.F.; Mellichamp, D.A.; Doyle, F.J.D., III. Process Dynamics and Control; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2011. [Google Scholar]
- Skogestad, S. Simple analytic rules for model reduction and PID controller tuning. J. Process Control 2003, 13, 291–309. [Google Scholar] [CrossRef] [Green Version]
- Chen, D.; Seborg, D. PI/PID controller design on direct synthesis and disturbance rejection. Ind. Eng. Chem. Res. 2002, 41, 4807–4822. [Google Scholar] [CrossRef]
- Pai, N.S.; Chang, S.C.; Huang, C.T. Tuning PI/PID controllers for integrating processes with deadtime and inverse response by simple calculations. J. Process Control 2010, 20, 726–733. [Google Scholar] [CrossRef]
- Nocedal, J.; Wright, S.J. Numerical Optimization; Springer: New York, NY, USA, 2006. [Google Scholar]
- Rugh, W.J.; Shamma, J.S. Research on gain scheduling. Automatica 2000, 36, 1401–1425. [Google Scholar] [CrossRef]
- Zhu, Y.C. Multivariable System Identification for Process Control; Elsevier: London, UK, 2001. [Google Scholar]



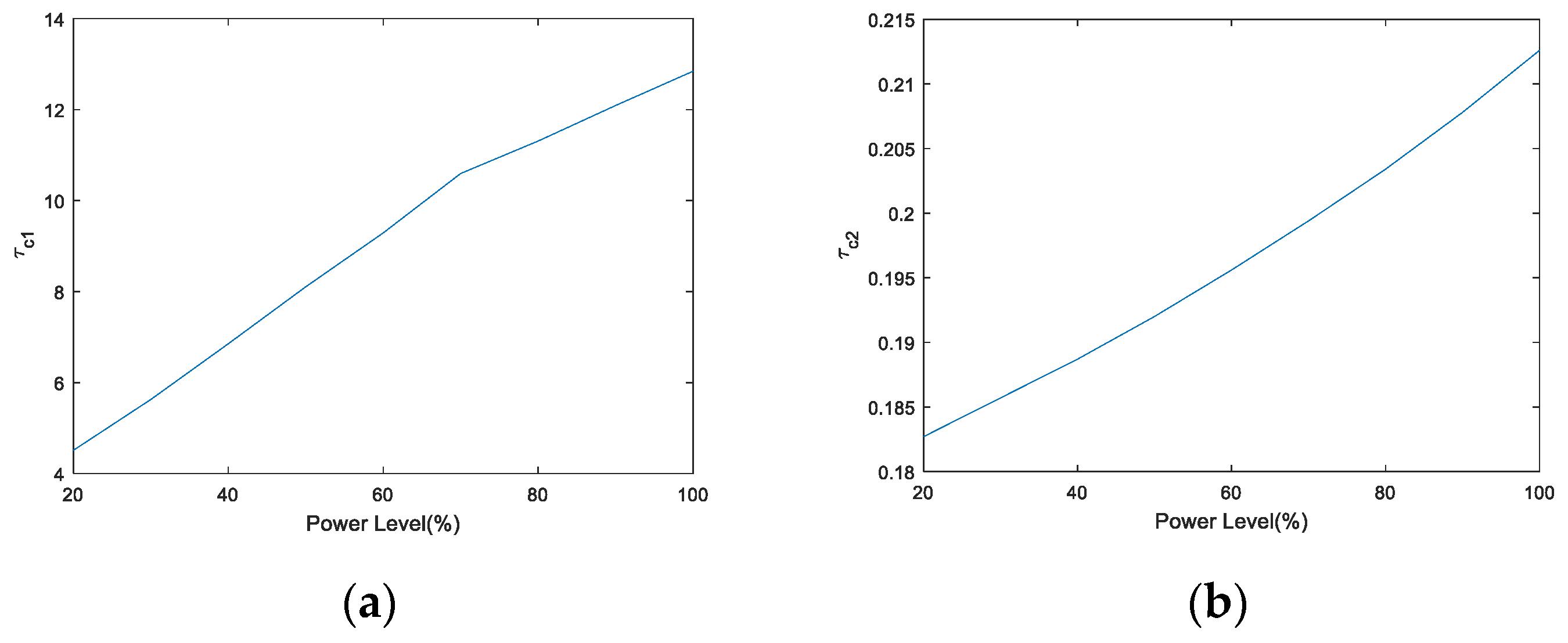

| Case | Model | Controller | Kc | ti | td |
|---|---|---|---|---|---|
| A | |||||
| B | |||||
| C |
| Power | k1 | k2 | t1 | t2 | t3 | t4 | ||
|---|---|---|---|---|---|---|---|---|
| 20% | 4.5101 | 0.1827 | 1.4846 | 5.4187 | 0.3000 | 1.4376 | 9.1116 | 0.9112 |
| 30% | 5.6275 | 0.1857 | 1.5352 | 3.5098 | 0.3000 | 1.4391 | 11.3479 | 1.1348 |
| 40% | 6.8527 | 0.1887 | 1.5922 | 2.3823 | 0.3000 | 1.4406 | 13.7997 | 1.3800 |
| 50% | 8.1047 | 0.1920 | 1.6538 | 1.7115 | 0.3000 | 1.4423 | 16.3055 | 1.6305 |
| 60% | 9.2895 | 0.1956 | 1.7213 | 1.3078 | 0.3000 | 1.4441 | 18.6767 | 1.8677 |
| 70% | 10.5954 | 0.1994 | 1.7973 | 1.0088 | 0.3000 | 1.4460 | 21.2904 | 2.1290 |
| 80% | 11.3089 | 0.2034 | 1.8823 | 0.8875 | 0.3000 | 1.4480 | 22.7195 | 2.2720 |
| 90% | 12.0898 | 0.2078 | 1.9786 | 0.7784 | 0.3000 | 1.4502 | 24.2834 | 2.4283 |
| 100% | 12.8437 | 0.2126 | 2.0877 | 0.6912 | 0.3000 | 1.4526 | 25.7937 | 2.5794 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, Z.; Fan, Q.; Zhao, J. Gain-Scheduled Equivalent-Cascade IMC Tuning Method for Water Level Control System of Nuclear Steam Generator. Processes 2020, 8, 1160. https://doi.org/10.3390/pr8091160
Xu Z, Fan Q, Zhao J. Gain-Scheduled Equivalent-Cascade IMC Tuning Method for Water Level Control System of Nuclear Steam Generator. Processes. 2020; 8(9):1160. https://doi.org/10.3390/pr8091160
Chicago/Turabian StyleXu, Zuhua, Qingli Fan, and Jun Zhao. 2020. "Gain-Scheduled Equivalent-Cascade IMC Tuning Method for Water Level Control System of Nuclear Steam Generator" Processes 8, no. 9: 1160. https://doi.org/10.3390/pr8091160





