Numerical Analyses of Heterogeneous CLC Reaction and Transport Processes in Large Oxygen Carrier Particles
Abstract
1. Introduction
2. The Numerical Methods and the Physical Models
2.1. Numerical Methods
2.2. The Geometrical Model and Boundary Conditions
3. Results and Discussion
3.1. Characteristics of Heterogeneous Reaction and Conjugate Transports of a Single Large OC Particle
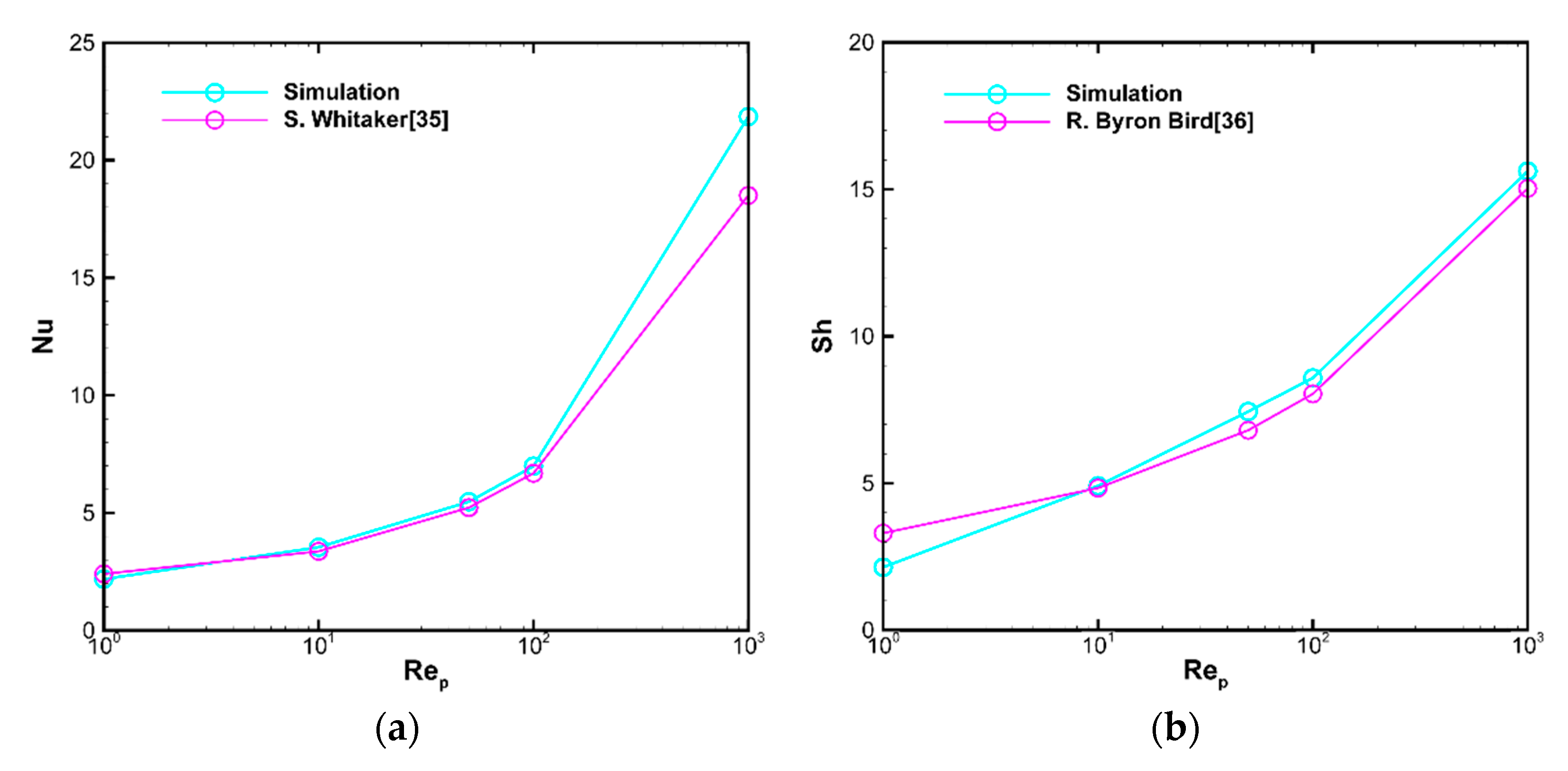
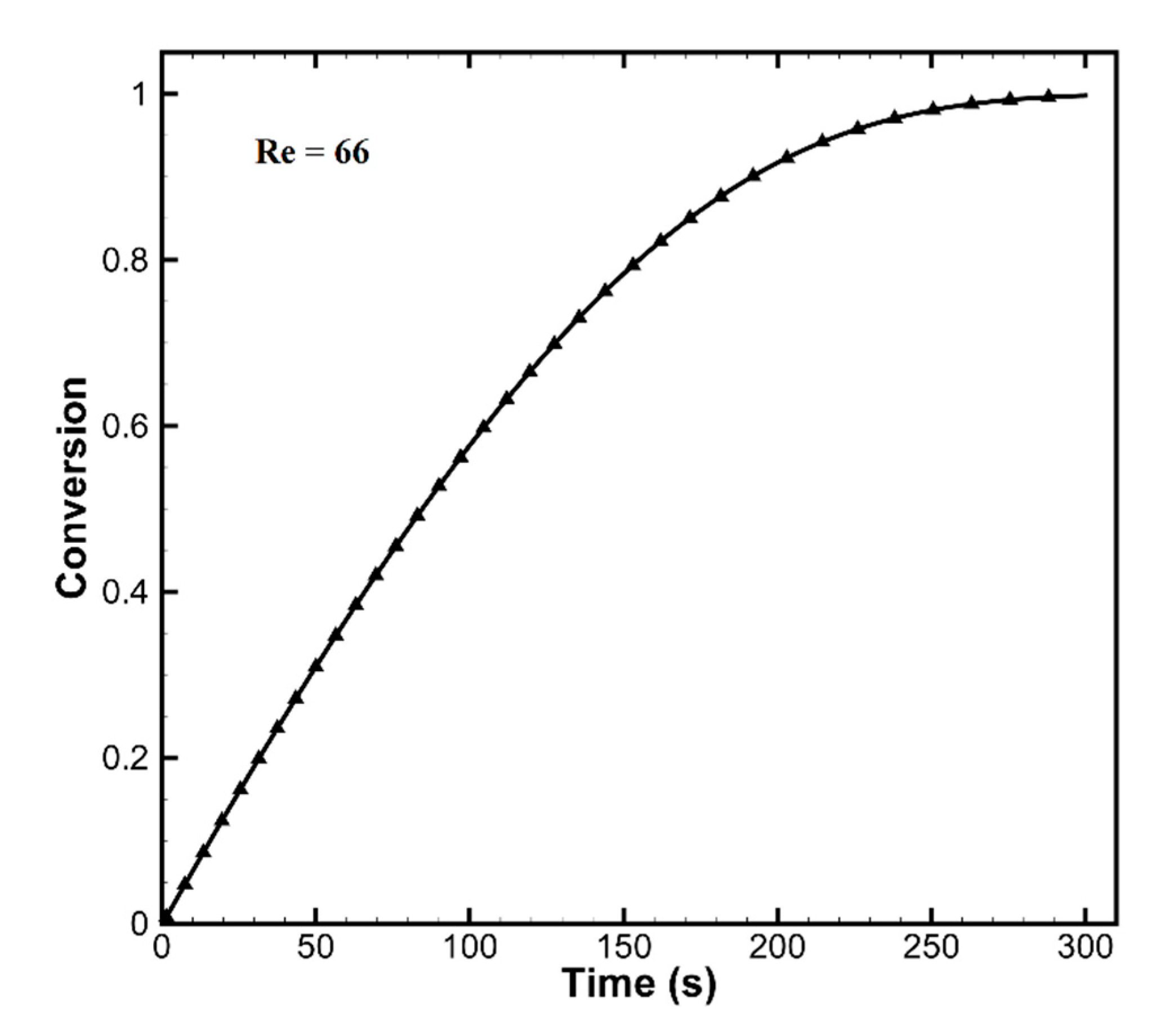
3.1.1. Validation of Numerical Methods
3.1.2. Effects of the External Convection
3.1.3. Effects of OC Particle Properties
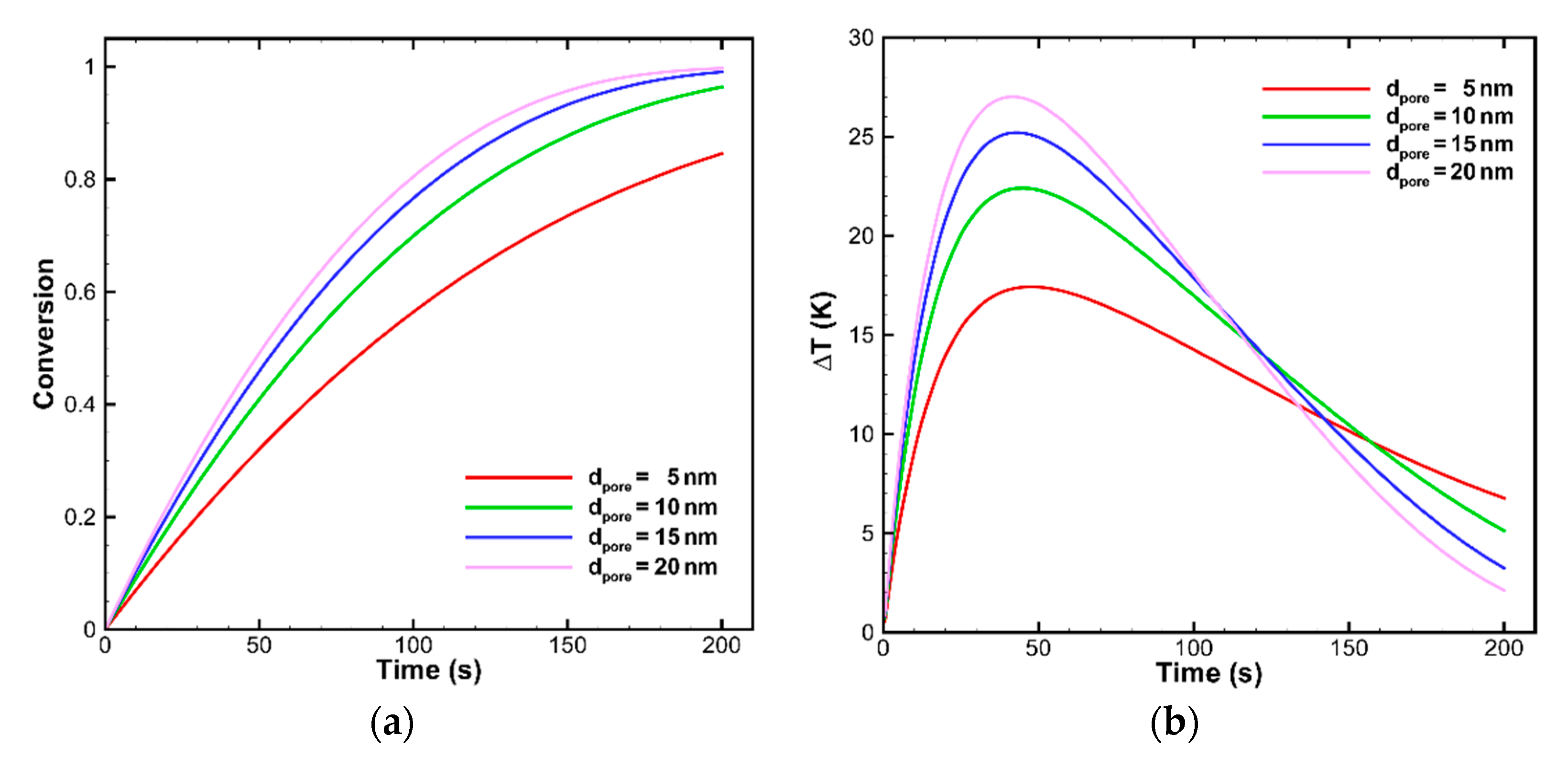
Internal Pore Size of OC Particles
Oxygen Carrier Load
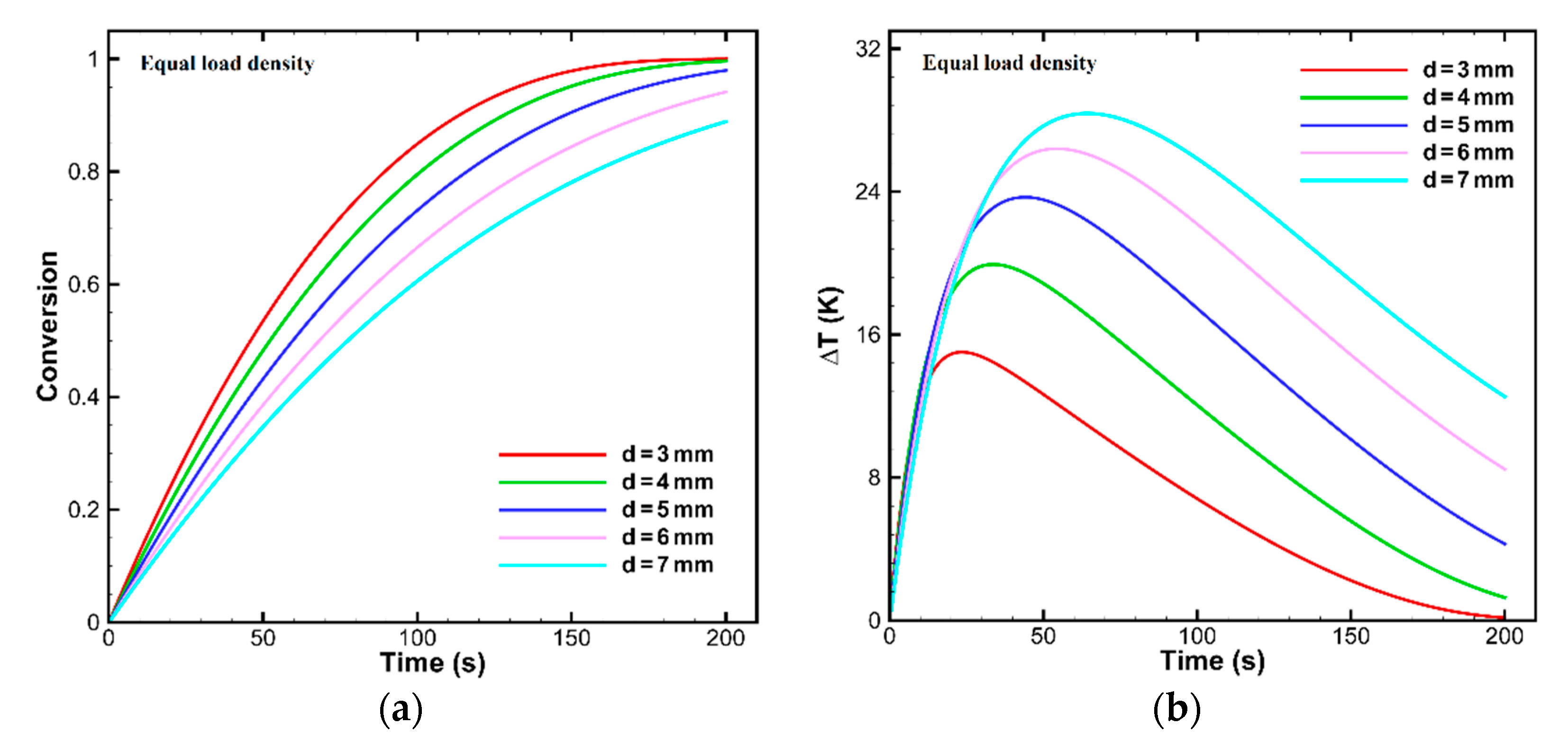
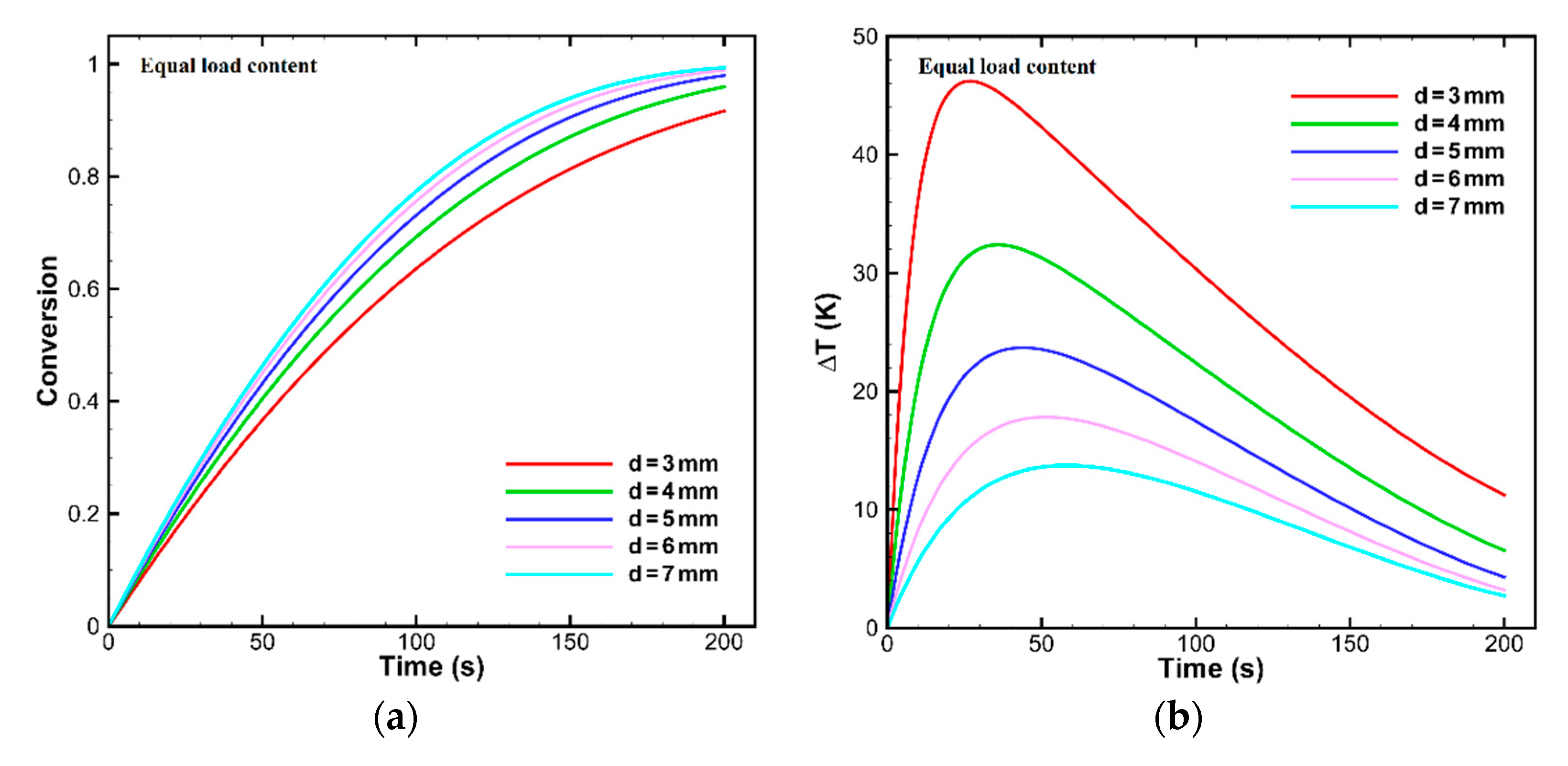
OC Particle Sizes
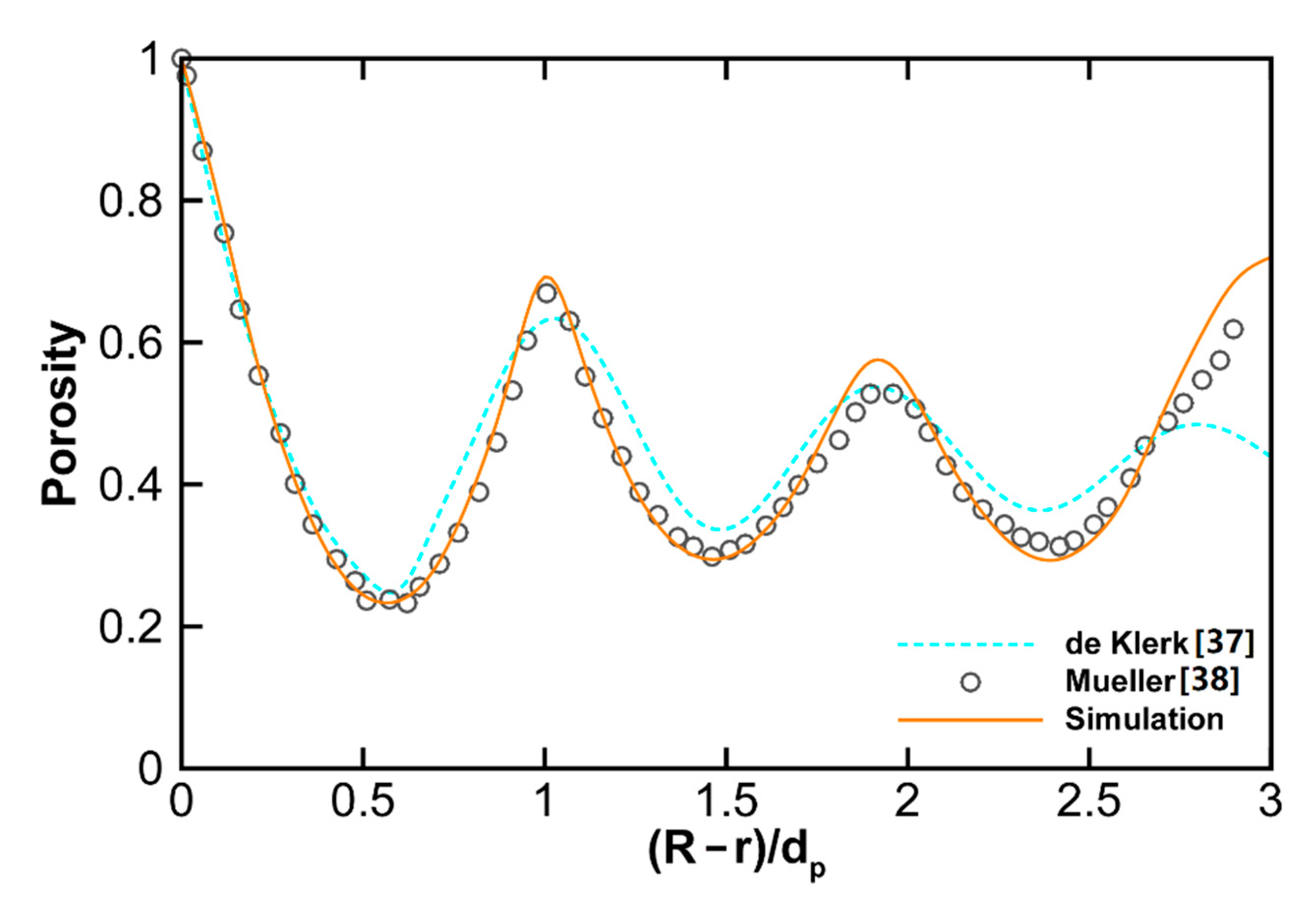
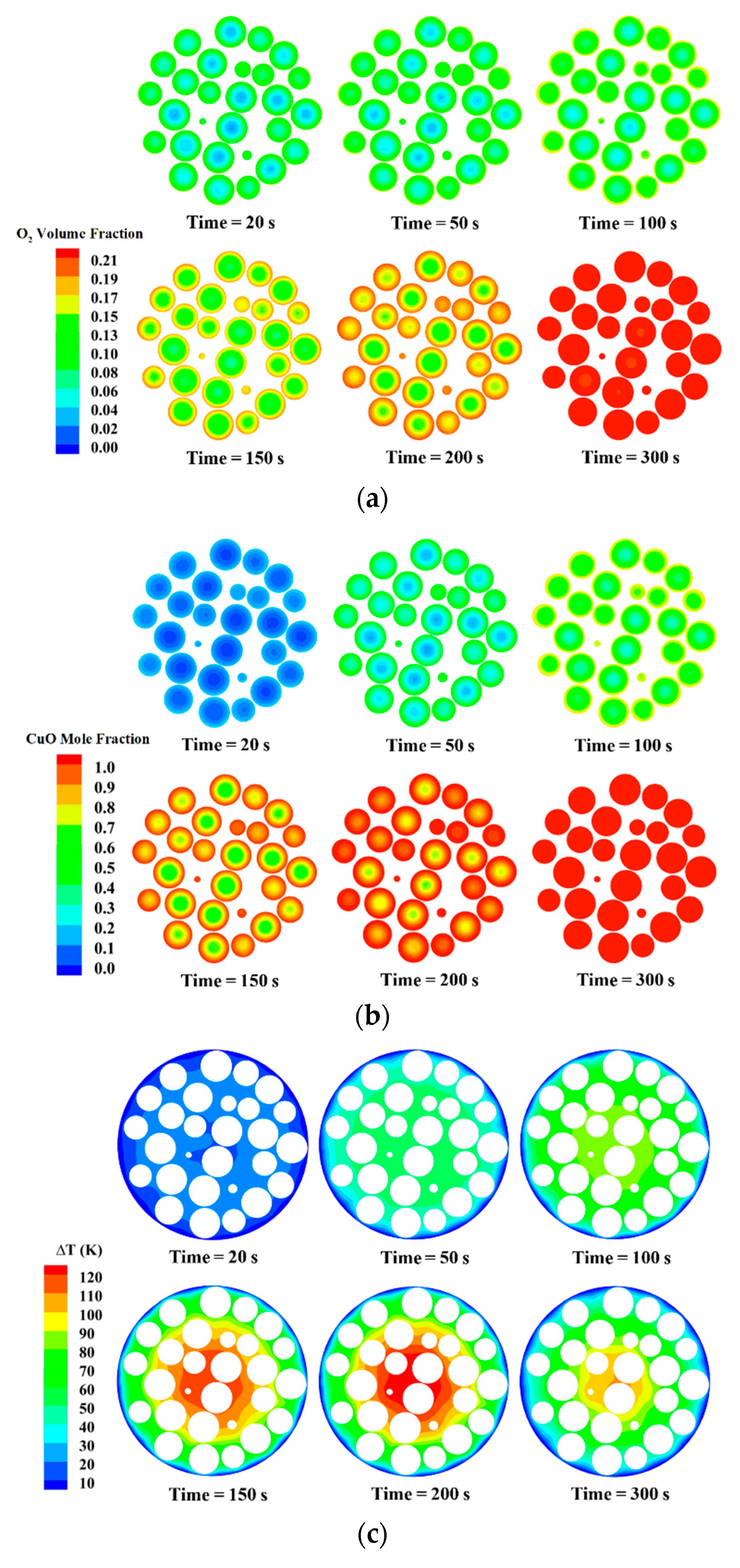
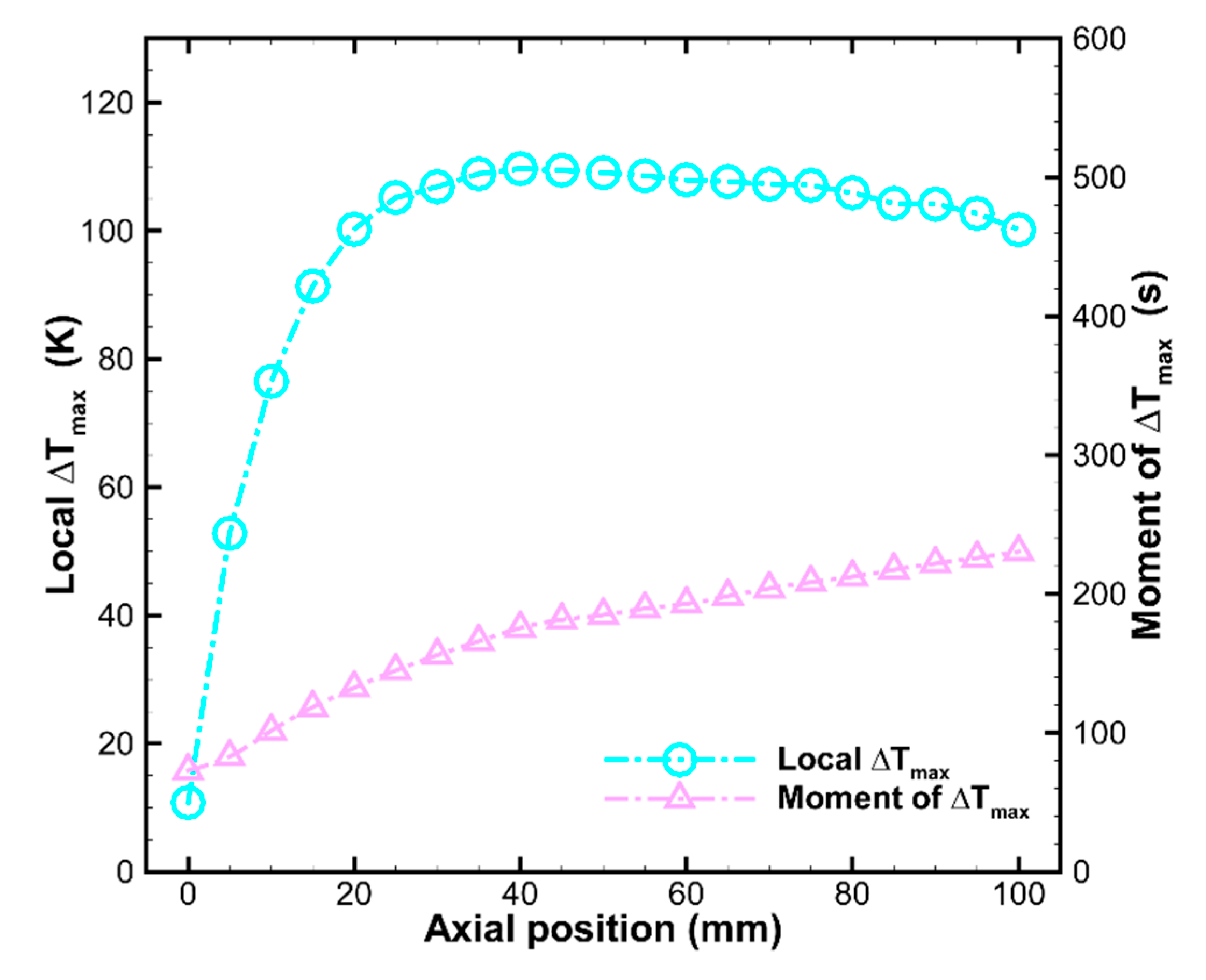
3.2. The Reaction and Transport Characteristics in a Random Packed Bed
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Latin letters | |
| Cg | gas concentration, mol/m3 |
| Cp | specific heat, J/(kg K) |
| Cs | solid concentration in surface, mol/m2 |
| DKnud | Knudsen diffusivity, m2/s |
| Dm | molecular diffusivity, m2/s |
| dpore | particle pore size, nm |
| Eact | activation energy kJ/mol |
| J | mass diffusion flux, kg m−2 s−1 |
| k0 | pre-expontential factor, 1/s |
| ks | chemical kinetic constant, m/s |
| n | gas rate exponent, dimensionless |
| Nu | Nusselt number, dimensionless |
| Pr | Prandtl number, dimensionless |
| Rep | particle Reynolds number, dimensionless |
| Rg | gas contant, J mol−1 K−1 |
| Rs | reaction rate, mol/(m3 s) |
| Sc | Schmidt number, dimensionless |
| Sh | Sherwood number, dimensionless |
| Sv | surface to volume of oxygen carrier, m2/m3 |
| ν | dynamic viscosity, Pa s |
| Xs | solid conversion, dimensionless |
| Greek letters | |
| α | stoichiometric number, dimensionless |
| β | temperature exponent, dimensionless |
| ε | particle porosity, dimensionless |
| η | simplified grain model function |
| λ | thermal conductivity, W/(m2 K) |
| μ | kinematic viscosity, m2/s |
| ρ | density, kg/m3 |
| υ | velocity, m/s |
| Φ | oxygen carrier load, kmol/m3 |
References
- Lyngfelt, A.; Leckner, B.; Mattisson, T. A fluidized-bed combustion process with inherent CO2 separation: Application of chemical-looping combustion. Chem. Eng. Sci. 2001, 56, 3101–3113. [Google Scholar] [CrossRef]
- Kronberger, B.; Johansson, E.; Loffer, G.; Mattisson, T.; Lyngfelt, A.; Hofbauer, H. A two-compartment fluidized bed reactor for CO2 capture by chemical-looping combustion. Chem. Eng. Technol. 2004, 27, 1318–1326. [Google Scholar] [CrossRef]
- De Diego, L.F.; Garcia-Labiano, F.; Gayan, P.; Romeo, J.C.; Palacios, J.L.; Adánez, J. Operation of a 10 kWth chemical-looping combustor during 200 h with a CuO-Al2O3 oxygen carrier. Fuel 2007, 86, 1036–1045. [Google Scholar] [CrossRef]
- Abad, A.; Adánez, J.; Garcia-Labiano, F.; de Diego, L.F.; Gayá, P. Modeling of the chemical-looping combustion of methane using a Cu-based oxygen-carrier. Combust. Flame 2010, 157, 602–615. [Google Scholar] [CrossRef]
- Noorman, S.; van Sint Annaland, M.; Kuipers, J. Experimental validation of packed bed chemical-looping combustion. Chem. Eng. Sci. 2010, 65, 92–97. [Google Scholar]
- Guo, X.; Sun, Y.; Li, R.; Yang, F. Experimental investigations on temperature variation and inhomogeneity in a packed bed CLC reactor of large particles and low aspect ratio. Chem. Eng. Sci. 2014, 107, 266–276. [Google Scholar] [CrossRef]
- Noorman, S.; van Sint Annaland, M.; Kuipers, H. Packed bed reactor technology for chemical-looping combustion. Ind. Eng. Chem. Res. 2007, 46, 4212–4220. [Google Scholar]
- Noorman, S.; Gallucci, F.; van Sint Annaland, M.; Kuipers, J.A.M. Experimental investigation of chemical-looping combustion in packed beds: A parametric study. Ind. Eng. Chem. Res. 2011, 50, 1968–1980. [Google Scholar]
- Noorman, S.; Gallucci, F.; van Sint Annaland, M.; Kuipers, J.A.M. A theoretical investigation of CLC in packed beds. Part 2: Reactor model. Chem. Eng. J. 2011, 167, 369–376. [Google Scholar] [CrossRef]
- Ocone, R. Transport phenomena in packed bed reactor technology for chemical looping combustion. Chem. Eng. Res. Des. 2012, 90, 1625–1631. [Google Scholar]
- Hamers, H.P.; Gallucci, F.; Cobden, P.D.; Kimball, E.; van Sint Annaland, M. CLC in packed beds using syngas and CuO/Al2O3: Model description and experimental validation. Appl. Energy 2014, 119, 163–172. [Google Scholar] [CrossRef]
- Porrazzo, R.; White, G.; Ocone, R. Aspen Plus simulations of fluidised beds for chemical looping combustion. Fuel 2014, 136, 46–56. [Google Scholar] [CrossRef]
- Tijani, M.M.; Mostafavi, E.; Mahinpey, N. Process simulation and thermodynamic analysis of a chemical looping combustion system using methane as fuel and NiO as the oxygen carrier in a moving-bed reactor. Chem. Eng. Process. 2019, 144, 107636. [Google Scholar] [CrossRef]
- Dixon, A.G.; Nijemeisland, M. CFD as a Design Tool for Fixed-Bed Reactors. Ind. Eng. Chem. Res. 2001, 40, 5246–5254. [Google Scholar]
- Jafari, A.; Zamankhan, P.; Mousavi, S.M.; Pietarinen, K. Modeling and CFD simulation of flow behavior and dispersivity through randomly packed bed reactors. Chem. Eng. J. 2008, 144, 476–482. [Google Scholar] [CrossRef]
- Eppinger, T.; Seidler, K.; Kraume, M. DEM-CFD simulations of fixed bed reactors with small tube to particle diameter ratios. Chem. Eng. J. 2011, 166, 324–331. [Google Scholar]
- Behnam, M.; Dixon, A.G.; Nijemeisland, M.; Stitt, E.H. A new approach to fixed bed radial heat transfer modeling using velocity fields from computational fluid dynamics simulations. Ind. Eng. Chem. Res. 2013, 52, 15244–15261. [Google Scholar] [CrossRef]
- Dong, Y.; Sosna, B.; Korup, O.; Rosowski, F.; Horn, R. Investigation of radial heat transfer in a fixed-bed reactor: CFD simulations and profile measurements. Chem. Eng. J. 2017, 317, 204–214. [Google Scholar] [CrossRef]
- Dixon, A.G.; Ertan Taskin, M.; Hugh Stitt, E.; Nijemeisland, M. 3D CFD simulations of steam reforming with resolved intraparticle reaction and gradients. Chem. Eng. Sci. 2007, 62, 4963–4966. [Google Scholar]
- Wehinger, G.D.; Eppinger, T.; Kraume, M. Evaluating catalytic fixed-bed reactors for dry reforming of methane with detailed CFD. Chem. Ing. Tec. 2015, 87, 734–745. [Google Scholar]
- Dong, Y.; Geske, M.; Korup, O. What happens in a catalytic fixed-bed reactor for n-butane oxidation to maleic anhydride? Insights from spatial profile measurements and particle resolved CFD simulations. Chem. Eng. J. 2018, 350, 799–811. [Google Scholar] [CrossRef]
- Zhang, M.; Dong, H.; Geng, Z. A particle-resolved CFD model coupling reaction-diffusion inside fixed-bed reactor. Adv. Powder Technol. 2019, 30, 1226–1238. [Google Scholar]
- Khakpoor, N.; Mostafavi, E.; Mahinpey, N.; De la Hoz Siegler, H. Oxygen transport capacity and kinetic study of ilmenite ores for methane chemical-looping combustion. Energy 2019, 169, 329–337. [Google Scholar]
- Guo, X.; Zhu, Z. CFD based modeling on chemical looping combustion in a packed bed reactor. Chem. Eng. Sci. 2015, 138, 303–314. [Google Scholar] [CrossRef]
- Georgakis, C.; Chang, C.W.; Szekely, J. A changing grain size model for gas-solid reactions. Chem. Eng. Sci. 1979, 34, 1071–1075. [Google Scholar]
- Garcia-Labiano, F.; De Diego, L.F.; Adanez, J.; Abad, A.; Gayán, P. Temperature variations in the oxygen carrier particles during their reduction and oxidation in a chemical-looping combustion system. Chem. Eng. Sci. 2005, 60, 851–862. [Google Scholar] [CrossRef]
- Guo, X.; Dai, R. Numerical simulation of flow and heat transfer in a random packed bed. Particuology 2010, 8, 293–299. [Google Scholar] [CrossRef]
- Noorman, S.; Gallucci, F.; van Sint Annaland, M.; Kuipers, H.J.A.M. Experimental investigation of a CuO/Al2O3 oxygen carrier for chemical-looping combustion. Ind. Eng. Chem. Res. 2010, 49, 9720–9728. [Google Scholar]
- ANSYS. Fluent Theory Guide; ANSYS Inc.: Canonsburg, PA, USA, 2012. [Google Scholar]
- Noorman, S.; Gallucci, F.; van Sint Annaland, M.; Kuipers, J.A.M. A theoretical investigation of CLC in packed beds. Part 1: Particle model. Chem. Eng. J. 2011, 167, 297–307. [Google Scholar] [CrossRef]
- Zeng, S.; Hunt, A.; Greif, R. Mean free path and apparent thermal conductivity of a gas in a porous medium. J. Heat Transf. 1995, 117, 758–761. [Google Scholar] [CrossRef]
- Fuller, E.N.; Schettler, P.D.; Giddings, J.C. New method for prediction of binary gas-phase diffusion coefficients. Ind. Eng. Chem. 1966, 58, 18–27. [Google Scholar] [CrossRef]
- Van den Aarsen, F.G. Fluidised Bed Wood Gasifier: Performance and Modelling. Ph.D. Thesis, University of Twente, Enschede, The Netherlands, 1985. [Google Scholar]
- Partopour, B.; Dixon, A.G. An integrated workflow for resolved-particle packed bed models with complex particle shapes. Powder Technol. 2017, 322, 258–272. [Google Scholar] [CrossRef]
- Whitaker, S. Forced convection heat transfer correlations for flow in pipes, past flat plates, single cylinders, single spheres, and for flow in packed beds and tube bundles. AIChE J. 1972, 18, 361–371. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena, 2nd ed.; Wiley: New York, NY, USA, 2002; pp. 676–687. [Google Scholar]
- De Klerk, A. Voidage variation in packed beds at small column to particle diameter ratio. AIChE J. 2003, 49, 2022–2029. [Google Scholar] [CrossRef]
- Mueller, G.E. Numerically packing spheres in cylinders. Powder Technol. 2005, 159, 105–110. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Process. 1952, 48, 89–94. [Google Scholar]








| Kinetic Parameters | Symbol | CH4 | O2 |
|---|---|---|---|
| Rate exponent | n | 0.6 | 1 |
| Pre-exponential factor | k0 | 0.0099 | 0.0047 |
| Activation energy | Eact | 60 | 15 |
| Parameters | Symbol | Value |
|---|---|---|
| Reynolds number | Rep, - | 100 |
| Operating temperature | T, K | 873 |
| Internal pore size | dpore, nm | 12 |
| OC particle size | d, mm | 5 |
| Oxygen carrier load | Φ, kmol/m3 | 1.88 |
| Parameters | Symbol | Value |
|---|---|---|
| Reynolds number | Rep, - | 1, 10, 50, 100, 1000 |
| Internal pore size | dpore, nm | 5, 10, 15, 20 |
| OC particle size | d, mm | 3, 4, 5, 6, 7 |
| Oxygen carrier load | Φ, kmol/m3 | 1.5, 2.0, 2.5 |
| Parameters | Value |
|---|---|
| Base size, mm | 3, 4, 5 |
| Surface size | 8% of base size |
| Surface grow rate | 1.5 |
| Boundary layers | 2 |
| Thickness of the layers | 2% of base size |
| Reactor Dimensions | Symbol | Value |
|---|---|---|
| Tube diameter | D, mm | 30 |
| Particle diameter | d, mm | 5 |
| Packing height | x, mm | 100 |
| Particle properties | ||
| Average density | ρ, kg/m3 | 1496 |
| Specific heat | Cp, J/(kg·K) | 1147 |
| Thermal conductivity | λs, W/(m·K) | 0.341 |
| Particle porosity | ε, - | 0.18 |
| Internal pore size | dpore, nm | 12 |
| Initial Cu load | Φ, kmol/m3 | 1.88 |
| Operation conditions | ||
| Inlet temperature | T, K | 873 |
| Inlet O2 volume fraction | Yoxygen, % | 21 |
| Reynolds number | Rep, - | 66 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huo, G.; Guo, X. Numerical Analyses of Heterogeneous CLC Reaction and Transport Processes in Large Oxygen Carrier Particles. Processes 2021, 9, 125. https://doi.org/10.3390/pr9010125
Huo G, Guo X. Numerical Analyses of Heterogeneous CLC Reaction and Transport Processes in Large Oxygen Carrier Particles. Processes. 2021; 9(1):125. https://doi.org/10.3390/pr9010125
Chicago/Turabian StyleHuo, Guanping, and Xueyan Guo. 2021. "Numerical Analyses of Heterogeneous CLC Reaction and Transport Processes in Large Oxygen Carrier Particles" Processes 9, no. 1: 125. https://doi.org/10.3390/pr9010125
APA StyleHuo, G., & Guo, X. (2021). Numerical Analyses of Heterogeneous CLC Reaction and Transport Processes in Large Oxygen Carrier Particles. Processes, 9(1), 125. https://doi.org/10.3390/pr9010125





