Multi-Objective Coordinated Optimal Allocation of DG and EVCSs Based on the V2G Mode

Abstract

With the vigorous promotion of new energy sources and the development of vehicle-to-grid (V2G) technology, the influence of the V2G mode should be considered in the joint optimal allocation of Distributed Generation (DG) and electric vehicle charging stations (EVCSs). The timing characteristics of the intermittent output of DG, conventional demand for load, and charging load of the electric vehicle (EV) are considered, as is its participation in grid interaction to examine the construction of typical scenarios and the EV cluster dispatching strategy. From the perspective of comprehensively planning the coordination of the distribution network, a DG-EVCSs bi-level joint planning model is established under the peak and valley price mechanism, with the sub-objectives of obtaining a comprehensive profit and high quality of voltage, curbing system load fluctuations, and satisfactorily charging the EV. An improved harmony particle swarm optimization algorithm is proposed to solve the bi-level model. The proposed method was tested on the IEEE-33 and the PG&E-69 (Pacific Gas and Electric Company) bus distribution systems, and the results show that the optimized configuration model that considers the V2G mode can improve the overall performance of the planning scheme, promote the use of clean energy, smoothen the load fluctuations of the system, and improve the quality of voltage and charging satisfaction of EV users.

1. Introduction

With increasing concerns about environmental pollution and the use of fossil fuels for energy, a growing number of applications are being proposed for distributed generation (DG) and electric vehicles (EV) [1,2,3,4]. The interconnection between large-scale distributed generation and electric vehicle charging stations (EVCSs) is expected to have an impact on the security and reliability of the distribution network. Therefore, the optimal allocation of DG and EVCSs has received extensive research attention in recent years.

The authors of [5] proposed a mixed-integer linear programming model to solve the problems of planning electrical distribution systems and allocating EVCSs, and proposed a robust optimal allocation scheme for the latter. An analytical expression was proposed in [6] for the evaluation of DG site selection schemes and involved transforming the random mixed-integer nonlinear programming problem into a deterministic integer problem to solve the DG programming problem. The work in [7] proposed an optimal allocation model of EVCSs, with the goal of minimizing the total annual cost of the charging system. In view of the complexity of the optimization model, a two-step equivalence method was proposed to transform the optimization model into a mixed-integer second-order cone programming problem through equivalence and precision relaxation. The capacity of the EVCSs was determined by considering the impact of traffic flow in [8], and the charging requirements of the infrastructure were integrated into the model to evaluate the economics of candidate schemes.

The above research originated in the separate planning of DG and EVCSs, without considering the coordination between them. The joint planning of DG and EVCSs is conducive to promoting the complementarity between the time-series characteristics of the output of DG and the charging load, to realize the on-site consumption of DG by EVs and improve the permeability of DG. Based on this, the authors of [9] designed a regional EVCSs system using wind power, photovoltaic, and energy storage systems. The minimum operational cost was taken as the objective function, and support vector regression was used to predict the on-grid price and the electricity market price. A two-stage stochastic programming model of EVCSs and photovoltaics was established in [10], and a generalized Benders decomposition algorithm was proposed to solve it. The work in [11] developed a grasshopper optimization algorithm to optimize the allocation of DG and EVCSs to reduce energy loss and improve the coefficient of voltage stability of the system.

With the development of vehicle-to-grid (V2G) technology, EVs will be connected to the grid as a controllable load and a mobile energy storage device and will participate in the dispatching of the power grid. The V2G mode will have an impact on power flow, network loss, the voltage quality. However, the research in [9,10,11] did not consider the influence of the V2G mode on distribution network planning, where this is important for engineering applications [12,13].

In this paper, a bi-level optimal allocation model for DG-EVCSs is established, considering the interaction between electric vehicles and the distribution network. The k-means++ clustering algorithm is used to establish typical daily scenarios of the wind-photovoltaic load. Based on the charging model for the electric vehicle, the bi-level optimal allocation model of DG-EVCSs is established by considering the peak and valley prices. At the upper planning level, an objective function is established based on comprehensive profit, voltage quality, the fluctuation in system load, and EV charging satisfaction. At the lower EV cluster scheduling level, the power flow is optimized in each typical scenario through the orderly management of the charging and discharging of the EV. The improved harmony particle swarm optimization (I-HSPSO) algorithm is proposed to solve the bi-level programming model. Finally, simulations based on the IEEE-33 bus distribution network and the PG and E-69bus distribution network are used to verify the effectiveness of the proposed model and its solution.

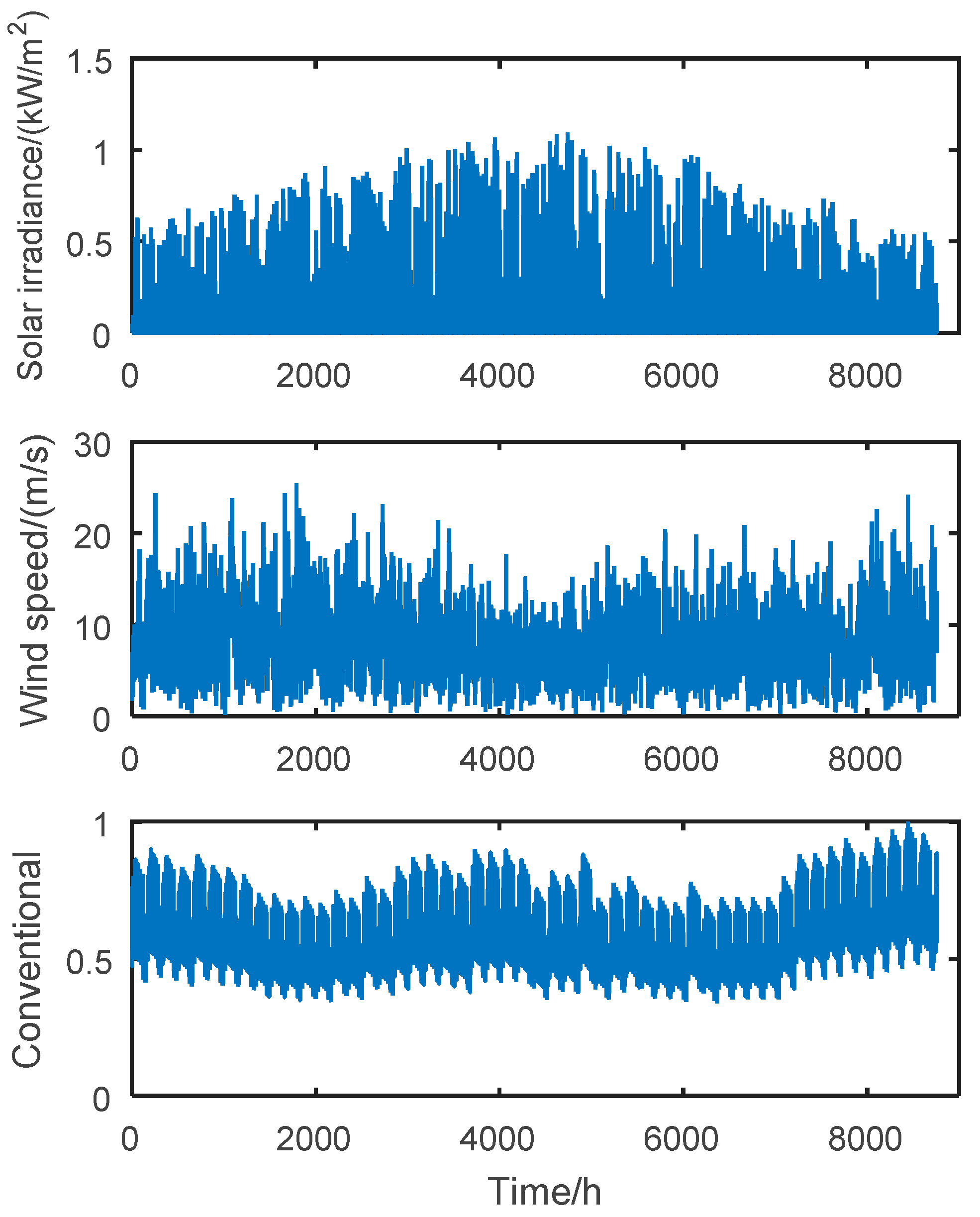
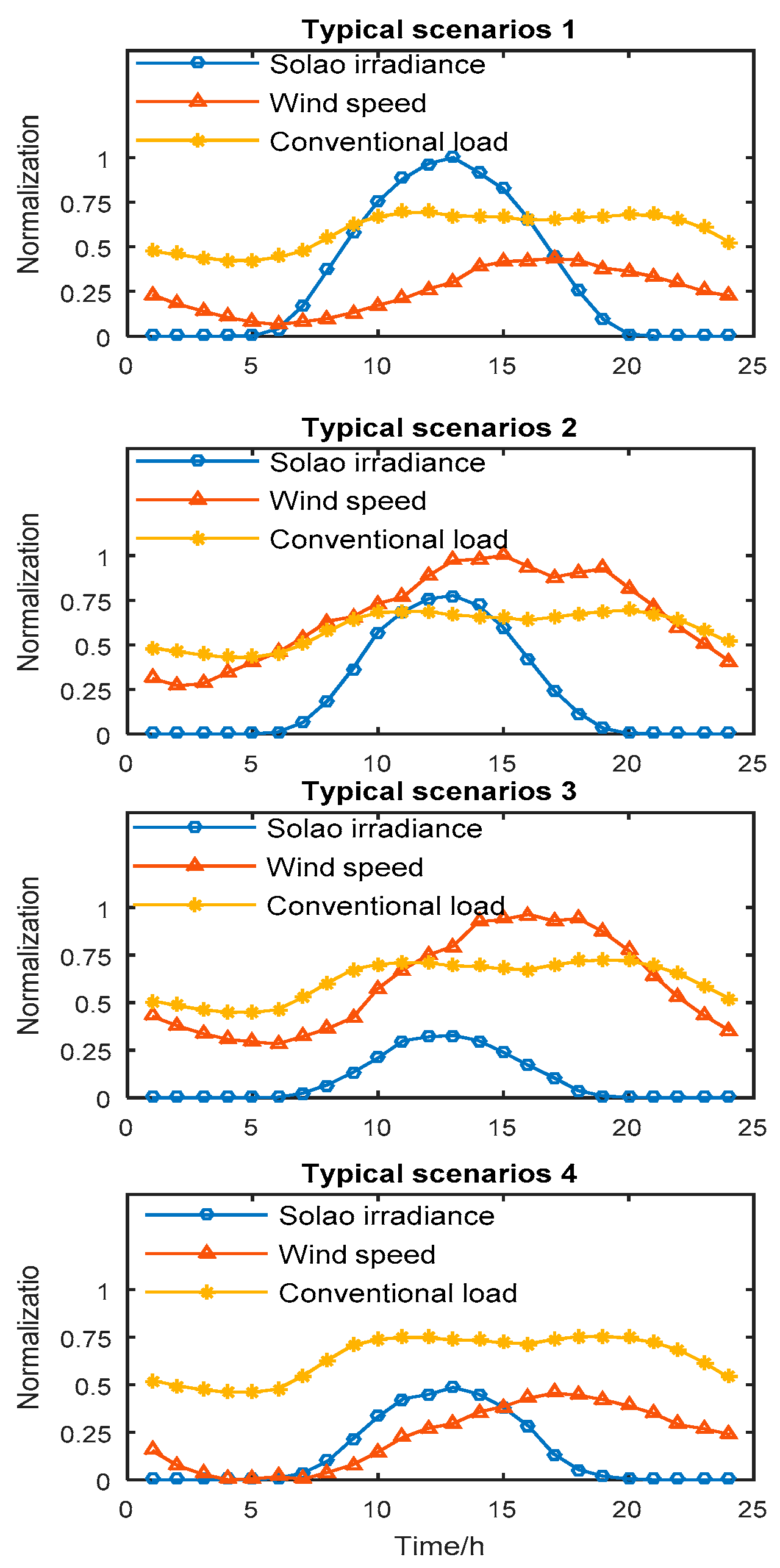
2. Construction of Typical Wind-Photovoltaic Load Scenarios

Distributed wind generation (DWG), photovoltaic generation (PVG), and load feature high uncertainty. The outputs of DWG and PVG are mainly affected by natural factors, such as wind speed and solar irradiance. The sampling period of wind speed is 15 s, but the period of photovoltaic and load data can only be 1 h, so all the data frequency is taken as 1 h. The wind speed, solar irradiance, and conventional demand for load for 8760 h a year in the planning area are presented in Figure 1.

It is clear from Figure 1 that the wind speed is high, and fluctuates significantly in spring and winter, and the solar irradiance in summer is clearly stronger than that in the other seasons. The conventional demand for load is higher in summer and winter. Therefore, it is necessary to consider the sequential temporal fluctuation in typical wind-photovoltaic load scenarios when planning the distribution network.

To avoid excessive calculations in the model, we use the k-means++ clustering algorithm [14] to optimize the scenario based on historical data for the planning area. Representative typical scenarios are thus extracted, and the validity of the results of clustering was verified based on the pseudo F-statistic (PFS) [15] to improve the computational efficiency of the model, while ensuring the distribution characteristics of the original scenarios.

The outputs of photovoltaic and wind power are closely related to wind speed and solar irradiance, respectively, and can be expressed as follows [16]:

$$P_{\mathrm{PV}}=\{\begin{array}{cc}{P}_{\mathrm{P}}\frac{h}{h_{\mathrm{s}}}\hfill & h\le h_{\mathrm{s}}\\ P_{\mathrm{P}}\hfill & h>h_{\mathrm{s}}\end{array},$$

(1)

where P_PV indicates the output power of PVG, P_P indicates the rated output of photovoltaic power, h and h_s, respectively, indicate the actual solar irradiance and the rated solar irradiance.

$$P_{\mathrm{DW}}=\{\begin{array}{cc}0\hfill & 0\le v<v_{\mathrm{i}}\mathrm{or}{v}_{\mathrm{o}}\le v\\ P_{\mathrm{D}}\frac{v-v_{\mathrm{i}}}{v_{\mathrm{s}}-v_{\mathrm{i}}}\hfill & v_{\mathrm{i}}\le v<v_{\mathrm{s}}\\ P_{\mathrm{D}}\hfill & v_{\mathrm{s}}\le v<v_{\mathrm{o}}\end{array},$$

(2)

where P_DW indicates the output power of DWG, P_D indicates the rated output of wind power, v indicates the actual wind speed, v_i indicates the cut-in wind speed, v₀ indicates the cut-off wind speed, and v_s indicates the rated wind speed.

3. Charging and Discharging Model of EV in V2G Mode

There are four common types of EVs: buses, taxis, commercial cars, and private cars. According to the forecasts of vehicle ownership in 2020, there were a between 784,600 to 959,900 buses, 18,776 to 2,294,800 taxis, 8,022,000 to 9,805,200 business cars, and 74,687,400 to 91,284,600 private cars in China [17].Assuming that the ratio of the number of private electric cars to the total number of private cars is 10%, and the ratio of the number of each of other types of electric vehicles to the total number of respective vehicles in their categories is 15%, we can estimate that the ratio of number of electric buses, electric taxis, electric business cars, and electric private cars is 1: 2.4: 10.2: 63.5.

The charging mode of the EV is influenced by the initial state of charge (SOC), charging mode, charging power, and charging time. In addition, the demands for charging different types of EV are different. For example, the power consumption per 100 km of private electric vehicles is 20~30 kW·h and the battery capacity is 32 kW·h. The rechargeable period for private electric vehicles can be divided into a rest period at night and a work period during the day, namely 18:00~7:00 h and 8:00~17:00 h, respectively, and the charging power is 7 kW. The initial durations of charging for the two periods respectively satisfy the normal distributions N (9, 0.52) and N (19, 1.52). The modes and parameters of charging of the other types of electric vehicles are provided in [17].

In this paper, the Monte Carlo simulation was used to calculate the required duration of charging of the EV, which is expressed as T_f:

$$T_{\mathrm{f}}=\frac{(SO{C}_{\mathrm{e}}-SO{C}_0)}{\eta \cdot P_{\mathrm{e}}}\cdot E_{\mathrm{e}}\cdot 60,$$

(3)

where SOC_e indicates the percentage of batter capacity after charging, SOC₀ indicates the percentage before charging, η indicates the charging efficiency, P_e indicates the charging power, and E_e indicates the battery capacity.

The EV charging limit time T_lim is determined according to the chargeable period of each type of EV, and the actual EV charging time is T_cd = min (T_f, T_lim).

With large-scale EVs in parallel in the grid, grouping electric vehicles into clusters and using cluster scheduling can help reduce the difficulty of system scheduling. For large-scale EVs, the daily charging mode has a certain rule of distribution. We thus developed a cluster scheduling strategy based on the EV charging model.

To participate in the V2G process, a number of complex factors need to be considered for buses, taxis, and official vehicles including operational needs and corporate willingness, while the participation of private cars depends on the willingness of their owners. Therefore, we used private electric cars as the object of scheduling of V2G to participate in EV cluster scheduling. The other three types of electric vehicles still used the plug-and-charge disorder charging mode.

The grid-connected time of the EV T_star, required charging time T_e, and off-grid time T_end are selected as the discriminant bases for EV cluster division, and the process consists of three steps:

(1)

According to the willingness of the users, EVs can be divided into two categories: owners willing to participate in V2G and owners unwilling to participate in V2G.

(2)

The required charging time of the EV T_f for the willing-to-participate group is calculated. If T_f is less than the charging time limit T_lim, the given of EV is classed in the same cluster as the unwilling-to-participate group owing to its lack of V2G capabilities.

(3)

We cluster EVs the owners of which were willing and able to participate in V2G according to T_star, T_e, and T_end. For example, when an EV was connected to the grid from 18:00~19:00 h, the charging time was three to four h, and the off-grid time was 7:00 h the next day. Such EVs were placed in the same cluster.

The total grid-connection time of the EV is set to T_total. To avoid the loss of battery owning to frequent charging and discharging, the maximum daily discharge frequency of EVs under the V2G mode was set to one. The discharge operation was not allowed until the initial charging of the EVs was complete, and the discharge was terminated before reaching the maximum allowable discharge level. Then, secondary charging was performed according to the scheduling instructions until charging was terminated. The charging and discharging time distributions of the EV are shown in Figure 2. T_delay indicates the first delay in charging, T_delay2 indicates the delay, T_delay3 indicates the second delay, T_e and T_e2, respectively, indicate the charging and discharging times, T_e3 indicates the second charging time, and T_end indicates the off-grid time of the EV.

For different clusters of the EV, the EV cluster scheduling strategy can be formulated by setting T_delay, T_delay2, T_delay3, T_e2, and T_e3.

4. Bi-Level Optimization Model

The bi-level model is a hierarchical system optimization model, in which the upper and low levels have their own mathematical models. We use programming as the upper level and EV cluster scheduling as the lower level to build a multi-objective optimization model of DG and EV charging stations.

4.1. Mathematical Model of the Upper Level

The decision variables of the upper level planning problem are the locations and capacity of DG and EVCSs. A multi-objective optimization model is established with the objective of obtaining the maximum overall profit, optimal voltage quality, minimum fluctuations in system load, and the maximum charging satisfaction of the EV.

Comprehensive profit F₁

$$\max F_1=C_{\mathrm{SS}}+C_{\mathrm{B}}-C_{\mathrm{inv}}-C_{\mathrm{OM}}-C_{\mathrm{loss}}+C_{\mathrm{env}},$$

(4)

where C_SS indicates the profit of the distribution company, C_B indicates the subsidy from the government for renewable energy sources, C_inv indicates the investment on intermittent DG and EVCSs, C_OM indicates the maintenance fee for DG and EVCSs, C_loss indicates the cost of network loss, and C_env indicates the environmental profit due to the use of clean energy.

$$C_{\mathrm{SS}}={\displaystyle \sum _{l=1}^{k_{\mathrm{s}}}{T}_l{\displaystyle \sum _{t=1}^{24}\left(\begin{array}{l}{c}_{\mathrm{o}}(t)\cdot P_{l,t,\mathrm{L}}-c_{\mathrm{i}}(t)\cdot (P_{l,t,\mathrm{L}}-P_{l,t,\mathrm{DWG}}-P_{l,t,\mathrm{PV}}+P_{{}_{l,t,\mathrm{EV}}}^{\mathrm{c}}-P_{{}_{l,t,\mathrm{EV}}}^{\mathrm{d}})+\\ (c_{\mathrm{e}}(t)\cdot P_{{}_{l,t,\mathrm{EV}}}^{\mathrm{c}}-c_{\mathrm{f}}(t)\cdot P_{{}_{l,t,\mathrm{EV}}}^{\mathrm{d}}-c_{\mathrm{b}}\cdot P_{{}_{l,t,\mathrm{EV}}}^{\mathrm{d}})\end{array}\right)}},$$

(5)

where c_o(t), c_i(t), c_e(t), and c_f(t), respectively, indicate the sale price of electricity charged by the distribution company, the price it pays, the unit charging cost of EVCSs, and the discharge compensation coefficient at time t. k_s indicates the number of typical scenarios, T_l indicates the probability for l_th typical scenario obtaining, P_l,t,L, P_l,t,DWG and P_l,t,PV, respectively, indicate the load demand, output power of DWG, and output power of PV at time t, P_cl,t,EV and P_dl,t,EV, respectively, indicate the charging and discharging powers of the EV at time t, and c_b indicates the compensation coefficient of battery loss.

$$C_{\mathrm{B}}={\displaystyle \sum _{l=1}^{k_{\mathrm{s}}}{T}_l{\displaystyle \sum _{t=1}^{24}(c_{\mathrm{b},\mathrm{DWG}}{P}_{l,t,\mathrm{DWG}}+}}{c}_{\mathrm{b},\mathrm{PV}}{P}_{l,t,\mathrm{PV}}),$$

(6)

where c_b,DWG and c_b,PV respectively indicate unit subsidies from the government for DWG and PV.

$$C_{\mathrm{inv}}=\left({\displaystyle \sum _{j=1}^{n_{{}_{\mathrm{DWG}}}}{c}_{\mathrm{t}1}{P}_{j,\mathrm{DWG}}}+{\displaystyle \sum _{j=1}^{n_{{}_{\mathrm{PV}}}}{c}_{\mathrm{t}2}{P}_{j,\mathrm{PV}}}+{\displaystyle \sum _{j=1}^{n_{{}_{\mathrm{EV}}}}(c_g+c_{\mathrm{t}3}{P}_{j,EV})}\right)\cdot \frac{r{(1+r)}^{n_1}}{{(1+r)}^{n_1}-1},$$

(7)

where n_DWG, n_PV, and n_EV, respectively, indicate the number of candidate nodes for DWG, PVG, and EVCSs, P_j,DWG, P_j,PV, and P_j,EV, respectively, indicate the capacity for DWG, PVG, and EVCSs at node j, c_t1, c_t2, and c_t3, respectively, indicate the costs of construction of unit capacity of the DWG, PVG, and EVCSs, c_g indicates the fixed investment cost of EVCSs, r indicates the discount rate, and n₁ indicates the service life of the equipment.

$$C_{\mathrm{OM}}={\displaystyle \sum _{l=1}^{k_{\mathrm{s}}}{T}_l{\displaystyle \sum _{t=1}^{24}(c_{\mathrm{om}1}{P}_{l,t,\mathrm{DWG}}+c_{\mathrm{om}2}{P}_{l,t,\mathrm{PV}})}}+{\displaystyle \sum _{j=1}^{n_{{}_{\mathrm{EV}}}}(c_{\mathrm{om}3}{P}_{j,\mathrm{EV}})},$$

(8)

where c_om1 and c_om2 respectively indicate the unit maintenance fees for DWG and PVG, and c_om3 indicates the amortized unit maintenance fee for EVCSs.

$$C_{\mathrm{loss}}={\displaystyle \sum _{l=1}^{k_{\mathrm{s}}}{T}_l{\displaystyle \sum _{t=1}^{24}{c}_{\mathrm{o}}{P}_{l,t,\mathrm{loss}}}},$$

(9)

where P_l,t,loss indicates the system loss at time t.

$$C_{\mathrm{env}}={\displaystyle \sum _{l=1}^{k_{\mathrm{s}}}{T}_l{\displaystyle \sum _{t=1}^{24}\left((P_{l,t,\mathrm{DWG}}+P_{l,t,\mathrm{PV}}){\displaystyle \sum _{s=1}^{N_{\mathrm{env}}}{x}_s(a_s+b_s)+}\frac{P_{l,t,\mathrm{EV}}}{e_{\mathrm{EV}}}{c}_{\mathrm{co}2}\Delta \right)}},$$

(10)

where C_env indicates the social welfare of renewable energy sources and reduced emissions due to EVs, N_env indicates the types of pollutant gases, x_s, a_s, and b_s, respectively, indicate the emission levels of the sth kind of pollution gas, e_EV indicates the energy consumed by an EV over 100 miles, c_co2 indicates the CO₂ trading tax fee in the international market, and Δ indicates the difference between EVs and conventional vehicles.

Voltage quality F₂

$$\max F_2={\displaystyle \sum _{l=1}^{k_{\mathrm{s}}}\frac{T_l}{365\cdot 24}{\displaystyle \sum _{i=1}^Z{\displaystyle \sum _{t=1}^{24}\frac{(U_i(t)-U_{i\min })}{(U_{ir}-U_{i\min })}}}}\cdot \frac{(U_{i\max }-U_i(t))\left|P_i(t)\right|}{(U_{i\max }-U_{ir}){\displaystyle \sum _{j=1}^Z\left|P_j(t)\right|}},$$

(11)

where Z indicates the number of system nodes, U_ir indicates the voltage rating at node i, P_i(t) indicates the injected active power at the i-th node at time t, U_i(t) indicates the voltage of the i-th node at time t, and U_imax and U_imin, respectively, indicate the upper and lower limits of voltage at the i-th node.

System load fluctuation F₃

$$\min F_3={\displaystyle \sum _{l=1}^{k_{\mathrm{s}}}\frac{T_l}{365}\sqrt{\frac{{\displaystyle \sum _{t=1}^{24}{(P_{l,t,\mathrm{e}}-P_{l,\mathrm{ave}})}^2}}{24}}},$$

(12)

$$P_{l,t,\mathrm{e}}=P_{l,t,\mathrm{L}}+P_{l,t,\mathrm{EV}}-P_{l,t,\mathrm{DG}},$$

(13)

where P_l,t,e indicates the equivalent load of the system at time t under scenario l, and P_l,ave indicates its average load under scenario l.

Charging satisfaction of EVF₄

$$\max F_4={\displaystyle \sum _{l=1}^{k_{\mathrm{s}}}\frac{T_l}{365}\left({\alpha }_1\cdot c_{l,\mathrm{wcd}}+{\alpha }_2\cdot \frac{1}{c_{l,\mathrm{cb}}}\right)},$$

(14)

where c_l,wcd indicates the completion of charging of the EV cluster under scenario l, c_l,cb indicates the unit charging cost of the EV cluster under scenario l, and α₁ and α₂ respectively indicate the weight of complete charging and unit charging cost satisfaction.

The above four objective functions are normalized as follows:

$$f_i^{*}=\{\begin{array}{ll}{F}_i/F_i^{\max }\hfill & i=1,2,4\\ F_i^{\min }/F_i\hfill & i=3\end{array},$$

(15)

where $f_i^{*}$ indicates the normalized value of the sub-objective function F_i, and $F_i^{\max }$ and $F_i^{\min }$ indicate the optimal values of the subobjective function in the optimization process.

The multiple objective functions were aggregated into comprehensive evaluation indices maxf_U by linear weighting:

$$\max f_{\mathrm{U}}={\displaystyle \sum _{i=1}^4{w}_i\cdot f_i^{*}},$$

(16)

where w_i indicates the weight of the sub-objective function $f_i^{*}$. In this paper, the weight coefficient of the sub-objective function is determined based on the Analytic Hierarchy Process (AHP) [18].

The constraints on the upper-level optimization model are:

$$P_{\mathrm{DG}i}\le P_{{}_{\mathrm{DG}i}}^{\max },$$

(17)

$${\displaystyle \sum P_{\mathrm{DG}i}}\le P_{\mathrm{DG}}^{\max },$$

(18)

$$P_{{}_{\mathrm{EV}i}}^{\min }\le P_{\mathrm{EV}i}\le P_{{}_{\mathrm{EV}i}}^{\max },$$

(19)

where P_DGi indicates the installed capacity of DG at node i, $P_{\mathrm{DG}i}^{\max }$ indicates the installed capacity limit of DG at node i, $P_{\mathrm{DG}}^{\max }$ indicates the limit of the total installed capacity of DG in the system, P_EVi indicates the installed capacity of the EVCSs at node i, and $P_{\mathrm{EV}i}^{\max }$ and $P_{\mathrm{EV}i}^{\min }$, respectively, indicate the upper and lower limits of the installed capacity of the EVCSs at node i.

4.2. Mathematical Model of the Lower Level

Based on DG and the EVCSs planning scheme determined by the upper level, the lower layer formulates the cluster scheduling strategy for the EVs, and manages their charging and discharging in an orderly manner to achieves the optimal overall operation of the system. The objective function of the lower level can be expressed as:

$$\max f_{\mathrm{L}}=w_1\cdot f_{l,1}^{*}+w_2\cdot f_{l,2}^{*}+w_3\cdot f_{l,3}^{*}+w_4\cdot f_{l,4}^{*},$$

(20)

$$F_{l,1}=C_{l,\mathrm{S}}+C_{l,\mathrm{B}}-C_{l,\mathrm{OM}}-C_{l,\mathrm{loss}}+C_{l,\mathrm{env}},$$

(21)

$$F_{l,2}=\frac{1}{24}{\displaystyle \sum _{i=1}^Z{\displaystyle \sum _{t=1}^{24}\frac{(U_i(t)-U_{i\min })}{(U_{ir}-U_{i\min })}}}\cdot \frac{(U_{i\max }-U_i(t))\left|P_i(t)\right|}{(U_{i\max }-U_{ir}){\displaystyle \sum _{j=1}^Z\left|P_j(t)\right|}},$$

(22)

$$F_{l,3}=\sqrt{{\displaystyle \sum _{t=1}^{24}{(P_{l,t,\mathrm{e}}-P_{l,\mathrm{ave}})}^2}/24},$$

(23)

$$F_{l,4}={\alpha }_1\cdot c_{l,\mathrm{wcd}}+{\alpha }_2/c_{l,\mathrm{cb}},$$

(24)

where $f_{l,1}^{*}$, $f_{l,2}^{*}$, $f_{l,3}^{*}$, and $f_{l,4}^{*}$, respectively, indicate the normalized values of the comprehensive profit index F_l,1, the voltage quality index F_l,2, the system load fluctuation index F_l,3, and the EV charging satisfaction index F_l,4.

The constraints on the lower-level optimization model are:

$$\{\begin{array}{c}{P}_i-U_i{\displaystyle \sum _{j\in i}{U}_j(G_{ij}\cos {\theta }_{ij}+B_{ij}\sin {\theta }_{ij})=0}\\ Q_i-U_i{\displaystyle \sum _{j\in i}{U}_j(G_{ij}\sin {\theta }_{ij}-B_{ij}\cos {\theta }_{ij})=0}\end{array},$$

(25)

$$U_{i\min }\le U_i\le U_{i\max },$$

(26)

$$I_{ij}\le I_{ij}^{\max },$$

(27)

$$SO{C}_{\min }\le SOC\le SO{C}_{\max },$$

(28)

$$SO{C}_{\mathrm{end}}\le SO{C}_{\mathrm{ex}},$$

(29)

$$T_{\mathrm{delay}}+T_{\mathrm{e}}+T_{\mathrm{delay}2}+T_{\mathrm{e}2}+T_{\mathrm{delay}3}+T_{\mathrm{e}3}\le T_{\mathrm{total}},$$

(30)

where P_i and Q_i, respectively, indicate the injected active power and the injected reactive power at the i-th node, U_i and U_j, respectively, indicate the voltage at the i-th node and the j-th node, G_ij, and B_ij, respectively, indicate the conductance and susceptance between the i-th and the j-th nodes, θ_ij indicates the difference in voltage angle between the i-th and the j-th nodes; U_imax and U_imin, respectively, indicate the upper and lower limits of voltage at the i-th node, I_ij indicates the actual current through the branch ij, I_maxij indicates the maximum current through the branch ij, SOC_max and SOC_min, respectively, indicate the upper and lower limits of battery capacity, SOC_ex indicates the expected value of SOC at the end of charging, and SOC_end indicates the actual value of SOC when the EV is off the grid.

5. Optimal Solution of the Proposed Bi-Level Model

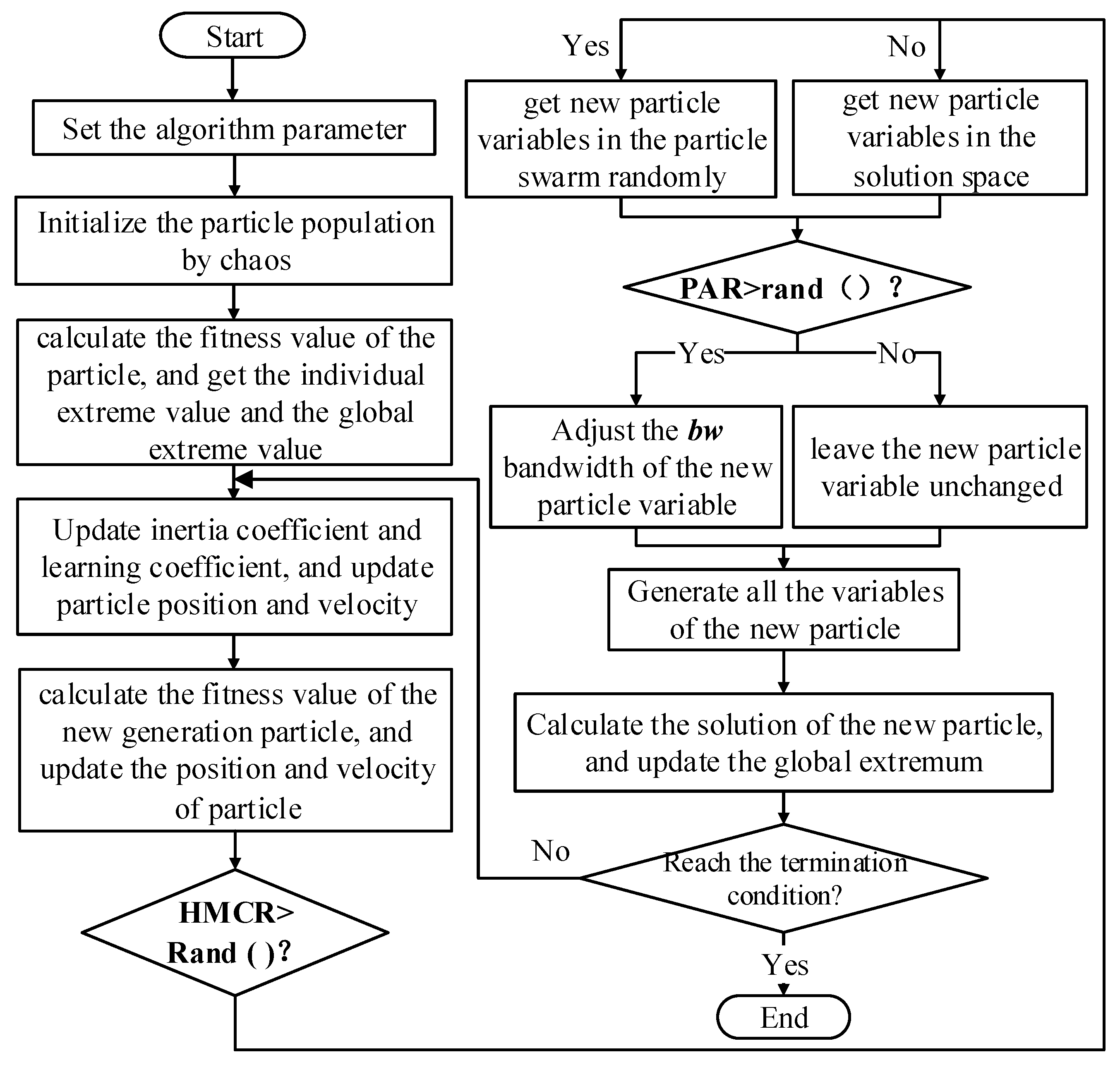
5.1. Improved Harmonic Particle Swarm Optimization

Particle swarm optimization (PSO) simulates the principle of foraging by a swarm of birds and has the advantages of simple calculation and strong directionality [19]. However, the global search ability of the PSO algorithm is poor, and it can easily fall into the local optimum in the later stage. Therefore, this paper optimizes the PSO algorithm to improve its convergence-related.

Chaos is a kind of irregular state of motion with strong nonlinearity. The initialization of the particle swarm by introducing a chaos variable is beneficial for generating a more uniform initial particle swarm. To improve the ergodic property of the initial particle in the search space, chaotic initialization is carried out on the particle swarm:

$$x_{i,j}=x_j^{\min }+(x_j^{\max }-x_j^{\min }){\chi }_{i,j},$$

(31)

$${\chi }_{i,j+1}=\lambda \cdot {\chi }_{i,j}(1-{\chi }_{i,j}),$$

(32)

where x_i,j indicates the j-dimension value of particle i, $x_j^{\max }$ and $x_j^{\min }$, respectively, indicate the upper and lower limits, x_i,j indicates the sequences of chaotic variables generated by the logistic model, the chaotic parameters λ is set to four.

Of the PSO parameters, the optimization of the inertial coefficient ω is beneficial for balancing the global and the local search capabilities of the PSO algorithm. The optimization is expressed as follows:

$$\omega =\frac{{\omega }_{\max }-{\omega }_{\min }}{2}\cdot \cos (\mathsf{\pi }\cdot t/T_{\mathrm{PSO}})+\frac{{\omega }_{\max }+{\omega }_{\min }}{2},$$

(33)

where ω_max and ω_min, respectively, indicate the upper and lower limits of the inertial coefficient, t indicates the number of iterations at the given time, and T_PSO indicates the maximum number of iterations.

The learning coefficients c₁ and c₂, respectively, reflect the self-cognition ability and social cognition ability of the particle. The optimization of the learning coefficient can strengthen the self-learning ability of the particle swarm in the initial stage to avoid falling into the local optimum, and improves its ability to learn from the optimal solution for the group to find the optimal solution:

$$\{\begin{array}{c}{c}_1=c_{1\max }+t(c_{1\min }-c_{1\max })/T_{\mathrm{PSO}}\\ c_2=c_{2\min }+t(c_{2\max }-c_{2\min })/T_{\mathrm{PSO}}\end{array},$$

(34)

The harmony search (HS) principle is introduced in this paper. Although the directivity of the HS algorithm is not strong, it has the characteristic of expanding the search range in the later stage of execution. Therefore, a novel combination harmony principle of the HS algorithm is introduced to the particle optimization process of the PSO algorithm, and the optimal particle is found within the search space with a certain probability in each iteration to improve the performance of the algorithm in terms of global search.

The flow of calculation of the improved harmony search particle swarm optimization (I-HSPSO) is shown in Figure 3.

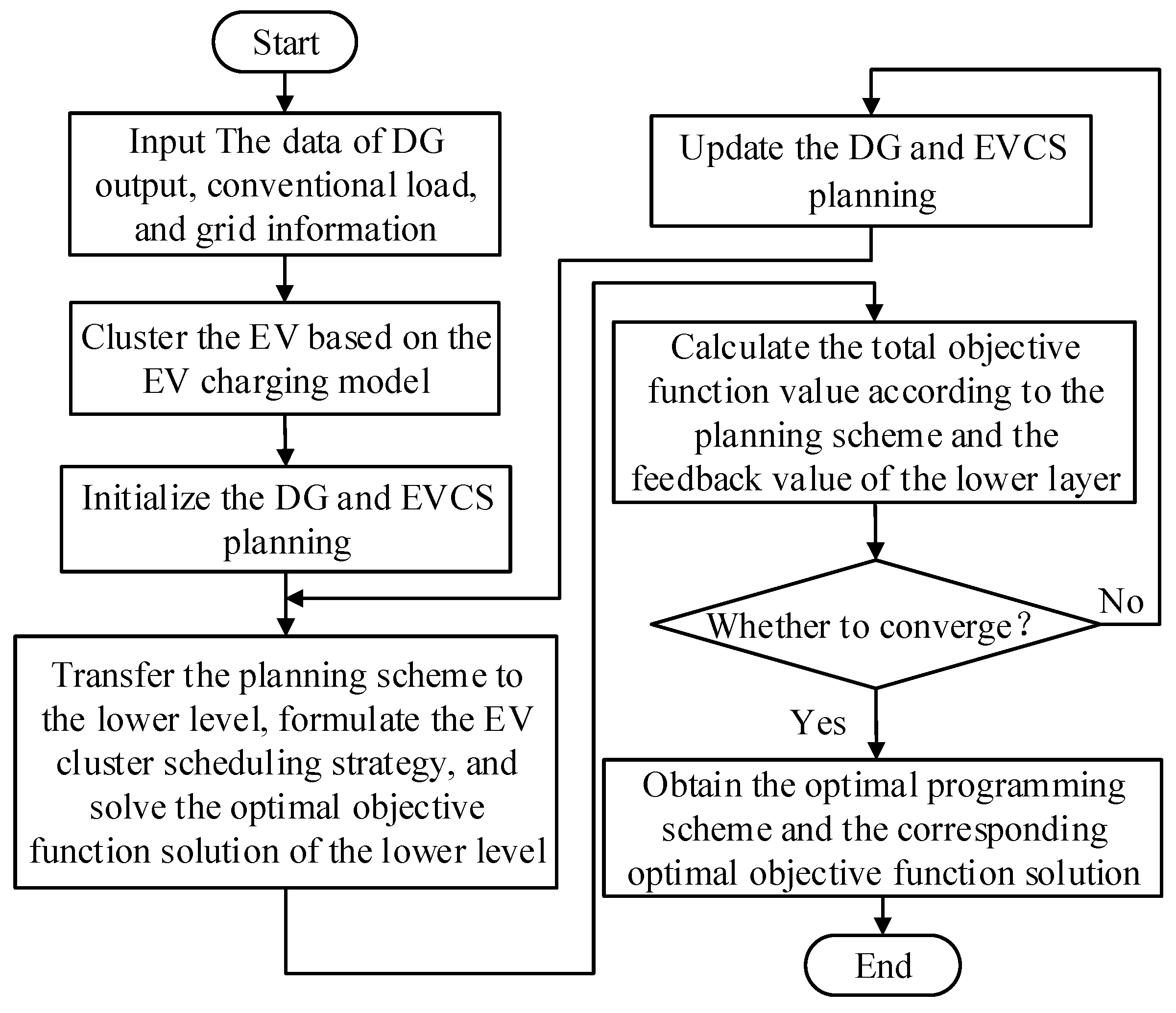
5.2. Flowchart of Bi-Level Programming Model

The flow of the bi-level optimization model established in this paper is shown in Figure 4.

The bi-level optimization model is solved based on the I-HSPSO algorithm, where the upper level makes decisions on site selection and capacity determination of DG and the EVCSs, and the lower level formulates the scheduling strategy for each EV cluster. At the lower level, the charging and discharging of the EV are managed in an orderly manner to optimize power flow in each typical scenario, and the optimal solution maxf_L is fed back to the upper level, where the optimal solution maxf_U of the overall objective function is calculated according to the scheme and maxf_L to obtain the optimal scheme for DG and the EVCSs.

6. Case Study

6.1. Parameters of the IEEE-33 Bus Test System

In this paper, the IEEE-33 bus test system was used for a simulation analysis of the proposed DG-EVCSs planning, and is shown in Figure 5. The system parameters are described in [20].

It was assumed that the number of EVs in the planning area was 900, and that they were evenly distributed among sub-stations. According to the ratio of each type of EV, the number of private electric vehicles was 740. It was assumed that the ratio of EV users willing to participate in the V2G mode was 90%, efficiency of charging and discharging efficiency was 90%, charging and discharging power was 7 kW, and the compensation coefficient of battery loss was 0.854 CNY/kWh. The peak and valley prices were used to calculate the prices of electricity for the distribution network and the EVCSs, and the values are shown in

Table 1. Peak and valley price.

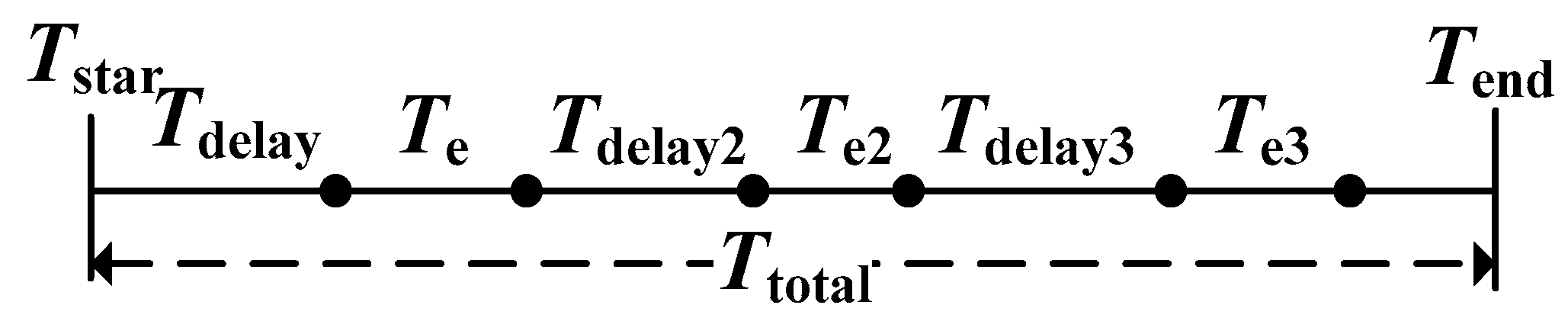
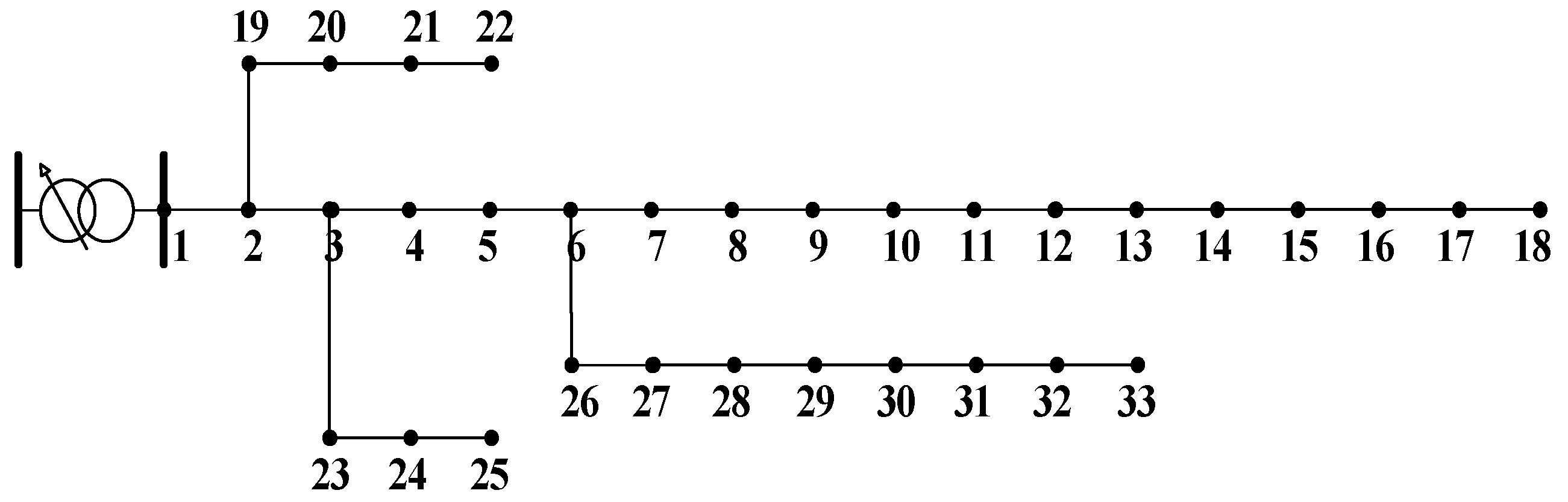
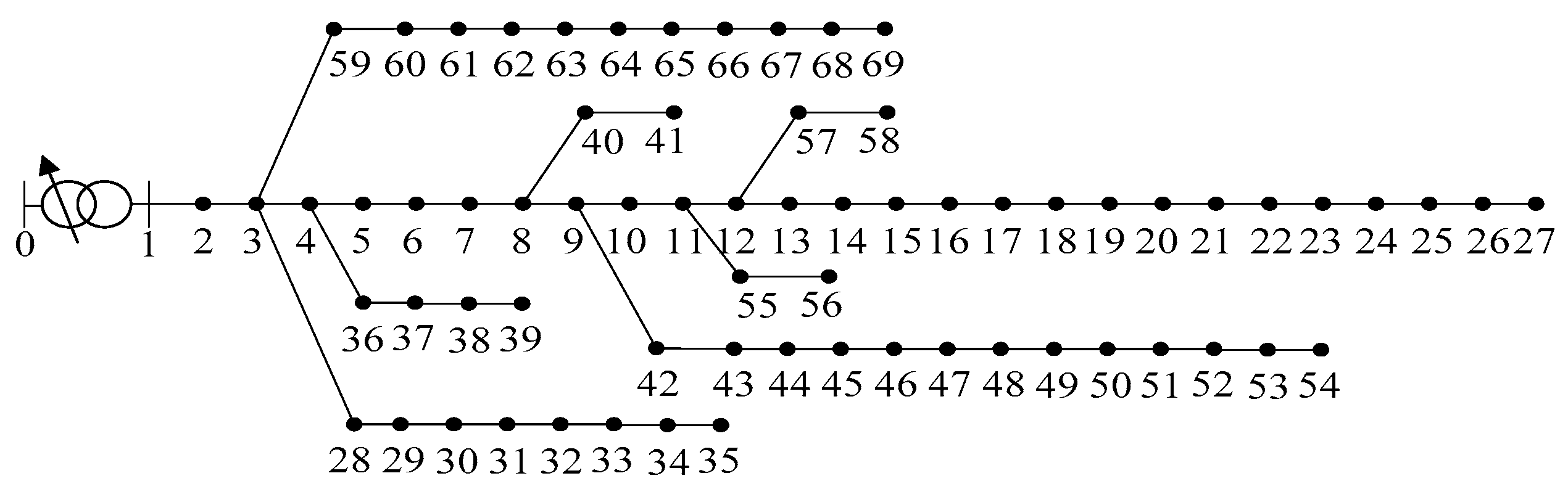
	Electricity Cost Price/(CNY/kWh)	Electricity Sale Price/(CNY/kWh)	Charging Cost of EV/(CNY/kWh)	Discharge Compensation Coefficient/(CNY/kWh)
Peak time	0.6129	1.11	1.5	2.20
Normal time	0.4430	0.68	1.0	1.23
Valley time	0.2189	0.35	0.75	0.35

.

For the IEEE-33 bus test system, the DWG candidate nodes were nodes 13, 23, and 31, the PV candidate nodes were nodes 7, 21, and 28, and the EVCSs candidate nodes were nodes 4, 8, 14, 20, and 29. The weights of the completion of charging and unit charging cost satisfaction α₁ and α₂ were 0.4 and 0.6, respectively. The weight coefficients of the sub-objective function w₁, w₂, w₃, and w₄ are 0.375, 0.125, 0.125, and 0.375, respectively. The rated power for DG was 100 kW, the cut-in wind speed, rated wind speed, and cut-off wind speed of DWG were 13.5 m/s, 3 m/s, and 20 m/s, respectively, and the rated solar irradiance of PV was 1 kW/m². The government subsidy c_b,DWG was 0.1 CNY/kWh and c_b,PV was 0.36 CNY/kWh. The capacity construction costs c_t1, c_t2, and c_t3 were 5381 CNY/kWh, 4735 CNY/kWh, and 6000 CNY/kWh, respectively. The fixed investment cost of the EVCSs is 3,000,000 CNY. The service life of the equipment n₁ was 20 years, and the discount rate was 8%. The unit maintenance fees were c_om1 = 0.0296 CNY/kWh and c_om2 = 0.0096 CNY/kWh, and the amortized unit maintenance fee for the EVCSs was 100 CNY/kWh. The energy consumed by an EV over 100 miles was 21.5 kWh, the CO₂ trading tax fee in the international market was 80 CNY/ton, and the difference between the EVs and conventional vehicles over 100 miles Δ was 7 kg. The cost parameters of environmental pollution are shown in

Table 2. Cost parameters of environmental pollution.

Contaminant	xs/(kg/MWh)	as/(CNY/kg)	bs/(CNY/kg)
CO2	639.2	0.01	0.02
SO2	3.587	1.00	6.00
NOx	1.544	2.00	8.00

.

The four typical scenarios of wind speed, solar irradiance, and conventional demand for load, obtained based on the maximum principle of the pseudo F-statistic (PFS), are shown in Figure 6. Based on the uncertainty of wind power and light, four typical scenarios constructed in this paper represent the fluctuations of wind speed and light throughout the year.

6.2. Analysis of Results

The following three schemes were used for the optimization for DG and the EVCSs.

Scheme 1: Multi-objective planning model of the DG-EVCSs in V2G mode.

Scheme 2: Multi-objective planning model of the DG-EVCSs in the plug-and-charge charging mode.

Scheme 3: Planning model of the DG-EVCSs in V2G mode maximize comprehensive profit.

The results of the optimization of the DG-EVCSs, based on the above three schemes, are shown in

Table 3. Optimal results of allocation of different schemes.

Scheme	Optimal Allocation Results		Capacity/kW
Scheme 1	DG	13(10).23(8).31(10).7(7)	3500
	EVCSs	20(309).4(254).8(288).14(211).29(296)	1358
Scheme 2	DG	13(10).23(6).31(7).28(7)	3000
	EVCSs	20(290).4(150).8(387).14(248).29(173)	1248
Scheme 3	DG	13(8).23(3).31(9).7(1).21(9).28(7)	3700
	EVCSs	20(327).4(293).8(348).14(202).29(291)	1461

. It lists the optimal planning schemes determined using the time frame of year, including the four scenarios shown in Figure 6. The corresponding DG consumption and charging load acceptance under the three schemes are shown in Table 3.

In the DG planning scheme, 13(10) indicates that 10 distributed generators were installed in node 13, and in the EVCSs planning scheme, 20(309) indicates that the capacity of the charging station at node 20 was 309 kW.

The comprehensive evaluation indices of the three schemes are shown in

Table 4. Comprehensive evaluation indices of the three schemes.

Scheme	Scheme 1	Scheme 2	Scheme 3
Comprehensive profit/10,000 CNY	1199.238	1204.678	1251.675
Voltage quality/pu	0.845	0.831	0.823
System load fluctuation/kW	504.026	530.489	662.976
Charging satisfaction of EV/%	0.911	0.840	0.866
Comprehensive evaluation indices/pu	0.933	0.897	0.899

.

According to the data in the table, the comprehensive evaluation of Scheme 1 was the best, while that of Scheme 2 was similar to the evaluation of Scheme 3.

The specific indicators of the comprehensive benefits of the three schemes are shown in

Table 5. Specific indicators of comprehensive benefits.

Scheme	Scheme 1	Scheme 2	Scheme 3
Electricity sale benefits/10,000 CNY	1514.417	1514.417	1514.417
Charging station sales revenue/10,000 CNY	550.484	603.089	668.442
Electricity purchasing cost/10,000 CNY	587.752	648.469	658.807
Investment and construction cost/10,000 CNY	422.985	388.860	433.661
Maintenance cost/10,000 CNY	47.442	41.756	41.501
Government subsidy benefits/10,000 CNY	144.806	130.280	167.040
System network loss cost/10,000 CNY	38.979	40.556	42.882
Environmental benefits/10,000 CNY	86.689	76.533	78.627

, and those of EV charging satisfaction are shown in

Table 6. Specific indicators of EV charging satisfaction.

Scheme	Scheme 1	Scheme 2	Scheme 3
Charging completion of EV/%	86.162	80.139	88.299
Unit charging cost of EV/(CNY/kWh)	1.060	1.155	1.171

.

Compared with Scheme 2, Scheme 1 took into account the V2G effect of the EVs, which helped manage their charging and discharging in an orderly manner, optimize power flow, and improve the consumption capacity of the distribution network to DG. The clean energy consumption of the three schemes is shown in

Table 7. Clean energy consumption.

Scheme	Scheme 1	Scheme 2	Scheme 3
Consumption of DG/MWh	12,067	10,537	10,656
Total acceptance of charging load/MWh	5612	5220	5751

. Compared with Scheme 2, the planning capacity of Scheme 1 increased by 500 kW, and the consumption of DG increased by 1530 MWh. The increase in DG consumption increased the costs of investment, construction, and maintenance of Scheme 1, but also increased income from government subsidies income and reduces the cost of power from the distribution company owing to the superior power grid.

When the capacities of the EVCSs of the two schemes were compared, the planned capacity of Scheme 1 was found to be higher than that of Scheme 2. Compared with the plug-and-charge charging mode, the V2G mode was more conducive to promoting the acceptance of charging load. Therefore, the EV charging completion of Scheme 1 was 6.023% higher than that of Scheme 2, and its charging load acceptance increased by 392 MWh.

In terms of environmental benefits, Table 7 shows that the scheme considering the V2G mode was conducive to promoting the consumption of DG and the charging load and improving the consumption of clean energy in the distribution network.

In terms of the cost of network loss, compared with Scheme 2, the cost of Scheme 1 was reduced by 3.89%, which indicates that appropriate management of charging and discharging can optimize the power flow and reduce network loss.

In terms of EV charging satisfaction, Scheme 2 used the plug-and-charge charging mode, and thus its unit charging cost was high. Scheme 1 responded to the peak and valley prices by scheduling the charging and discharging loads of the EV; its unit charging cost was thus 8.23% lower than that of Scheme 2. The reduction in unit charging cost and the increase in EV charging completion resulted in a 7.1% increase in EV charging satisfaction in Scheme 1.

Compared with Scheme 1, Scheme 3 considered only the comprehensive benefits, and mainly increased them by expanding the acceptance of EV charging load while ignoring voltage quality and load fluctuation. Because Scheme 3 did not take into account EV charging satisfaction, the demand or it by EV users could not be guaranteed, and the unit charging cost was relatively high. Although the comprehensive benefits increased by 524,370 CNY, the higher charging cost led to a decrease in the willingness of EV users to participate in V2G.

In terms of the system load fluctuation index, the net load fluctuation surfaces of the three schemes are shown in Figure 7.

As shown in Figure 7, the surface of the net load fluctuation of Scheme 1 was the smoothest, and its load fluctuation index was 4.99% lower than that of Scheme 2, which indicates that load fluctuation was suppressed in the V2G mode. In Scheme 3, the excessive acceptance of charging load led to the most serious fluctuation in net load. The load fluctuation index of Scheme 3 reached 662.976 kW, an increase of 31.54% compared with Scheme 1. The voltage quality of Scheme 1 was the highest, whereas the disordered access of charging loads in Scheme 3 not only aggravated the fluctuation of system load, but also causes further deterioration in voltage quality.

6.3. Case Study Using PG and E-69 Bus Test System

To further verify the effectiveness of the optimization model proposed in this paper, the PG and E-69 bus test system, shown in Figure 8, was used. The system parameters are described in [21].

For the PG and E-69 bus test system, the DWG candidate nodes were nodes 10, 33, and 38, the PV candidate nodes were nodes 21, 50, and 66, and the EVCSs candidate nodes were nodes 14, 32, 40, 45, and 61. The results of optimization of DG and the EVCSs of the three schemes are shown in

Table 8. Optimization results.

Scheme	Optimal Allocation Results		Capacity/kW
Scheme 1	DG	10(9).33(2).38(10).21(1).50(5).66(4)	3100
	EVCSs	14(259).31(237).40(257).45(258).61(299)	1310
Scheme 2	DG	10(6).33(2).38(10).21(3).50(10)	3100
	EVCSs	14(232).31(187).40(245).45(150).61(242)	1056
Scheme 3	DG	33(7).38(10).21(8).50(10).66(10)	4500
	EVCSs	14(442).31(439).40(331).45(308).61(389)	1909

, and the corresponding objective functions are shown in

Table 9. Comprehensive evaluation index.

Scheme	Scheme 1	Scheme 2	Scheme 3
Comprehensive profit/10,000 CNY	1147.366	1202.422	1320.579
Voltage quality/pu	0.990	0.989	0.987
System load fluctuation/kW	492.478	524.166	866.618
Charging satisfaction of EV/%	0.904	0.829	0.870
Comprehensive evaluation indices/pu	0.905	0.880	0.886

.

According to the data in the table, the comparative advantages and disadvantages of the three schemes were similar to the results of optimization of the IEEE-33 bus test system, and Scheme 1 was the optimal scheme. Based on the results of the PG and E-69 bus test system, the validity of the model proposed in this paper was verified again. The difference between different regions or countries is mainly reflected in the peak or valley electricity prices, which does not affect the overall applicability of the model.

6.4. Comparison of Algorithm Performance

In this paper, the proposed I-HSPSO algorithm and PSO algorithm were tested by using the test functions f₁(x)~f₄(x), and the optimal value of the four test functions was zero.

$$f_1(x)={\displaystyle \sum _{i=1}^n{x}_i^2},$$

(35)

$$f_2(x)={\displaystyle \sum _{i=1}^n\left|x_i\right|}+{\displaystyle \prod _{i=1}^n\left|x_i\right|},$$

(36)

$$f_3(x)=0.5+\frac{{\sin }^2\sqrt{x_1^2+x_2^2}-0.5}{{\left[1+0.001\left(x_1^2+x_2^2\right)\right]}^2},$$

(37)

$$f_4(x)={\displaystyle \sum _{i=1}^n\left[x_i^2-10\cdot \cos (2\pi x_i)+10\right]},$$

(38)

MATLAB was used for programming, the particle swarm size of the algorithm was 50, the number of iterations was 1000, and each algorithm was run independently 100 times. The results of the two algorithms are shown in

Table 10. Results of algorithm simulation.

Function	Algorithm	Best Value	Worst Value	Mean Value
f1	PSO	3.832 × 10−23	2.194 × 10−5	2.577 × 10−7
	I−HSPSO	9.001 × 10−24	9.168 × 10−8	4.258 × 10−9
f2	PSO	0.1795	143.274	14.165
	I−HSPSO	3.745 × 10−4	1.992 × 10−1	1.849 × 10−2
f3	PSO	9.368 × 10−13	0.009	0.004
	I−HSPSO	0	0.009	6.802 × 10−4
f4	PSO	3.980	29.849	12.696
	I−HSPSO	3.836 × 10−24	9.949	3.872

.

According to the results for the f₁(x) function, the I-HPSO algorithm was superior to the PSO algorithm in terms of searching for single-peak convex functions. The function f₂(x) had local extrema around the global optimal value. For such functions with local extremum, compared with the PSO algorithm, the I-HSPSO had stronger global optimization ability. Therefore, all indices in the results of its simulation improved significantly. The function f₃(x) had numerous minima and oscillated strongly. The function f₄(x) was a nonlinear multi-modal function with jumping peaks, which made it difficult to find the global optimal solution. For such functions as f₃(x) and f₄(x), which struggled to find the global extremum, the results show that I-HSPSO had a stronger searching ability. Thus, the I-HSPSO algorithm proposed in this paper significantly improved algorithm performance.

7. Conclusions

In this paper, a multi-objective optimization model of the DG-EVCSs was established by considering the V2G technology of EVs. Based on the I-HSPSO algorithm, a bi-level programming model was solved. The conclusions of this study are as follows:

• Considering the planning of DG and EVCSs in the V2G mode is conducive to improving the consumption of clean energy and optimizing power flow. In this way, network loss and load fluctuations can be reduced, the quality of voltage can be improved, and a scheme with better overall performance can be obtained.
• In the distribution network with peak and valley prices, the V2G mode can reduce the unit charging cost for EV users, improve EV charging satisfaction, and satisfy the interests of both the distribution company and EV users.
• The objective here was the comprehensive optimization of four indices such as comprehensive profit, voltage quality, system load fluctuation, and EV charging satisfaction so that the objective function of the planning model was complex, which is conducive to considering multiple demands and improving the comprehensive performance of the planning scheme.
• The proposed I-HSPSO algorithm converged quickly, and had a strong global optimization ability, because of which it did not easily to fall into the local optimum. Its performance thus improved.