1. Introduction
Since the industrial revolution, the increase of CO
content in the atmosphere has led to the increase of the greenhouse effect year by year, which leads to a series of extreme weather problems [
1,
2,
3]. CO
emissions come mainly from the combustion of fossil fuels, especially coal-fired power plants, which are recognized as point sources of CO
emissions that exacerbate greenhouse effects. The capture and recovery of CO
are the key measures for effective emission reduction [
4]. Compared with other carbon dioxide capture theories, the post-combustion amine capture technology is the closest technology to commercial operation and is suitable for the transformation of existing power plants. It is the mainstream technology of carbon capture at present [
5,
6,
7].
Hence, since the implementation of the Post-combustion CO
Capture Process (PCCP), scholars in the process control field and engineers have invested a lot of time and money to solve and improve the capture performance of CO
capture systems [
8]. U.S. technology company CANSOLV achieved cost reduction by combining CO
capture and capture of pollutants, such as CO
, nitrogen oxides, and mercury [
9]. The Center for International Cooperation on CO
Capture, Storage and Utilization (iCCSU), established by Professor Tong Baidong, Hunan University in September 2009, has carried out fruitful applied basic research and key technology development on the frontier of CO
capture, separation and purification, and solidification of carbon dioxide materials [
10].
Regarding the industrial process, under the background of the chemical process industry, the improvement space of the process operation will always exist. In view of the technology that PCCP can improve the efficiency of power generation by improving the operation process, scholars have carried out a lot of research in recent years [
11,
12].
Figure 1 shows traditional power plants and carbon dioxide capture processes.
Shan et al. [
13] proposed a model of absorption tower and desorption tower based on the kinetic relationship between the column enhancement factor and the chemical reaction and verified it in MATLAB/Simulink. In [
14], under the open loop condition, the flue gas flow is fixed, and the other inputs remain constant. The dynamic response of the absorption tower model established in Modelica is compared with the dynamic response in the actual plant, and the correctness of the absorption tower model is verified. In terms of model establishment, the above studies only verified a certain link of the system, and did not conduct a systematic dynamic analysis of the overall model. On this basis, Lin et al. [
15] established a complete CO
capture system model in Aspen Plus Dynamics and determined the factors that affect CO
removal performance, energy efficiency, and the long-term stability of the absorption/stripping CO
capture process using monoethanolamine solution. Three important factors, namely lean solvent flow rate, lean solvent load, and water replenishment of the balance system, provide guidance for the dynamic modeling of the CO
capture system. Kvamsdal et al. [
16] designed a CO
dynamic capture model based on the rate level in Matlab and compared the data obtained in the steady-state and dynamic tests with the data collected in VOCC (validation of carbon capture) to verify the accuracy of the model when the absorption tower is in a specific working condition. Subraveti et al. [
17] established an equilibrium model based on the post-combustion CO
capture model in Modelica and used steady-state experimental data to adjust the model coefficients related to mass/heat transfer and chemical reactions to make the model more suitable for actual plants under nominal operating conditions.
The study of PCCP operation control by Mechleri et al. [
18] was carried out using conventional single-loop disturbance suppression methods, such as stabilizing the CO
content of the intake channel, keeping the steam temperature and heat capacity of the reboiler constant, maintaining the MEA content of the stripping unit constant, etc. Lin et al. proposed two different proportional-integral (PI) control strategies to maintain the desired absorption efficiency by using the lean solvent flow rate and reboiler input heat as manipulation variables [
19]. Beedelbayev et al. gave the single machine type only for the absorber MPC control scheme [
20]. Panahi and Skogtogad implemented a MPC control strategy using the degree of CO
recovery and reboiler temperature as controlled variables [
21,
22]. From the current research situation, existing PCCP dynamic research focuses on the study of the dynamic characteristics of a single tower or a single unit and simple PI control algorithms.
However, the complete dynamic performance of the capture rate of the actual power plant PCCP device under the condition of flue gas disturbance is still lacking. In variable operating conditions, the control effect is not particularly ideal. For the purpose of solving the problem of the slow response and system constraint of PCCP regulating systems in variable working conditions,
Section 1 introduces the background, motivation, and contribution.
Section 2 introduces the dynamic behavior of the system, establishes the complete CO
capture system in the Aspen Plus and Aspen Plus Dynamics, and determines the state space model with high fitting degree according to the experimental data in
Section 3.
Section 4 shows the design of the MPC controller in the Matlab/Simulink and establishes the capture rate adjustment model of the CO
capture system; the system simulation is qualitatively analyzed according to the performance index. It is found that the MPC algorithm can achieve the given capture rate results more accurately and stably than the conventional PID algorithm regulation system, and the regulation system has good control performance, which provides a reference for the flexible design of the PCCP capture rate.
2. Description of the Post-Combustion Capture CO System
Studies have shown that the core of CO
capture technology is to improve the operation process by implementing advanced control technology on the CO
capture device. MEA is the best choice for the CO
absorbent with its absorptivity of up to 90% [
23,
24]. Therefore, capture CO
equipment and its process based on MEA combustion are the most commercially attractive options in the world.
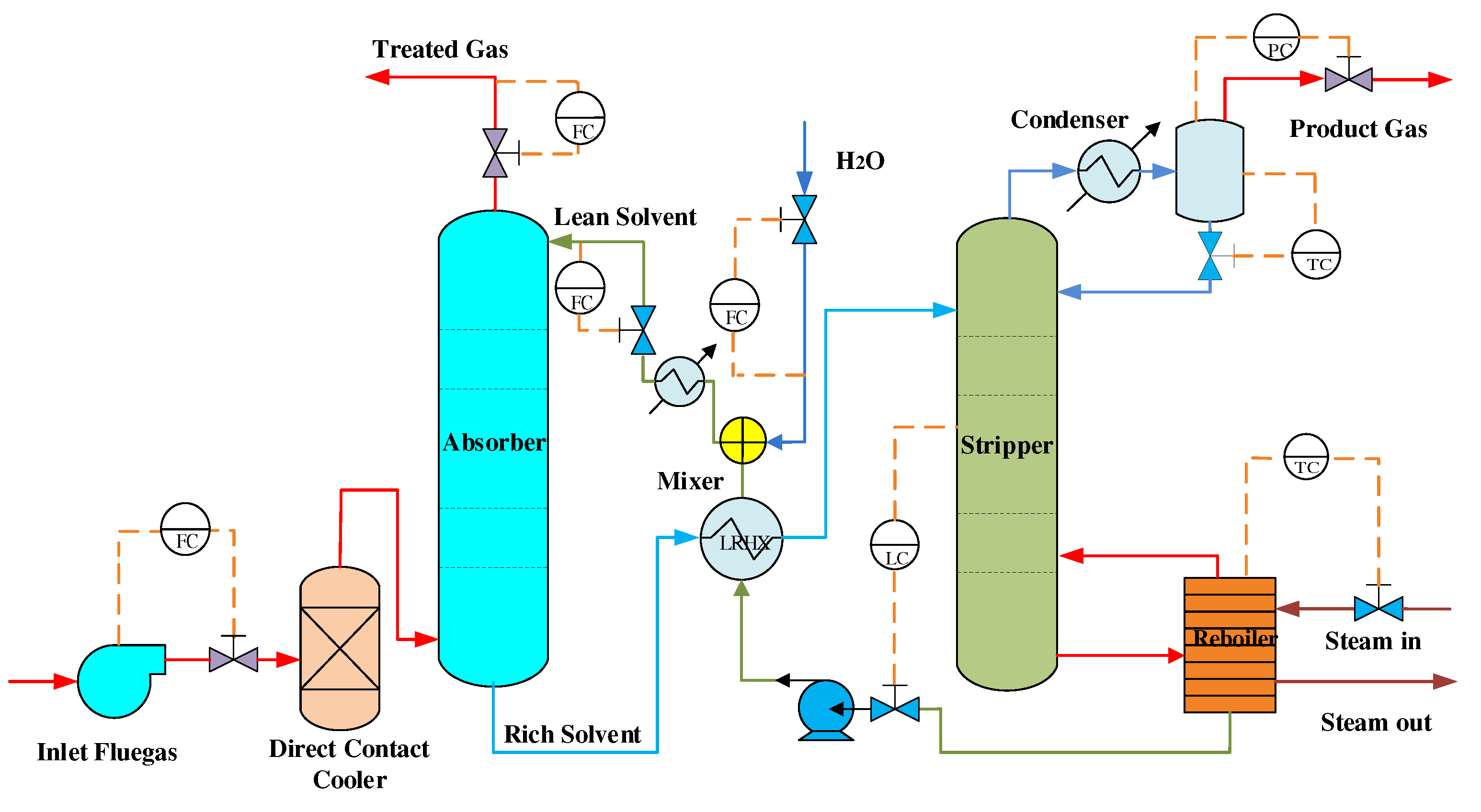
Figure 2 shows a schematic diagram of the CO
capture device after combustion in an amine-based power plant.
As shown in
Figure 2, after desulfurization [
25], the flue gas reacts with the MEA solvent flowing into the top of the tower by fan pressurization to remove carbon dioxide from the furnace gas. The rich liquid absorbs carbon dioxide from the bottom of the absorption unit and then heats up into the stripping unit. The lean solvent produced by the reaction is recycled from the bottom of the stripping unit to the absorption unit, and the analytical carbon dioxide is purified. Finally, the high-pressure carbon dioxide gas is used. To maintain the water balance of the system, water is replenished in the system [
26].
2.1. Mathematical Model of a Post-Combustion Capture CO System
In the mathematical model, the description of the absorption unit and the stripping unit is consistent. The difference is that the reboiler unit is added to the stripping unit and the gas is stripped at the high temperature produced by it. The mathematical model of each unit reflects the dynamic behavior of each part of the system.
2.1.1. Modeling Assumptions
The assumptions used in the modeling of the PCCP plant are:
All reactions reach equilibrium.
The velocity of any section of the axial surface is constant, and the pressure drop is linear along the axial direction of the tower.
Mass and heat transfer are described by the two-film theory [
27].
The interface between the liquid film and the gas film is in phase equilibrium.
Solution degradation is negligible.
No heat losses to the surrounding area.
2.1.2. Absorption and Stripping Units
Equations (
1)–(
4) describe the mass and energy balances along the axial direction in the two reaction towers.
Here, (mol/m) and (mol/m) are the gas and liquid concentrations of each component, F (m/s) is phase volumetric flow, (m) is the radius of the reaction column, (mol/m/s) is the molar flux i the component, T (K) is the temperature of the liquid and gas phases, (m/ m) is the gas–liquid contact area, is the length of the reaction column, (kJ/kmol) is heat capacity, and Q (kJ/ms) is the heat transfer rate. The i components in the column are MEA, N, CO, and HO. In the absorption unit, is the operating variable to control the carbon dioxide capture rate and is a disturbance from the power plant.
2.1.3. Heat Exchanger Model
The lean-rich heat exchanger considered in the process is assumed to be a counter-current shell and tube heat exchanger.
where
T (
K) is the temperature,
(m
/s) is volume flow,
V (m
) is volume,
(kJ/s) is the heat transfer rate,
(kmol/m
) represents the average molar density, and the subscripts tube, shell, in, and out represent the management side, shell side, inlet, and outlet of the heat exchanger, respectively.
2.1.4. Reboiler Model
In the reboiler unit, the CO
-absorbed rich solvent is heated to break the chemical bond between the CO
and MEA. The remaining components (H
O, CO
and MEA) evaporate and enter the bottom of the stripper. The solvent with low amount of CO
exists from the bottom of the reboiler and enters a new cycle. Its mass and energy balance are shown in Equations (
7) and (
8):
The components i are MEA, CO, and HO. (kmol) is the mass holdup of component i, F (kmol/s) is the molar flow rate, F and L are the flow rates of steam and liquid, and the subscripts in and out represent the input and output. In the description of energy balance, (K) is temperature, (kmol/m) is density, (kJ/kmol) is molar heat capacity, V (m) is retention volume, H (kJ) is enthalpy, and (kJ/s) is heat input.
2.2. Steady-State and Dynamic Model
The steady-state model uses ELECNRTL physical method and CO
–MEA–H
O systems containing the following five equilibrium reactions to describe the absorption equilibrium in the system.
The kinetic reversible reactions involve can be expressed as:
The power plant lean solvent flowrate is 0.458 kg/s [
28] and the CO
capture rate is fixed at 70%. The reboiler type in the stripper is selected. Flue gas condition in PCC plant is shown in
Table 1. The parameters corresponding to the absorber and the stripper are shown in
Table 2.
The size of absorber/stripper is added to the steady-state model under the above optimal working conditions, and the parameters needed for the dynamic models such as the liquid level and pressure are set. The steady-state model is derived as the initial value file of dynamic model driven by pressure. Compared with the equilibrium-based model, the rate-based model can predict and simulate the results more accurately. Therefore, the rate model is recognized as the most reliable process model of absorption and desorption. However, the dynamic simulation in the Aspen Plus Dynamics does not support the rate level model, so the equilibrium level model is selected in this paper [
17]. The steady-state model of the post-combustion CO
capture system in Aspen Plus is shown in
Figure 3.
The system capture rate is defined as
where CO
% represents the CO
capture rate,
is the CO
moles flow in flue gas, and the subscripts in and out represent exports and imports. Under the above definition, we can obtain the nonlinear distribution of carbon dioxide capture system under specified working conditions (capture rate 63.05–80.25%, flue gas flowrate 0.125–0.136 kg/s, and lean solvent flowrate 0.439–0.472 kg/s) by dynamic analysis in aspen plus dynamics (
Figure 4).
According to the analysis of the trapping rate distribution in the figure, when the flue gas flow is at a high flow rate and the lean liquid flow is at a low flow rate, the capture rate is low. When the flue gas flow is at a low flow rate but the lean solvent flow is high, the system capture rate is increased quickly, which improves the ability of the collection system to operate flexibly. However, in steady state operation, only points can be taken individually to obtain singular information of a certain working condition, and it is impossible to flexibly study the changes of the system with input. Therefore, dynamic testing of the system in Aspen plus Dynamics was performed to understand that the system is dynamically changing.
We have conducted a dynamic test on the system, as shown in
Figure 5. We perturb the flue gas flow and lean solvent flow by
, and it can be seen that it is consistent with the steady-state operation trend. When the flue gas flow rate increases, the MEA solution cannot completely absorb the CO
in the flue gas, resulting in an increase in the outlet CO
concentration and a decrease in the capture rate. When the lean solvent flow rate increases, the CO
in the flue gas is completely absorbed by the MEA solution, and the carbon capture rate increases. From the viewpoint of mass transfer kinetics, according to the two-film theory analysis, the transfer of gas and liquid phases in the two-film and the absorption of CO
by MEA require a certain amount of time for diffusion and material conversion. The increase in the gas flow rate reduces the reaction time of the gas–liquid phase in the film, and MEA is too late to absorb CO
. Therefore, increasing the flue gas flow rate will gradually reduce the capture rate. Increasing the flow rate of the absorbent enables the limited carbon dioxide in the flue gas to be fully captured, thus greatly improving the capture rate of the system.
4. Simulation and Results Analysis
The dynamic characteristic model of rear combustion CO
capture in a power plant with lean solvent flow as the controlled input, carbon dioxide capture rate as the controlled output, and flue gas flow as the disturbance variable as established in Matlab/Simulik. This paper takes the principles of small overshoot, fast response speed, and good tracking of a set value. The control effect of the system after combustion was verified by simulation experiments and compared with traditional PID. The key parameters of the tuning controller are shown in
Table 4.
This paper generally does not adopt the differential term in the PID controller because of the more interference in the actual control in the PID control strategy. Since the sampling time is 0.01 h in the actual chemical simulation and system identification, the sampling time in this paper is 36 s. First, both kinds of simulation add Gaussian distributed random signal.
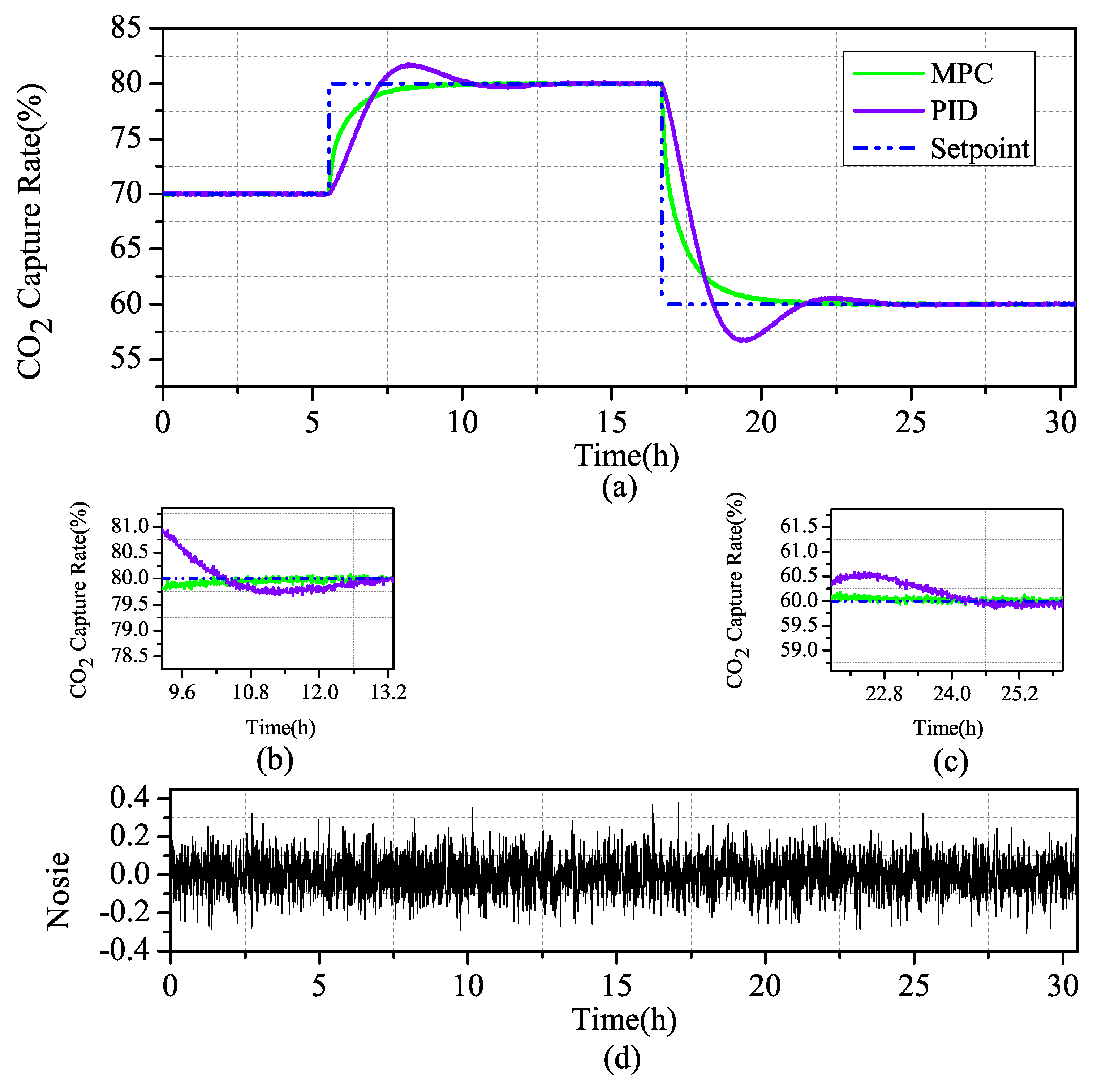
Transient response to a step change of lean solvent flow: In Scenario 1 of a given reference value input to a two-segment step signal, when the system runs stably for 4.1 h, the system steps up under the condition of a setting value of 70% and changes the setting value to 80%. When the system is under stable operation, at 18.0 h, the set value is reduced from 80% to 60%, and the stability of the controller design is investigated.
Transient response to a ramp change of lean solvent flow: Scenario 2 starts with steady-state operation. The three-stage slope signal was investigated: (a) at 1.4 h, to give reference to the descent ramp signal and decreased to 15% at a rate of 9%/h; (b) at this stage of steady operation to 11.1 h, a rising signal at a rate of 10.8%/h, steady state operation to 23.6 h; and(c) at 23.6 h, at a rate of 0.9%/h, and stable operation to 3.0 h, comprehensively consider the stability of the MPC and PID control when the system is undergoing a large decline, a large rise, and a small rise.
The simulation results in
Figure 10 and
Figure 11 show that the output of the CO
capture system increases with the increase of the measured input value, which is in line with the actual process. When the system changes slightly, the overshoot of the PID is not high, but the MPC has almost no overshoot. When the system decreases greatly, the overshoot of the PID increases obviously, while the overshoot of the MPC maintains almost no overshoot stability.
The results in
Table 5 show that, in terms of rapid performance, the CO
capture system under MPC control is higher than that under traditional PID control, although the rise time are higher than those under PID control. Under the MPC control strategy and the PID control strategy, the overshoot difference is two orders of magnitude, which is obviously better than the control. When the steady-state time of the system is analyzed, it can be seen that, under the condition of sudden change of set value, the system under MPC control can pull the system back to the stable state more quickly, while the traditional PID still has to go through a large fluctuation before it can gradually stabilize. The robustness of MPC is greatly improved compared with that of PID, by multiplying the absolute value error integral by time. According to the overall analysis, the MPC achieved a better control effect.
Through the comparative analysis of
Figure 12 and
Figure 13, it can be seen that MPC and PID control strategies can control the system in a stable state after a period of time, but, in terms of stability, MPC is obviously better than PID, for control effect. During the large change of the system, the fluctuation of the PID adjusted system changes greatly, and only after two periods of fluctuation near the set value can the set value be returned. During the small change of the system, although the PID has a small shock, it quickly returns to the set value. It can be seen that the regulation performance is still better in PID when faced with small changes in the system, but, in MPC, where the regulation time is longer and the control system is more stable and slower when the system changes substantially, the MPC-regulated system has almost no fluctuation under noise disturbance and stable fluctuation near the set value.
5. Conclusions
The process of MEA Absorption of CO to implement high-quality and high-performance predictive control algorithms is limited by low-quality and imprecise mathematical models. This challenge could be dealt with using a high-performance model identification algorithm, which as far as possible considers all actual operations of the process. In this work, we built the rate-based steady-state Aspen Plus model and established a dynamic model of the PCCP system based on the equilibrium level, which was driven by pressure in the Aspen Plus Dynamics. The non-linear distribution of the CO capture system under different operating conditions was analyzed. In Aspen Plus Dynamic, the dynamic characteristics of the system were analyzed and explained from the perspective of mass transfer, and the lean solvent flow rate was determined as the main control variable of the system. The system model was identified under open-loop experimental data. Then, the identified model-based predictive controller was designed for the process of MEA absorption of CO. Finally, its performance was compared with the traditional PID control performance.
The simulation results and performance analysis index show that the subspace identification model-based MPC control strategy can improve the dynamic adjustment ability of the system, the time that the system reaches the steady state can be shortened, and it has stronger anti-interference ability and more robust performance. If a controlled system can reach the steady state earlier in the actual industry, it means more considerable economic benefits.