Effects of Osmotic Dehydration on the Hot Air Drying of Apricot Halves: Drying Kinetics, Mass Transfer, and Shrinkage
Abstract
1. Introduction
2. Materials and Methods
2.1. Material
2.2. Methods
2.2.1. Cutting in Halves and Sulfurization
2.2.2. Osmotic Dehydration
2.2.3. Hot Air Drying (HAD)
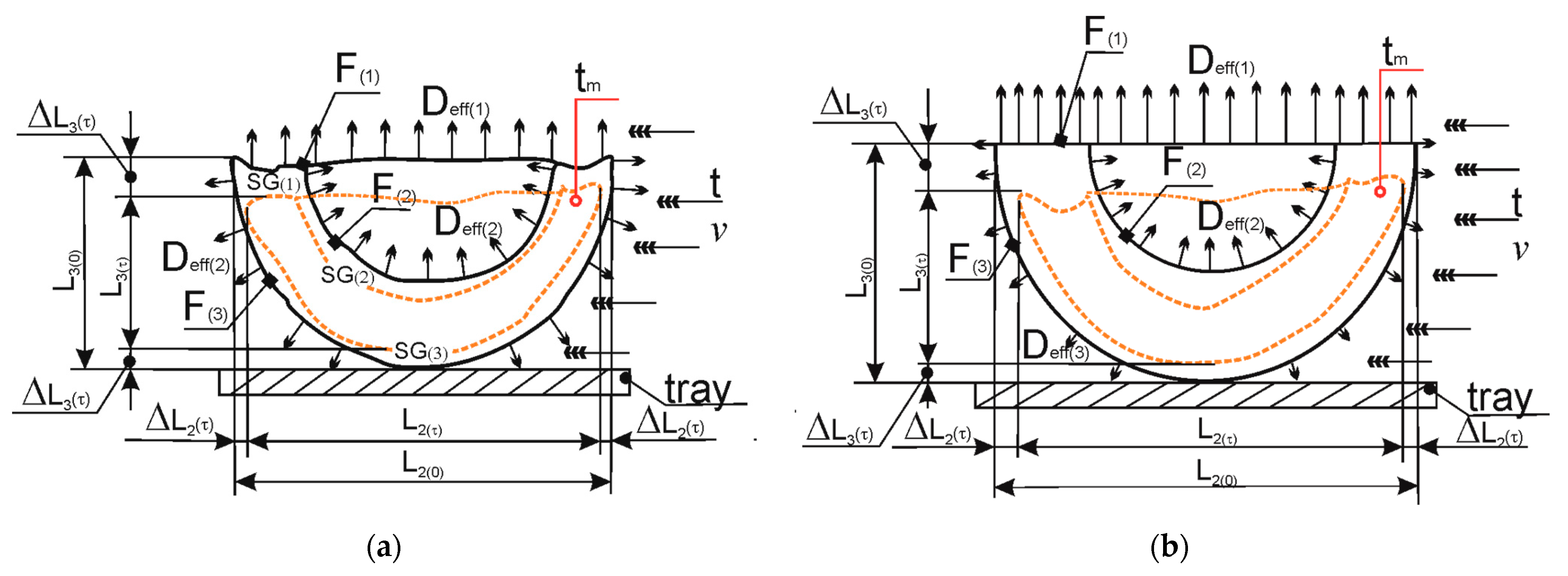
2.2.4. Measuring of Volume and Shrinkage
2.2.5. Modeling of Osmotic Dehydration and Hot Air Drying
2.2.6. Determination of Water and Solute Diffusivities
2.2.7. Determination of Activation Energy
2.2.8. Experimental Design and Statistical Analysis of the Results
- effects of concentration and temperature of the osmotic solution on the drying behavior of apricot halves during OD, the kinetics of water loss, solid gain, shrinkage, and diffusivity coefficients;
- effects of the OD process parameters on the drying behavior of apricot halves during HAD, kinetics, shrinkage, diffusivity coefficients, and activation energy.
3. Results
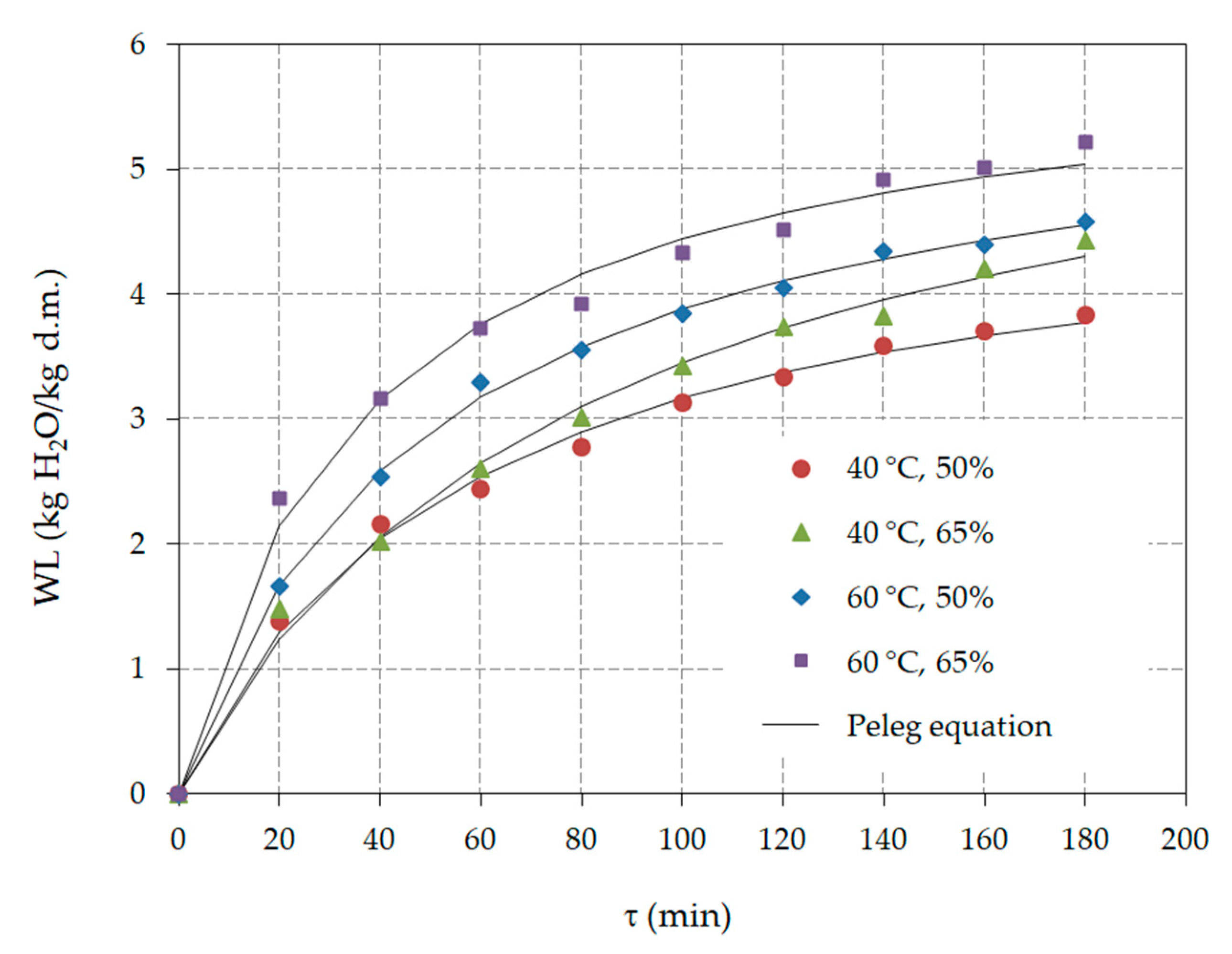
3.1. Osmotic Dehydration
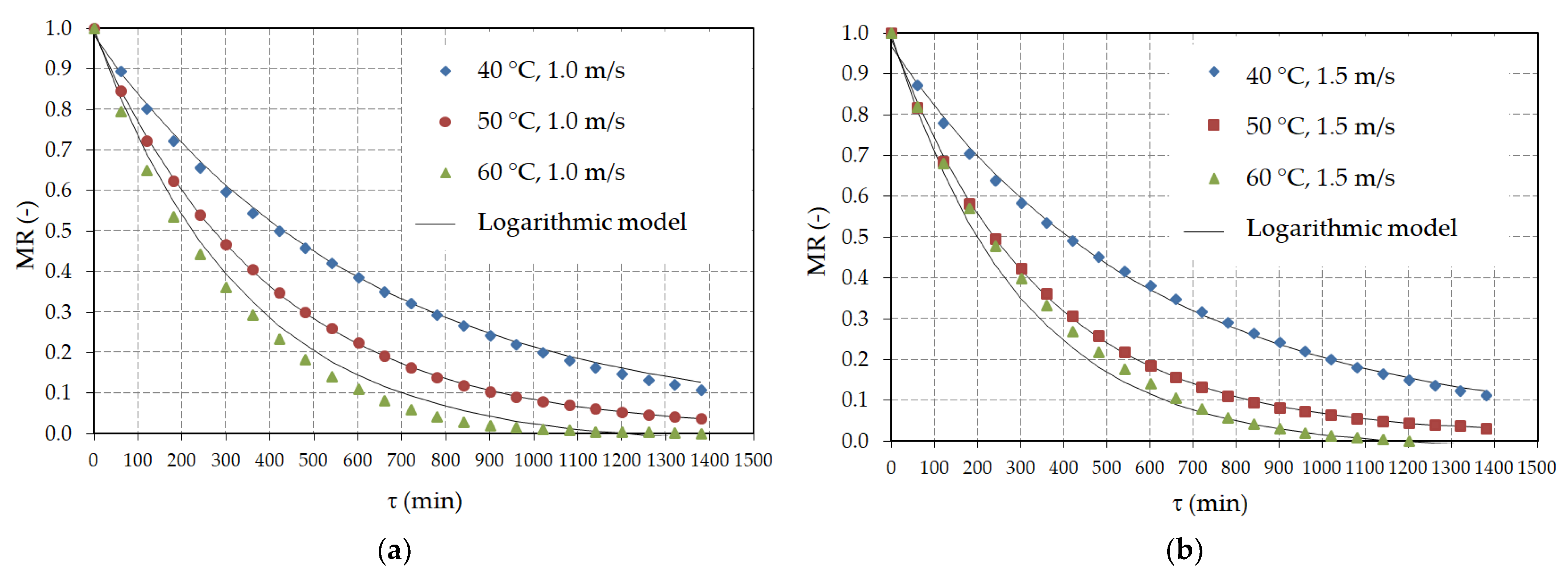
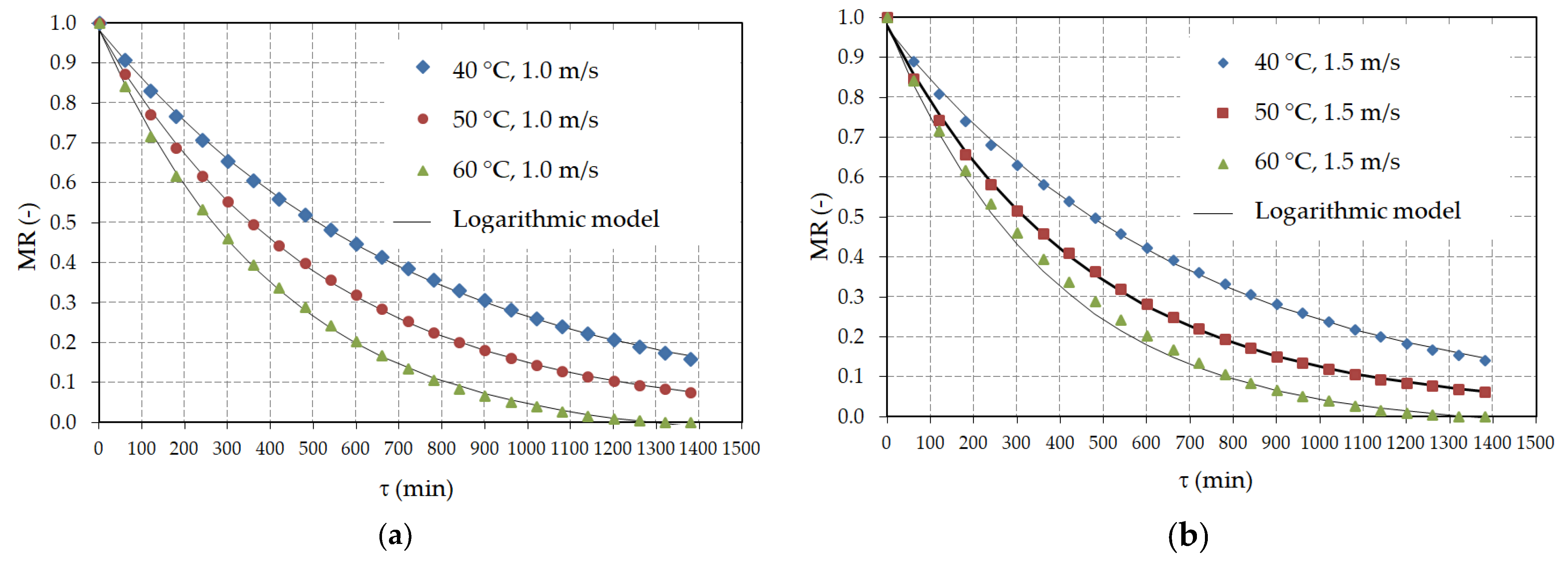
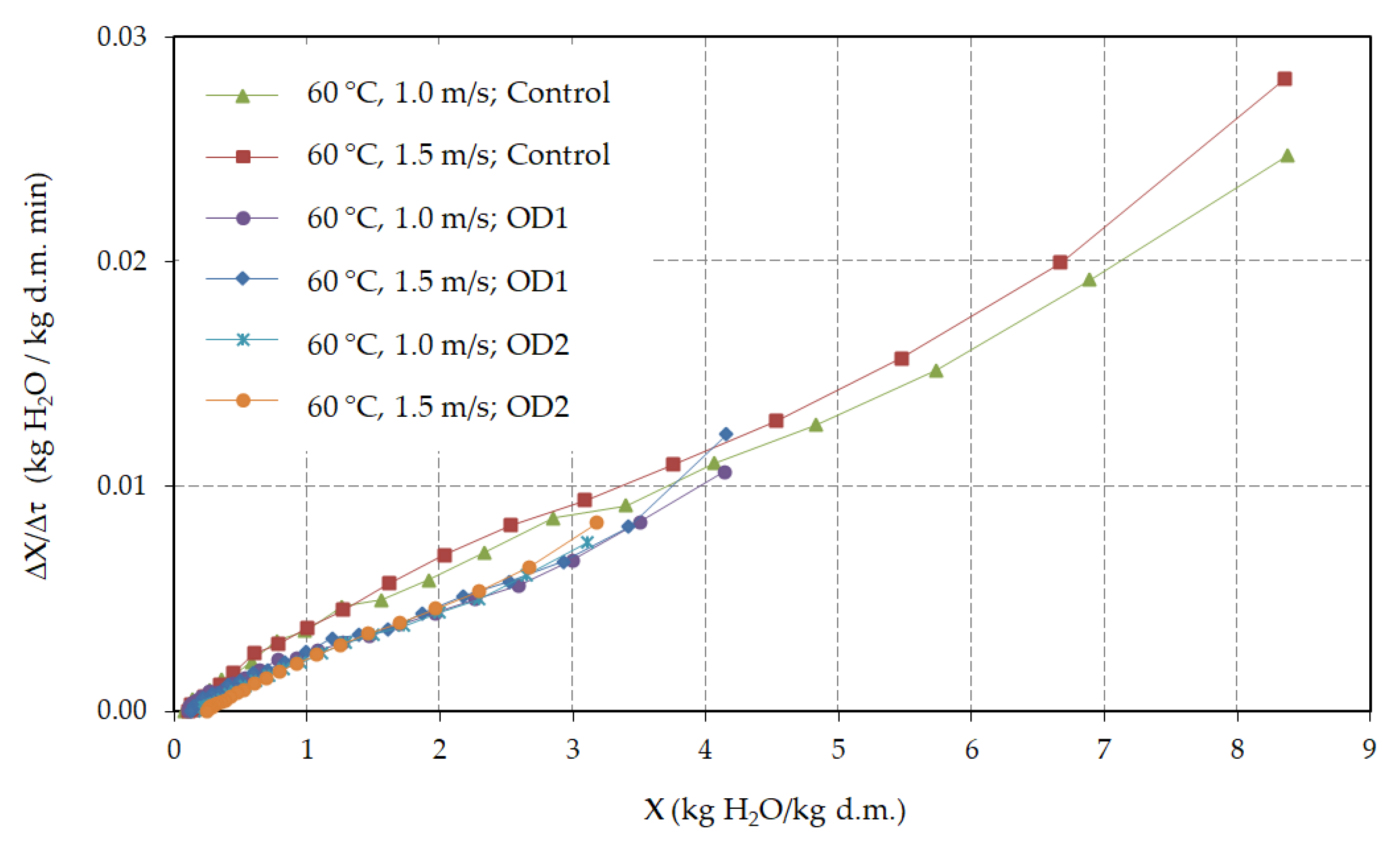
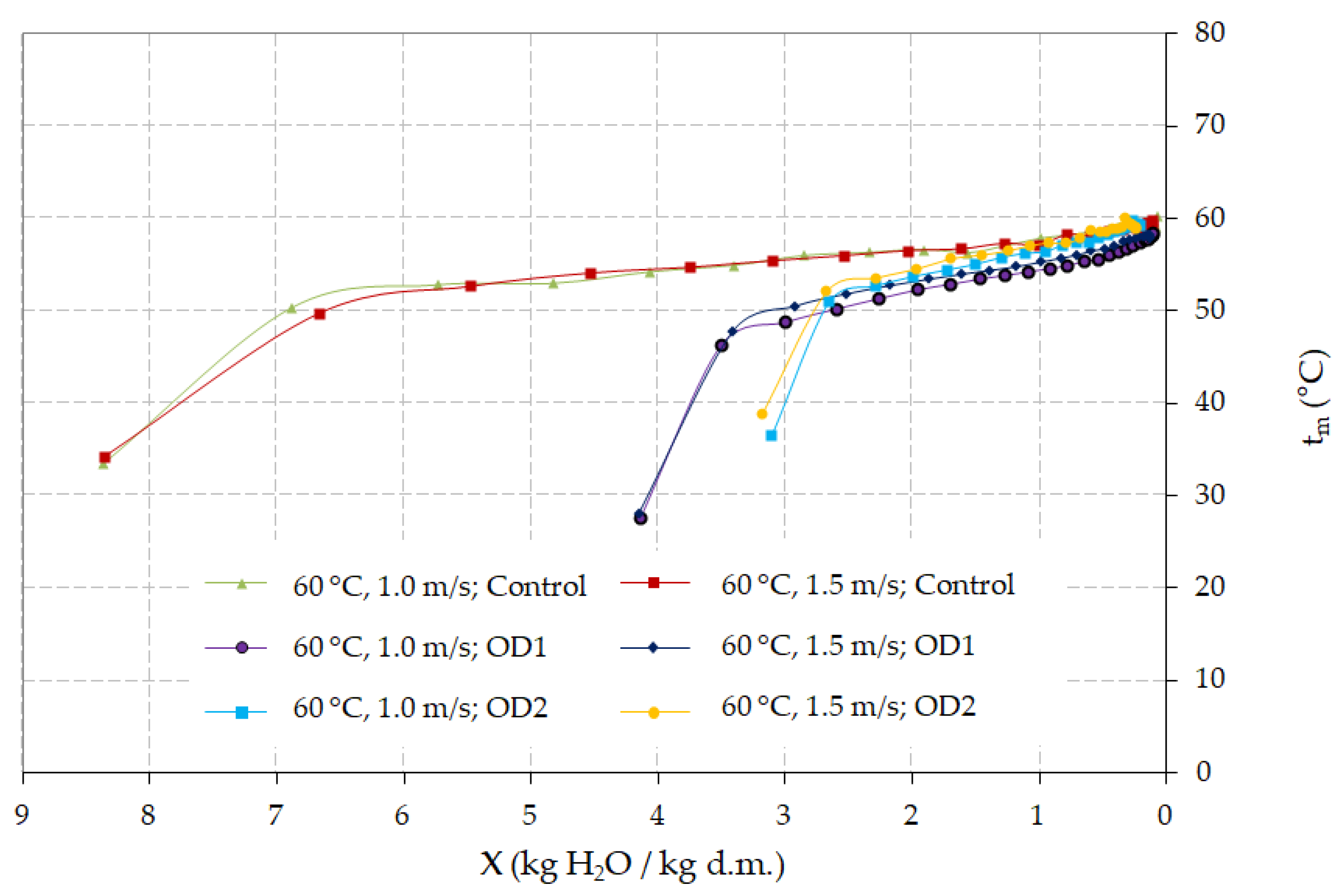
3.2. Hot Air Drying
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Miodragović, M.; Magazin, N.; Keserović, N.; Milić, B.; Popović, B.; Blagojević, B.; Klajdžić, J. The Early Perfomance and Fruit Properties of Apricot Cultivars Grafted on Pruns spinosa L. Interstock. Sci. Hortic. 2019, 250, 199–206. [Google Scholar] [CrossRef]
- Miodragović, M.; Keserović, Z.; Milić, B.; Dorić, M.; Magazin, N. Physical and Chemical Fruit Properties of Apricot Cultivars and Selections from Novi Sad within High-Density Growing System. J. Pomol. 2015, 49, 37–42. (In Serbian) [Google Scholar]
- Vukoje, V.; Pavkov, I.; Miljatović, A. Economic Aspects of Dried Fruit Production by Combined Technology. Econ. Agric. 2018, 65, 1031–1044. [Google Scholar] [CrossRef]
- Vukoje, V.; Pavkov, I. Analysis of Economic Justification of Drying of Apricots by Combined Technology. J. Process. Energy Agric. 2010, 14, 40–43. Available online: https://scindeks-clanci.ceon.rs/data/pdf/1821-4487/2010/1821-44871001040V.pdf (accessed on 17 November 2020).
- Keserović, Z.; Magazin, N.; Milić, B.; Igić, M.; Miodragović, M.; Kalajdžić, J. New Apricot Cultivar—“Buda”. J. Pomol. 2018, 52, 27–31. [Google Scholar]
- Karabulut, I.; Tugca, B.; Sislioglu, K.; Gokbulut, I.; Ozdemir, I.S.; Seyhan, F.; Ozturk, K. Chemical Composition of Apricots Affected by Fruit Size and Drying Methods. Dry. Technol. 2018, 36, 1937–1948. [Google Scholar] [CrossRef]
- Türkyılmaz, M.; Tağı, S.; Özkan, M. Changes in Chemical and Microbial Qualities of Dried Apricots Containing Sulphur Dioxide at Different Levels During Storage. Food Bioprocess Technol. 2013, 6, 1526–1538. [Google Scholar] [CrossRef]
- Sağırlı, F.; Tağı, S.; Özkan, M.; Yemiş, O. Chemical and Microbial Stability of High Moisture Dried Apricots During Storage. J. Sci. Food Agric. 2008, 88, 858–869. [Google Scholar] [CrossRef]
- Madrau, M.C.; Piscopo, A.; Sanguinetti, A.M.; Del Caro, A.; Poiana, M.; Romeo, F.V.; Piga, A. Effect of Drying Temperature on Polyphenolic Content and Antioxidant Activity of Apricots. Eur. Food Res. Technol. 2009, 228, 441–448. [Google Scholar] [CrossRef]
- Mir, M.A.; Hussain, P.R.; Fouzia, S.; Rather, A.H. Effect of Sulphiting and Drying Methods on Physic-Chemical and Sensorial Quality of Dried Apricots During Ambient Storage. Int. J. Food Sci. Technol. 2009, 44, 1157–1166. [Google Scholar] [CrossRef]
- Torreggiani, D.; Bertolo, G. Osmotic Pre-treatment in Fruit Processing: Chemical, Physical and Structural Effects. J. Food Eng. 2001, 49, 247–253. [Google Scholar] [CrossRef]
- Sakooei-Vayghan, R.; Peighambardoust, S.H.; Hesari, J.; Peressini, D. Effects of Osmotic Dehydration (with and without sonication) and Pectinbased Coating Pretreatments on Functional Properties and Color of Hot-Air Dried Apricot Cubes. Food Chem. 2020, 311, 125978. [Google Scholar] [CrossRef] [PubMed]
- Ispir, A.; Togrul, I.T. The Influence of Application of Pretreatment on the Osmotic Dehydration of Apricots. J. Food Process. Preserv. 2009, 33, 58–74. [Google Scholar] [CrossRef]
- Ciurzynska, A.; Kowalska, H.; Czajkowska, K.; Lenart, A. Osmotic Dehydration in Production of Sustainable and Healthy Food. Trends Food Sci. Technol. 2016, 59, 186–192. [Google Scholar] [CrossRef]
- Rastogi, N.K.; Niranjan, K. Enhanced Mass Transfer During Osmotic Dehydration of High Pressure Treated Pineapple. J. Food Sci. 1998, 63, 508–511. [Google Scholar] [CrossRef]
- Wiktor, A.; Sledz, M.; Nowacka, M.; Chudoba, T.; Witrowa-Rajchert, D. Pulsed Electric Field Pretreatment for Osmotic Dehydration of Apple Tissue: Experimental and Mathematical Modeling Studies. Dry. Technol. 2014, 32, 408–417. [Google Scholar] [CrossRef]
- Nowacka, M.; Wiktor, A.; Sledz, M.; Jurek, N.; Witrowa-Rajchert, D. Drying of Ultrasound Pretreated Apple and its Selected Physical Properties. J. Food Eng. 2012, 113, 427–433. [Google Scholar] [CrossRef]
- Vega-Galaves, A.; Uribe, E.; Perez, M.; Tabilo-Munizaga, G.; Vegara, J.; Garcia-Segovia, P.; Lara, E.; Di Scala, K. Effect of High Hydrostatic Pressure Pretreatment on Drying Kinetics, Antioxidant Activity, Firmness and Microstructure of Aloe Vera (Aloe barbadensis Miller) gel. LWT 2011, 44, 384–391. [Google Scholar] [CrossRef]
- Rodríguez, M.M.; Rodriguez, A.; Mascheroni, R.H. Color, Texture, Rehydration Ability and Phenolic Compounds of Plums Partially Osmodehydrated and Finish-Dried by Hot Air. J. Food Process. Preserv. 2015, 39, 2647–2662. [Google Scholar] [CrossRef]
- Riva, M.; Campolongo, S.; Leva, A.A.; Maestrelli, A.; Torreggiani, D. Structure–Property Relationships in Osmo-Air-Dehydrated Apricot Cubes. Food Res. Int. 2005, 38, 533–542. [Google Scholar] [CrossRef]
- Mrad, N.D.; Bonazzi, B.; Boudhrioua, N.; Kechaou, N.; Courtois, F. Influence of Sugar Composition on Water Sorption Isotherms and on Glass Transition in Apricots. J. Food Eng. 2012, 111, 403–411. [Google Scholar] [CrossRef]
- Kešelj, K.; Babić, M.; Pavkov, I.; Radojčin, M.; Stamenković, Z.; Tekić, D.; Ivanišević, M. Effects of Storage and Sulfurization with Sulfur Dioxide of Different Concentration on Changes in the Color of Cried Apricots. J. Process. Energy Agric. 2019, 23, 190–194. [Google Scholar] [CrossRef]
- Pavkov, I.; Babić, L.; Babić, M. Mathematical Model of the Apricot Kinetic Osmotic Drying. J. Process. Energy Agric. 2007, 11, 98–101. (In Serbian). Available online: https://scindeks.ceon.rs/article.aspx?artid=1450-50290703098P (accessed on 7 December 2020).
- Ispir, A.; Togrul, I.T. Osmotic Dehydration of Apricot: Kinetics and the Effect of Process Parameters. Chem. Eng. Res. Des. 2009, 87, 166–180. [Google Scholar] [CrossRef]
- Khoyi, M.R.; Hesari, J. Osmotic Dehydration Kinetics of Apricot Using Sucrose Solution. J. Food Eng. 2007, 78, 1355–1360. [Google Scholar] [CrossRef]
- Rahimi, J.; Singh, A.; Adewale, P.O.; Adedeji, A.A.; Ngadi, M.O.; Raghavan, V. Effect of Carboxylmethyl Cellulose Coating and Osmotic Dehydration on Freeze Drying Kinetics of Apple Slice. Foods 2013, 2, 170–182. [Google Scholar] [CrossRef] [PubMed]
- Pavkov, I.; Babić, L.; Babić, M.; Radojčin, M. Kinetics of the Combined Drying Technology of Pear Slice (Pyrus). J. Process. Energy Agric. 2009, 13, 111–116. Available online: https://scindeks.ceon.rs/article.aspx?artid=1821-44871104217P (accessed on 10 December 2020).
- Mohsenin, N.N. Physical Properties of Plant and Animal Materials; Gordon and Breach Sci. Publ.: New York, NY, USA, 1986; pp. 23–25. [Google Scholar]
- Radojčin, M.; Babić, M.; Pavkov, I.; Stamenković, Z. Osmotic Drying Effects on the Mass Transfer and Shrinkage of Quince tissue. J. Process. Energy Agric. 2015, 19, 113–119. Available online: https://scindeks.ceon.rs/article.aspx?artid=1821-44871503113R (accessed on 10 December 2020).
- Assis, F.R.; Morais, R.M.S.C.; Morais, A.M.M.B. Mathematical Modeling of Osmotic Dehydration Kinetics of Apple Cubes. J. Food Process. Preserv. 2017, 41, 1–16. [Google Scholar] [CrossRef]
- Lewis, W.K. The Rate of Drying of Solid Materials. ACES 1921, 13, 427–432. [Google Scholar] [CrossRef]
- Page, C. Factors Influencing the Maximum Rates of Air Drying of Shelled Corn in Thin Layer. Master’s Thesis, Purdue University, Lafayette, IN, USA, 1949. Unpublished work. [Google Scholar]
- Overhults, D.G.; White, H.E.; Hamilton, H.E.; Ross, I.J. Drying Soybeans With Heated Air. Trans. ASAE 1973, 16, 112–113. [Google Scholar] [CrossRef]
- Yagcıoglu, A.; Degirmencioglu, A.; Cagatay, F. Drying Characteristics of Laurel Leaves Under Different Drying Conditions. In Proceedings of the 7th International Congress on Agricultural Mechanization and Energy, Adana, Turkey, 26–27 May 1999; pp. 565–569. [Google Scholar]
- Henderson, S.M.; Pabis, S. Grain drying theory I. Temperature Effect on Drying Coefficient. J. Agric. Eng. Res. 1961, 6, 169–174. [Google Scholar]
- Karathanos, V.T.; Belessiotis, V.G. Application of a Thin Layer Equation to Drying Data of Fresh and Semi-Dried Fruits. J. Agric. Eng. Res. 1999, 74, 355–361. [Google Scholar] [CrossRef]
- Verma, L.R.A.; Bucklin, J.B.; Endan, F.T.W. Effects of Drying Air Parameters on Rice Drying Models. Trans. ASABE 1985, 28, 296–301. [Google Scholar] [CrossRef]
- Henderson, S.M. Progress in Developing the Thin Layer Drying Equation. Trans. ASABE 1974, 17, 1167–1172. [Google Scholar] [CrossRef]
- Yaldız, O.; Ertekin, C. Thin Layer Solar Drying Some Different Vegetables. Dry. Technol. 2001, 19, 583–596. [Google Scholar] [CrossRef]
- Kassem, A.S. Comparative Studies on Thin Layer Drying Models for Wheat. In Proceedings of the 13th International Congress on Agricultural Engineering, Rabat, Morocco, 2–6 February 1998; Bartali, E.H., Ed.; ANAFIDE: Rabat, Morocco, 1998. [Google Scholar]
- Crank, J. Mathematics of Diffusion, 2nd ed.; Clarendon Press: Oxford, UK, 1975; pp. 24–68. [Google Scholar]
- Kayran, S.; Doymaz, I. Infrared Drying and Effective Moisture Diffusivity of Apricot Halves: Influence of Pretreatment and Infrared Power. J. Food Process. Preserv. 2017, 41, 1–8. [Google Scholar] [CrossRef]
- Ruiz-Lopez, I.I.; Ruiz-Espinosa, H.; Luna-Guevara, M.L.; Garcia-Alvarado, M.A. Modeling and Simulation of Heat and Mass Transfer During Drying of Solids With Hemispherical Shell Geometry. Comput. Chem. Eng. 2011, 35, 191–199. [Google Scholar] [CrossRef]
- Bon, J.; Simal, S.; Rossello, C.; Mulet, A. Drying Characteristic of Hemispherical Solids. J. Food Eng. 1997, 34, 109–122. [Google Scholar] [CrossRef]
- Togrul, I.T.; Ispir, A. Effect on Effective Diffusion Coefficients and Investigation of Shrinkage During Osmotic Dehydration of Apricot. Energy Convers. Manag. 2007, 48, 2611–2621. [Google Scholar] [CrossRef]
- Junior, J.L.B.; Mancini, M.C.; Hubinger, M.D. Mass Transfer Kinetics and Mathematical Modeling of the Osmotic Dehydration of Orange-Fleshed Honeydew Melon in Corn Syrup and Sucrose Solutions. Int. J. Food Sci. Technol. 2013, 48, 2463–2473. [Google Scholar] [CrossRef]
- Archibald, R.; Melton, L. The Anatomy of the Fleshy Pericarp of Maturing Moorpac Apricots, Prunus Armeniaca. N. Z. J. Bot. 1987, 25, 181–184. [Google Scholar] [CrossRef]
- Mandala, I.G.; Anagnostaras, E.F.; Oikonomou, C.K. Influence of Osmotic Dehydration Conditions on Apple Air Drying Kinetics and their Quality Characteristics. J. Food Eng. 2005, 69, 307–316. [Google Scholar] [CrossRef]
- Barat, J.M.; Fito, P.; Chiralt, A. Modeling of Simultaneous Mass Transfer and Structural Changes in Fruit Tissues. J. Food Eng. 2001, 49, 77–85. [Google Scholar] [CrossRef]
- Yang, J.; Di., Q.; Jiang, Q.; Zhao, J. Application of Pore Size Analyzers in Study of Chinese Angelica Slices Drying. Dry. Technol. 2010, 28, 214–221. [Google Scholar] [CrossRef]
- Guine, R.P.F.; Castro, J.A.A.M. Pear Drying Process Analysis: Drying Rates and Evaluation of Water and Sugar Concentrations in Space and Time. Dry. Technol. 2002, 20, 1515–1526. [Google Scholar] [CrossRef]
- Bozkir, O. Thin-layer Drying and Mathematical Modeling for Washed Dry Apricots. J. Food Eng. 2006, 77, 146–151. [Google Scholar] [CrossRef]
- Sankat, C.K.; Castaigne, F.; Maharaj, R. The Air Drying Behaviour of Fresh and Osmotically Dehydrated Banana Slices. Int. J. Food Sci. Technol. 1996, 3, 123–135. [Google Scholar] [CrossRef]
- Azoubel, P.M.; El-Aouar, A.A.; Tonon, R.V.; Kurozawa, L.M.; Graziella, C.A.; Murr, F.E.X.; Park, K.J. Effect of Osmotic Dehydration on the Drying Kinetics and Quality of Cashew Apple. Int. J. Food Sci. Technol. 2009, 44, 980–986. [Google Scholar] [CrossRef]
- Igual, M.; Garcia-Martinez, E.; Martina-Espraza, M.E.; Martinez-Navarrete, N. Effect of Processing on the Drying Kinetics and Functional Value of Dried Apricot. Food Res. Int. 2012, 47, 284–290. [Google Scholar] [CrossRef]
- Doymaz, I. Effect of Pre-treatments Using Potassium Metabisulphide and Alkaline Ethyl Oleate on the Drying Kinetics of Apricots. Biosyst. Eng. 2004, 89, 281–287. [Google Scholar] [CrossRef]
- Bon, J.; Rossello, C.; Femenia, A.; Eim, V.; Simal, S. Mathematical Modeling of Drying Kinetics for Apricots: Influence of the External Resistance to Mass Transfer. Dry. Technol. 2007, 25, 1829–1835. [Google Scholar] [CrossRef]
- Krzykowski, A.; Dziki, D.; Rudy, S.; Gawlik-Dziki, U.; Janiszewska-Turak, E.; Biernacka, B. Wild Strawberry Fragaria vesca L.: Kinetics of Fruit Drying and Quality Characteristics of the Dried Fruits. Processes 2020, 8, 1265. [Google Scholar] [CrossRef]



| Model Number | Model Name | Model Equation | References |
|---|---|---|---|
| 1 | Newton 1 | MR = exp(−kτ) | [31] |
| 2 | Page | MR = exp(−kτn) | [32] |
| 3 | Modified Page | MR = exp(−(kt)n) | [33] |
| 4 | Logarithmic | MR = a exp(−kτ) + b | [34] |
| 5 | Henderson and Pabis | MR = a exp(−kt) | [35] |
| 6 | Modified Henderson and Pabis | MR = a exp(−k1τ)+ b exp(−k2τ) + c exp(−k3τ) | [36] |
| 7 | Verma | MR = a exp(−k1τ) + (1 − a) exp(−k2τ) | [37] |
| 8 | Two Term | MR = a exp(−k1τ) + b exp(−k2τ) | [38] |
| 9 | Two Term Exponential | MR = a exp(−kt) + (1 − a) exp(−kat) | [39] |
| 10 | Diffusion Approach | MR = a exp(−kt) + (1 − a) exp(−kbt) | [40] |
| 1 t (°C) | C (%) | WL (kg H2O/kg d.m.) | SG (kg d.m./kg i.d.m.) | Ratio WL/SG (−) |
|---|---|---|---|---|
| 40 | 50 | 3.832 ± 0.402 c | 0.394 ± 0.004 b | 9.711 |
| 40 | 65 | 4.429 ± 0.390 bc | 0.478 ± 0.059 c | 9.258 |
| 60 | 50 | 4.578 ± 0.441 ba | 0.517 ± 0.017 cb | 8.843 |
| 60 | 65 | 5.214 ± 0.018 a | 0.568 ± 0.013 a | 9.219 |
| Parameter | 1 t | C | kw1 or s1 | kw2 or s2 | R2 | RMSE | χ2 | CRV |
|---|---|---|---|---|---|---|---|---|
| WL | 40 | 50 | 11.544 | 0.200 | 0.9955 | 0.0767 | 0.0073 | 3.258 |
| 65 | 13.0325 | 0.1597 | 0.9937 | 0.0153 | 0.0135 | 4.055 | ||
| 60 | 50 | 8.5438 | 0.1724 | 0.9985 | 0.0527 | 0.0034 | 1.827 | |
| 65 | 6.0601 | 0.1646 | 0.9916 | 0.1369 | 0.0234 | 4.188 | ||
| SG | 40 | 50 | 155.82 | 1.6133 | 0.9916 | 0.0114 | 0.0001 | 5.195 |
| 65 | 176.64 | 1.1571 | 0.9889 | 0.0153 | 0.0002 | 6.372 | ||
| 60 | 50 | 120.99 | 1.2826 | 0.9948 | 0.0115 | 0.0001 | 4.113 | |
| 65 | 80.298 | 1.3699 | 0.9872 | 0.0188 | 0.0044 | 5.851 |
| Osmotic Solution | Water Loss | Solid Gain | |||||
|---|---|---|---|---|---|---|---|
| 1 t
(°C) |
C (%) |
Dew (m2/s) | R2 |
WLeq (kg H2O/kg d.m.) |
Des (m2/s) | R2 |
SGeq (kg d.m./kg i.d.m.) |
| 40 | 50 | 5.500 × 10−9 | 0.9337 | 7.11 ± 0.17 | 8.315 × 10−10 | 0.9165 | 0.476 ± 0.051 |
| 65 | 6.149 × 10−9 | 0.9675 | 7.75 ± 0.36 | 1.00 × 10−9 | 0.9527 | 0.593 ± 0.036 | |
| 60 | 50 | 6.728 × 10−9 | 0.9144 | 7.47 ± 0.21 | 1.076 × 10−9 | 0.9131 | 0.562 ± 0.017 |
| 65 | 7.387 × 10−9 | 0.9183 | 7.93 ± 0.14 | 1.113 × 10−9 | 0.8831 | 0.783 ± 0.044 | |
| Model | Pretreatment | Air Velocity (m/s) | Air Temperature (°C) | R2 | RMSE | χ2 | CRV (%) |
|---|---|---|---|---|---|---|---|
| Logarithmic | Control | 1.0 | 40 | 0.9991 | 0.0073 | 0.00006 | 1.8987 |
| 50 | 0.9998 | 0.0040 | 0.00002 | 1.4648 | |||
| 60 | 0.9994 | 0.0071 | 0.00006 | 3.2927 | |||
| 1.5 | 40 | 0.9981 | 0.0108 | 0.00013 | 2.8735 | ||
| 50 | 0.9996 | 0.0055 | 0.00003 | 2.2259 | |||
| 60 | 0.9991 | 0.0083 | 0.00008 | 4.2288 | |||
| OD1 1 | 1.0 | 40 | 0.9995 | 0.0053 | 0.00003 | 1.2226 | |
| 50 | 0.9996 | 0.0051 | 0.00003 | 1.5199 | |||
| 60 | 0.9995 | 0.0062 | 0.00004 | 2.4909 | |||
| 1.5 | 40 | 0.9989 | 0.0081 | 0.00008 | 1.9853 | ||
| 50 | 0.9993 | 0.0070 | 0.00006 | 2.2776 | |||
| 60 | 0.9992 | 0.0078 | 0.00007 | 3.2759 | |||
| OD2 | 1.0 | 40 | 0.9996 | 0.0044 | 0.00002 | 0.9191 | |
| 50 | 0.9999 | 0.0028 | 0.00001 | 0.7534 | |||
| 60 | 0.9994 | 0.0065 | 0.00005 | 2.4677 | |||
| 1.5 | 40 | 0.9991 | 0.0067 | 0.00005 | 1.4597 | ||
| 50 | 0.9997 | 0.0044 | 0.00002 | 1.2701 | |||
| 60 | 0.9997 | 0.0045 | 0.00002 | 1.7620 |
| Model | Pretreatment | Air Velocity (m/s) | Air Temperature (°C) | a 1 (−) | b (−) | k (min−1) |
|---|---|---|---|---|---|---|
| Logarithmic | Control | 1.0 | 40 | 0.9558 | 0.0256 | 0.0016 |
| 50 | 0.9828 | 0.0070 | 0.0025 | |||
| 60 | 1.0250 | −0.0287 | 0.0030 | |||
| 1.5 | 40 | 0.9360 | 0.0313 | 0.0017 | ||
| 50 | 0.9696 | 0.0155 | 0.0029 | |||
| 60 | 1.0135 | −0.0193 | 0.0034 | |||
| OD1 | 1.0 | 40 | 0.9649 | 0.0192 | 0.0014 | |
| 50 | 0.9747 | 0.0094 | 0.0019 | |||
| 60 | 1.0349 | −0.0474 | 0.0024 | |||
| 1.5 | 40 | 0.9557 | 0.0178 | 0.0014 | ||
| 50 | 0.9624 | 0.0146 | 0.0022 | |||
| 60 | 1.0122 | −0.0297 | 0.0026 | |||
| OD2 | 1.0 | 40 | 0.9576 | 0.0279 | 0.0012 | |
| 50 | 0.9193 | 0.0715 | 0.0019 | |||
| 60 | 0.9985 | 0.0050 | 0.0027 | |||
| 1.5 | 40 | 0.9268 | 0.0507 | 0.0013 | ||
| 50 | 0.9060 | 0.0797 | 0.0022 | |||
| 60 | 0.9756 | 0.0236 | 0.0029 |
| Pretreatment | Air Velocity (m/s) | Air Temperature (°C) | Deff 1 (m2/s) | R2 |
|---|---|---|---|---|
| Control | 1.0 | 40 | 5.431 × 10−10 | 0.999 |
| 50 | 8.933 × 10−10 | 0.998 | ||
| 60 | 1.585 × 10−9 | 0.957 | ||
| 1.5 | 40 | 5.984 × 10−10 | 0.999 | |
| 50 | 9.328 × 10−10 | 0.994 | ||
| 60 | 1.970 × 10−9 | 0.988 | ||
| OD1 | 1.0 | 40 | 4.028 × 10−10 | 0.999 |
| 50 | 5.662 × 10−10 | 0.999 | ||
| 60 | 1.065 × 10−9 | 0.887 | ||
| 1.5 | 40 | 4.304 × 10−10 | 0.999 | |
| 50 | 6.103 × 10−10 | 0.999 | ||
| 60 | 1.262 × 10−9 | 0.987 | ||
| OD2 | 1.0 | 40 | 3.002 × 10−10 | 0.999 |
| 50 | 4.198 × 10−10 | 0.994 | ||
| 60 | 6.777 × 10−10 | 0.991 | ||
| 1.5 | 40 | 3.019 × 10−10 | 0.999 | |
| 50 | 4.513 × 10−10 | 0.990 | ||
| 60 | 7.259 × 10−10 | 0.983 |
| Pretreatment | Air Velocity (m/s) | Ea1 (kJ/mol) | R2 |
|---|---|---|---|
| Control | 1.0 | 46.379 | 0.996 |
| 1.5 | 51.514 | 0.973 | |
| OD1 | 1.0 | 42.005 | 0.953 |
| 1.5 | 46.469 | 0.974 | |
| OD2 | 1.0 | 35.216 | 0.985 |
| 1.5 | 37.987 | 0.995 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pavkov, I.; Radojčin, M.; Stamenković, Z.; Kešelj, K.; Tylewicz, U.; Sipos, P.; Ponjičan, O.; Sedlar, A. Effects of Osmotic Dehydration on the Hot Air Drying of Apricot Halves: Drying Kinetics, Mass Transfer, and Shrinkage. Processes 2021, 9, 202. https://doi.org/10.3390/pr9020202
Pavkov I, Radojčin M, Stamenković Z, Kešelj K, Tylewicz U, Sipos P, Ponjičan O, Sedlar A. Effects of Osmotic Dehydration on the Hot Air Drying of Apricot Halves: Drying Kinetics, Mass Transfer, and Shrinkage. Processes. 2021; 9(2):202. https://doi.org/10.3390/pr9020202
Chicago/Turabian StylePavkov, Ivan, Milivoj Radojčin, Zoran Stamenković, Krstan Kešelj, Urszula Tylewicz, Péter Sipos, Ondrej Ponjičan, and Aleksandar Sedlar. 2021. "Effects of Osmotic Dehydration on the Hot Air Drying of Apricot Halves: Drying Kinetics, Mass Transfer, and Shrinkage" Processes 9, no. 2: 202. https://doi.org/10.3390/pr9020202
APA StylePavkov, I., Radojčin, M., Stamenković, Z., Kešelj, K., Tylewicz, U., Sipos, P., Ponjičan, O., & Sedlar, A. (2021). Effects of Osmotic Dehydration on the Hot Air Drying of Apricot Halves: Drying Kinetics, Mass Transfer, and Shrinkage. Processes, 9(2), 202. https://doi.org/10.3390/pr9020202










