Combined Approach to Analysis and Regulation of Thermodynamic Processes in the Energy Technology Complex

Abstract

The purpose of this work is to increase the theoretical and methodological approaches to value and regulate the dynamics of management processes. Application of these dynamics is implemented via methods of improving the quality of management of complex energy technology systems in the organization of recycling processes. As a result of the research, a technological model of a rotary kiln with a division into separate sections corresponding to the combustion zones for the production of cement clinker in recycling technology was developed. Mathematical modeling, analytical calculations of thermodynamic and gas-dynamic processes in the drums of rotating furnaces, and experimental studies were carried out. As a scientific novelty, an approximation of piecewise linear functions is obtained for modeling the processes of improving the quality of control by the criterion of reducing the error of data transmission for monitoring and regulating the thermodynamic parameters of the furnace via analog-to-digital methods. An algorithmic scheme of the method of in-depth analysis of management quality using data science tools in the concept of combining organizational, economic, technical, technological, and mathematical methods and methods of data collection, processing, and storage of big data is developed. This made it possible to apply the models in the formed energy technology complex using learning neural network algorithms. The possibilities of applying the methodology of combining methods for in-depth analysis and modeling of thermodynamic processes in an energy technological complex with any composition of equipment for the production of cement clinker are substantiated.

1. Introduction

This article proposes a combined approach to improving the energy, environmental, and economic efficiency of industrial power engineering devices. This was done using the combination or consistent application of organizational, technical, technological, and mathematical models and methods of analysis and regulation of thermodynamic processes. This approach provides a more complete use of the results of process modeling to achieve the quality of regulation of thermodynamic processes in the formed energy technological complex of technical devices and technologies of industrial energy according to the criterion of the overall efficiency of processes.

The complexity of integrated assessment and regulation of thermodynamic parameters of power technology installations determines the need to combine organizational, technical, technological, and mathematical models and methods for improving quality and efficiency. The dynamics and variety of thermodynamic parameters make it necessary to use a large database derived from big data. A particular problem is presented by processes whose thermodynamic parameters change abruptly or exponentially. This makes it necessary to use piecewise linear functions that are widely used in electronics to represent signal transmission processes. These features determine the additional use of tools for deeper analysis and digital modeling of processes in data science [1]. It is based on providing real-time control and regulation using neural network algorithms for deep machine learning using artificial intelligence. Such processes occur, for example, when regulating the energy efficiency of rotary kilns for the production of building materials in the transition from the use of traditional raw materials to resources of recycled origin in the production of cement clinker. Such a transition to a high-tech process is effective according to the criteria for ensuring total efficiency, considering the energy and technology complex (ETC). At the same time, there is often a decrease in the stability of development processes due to abrupt changes in the structure of relationships between its objects.

The insufficient level of total efficiency of these technologies and methods of regulation requires radical improvements. They are often distinguished by the singularity (unusual) of the processes of transition to new technologies, methods of analysis, and regulation of processes. This can be expressed in exponential, hyperbolic, or even abrupt (for example, sawtooth form of signals) changes in indicators/properties of total efficiency with zero or minimal transition time to a new level. This is due to the challenges of the external environment of developed countries with economies of the fifth to sixth order, when nature is needed, as well as the resource-saving transformation of public consciousness, defined as “high-hume” methods. In many countries, the prevailing conditions of the first to third organizational and technological structures of the economy, i.e., the evolutionary processes of applying technologies and methods, are characterized by relatively low indicators of total efficiency and the speed of their changes. During the transition to the fourth OTS (organizational and technological structure), the dynamics of indicators gradually increases on the basis of scaling the levels of innovative transformations achieved in the past and the modernization of products, works or services, technologies, and management methods. Revolutionary processes of high-tech transformations of the material type (the term is widely used in the world of “high-tech” practice) are necessary in the transition to the fifth and, especially, the sixth modes of economy. The complexity of interconnections between energy and industrial facilities determines the need for the proposed concept of combining organizational/economic, energy technological, and mathematical methods as a tool for describing and ensuring total efficiency. Overcoming the growing discrepancies in the assessment of differences in the level and dynamics of transformation necessitates the task of reducing the contradiction between the objectively evolutionarily increasing cost of fuel, materials, and raw materials of industry and the inappropriate increase in the efficiency of the equipment using them. The discrepancy between the lack of innovative capabilities of low-tech equipment and the emerging unique needs for energy saving is investigated. It is advisable to refer to the experience and forecasts of developed countries; in Germany, by 2025, energy facilities consuming nuclear and coal fuels should be closed, and, by 2035, the share of energy resources should be 8% [2]. At the same time, the volumes of a new type of material resource with the energy potential of development, i.e., solid household waste in the amount of about 0.5 billion tons or 500 kg/person, are added every year [3,4]. The unsolved problems of energy saving determine the need to improve the quality of assessment and regulation of the dynamics of processes for controlling the thermodynamic parameters of power plants.

In accordance with the strategy for the development of post-carbon energy for existing production facilities, this article provides solutions to three tasks aimed at achieving the goal. General task 1 is to justify and organize a set of measures in projects to reduce anthropogenic loads on the environment, thereby creating resource- and energy-saving technologies at individual installations. The formation of an ETC leads to an abrupt increase in the amount of data required for the development of measures. The problem is partially solved by poorly effective methods of traditional analysis based on big data, requiring data filtering. Therefore, task 2 is solved using the tools of deeper analysis and digital modeling in a comprehensive method for evaluating and modeling processes in data science [1,5,6,7]. It is based on providing real-time management of complex systems using neural network algorithms for deep machine learning using artificial intelligence. The increase in dynamics is achieved via new capabilities for obtaining a machine-readable type of signal transmission control system at the output of the developed system to increase the speed and reliability of evaluating and regulating the parameters of the power plant. Task 3 is to develop a set of basic equipment that generates heat and electricity, including objects of mechanics, electric drive technology, and automation of data collection for the results of the application of methods in data science.

The purpose of this work is to increase the theoretical and methodological approaches to value and regulate dynamics of management processes. Application of these dynamics is implemented via methods of improving the quality of management of complex energy technology systems in the organization of recycling processes.

Review of the Authors’ Research on the Topic of the Article

Ongoing research on the application of neural network technologies in the energy sector is concentrated in the field of regulation [8]. This paper proposes to take into account the world experience on the basis of obtained experimental data, combine calculation methods, and introduce adaptive weight coefficients for them. The author has studied coal dust combustion for a long time and has experience that allows us to assess the reliability of the results of neural network forecasting in this area [9]. In addition, for the first time in the world, it is proposed to link the experimental data obtained using new approximation methods with the theory of heat and mass transfer. New approximation methods have already been successfully applied by the author [10]. For a similar combustion problem, the author has a theoretical basis for research [11]. Studies of the processes of combustion and preparation of solid fuels are conducted by scientists in many countries. The most complete understanding of the preparation of coal dust at thermal power plants can be obtained in [12]. One of the main conditions for efficient and high-quality combustion of solid fuel is to take into account its poly-fraction composition, which was confirmed by mathematical models of the authors [13], in addition to the presence of a sufficient amount of air as an oxidizer and the fineness of grinding coal dust, as noted in [14]. There are different models of fuel combustion. In addition, we should not forget about the basics of the theory of practical combustion, which developed in parallel with research in the field of mathematical modeling. In the context of the lack of natural gas in some coal-producing countries, new methodological approaches to solving the problems of lignite sieving and burning have begun to develop. In [12], the topic of dust sieving with approximation of the obtained results was raised for the first time, which was subsequently reflected in the already mentioned work. Modern computer programs for mathematical modeling of the coal dust combustion process take into account the thermophysical characteristics of the fuel, i.e., the average determining (equivalent) particle size. It should be noted that the existing software packages provide an idea of the distribution of temperature, velocity, and concentration fields, which are associated with known dependencies, but the accuracy and reliability of the results obtained do not always meet the criteria necessary to start designing a boiler unit or changing dust preparation systems. In any case, it is necessary to conduct experimental studies and compare them with the results of computer modeling. The solution of the problem identified by the author will increase the accuracy of modeling.

Studies by such authors as Rosendahl support the theory of the weak methodological security of heat transfer processes in high-temperature installations; this researcher together with Mando published an article with a unique mathematical model [15]. In [16], Asotani et al. also considered a model of the behavior of coal particles in a mixture with air, and the proposed mathematical model correlated well with [15], as well as with some provisions of the authors’ proposals [17]. The mathematical models proposed in the review do not contradict each other, nor do they contradict the fundamental laws of physics, particularly heat transfer.

In this study, the authors propose an algorithm for a holistic understanding of the content of the article, its purpose, methods, and methodology.

At the beginning of the article, the theoretical justification of the application of the technology is given, and the basic principles underlying the creation of a new technology are identified. Results encompass new knowledge about the formation of thermodynamic and economic analysis in order to optimize the operation of a thermal power plant according to the study of applicable thermodynamic, mechanical, heat, and mass transfer and management laws. Scientific significance constitutes obtaining essential and important new knowledge for the world science. The applied significance lies in the use of this knowledge to create a computer model of a thermal power plant.

Furthermore, the authors propose to formulate the concept of technology, along with scientific justification of the concept, to search for technological approaches allowing the implementation of the concept, to identify advantages over alternative approaches, to determine the feasibility of further development of the technological concept, and to assess the risks of its implementation. The planned result includes the methods of applying the previously studied phenomena and the acquired knowledge to solve practical problems of maximum optimization of the power plant operation, in addition to the presentation of the results in a scientific and technical report on the research work, with results of the study of a computer model. The scientific significance lies in the creation of new knowledge important for the world of science in the form of universal algorithms. The applied significance lies in the use of this knowledge to create software that implements the algorithm of the power plant.

Experimental proof of concept, modeling, and testing are provided. The final goal of the research is to test the operability of the software on existing power plants, whereby the scientific significance also lies in the universalization of the created solutions, which is important for the global energy industry and creates prerequisites for a significant economic effect. The applied significance lies in the replication of the created software on a global scale.

2. Materials and Methods

The proposed method of technical and economic analysis can be considered as one of the steps to complete digitalization of control systems for new-generation thermal power plants.

The proposed study aims at a systematic study of nonoptimal modes of operation of thermal power plants using knowledge of the laws of mechanics, thermodynamics, heat, and mass transfer and management, as well as the development of algorithms and software for optimization of the control system of a thermal power complex.

The top-level program with elements of artificial intelligence, embedded in the control system to optimize the operation of the power plant, is adaptive and trainable. When the program is first turned on, it must test the sensor system of the power plant. After the power plant operation mode is stabilized, the self-learning system records the sensor readings.

The research is analyzed, the main stages of development of the energy method of thermodynamic analysis of heat exchange devices and processes are highlighted, and the most promising developments in the field of thermodynamics and thermo-economic analysis are identified.

Methodological approaches for economic and thermodynamic analysis using new methods of approximation of piecewise linear functions are developed. In addition, it is proposed to use this method not only to optimize heat losses, but also to analyze exergy according to the fundamental principles of physics.

In addition to the above calculations, all measurement divergences can be calculated using a mathematical model that is developed taking into account the results of thermodynamic modeling.

Thus, the project is aimed at combining the algorithm of the economic analysis method and the power plant control algorithm according to the analysis of the sensor data array.

The approach is proposed for the first time, as the authors have not identified any analogues in publications, patents, and programs. Accordingly, the proposed method can be adapted for any control system of a thermal power plant of any capacity. Thus, the proposed methods and approaches allow us to successfully solve the tasks set and complete the project at a level significantly higher than the world level.

The conditions of the singularity of development correspond to many forecasts, confirming the well-known methodological proposals of Adizes [18] that favor creating biosimilar management structures of “live” organizations. Sen and Lalu noted that [19,20] holacratic flexible (agile) methods of creating self-governing teams of different profiles are effective. They correspond to the spiral dynamics model of the so-called “turquoise enterprises” [20]. However, including the competent personnel in the control and regulation system does not solve the problems. The quality of control of thermodynamic parameters of power technological installations due to the inclusion of the human factor in the control system leads to low speed and reliability of regulation. More concrete forecasts for the development of intellectual resources by Frumin [21] highlighted the increase in the number of digital and network companies such as “Amazon”. The considered methods solve a set of problems of organizing high-tech development processes using the integration of diversified resources. However, through assessing their overall compliance with the concept of combining methods to ensure total efficiency, we can note their insufficient focus on solving these research problems.

There is a known method for controlling elements of an energy technology complex using a neural network [22], involving regulation of the water level in the drum of a power boiler unit using a Hopfield network. The disadvantage of this method is the lack of scaling in relation to various objects of heat and power engineering. The costs of implementing management tasks using deep neural networks are high due to the uniqueness of the software. The same can be said about electric heating methods [23], which are usually implemented with the release of volatile substances. This determines the increased energy consumption costs of the electric drive mechanisms, as well as the increased risk of an emergency stop due to low control reliability. By using methods in data science in terms of assessing compliance with the trends of modern development it would exclude such a technology from the list of possible options already at the stage of expert evaluation of the database.

For this reason, methods of electric heating without preliminary preparation for particle size by continuous pouring and flaring in a rotating drum reactor inclined relative to the horizontal plane are ineffective. They are also characterized by heating, release, and burning of volatile substances with the removal of a mixture of volatile substances and combustion products from the reactor into the atmosphere. The method is implemented according to the technological schemes of a number of authors [24]. The disadvantage of this method is the supply of unprepared carbon particles for activation. There are known methods that use pre-preparation of the initial product, for example [25]. The disadvantage of this method is a large loss of heat and product, as well as a large consumption of electricity.

Considerable attention was paid to the issues of automatic control of the energy technology complex in the publications of Salikhov [26,27]. The simplest control methods using neural networks in relation to rotating furnaces were studied in detail in [28,29]. However, the absence of the concept of combining methods does not provide the necessary characteristics for the depth of analysis and the quality of management according to the criterion of ensuring total efficiency.

The proposed automatic control systems are characterized by relatively low reliability due to the lack of backup channels for converting control actions and automatic diagnostics. There is also no possibility of equalizing the temperature throughout the entire volume of the furnace, which would reduce fuel consumption and atmospheric pollution during the operation of the heat and power technology complex. The main reason is also the nonuse of the proposed complex analytical method in data science in the concept of combining methods.

3. Problems of Research of Methods for Imperfection Processes for Monitoring and Regulating the Speed of Control Signals

There are two groups of models and methods for ensuring efficiency and quality: organizational/economic and technical/technological.

Performance and quality indicators are factors in the structural analysis of systems. The first ones represent an algorithm for converting resources into results of activity. Therefore, it is proposed to evaluate them using the ratio of the values of results (outputs of the system) and resources (inputs) that are different in essence and dimension. The latter determine the structure of the system in the “causes–results” ratio. Therefore, quality indicators should be evaluated in a level-by-level way by comparing performance indicators of the same name (for example, actual and target or standard fuel consumption, efficiency). The peculiarity of power engineering is that the energy and environmental efficiency of technical and technological systems is more often understood in the quality assessment. The total efficiency indicator is understood by us in the organizational and economic approach to assessing the economic effects and costs of energy and technology development.

We present a model of the processes of combining diversified resources using methods in data science. This method provides digital implementation of the total efficiency improvement project. Technical and technological problems of controlling and regulating the speed and reliability of signal transmission processes have a number of aspects. The most significant and quick solutions are the following: when transmitting signals in an analog way, there may be oscillations accompanied by the Gibbs effect, and, when transmitting a signal in a digital way, there is a “blurring” of the image. In addition, in both cases, the mathematical description of sine–cosine functions in the approximation inevitably leads to an error. The authors developed a model of a rotary kiln divided into separate zones (Figure 1). These features that determine the possibility of increasing total efficiency are especially evident in the transit zone 6, the burning zone 7, and the cooling zone of the finished product 8. Existing furnaces differ in the average thermodynamic characteristics of total efficiency shown in

Table 1. Comparative characteristics of total efficiency of rotary kilns for the production of cement clinker/recycling of raw materials [28].

Specifications	Russia	European Union
Energy: Thermodynamic efficiency	72.8/73.1	78.5/79.8
Environmental: Emissions of harmful substances into the atmosphere, CO2, mg/m3	4.8/4.0	4.2/3.4
Technical and economic: Specific heat consumption for the production of 1 kg of the finished product, kJ/kg	5403/5224	4968/4679

for two options: when using standard technology (in the numerator) and under recycling conditions (in the denominator). It should be noted that, during recycling, rotary kilns are used, the purpose of which is primarily to reduce the consequences of environmental pollution from industrial waste and emissions into the atmosphere; thus, their use is possible for various technological processes.

The development of rotary kilns for recycling materials is a rather complex and multiparametric task. The table shows the possibilities of reducing fuel consumption and improving the environmental performance of high-tech recycling processes. This confirms an increase in the thermodynamic efficiency of such an installation in comparison with a conventional rotary kiln. We need methods for optimizing fuel use according to total efficiency criteria using neural network algorithms to improve the quality of data collection, processing, and parameter control through data science tools.

The subject of the study was the processes occurring in three zones—6, 7, and 8. They are the most significant for increasing total efficiency and are described by the following well-known dependencies, characterized by a high rate of change (for example, exponential and hyperbolic types) [24,25]:

The combustion temperature is

$$T_{flame}=\frac{Q_{fuel}-Q_{air}-Q_{rad}}{V_{com.pr}\cdot C_{com.pr}},$$

(1)

where $Q_{fuel}$ is the fuel calorific value, ${\mathrm{J}/\mathrm{m}}^3$, $Q_{air}$ is the amount of heat introduced by secondary air, ${\mathrm{J}/\mathrm{m}}^3$, $Q_{rad}$ is the amount of radiant heat of the torch, ${\mathrm{J}/\mathrm{m}}^3$, $V_{com.pr}$ is the volume of combustion products, ${\mathrm{m}}^3$, and $C_{com.pr}$ is the heat capacity of combustion products, J/(m³·K).

The coefficient of the rate of chemical oxidation reaction is

$$k=A\cdot e^{-\frac{E}{RT}},$$

(2)

where $A$ is a preexponential multiplier, $e$ is the base of the natural logarithm, $E$ is the activation energy, ${\mathrm{J}/\mathrm{m}}^3$, $R$ is the gas constant of a specific fuel component, J/(m³·K), and $T$ is the ignition temperature of the component, k.

The length of the diffusion torch lf can be calculated using an empirical formula, transformed by the authors from [14].

$$l_f=d_0\cdot \left(6.4n_{air}+3.3\right)\cdot {\left({\rho }_0/{\rho }_f\right)}^{0.5},$$

(3)

where $d_0$ is the diameter of the burner mouth, m, $n_{air}$ is the mass of air theoretically required for combustion of the fuel, kg of air/kg of fuel, ${\rho }_0$ is the fuel density, kg/m³, and ${\rho }_f$ is the density of the gaseous medium in the flare, kg/m³. The exponential type of dependencies in critical zones determines special requirements for methods for evaluating and regulating the transmission of signals from automation equipment. Indeed, the quality of management of multi-zone controllers and controllers can be improved by using neural network algorithms of the ANSYS program as components of the Data Science Toolkit. The variety of estimated parameters determines significant difficulties in transmitting reliable signals from the control object to monitoring devices, which often have amplitude jumps and signal shape distortions. New mathematical methods for modeling are needed [20].

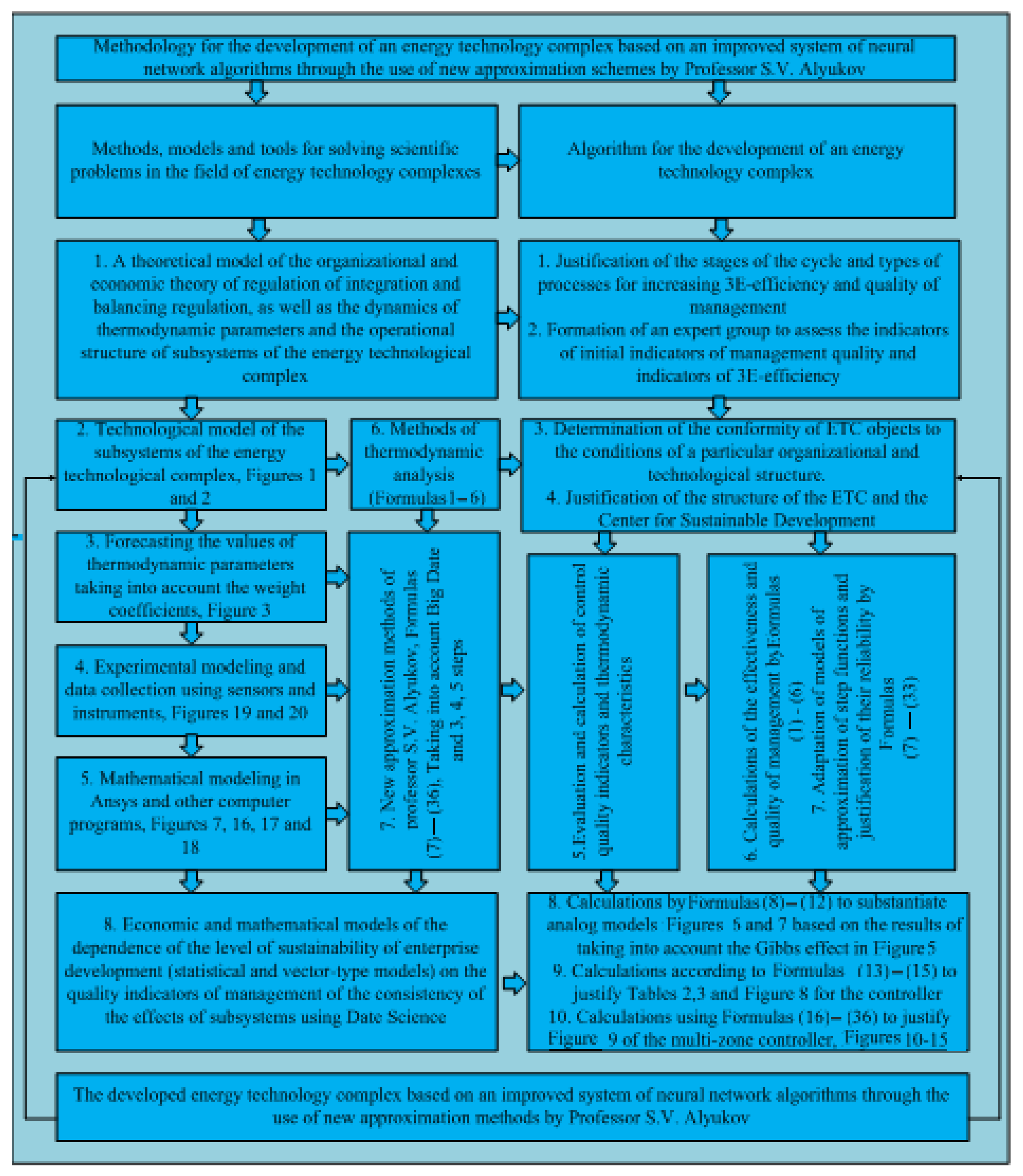
4. The Proposed Methodology: Organization of Mathematical Models and Algorithms Development Processes

We propose a special organization of information processing processes that meet the requirements of the concept of combining methods using neural networks of the Data Science Toolkit. It is necessary to ensure the use of new methods for approximating the functions of describing step-by-step processes to improve the quality of control (Figure 2). It is proposed to regulate them with special management functions used in the new organizational structure of the sustainable development center (SDC) complex [30,31]. It differs in that the center for sustainable development pays special attention to the process of collecting data using the big data method and implementing the Data Science Toolkit. The need for their processing in order to regulate and optimize the process of obtaining the final product through a more advanced and complex data science method is indicated. This will reduce a number of problems associated with management and regulation, particularly with reducing fuel and heat consumption for the production of 1 kg of finished product.

Let us describe the main elements of the proposed scheme with special management functions used in the new organizational structure of the SDC-formed ETC. This involves the function of collecting data from auxiliary equipment (pumps, fans, feeders, etc.), as well as accumulating a cloud of data from temperature and pressure sensors (performed using big data methods). Of particular importance is the function of the subsystem for monitoring and diagnosing the residual life of equipment (the initial element of the data science subsystem). It is performed by subsystems for collecting thermodynamic and gas-dynamic data from a rotating furnace, as well as a system for collecting, processing, and storing data. Other subsystems and tools of this method make it necessary to develop and apply special technical, technological, and mathematical models and methods to improve the quality of control of the relationships between the objects of the ETC and the combustion processes inside the drum of a rotating furnace.

The solution of task 2 of the study is carried out in three directions. At Step 2.1, an expert assessment of the initial state of the object under study should be carried out on the basis of a set of parameters of energy, environmental, and economic efficiency. As a result, a database is created for working with tables of the Pandas type, among others, for setting a research task for subsequent modeling. Step 2.2 is to develop or adapt mathematical models and algorithms and test them using the capabilities of trained neural networks, as well as learn algorithmic training in the generated ETC. They differ in the possibilities of approximation of piecewise linear functions of the representation of signal transmission processes from the control object to the controller that regulates parameter changes. Step 2.3 involves the development or use of computer programs (Ansys, Anaconda, Python, etc.) to determine the optimal design parameters of the power and process plant. Therefore, the methodological approach to the formation of an energy technology complex in the concept of combining methods using the Data Science Toolkit should be distinguished by using the capabilities of two-layer neural networks for mathematical modeling of processes, as well as justifying the choice of parameters and ways to increase energy, environmental, and economic efficiency. The multilayered nature of networks and the requirements for the depth of total efficiency analysis determined the choice of the big data collection method.

To implement the Step 2.1 design methodologies presented above, the original state of the object is characterized by the above parameters of total effectiveness of the system of heat and power and technological equipment which generated a complex (see Table 1) for rotary kilns: the product produced, the fuel burned, the excess air coefficient, the product temperature, the torch temperature, the furnace body temperature, and others necessary for further modeling. To assess the possibilities of increasing this level, it is necessary to use the main theoretical dependences of indicators/properties of total efficiency on the speed and reliability of transmission of regulatory and control signals in estimates of thermodynamic parameters of a rotating furnace. Figure 3 presents a series of graphs showing the deviations of the predicted values of the flare length. This dependence allows setting requirements for the quality control parameters of the total efficiency of the combustion process. Dependencies are shown, one of which corresponds to the real state of the parameters, whereas the others differ in weight coefficients. This means that, in order to improve the quality of management, it is necessary to use the critical zones in Figure 1 to regulate the following thermodynamic parameters: the amount of secondary air supplied to ensure stable combustion, the speed of flame propagation, and the amount of fuel.

The analysis of the organizational and technological problems allowed formulating the hypothesis of increasing efficiency as the ability of qualitative and quantitative representations of processes improving the dynamics and regulators of signals in a generalized structure of energy complexes for various purposes via the data science methods of in-depth analysis, modeling, and programming for the organization, project planning, monitoring, and regulation of speed and reliability to enhance the total efficiency of rotary kilns. As a result, there should be an assessment of the state of the object system under study according to total efficiency indicators, and a database should be created for working with tables (such as Pandas) and setting the research task for subsequent modeling.

Step 2.2 of the methodology consists of developing or adapting special mathematical models and algorithms that use well-known methods and thermodynamic dependencies, according to new data sampling systems of energy and technology. The speed of the model response to any changes in the combustion process dynamics is characterized by the adaptation parameter. The model training process consists of choosing the best adaptation parameter on the basis of samples on a retrospective material.

The model can only be adapted if certain weight coefficients of the controlled parameters are used, in which case neural network algorithms become trainable.

Achieving the performance targets for the characteristics of the fifth to sixth economic order requires improving the methodological support for the implementation of the theory and practice of enterprise management. This determined the need to develop an algorithmic scheme for presenting the methodology to ensure a regulated improvement in the quality of management according to the proposed criterion for improving total efficiency (Figure 4).

Mathematical models are employed to describe time series. Imagine that the time series $x_{\tau }$ generated by some model can be represented in the authors’ adaptation as two components [26,27]:

$$x_{\tau }={\xi }_{\tau }+{\epsilon }_{\tau },$$

(4)

where ${\epsilon }_{\tau }$ is a time series component generated by a random non-autocorrelated process with a zero mathematical expectation and finite dispersion, which affects only the value of the synchronous series term, while ${\xi }_{\tau }$ is a time series component generated by a deterministic function or a random process, which determines the value of several or all subsequent series terms.

When building the predictive model, a hypothesis is put forward on the dynamics of the function ${\xi }_{\tau }$ depending on the time argument. The considered models are endowed with adaptive properties, i.e., the ability to adjust the initial hypothesis or to replace it with another one, which is more adequate in terms of prediction accuracy.

The simplest adaptive model is based on calculating the exponential average. The basis of exponential smoothing is formed by the calculation of exponential averages; it is carried out according to the recurrence formula.

$$S_{\tau }=\gamma \cdot x_{\tau }+\beta \cdot S_{\tau -1},$$

(5)

where $S_{\tau }$ is the value of the exponential average at the moment $\tau$, and $\gamma$ is the smoothing parameter, wherein γ = const and 0 < γ < 1; β = 1 − γ.

Transforming Equation (5), we obtain

$$S_{\tau }=S_{\tau -1}+\gamma \cdot \left(x_{\tau }-S_{\tau -1}\right),$$

(6)

where the exponential average at the moment τ is expressed here as the exponential average of the previous moment plus the fraction $\gamma$ of the difference between the current observation and the exponential average of the past moment. The value $S_{\tau }$ is the weighted sum of all the series terms. Moreover, the weights fall exponentially depending on the antiquity of the observation. The value of $S_{\tau }$ has the same mathematical expectation as the series x but a smaller dispersion. A smaller value of $\gamma$ leads to a greater reduction in the dispersion of the exponential average and greater suppression of the oscillations of the initial series.

When using the dependencies in Equations (4)–(6), there are a number of difficulties associated with the use of reliable data on thermodynamic processes occurring inside a rotating furnace. In particular, if there is an error in data transmission, the weights must be adjusted. It is necessary to improve the quality of management with the introduction of new methods for approximating step functions representing exponential processes of changes in thermodynamic parameters of the amount of secondary air, submitted for sustainable development of combustion, flame propagation speed and fuel quantity, and data transmission and processing for monitoring and regulation. The collection of information from learning neural network algorithms for complex energy technological objects is currently difficult.

5. Using the Proposed Methodology Together with Methods of Approximation of Functions for Modeling Processes of Control and Regulation of Control Parameters

The studied processes of the organization of interaction of energy technological objects and improving the quality of management of control and regulation processes are characterized by piecewise step functions. This increases the expediency of their approximation for analytical purposes. A well-known approximation method is the Fourier series expansion.

$$f={\displaystyle \sum _{k=1}^{\infty }{c}_k\cdot {\mathsf{\phi }}_k},$$

(7)

where $\left\{{\mathsf{\phi }}_1,{\mathsf{\phi }}_2,\dots ,{\mathsf{\phi }}_n,\dots \right\}$ is represented as an orthogonal system in a functional Hilbert space $L_2\left[-\mathsf{\pi }; \mathsf{\pi }\right]$ with measurable functions f = total efficiencies with Lebesgue-integrable squares, $f\in L_2[-\mathsf{\pi },\mathsf{\pi }], c_k=\left(f_k\cdot {\mathsf{\phi }}_k\right)/{\Vert {\mathsf{\phi }}_k\Vert }^2$.

The trigonometric system used involves 2π periodic functions $\left\{1, \sin nx, \cos nx; n\in N\right\}$ of orthogonal type. Such a system adequately describes the total efficiency of jump-like processes of object transition ETC to high-tech methods of organizing activities by factors of the fifth to sixth economic order. Model 7 can also be used to represent the quality of signal transmission control of controllers and other controllers of power technology complex installations (in this case, in the production of cement clinker). Indeed, such signals can be converted in a similar way. It uses mathematical models of physical processes that describe the types of flows known in theory: compressible and incompressible, stationary and nonstationary, laminar (including non-Newtonian fluids), etc.

We show that the use of Fourier series for the approximation of piecewise linear functions leads to a sufficiently high error in calculating the total efficiency and control quality indicators during approximation. In addition, we highlight specific jump waves of the approximating function for evaluating the indicators/properties according to the studied parameters of the thermodynamic nature for generating technological installations in the vicinity of the break points $O_{\mathsf{\delta }}=\left(x_0\right)$. This problem occurs when using ANSYS CFX for modeling physical processes that describe the types of flows known in theory: compressible and incompressible, stationary and nonstationary, and laminar (including non-Newtonian fluids). This follows from the fact that, when using Equations (4)–(6), problems of data collection, processing, sampling, and management of energy technology complexes are not properly solved. The expansion of the interaction space and equipment composition makes it difficult to transmit data in real time or at intervals of less than 1 h. There is a condition for such points,

$$\begin{array}{c}\sup \\ x\in O_{\mathsf{\delta }}/\left\{x_0\right\}\end{array}\left|f\left(x\right)-S_n\left(x\right)\right|\underset{n\to \infty }{\to }A\ne 0,$$

(8)

where $S_n\left(x\right)$ is the partial sum of the Fourier series. For example, for the following function:

$$f_0\left(x\right)=\mathrm{sign}\left(\sin x\right) ,$$

(9)

with rectangular current pulses x = π/m, where m = 2[(n + 1)/2] and [A] is the integer part of a number A, the following represents the maximum point of the partial sum $S_n\left(f_0\right)$ of Fourier series:

$$S_n\left(f_0,\mathsf{\pi }/m\right)\underset{n\to \infty }{\to }\frac{2}{\mathsf{\pi }}{\displaystyle \underset{0}{\overset{\mathsf{\pi }}{\int }}\frac{\sin t}{t}dt\approx 1.17898},$$

(10)

where the absolute error is shown in Figure 5. This representation of the process is acceptable when modeling organizational decision-making processes at the beginning of the transition to a high-tech method of energy saving. However, the waveform of the control signals of the multizone controller is determined by thermodynamic and hydro-gas dynamic processes for evaluating the thermodynamic parameters of the amount of secondary air supplied to ensure stable combustion, the flame propagation speed, and the amount of fuel.

This will reduce the quality of management. It can lead to a failure in data transmission, as well as to increased errors in data processing and transmission to the neural network. In the ANSYS CFX program, when simulating physical processes that describe the types of flows known in theory (compressible and incompressible, stationary and nonstationary, and laminar, including non-Newtonian fluids), there may be an inconsistency of the solution or an increased error in comparison with experimental data. This is due to the relative error of the ideal representation of the step function, which is more than 17% [32,33]. It is not acceptable for regulating parameters on the basis of the criteria of speed and reliability of signal transmission in such installations. This is due to the fact that an increased error leads to an increase in fuel consumption and, most importantly, it can lead to a product of poor quality at the exit of the rotary kiln.

In Figure 6, curve 3 corresponds to the graph of the approximating function of the indicator/property for 20 terms of the following series:

$$f_n\left(x\right)={\displaystyle \sum _{n=1}^{20}{c}_n\cdot {\mathsf{\phi }}_n}.$$

(11)

The high approximation error with the Gibbs effect is obvious [32,33]. Its unacceptability is confirmed by subsequent physical modeling of processes in the furnace. For functions with limited variation on a segment [a,b], with an isolated break point $x_0\in \left(a,b\right)$, the condition is met [32,33]. Such conditions are typical for a few options for organizing transitions to high-energy-saving technologies based on factors of the fifth to sixth order. To a greater extent, this corresponds to options for improving the quality of signal transmission control in controllers—the efficiency of the studied objects. To confirm these facts, we present the results of physical modeling on the photo of thermal imaging of a rotating furnace (Figure 6).

As can be seen from Figure 7, the rotating furnace has increased heat losses, which also makes it clear that the division of the furnace into separate sections corresponding to the critical zones in Figure 1 was correct. We justify this by modeling the processes in Step 7 of the algorithmic scheme in Figure 5 using the following mathematical justification:

$$\begin{array}{c}\lim \\ n\to \infty \end{array}{S}_n\left(f,x_0+\mathsf{\pi }/m\right)=f\left(x_0,0\right)+\frac{d}{2}\left(\frac{2}{\mathsf{\pi }}{\displaystyle \underset{0}{\overset{\mathsf{\pi }}{\int }}\frac{\sin t}{t}dt-1}\right),$$

(12)

where $d=f\left(x_0+0\right)-f\left(x_0-0\right)$.

We show that Δ = Δ(x) and δ = δ(x), i.e., the absolute and relative approximation errors, respectively, do not have an increase limit. This does not matter for organizational transformation processes. However, to apply that part of the ANSYS CFX program, mathematical models of physical processes describing the types of gas-dynamic flows are used (Figure 7). Indeed, physical modeling allows us to see the process of flame propagation in a circular channel, limited, for example, by the size of a rotating furnace. This can be confirmed by previously performed calculations of the authors’ gas mixture flow parameters at Step 5 of the algorithmic scheme and the dependencies in Equations (1)–(6), which correspond to Step 6 of the same scheme.

This type of flow of a mixture of natural gas and air from the burner nozzle is satisfactorily shown by Equations (1)–(6) in Step 6 of the algorithmic scheme in Figure 4. This confirms the following conclusion about the absence of convergence of the Fourier series for the considered type of processes:

$$\begin{array}{l}\begin{array}{c}\lim \\ n\to \infty \end{array}\mathsf{\Delta }\left(x_0+\mathsf{\pi }/m\right)=\begin{array}{c}\lim \\ n\to \infty \end{array}\left|S_n\left(f,x_0+\mathsf{\pi }/m\right)-f\left(x_0+\mathsf{\pi }/m\right)\right|=\\ =\left|\begin{array}{c}\lim \\ n\to \infty \end{array}{S}_n\left(x_0+\mathsf{\pi }/m\right)-\begin{array}{c}\lim \\ n\to \infty \end{array}f\left(x_0+\mathsf{\pi }/m\right)\right|=\\ =\left|f\left(x_0+0\right)+\frac{d}{2}\left(\frac{2}{\mathsf{\pi }}{\displaystyle \underset{0}{\overset{\mathsf{\pi }}{\int }}\frac{\sin t}{t}dt-1}\right)-f\left(x_0+0\right)\right|=\\ =\left|\frac{d}{2}\left(\frac{2}{\mathsf{\pi }}{\displaystyle \underset{0}{\overset{\mathsf{\pi }}{\int }}\frac{\sin t}{t}dt-1}\right)\right|=\mathsf{\Delta }\left(d\right). \end{array}$$

(13)

Furthermore, the function $\mathsf{\Delta }\left(d\right)$ represents an infinitely large quantity, since

$$\forall M>0\exists d=d*\left(M\right)>0\forall d:\left|d\right|>d*\Rightarrow \mathsf{\Delta }\left(d*\right)=\left|\frac{d*}{2}\left(\frac{2}{\mathsf{\pi }}{\displaystyle \underset{0}{\overset{\mathsf{\pi }}{\int }}\frac{\sin t}{t}dt-1}\right)\right|>M.$$

(14)

You can take $d*$, for example,

$$\left[2M\mathsf{\pi }/\left(\frac{2}{\mathsf{\pi }}{\displaystyle \underset{0}{\overset{\mathsf{\pi }}{\int }}\frac{\sin t}{t}dt-\mathsf{\pi }}\right)\right]+1.$$

(15)

The proof is the same for the relative error $\mathsf{\delta }\left(x\right)=\mathsf{\Delta }\left(x\right)/\left|f\left(x\right)\right|$.

At a constant value $d>R \left(d\ne 0\right)$ and for any M > 0, the function is selected $f\left(x\right)\in L_2\left[a,b\right]$, for which $\mathsf{\delta }\left(x_0+0,d\right)=\mathsf{\Delta }\left(x_0+0,d\right)/\left|f\left(x_0+0\right)\right|>M$.

As a similar function, let us take a function that has $\left|f\left(x_0+0\right)\right|<\mathsf{\Delta }\left(x_0+0,d\right)/M, f\left(x_0+0\right)\ne 0$.

Note that, even on the set of continuous functions $C [-\mathsf{\pi }, \mathsf{\pi }]$, Fourier series, as known, do not have to converge at every point. In organizational processes, this convergence is necessary to achieve and stabilize the compromise of sustainability goals and total effectiveness of high-tech transformations. To improve the quality of control and reliability of signal transmission processes, this condition is necessary. Therefore, we propose an approximation of a step function of the best type on the basis of the following recursive functions [32,33]:

$$\left\{f_n\left(x\right)|f_n\left(x\right)=\sin \left(\left(\mathsf{\pi }/2\right)f_{n-1}\left(x\right)\right), f_1\left(x\right)=\sin \left(x\right); n-1\in N\right\}\subset C^{\infty }[-\mathsf{\pi },\mathsf{\pi }].$$

(16)

The recording form is based on the use of trigonometric expressions in the form of attachments. In this case, we get four graphs of the function of dependence of total efficiency in the new organizational structure of the sustainable development center (SDC) ETC on the degree of quality of interaction management of its objects. By increasing the number of functions interpreted by the approximation of the recursive function in Equation (16) to five, clarity is provided in determining the beginning of high-tech and energy-saving measures for time periods x. For controllers and regulators, the graph shows an improvement in the quality of evaluation and regulation using the additional management functions listed above. Successive approximations to the ideal waveform can be shown when calculating the temperature and heating rate of the material in zones 6, 7, and 8 in Figure 1; using Equations (1)–(3), the calculation method will receive the value of the length of the initial section of the torch, depending on the exit speed of the mixture of air and natural gas from the mouth of the burner, compared with the processed Equations (4)–(6), as shown in

Table 2. Results of research on Equations (1)–(6).

Air Excess Factor, α	Length of the Initial Section of the Torch, l0, m, When Using Equations (1)–(3)	Length of the Initial Section of the Torch, l0, m, When Using Equations (4)–(6)
1.15	0.91	0.97
1.10	0.86	0.91
1.05	0.83	0.88

. It should be noted that the results of the calculations are summarized in Table 2, corresponding to Step 6 of the algorithmic scheme in Figure 5. Weight coefficients are an integral part of neural networks. Thus, Table 2 shows the difference between analytical data and data when transmitting signals for a neural network from the object of research—a rotating furnace. Similarly, you can study not only the length of the initial section of the torch, but also the total length of the torch in the drum of the rotating furnace, as shown later.

Thus, according to Table 2, there are significant differences between the experimental data processed using weight coefficients and those obtained during the calculation. This is primarily due to the inaccurate choice of weight coefficients. Another conclusion from the analysis in Table 2 can be the assumption that the use of weight coefficients for learning neural networks should be constantly improved, particularly with the help of new approximation methods, as shown later.

Figure 4 shows the results of studies using standard weight coefficients using Equations (1)–(6) to describe the corresponding processes; it is necessary to take into account that, when considering this algorithm of actions, even for small values of n, the graphs of the original and approximating functions converge very closely. This is typical for the processes of heat propagation in the volume of the drum of a rotating furnace, particularly for the temperature field changing in space. In addition, there are practically no fluctuations in straight sections, which consequently leads to a decrease in the influence of the Gibbs effect on the approximation of the original function. Estimates of convergence and approximation errors for piecewise linear functions allow us to quantify the effects of increasing speed and reliability. Previously, the authors in [32,33] proved that the sequence of approximating functions converges normally to the original function, and this statement is true for the space L1[0,π/2] and L2[0,π/2]. We present the sequence of proof of this statement in an abbreviated form (a full description can be found in [32,33]).

When using a sequence that is invariant with respect to the sequence f_n(x) functions, we receive

$$\left\{{\mathsf{\phi }}_n\left(x\right)|{\mathsf{\phi }}_n\left(x\right)=1-\exp \left(-{\left(\mathsf{\pi }/2\right)}^{n-1}\cdot x\right), n\in N\right\}\subset C^{\infty }[0,\mathsf{\pi }/2].$$

(17)

We prove that $f_n\left(x\right)\ge {\mathsf{\phi }}_n\left(x\right), \forall n\in N, \forall x\in [0,\mathsf{\pi }/2]$. The set of break points of a function $f_0(x)$ is equal to zero. Then, given the nonnegativity and the boundedness of functions f_n(x) and φ_n(x) on the segment under consideration, in space L1[0,π/2], we receive

$$\begin{array}{l}{\Vert f_0\left(x\right)-f_n\left(x\right)\Vert }_{L_1\left[0,\mathsf{\pi }/2\right]}={\displaystyle \underset{0}{\overset{\mathsf{\pi }/2}{\int }}\left(1-f_n\left(x\right)\right)}dx\le {\displaystyle \underset{0}{\overset{\mathsf{\pi }/2}{\int }}\left(1-{\mathsf{\phi }}_n\left(x\right)\right)}dx=\\ ={\left(2/\mathsf{\pi }\right)}^{n-1}\left(1-\exp \left(-{\left(\mathsf{\pi }/2\right)}^n\right)\right). \end{array}$$

(18)

Since

$$\begin{array}{c}\lim \\ n\to \infty \end{array}{\left(2/\mathsf{\pi }\right)}^{n-1}\left(1-\exp \left(-{\left(\mathsf{\pi }/2\right)}^n\right)\right),$$

(19)

we get

$${\Vert f_0\left(x\right)-f_n\left(x\right)\Vert }_{L_1\left[0,\mathsf{\pi }/2\right]}\underset{n\to \infty }{\to }0.$$

(20)

In a functional Hilbert space, L2[0,π/2], with the metric

$$\mathsf{\rho }\left(x,y\right)={\left({\displaystyle \underset{0}{\overset{\mathsf{\pi }/2}{\int }}{\left(x\left(t\right)-y\left(t\right)\right)}^{2}dt}\right)}^{1/2} ,$$

(21)

we have

$$\begin{array}{l}{\Vert f_0\left(x\right)-f_n\left(x\right)\Vert }_{L_2\left[0,\mathsf{\pi }/2\right]}={\left({\displaystyle \underset{0}{\overset{\mathsf{\pi }/2}{\int }}{\left(1-f_n\left(x\right)\right)}^2}dx\right)}^{1/2}\le {\left({\displaystyle \underset{0}{\overset{\mathsf{\pi }/2}{\int }}{\left(1-{\mathsf{\phi }}_n\left(x\right)\right)}^2}dx\right)}^{1/2}=\\ ={\left(\frac{{\left(2/\mathsf{\pi }\right)}^{n-1}}{2}\left(1-\exp \left(-2{\left(\mathsf{\pi }/2\right)}^n\right)\right)\right)}^{1/2}. \end{array}$$

(22)

Given that

$$\begin{array}{c}\lim \\ n\to \infty \end{array}{\left(\frac{{\left(2/\mathsf{\pi }\right)}^{n-1}}{2}\left(1-\exp \left(-2{\left(\mathsf{\pi }/2\right)}^n\right)\right)/2\right)}^{1/2}=0,$$

(23)

we get that, in this space,

$${\Vert f_0\left(x\right)-f_n\left(x\right)\Vert }_{L_2\left[0,\mathsf{\pi }/2\right]}\underset{n\to \infty }{\to }0.$$

(24)

The sequence converges on average to the original function.

Thus, the sequence of the total efficiency function f_n(x) into space L1[−π,π] and L2[−π,π] is fundamental, and, in space C[−π,π], the sequence f_n(x) is not fundamental. This means that the proposed approximation can be applied to improve the quality of organizational and technical management.

Numerical verification of the calculation error using the new approximation scheme is shown below.

To estimate the approximation error, we use the relation ${\mathsf{\phi }}_n\left(x\right)\le f_n\left(x\right)\le {\mathsf{\Psi }}_n\left(x\right)$ (Figure 8), where ${\mathsf{\Psi }}_n\left(x\right)={\left(\mathsf{\pi }/2\right)}^{n-1}\cdot x, x\in [0,\mathsf{\pi }/2], n\in N$.

Functions ${\mathsf{\phi }}_n\left(x\right)$ and ${\mathsf{\Psi }}_n\left(x\right)$ are constructed from the condition of equality of derivatives at zero ${\mathsf{\phi }}_n^{\prime }\left(0\right)={\mathsf{\Psi }}_n^{\prime }\left(0\right)=f_n^{\prime }\left(0\right)$; this allows getting a narrow interval for estimating the approximation error.

The limiting functions in this case are the dependences of the controlled parameters of the studied processes of increasing total efficiency for the parameters of the rotating furnace torch. Indeed, a smaller approximation error was found using the proposed method when using the parameters of the combustion temperature and the length of the torch. This is typical for the studied zones of the furnace in Figure 1, shown in calculations using Equations (1)–(3), where the length of the initial section of the torch depends on the rate of exit of the mixture of natural gas and air from the mouth of the burner. The same values of the weight coefficients are obtained using Equations (4)–(6), taking into account new approximation methods (

Table 3. Results of using new approximation methods for modeling the processes of signal transmission from a rotating furnace.

Air Excess Factor, α	Length of the Initial Section of the Torch, l0, m, Using Equations (1)–(6) and New Approximation Methods as in Our Previous Works [9,29]	Relative Error
1.15	0.926	0.017
1.10	0.846	0.019
1.05	0.875	0.016

).

It should be noted that the results of calculations are summarized in Table 2 and correspond to Step 7 of the algorithmic scheme in Figure 5. Table 3 shows the difference between data obtained without using approximation and data when transmitting signals for a neural network using the original weight coefficients.

As can be seen from Table 3, the use of new approximation methods gives small relative errors in the calculations (Figure 8). Another conclusion from the analysis of Table 3 can be the assumption that the use of weight coefficients for learning neural networks should be constantly improved, in particular with the help of new approximation methods.

In space L1[0,π/2], the estimates for absolute and relative error are equal to

$$\frac{{\left(2/\mathsf{\pi }\right)}^{n-1}}{2}\le {\Vert f_0\left(x\right)-f_n\left(x\right)\Vert }_{L_1\left[0,\mathsf{\pi }/2\right]}\le {\left(2/\mathsf{\pi }\right)}^{n-1}\left(1-\exp \left(-{\left(\mathsf{\pi }/2\right)}^n\right)\right),$$

(25)

$$\frac{{\left(2/\mathsf{\pi }\right)}^n}{2}\le {\Vert f_0\left(x\right)-f_n\left(x\right)\Vert }_{L_1\left[0,\mathsf{\pi }/2\right]}\le {\left(2/\mathsf{\pi }\right)}^n\left(1-\exp \left(-{\left(\mathsf{\pi }/2\right)}^n\right)\right).$$

(26)

In space L2[0,π/2], these estimates take the form

$${\left(\frac{{\left(2/\mathsf{\pi }\right)}^{n-1}}{3}\right)}^{1/2}\le {\Vert f_n\left(x\right)-f_0\left(x\right)\Vert }_{L_2\left[0,\mathsf{\pi }/2\right]}\le {\left(\frac{{\left(2/\mathsf{\pi }\right)}^{n-1}}{2}\left(1-\exp \left(-{\left(\mathsf{\pi }/2\right)}^n\right)\right)\right)}^{1/2},$$

(27)

$${\left(\frac{{\left(2/\mathsf{\pi }\right)}^{n-1}}{3}\right)}^{1/2}\le \left({\Vert f_n\left(x\right)-f_0\left(x\right)\Vert }_{L_2\left[0,\mathsf{\pi }/2\right]}\right)/{\left(\mathsf{\pi }/2\right)}^{1/2}\le {\left(\frac{{\left(2/\mathsf{\pi }\right)}^n}{2}\left(1-\exp \left(-{\left(\mathsf{\pi }/2\right)}^n\right)\right)\right)}^{1/2}.$$

(28)

Graphs of upper and lower relative error estimates $\mathsf{\delta }$ in relation to $n\in N$ for the space L1[0,π/2] (curves 1) and space L2[0,π/2] (curves 2) are shown in Figure 8. In this case, the calculation error is quite small and falls within the acceptable range of regulating the parameters of the rotating furnace torch, especially when using a multizone controller.

Table 4. Results with new weight coefficients, as well as using new approximation methods.

Air Excess Factor, α	The Length of the Initial Section of the Torch, L0, m, Using Equations (1)–(6) and New Approximation Methods as in Our Previous Works [9,29] and New Weight Coefficients	Relative Error
1.15	0.916	0.061
1.10	0.837	0.059
1.05	0.878	0.064

shows how much the calculations of the initial section of the flare improve when using new weight coefficients and new approximation methods. When using Equations (1)–(3), the values of the length of the initial section of the torch depending on the rate of exit of a mixture of natural gas and air from the mouth of the burner are calculated. They are proposed to be supplemented by processing new weight coefficients using Equations (4)–(6).

The calculation results are summarized in Table 4 and correspond to Steps 5–7 of the algorithmic scheme in Figure 5. Thus, Table 4 shows the difference between the data obtained using the mathematical dependencies as in our previous works [9,29] with the original weight coefficients and the improved ones.

As can be seen from Table 4, when using new weight coefficients and new approximation methods, it gives small relative errors in the calculations. Another conclusion from the analysis of Table 4 can be the statement that the use of new weight coefficients for learning neural networks and new approximation methods gives an even smaller error in signal transmission (Figure 9).

In the sequence of approximating functions, a number was used as a constant multiplier $\mathsf{\pi }/2$, although it is clear that it is possible to take a different multiplier. Moreover, the multiplier can also be variable. Instead of the sine, the proposed approximation method can use the cosine and other trigonometric functions, as well as their combinations. This selection of functions is necessary for modeling the types of controllers and controllers that differ in input and output characteristics. In addition, the choice of the function affects further changes in the weight coefficients.

For example, using the procedure

$$f(x)=\cos (S(S\dots (S(x)))),$$

(29)

where $S(x)=(\mathsf{\pi }/2)\sin x$, we can get a sequence of approximating functions describing short-term pulses (Figure 10) in the controller. On the basis of a multizone controller, economical, high-precision, and reliable control systems for thermal heating installations can be implemented, particularly systems for controlling the thermal field of rotating furnaces of materials using recycled raw materials (for example, cement clinker and activated carbon for industrial purposes). The obtained experimental data can be used in correlations for rotating furnaces of various types. In addition, the principles of multizone integration transformation can be effectively applied to the construction of the following systems: water pumps of any functional purpose, water supply recycling systems for industrial enterprises and agriculture, and oil pump control systems for industrial machinery.

Advantages of the proposed systems are as follows: high quality of finished products, reduction in physical losses in the process of obtaining materials using recycled raw materials, and improved quality of regulation in static and dynamic modes of operation of control systems.

Oscillations appear when considering discontinuous gas flows jointly with the use of central difference methods (Figure 8).

Using the resulting three-dimensional (3D) representation of processes requires analyzing the dependencies, for example, of pressure on the location in space of the drum of a rotating furnace. In this case, you can focus on the division of zones made in Figure 1. Figure 11 shows the oscillations when solving mathematical problems in the field of gas dynamics, as well as when transmitting signals. Note that the graph in Figure 11 can be transformed. Such algorithmic procedures correspond to Step 7 of Figure 3.

Obviously, the discrepancy between the real and approximating dependencies is not more than tenths of a percent.

The proposed approximation methods also allow us to approximate step functions with different lengths of intervals corresponding to positive and negative values of the initial step dependence. For example, if, as an initial function, we take

$$f_1(x)=-0.7\sin x,$$

(30)

then, using the approximating procedure, we get a sequence of functions, the graphs of which are shown in Figure 12. Note that it is possible to construct approximations for step functions with any ratio of intervals corresponding to the positive and negative values of the original step function. In ETC, these functions describe the processes of transmitting signals from the cement clinker furnace to the controller. This increases the possibility of reverse effects on thermodynamic parameters. When implementing the theory and methods of controlling neural networks in application to thermal and electrical equipment, there are problems of a practical and scientific nature. Existing energy technology complexes include equipment that generates heat and electricity, as well as mechanical and electric drive equipment. They require improvement and development of the theory of automatic control, including neural control based on collecting data about system parameters using controllers and processing using software with the ability to train a neural network. In the algorithmic scheme of Figure 5, this corresponds to Step 8 when using standard Equations (1)–(6) and new approximation methods as in our previous works [9,29], shown in Equations (7)–(30). Figure 12 shows graphs of several approximations when approximating a function, which is typical for estimating oscillations during signal transmission, as well as when converting thermodynamic functions.

In this paper, we also propose some other methods for approximating piecewise linear functions. For example, the function

$$f(x)=((P-1)/A(x))\cos \left((\mathsf{\pi }/2)x\right),$$

(31)

where

$$A(x)={(P^2-{(P-1)}^2{\sin }^2((\mathsf{\pi }/2)x))}^{1/2},$$

(32)

if the parameter values are large enough, can be used to approximate step functions.

Functions

$$f_1(x)=(2/\mathsf{\pi })\arcsin \left(\left(1-(1/P)\right)\sin \left((\mathsf{\pi }/2)x\right)\right),$$

(33)

and

$$f_2(x)=(2/\mathsf{\pi })\arcsin \left(\left(1-(1/P)\right)\sin \left((\mathsf{\pi }/2)xf(x)\right)\right),$$

(34)

can be used to approximate saw-tooth piecewise linear functions.

To approximate the function

$$f(x)=\left|x\right|,$$

(35)

you can use analytical functions such as

$$f(x)=(B^2(x)+2P)/2PB(x),$$

(36)

and

$$f(x)=x+2/B(x),$$

(37)

where

$$B(x)=Px+{({(Px)}^2+2P)}^{1/2}.$$

(38)

In the generated ETC, the graph in Figure 13 can be used to describe the signal transmission processes that regulate the effect of the excess air coefficient on the length of the torch. The graph in Figure 14 is convenient for displaying the processes of influence of the fuel type on the length of the torch. Indeed, the graph of the dependence of the torch length is shown below according to the results of physical modeling (Figure 15).

The length of the torch and the temperature are determined using Equations (1) and (2), while the value of the radiant flux Qrad, Wt/m², which they depend on, is determined by the following well-known formula:

$$Q_{rad}=5,67\cdot {\epsilon }_m\cdot \left[{\epsilon }_f{\left(\frac{T_f}{100}\right)}^4-a_{com}{\left(\frac{T_m}{100}\right)}^4\right]\cdot F,$$

(39)

where ε_m, ε_f are the coefficients of black material and torch, respectively, T_m, T_f are the temperature of the material and torch, respectively, K, a_com is the degree of gas absorption capacity, and F is the heat transfer area, m².

The thin lines in Figure 13 and Figure 14 interpret the decreasing levels of total efficiency with a decrease in the quality of control of the thermodynamic parameters of the rotating furnace, which affect the decrease in the speed and reliability of signal transmission.

Step 2.3 of the developed methodology involves the development or use of computer programs such as Ansys, Anaconda, and Python to determine the optimal design parameters of the power and technological installation. Consequently, the methodological approach to the formation of the energy technology complex is characterized by using the capabilities of two-layer neural networks for mathematical modeling of processes and justification of the choice of parameters and methods for improving energy, environmental, and economic efficiency. Modeling the combustion process in rotary kilns is carried out using the capabilities of well-known software products. The following turbulence models are also used: algebraic, two-parameter differential RANS (The Reynolds-averaged Navier–Stokes equations) k–ε, and k–ω including time-averaged transport equations for flows with large Re numbers. The authors used a two-parameter differential Menter model, a model of large vortices or large structures LES (large eddy simulation), a model of an unconnected or free vortex DES (detached eddy simulation), and a model that takes into account the scale of turbulent pulsations SAS (scale adaptive simulation).

The results obtained allow solving one of the important modeling tasks at this stage of its development, i.e., reducing the calculation time and the adequacy of the constructed model for similar installations and devices, which corresponds to Steps 4–7 in the algorithmic scheme in Figure 5. Next, we present the continuation of the simulation of the burning process in Figure 15. Figure 16 and Figure 17 show the solid-state model and the rotary kiln combustion model.

The results obtained during the simulation are summarized in

Table 5. Results of physical modeling of the total length of the torch in a rotary kiln/furnace with material recycling.

Air Excess Factor, α	The Length of the Torch, lf, m
1.15	12.15/12.96
1.10	13.95/14.57
1.05	15.50/15.87

.

Large values for a rotary kiln with material recycling mean that, in this case, the combustion process is delayed, which in principle corresponds to the previously made conclusions from Equations (1)–(6), as shown in Figure 3 and Table 1, Table 2, Table 3 and Table 4.

Thus, according to Table 5, there are significant differences between the model data processed using a computer program and those obtained during the calculation. This is primarily due to the inaccurate choice of the grid and the modeling method. Another conclusion from the analysis of Table 5 can be the statement that the use of new approximation methods for learning neural networks reduces the calculation error, which corresponds to Step 7 in the algorithmic scheme in Figure 5.

When solving problem 3, physical modeling actions are implemented for the subsequent determination of structural elements of heat/power and technological equipment, with automatic control of thermal and electrical parameters in the scheme of a single controller for regulating equipment parameters according to the theory of electro- and thermodynamic similarity. It is proposed to control electric drives of the energy technology complex on the basis of a multizone controller for more effective self-diagnosis and redundancy of fuel and energy systems. It should also be taken into account that the authors propose new methods for approximating piecewise linear functions when transmitting a signal from a control object to a controller.

The considered proposals can also be adapted for systems such as a power technological complex of a rotating cement clinker furnace, a hybrid power technological complex for the production of multifunctional materials, electrometallurgical production of graphite electrodes, and a gas-dynamic warning system for the process of double arcing in a low-temperature electric arc plasma torch.

6. Description of Signal Transmission Processes in the Control and Regulation Mechanism of Heat Engineering Elements

The widespread use of piecewise linear functions is explained by the simplicity of their structure, which involves straight lines and their segments. This makes it possible in many cases to obtain solutions using the methods of linear system theory. However, problems arise when constructing solutions for the entire domain of determining a piecewise linear function, linking solutions by sections with the need to use special mathematical methods. To simplify calculations, working with piecewise linear functions, in many cases, they resort to approximation methods at Step 2.2 for solving modeling problems using the data science method.

Simulations were performed using the standard k–omega model. The authors also propose to use in the calculations the original version of the approximation of the generalized functions used in the simulation, which are derived from the delta-function.

At the same time, as indicated in our previous works [9,29], we developed new methods of approximation of generalized functions.

The delta function is a derivative of the Heaviside function or the unit jump function, which is defined as

$$H(x)=\{\begin{array}{l}1, \forall x>0;\\ 0, \forall x<0.\end{array}$$

(40)

As indicated in our previous works [9,29], we suggested approximating the Heaviside function via a sequence of functions of the form $H_n(x)=0.5(1+f_n(x))$, where the sequence of recursive functions is determined by the following relationship:

$$\left\{ f_n(x) |\begin{array}{l}{f}_n(x)=\sin \left((\mathsf{\pi }/2)\cdot f_{n-1}(x)\right), \\ f_1(x)=\sin x; n-1\in N \end{array}\right\}\subset C^{\infty }[-\mathsf{\pi }/2, \mathsf{\pi }/2].$$

(41)

Finding the first derivatives of the Heaviside function approximations, we obtain successive approximations for the delta function.

7. Experimental Data on the Results of the Furnace Operation

A constant heat regime of the furnace is necessary to ensure the stationary processes occurring in it. As a rule, the stability of the firing mode is supported by changes in fuel consumption when the furnace is constantly powered, which is accompanied by various transients (changes in the position and length of the furnace zones, the amount of CO₂ released, the amount of heat entering the cold part of the furnace, etc.). Such transients are temporary disturbances, the magnitude of which depends on the control action. Large values of control actions can themselves be the reasons for the further output of the furnace from normal operation. Since the thermal mode of the furnace is determined by the volume-specific heat output, the optimal thermal mode corresponds to a certain value of the heat voltage. The highest value of the volumetric heat stress corresponds to the situation when complete combustion of fuel is impossible (that is, there is a risk of under-fire), and the lowest corresponds to when the capacity is too large (that is, the furnace operates in an uneconomical mode). You can select an acceptable range of changes in the volumetric heat stress, at which you should maintain a constant performance. At the boundaries of the interval, a constant thermal mode is maintained with a change in performance. This restriction will reduce the harmful effect of transients on the furnace operation, reduce the specific fuel consumption for firing, and prevent situations related to under-burning of fuel and operation of the furnace in an uneconomical mode. The general dependence is found that the further the fuel is ignited from the nozzle, the shorter the torch is. The authors present the results of their research on a rotary kiln in Figure 18 and Figure 19.

The data obtained as a result of experimental studies are summarized in

Table 6. Dependence of the torch length on the coefficient of excess air during natural gas combustion in rotary kilns/furnaces with recycling.

Air Excess Factor, α	The Length of the Torch, lf, m
1.15	11.43/11.55
1.10	13.54/13.98
1.05	15.76/15.86

. In contrast to the data in Table 6, the actual data obtained at the research object are shown here.

Large values for a rotary kiln with material recycling mean that the combustion process is delayed in this case, which in principle corresponds to the previously made conclusions from Equations (1)–(6), as shown in Figure 3 and Figure 4 and Table 1, Table 2, Table 3, Table 4 and Table 5.

According to Table 6, there are significant differences between the experimental data processed using the controller and those obtained during the calculation. This is primarily due to the inaccurate choice of the signal transmission system from the rotary kiln to the controller. Another conclusion from the analysis of Table 6 can be the statement that the use of new approximation methods for training neural networks in data processing reduces the calculation error, which corresponds to Step 7 in the algorithmic scheme in Figure 5.

8. Results

To simplify calculations, working with piecewise linear functions, approximation methods are used in many cases. The use of Fourier series also has certain disadvantages. For example, with a relatively small number of terms in the Fourier series used to decompose a piecewise linear function, the approximating function has a pronounced wave-like character even within one rectilinear section of the piecewise linear function, which leads to a sufficiently large approximation error. In addition, for the plot of the approximating function, an increased approximation error appears in the vicinity of the break points of the original function. This manifests the so-called Gibbs effect, and, with an increase in the number of harmonics, the Gibbs effect does not disappear, which leads to extremely negative consequences of using the approximating function. In this paper, the developed method is used as a method of approximation of functions, which allows reducing the error of data processing results.

The results of mathematical and physical modeling, through application of the ANSYS program, confirm the theoretical and methodological constructions and the hypothesis of increasing total efficiency via methods of improving the quality of control over the dynamics of thermodynamic parameters. The differences with the experimental results are insignificant, taking into account the measurement error using modern devices certified by the European Union. As mentioned earlier, the error of the proposed calculation method using approximating functions instead of Fourier series makes the theoretical calculation more correlative with respect to the data obtained in the course of experiments. The error in mathematical modeling was reduced due to the use of specific grids and models used only for the flow of a heterogeneous mixture, i.e., a mixture of natural gas and air.

We compared the results of experimental studies using new approximation methods for processing signals from sensors and devices from a rotating furnace. They are summarized in

Table 7. Results of using new approximation methods on a real object of research.

Air Excess Factor, α	The Length of the Torch, lf, m
1.15	11.21/11.33
1.10	13.16/13.48
1.05	15.43/15.67

and correspond to Steps 5–7 of the algorithmic scheme in Figure 5. The data obtained on a real object of research are shown.

Therefore, they can be used in a learning neural network to build an optimization model of an energy technology complex (Step 8 of the algorithmic scheme).

As can be seen from Table 7, when using new approximation methods, only small relative errors occur when transmitting experimental data.

The authors emphasize that the obtained modeling results in ANSYS are very akin to the theoretical and experimental data. The differences are insignificant since the error in the experimental measurements was leveled by the use of modern tools certified by the European Union. The error in the mathematical modeling was reduced due to the use of the empirical data obtained by processing the signals from analogous equipment and subsequent sampling according to the technology developed by the authors. For example, this is evident for the velocity values v. During standard modeling without the use of sampled data, the velocity value ranged from 168–173 m/s, i.e., it averaged 170.5 m/s. At the same time, when using the authors’ developments, the value of the average velocity was 173.6 m/s. This value is the closest to the experimentally obtained values of 173.9 m/s. Thus, the maximum differences are obtained between the experimental data and computer modeling data without the use of the authors’ developments, while the maximum coincidence is shown between the average values according to the modeling results taking into account the sampled signals and the experiment (Figure 20).

9. Conclusions

• The abovementioned method of practical implementation of the research results involved the development or use of computer programs (Anaconda, Python, etc.) to determine the optimal design parameters of an energy and technological installation. The above-defined features of fuel and energy facilities and the complexity of process modeling made it advisable to use the capabilities of trained neural networks of a two-layer or deeper type. This was done on the basis of results of previously conducted mathematical modeling of processes and algorithmic justification of the choice of parameters, with ways to increase the total efficiency in the ETC according to the criteria for ensuring the necessary speed and reliability of signal transmission.
• A technological model of a rotary kiln was developed with its division into separate sections corresponding to the combustion zones. The degree of readiness of the product was determined, i.e., cement clinker and recycled raw materials. Experimental studies were carried out on rotating furnaces, and mathematical modeling of thermodynamic and gas-dynamic processes in the drum of a rotating furnace was carried out. As a result, experimental, calculated, and model data were compared. It should be noted that the research was conducted using data science methods using the Big Data Toolkit. Mathematical dependencies have been developed that allow processing data transmitted from the object of research—a rotating furnace—using analog-to-digital methods. The presented mathematical dependencies as in our previous works [9,29] allow reducing the error in data transmission.
• The results of using the new approximation method showed a fairly good convergence of the results obtained with experimental data.
• The considered theory and methods of analysis can also be adapted for systems such as a power technological complex of a rotating cement clinker furnace, a hybrid power technological complex for the production of multifunctional materials, electrometallurgical production of graphite electrodes, and a gas-dynamic warning system for the process of double arcing in a low-temperature electric arc plasma torch.
• The authors propose using neural network algorithms to predict the temperature of the flame in the zone of intense burning, which is most affected by the process of fuel combustion. The implementation of this feature allows quickly and accurately predicting the temperature in the zone of intense combustion of a rotary kiln even when burning different fuels and varying their ratio. When combined in a single neural network, these techniques will have a complex effect that increases the accuracy of the description of combustion and will vary the empirical coefficients used in these techniques depending on the type and properties of the fuel used and the geometry of the rotating furnace.