Effect of Aspect Ratio on the Mixing Performance in the Kenics Static Mixer
Abstract
:1. Introduction
2. Materials and Methods
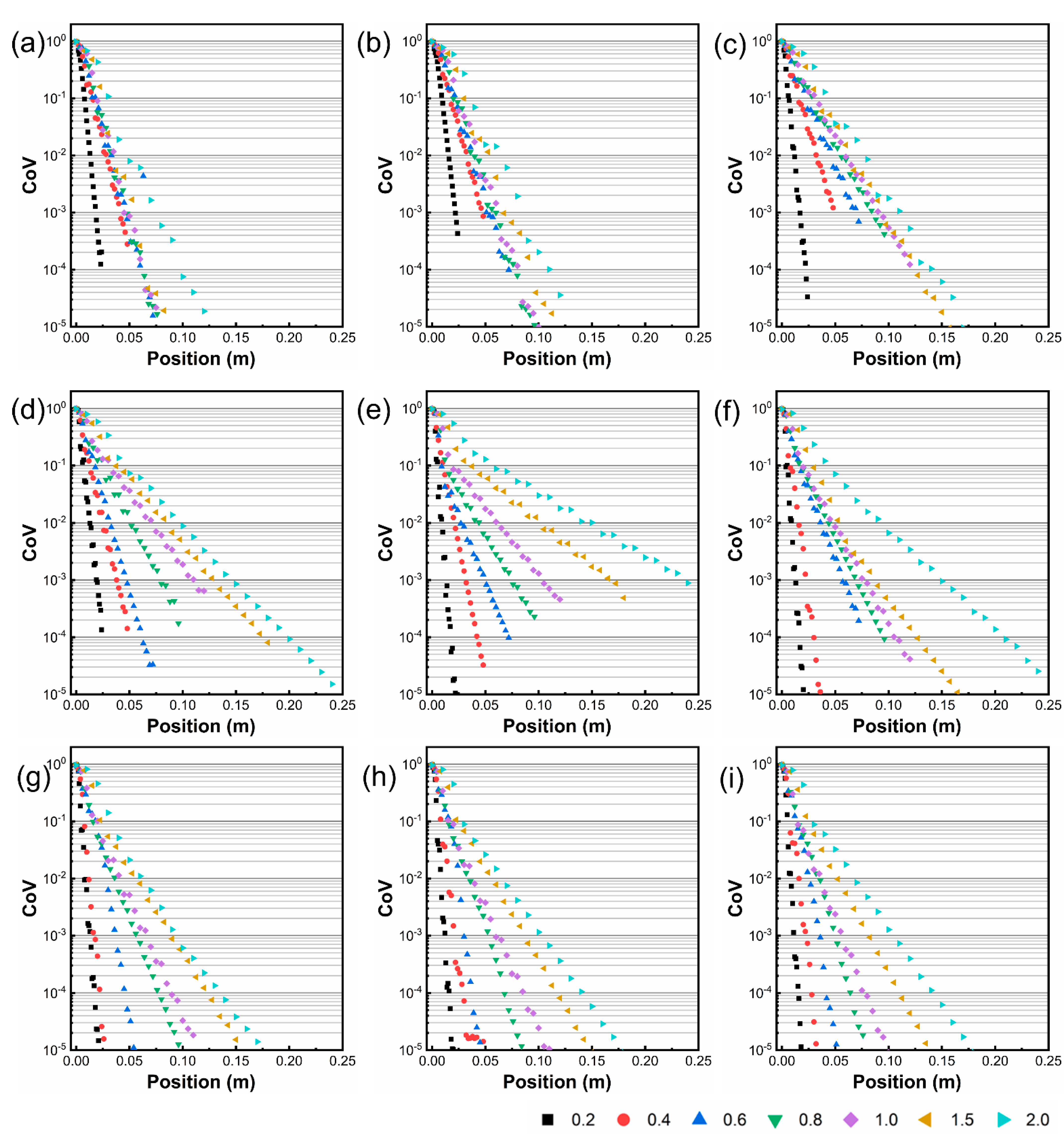
2.1. Coefficient of Variation
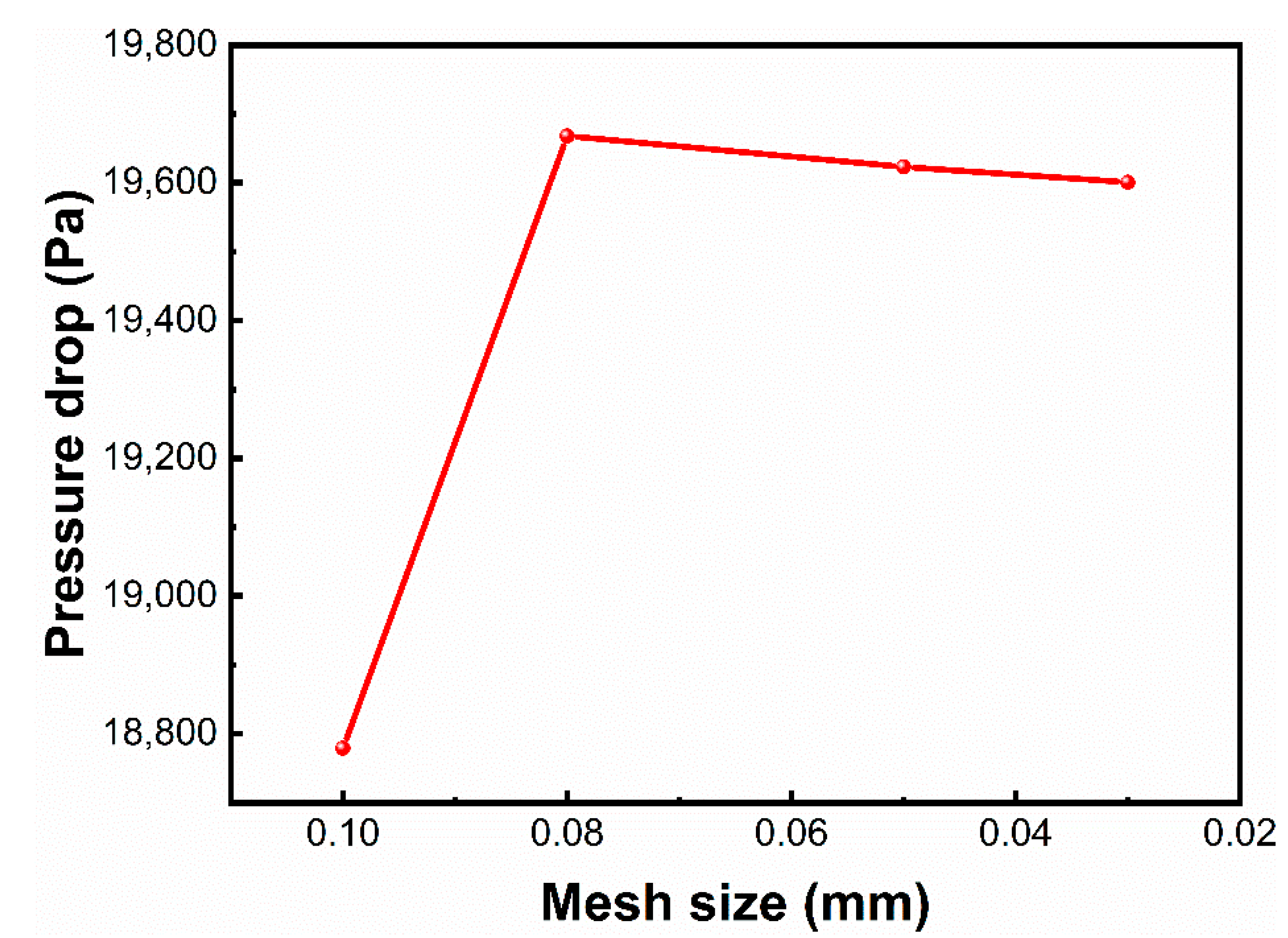
2.2. Computational Fluid Dynamics
3. Results and Discussion
3.1. Effect of Aspect Ratio on CoV
3.2. Effect of Aspect Ratio on Number of Elements
3.3. Effect of Aspect Ratio on Mixer Length
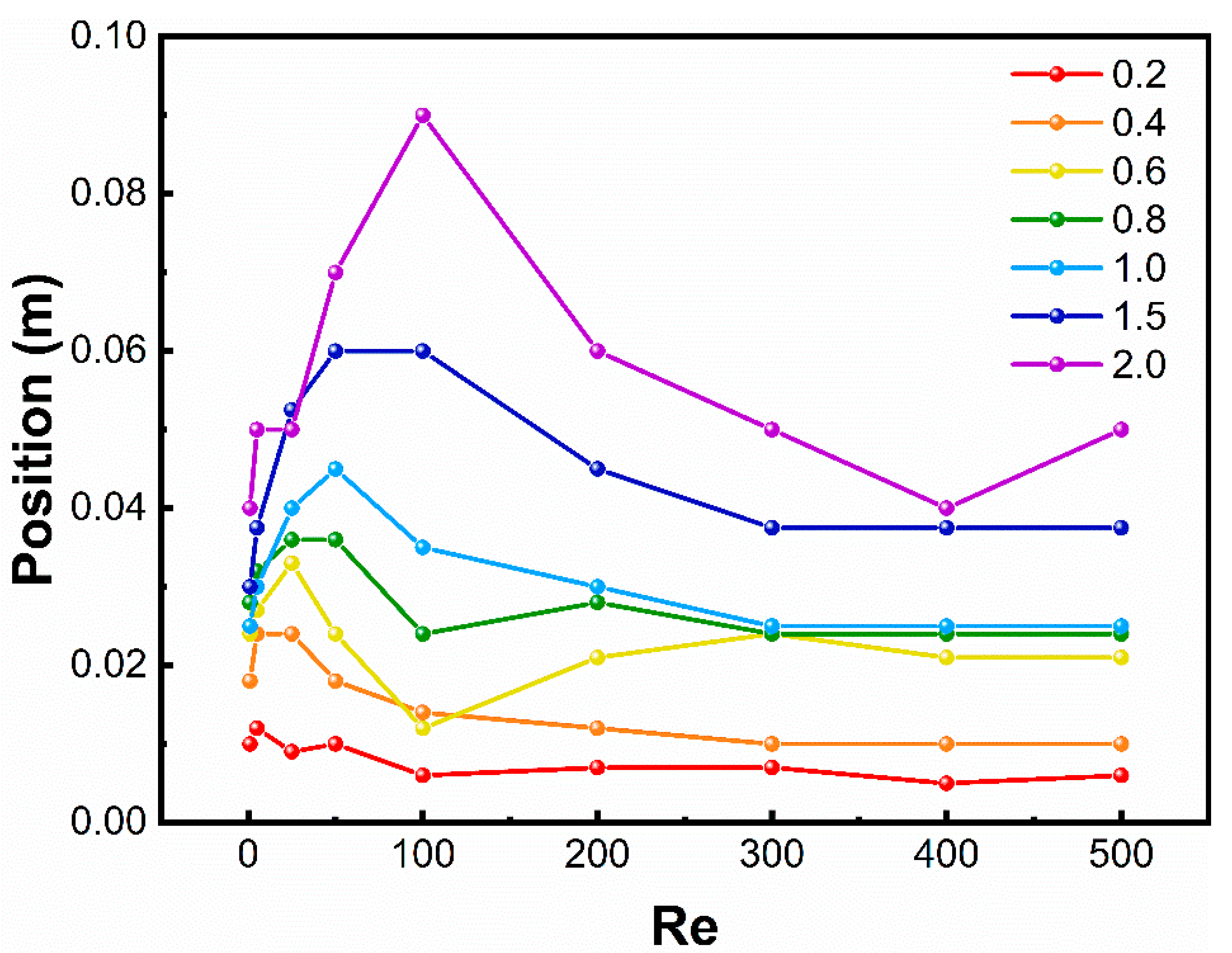
3.4. Effect of Aspect Ratio on Mixing Time
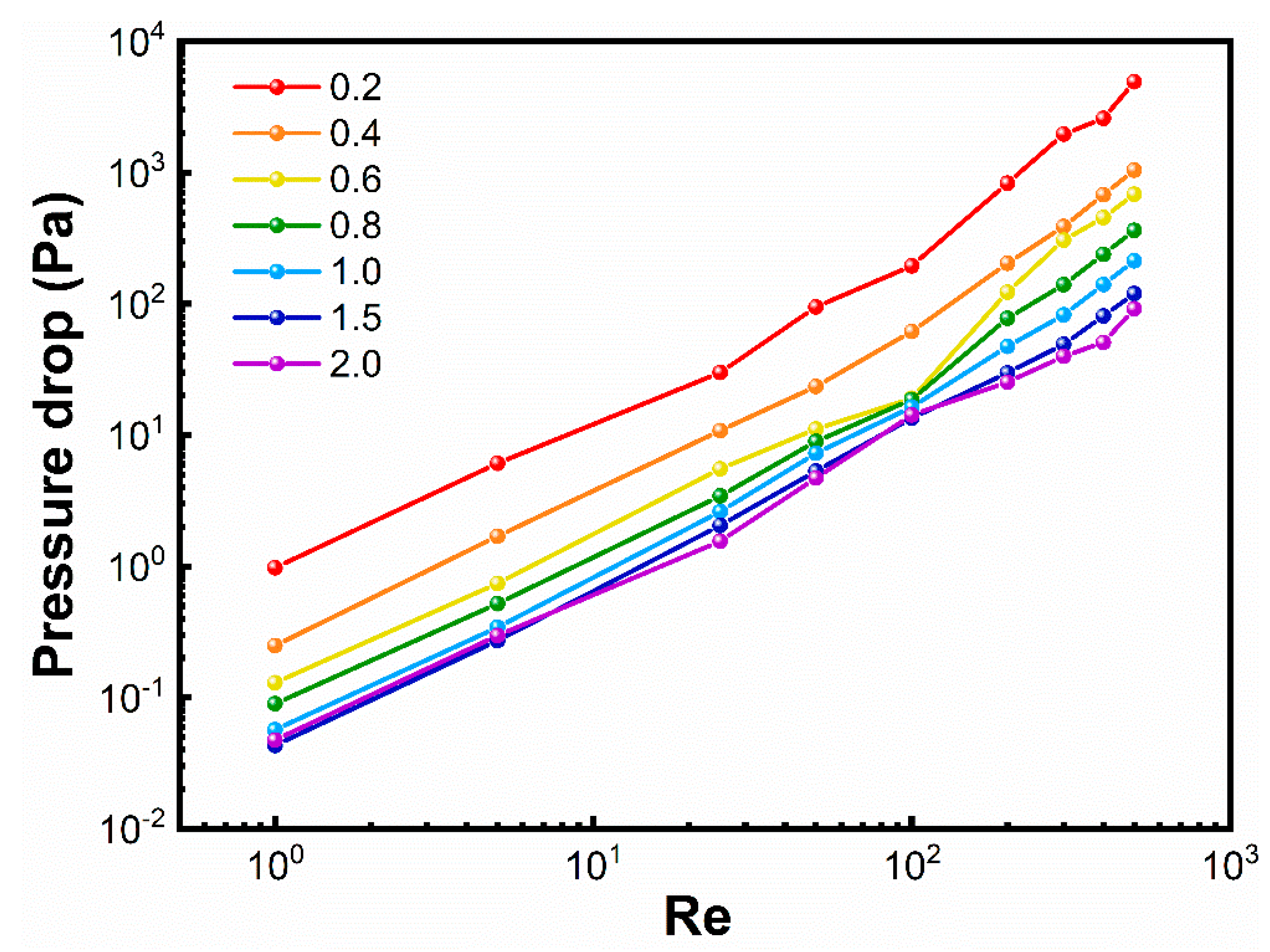
3.5. Effect of Aspect Ratio on Pressure Drop
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Roberge, D.M.; Zimmermann, B.; Rainone, F.; Gottsponer, M.; Eyholzer, M.; Kockmann, N. Microreactor Technology and Continuous Processes in the Fine Chemical and Pharmaceutical Industry: Is the Revolution Underway? Org. Process Res. Dev. 2008, 12, 905–910. [Google Scholar] [CrossRef]
- Poechlauer, P.; Braune, S.; Dielemans, B.; Kaptein, B.; Obermueller, R.; Thathagar, M. On-site-on demand production of hazardous chemicals by continuous flow processes. Chim. Oggi-Chem. Today 2012, 30, 51–54. [Google Scholar]
- Gutmann, B.; Cantillo, D.; Kappe, C.O. Continuous-Flow Technology—A Tool for the Safe Manufacturing of Active Pharmaceutical Ingredients. Angew. Chem. Int. Ed. 2015, 54, 6688–6728. [Google Scholar] [CrossRef]
- Plumb, K. Continuous Processing in the Pharmaceutical Industry: Changing the Mind Set. Chem. Eng. Res. Des. 2005, 83, 730–738. [Google Scholar] [CrossRef]
- Sagandira, C.R.; Siyawamwaya, M.; Watts, P. 3D printing and continuous flow chemistry technology to advance pharmaceutical manufacturing in developing countries. Arab. J. Chem. 2020, 13, 7886–7908. [Google Scholar] [CrossRef]
- Plutschack, M.B.; Pieber, B.; Gilmore, K.; Seeberger, P.H. The Hitchhiker’s Guide to Flow Chemistry. Chem. Rev. 2017, 117, 11796–11893. [Google Scholar] [CrossRef]
- Schaber, S.D.; Gerogiorgis, D.I.; Ramachandran, R.; Evans, J.M.B.; Barton, P.I.; Trout, B.L. Economic Analysis of Integrated Continuous and Batch Pharmaceutical Manufacturing: A Case Study. Ind. Eng. Chem. Res. 2011, 50, 10083–10092. [Google Scholar] [CrossRef] [Green Version]
- Taylor, R.A.; Penney, W.R.; Vo, H.X. Scale-up Methods for Fast Competitive Chemical Reactions in Pipeline Mixers. Ind. Eng. Chem. Res. 2005, 44, 6095–6102. [Google Scholar] [CrossRef]
- Levesque, F.; Bogus, N.J.; Spencer, G.; Grigorov, P.; McMullen, J.P.; Thaisrivongs, D.A.; Davies, I.W.; Naber, J.R. Advancing Flow Chemistry Portability: A Simplified Approach to Scaling Up Flow Chemistry. Org. Process Res. Dev. 2018, 22, 1015–1021. [Google Scholar] [CrossRef]
- Ir, J.I.I.; Lecjaks, Z. Pressure drop and homogenization efficiency of a motionless mixer. Chem. Eng. Commun. 1982, 16, 325–334. [Google Scholar] [CrossRef]
- Hobbs, D.M. Characterization of a Kenics Static Mixer under Laminar Flow Conditions. Ph.D. Thesis, The State University of NewJersey, New Brunswick, NJ, USA, 1997. [Google Scholar]
- Hobbs, D.M.; Muzzio, F.J. Effects of injection location, flow ratio and geometry on kenics mixer performance. Aiche J. 1997, 43, 3121–3132. [Google Scholar] [CrossRef]
- Alberini, F.; Simmons, M.J.H.; Ingram, A.; Stitt, E.H. Assessment of different methods of analysis to characterise the mixing of shear-thinning fluids in a Kenics KM static mixer using PLIF. Chem. Eng. Sci. 2014, 112, 152–169. [Google Scholar] [CrossRef] [Green Version]
- Kumar, V.; Shirke, V.; Nigam, K.D.P. Performance of Kenics static mixer over a wide range of Reynolds number. Chem. Eng. J. 2008, 139, 284–295. [Google Scholar] [CrossRef]
- Etchells Iii, A.W.; Meyer, C.F. Mixing in Pipelines. In Handbook of Industrial Mixing; Wiley: Hoboken, NJ, USA, 2003; pp. 391–477. [Google Scholar] [CrossRef]
- Wilcox, D.C. Turbulence Modeling for CFD; DCW Industries: La CaÒada, CA, USA, 2010. [Google Scholar]
- Wilcox, D.C. Formulation of the k-w Turbulence Model Revisited. AIAA J. 2008, 46, 2823–2838. [Google Scholar] [CrossRef] [Green Version]
- Wilcox, D.C. Simulation of Transition with a Two-Equation Turbulence Model. AIAA J. 1994, 32, 247–255. [Google Scholar] [CrossRef]
- Menter, F.R. Two-equation eddy-viscosity turbulence models for engineering applications. Aiaa J. 1994, 32, 1598–1605. [Google Scholar] [CrossRef] [Green Version]
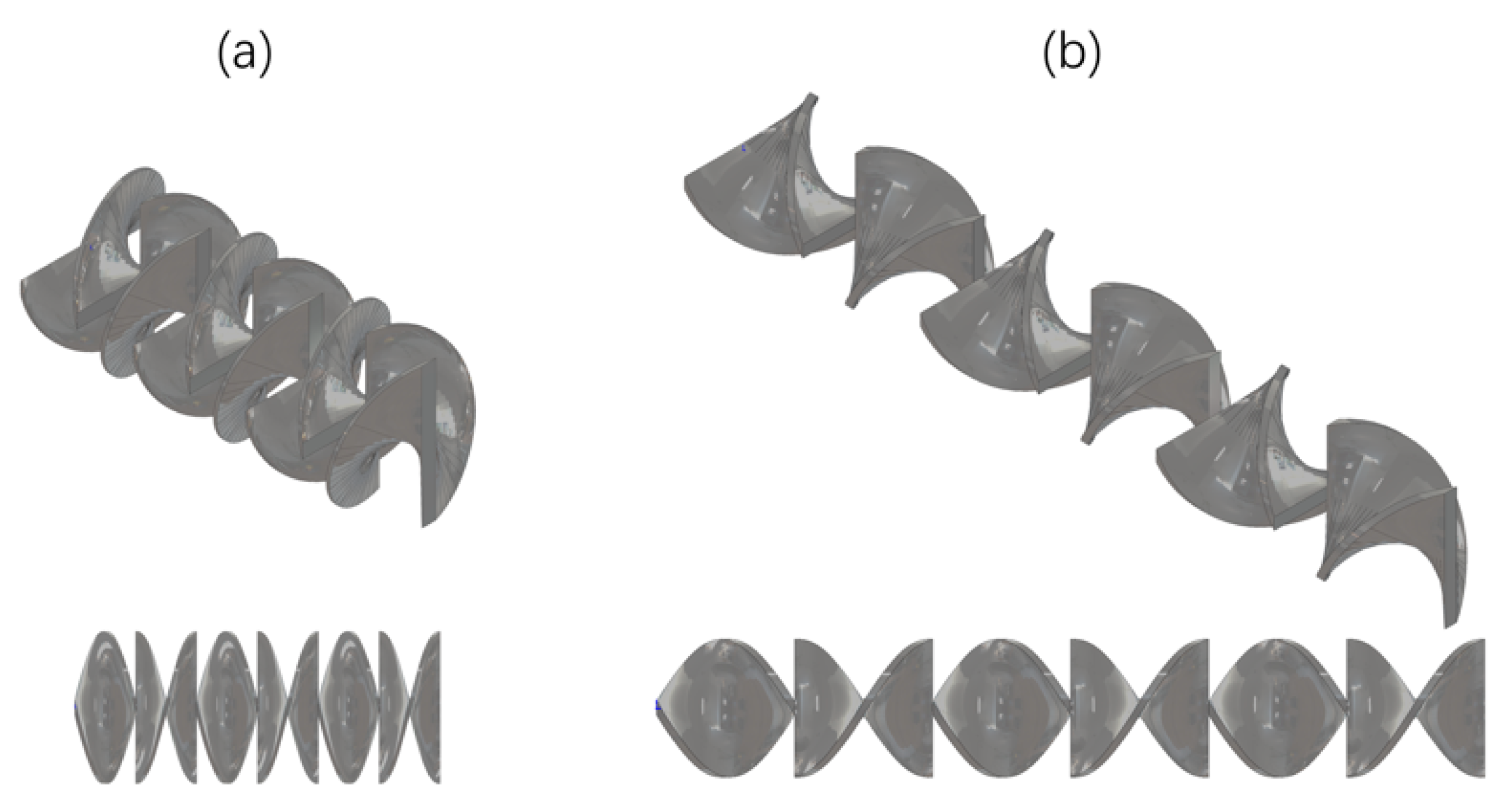
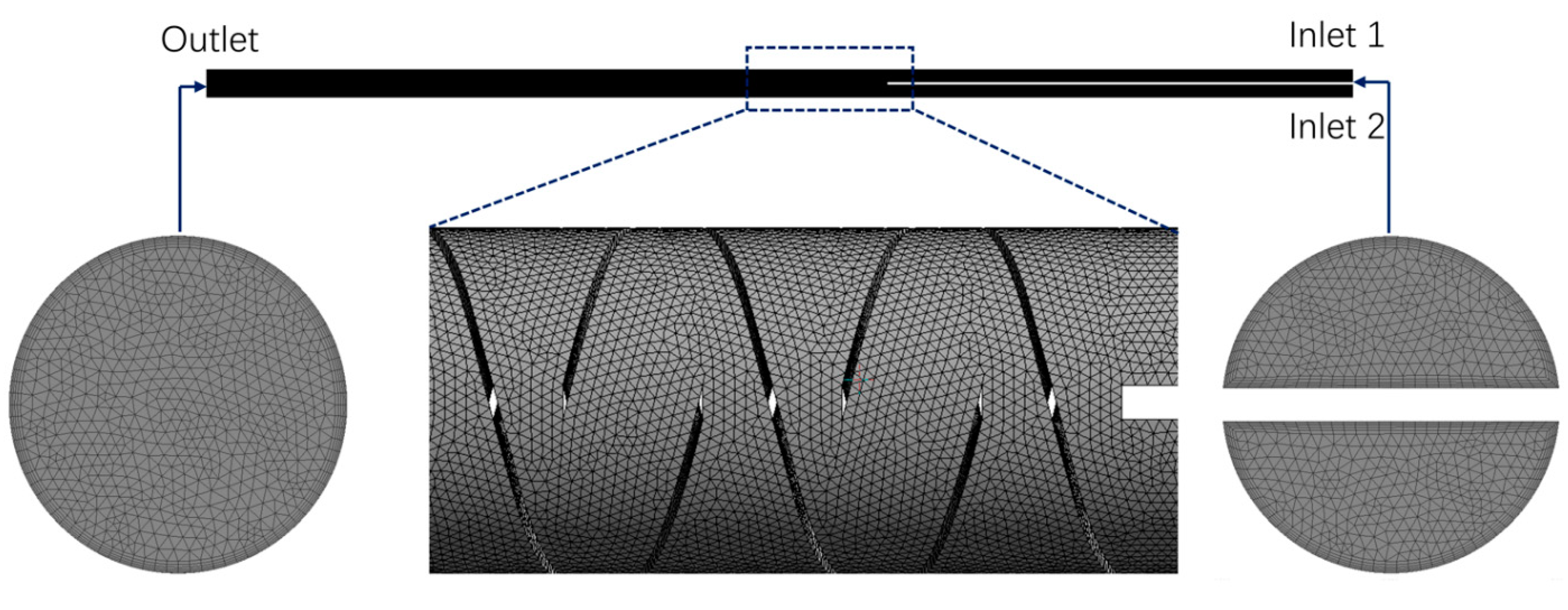









| Number | Diameter (mm) | Element Thickness (mm) | Aspect Ratio | Number of Elements |
|---|---|---|---|---|
| 1 | 5 | 0.5 | 0.2 | 24 |
| 2 | 5 | 0.5 | 0.4 | 24 |
| 3 | 5 | 0.5 | 0.6 | 24 |
| 4 | 5 | 0.5 | 0.8 | 24 |
| 5 | 5 | 0.5 | 1 | 24 |
| 6 | 5 | 0.5 | 1.5 | 24 |
| 7 | 5 | 0.5 | 2 | 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, X.; Yang, N.; Wang, R. Effect of Aspect Ratio on the Mixing Performance in the Kenics Static Mixer. Processes 2021, 9, 464. https://doi.org/10.3390/pr9030464
Jiang X, Yang N, Wang R. Effect of Aspect Ratio on the Mixing Performance in the Kenics Static Mixer. Processes. 2021; 9(3):464. https://doi.org/10.3390/pr9030464
Chicago/Turabian StyleJiang, Xingren, Ning Yang, and Rijie Wang. 2021. "Effect of Aspect Ratio on the Mixing Performance in the Kenics Static Mixer" Processes 9, no. 3: 464. https://doi.org/10.3390/pr9030464
APA StyleJiang, X., Yang, N., & Wang, R. (2021). Effect of Aspect Ratio on the Mixing Performance in the Kenics Static Mixer. Processes, 9(3), 464. https://doi.org/10.3390/pr9030464






