Modeling the Influence of Temperature, Light Intensity and Oxygen Concentration on Microalgal Growth Rate
Abstract
1. Introduction
2. Model Development
2.1. Representing Growth and Toxicity Rates
2.2. Dynamic Modeling
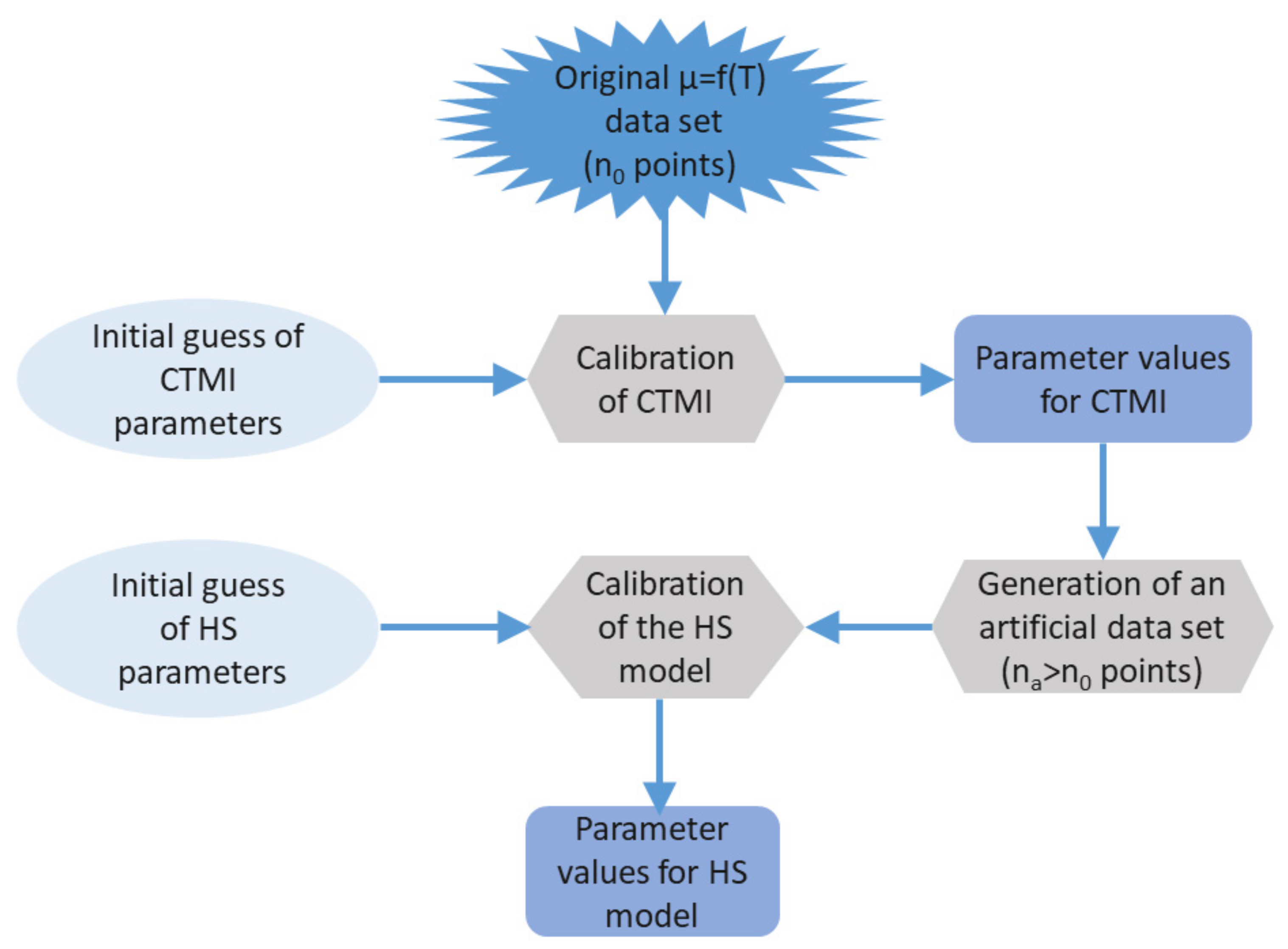
2.3. Parameter Estimation
2.4. Model Validation
3. Results and Discussion
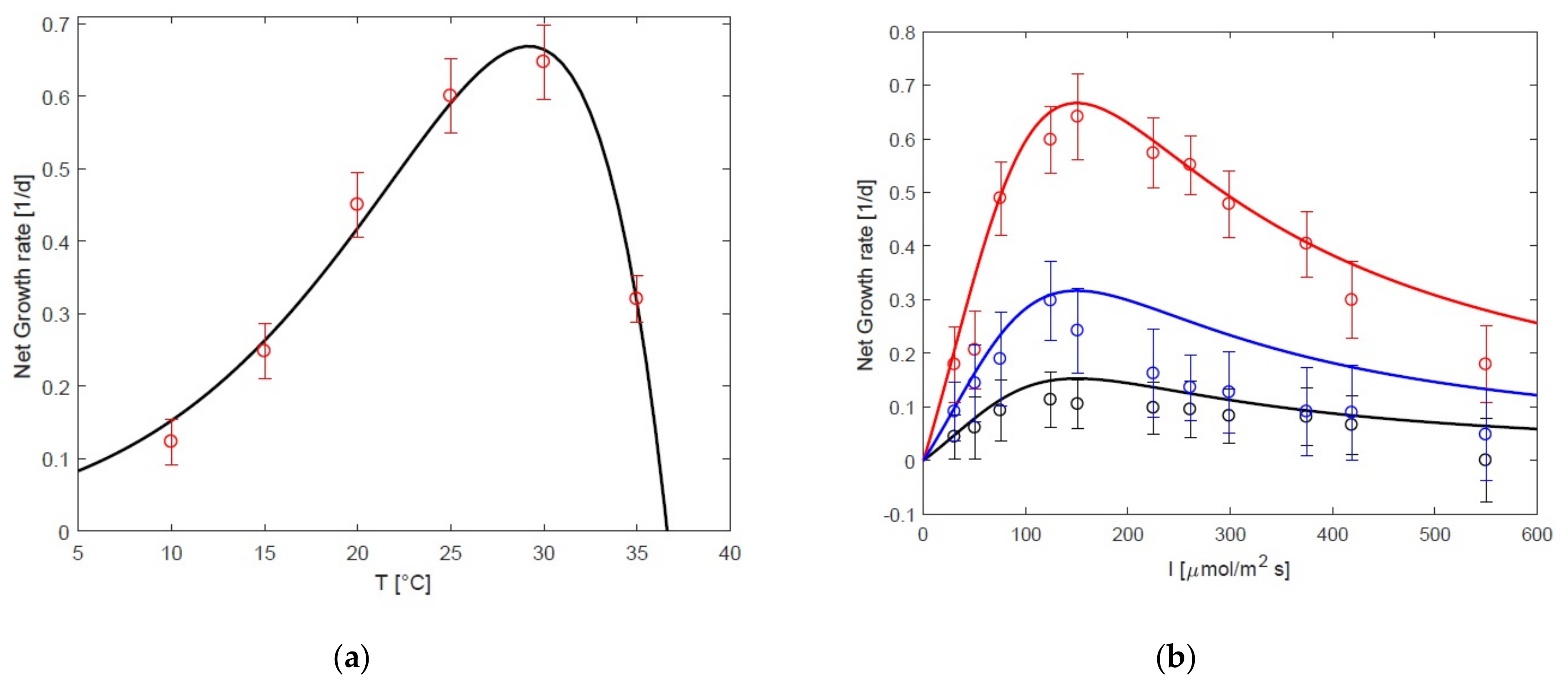
3.1. Static Growth Model as a Function of Temperature and Light
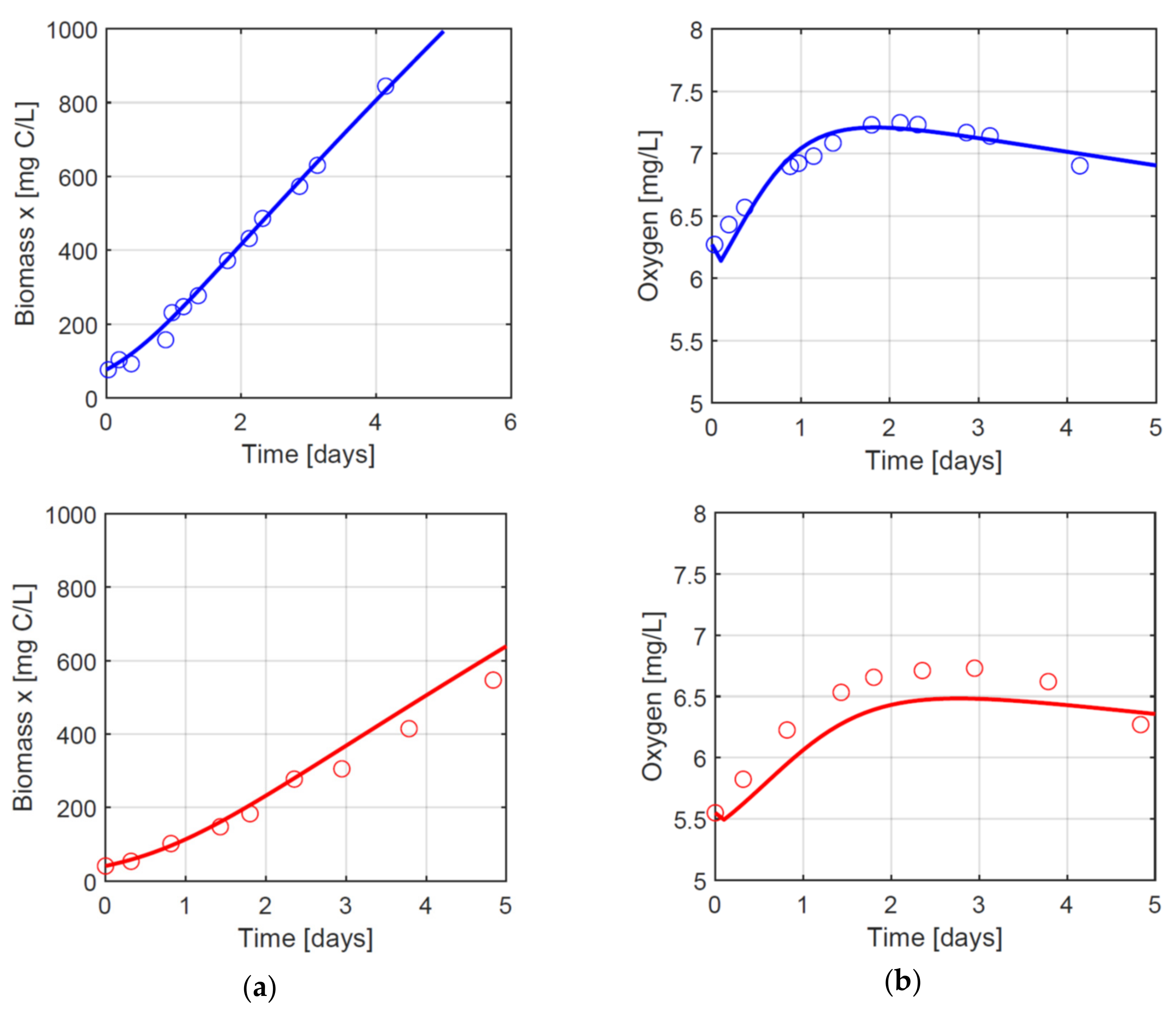
3.2. Growth in Dynamical Conditions
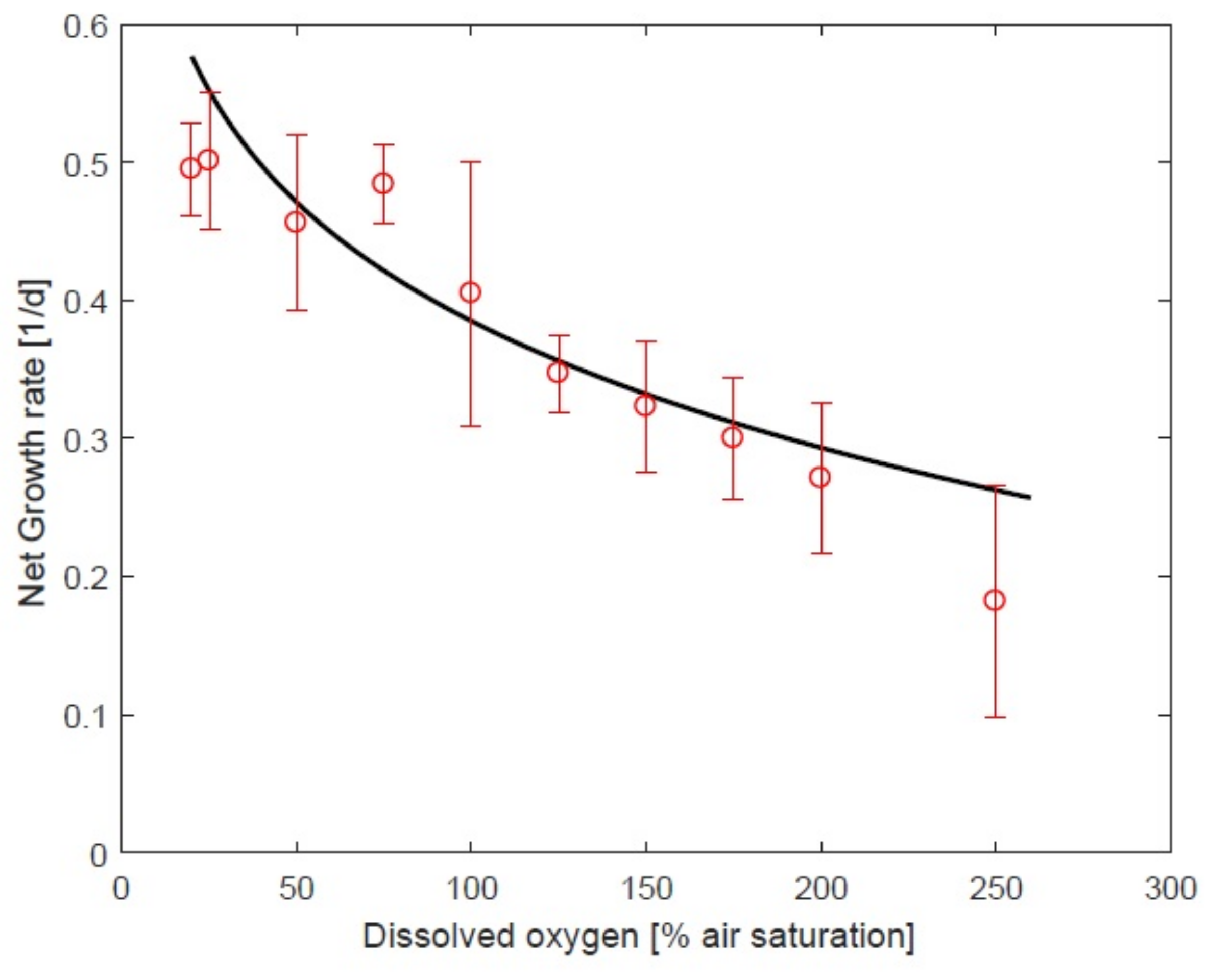
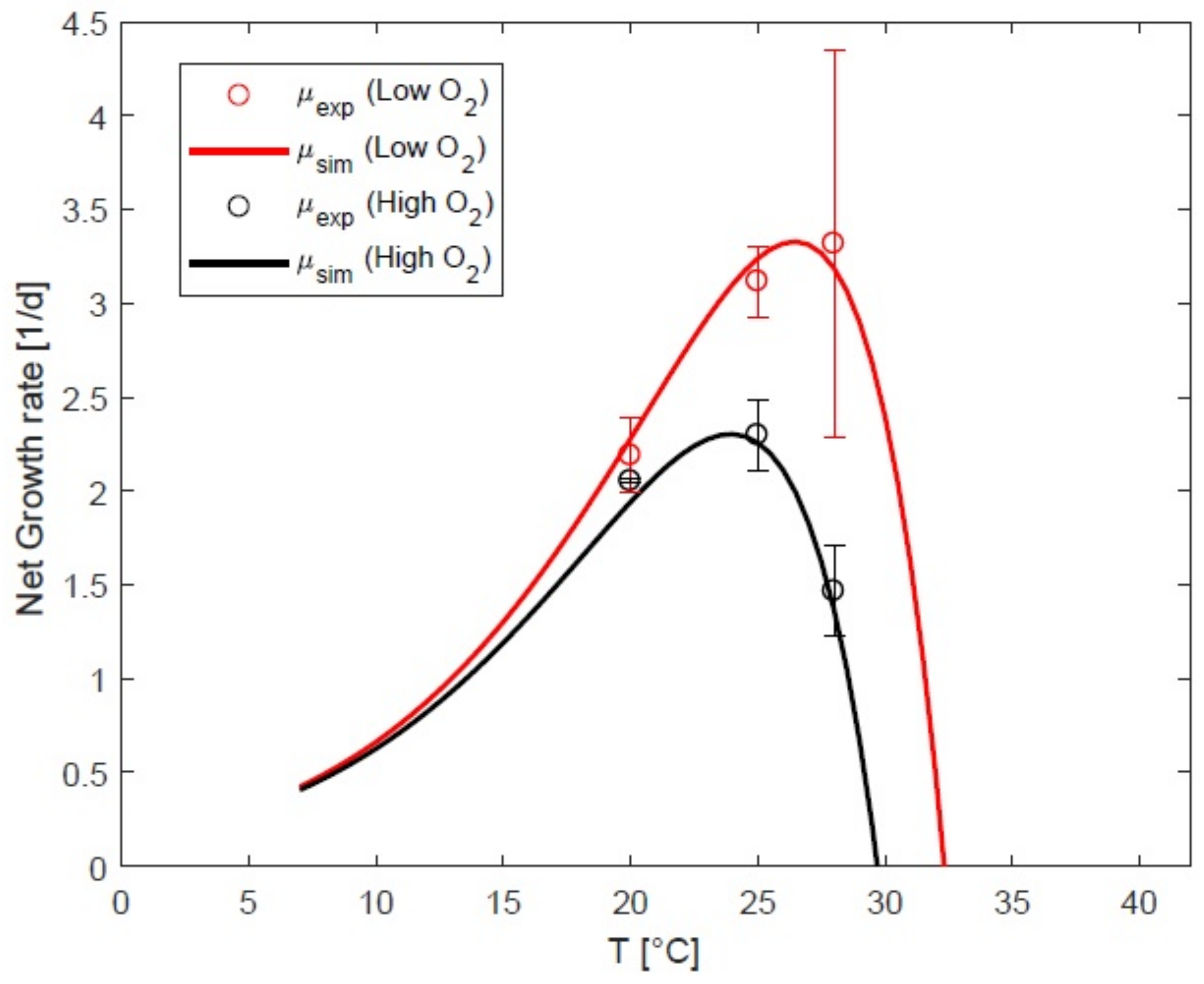
3.3. Impact of Oxygen on Response to Temperature
4. Discussion
4.1. Impact of Oxygen the Growth Rate
4.2. Sensitivity to Oxidative Stress
4.3. Calibration of Hinshelwood’s Model
4.4. Predicting and Reducing Oxidative Stress
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
Appendix B
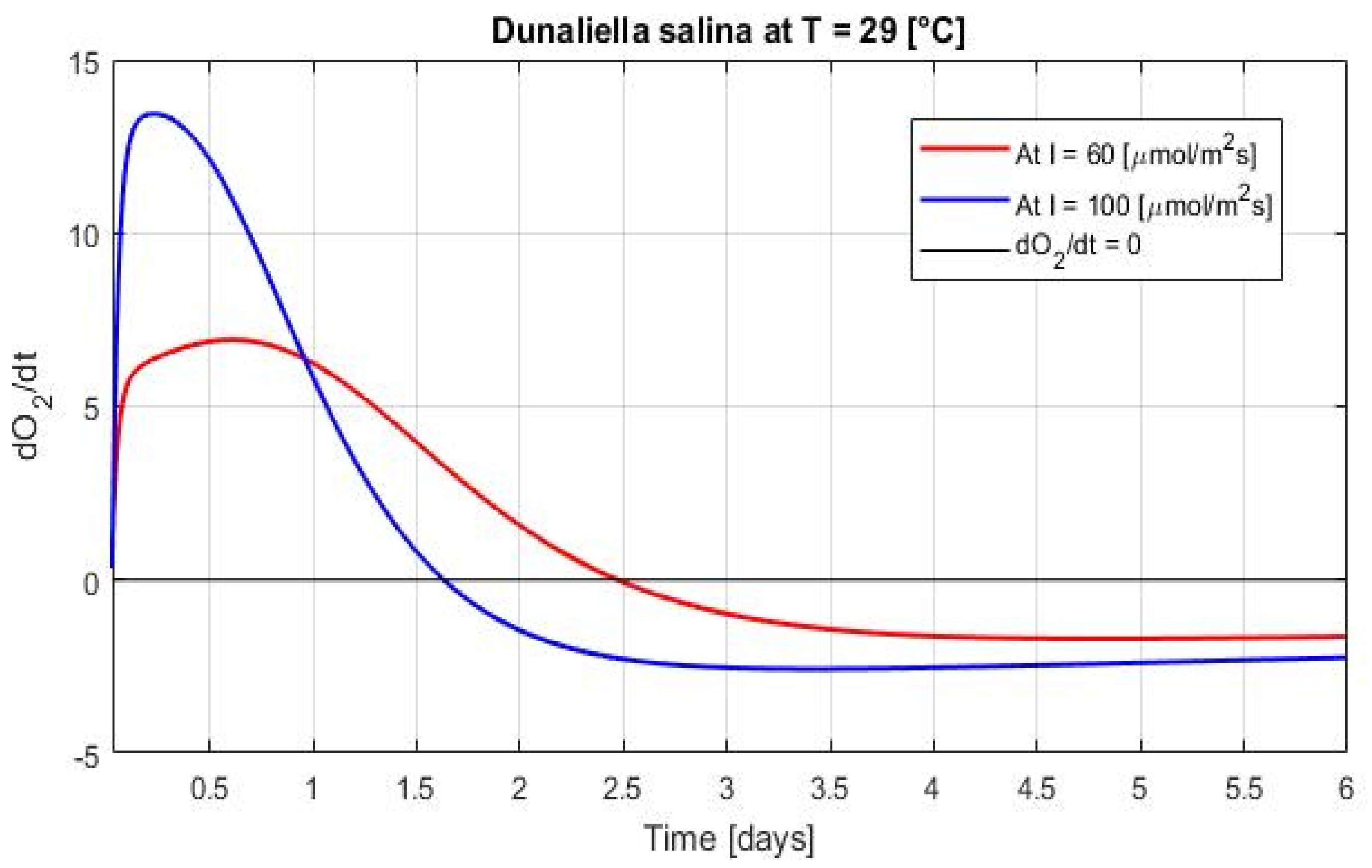
Appendix C

References
- Wijffels, R.H.; Barbosa, M.J. An outlook on microalgal biofuels. Science 2010, 329, 796–799. [Google Scholar] [CrossRef] [PubMed]
- Bernard, O. Hurdles and challenges for modelling and control of microalgae for CO2 mitigation and biofuel production. J. Process. Control. 2011, 21, 1378–1389. [Google Scholar] [CrossRef]
- Guedes, A.C.; Meireles, L.A.; Amaro, H.M.; Malcata, F.X. Changes in lipid class and fatty acid composition of cultures of Pavlova lutheri, in response to light intensity. J. Am. Oil Chem. Soc. 2010, 87, 791–801. [Google Scholar] [CrossRef]
- Sousa, C.; De Winter, L.; Janssen, M.; Vermuë, M.H.; Wijffels, R.H. Growth of the microalgae Neochloris oleoabundans at high partial oxygen pressures and sub-saturating light intensity. Bioresour. Technol. 2012, 104, 565–570. [Google Scholar] [CrossRef] [PubMed]
- Eilers, P.H.C.; Peeters, J.C.H. A model for the relationship method is easy to implement, is less expensive than the between light intensity and the rate of photosynthesis in phytoplankton. Ecol. Model. 1988, 42, 199–215. [Google Scholar] [CrossRef]
- Béchet, Q.; Laviale, M.; Arsapin, N.; Bonnefond, H.; Bernard, O. Modeling the impact of high temperatures on microalgal viability and photosynthetic activity. Biotechnol. Biofuels 2017, 10, 1–11. [Google Scholar] [CrossRef]
- Ras, M.; Steyer, J.-P.; Bernard, O. Temperature effect on microalgae: A crucial factor for outdoor production. Rev. Environ. Sci. Biotechnol. 2013, 12, 153–164. [Google Scholar] [CrossRef]
- Serra-Maia, R.; Bernard, O.; Goncalves, A.; Bensalem, S.; Lopes, F. Influence of temperature on Chlorella vulgaris growth and toxicity rates in a photobioreactor. Algal Res. 2016, 18, 352–359. [Google Scholar] [CrossRef]
- Foyer, C.H.; Bloom, A.J.; Queval, G.; Noctor, G. Photorespiratory metabolism: Genes, Mutants, energetics, and redox signaling. Annu. Rev. Plant Biol. 2009, 60, 455–484. [Google Scholar] [CrossRef]
- Murata, N.; Takahashi, S.; Nishiyama, Y.; Allakhverdiev, S.I. Photoinhibition of photosystem II under environmental stress. Biochim. Biophys. Acta Bioenerg. 2007, 1767, 414–421. [Google Scholar] [CrossRef]
- Pospíšil, P. Enzymatic function of cytochrome b559 in photosystem II. J. Photochem. Photobiol. B Biol. 2011, 104, 341–347. [Google Scholar] [CrossRef]
- Takeda, T.; Yokota, A.; Shigeoka, S. Resistance of photosynthesis to hydrogen peroxide in algae. Plant Cell Physiol. 1995, 36, 1089–1095. [Google Scholar] [CrossRef]
- Bernard, O.; Rémond, B. Validation of a simple model accounting for light and temperature effect on microalgal growth. Bioresour. Technol. 2012, 123, 520–527. [Google Scholar] [CrossRef] [PubMed]
- Bernard, O.; Mairet, F.; Chachuat, B. Modelling of microalgae culture systems with applications to control and optimization. In Tissue Engineering III: Cell—Surface Interactions for Tissue Culture; Portner, R., Kasper, C., Witte, F., Eds.; Springer International Publishing: Geneva, Switzerland, 2015; Volume 153, pp. 59–87. [Google Scholar]
- Béchet, Q.; Shilton, A.; Guieysse, B. Modeling the effects of light and temperature on algae growth: State of the art and critical assessment for productivity prediction during outdoor cultivation. Biotechnol. Adv. 2013, 31, 1648–1663. [Google Scholar] [CrossRef] [PubMed]
- Steele, J.H.; Baird, I.E. Further relations between primary production, chlorophyll, and particulate carbon. Limnol. Oceanogr. 1962, 7, 42–47. [Google Scholar] [CrossRef]
- Grimaud, G.M.; Mairet, F.; Sciandra, A.; Bernard, O. Modeling the temperature effect on the specific growth rate of phytoplankton: A review. Rev. Environ. Sci. Biotechnol. 2017, 16, 625–645. [Google Scholar] [CrossRef]
- Rosso, L.; Lobry, J.R.; Flandrois, J.P. An unexpected correlation between cardinal temperatures of microbial growth high-lighted by a new model. J. Theor. Biol. 1993, 162, 447–463. [Google Scholar] [CrossRef]
- Hinshelwood, C.N. Kinetics of the Bacterial Cell; Oxford University Press: London, UK, 1946. [Google Scholar]
- Huisman, J.; Weissing, F.J. Light-limited growth and competition for light in well-mixed aquatic environments: An elementary model. Ecology 1994, 75, 507–520. [Google Scholar] [CrossRef]
- Martínez, C.; Mairet, F.; Bernard, O. Theory of turbid microalgae cultures. J. Theor. Biol. 2018, 456, 190–200. [Google Scholar] [CrossRef]
- Sherwood, J.; Stagnitti, F.; Kokkinn, M.J.; Williams, W.D. Dissolved oxygen concentrations in hypersaline waters. Limnol. Oceanogr. 1991, 36, 235–250. [Google Scholar] [CrossRef]
- Aleya, L.; Dauta, A.; Reynolds, C.S. Endogenous regulation of the growth-rate responses of a spring-dwelling strain of the freshwater alga, Chlorella minutissima, to light and temperature. Eur. J. Protistol. 2011, 47, 239–244. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.-H.; Chang, F.-L.; Tsao, C.-Y.; Leu, J.-Y. Influence of growth phase and nutrient source on fatty acid composition of Isochrysis galbana CCMP 1324 in a batch photoreactor. Biochem. Eng. J. 2007, 37, 166–176. [Google Scholar] [CrossRef]
- Li, J.; Xu, N.S.; Su, W.W. Online estimation of stirred-tank microalgal photobioreactor cultures based on dissolved oxygen measurement. Biochem. Eng. J. 2003, 14, 51–65. [Google Scholar] [CrossRef]
- Raso, S.; Van Genugten, B.; Vermuë, M.; Wijffels, R.H. Effect of oxygen concentration on the growth of Nannochloropsis sp. at low light intensity. Environ. Biol. Fishes 2011, 24, 863–871. [Google Scholar] [CrossRef]
- Horton, R.L.; Seber, G.A.F.; Wild, C.J. Nonlinear regression. J. Mark. Res. 1990, 27, 244–245. [Google Scholar] [CrossRef]
- Sadino-Riquelme, M.C.; Rivas, J.; Jeison, D.; Hayes, R.E.; Donoso-Bravo, A. Making sense of parameter estimation and model simulation in bioprocesses. Biotechnol. Bioeng. 2020, 117, 1357–1366. [Google Scholar] [CrossRef] [PubMed]
- Edwards, K.F.; Thomas, M.K.; Klausmeier, C.A.; Litchman, E. Light and growth in marine phytoplankton: Allometric, taxonomic, and environmental variation. Limnol. Oceanogr. 2015, 60, 540–552. [Google Scholar] [CrossRef]
- Schwaderer, A.S.; Yoshiyama, K.; Pinto, P.D.T.; Swenson, N.G.; Klausmeier, C.A.; Litchman, E. Ecoevolutionary differences in light utilization traits and distributions of freshwater phytoplankton. Limnol. Oceanogr. 2011, 56, 589–598. [Google Scholar] [CrossRef]
- Murthy, K.C.; Vanitha, A.; Rajesha, J.; Swamy, M.M.; Sowmya, P.; Ravishankar, G.A. In vivo antioxidant activity of carotenoids from Dunaliella salina—A green microalga. Life Sci. 2005, 76, 1381–1390. [Google Scholar] [CrossRef] [PubMed]
- Frank, H.A.; Young, A.; Britton, G.; Cogdell, R.J. The photochemistry of carotenoids. In Advances in Photosynthesis and Respiration; Sharkey, T.D., Eaton-Rye, J., Eds.; Springer Science and Business Media: Secaucus, NJ, USA, 1999; Volume 8. [Google Scholar]
- De-Luca, R.; Bezzo, F.; Béchet, Q.; Bernard, O. Exploiting meteorological forecasts for the optimal operation of algal ponds. J. Process. Control. 2017, 55, 55–65. [Google Scholar] [CrossRef]
- Bonnefond, H.; Grimaud, G.; Rumin, J.; Bougaran, G.; Talec, A.; Gachelin, M.; Boutoute, M.; Pruvost, E.; Bernard, O.; Sciandra, A. Continuous selection pressure to improve temperature acclimation of Tisochrysis lutea. PLoS ONE 2017, 12, e0183547. [Google Scholar] [CrossRef] [PubMed]
- Ugwu, C.; Aoyagi, H.; Uchiyama, H. Photobioreactors for mass cultivation of algae. Bioresour. Technol. 2008, 99, 4021–4028. [Google Scholar] [CrossRef] [PubMed]


| Reference | Model | Species | Light Intensity | Temperature °C | pH | Oxygen Concentration |
|---|---|---|---|---|---|---|
| [8] | C | Chlorella vulgaris | 140 | From 20 to 35 | NC | E |
| [23] | C | Chlorella minutissima | From 30 to 550 | 10, 30 and 35 | NC | E |
| [24] | C | Isochrysis galbana | From 12 to 136 | From 10 to 40 | 9 | E |
| [25] | C and V | Dunaliella salina | From 60 to 100 | 29 | 7.5 | M |
| [26] | C | Nannochloropsis sp | 100 | 25 | 7.8 | M |
| Species | - | - | - | |||||||
| C. minutissima | ||||||||||
| I. galbana | ||||||||||
| Nannochloropsis sp. | ||||||||||
| C. vulgaris | ||||||||||
| D. salina |
| Parameter | |||||
|---|---|---|---|---|---|
| Unit | |||||
| Value |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López Muñoz, I.; Bernard, O. Modeling the Influence of Temperature, Light Intensity and Oxygen Concentration on Microalgal Growth Rate. Processes 2021, 9, 496. https://doi.org/10.3390/pr9030496
López Muñoz I, Bernard O. Modeling the Influence of Temperature, Light Intensity and Oxygen Concentration on Microalgal Growth Rate. Processes. 2021; 9(3):496. https://doi.org/10.3390/pr9030496
Chicago/Turabian StyleLópez Muñoz, Ignacio, and Olivier Bernard. 2021. "Modeling the Influence of Temperature, Light Intensity and Oxygen Concentration on Microalgal Growth Rate" Processes 9, no. 3: 496. https://doi.org/10.3390/pr9030496
APA StyleLópez Muñoz, I., & Bernard, O. (2021). Modeling the Influence of Temperature, Light Intensity and Oxygen Concentration on Microalgal Growth Rate. Processes, 9(3), 496. https://doi.org/10.3390/pr9030496






