Early-Stage Detection of Solid Oxide Cells Anode Degradation by Operando Impedance Analysis
Abstract
:1. Introduction
1.1. Operando Measurement Techniques for SOC Degradation
EIS-DRT Analysis for SOCs: A Summary
- Oxygen transfer at the FE is highlighted by a peak in the DRT at τ = 10−4 s (PA1); moreover, it is modeled with a parallel Resistance//Constant Phase Element (Ra1Qa1);
- The Hydrogen Oxidation Reaction (HOR) at the fuel electrode yields a peak at τ = 10−3 s (PA2) and it corresponds to a parallel Resistance//Constant Phase Element (Ra2Qa2);
- Similarly, the Oxygen Reduction Reaction (ORR) at the AE is modeled with another parallel Resistance//Constant Phase Element (Rc1Qc1) and it gives a peak in the DRT at τ = 10−1 s (Pc1).
- A finite-length Warburg element (WFLWa) modeling the gas transport to the fuel electrode. This process is highlighted by the peak at τ = 10−2 s (PA3);
- A Gerischer element (G), standing for gas transport at the mixed ionic-electronic conductor (MIEC) AE. It corresponds to the signal at τ = 10 s (PC1).
1.2. Aim of the Study
2. Materials and Methods
2.1. Experimental
2.1.1. Materials
2.1.2. Methods
- Start-up: When starting the test, the sealing paste is cured according to the instructions provided by the supplier, without exceeding a temperature rising rate of 1 K/min. During this phase, the cell is supplied with nitrogen at the fuel electrode and air at the air electrode. Once 1073 K are reached, the fuel electrode catalyst reduction begins.
- Reduction: Nitrogen is gradually substituted with hydrogen to reduce the fuel electrode catalysts from NiO to Ni.
- Stabilization: The cell is stabilized for at least 100 h at 1073 K, exposing the fuel electrode to a pure hydrogen atmosphere. A constant mild current load (250 mA/cm2) is set.
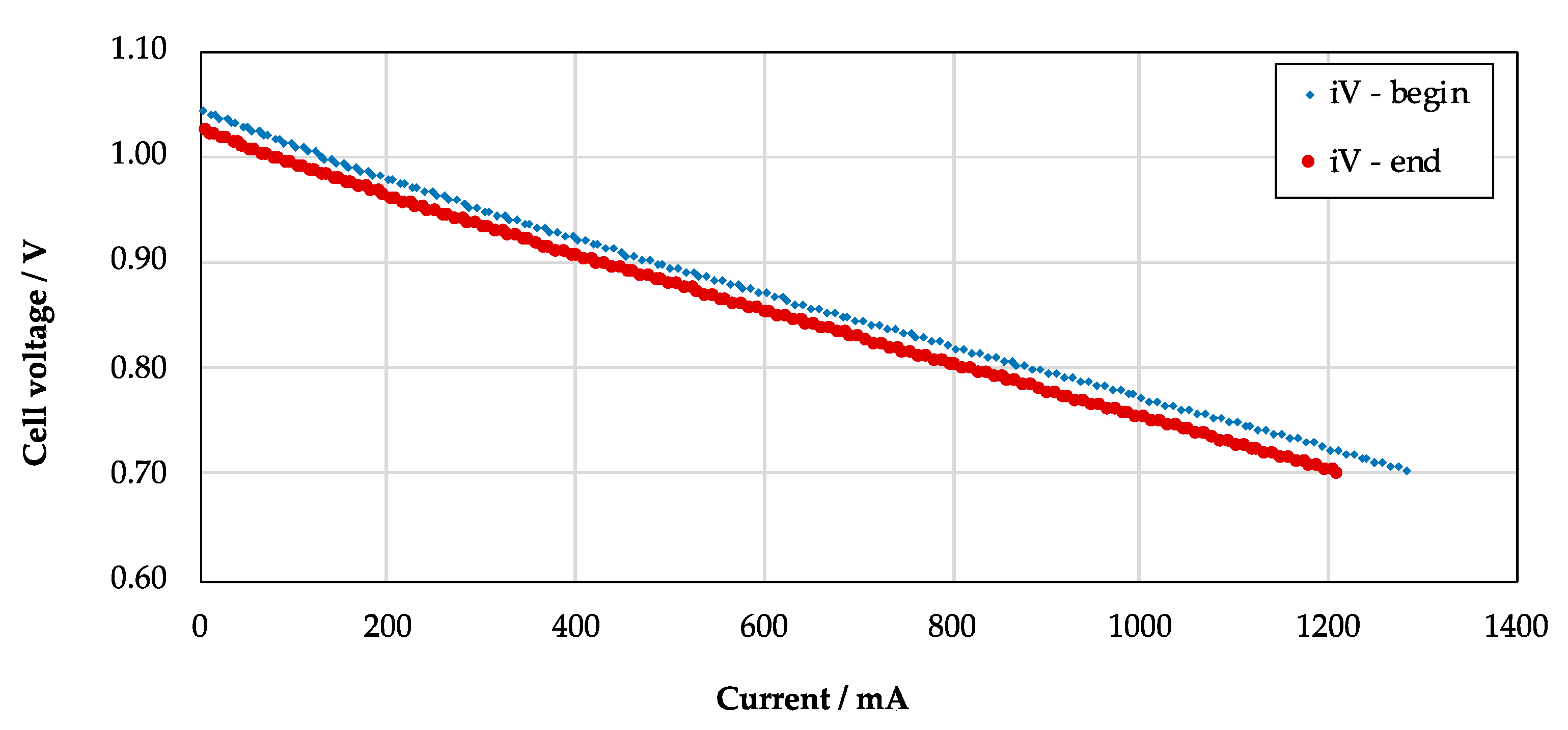
- Begin Reference: Reference performances are acquired at 1048 K, feeding the fuel electrode with a mixture of hydrogen (50 Sml/min) and nitrogen (150 Sml/min). The air electrode gas supply does not change (air, 300 Sml/min). Reference performance is characterized by both polarization and impedance analysis. For the further, the i-V curve of the cell is sampled with a potentiostat method, varying the working electrode potential from Open Circuit (OC) down to 0.7 V, by a rate of −40 mV/min, and then reverting to OC with a rising ramp of +40 mV/min. Then, for the latter, impedance is measured in galvanostatic mode with a single-sine method, applying a current wave of 20 mA amplitude. Electrochemical impedance is scanned from 100 kHz down to 100 MHz, acquiring 10 points per frequency decade, logarithmically spaced. Every single measurement is the average of 6 samplings. Impedance spectra are sampled at different selected points on the i-V curve (0, 100, 250, 500, and 750 mA/cm2). Both techniques are implemented through a BioLogic SP-240 analyzer, setting a voltage range of 0.5–1.5 V (resolution 20 μV) and a current range of 4A.
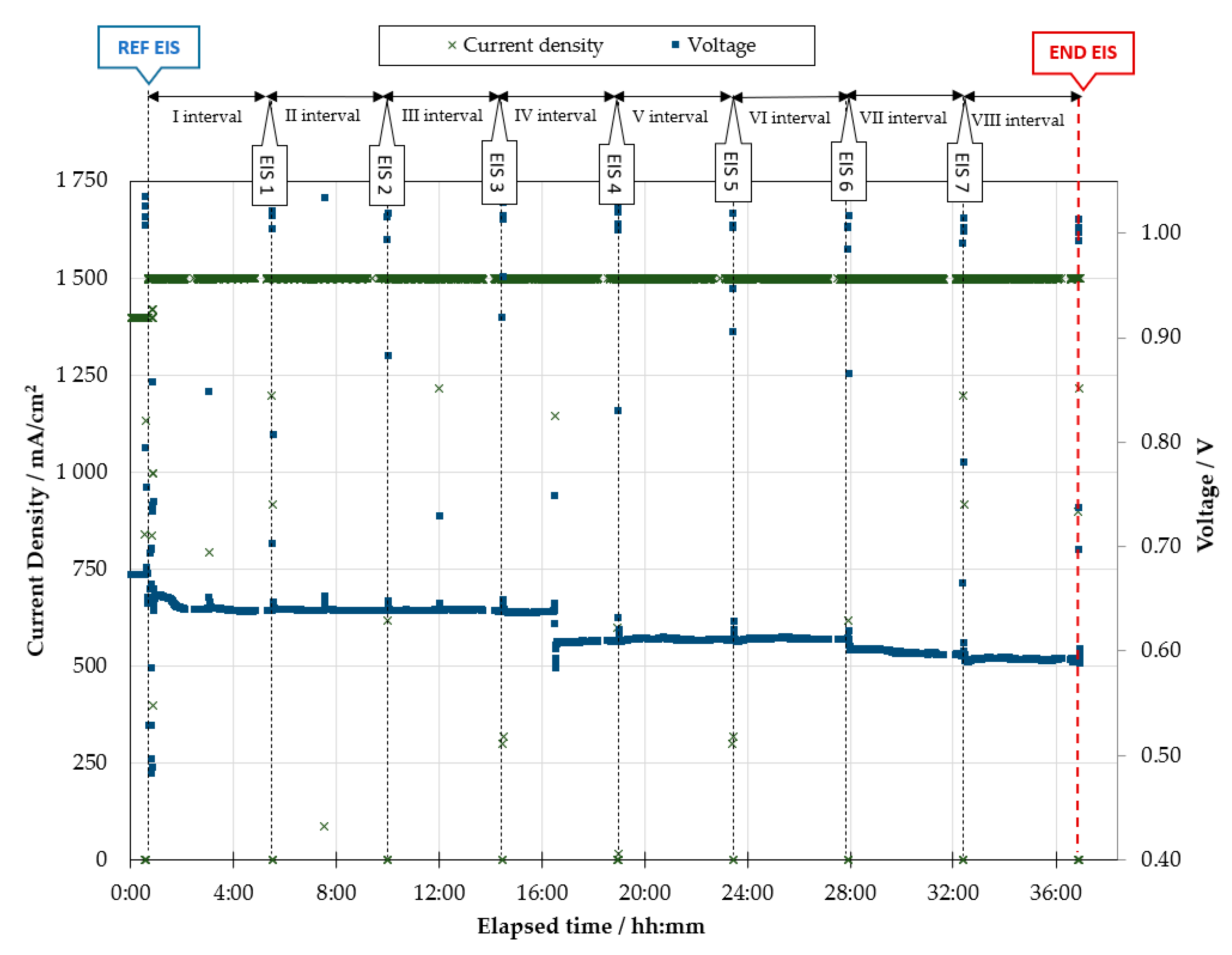
- Stress test: The cell temperature is kept at 1048 K and the gas flow rates and composition at both electrodes do not change regarding the reference characterization. The cell is continuously operated at 1500 mA/cm2 for time intervals of 4 h. After each 4-h time interval, the cell is brought back to OC to perform a galvanostatic EIS scan. The settings are the same as above: 20 mA single-sine current wave, 10 points per frequency decade, logarithmic spacing, 6 samplings per point. The impedance analysis is carried out at three current values of the polarization curve (0, 250, 500 mA/cm2), with both forward (from 100 kHz down to 100 MHz) and backward frequency scan (from 100 MHz up to 100 kHz). After the EIS characterization, constant load operation at 1500 mA/cm2 is restored for the following 4 h. This process is iterated as long as the working electrode potential is above 0.60 V.
- End Point: The final characterization is performed in the same conditions set for the beginning reference test. Both polarization and impedance are recorded, following the procedure already presented at the previous point 4.
- Shut down: The electric load is disconnected. Then, the cell is cooled down to room temperature (RT) with a decreasing temperature rate of −1 K/min, supplying former gas at the fuel electrode (hydrogen 5 Sml/min + nitrogen 95 Sml/min) and nitrogen at the air electrode (100 Sml/min).
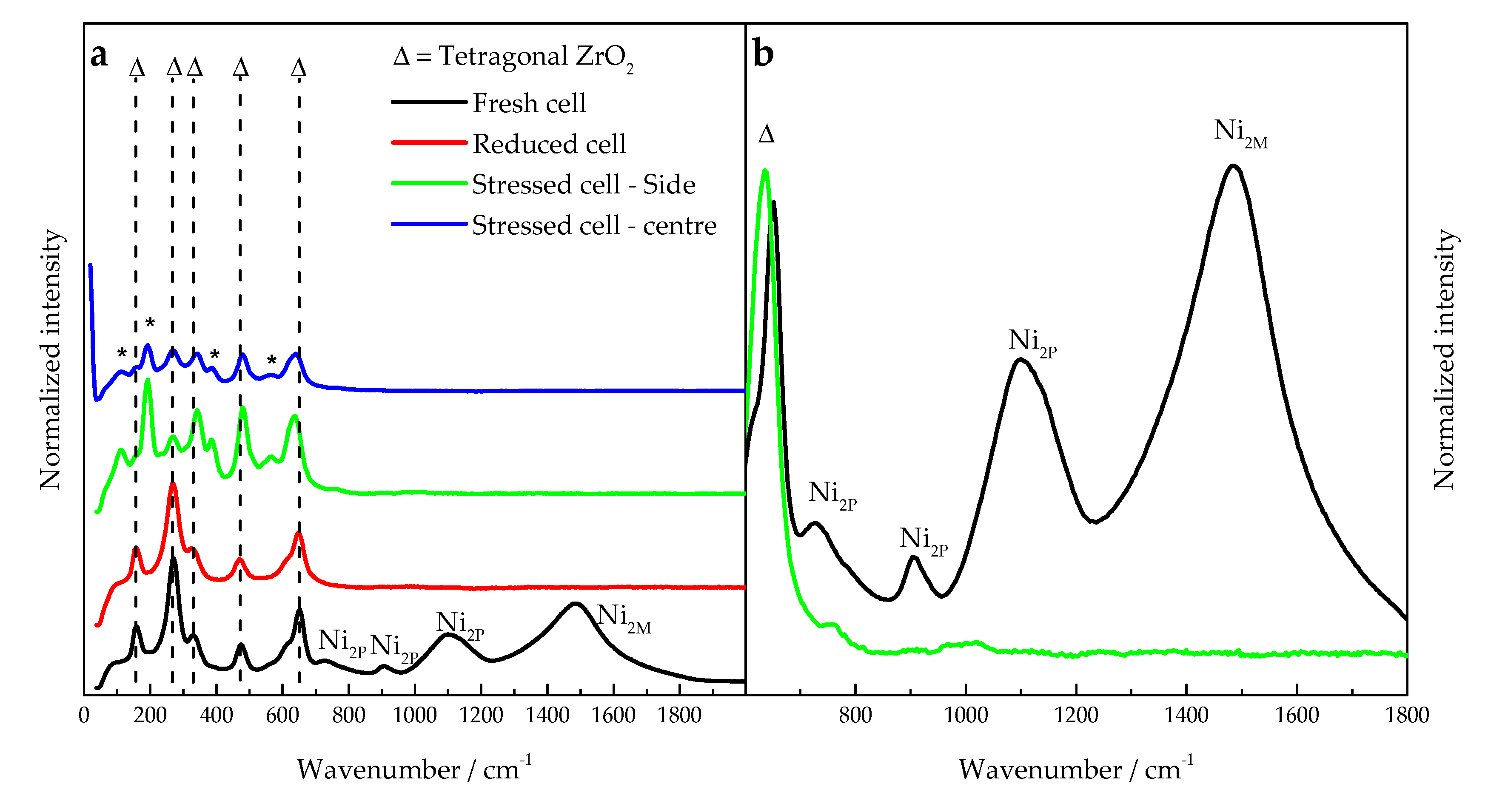
2.1.3. Cell Material Characterization
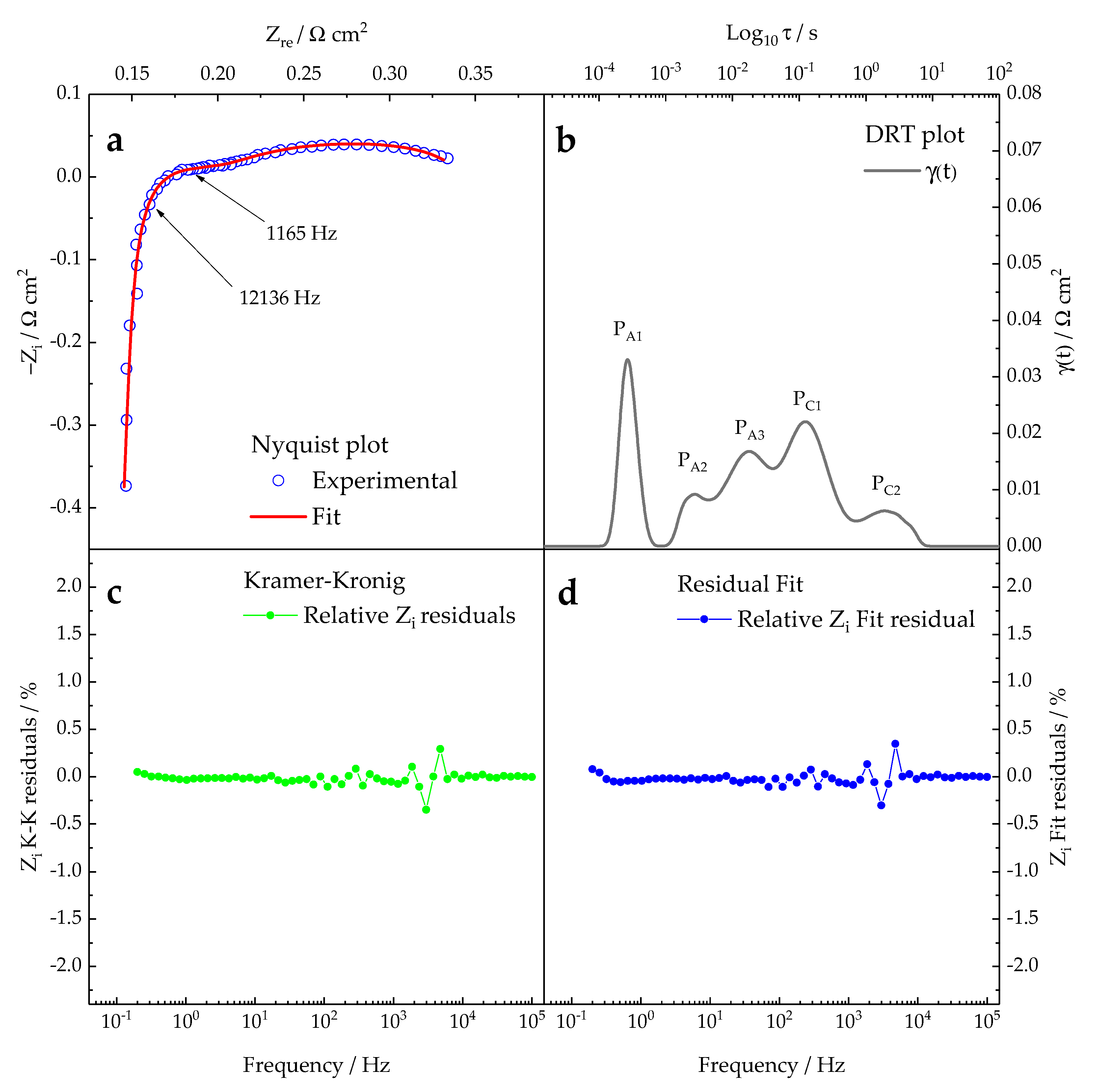
2.2. Impedance Data Post-Processing
3. Results
3.1. Experimental
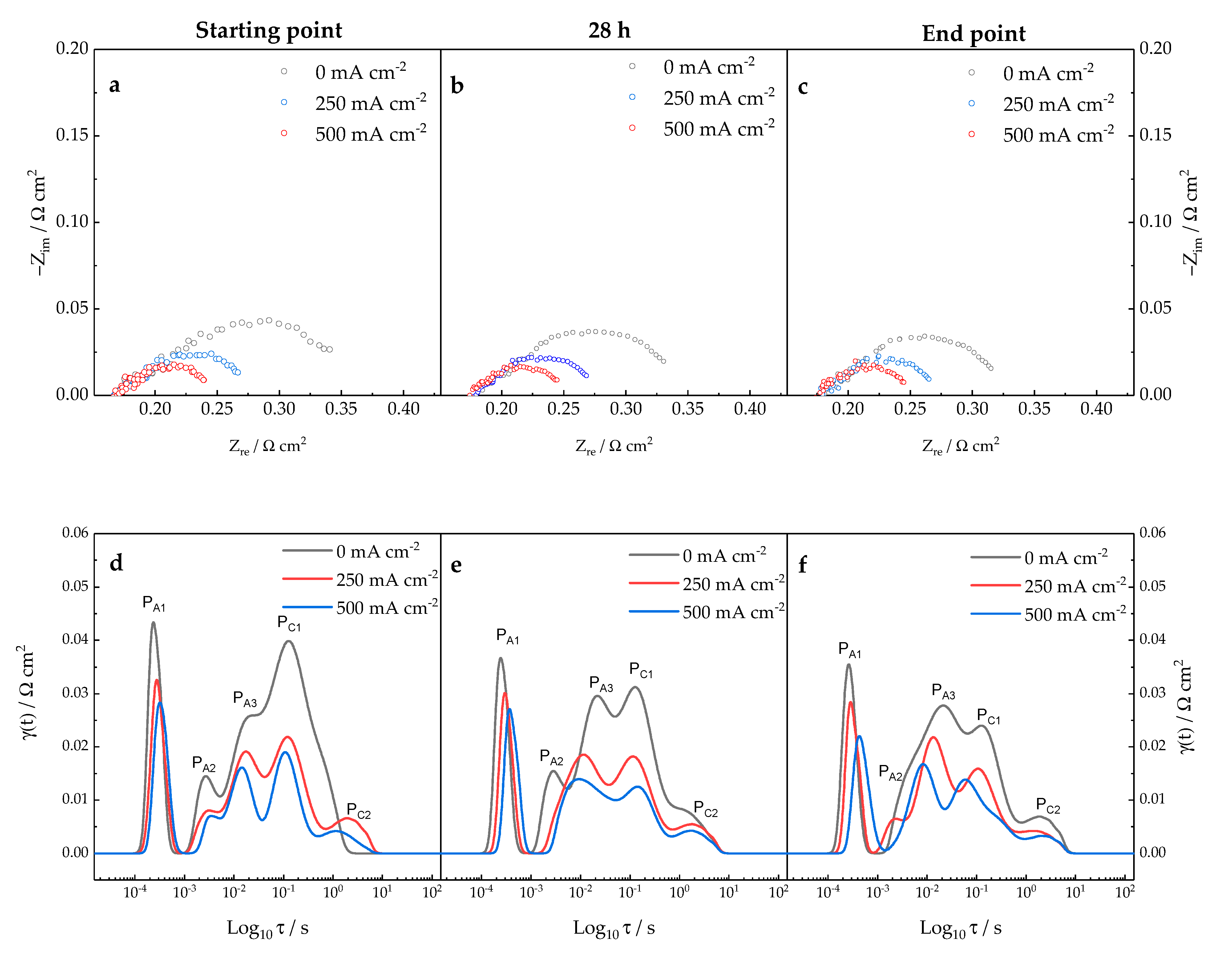
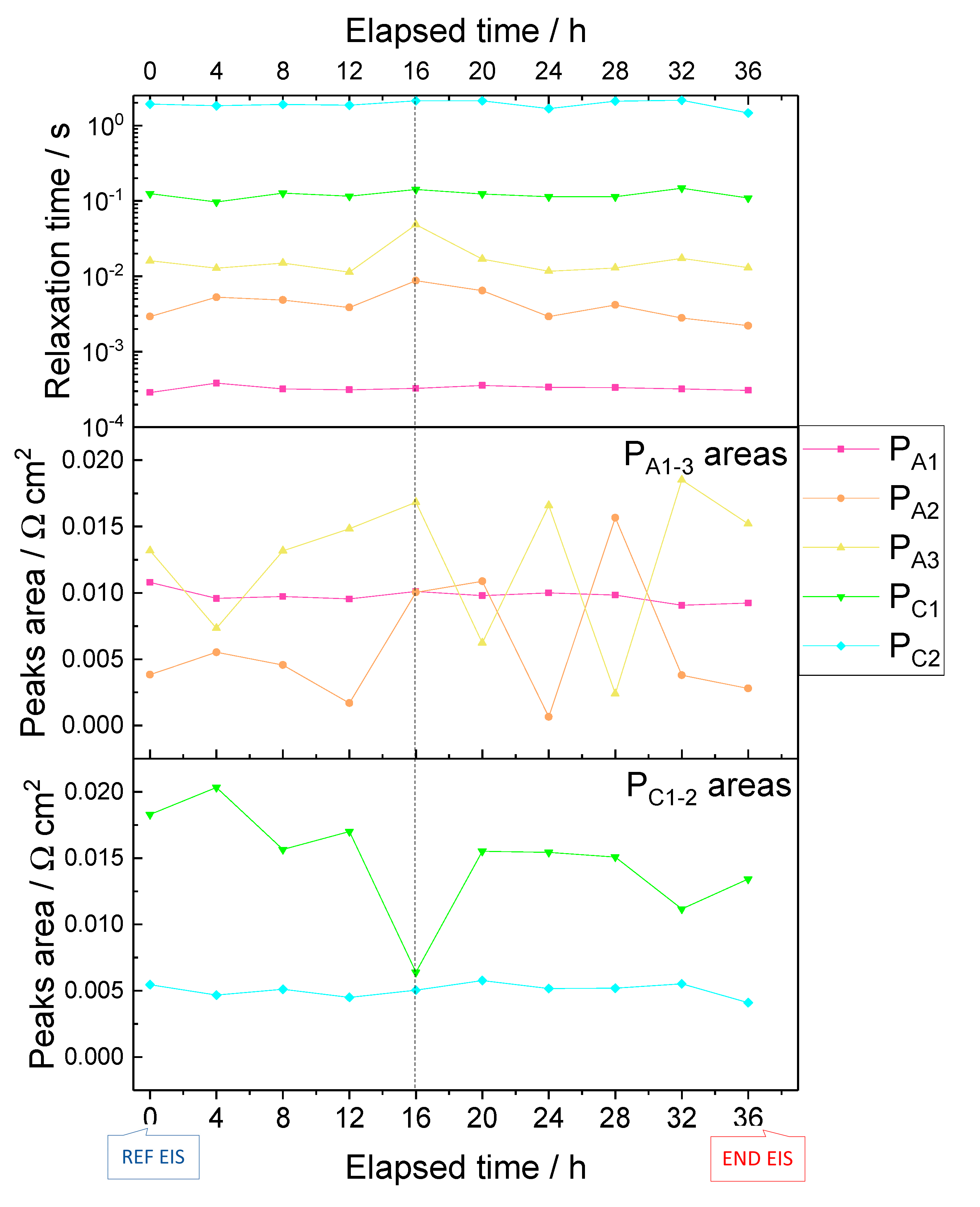
3.2. Diagnosis Investigation
- -
- -
- -
3.3. Diagnosis Validation
4. Discussion and Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| AE | Air Electrode |
| DAQ | Digital Acquistition System |
| DC | Direct Current |
| DRT | Distribution of Relaxation Times |
| ECM | Equivalent Circuit Model |
| EIS | Electrochemical Impedance Spectroscopy |
| FMC | Flow Meter Controller |
| FE | Fuel Electrode |
| HOR | Hydrogen Oxidation Reaction |
| MIEC | Mixed Ionic-Electronic Conductor |
| NLLS | Non-Linear Least Square |
| OC | Open Circuit |
| OCV | Open Circuit Voltage |
| ORR | Oxygen Reduction Reaction |
| rSOC | Reversible Solid Oxide Cell |
| RT | Room Temperature |
| SEM | Scanning Electron Microscopy |
| SOC | Solid Oxide Cell |
| SOFC | Solid Oxide Fuel Cell |
| TM | Temperature Measurement |
| TR | Temperature Regulation |
| YSZ | Yttria-stabilized Zirconia |
References
- Venkataraman, V.; Pérez-Fortes, M.; Wang, L.; Hajimolana, Y.S.; Boigues-Muñoz, C.; Agostini, A.; McPhail, S.J.; Maréchal, F.; Van Herle, J.; Aravind, P. Reversible solid oxide systems for energy and chemical applications—Review & perspectives. J. Energy Storage 2019, 24, 100782. [Google Scholar] [CrossRef] [Green Version]
- Posdziech, O.; Schwarze, K.; Brabandt, J. Efficient hydrogen production for industry and electricity storage via high-temperature electrolysis. Int. J. Hydrogen Energy 2019, 44, 19089–19101. [Google Scholar] [CrossRef]
- Bicer, Y.; Khalid, F. Life cycle environmental impact comparison of solid oxide fuel cells fueled by natural gas, hydrogen, ammonia and methanol for combined heat and power generation. Int. J. Hydrogen Energy 2020, 45, 3670–3685. [Google Scholar] [CrossRef]
- Choudhury, A.; Chandra, H.; Arora, A. Application of solid oxide fuel cell technology for power generation—A review. Renew. Sustain. Energy Rev. 2013, 20, 430–442. [Google Scholar] [CrossRef]
- Keçebaş, A.; Kayfeci, M.; Bayat, M. Electrochemical hydrogen generation. In Solar Hydrogen Production; Elsevier: Amsterdam, The Netherlands, 2019; pp. 299–317. [Google Scholar]
- David, M.; Ocampo-Martínez, C.; Sánchez-Peña, R. Advances in alkaline water electrolyzers: A review. J. Energy Storage 2019, 23, 392–403. [Google Scholar] [CrossRef] [Green Version]
- Bianchi, F.R.; Baldinelli, A.; Barelli, L.; Cinti, G.; Audasso, E.; Bosio, B. Multiscale Modeling for Reversible Solid Oxide Cell Operation. Energies 2020, 13, 5058. [Google Scholar] [CrossRef]
- Frank, M.; Deja, R.; Peters, R.; Blum, L.; Stolten, D. Bypassing renewable variability with a reversible solid oxide cell plant. Appl. Energy 2018, 217, 101–112. [Google Scholar] [CrossRef]
- Nguyen, V.N.; Fang, Q.; Packbier, U.; Blum, L. Long-term tests of a Jülich planar short stack with reversible solid oxide cells in both fuel cell and electrolysis modes. Int. J. Hydrogen Energy 2013, 38, 4281–4290. [Google Scholar] [CrossRef]
- Hanasaki, M.; Uryu, C.; Daio, T.; Kawabata, T.; Tachikawa, Y.; Lyth, S.M.; Shiratori, Y.; Taniguchi, S.I.; Sasaki, K. SOFC Durability against Standby and Shutdown Cycling. J. Electrochem. Soc. 2014, 161, F850–F860. [Google Scholar] [CrossRef]
- Cooper, S.J.; Brandon, N.P. An Introduction to Solid Oxide Fuel Cell Materials, Technology and Applications; Elsevier Ltd.: Amsterdam, The Netherlands, 2017. [Google Scholar]
- Petipas, F.; Fu, Q.; Brisse, A.; Bouallou, C. Transient operation of a solid oxide electrolysis cell. Int. J. Hydrogen Energy 2013, 38, 2957–2964. [Google Scholar] [CrossRef]
- Preininger, M.; Stoeckl, B.; Subotić, V.; Hochenauer, C.; Stöckl, B. Extensive analysis of an SOC stack for mobile application in reversible mode under various operating conditions. Electrochimica Acta 2019, 299, 692–707. [Google Scholar] [CrossRef]
- Baldinelli, A.; Barelli, L.; Bidini, G.; Discepoli, G. Economics of innovative high capacity-to-power energy storage technologies pointing at 100% renewable micro-grids. J. Energy Storage 2020, 28, 101198. [Google Scholar] [CrossRef]
- Pfeifer, T.; Reuber, S.; Hartmann, M.; Barthel, M.; Baade, J.; Matyáš, J.; Balaya, P.; Singh, D.; Wei, J. SOFC System Development and Held Trials for Commercial Applications. Process. High Temp. Supercond. 2016, 255, 61–75. [Google Scholar] [CrossRef]
- Khan, M.S.; Lee, S.-B.; Song, R.-H.; Lee, J.-W.; Lim, T.-H.; Park, S.-J. Fundamental mechanisms involved in the degradation of nickel–yttria stabilized zirconia (Ni–YSZ) anode during solid oxide fuel cells operation: A review. Ceram. Int. 2016, 42, 35–48. [Google Scholar] [CrossRef]
- Sasaki, K.; Susuki, K.; Iyoshi, A.; Uchimura, M.; Imamura, N.; Kusaba, H.; Teraoka, Y.; Fuchino, H.; Tsujimoto, K.; Uchida, Y.; et al. H2S Poisoning of Solid Oxide Fuel Cells. J. Electrochem. Soc. 2006, 153, A2023–A2029. [Google Scholar] [CrossRef]
- Sreedhar, I.; Agarwal, B.; Goyal, P.; Agarwal, A. An overview of degradation in solid oxide fuel cells-potential clean power sources. J. Solid State Electrochem. 2020, 24, 1239–1270. [Google Scholar] [CrossRef]
- Jiang, S.P.; Zhen, Y. Mechanism of Cr deposition and its application in the development of Cr-tolerant cathodes of solid oxide fuel cells. Solid State Ionics 2008, 179, 1459–1464. [Google Scholar] [CrossRef]
- Fergus, J. Effect of cathode and electrolyte transport properties on chromium poisoning in solid oxide fuel cells. Int. J. Hydrogen Energy 2007, 32, 3664–3671. [Google Scholar] [CrossRef]
- Trembly, J.; Gemmen, R.; Bayless, D. The effect of coal syngas containing HCl on the performance of solid oxide fuel cells: Investigations into the effect of operational temperature and HCl concentration. J. Power Sources 2007, 169, 347–354. [Google Scholar] [CrossRef]
- El Gabaly, F.; Mccarty, K.F.; Bluhm, H.; McDaniel, A.H. Oxidation stages of Ni electrodes in solid oxide fuel cell environments. Phys. Chem. Chem. Phys. 2013, 15, 8334–8341. [Google Scholar] [CrossRef]
- Li, X.; Blinn, K.; Chen, D.; Liu, M. In Situ and Surface-Enhanced Raman Spectroscopy Study of Electrode Materials in Solid Oxide Fuel Cells. Electrochem. Energy Rev. 2018, 1, 433–459. [Google Scholar] [CrossRef]
- Li, X.; Lee, J.-P.; Blinn, K.S.; Chen, D.; Yoo, S.; Kang, B.; Bottomley, L.A.; El-Sayed, M.A.; Park, S.; Liu, M. High-temperature surface enhanced Raman spectroscopy for in situ study of solid oxide fuel cell materials. Energy Environ. Sci. 2013, 7, 306–310. [Google Scholar] [CrossRef] [Green Version]
- Swallow, J.G.; Lee, J.K.; Defferriere, T.; Hughes, G.M.; Raja, S.N.; Tuller, H.L.; Warner, J.H.; Van Vliet, K.J. Atomic Resolution Imaging of Nanoscale Chemical Expansion in PrxCe1−xO2−δ during In Situ Heating. ACS Nano 2018, 12, 1359–1372. [Google Scholar] [CrossRef]
- Hwang, S.; Chen, X.; Zhou, G.; Su, D. In Situ Transmission Electron Microscopy on Energy-Related Catalysis. Adv. Energy Mater. 2020, 10, 1902105. [Google Scholar] [CrossRef]
- Stangl, A.; Munoz-Rojas, D.; Burriel, M. In situ and operando characterisation techniques for solid oxide electrochemical cells: Recent advances. J. Phys. Energy 2020, 3, 12001. [Google Scholar] [CrossRef]
- Baldinelli, A.; Barelli, L.; Bidini, G.; Di Cicco, A.; Gunnella, R.; Minicucci, M.; Trapananti, A. Advancements regarding in-operando diagnosis techniques for solid oxide cells NiYSZ cermets. AIP Conf. Proc. 2019, 2191, 020012. [Google Scholar] [CrossRef]
- Nielsen, J.; Hjelm, J. Impedance of SOFC electrodes: A review and a comprehensive case study on the impedance of LSM:YSZ cathodes. Electrochimica Acta 2014, 115, 31–45. [Google Scholar] [CrossRef] [Green Version]
- Nobili, F.; Tossici, R.; Marassi, R.; Croce, F.; Scrosati, B. An AC Impedance Spectroscopic Study of LixCoO2 at Different Temperatures. J. Phys. Chem. B 2002, 106, 3909–3915. [Google Scholar] [CrossRef]
- Pitarch-Tena, D.; Ngo, T.T.; Vallés-Pelarda, M.; Pauporté, T.; Mora-Seró, I. Impedance Spectroscopy Measurements in Perovskite Solar Cells: Device Stability and Noise Reduction. ACS Energy Lett. 2018, 3, 1044–1048. [Google Scholar] [CrossRef] [Green Version]
- Schwartz, M. The theory of impedance in biological systems. J. Biol. Phys. 1973, 1, 123–142. [Google Scholar] [CrossRef]
- Kornely, M.; Neumann, A.; Menzler, N.H.; Leonide, A.; Weber, A.; Ivers-Tiffée, E. Degradation of anode supported cell (ASC) performance by Cr-poisoning. J. Power Sources 2011, 196, 7203–7208. [Google Scholar] [CrossRef]
- Kromp, A.; Dierickx, S.; Leonide, A.; Weber, A.; Iverstiffee, E. Electrochemical Analysis of Sulfur-Poisoning in Anode Supported SOFCs Fuelled with a Model Reformate. J. Electrochem. Soc. 2012, 159, B597–B601. [Google Scholar] [CrossRef]
- Sumi, H.; Shimada, H.; Yamaguchi, Y.; Yamaguchi, T.; Fujishiro, Y. Degradation evaluation by distribution of relaxation times analysis for microtubular solid oxide fuel cells. Electrochimica Acta 2020, 339, 135913. [Google Scholar] [CrossRef]
- Dierickx, S.; Weber, A.; Ivers-Tiffée, E. How the distribution of relaxation times enhances complex equivalent circuit models for fuel cells. Electrochimica Acta 2020, 355, 136764. [Google Scholar] [CrossRef]
- Boukamp, B.A. A Nonlinear Least Squares Fit procedure for analysis of immittance data of electrochemical systems. Solid State Ionics 1986, 20, 31–44. [Google Scholar] [CrossRef] [Green Version]
- Macdonald, J.R. Impedance spectroscopy: Old problems and new developments. Electrochimica Acta 1990, 35, 1483–1492. [Google Scholar] [CrossRef]
- Bartoszek, J.; Liu, Y.-X.; Karczewski, J.; Wang, S.-F.; Mrozinski, A.; Jasiński, P. Distribution of relaxation times as a method of separation and identification of complex processes measured by impedance spectroscopy. In Proceedings of the 2017 21st European Microelectronics and Packaging Conference (EMPC) & Exhibition, Warsaw, Poland, 10–13 September 2017; pp. 1–5. [Google Scholar]
- Baldinelli, A.; Staffolani, A.; Bidini, G.; Barelli, L.; Nobili, F. An extensive model for renewable energy electrochemical storage with Solid Oxide Cells based on a comprehensive analysis of impedance deconvolution. J. Energy Storage 2021, 33, 102052. [Google Scholar] [CrossRef]
- Boukamp, B. Practical application of the Kramers-Kronig transformation on impedance measurements in solid state electrochemistry. Solid State Ionics 1993, 62, 131–141. [Google Scholar] [CrossRef] [Green Version]
- Wan, T.H.; Saccoccio, M.; Chen, C.; Ciucci, F. Influence of the Discretization Methods on the Distribution of Relaxation Times Deconvolution: Implementing Radial Basis Functions with DRTtools. Electrochimica Acta 2015, 184, 483–499. [Google Scholar] [CrossRef]
- Papurello, D.; Menichini, D.; Lanzini, A. Distributed relaxation times technique for the determination of fuel cell losses with an equivalent circuit model to identify physicochemical processes. Electrochimica Acta 2017, 258, 98–109. [Google Scholar] [CrossRef]
- Muñoz, C.B.; Pumiglia, D.; McPhail, S.J.; Montinaro, D.; Comodi, G.; Santori, G.; Carlini, M.; Polonara, F. More accurate macro-models of solid oxide fuel cells through electrochemical and microstructural parameter estimation—Part I: Experimentation. J. Power Sources 2015, 294, 658–668. [Google Scholar] [CrossRef] [Green Version]
- Leonide, A.; Sonn, V.; Weber, A.; Ivers-Tiffée, E. Evaluation and Modeling of the Cell Resistance in Anode-Supported Solid Oxide Fuel Cells. J. Electrochem. Soc. 2008, 155, B36–B41. [Google Scholar] [CrossRef]
- Macdonald, J.R. Impedance Spectroscopy: Emphasizing Solid Materials and Systems; Wiley-Interscience: Hoboken, NJ, USA, 1987. [Google Scholar]
- Adler, S.B.; Lane, J.A.; Steele, B.C.H. Electrode Kinetics of Porous Mixed-Conducting Oxygen Electrodes. J. Electrochem. Soc. 1996, 143, 3554–3564. [Google Scholar] [CrossRef]
- Basahel, S.N.; Ali, T.T.; Mokhtar, M.; Narasimharao, K. Influence of crystal structure of nanosized ZrO2 on photocatalytic degradation of methyl orange. Nanoscale Res. Lett. 2015, 10, 73. [Google Scholar] [CrossRef] [Green Version]
- Mironova-Ulmane, N.; Kuzmin, A.; Steins, I.; Grabis, J.; Sildos, I.; Pärs, M. Raman scattering in nanosized nickel oxide NiO. J. Phys. Conf. Ser. 2007, 93, 012039. [Google Scholar] [CrossRef]
- Burmistrov, I.; Agarkov, D.; Tartakovskii, I.; Kharton, V.; Bredikhin, S. Performance Optimization of Cermet SOFC Anodes: An Evaluation of Nanostructured NiO. ECS Meet. Abstr. 2015, 68, 1265–1274. [Google Scholar] [CrossRef] [Green Version]
- Mironova-Ulmane, N.; Kuzmin, A.; Sildos, I.; Puust, L.; Grabis, J. Magnon and Phonon Excitations in Nanosized NiO. Latv. J. Phys. Tech. Sci. 2019, 56, 61–72. [Google Scholar] [CrossRef] [Green Version]

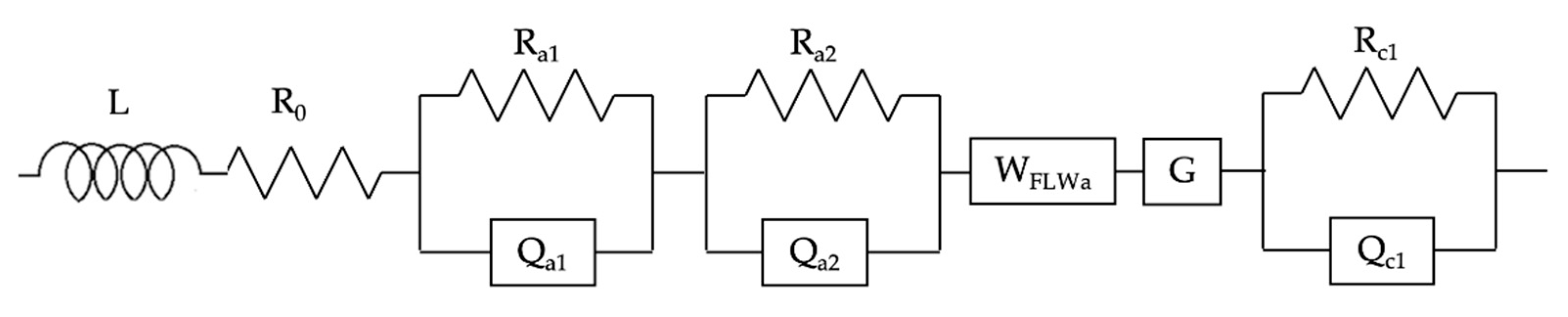





| Phenomenon | Variation With: | DRT Peak | ECM Element |
|---|---|---|---|
| Oxygen transport | Temperature | PA1 at τ = 10−4 s | Ra1Qa1 = |
| HOR | Hydrogen partial pressure, catalytic activity at the FE, temperature | PA2 at τ = 10−3 s | Ra2Qa2 = |
| ORR | Oxygen partial pressure, catalytic activity at the AE, temperature | PC1 at τ = 10−1 s | Rc1QC1 = |
| Mass transport FE (NiYSZ) | Reactants space velocity, utilization rate (current density) at the FE | PA3 at τ = 10−2 s | WFLWa = |
| Mass transport AE (GDC/LSCF) | Reactants space velocity, utilization rate (current density) at the AE | PC2 at τ = 10 s | G = |
| Electrolyte | Temperature | - | R0 |
| Wiring—Cell geometry | Not relevant | - |
| Layer | Composition | Thickness |
|---|---|---|
| Fuel Electrode | NiYSZ | 240 μm |
| Electrolyte | 8YSZ | 8 μm |
| Air Electrode | GDC-LSCF | 50 μm |
| TEST | Fuel Electrode | Air Electrode | Operating Settings | Duration | |||
|---|---|---|---|---|---|---|---|
| ID | X | Q | x | Q | T | Load | Hours |
| Start-up | 100% N2 | 50 | 21% O2 + 79% N2 | 300 | RT1 → 1073 | OC | 16 h |
| Reduction | 100% N2 → 100% H2 | 150 | 21% O2 + 79% N2 | 300 | 1073 | OC | 1.5 h |
| Stabilization | 100% H2 | 150 | 21% O2 + 79% N2 | 300 | 1073 | Constant j = 250 mA/cm2 | 100 h |
| Begin Ref | 25% H2 + 75% N2 | 200 | 21% O2 + 79% N2 | 300 | 1048 | i-V: OC → 0.7 V EIS: 0, 100, 250, 500, 750 mA/cm2 | 30 min 1 h |
| Stress test (repeated) | 25% H2 + 75% N2 | 200 | 21% O2 + 79% N2 | 300 | 1048 | Constant j = 1500 mA/cm2 EIS: 0, 100, 250, 500 mA/cm2 | 4 h 30 min |
| End Point | 25% H2 + 75% N2 | 200 | 21% O2 + 79% N2 | 300 | 1048 | i-V: OC → 0.7 V EIS: 0, 100, 250, 500, 750 mA/cm2 | 30 min 1 h |
| Shut down | 5% H2 + 95% N2 | 100 | 100% N2 | 100 | 1073 → RT | OC | c.a. 12 h |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Staffolani, A.; Baldinelli, A.; Barelli, L.; Bidini, G.; Nobili, F. Early-Stage Detection of Solid Oxide Cells Anode Degradation by Operando Impedance Analysis. Processes 2021, 9, 848. https://doi.org/10.3390/pr9050848
Staffolani A, Baldinelli A, Barelli L, Bidini G, Nobili F. Early-Stage Detection of Solid Oxide Cells Anode Degradation by Operando Impedance Analysis. Processes. 2021; 9(5):848. https://doi.org/10.3390/pr9050848
Chicago/Turabian StyleStaffolani, Antunes, Arianna Baldinelli, Linda Barelli, Gianni Bidini, and Francesco Nobili. 2021. "Early-Stage Detection of Solid Oxide Cells Anode Degradation by Operando Impedance Analysis" Processes 9, no. 5: 848. https://doi.org/10.3390/pr9050848
APA StyleStaffolani, A., Baldinelli, A., Barelli, L., Bidini, G., & Nobili, F. (2021). Early-Stage Detection of Solid Oxide Cells Anode Degradation by Operando Impedance Analysis. Processes, 9(5), 848. https://doi.org/10.3390/pr9050848








