A Novel Rotary Dryer Filled with Alumina Ceramic Beads for the Treatment of Industrial Wastewaters: Numerical Simulation and Experimental Study
Abstract
:1. Introduction
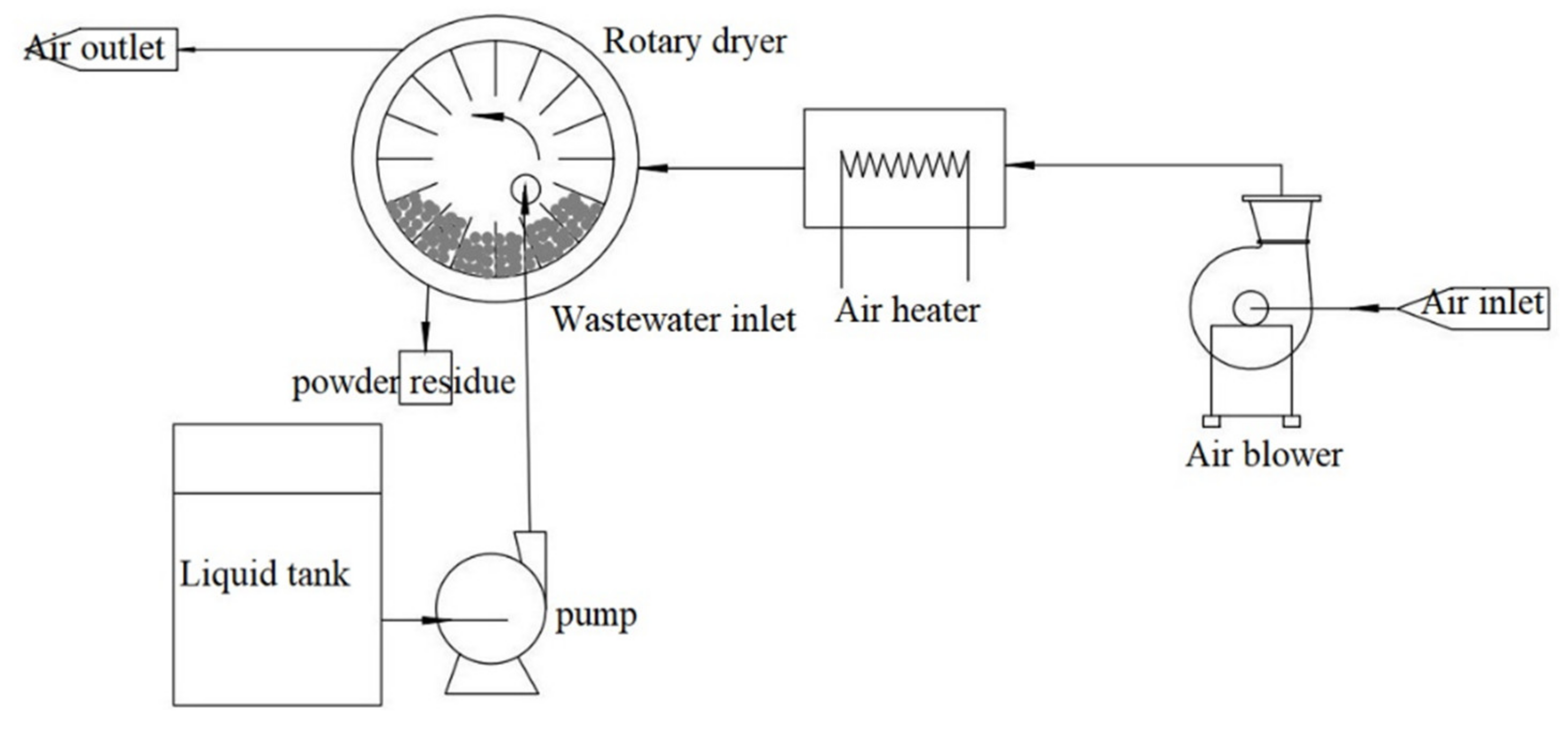
2. Simulations and Experiments
2.1. DEM Simulation
2.2. Experiments
3. Results and Discussions
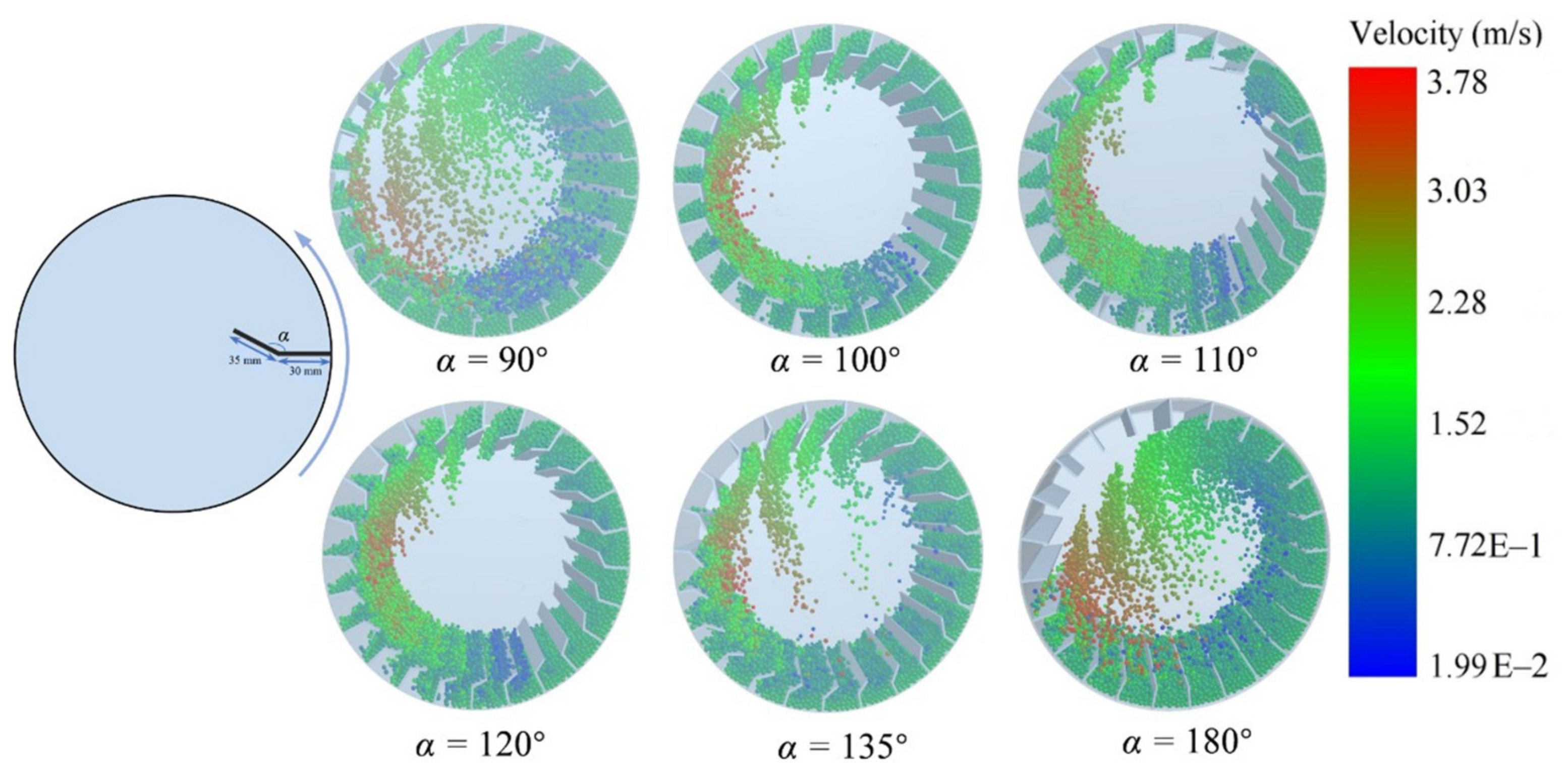
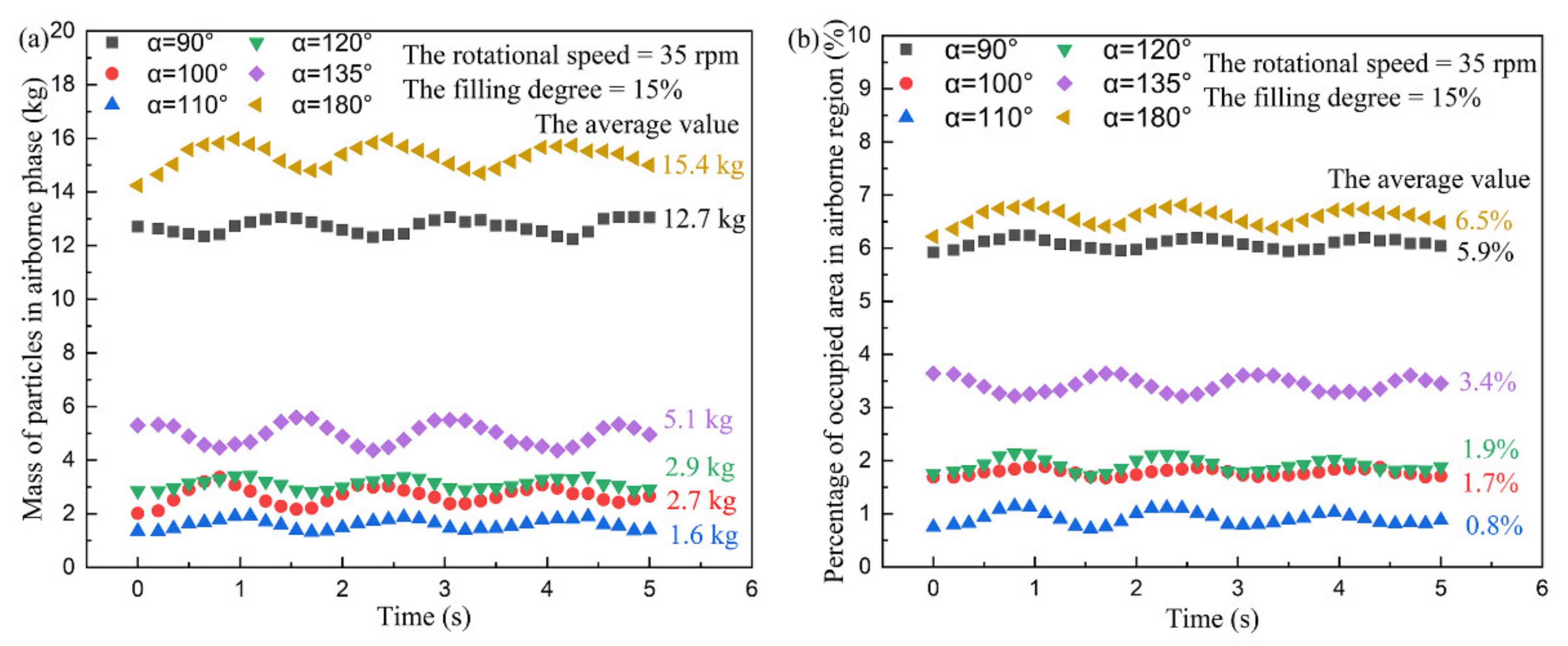
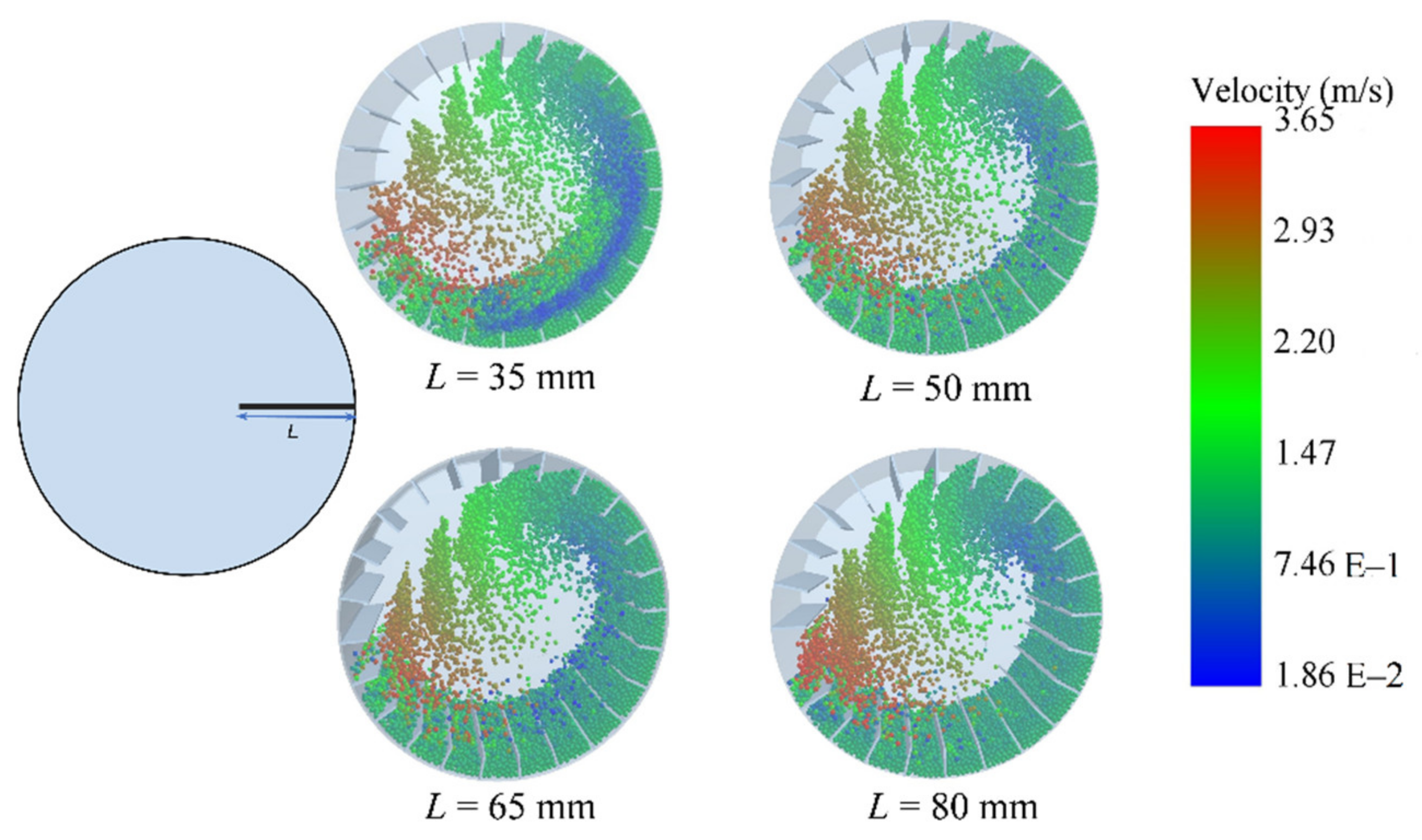
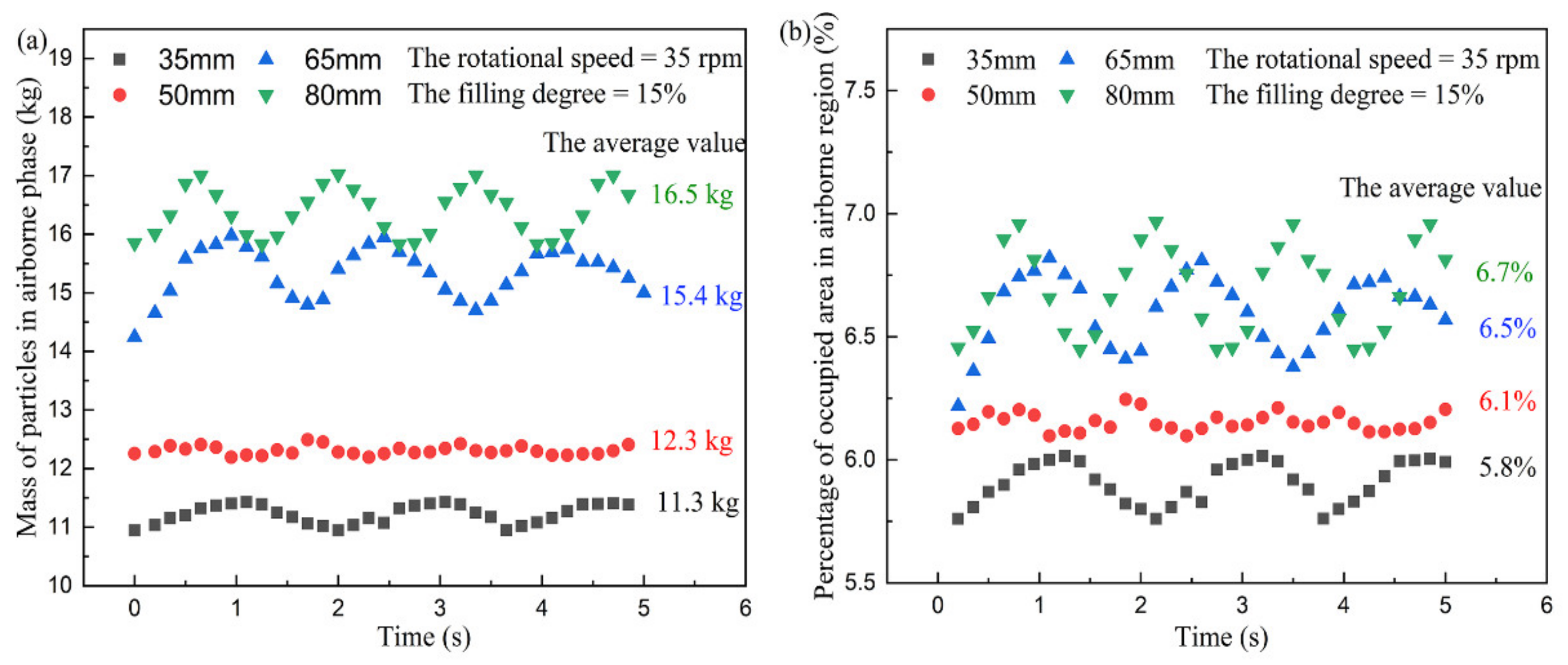
3.1. The Effects of Flight Structures
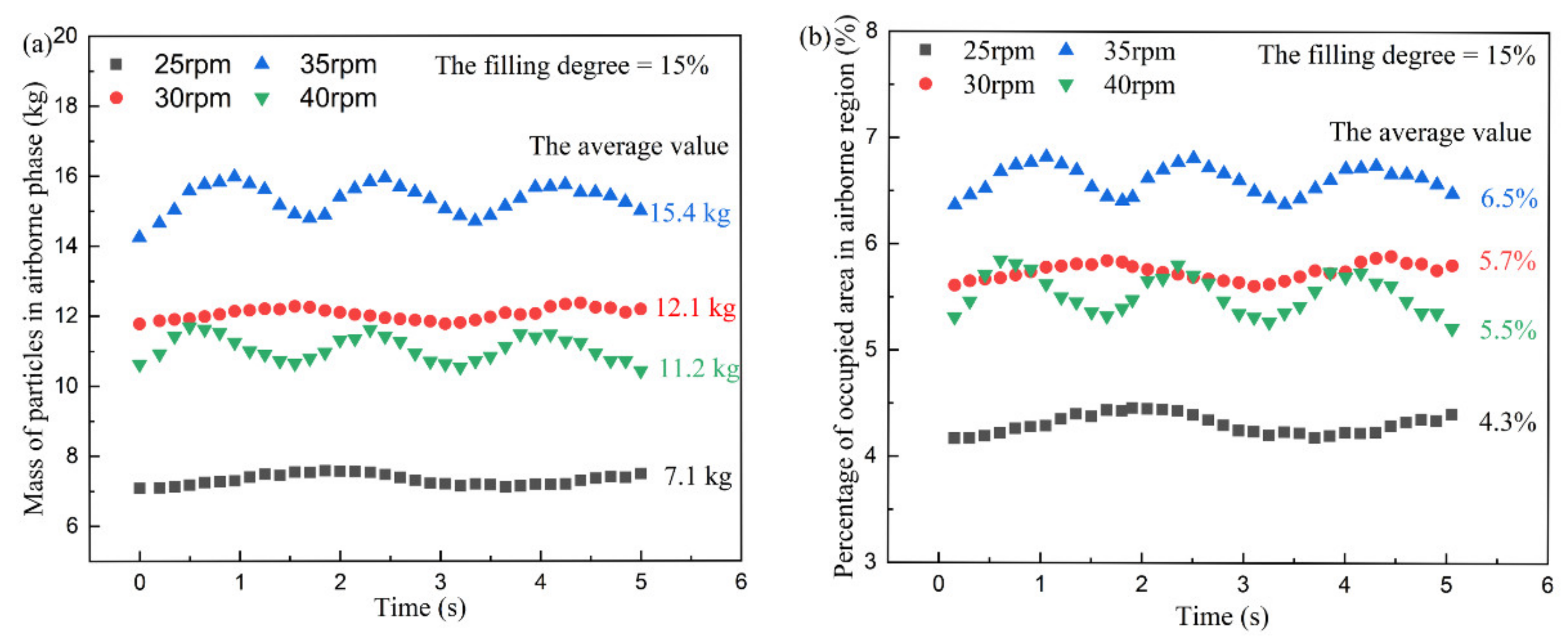
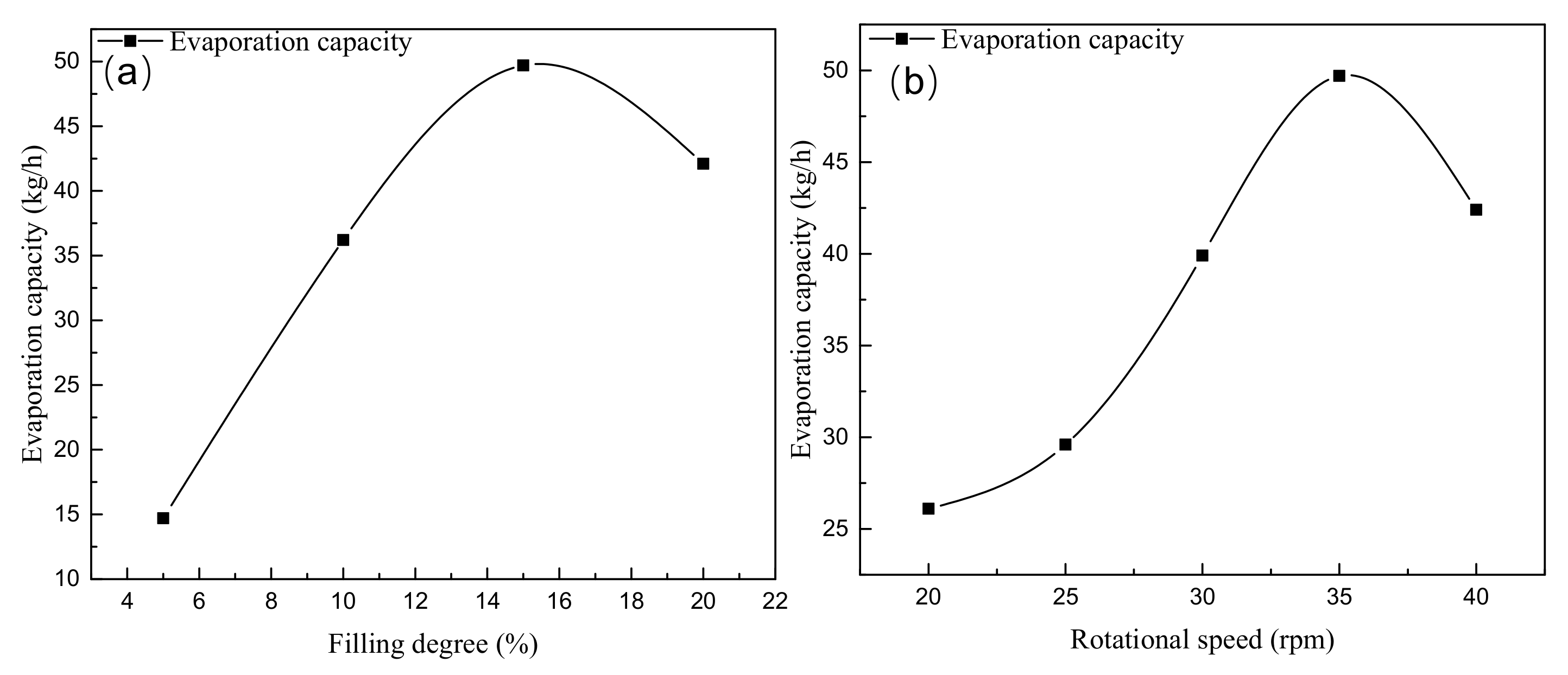
3.2. The Effect of Rotational Speeds
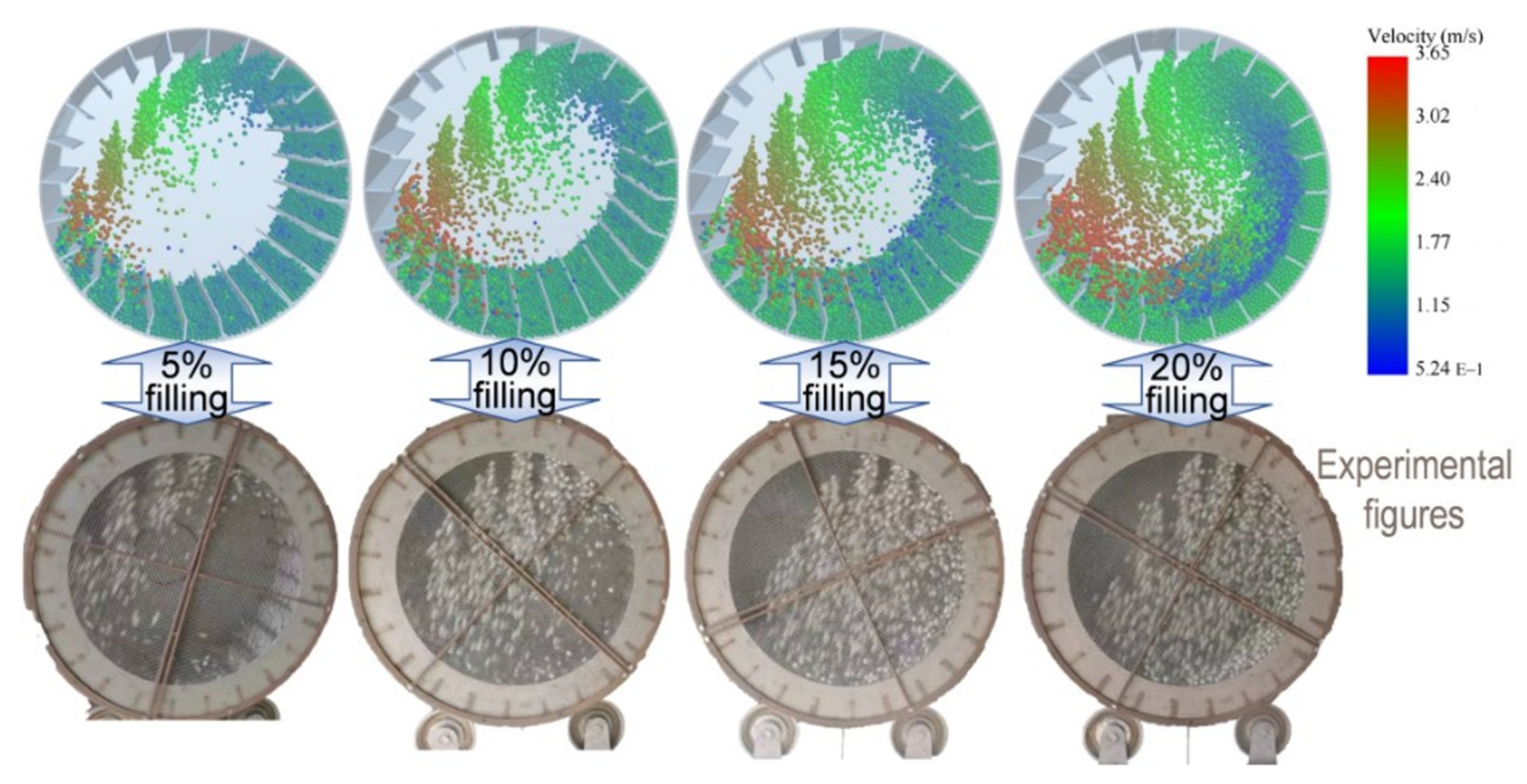
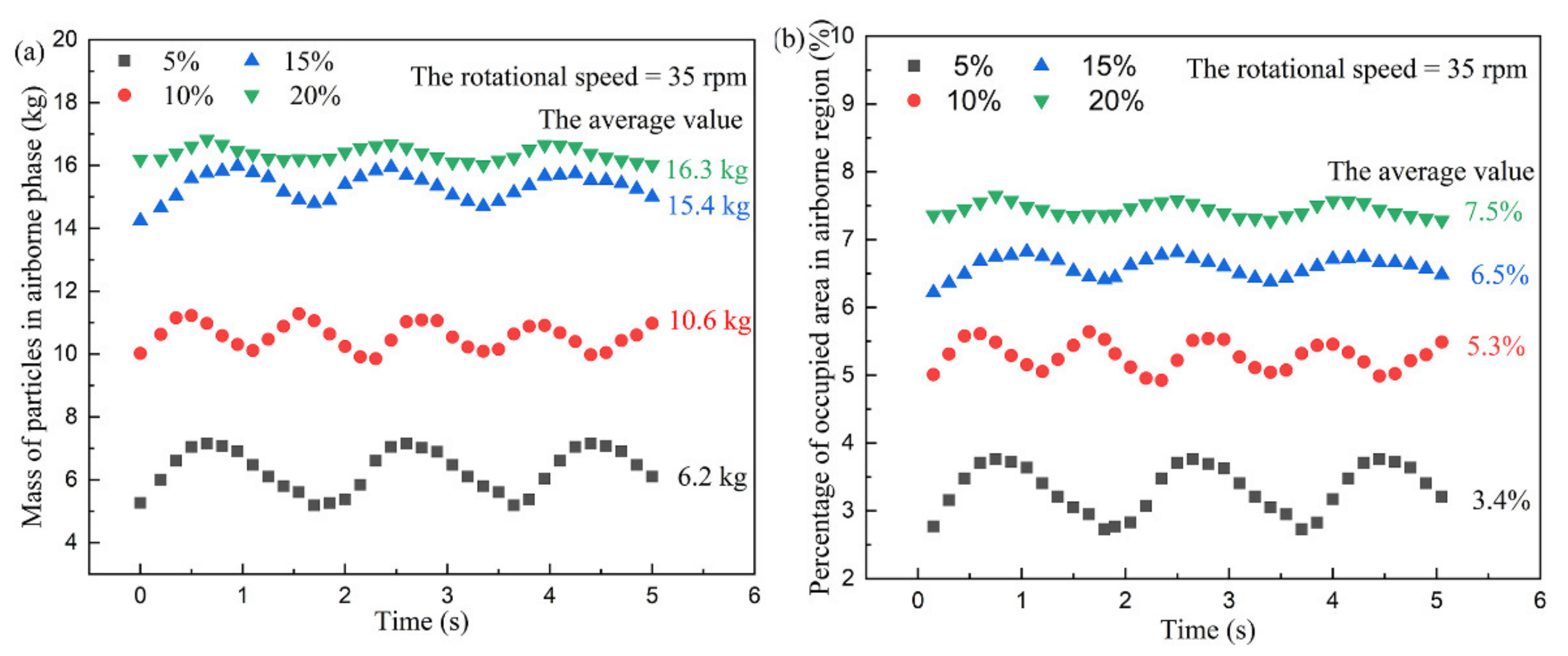
3.3. The Effect of Bead Filling Degrees
3.4. The Drying Experiments at Optimized Conditions
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| List of symbols | |
| F | Force [N] |
| g | Gravity [m s−2] |
| G | shear modulus [Pa] |
| G* | equivalent shear modulus [Pa] |
| I | moment of inertia [m s−2] |
| K | elastic constant [kg m−2] |
| l | length of flight [mm] |
| M | mass [kg] |
| m* | equivalent mass [kg] |
| R | radius [m] |
| R* | radius [m] |
| S | stiffness [Pa m] |
| Y | Young’s modulus [Pa] |
| Y* | equivalent Young’s modulus [Pa] |
| Greek symbols | |
| α | joint angle of the two-segment flights [°] |
| β | damping coefficient [−] |
| η | viscoelastic damping constant [kg s−1] |
| δ | overlap distance of two particles [m] |
| ν | Poisson ratio [−] |
| ω | rotational speed [rpm] |
References
- Lefebvre, O.; Moletta, R. Treatment of organic pollution in industrial saline wastewater: A literature review. Water Res. 2006, 40, 3671–3682. [Google Scholar] [CrossRef] [PubMed]
- Fu, F.L.; Wang, Q. Removal of heavy metal ions from wastewaters: A review. J. Environ. Manag. 2011, 3, 407–418. [Google Scholar] [CrossRef] [PubMed]
- Zhao, W.Y.; Zhou, M.; Yan, B.; Sun, X.; Liu, Y.; Wang, Y.; Xu, T.; Zhang, Y. Waste conversion and resource recovery from wastewater by ion exchange membranes: State-of-the-art and prospective. Ind. Eng. Chem. Res. 2018, 57, 6025–6039. [Google Scholar] [CrossRef]
- Chang, Y.; Deng, L.; Meng, X.; Zhang, W.; Wang, C.; Wang, Y.; Zhao, S.; Lin, L.; Crittenden, J.C. Closed-Loop Electrochemical Recycling of Spent Copper(II) from Etchant Wastewater Using a Carbon Nanotube Modified Graphite Felt Anode. Environ. Sci. Technol. 2018, 10, 5940–5948. [Google Scholar] [CrossRef]
- Bian, X.; Huang, Y.; Guo, R.; Xu, D.; Zhu, L.; Yang, J.; Qiu, Z. Research progress on salt separation and resource utilization in high salinity wastewater. Inorg. Chem. Ind. 2019, 51, 7–12. [Google Scholar]
- Russo, T.; Fucile, P.; Giacometti, R.; Sannino, F. Sustainable Removal of Contaminants by Biopolymers: A Novel Approach for Wastewater Treatment. Current State and Future Perspectives. Processes 2021, 9, 719. [Google Scholar] [CrossRef]
- Revollar, S.; Meneses, M.; Vilanova, R.; Vega, P.; Francisco, M. Quantifying the Benefit of a Dynamic Performance Assessment of WWTP. Processes 2020, 8, 206. [Google Scholar] [CrossRef] [Green Version]
- Fortes, M.C.B.; Silva, A.A.M.; Guimarães, R.C.; Ataide, C.H.; Barrozo, M.A.S. Pre-separation of siliceous gangue in apatite flotation. Ind. Eng. Chem. Res. 2007, 46, 7027–7029. [Google Scholar] [CrossRef]
- Silvério, B.; Arruda, E.; Duarte, C.; Barrozo, M. A novel rotary dryer for drying fertilizer: Comparison of performance with conventional configurations. Powder Technol. 2015, 270, 135–140. [Google Scholar] [CrossRef]
- Ding, Y.L.; Forster, R.; Seville, J.P.K.; Parker, D. Granular motion in rotating drums: Bed turnover time and slumping–rolling transition. Powder Technol. 2002, 124, 18–27. [Google Scholar] [CrossRef]
- Xie, L.X.; Xu, S.C.; Su, L.B. A High Efficiency and Energy Saving Evaporative Drying Device. Chinese Patent CN201921638583.5, August 2019. [Google Scholar]
- Hlosta, J.; Jezerská, L.; Rozbroj, J.; Žurovec, D.; Nečas, J.; Zegzulka, J. DEM investigation of the influence of particulate properties and operating conditions on the mixing process in Rotary Drums: Part 2—Process. Processes 2020, 8, 184. [Google Scholar] [CrossRef] [Green Version]
- Nascimento, S.M.; Lima, R.M.; Brandão, R.J.; Duarte, C.R.; Barrozo, M.A.S. Eulerian study of flights discharge in a rotating drum. Can. J. Chem. Eng. 2019, 97, 477–484. [Google Scholar] [CrossRef]
- Karali, M.A.; Specht, E.; Herz, F.; Mellmann, J.; Refaey, H.A. Unloading characteristics of flights in a flighted rotary drum operated at optimum loading. Powder Technol. 2018, 333, 347–352. [Google Scholar] [CrossRef]
- Hlosta, J.; Jezerská, L.; Rozbroj, J.; Žurovec, D.; Nečas, J.; Zegzulka, J. DEM Investigation of the Influence of Particulate Properties and Operating Conditions on the Mixing Process in Rotary Drums: Part 1—Determination of the DEM Parameters and Calibration Process. Processes 2020, 8, 222. [Google Scholar] [CrossRef] [Green Version]
- Höhner, D.; Wirtz, S.; Scherer, V. A study on the influence of particle shape and shape approximation on particle mechanics in a rotating drum using the discrete element method. Powder Technol. 2014, 253, 256–265. [Google Scholar] [CrossRef]
- Nascimento, S.; Santos, D.; Barrozo, M.; Duarte, C. Solids holdup in flighted rotating drums: An experimental and simulation study. Powder Technol. 2015, 280, 18–25. [Google Scholar] [CrossRef]
- Scherer, V.; Mönnigmann, M.; Berner, M.O.; Sudbrock, F. Coupled DEM–CFD simulation of drying wood chips in a rotary drum—Baffle design and model reduction. Fuel 2016, 184, 896–904. [Google Scholar] [CrossRef]
- Benhsine, I.; Hellou, M.; Lominé, F.; Roques, Y. Influence of flight shape on discharging profiles of granular material in rotary dryer. EPJ Web Conf. 2017, 140, 03023. [Google Scholar] [CrossRef] [Green Version]
- Nascimento, S.M.; De Lima, F.; Duarte, C.R.; Barrozo, M.A.D.S. Numerical Simulation and Experimental Study of Particle Dynamics in a Rotating Drum with Flights. Mater. Sci. Forum 2017, 899, 65–70. [Google Scholar] [CrossRef]
- Henein, H.; Brimacombe, J.K.; Watkinson, A.P. Experimental study of transverse bed motion in rotary kilns. Met. Mater. Trans. B 1983, 14B, 191–205. [Google Scholar] [CrossRef]
- Santos, D.A.; Barrozo, M.A.; Duarte, C.R.; Weigler, F.; Mellmann, J. Investigation of particle dynamics in a rotary drum by means of experiments and numerical simulations using DEM. Adv. Powder Technol. 2016, 27, 692–703. [Google Scholar] [CrossRef]
- Sheehan, M.E.; Britton, P.F.; Schneider, P.A. A model for solids transport in flighted rotary dryers based on physical considerations. Chem. Eng. Sci. 2005, 60, 4171–4182. [Google Scholar] [CrossRef]
- Geng, F.; Yuan, Z.; Xu, D. Three Dimensional Numerical Simulation of Mixing Process of Particles in Rotary Dryer. Chin. J. Appl. Mech. 2008, 25, 529–534. [Google Scholar]
- Hill, K.M.; Kakalios, J. Reversible axial segregation of rotating granular media. Phys. Rev. E 1995, 52, 4393–4400. [Google Scholar] [CrossRef]
- Havlík, J.; Dlouhý, T. Indirect Dryers for Biomass Drying—Comparison of Experimental Characteristics for Drum and Rotary Configurations. Chem. Eng. 2020, 4, 18. [Google Scholar] [CrossRef] [Green Version]
- Xie, G.; Zhang, X.; Cai, J.; Sun, W.; Zhang, K.; Zhang, S. Development of a Novel Shaft Dryer for Coal-Based Green Needle Coke Drying Process. Appl. Sci. 2019, 9, 3301. [Google Scholar] [CrossRef] [Green Version]
- Kaveh, M.; Abbaspour-Gilandeh, Y.; Taghinezhad, E.; Witrowa-Rajchert, D.; Nowacka, M. The Quality of Infrared Rotary Dried Terebinth (Pistacia atlantica L.)-Optimization and Prediction Approach Using Response Surface Methodology. Molecules 2021, 26, 1999. [Google Scholar] [CrossRef]
- Silveira, J.C.; Brandao, R.J.; Lima, R.M.; Machado, M.V.; Barrozo, M.A.; Duarte, C.R. A fluid dynamic study of the active phase behavior in a rotary drum with flights of two and three segments. Powder Technol. 2020, 368, 297–307. [Google Scholar] [CrossRef]
- Geng, F.; Li, Y.; Yuan, L.; Liu, M.; Wang, X.; Yuan, Z.; Yan, Y.; Luo, D. Experimental study on the space time of flexible filamentous particles in a rotary dryer. Exp. Therm. Fluid Sci. 2013, 44, 708–715. [Google Scholar] [CrossRef]
- Thibault, J.; Alvarez, P.I.; Blasco, R.; Vega, R. Modeling the Mean Residence Time in a Rotary Dryer for Various Types of Solids. Dry. Technol. 2010, 28, 1136–1141. [Google Scholar] [CrossRef]
- Jahani, M.; Farzanegan, A.; Noaparast, M. Investigation of screening performance of banana screens using LIGGGHTS DEM solver. Powder Technol. 2015, 283, 32–47. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical mode for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Stevens, A.; Hrenya, C. Comparison of soft-sphere models to measurements of collision properties during normal impacts. Powder Technol. 2005, 154, 99–109. [Google Scholar] [CrossRef]
- Le Guen, L.; Huchet, F.; Dumoulin, J.; Baudru, Y.; Tamagny, P. Convective heat transfer analysis in aggregates rotary drum reactor. Appl. Therm. Eng. 2013, 54, 131–139. [Google Scholar] [CrossRef]
- Chou, S.; Liao, C.; Hsiau, S. An experimental study on the effect of liquid content and viscosity on particle segregation in a rotating drum. Powder Technol. 2010, 201, 266–272. [Google Scholar] [CrossRef]
- Zhou, Y.; Shi, C.; Dong, G. Analysis of a mechanical vapor recompression wastewater distillation system. Desalination 2014, 353, 91–97. [Google Scholar] [CrossRef]
- Tang, Z.W.; Wang, J.; Huang, H.; Nie, C. Design of a spray evaporation tower for high-salinity oilfield waster and numerical simulation of its flow field. Environ. Technol. 2017, 35, 27–33. [Google Scholar]




| Normal Elasic Constant | (5) | |
| Normal viscoelastic damping constant | (6) | |
| Tangential Elastic constant | (7) | |
| Tangential viscoelastic damping constant | (8) | |
| Normal stiffness | (9) | |
| Tangential stiffness | (10) | |
| Young’s modulus | (11) | |
| shear modulus | (12) | |
| Equivalent particle mass | (13) | |
| Equivalent particle radius | (14) |
| Ceramic Beads | Stainless Steel | |
|---|---|---|
| Density (kg/m3) | 2100 | 7900 |
| Restitution coefficient | 0.5 | 0.9 |
| Poisson ratio (−) | 0.29 | 0.3 |
| Young’s modulus (Pa) | 5.16 × 107 | 2 × 1011 |
| Particle-particle | Particle-wall | |
| Coefficient static friction | 0.3 | 0.5 |
| Coefficient of rolling friction | 0.01 | 0.01 |
| pH | Total Dissolved Solids (mg/L) | Cl− (mg/L) | SO42− (mg/L) | Na+ (mg/L) | Ca2+ (mg/L) | Mg2+ (mg/L) |
|---|---|---|---|---|---|---|
| 8–10 | 90,600 | 48,130 | 7280 | 34,200 | 469 | 131 |
| pH | Ammonia Nitrogen (mg/L) | Suspended Solids (mg/L) | Ca2+ (mg/L) | Mg2+ (mg/L) | Fe3+ (mg/L) | Cl− (mg/L) |
|---|---|---|---|---|---|---|
| 5.5–6.1 | 900 | 800 | 50 | 150 | 60 | 640 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, L.; Yang, L.; Su, L.; Xu, S.; Zhang, W. A Novel Rotary Dryer Filled with Alumina Ceramic Beads for the Treatment of Industrial Wastewaters: Numerical Simulation and Experimental Study. Processes 2021, 9, 862. https://doi.org/10.3390/pr9050862
Xie L, Yang L, Su L, Xu S, Zhang W. A Novel Rotary Dryer Filled with Alumina Ceramic Beads for the Treatment of Industrial Wastewaters: Numerical Simulation and Experimental Study. Processes. 2021; 9(5):862. https://doi.org/10.3390/pr9050862
Chicago/Turabian StyleXie, Lixin, Lingling Yang, Libo Su, Shichang Xu, and Wen Zhang. 2021. "A Novel Rotary Dryer Filled with Alumina Ceramic Beads for the Treatment of Industrial Wastewaters: Numerical Simulation and Experimental Study" Processes 9, no. 5: 862. https://doi.org/10.3390/pr9050862
APA StyleXie, L., Yang, L., Su, L., Xu, S., & Zhang, W. (2021). A Novel Rotary Dryer Filled with Alumina Ceramic Beads for the Treatment of Industrial Wastewaters: Numerical Simulation and Experimental Study. Processes, 9(5), 862. https://doi.org/10.3390/pr9050862







