Transient Permeabilization of Living Cells: Combining Shear Flow and Acoustofluidic Trapping for the Facilitated Uptake of Molecules
Abstract
:1. Introduction
2. Methods and Materials
2.1. Cells and Cell Culture
2.2. SAW Chip
2.3. Microfluidic Channels
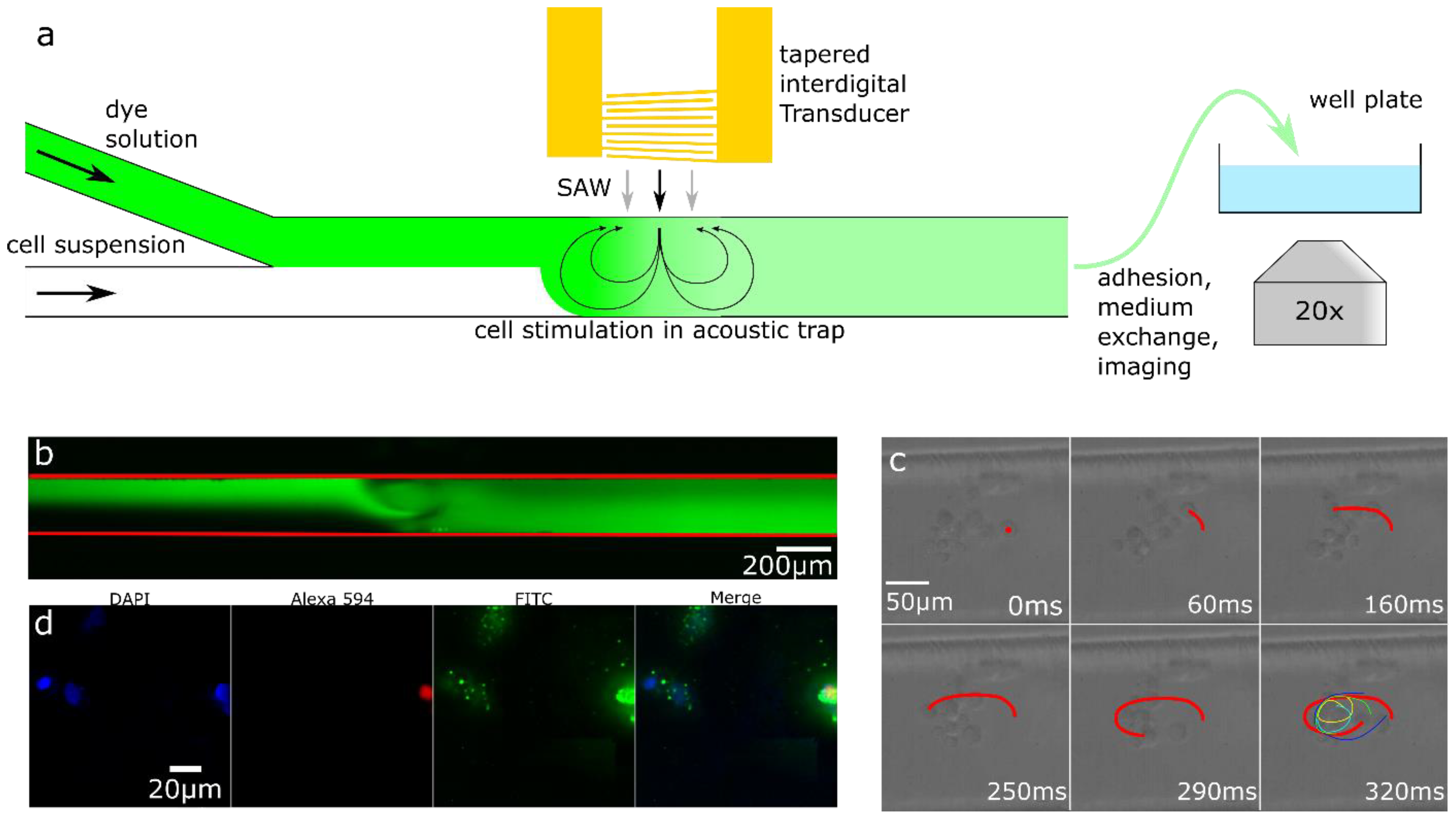
2.4. Acoustofluidic Permeabilization
2.5. Data Processing
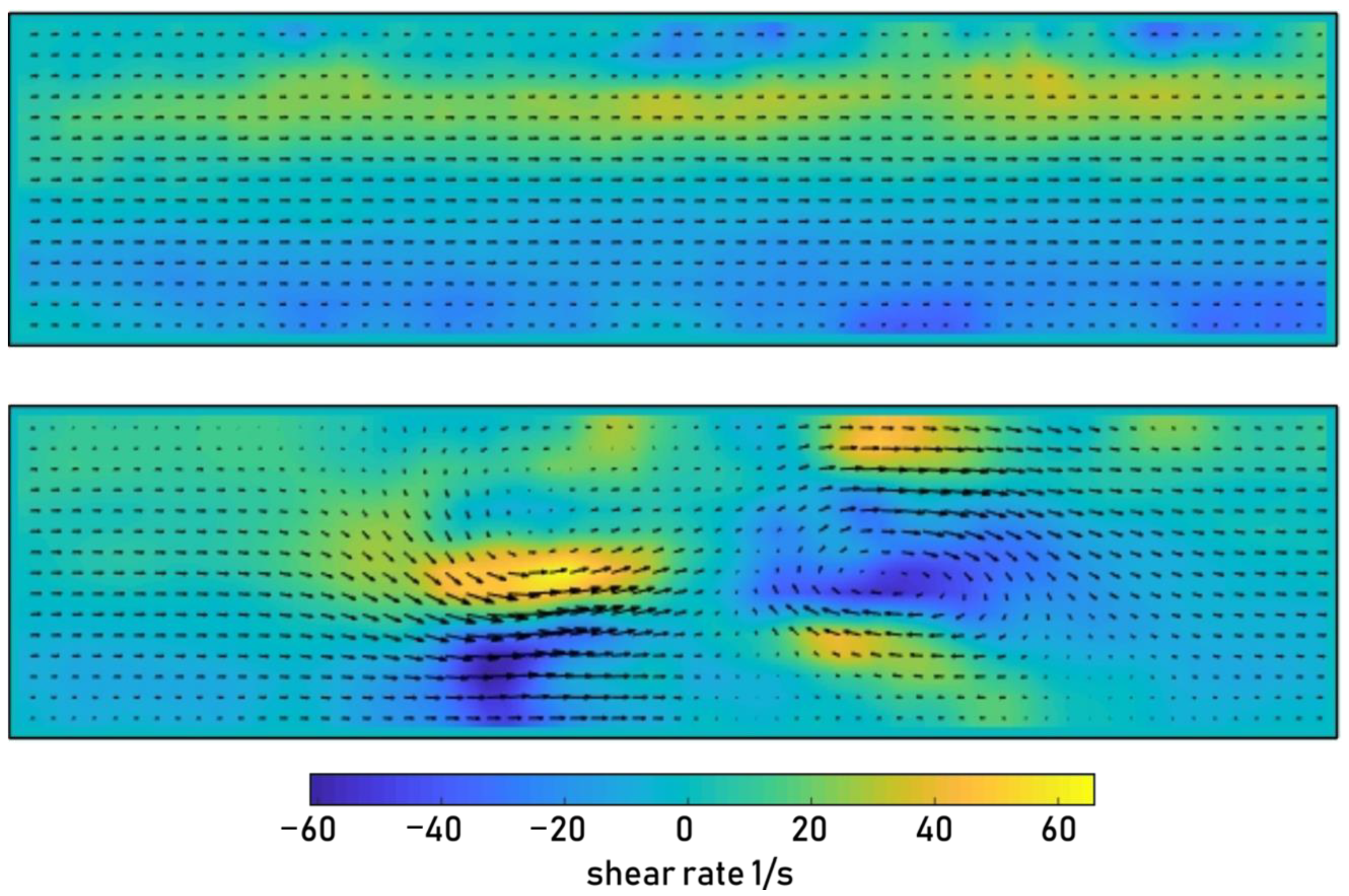
2.6. Particle Image Velocimetry
3. Results and Discussion
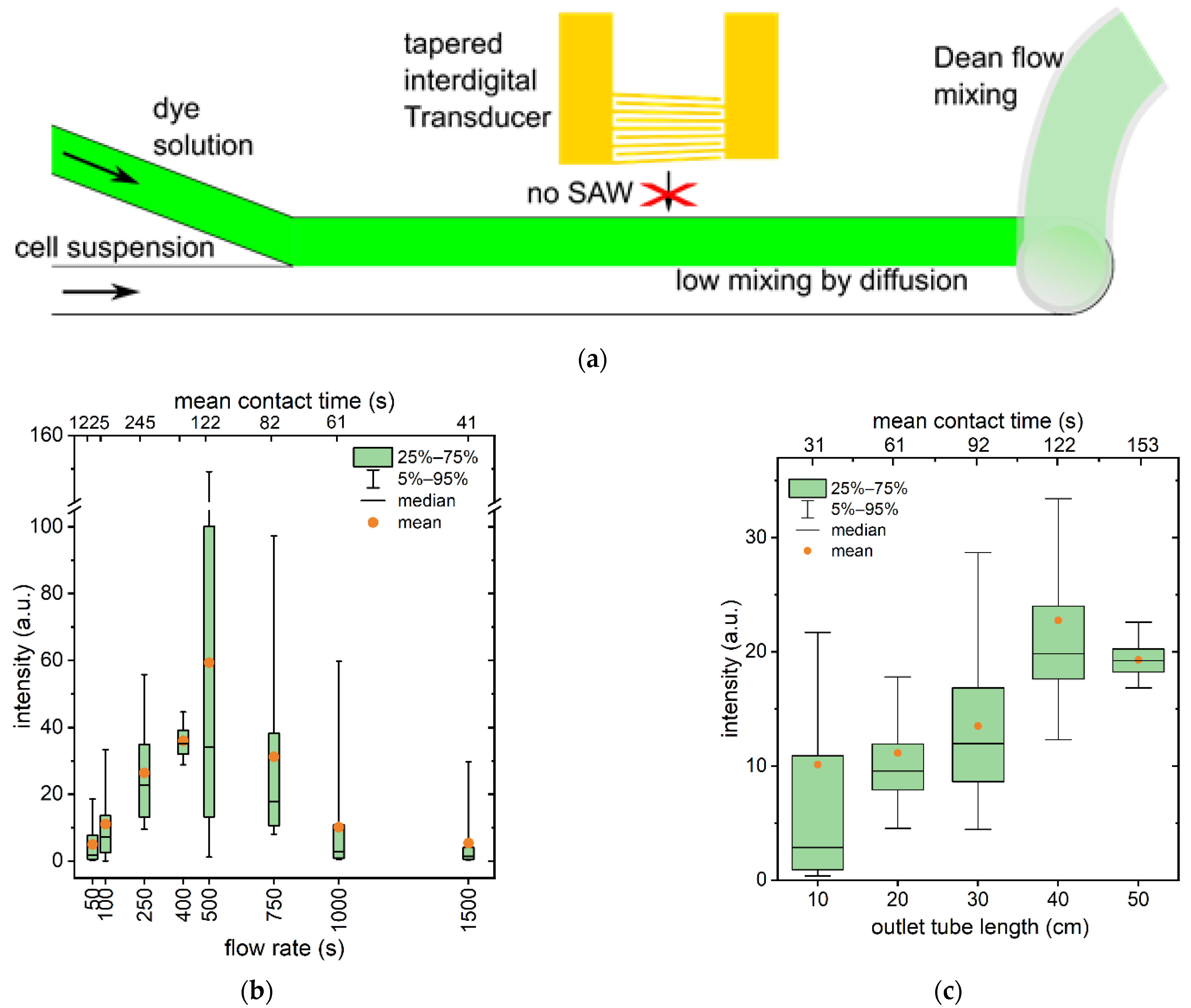
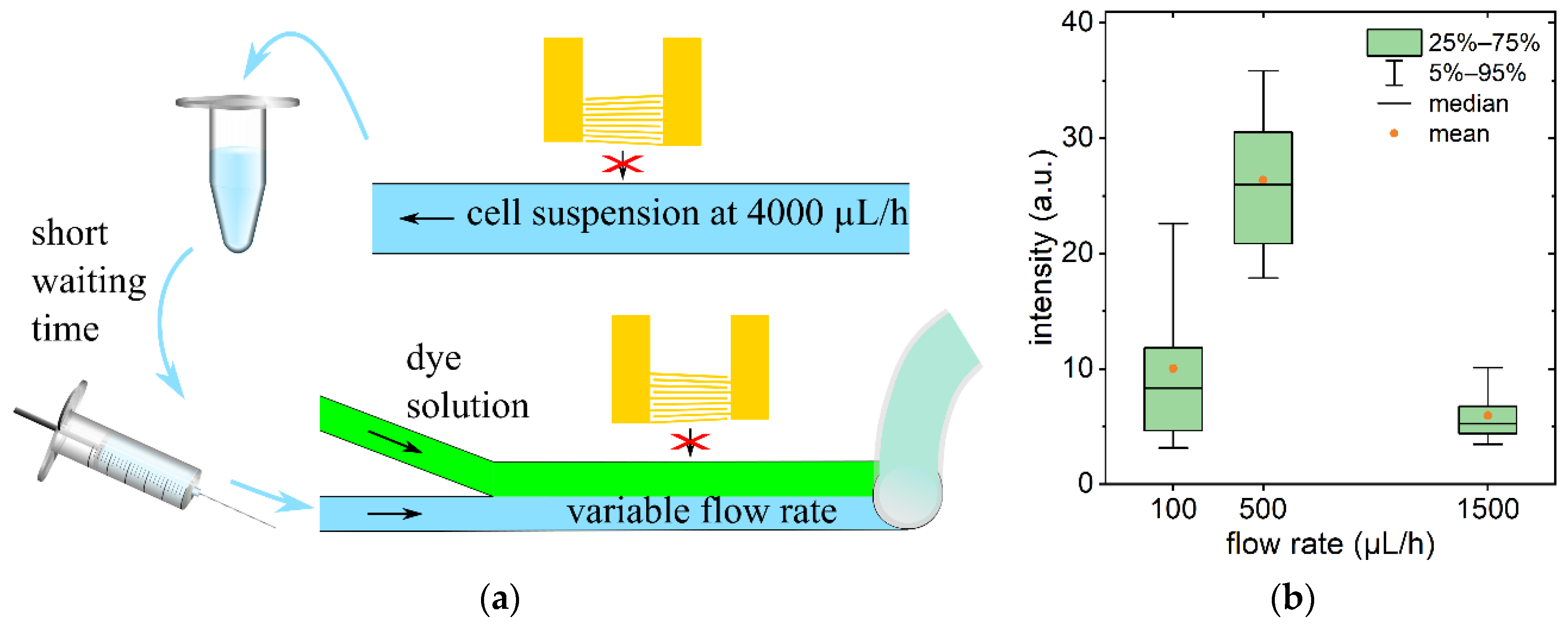
3.1. Shear Flow Induced Permeabilization without Acoustic Trapping
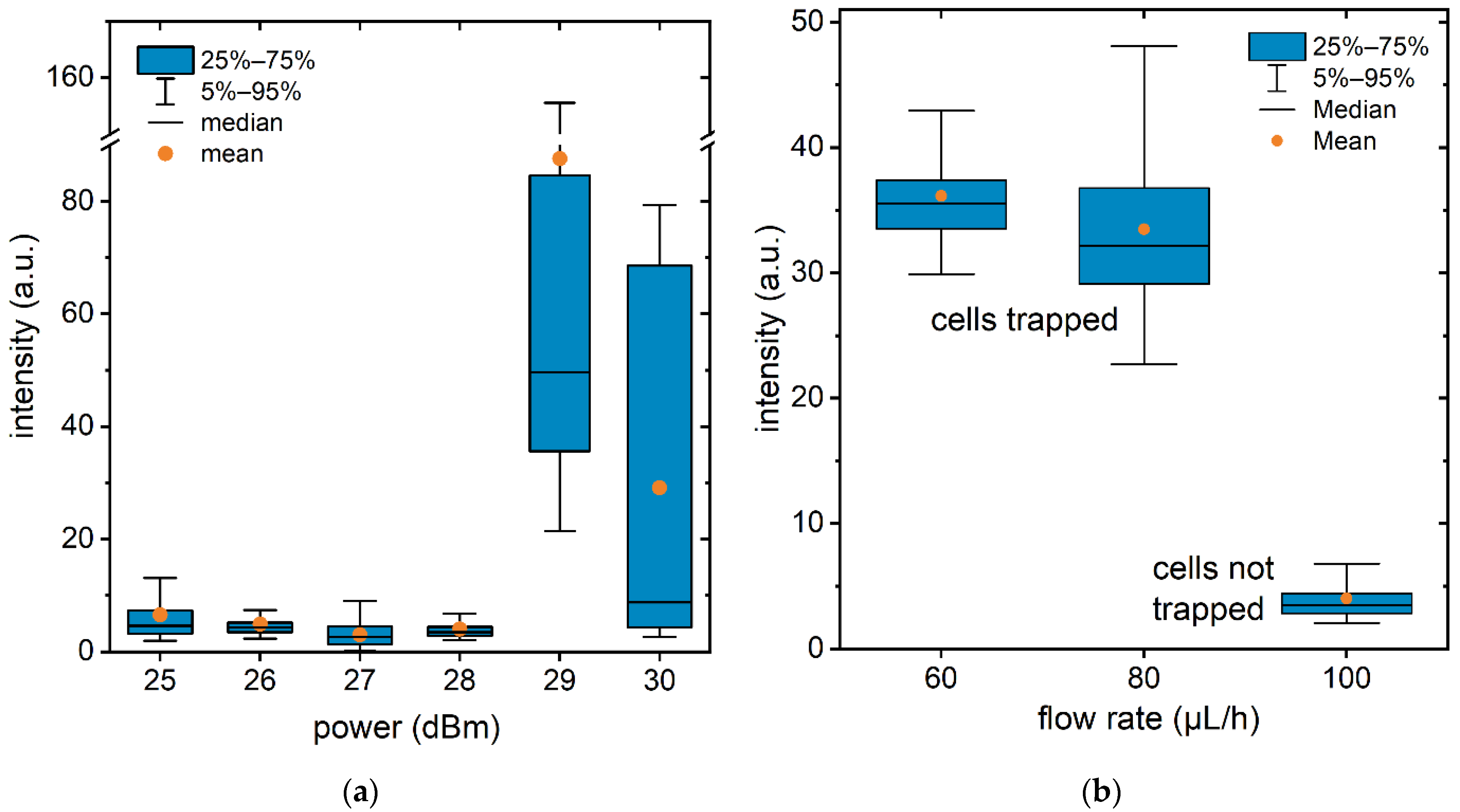
3.2. Acoustofluidic Trapping and Stimulated Uptake Employing Surface Acoustic Waves
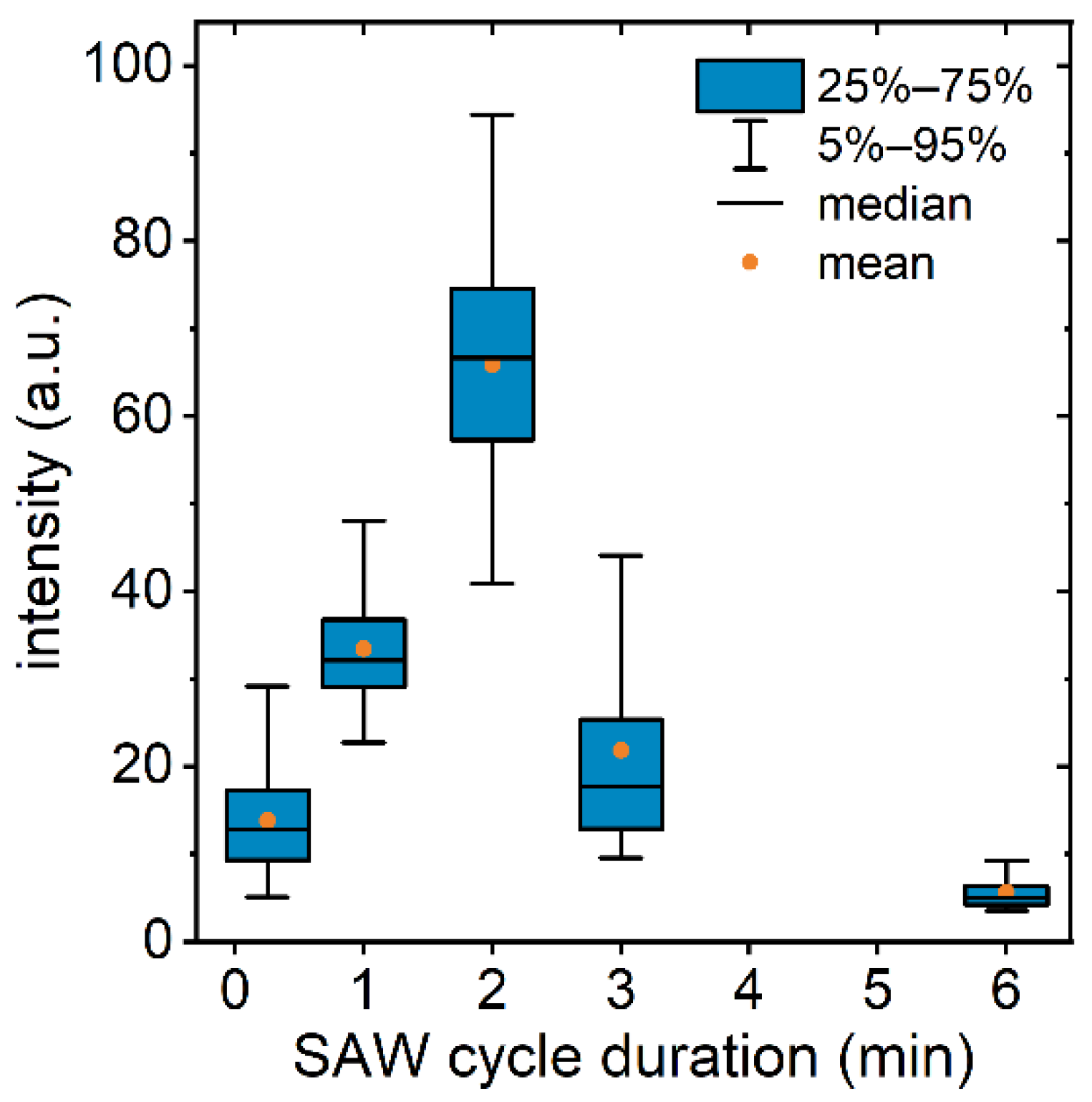
3.3. SAW Cycle Duration
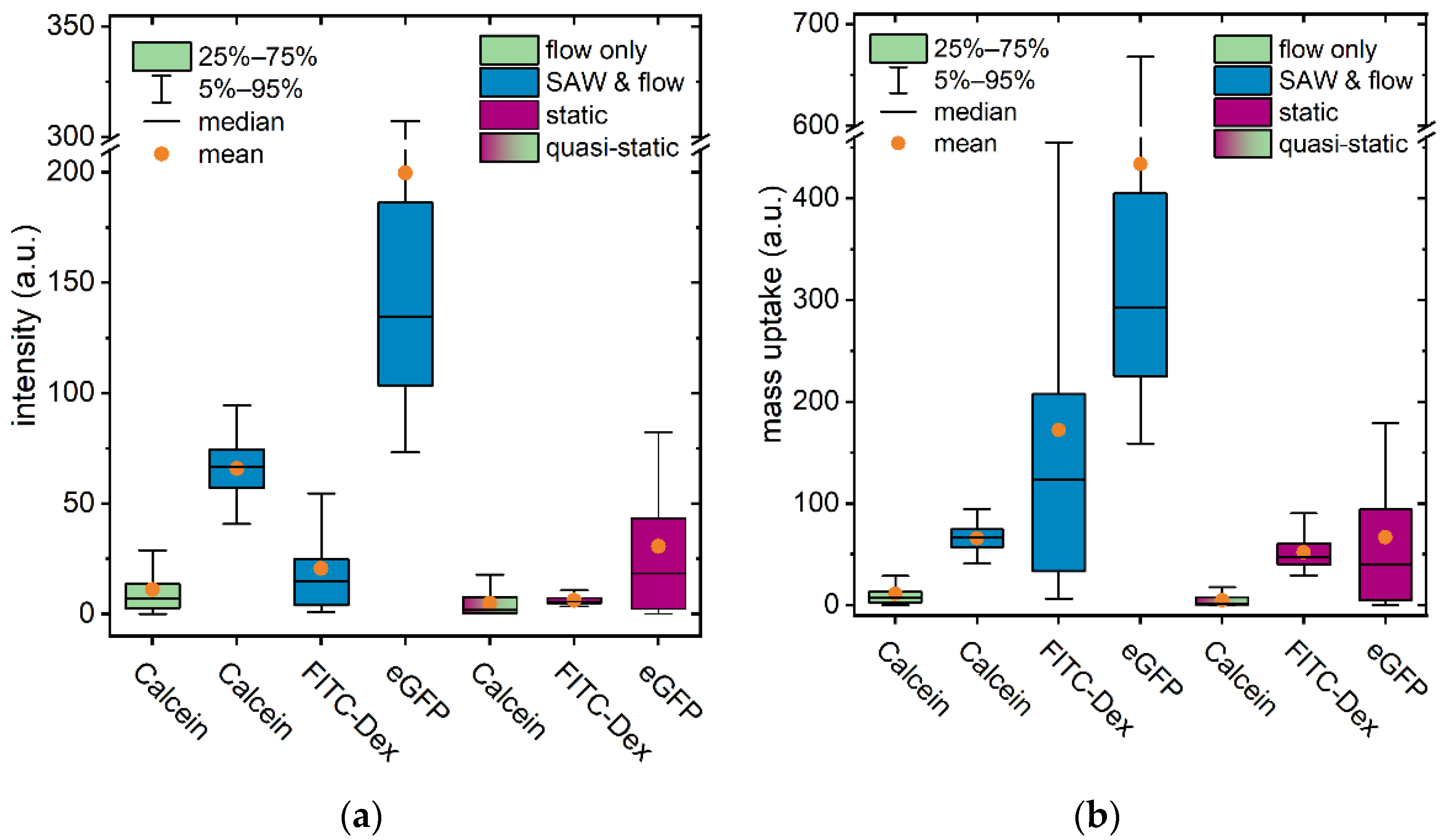
3.4. Applicability for Various Molecular Weights
4. Conclusions and Outlook
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Stewart, M.P.; Langer, R.; Jensen, K.F. Intracellular Delivery by Membrane Disruption: Mechanisms, Strategies, and Concepts. Chem. Rev. 2018, 118, 7409–7531. [Google Scholar] [CrossRef]
- Gehl, J. Electroporation: Theory and methods, perspectives for drug delivery, gene therapy and research. Acta Physiol. Scand. 2003, 177, 437–447. [Google Scholar] [CrossRef]
- Weaver, J.C. Electroporation of cells and tissues. IEEE Trans. Plasma Sci. 2000, 28, 24–33. [Google Scholar] [CrossRef] [Green Version]
- Weaver, J.C.; Chizmadzhev, Y.A. Theory of electroporation: A review. Bioelectrochem. Bioenergy 1996, 41, 135–160. [Google Scholar] [CrossRef]
- Rubinsky, B. Irreversible electroporation in medicine. Technol. Cancer Res. Treat. 2007, 6, 255–259. [Google Scholar] [CrossRef] [PubMed]
- Scheffer, H.J.; Nielsen, K.; De Jong, M.C.; Van Tilborg, A.A.J.M.; Vieveen, J.M.; Bouwman, A.; Meijer, S.; Van Kuijk, C.; Van Den Tol, P.; Meijerink, M.R. Irreversible electroporation for nonthermal tumor ablation in the clinical setting: A systematic review of safety and efficacy. J. Vasc. Interv. Radiol. 2014, 25, 997–1011. [Google Scholar] [CrossRef] [PubMed]
- Mitragotri, S. Healing sound: The use of ultrasound in drug delivery and other therapeutic applications. Nat. Rev. Drug Discov. 2005, 4, 255–260. [Google Scholar] [CrossRef]
- Lentacker, I.; De Cock, I.; Deckers, R.; De Smedt, S.C.; Moonen, C.T.W. Understanding ultrasound induced sonoporation: Definitions and underlying mechanisms. Adv. Drug Deliv. Rev. 2014, 72, 49–64. [Google Scholar] [CrossRef] [Green Version]
- Sheikh, S.; Pallagatti, S.; Singh, B.; Puri, N.; Singh, R.; Kalucha, A. Sonoporation, a redefined ultrasound modality as therapeutic aid: A review. J. Clin. Exp. Dent. 2011, 3, 228–234. [Google Scholar] [CrossRef]
- Mehier-Humbert, S.; Bettinger, T.; Yan, F.; Guy, R.H. Plasma membrane poration induced by ultrasound exposure: Implication for drug delivery. J. Control. Release 2005, 104, 213–222. [Google Scholar] [CrossRef]
- Belling, J.N.; Heidenreich, L.K.; Tian, Z.; Mendoza, A.M.; Chiou, T.-T.; Gong, Y.; Chen, N.Y.; Young, T.D.; Wattanatorn, N.; Park, J.H.; et al. Acoustofluidic sonoporation for gene delivery to human hematopoietic stem and progenitor cells. Proc. Natl. Acad. Sci. USA 2020, 117, 10976–10982. [Google Scholar] [CrossRef]
- Hanasaki, I.; Walther, J.H.; Kawano, S.; Koumoutsakos, P. Coarse-grained molecular dynamics simulations of shear-induced instabilities of lipid bilayer membranes in water. Phys. Rev. E 2010, 82, 051602. [Google Scholar] [CrossRef] [Green Version]
- Hallow, D.M.; Seeger, R.A.; Kamaev, P.P.; Prado, G.R.; LaPlaca, M.C.; Prausnitz, M.R. Shear-induced intracellular loading of cells with molecules by controlled microfluidics. Biotechnol. Bioeng. 2008, 99, 846–854. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramesan, S.; Rezk, A.R.; Dekiwadia, C.; Cortez-Jugo, C.; Yeo, L.Y. Acoustically-mediated intracellular delivery. Nanoscale 2018, 10, 13165–13178. [Google Scholar] [CrossRef]
- Ramesan, S.; Rezk, A.R.; Yeo, L.Y. High frequency acoustic permeabilisation of drugs through tissue for localised mucosal delivery. Lab Chip 2018, 18, 3272–3284. [Google Scholar] [CrossRef] [PubMed]
- Hodgson, R.P.; Tan, M.; Yeo, L.; Friend, J. Transmitting high power rf acoustic radiation via fluid couplants into superstrates for microfluidics. Appl. Phys. Lett. 2009, 94, 024102. [Google Scholar] [CrossRef]
- Sritharan, K.; Strobl, C.J.; Schneider, M.F.; Wixforth, A.; Guttenberg, Z. Acoustic mixing at low Reynold’s numbers. Appl. Phys. Lett. 2006, 88, 054102. [Google Scholar] [CrossRef]
- Wixforth, A. Acoustically Driven Programmable Microfluidics for Biological and Chemical Applications. J. Lab. Autom. 2006, 11, 399–405. [Google Scholar] [CrossRef]
- Dean, S.; Rathgeber, A.; Wassermeier, M.; Wixforth, A. Acoustic ‘Distributed Source’ Mixing of Smallest Fluid Volumes. J. ASTM Int. 2005, 2, 12829. [Google Scholar] [CrossRef]
- Westerhausen, C.; Schnitzler, L.; Wendel, D.; Krzysztoń, R.; Lächelt, U.; Wagner, E.; Rädler, J.; Wixforth, A. Controllable Acoustic Mixing of Fluids in Microchannels for the Fabrication of Therapeutic Nanoparticles. Micromachines 2016, 7, 150. [Google Scholar] [CrossRef] [Green Version]
- Frommelt, T.; Kostur, M.; Wenzel-Schäfer, M.; Talkner, P.; Hänggi, P.; Wixforth, A. Microfluidic mixing via acoustically driven chaotic advection. Phys. Rev. Lett. 2008, 100, 1–4. [Google Scholar] [CrossRef] [PubMed]
- Streibl, M.; Wixforth, A.; Kotthaus, J.P.; Govorov, A.O.; Kadow, C.; Gossard, A.C. Imaging of acoustic charge transport in semiconductor heterostructures by surface acoustic waves. Appl. Phys. Lett. 1999, 75, 4139–4141. [Google Scholar] [CrossRef] [Green Version]
- Xia, Y.; Whitesides, G.M. Soft Lithography. Annu. Rev. Mater. Sci. 1998, 28, 153–184. [Google Scholar] [CrossRef]
- Illes, B.; Hirschle, P.; Barnert, S.; Cauda, V.; Wuttke, S.; Engelke, H. Exosome-Coated Metal—Organic Framework Nanoparticles: An Efficient Drug Delivery Platform. Chem. Mater. 2017, 29, 8042–8046. [Google Scholar] [CrossRef]
- Maier, K.; Wagner, E. Acid-Labile Traceless Click Linker for Protein Transduction. J. Am. Chem. Soc. 2012, 134, 10169–10173. [Google Scholar] [CrossRef] [Green Version]
- Thielicke, W.; Stamhuis, E.J. PIVlab—Towards User-friendly, Affordable and Accurate Digital Particle Image Velocimetry in MATLAB. J. Open Res. Softw. 2014, 2. [Google Scholar] [CrossRef] [Green Version]
- Clarke, M.S.F.; McNeil, P.L. Syringe loading introduces macromolecules into living mammalian cell cytosol. J. Cell Sci. 1992, 102 Pt 3, 533–541. [Google Scholar] [CrossRef]
- Dean, W.R. Fluid Motion in a Curved Channel. Proc. R. Soc. A Math. Phys. Eng. Sci. 1928, 121, 402–420. [Google Scholar] [CrossRef] [Green Version]
- Sharei, A.; Zoldan, J.; Adamo, A.; Sim, W.Y.; Cho, N.; Jackson, E.; Mao, S.; Schneider, S.; Han, M.-J.; Lytton-Jean, A.; et al. A vector-free microfluidic platform for intracellular delivery. Proc. Natl. Acad. Sci. USA 2013, 110, 2082–2087. [Google Scholar] [CrossRef] [Green Version]
- Geislinger, T.M.; Franke, T. Hydrodynamic lift of vesicles and red blood cells in flow—From Fåhræus & Lindqvist to microfluidic cell sorting. Adv. Colloid Interface Sci. 2014, 208, 161–176. [Google Scholar] [CrossRef]
- De Haas, K.H.; Blom, C.; van den Ende, D.; Duits, M.H.G.; Mellema, J. Deformation of giant lipid bilayer vesicles in shear flow. Phys. Rev. E 1997, 56, 7132–7137. [Google Scholar] [CrossRef] [Green Version]
- Debye, P.; Hückel, E. Zur Theorie der Elektrolyte. I. Gefrierpunktserniedrigung und verwandte Erscheinungen. Phys. Z. 1923, 24, 305. [Google Scholar]
- Evans, E.; Heinrich, V.; Ludwig, F.; Rawicz, W. Dynamic tension spectroscopy and strength of biomembranes. Biophys. J. 2003, 85, 2342–2350. [Google Scholar] [CrossRef] [Green Version]
- Tamba, Y.; Ariyama, H.; Levadny, V.; Yamazaki, M. Kinetic Pathway of Antimicrobial Peptide Magainin 2-Induced Pore Formation in Lipid Membranes. J. Phys. Chem. B 2010, 114, 12018–12026. [Google Scholar] [CrossRef] [PubMed]
- Akimov, S.A.; Volynsky, P.E.; Galimzyanov, T.R.; Kuzmin, P.I.; Pavlov, K.V.; Batishchev, O.V. Pore formation in lipid membrane II: Energy landscape under external stress. Sci. Rep. 2017, 7, 12509. [Google Scholar] [CrossRef] [Green Version]
- Blicher, A.; Wodzinska, K.; Fidorra, M.; Winterhalter, M.; Heimburg, T. The temperature dependence of lipid membrane permeability, its quantized nature, and the influence of anesthetics. Biophys. J. 2009, 96, 4581–4591. [Google Scholar] [CrossRef] [Green Version]
- Petronilli, V.; Miotto, G.; Canton, M.; Brini, M.; Colonna, R.; Bernardi, P.; Di Lisa, F. Transient and Long-Lasting Openings of the Mitochondrial Permeability Transition Pore Can Be Monitored Directly in Intact Cells by Changes in Mitochondrial Calcein Fluorescence. Biophys. J. 1999, 76, 725–734. [Google Scholar] [CrossRef] [Green Version]
- Beattie, G.M.; Crowe, J.H.; Lopez, A.D.; Cirulli, V.; Ricordi, C.; Hayek, A. Trehalose: A Cryoprotectant That Enhances Recovery and Preserves Function of Human Pancreatic Islets After Long-Term Storage. Diabetes 1997, 46, 519–523. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Van Die, I.M.; Bergmans, H.E.N.; Hoekstra, W.P.M. Transformation in Escherichia coli: Studies On The Role Of The Heat Shock In Induction Of Competence. Microbiology 1983, 129, 663–670. [Google Scholar] [CrossRef] [Green Version]
- Yamamoto, K.; Ando, J. Endothelial cell and model membranes respond to shear stress by rapidly decreasing the order of their lipid phases. J. Cell Sci. 2013, 126, 1227–1234. [Google Scholar] [CrossRef] [Green Version]
- Färber, N.; Westerhausen, C. Broad lipid phase transitions in mammalian cell membranes measured by Laurdan fluorescence spectroscopy. Rev. Sci. Rep. 2021. [Google Scholar] [CrossRef]
- De Haas, K.H.; Blom, C.; van den Ende, D.; Duits, M.H.G.; Haveman, B.; Mellema, J. Rheological Behavior of a Dispersion of Small Lipid Bilayer Vesicles. Langmuir 1997, 13, 6658–6668. [Google Scholar] [CrossRef] [Green Version]
| Fluorescent Species | Brightness |
|---|---|
| Calcein | 1 |
| FITC–dextran | 0.12 |
| eGFP | 0.46 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kamenac, A.; Schilberth, F.L.; Wagner, E.; Wixforth, A.; Lächelt, U.; Westerhausen, C. Transient Permeabilization of Living Cells: Combining Shear Flow and Acoustofluidic Trapping for the Facilitated Uptake of Molecules. Processes 2021, 9, 913. https://doi.org/10.3390/pr9060913
Kamenac A, Schilberth FL, Wagner E, Wixforth A, Lächelt U, Westerhausen C. Transient Permeabilization of Living Cells: Combining Shear Flow and Acoustofluidic Trapping for the Facilitated Uptake of Molecules. Processes. 2021; 9(6):913. https://doi.org/10.3390/pr9060913
Chicago/Turabian StyleKamenac, Andrej, Felix L. Schilberth, Ernst Wagner, Achim Wixforth, Ulrich Lächelt, and Christoph Westerhausen. 2021. "Transient Permeabilization of Living Cells: Combining Shear Flow and Acoustofluidic Trapping for the Facilitated Uptake of Molecules" Processes 9, no. 6: 913. https://doi.org/10.3390/pr9060913
APA StyleKamenac, A., Schilberth, F. L., Wagner, E., Wixforth, A., Lächelt, U., & Westerhausen, C. (2021). Transient Permeabilization of Living Cells: Combining Shear Flow and Acoustofluidic Trapping for the Facilitated Uptake of Molecules. Processes, 9(6), 913. https://doi.org/10.3390/pr9060913







