Multi-State Load Demand Forecasting Using Hybridized Support Vector Regression Integrated with Optimal Design of Off-Grid Energy Systems—A Metaheuristic Approach

Abstract

The prediction accuracy of support vector regression (SVR) is highly influenced by a kernel function. However, its performance suffers on large datasets, and this could be attributed to the computational limitations of kernel learning. To tackle this problem, this paper combines SVR with the emerging Harris hawks optimization (HHO) and particle swarm optimization (PSO) algorithms to form two hybrid SVR algorithms, SVR-HHO and SVR-PSO. Both the two proposed algorithms and traditional SVR were applied to load forecasting in four different states of Nigeria. The correlation coefficient (R), coefficient of determination (R²), mean square error (MSE), root mean square error (RMSE), and mean absolute percentage error (MAPE) were used as indicators to evaluate the prediction accuracy of the algorithms. The results reveal that there is an increase in performance for both SVR-HHO and SVR-PSO over traditional SVR. SVR-HHO has the highest R² values of 0.9951, 0.8963, 0.9951, and 0.9313, the lowest MSE values of 0.0002, 0.0070, 0.0002, and 0.0080, and the lowest MAPE values of 0.1311, 0.1452, 0.0599, and 0.1817, respectively, for Kano, Abuja, Niger, and Lagos State. The results of SVR-HHO also prove more advantageous over SVR-PSO in all the states concerning load forecasting skills. This paper also designed a hybrid renewable energy system (HRES) that consists of solar photovoltaic (PV) panels, wind turbines, and batteries. As inputs, the system used solar radiation, temperature, wind speed, and the predicted load demands by SVR-HHO in all the states. The system was optimized by using the PSO algorithm to obtain the optimal configuration of the HRES that will satisfy all constraints at the minimum cost.

1. Introduction

Electricity is paramount for the socio-economic development of every nation [1]. It affects every part of human life such as education, entertainment, healthcare, and transport. However, this vital commodity remains a luxury for a significant portion of the world’s population. A total of 1.1 billion people, representing 14% of the global population, had no access to electricity in 2016, according to the International Energy Agency [2]. The lack of electricity affects developing countries the most, especially those in sub-Saharan Africa (SSA) and Asia. Consequently, the lack of electricity has restricted the development of these countries. Most of the countries in these regions show disparities in electrification rates between urban and rural areas [3]. Such is the case in Nigeria, a sovereign country in West Africa.

With a population of over 190 million, Nigeria has a peak load demand of 17,700 MW [4]. In 2017, the country recorded an all-time peak electricity generation of 5074 MW generated from 28 grid-connected power plants [4]. Nigeria’s national electrification rate is only 58%, with a substantial disparity between urban areas (78%) and rural areas (39%) [5]. Grid extension to rural areas is limited by poor road connectivity, geographical remoteness, rough terrain, dense jungles, low energy usage, high supply costs, low incomes for households, and scattered consumer settlement [3,6]. People in rural areas thus depend on diesel generators for electricity supply which has negative consequences arising from noise pollution, carbon dioxide emissions, and the need for frequent maintenance with associated high fuel costs [7].

In the wake of environmental concerns over climate change, the Nigerian electrical power industry is advised to depend on renewable energy (RE) sources for electricity generation [1]. These RE sources include biomass, geothermal, wind, small hydro, and solar and have the advantages of being free, eco-friendly, and inexhaustible [8]. The main disadvantage of using RE sources for electricity generation, particularly wind and solar, is their intermittent nature. This disadvantage generally requires oversizing the system components, resulting in significant investment costs [7]. This is the key factor for the popularity of hybrid renewable energy systems (HRESs) as an effective way of generating electricity in rural areas of the SSA region. An HRES consists of two or more renewable energy sources, energy storage facilities, and electronic equipment. Unlike renewable energy systems from a single source, HRESs are more stable and more efficient and produce electricity at lower costs [7].

In developing countries, optimal design-related studies on HRESs have been reported in the literature. These designs of HRESs are to cater to different applications. A study by [9] developed an HRES for automotive applications, utilizing a PV array combined with transportation means running on PEM fuel cell/NiCd battery. Their study, which used both a logic-based ‘algebraic controller’ and a standard PI controller, showed that both control strategies perform equally well in enabling the HRES to meet its objectives under typical operating conditions and sudden cloud cover conditions; however, battery SOC maintenance is better and the system consumes less hydrogen with PI control at consistently high bus speeds. The goal of optimizing the sizing of a PV/fuel cell/battery system was studied by [10] for desalinating seawater at NEOM city, in Saudi Arabia. Their study was to determine the ideal techno-economic feasibility of three scenarios: one was a hybrid system of solar photovoltaics (PV), a fuel cell (FC) with a hydrogen storage system, and a battery system (BS), while the second and third scenarios were based on hybrid PV/BS and PV/FC with a hydrogen storage system, respectively. Their result showed that PV/FC/BS is the optimum configuration. The main goal of these studies was to determine the best size of each component to maximize or minimize the objective function(s) while satisfying all the constraints [3]. Reviewing all the studies in this field is beyond the scope of this study. However, for illustrative purposes, a few will be mentioned, such as the study by Sawle et al. [11], who applied the genetic algorithm (GA) and particle swarm optimization (PSO) algorithm to optimally design an off-grid PV/wind/biomass hybrid energy system. As an objective function, the cost of energy (COE) was minimized. Dufo-Lopez and Bernal-Agustin [12] used a multi-objective evolutionary algorithm (MOEA) and GA to find the optimal combination of the hybrid system components and control strategies. The algorithm sought to minimize the total cost and greenhouse gas emissions for the entire life span of the installation. Traoré et al. [13] presented an enhanced GA to optimally design an off-grid PV/wind/battery hybrid micro-grid (MG) system to supply a particular load demand. A loss of power supply probability (LPSP) technique was used for carrying out the reliability analysis of the hybrid MG system. Askarzadeh and dos Santos Coelho [14] optimized a hybrid renewable energy system of PV/wind/battery for electrification of a remote area in Iran, using the PSO algorithm. The algorithm minimized the life cycle cost (LCC) of the system while maintaining system reliability. Maleki et al. [15] presented a model and optimization of a PV/wind/battery hybrid system for electrification of a remote area in Iran by a PSO algorithm-based Monte Carlo method. Similarly, a study by [16] designed an optimal island HRES composed of wind, tidal current, battery, and diesel using an improved multi-objective grey wolf optimizer (IMOGWO). Their study, which was aimed to determine the optimal size of the hybrid energy system, showed that it is possible to scale the system optimally using IMOGWO, and the energy management strategy efficiently matches the system’s operational requirements. In addition, a comparison of hybrid systems with and without tidal current turbines was conducted to confirm that the use of tidal current turbines can contribute to improving system reliability and lowering system investment, particularly in places with high tidal currents.

Gurubel et al. [17] proposed an optimal sizing strategy based on RE source neural forecasting and metaheuristic optimization. A recurrent multilayer perceptron (RMLP) was used to predict solar irradiance, wind speed, and load demand variability, while for optimal sizing, the clonal selection algorithm (CSA) was used. Ringwood and Bofelli [18] applied artificial neural network (ANN) models to forecast electricity demand in the Republic of Ireland. A comparative analysis of ANN and linear models was conducted, where ANN models were found to outperform linear models. Raza and Khosravi [19] reviewed the intelligence-based load demand forecasting techniques for smart grids and buildings. The research reviewed artificial intelligence (AI) models in detail and in terms of load forecasting techniques. The authors evaluated the performance of the models and techniques and identified gaps in the research. The study revealed that there is reliance, by the ANN-based forecasting model, on the number of parameters. These parameters include forecast model architecture, input combination, activation functions, and training algorithm of the network.

Javier [20] used a long short-term memory (LSTM) recurrent neural network to estimate 284 stocks from the Standard and Poor’s (S&P) 500 stock market index. The author also applied exponential smooth time series (ETS) and the autoregressive integrated moving average (ARIMA) model to forecast the same stock. The mean absolute error (MAE) obtained from their predictions was compared, and the results showed a significant reduction in prediction errors when LSTM was applied. Abbasimehr et al. [21] proposed a demand forecasting method based on multilayer LSTM networks. The proposed method was compared with ARIMA, ETS, ANN, k-nearest neighbors (KNN), recurrent neural network (RNN), support vector machine (SVM), and single-layer LSTM using demand data of a furniture company. The experimental results indicated that the proposed method is superior among the tested methods in terms of performance measures. Azadeh et al. [22] proposed a multilayer perceptron (MLP) neural network in order to predict renewable energy consumption in Iran. Environmental and economic factors were considered as input to the model and renewable energy consumption as output. To demonstrate the usefulness of the proposed model, real data for the input parameters collected for eleven years (1996–2006) were used. The results displayed a high accuracy of about 99.9%. Hayati and Shirvany [23] applied an MLP neural network to short-term load forecasting in Illam State, Iran. The MLP was trained and tested using three years (2004–2006) of data. The results showed that the MLP network has the lowest forecasting error and can be considered as a good model for short-term load forecasting.

As highlighted in the literature review, studies that have integrated probabilistic estimation of the dynamic behavior of the load demand profile in their optimal design process are limited, especially in developing countries. Such integration is essential for accurate short-term load forecasting based on the historical daily load data and weather data, along with current and forecasted weather data [17]. Several studies have been carried out on load demand forecasting using AI-based models, but very few focused on the application of different learning techniques and optimization of the network architecture.

To the best of the authors’ knowledge, the application of hybrid support vector regression (SVR) with the emerging Harris hawks optimization (HHO) algorithm for short-term load forecasting has not been reported in the literature. Therefore, this study aims to (i) combine SVR with HHO and PSO to form two hybrid SVR algorithms, SVR-HHO and SVR-PSO; (ii) apply both the two proposed algorithms and traditional SVR to load forecasting in four different states of Nigeria and evaluate their prediction accuracy; (iii) design a hybrid renewable energy system (HRES) that consists of photovoltaics, wind turbines, and batteries; (iv) apply PSO based on the SVR predictor model with the highest prediction accuracy, in order to determine the optimal sizes of three generation systems (PV/wind/battery, PV/battery, and wind/battery systems) in all the states. The same procedure is carried out by GA, and the results of both algorithms are compared.

It is worthy of note that the choice of PSO is based on whether it solves some limitations of heuristics and evolutionary programming as an optimization technique. Some of the challenges encountered using several optimization techniques include algorithm complexity, numerical difficulties when the penalty is large, and the inability to identify a global optimum. The PSO technique, which combines social psychology principles in socio-cognition human agents and evolutionary computations, has been shown to be flexible, well balanced, and easy to apply, and to enhance and adapt to the global and local exploration abilities. Furthermore, PSO has some special properties such as it does not use the gradient of an objective function, and its utilization for continuous real numbers, which makes it comparatively more efficient than other techniques [11].

The rest of the paper is structured as follows: The SVR, HHO, PSO, and hybrid SVR algorithms and the proposed methodologies are introduced in Section 2. The system configuration, operation strategy, and mathematical models for the hybrid energy system are presented in Section 3. Section 4 defines the objective function of the optimal sizing problem subject to certain operational constraints. Section 5 presents the predicted load demands by traditional SVR and hybrid SVR algorithms, as well as optimal sizing results for three generation systems. Finally, Section 6 concludes this paper.

2. Methods

This study proposes a hybrid support vector regression (SVR) with Harris hawks optimization (HHO) for short-term load forecasting in remote areas located in the states of Kano, Abuja, Niger, and Lagos, Nigeria. Multi-state load forecasting is paramount, but considering the nature of the dataset obtained from these locations, creating a reliable predictive model is always difficult. For the development of the model, the dataset was randomly divided into two parts called the calibration set, and the verification set. The calibration set was used for the training process and model construction, while the verification set was used for examining the performance accuracy of each candidate model.

The main motive for employing different optimization algorithms for models is attributed to the difficulty in understanding whether a specific algorithm is superior to the others in practice. Additionally, the process of selecting a more accurate algorithm is relatively tough as there exist numerous statistical matrices for the evaluation of models as well as three different approaches including several input combinations. All input data were collected, pre-processed, and normalized based on Equation (1). The normalization of the data was performed before the model training, which is usually conducted to increase the accuracy and speed of the model. This process is very important as it enhances the effectiveness of the predictive models. Computational models such as regression models and AI-based models are usually evaluated using different statistical indicators, which provide more information about each adopted approach, besides providing a clear and realistic impression of the performance of each predictive model separately. Furthermore, identifying the statistical measures that are effectively used to assess the performance of a certain model is also very significant in the selection of the best predictive model.

$$y=0.05+\left(0.95\times \left(\frac{x-x_{min}}{x_{max}-x_{min}}\right)\right)$$

(1)

where $y$ is the normalized data, $x$ is the measured data, and $x_{max}$ and $x_{min}$ are the maximum and minimum values of the measured data, respectively.

For effective modeling and forecasting, external or internal validation techniques are paramount. In AI-based models, validation is generally conducted to fit the model into the given dataset according to the employed indicators to achieve a reliable result for the prediction of the unknown dataset. Due to problems such as overfitting, satisfactory calibration performance is not usually in agreement with the testing performance. In the validation approach, various kinds of validation methods can be utilized including cross-validation (also known as k-fold cross-validation), holdout, and leave-one-out. The holdout technique is generally regarded as the simplest form of k-fold, whereby the data are randomly categorized into two sets called the training/calibration data and the verification/testing data. One of the main advantages of this method is that in every single round, the training and validation sets are independent of one another. This leads to a sound foundation in model optimization. In this research, the data were divided into two parts as stated above: 70% for the training phase and 30% for the testing phase. The model combination is presented in Equation (2). It is important to note that other methods could be used for validating and portioning the data. The proposed overall model development flowchart is presented in Figure 1.

$$\mathrm{Load} \mathrm{Demand} \left(W\right)=f\left\{\begin{array}{c}M1=\left(\mathrm{Temperature}\right)\\ M2=\left(\mathrm{Temperature}+\mathrm{wind}\right)\\ M3=\left(\mathrm{Temperature}+\mathrm{wind}+\mathrm{solar} \mathrm{radiation}\right)\end{array}\right.$$

(2)

2.1. Support Vector Regression

The idea of support vector machines (SVMs), which are an observer-based learning technique, was first presented by Vapnik in 1995 [24], and they have recently been used effectively in various fields of engineering science such as hydrological modeling, where the first application was by [25]. SVMs are an effective learning technique based on the theory of bounded optimization that uses the structural minimization principle. SVMs are generally split into: support vector classifiers (SVCs), dealing with classification problems, and SVR, performing regression analysis. The function of SVR is expressed as

$$f\left(x\right)=w\times \mathsf{\varphi }\left(x\right)+b$$

(3)

where $w$ represents the weight vector assigned to each feature, $\mathsf{\varphi }$ is the transfer function, and $b$ is a bias. To find an appropriate SVR function $f\left(x\right)$, the regression problem can be stated as

$$\mathrm{Minimize}: \frac{1}{2}{\Vert w\Vert }^2+C{\sum }_{i=1}^N\left({\xi }_i+{\xi }_i^{\ast }\right)$$

(4)

$$\mathrm{Subject} \mathrm{to}:\left\{\begin{array}{c}{y}_i-f\left(x\right)\le \mathsf{\epsilon }+{\xi }_i\\ f\left(x\right)-y_i\le \mathsf{\epsilon }+{\xi }_i^{\ast }\\ {\xi }_i,{\xi }_i^{\ast }\ge 0, i=1, 2, 3,\dots .,N \end{array}\right.$$

(5)

where $C$ is the penalty parameter, ${\xi }_i$ and ${\xi }_i^{\ast }$ are the slack variables, and $\mathsf{\epsilon }$ denotes the size of the tube and displays the optimization performance. The solution of the non-linear regression function can be obtained by applying the Lagrangian functions as follows:

$$f\left(x\right)={\sum }_{i=1}^N\left({\alpha }_i-{\alpha }_i^{\ast }\right) K\left(x,x_i\right)+b$$

(6)

where $K\left(x,x_i\right)$ is the kernel function; ${\alpha }_i$ and ${\alpha }_i^{\ast }$ are dual variables; and ${\alpha }_i$ and ${\alpha }_i^{\ast }$ are >0. There are many kernel functions, such as polynomial, sigmoid, linear, and radial basis functions (RBF). Among the kernel functions, the most popular kernel used in the literature is the RBF kernel [26]. Thus, the RBF kernel was adopted in this study. The RBF kernel used here is that defined by [26,27].

$$K\left(x,x_i\right)=\exp (-\mathsf{\gamma }{\Vert x_i-x\Vert }^2)$$

(7)

where $\mathsf{\gamma }$ is the kernel parameter. SVR performance is influenced by three parameters, $C$, $\gamma$, and $\mathsf{\epsilon }$. A detailed description of SVR and SVM is available in [28].

2.2. Harris Hawks Optimization

HHO is a novel algorithm based on Harris hawks’ hunting process [29]. In recent years, the HHO algorithm has been effectively applied for optimizing many intricate engineering problems [30]. Usually, hawks operate alone, except for Harris hawks, which work together to hunt and chase. The HHO algorithm mimics Harris hawks’ cooperative behavior and hunting style in nature. Four movements are included in the hunting style of HHO: tracing, encircling, approaching, and attacking. This hunting style is based on three main steps: the exploration capability, the transition from exploration to exploitation, and, finally, the exploitation phase (Figure 2). The first stage is the exploration capability and is stated as

$$X\left(t+1\right)=\left\{\begin{array}{c}{X}_{rand}\left(t\right)-r_1\left|X_{rand}\left(t\right)-2r_{2}X\left(t\right)\right| if q\ge 0.5\\ X_{rabbit}\left(t\right)-X_a\left(t\right)-r_3\left(LB+r_4\left(UB-LB\right)\right) if q<0.5\end{array}\right.$$

(8)

$$X_a\left(t\right)=\frac{1}{N}{\sum }_1^N{X}_i\left(t\right)$$

(9)

where $X_a\left(t\right)$ is the average location of Harris hawks, N is the number of Harris hawks (search agent number), $X\left(t+1\right)$ is the location of the hawks in the following iteration t + 1, $X_i\left(t\right)$ is the current position of the Harris hawk at iteration t, $X_{rand}\left(t\right)$ is a randomly selected hawk, $X_{rabbit}\left(t\right)$ is the position of the rabbit (prey), LB and UB are the lower and upper bands, respectively, and $q$, $r_1$, $r_2$, $r_3$, and $r_4$ are random values varying between 0 and 1.

The second stage is the transition from exploration to exploitation when the hawk energy is reduced during hunting. The hunting escape energy E can be formulated as

$$E=2E_0(1-\frac{t}{T})$$

(10)

where $E_0$ is the initial energy during each progression ($E_0$ ∈ [−1, 1]) and $T$ is the maximum iteration size. In the HHO algorithm, the state of the rabbit (prey) can be determined based on the direction of the contrast of $E$. In Equation (10), $E$ stands for the rabbit energy. HHO can calculate the rabbit state dependent on the variation trend of $E$.

The third stage is the exploitation phase, which is predominantly planned to enhance local solutions based on the latest solutions available. In this stage, based on the prey escape and hawk hunting, the hawks suddenly attack the prey identified in the past stage. The besiege type to catch the rabbit is chosen based on both $E$ and $X$ values; the hard one is taken when | $E$ | < 0.5, and the soft one is taken when | $E$ | ≥ 0.5. The HHO algorithm has four strategies to mimic the stage of the attack: soft besiege, soft besiege with rapid progressive dives, hard besiege, and hard besiege with rapid progressive dives (Figure 2) [29,30].

2.3. Particle Swarm Optimization

The PSO algorithm was introduced by Kennedy and Eberhart in 1995 [32]. It is a population-based search algorithm inspired by the social behavior and movement dynamics of animals. The initial intent of the particle swarm optimization concept was to graphically simulate animals’ social behavior, such as bird flocking, to discover patterns that govern the ability of birds to fly synchronously, and to suddenly change direction with regrouping in an optimal formation. From this initial objective, the concept evolved into a simple and efficient optimization algorithm.

In PSO, the population is referred to as ‘swarm’, and individuals are referred to as ‘particles’. Using the metaphor of well-known birds, the algorithm manipulates a population of individual members in the swarm to establish a region of the search space. Each member moves with a definite velocity within the search space and keeps track of its position where it has found itself. This information is communicated among all members within the swarm. The general principles of the PSO algorithm are explained below.

Suppose that the search space is $n$-dimensional, and each particle has a position vector $X_i$ and a velocity vector $V_i$. The position vector $X_i$ and the velocity vector $V_i$ of the $i^{th}$ particle in the $n$-dimensional search space can be represented as $X_i=\left(x_{i1},x_{i2},\dots ,x_{in}\right)$ and $V_i=\left(v_{i1},v_{i2},\dots ,v_{in}\right),$ respectively. Each member has a memory of the best position in the search space where it has found itself $\left(Pbes{t}_i\right)$ and knows the best position found by all the members in the swarm$\left(Gbest\right)$. Let $Pbes{t}_i=\left(x_{i1}^{Pbest},x_{i2}^{Pbest},\dots ,x_{in}^{Pbest}\right)$ and $Gbest=\left(x_1^{Gbest},x_2^{Gbest},\dots ,x_n^{Gbest}\right)$ be the best position of individual $i$ and all the individuals in the swarm, respectively. At each step, the velocity and position of the $i^{th}$ particle will be updated according to the following equations:

$$V_i^{k+1}=\omega V_i^k+c_1{r}_1\times \left(Pbes{t}_i^k-X_i^k\right)+c_2{r}_2\times \left(Gbes{t}^k-X_i^k\right)$$

(11)

$$X_i^{k+1}=X_i^k+V_i^{k+1}$$

(12)

where $V_i^{k+1}$ is the velocity of individual $i$ at iteration $k+1$, $V_i^k$ is the velocity of individual $i$ at iteration $k$, $\omega$ is the inertia weight parameter, $c_1$ and $c_2$ are the cognitive and social parameters, respectively, $r_1$ and $r_2$ are random numbers between 0 and 1, $X_i^k$ is the position of individual $i$ at iteration$k$, $Pbes{t}_i^k$ is the best position of individual $i$ at iteration $k$, and $Gbes{t}^k$ is the best position of the group until iteration $k$.

The inertia weight parameter in Equation (11) is used to assess the impact of the preceding history of velocities on the succeeding ones. Therefore, $\omega$ shows a compromise between a wider and a local exploration ability of the swarm. In essence, a big inertia weight parameter encourages a wider exploration, while a small one encourages a local exploration. Experimental results suggest that it is preferable to initialize it to a large value, giving priority to the global exploration of the search space, gradually decreasing it in order to obtain a refined solution.

2.4. Hybrid SVR Algorithms

To enhance the performance of SVR, the parameters of the SVR model must be carefully defined. The strength of the SVR model depends on the accurate selection of these three parameters, $C$, $\gamma$, and $\epsilon$ [33]. However, these parameters with a wide range make the search space very large, as well as making it hard to select accurate parameters. Hence, this problem can be categorized as an optimization problem and needs to be resolved by using optimization techniques. The combination of the SVR model with HHO and PSO, which are nature-inspired algorithms, resulted in the following hybrid models: SVR-HHO and SVR-PSO, respectively. The nature-inspired algorithms were used to select the SVR model parameters, $C$, $\mathsf{\gamma }$, and $\mathsf{\epsilon }$. The flowchart of the hybrid SVR-HHO and SVR-PSO models developed in this study is illustrated in Figure 3.

The data values were divided into two sets for the development of prediction models (i.e., SVR-HHO, and SVR-PSO): one set for model training, and another set for testing. A total of 70% of the data were used for training in the present research, while the remaining 30% were used for testing. To provide an unbiased estimation of model performance, model performance analysis was conducted using the testing dataset. At various states, the availability of data was different. Different periods were therefore used for the training and validation of the models at the various states. Tables 1 and 2 provide the data periods used for model training and testing at the various states.

2.5. Evaluation Criteria of the Models

Both the two proposed algorithms and the traditional SVR models were assessed using several performance evaluation criteria including the correlation coefficient (R), coefficient of determination (R²), mean square error (MSE), root mean square error (RMSE), and mean absolute percentage error (MAPE). The R² indicates the discrepancy between the observed and predicted values; for the best network, the R² value should be high both in training and validation. The higher the R², the better the prediction. Its value ranges between −∞ and 1, with higher values indicating better agreement. The R is a significant factor that can be utilized to efficiently discover the robustness of the relationship between predicted and simulated data points. Relative errors (MSE, RMSE, and MAPE) can be expressed by assuming the absolute errors divided by the number of total observations. This indicator is widely used in science and engineering sectors to assess predictive models because it provides significant information on how closely the simulated data points match actual ones. Percentage errors (MAPE) have the advantage of being scale-independent, meaning they are frequently used to compare the forecast performance between different data series [34]. RMSE is a statistical parameter often used to compare the forecasting errors of several models. Lower RMSE values usually point to better predictions. The selection process of the best predictive model is of great importance to achieve highly accurate predictions. Therefore, in this study, five statistical parameters were used to assess the performances of each predictive approach. These quantitative parameters are

$$R^2=1-\frac{{\sum }_{i=1}^N{\left[O_{obsi}-O_{comi}\right]}^2}{{\sum }_{i=1}^N{\left[O_{obsi}-{\overline{O}}_{obsi}\right]}^2}$$

(13)

$$RMSE=\sqrt{\frac{{\sum }_{i=1}^N{(o_{obsi}-o_{comi})}^2}{N}}$$

(14)

$$R=\frac{{\sum }_{i=1}^N\left(O_{obsi}-{\overline{O}}_{obsi}\right)\left(O_{comi}-{\overline{O}}_{comi}\right)}{\sqrt{{\sum }_{i=1}^N{\left(O_{obsi}-{\overline{O}}_{obsi}\right)}^2}{\sum }_{i=1}^N{\left(O_{comi}-{\overline{O}}_{comi}\right)}^2}$$

(15)

$$MSE=\frac{1}{N}{\sum }_{i=1}^N{(O_{obsi}-O_{comi})}^2$$

(16)

$$MAPE=\frac{1}{N}\left[{\sum }_{i=1}^N\left|\frac{O_{obsi}-O_{comi}}{O_{obsi}}\right|\right]$$

(17)

where N, $O_{obsi}$, ${\overline{O}}_{obsi}$, $O_{comi}$ and ${\overline{O}}_{comi}$ are data number, observed data, averaged value of the observed data, computed values, and averaged value of the computed values, respectively.

3. Sizing Formulation

The schematic description of the off-grid solar PV/wind/battery HRES is shown in Figure 4. The HRES consists of solar photovoltaic panels (PVs), wind turbines (WTs), and a battery bank to store excess energy and improve system reliability. In this system, when the power generated by the renewable energy sources $\left(P_{Gen}\right)$ at time t matches the load demand $\left(P_{Load}\right)$, the total power generated is injected into the load through an inverter. When the power generated is higher than the load demand, excess energy will be stored in the battery bank. Conversely, when the load demand is higher than the power generated, the storage system will come on board to supply the difference. In a situation whereby the load demand exceeds the power generated by the renewable energy sources plus that supplied by the storage system, some fraction of the load must be shed, leading to a loss of load. A DC-coupled HRES configuration was considered in this study because it is easy to implement and more efficient and economic, and it eliminates the need for frequency and voltage control of individual sources connected to the bus [35].

3.1. Modeling the System Components

3.1.1. Photovoltaic System

The output power of a PV panel $(p_{PV})$ in watts (W) at time t can be obtained from the available solar radiation using the following equation:

$$p_{PV}\left(t\right)=Y_{PV}\times \left(\frac{I\left(t\right)}{1000}\right)\times \left[1+{\alpha }_P\left(T_C-25\right)\right]$$

(18)

where $Y_{PV}$ is the rated power of the PV panel (W), $I$ is the solar radiation (W/m²), ${\alpha }_P$ is the temperature coefficient (%/°C), and $T_C$ is the PV panel temperature (°C). If the number of PV panels is $N_{PV}$, the overall produced power is $P_{PV}\left(t\right)=N_{PV}\times p_{PV}\left(t\right)$.

3.1.2. Wind Turbine

For a wind turbine, wind speed is the most important factor. When the wind speed equals or exceeds the cut-in value, the wind turbine generator will start generating power. If the wind speed exceeds the cut-out value, the wind turbine generator stops running to protect the generator. The produced power of a wind turbine $\left(p_{WT}\right)$ at time t is obtained as follows:

$$p_{WT}\left(t\right)=\left\{\begin{array}{c}0\\ P_r\\ P_r\end{array}\right.\frac{v\left(t\right)-V_{ci}}{V_r-V_{ci}} \begin{array}{c} v\left(t\right)\le V_{ci} or v\left(t\right)\ge V_{co}\\ V_{ci}<v\left(t\right)<V_r\\ V_r<v\left(t\right)<V_{co}\end{array}$$

(19)

where $v\left(t\right)$ is the wind speed at time t, $P_r$ is the rated power of the wind turbine, and $V_{ci}$, $V_{co}$, and $V_r$ are cut-in, cut-out, and rated wind speed of the turbine, respectively. If the number of wind turbines is $N_{WT}$, the overall produced power is $P_{WT}\left(t\right)=N_{WT}\times p_{WT}\left(t\right)$.

3.1.3. Battery

The purpose of using a battery is for energy storage, and it is utilized to cover the difference between supply (from PV and wind turbines) and load demand. The input power of the battery can be negative or positive due to the charging and discharging process. The state of charge $\left(SOC\right)$ of a battery with the corresponding productivity and time consumption is obtained as follows:

When $P_{PV}\left(t\right)+P_{WT}\left(t\right)=\frac{P_{Load}\left(t\right)}{{ɳ}_{Inv}},$ the capacity of the battery is stable and will not change. When the total output power of PV panels and wind turbines is greater than the load demand, $P_{PV}\left(t\right)+P_{WT}\left(t\right)>\frac{P_{Load}\left(t\right)}{{ɳ}_{Inv}},$ the battery bank is in a charging state. The charge quantity of the battery at time t can be obtained as

$$SOC\left(t\right)=SOC\left(t-1\right) \times \left(1-\sigma \right)+\left[\left(P_{PV}\left(t\right)+P_{WT}\left(t\right)\right)-\frac{P_{Load}\left(t\right)}{{ɳ}_{Inv}} \right]\times {ɳ}_{BC}$$

(20)

where $SOC\left(t\right)$ and $SOC\left(t-1\right)$ are the charge quantities of the battery bank at time $t$ and $t-1$, σ is the hourly self-discharge rate, ${ɳ}_{Inv}$ is the inverter efficiency, $P_{Load}\left(t\right)$ is the load demand for a particular hour, and ${ɳ}_{BC}$ is the charging efficiency of the battery bank.

When the total output power of PV panels and wind turbines is less than the load demand, $P_{PV}\left(t\right)+P_{WT}\left(t\right)<\frac{P_{Load}\left(t\right)}{{ɳ}_{Inv}},$ the battery bank is in a discharging state. The charge quantity of the battery at time t can be obtained as

$$SOC\left(t\right)=SOC\left(t-1\right)\times \left(1-\sigma \right)-\left[\frac{P_{Load}\left(t\right)}{{ɳ}_{Inv}}-\left(P_{PV}\left(t\right)+P_{WT}\left(t\right)\right)\right] / {ɳ}_{BD}$$

(21)

where ${ɳ}_{BD}$ is the discharging efficiency of the battery bank.

3.1.4. Converters/Inverters

Two DC/DC converters, one AC/DC converter, and one DC/AC inverter were used for the power conversion in the proposed HRES. The efficiency of all these power conversion devices was set at 95%. The inverter’s losses are a function of its efficiency which is used to relate DC load input to AC load output as follows:

$$P_{Inv-Load}\left(t\right)=\left(P_{Gen-Inv}\left(t\right)+P_{Bat-Inv}\left(t\right)\right)\times {ɳ}_{Inv}$$

(22)

where $P_{Inv-Load}\left(t\right), P_{Gen-Inv}\left(t\right),$ and $P_{Bat-Inv}\left(t\right)$ are the total power injected into the load (AC), power transferred from the renewable energy sources (DC), and the battery (DC) at time t, respectively.

3.1.5. Reliability

Power reliability analysis plays an important role in the hybrid energy system design process because of the intermittent generation characteristics of PV and WT. When the power supply by the HRES is less than the demand, this places the hybrid energy system into a loss of power supply (LPS) scenario, expressed as

$$LPS\left(t\right)=P_{Load}\left(t\right)-P_{avail}\left(t\right)$$

(23)

The available power from the HRES at a time, $P_{avail }\left(t\right),$ can be obtained by Equation (24).

$$P_{avail}\left(t\right)=[P_{PV}\left(t\right)+P_{WT}\left(t\right)+P_{Bat}\left(t\right)]\times {ɳ}_{Inv}$$

(24)

There are many techniques for carrying out reliability analysis, the most prominent among them being the loss of power supply probability (LPSP) technique, defined by Equation (25).

$$LPSP=\frac{{\sum }_{t=0}^{T}LPS\left(t\right) }{{\sum }_{t=0}^T{P}_{Load}\left(t\right)}=\frac{{\sum }_{t=0}^{T}Power failure time}{T}$$

(25)

where $T$ is the number of hours in the study.

An LPSP of 0 means that the load demand will always be satisfied, and an LPSP of 1 means that the load demand will never be satisfied.

4. Problem Formulation

4.1. Objective Function

The objective function of this optimal sizing problem is to minimize the total annual cost $\left(C_{TA}\right)$ of the system. The $\left(C_{TA}\right)$ consists of the annual capital cost $\left(C_{AC}\right)$ and the annual maintenance cost $\left(C_{AM}\right)$. To optimally size the off-grid hybrid energy system, the optimization problem defined by Equation (26) must be solved by using an optimization technique.

$$Minimize C_{TA}=C_{AC}+C_{AM}$$

(26)

The capital cost occurs at the beginning of a project, while the maintenance cost occurs during the project life.

In order to convert the initial capital cost to the annual capital cost, the capital recovery factor$\left(CRF\right)$, defined by Equation (27), was used. The capital recovery factor is a ratio used to calculate the present value of an annuity (a series of equal annual cash flows).

$$CRF=\frac{i{\left(1+i\right)}^n}{{\left(1+i\right)}^n-1}$$

(27)

where $\left(i\right)$ is the interest rate and $\left(n\right)$ denotes the life span of the system in years.

The lifetime of the proposed hybrid renewable energy system project was considered to be 20 years. During the project’s lifetime, some components of the PV/wind/battery system need to be replaced. The lifetime of a battery was assumed to be 5 years. By using the single payment present worth factor, we have

$$C_{Bat}=P_{Bat}\times \left(1+\frac{1}{{\left(1+i\right)}^5}+\frac{1}{{\left(1+i\right)}^{10}}+\frac{1}{{\left(1+i\right)}^{15}}\right)$$

(28)

where $C_{Bat}$ is the present worth of the battery and $P_{Bat}$ is the battery price.

Similarly, the lifetime of the converter/inverter was assumed to be 10 years. By using the single payment worth factor, we have

$$C_{Conv/Inv}=P_{Conv/Inv}\times \left(1+\frac{1}{{\left(1+i\right)}^{10}}\right)$$

(29)

where $C_{Conv/Inv}$ is the present worth of the converter/inverter and $P_{Conv/Inv}$ is the price of the converter/inverter.

For this system, the total annual capital and maintenance costs were obtained by Equations (30) and (31), respectively.

$$C_{AC}=CRF\times \left[N_{PV}\times C_{PV}+N_{WT}\times C_{WT}+N_{Bat}\times C_{Bat}+N_{Conv/Inv}\times C_{Conv/Inv}\right]$$

(30)

where $N_{PV}$ is the number of PV panels, $C_{PV}$ is the unit cost of a PV panel, $N_{WT}$ is the number of wind turbines, $C_{WT}$ is the unit cost of a wind turbine, $N_{Bat}$ is the number of batteries, $C_{Bat}$ is the present worth of a battery, $N_{Conv/Inv}$ is the number of converters/inverters, and $C_{Conv/Inv}$ is the present worth of converters/inverters.

$$C_{AM}=C_{PV-Mtn}\times N_{PV}+C_{WT-Mtn}\times N_{WT}$$

(31)

where $C_{PV-Mtn}$ and $C_{WT-Mtn}$ are the annual maintenance costs of a PV panel and wind turbine, respectively. The maintenance costs of batteries and converter/inverter systems were ignored.

4.2. Constraints

For the hybrid PV/wind/battery-based system, the following constraints should be satisfied:

$$N_{PV}=Integer, 0\le N_{PV}\le N_{PV-Max}$$

(32)

$$N_{WT}=Integer, 0\le N_{WT}\le N_{WT-Max}$$

(33)

$$N_{Bat}=Integer, 0\le N_{Bat}\le N_{Bat-Max}$$

(34)

where $N_{PV-Max},N_{WT-Max}$, and $N_{Bat-Max}$ are the maximum number of PV panels, wind turbines, and batteries, respectively.

At any time, the charge quantity of the battery bank should satisfy the constraint of $SOC\left(t_{min}\right)\le SOC\left(t\right)\le SOC\left(t_{max}\right)$.

The maximum charge quantity of the battery bank $SOC\left(t_{max}\right)$ takes the value of the nominal capacity of the battery bank $\left(S_{Bat}\right)$, and the minimum charge quantity of the battery bank $SOC\left(t_{min}\right)$ is obtained by the maximum depth of discharge $\left(DOD\right)$.

$$SOC\left(t_{min}\right)=\left(1-DOD\right)\times S_{Bat}$$

(35)

5. Results and Discussion

The main objective of this study was to develop hybrid SVR algorithms (SVR-HHO, and SVR-PSO) and compare their effectiveness in predicting the load demand variability of remote areas located in Kano, Abuja, Niger, and Lagos State of Nigeria (a multi-state approach). For this aim, in each state, the load profile of a remote block of flats consisting of 10 apartments was obtained through a survey. The number of electrical appliances, their ratings, and time of usage for all the apartments were considered. The hourly load data were computed by physical monitoring and recording of an hourly variation of the unrestricted load in a 24-h window. The bar plot of the raw data for the four remote locations is presented in Figure 5. Therefore, this section presents the results obtained in both quantitative and visualized forms. Prior to the model simulation, pre-processing of the data was carried out using various methods including normalization, and reliability analysis. For computational analysis (time series data), understanding the effect of individual inputs is crucial in determining the robustness of the predictive models. Hence, stationary and reliability analysis was conducted for all the study areas using the Cronbach’s alpha method and unit root test (i.e., using augmented Dickey–Fuller (ADF)). It should be noted that for any time series, the preliminary analysis of a single parameter or input is quite significant for the reason that its prediction accuracy could potentially add to the performance efficiency of the models. As reported in [36,37], the internal consistency of the parameter can have a positive impact if the Cronbach’s alpha values exceed the threshold of 0.7. According to [38], in order to obtain reliable and valid outcomes that safeguard the stationarity of all the parameters, the ADF test is paramount. The experimental data used in the present work satisfied the aforementioned criteria.

Although the selection of input variable combination is effective using linear sensitivity analysis, many studies such as [39,40,41,42] criticized the conventional method of using Pearson correlation as the input selection approach and recommended the application of complex chaotic systems such as non-linear kernels, GA, and kernel-PCA. In this study, both linear and non-linear sensitivity analyses were tested and verified. From the analysis, it was observed that there is good agreement between the two approaches. The determination of model combinations using linear and non-linear approaches has been reported in several studies [43,44,45,46]. The correlation matrix of the four states (Figure 6) shows that the most effective variable with the target value follows the following hierarchy: ambient temperature (°C) > wind speed (m/s) > solar radiation (W/m²) for Kano, Abuja, and Niger. The hierarchy order for Lagos is: wind speed (m/s) > ambient temperature (°C) > solar radiation (W/m²). A strong correlation for temperature was observed for Lagos, Kano, Niger, and Abuja, with 0.72, 0.71, 0.67, and 0.61, respectively. Similarly, a good to marginal correlation was attained by wind speed, with values of 0.53, 0.51, 0.39, and 0.83 for Kano, Abuja, Niger, and Lagos, respectively. However, a marginal to fair correlation coefficient was observed by solar radiation, with values of 0.37, 0.42, 0.28, and 0.29 for Kano, Abuja, Niger, and Lagos, respectively.

5.1. Results of Machine Learning and Metaheuristic Algorithms

The simulation was conducted in MATLAB 9.3 (R2020a). The best architecture of the SVR model was optimized and selected through the use of the trial-and-error method. According to suggestions in the literature [47,48,49,50], a qualified model is one that meets the requirements of most statistical evaluation criteria. The model simulation was evaluated using the most utilized performance criteria including R², MSE, RMSE, R, and MAPE in both calibration and verification. Based on model combinations (Equation (2)), the simulated results in terms of quantitative assessment are presented in

Table 1. Results of evaluation for traditional SVR models (Kano, Abuja, Niger, and Lagos).

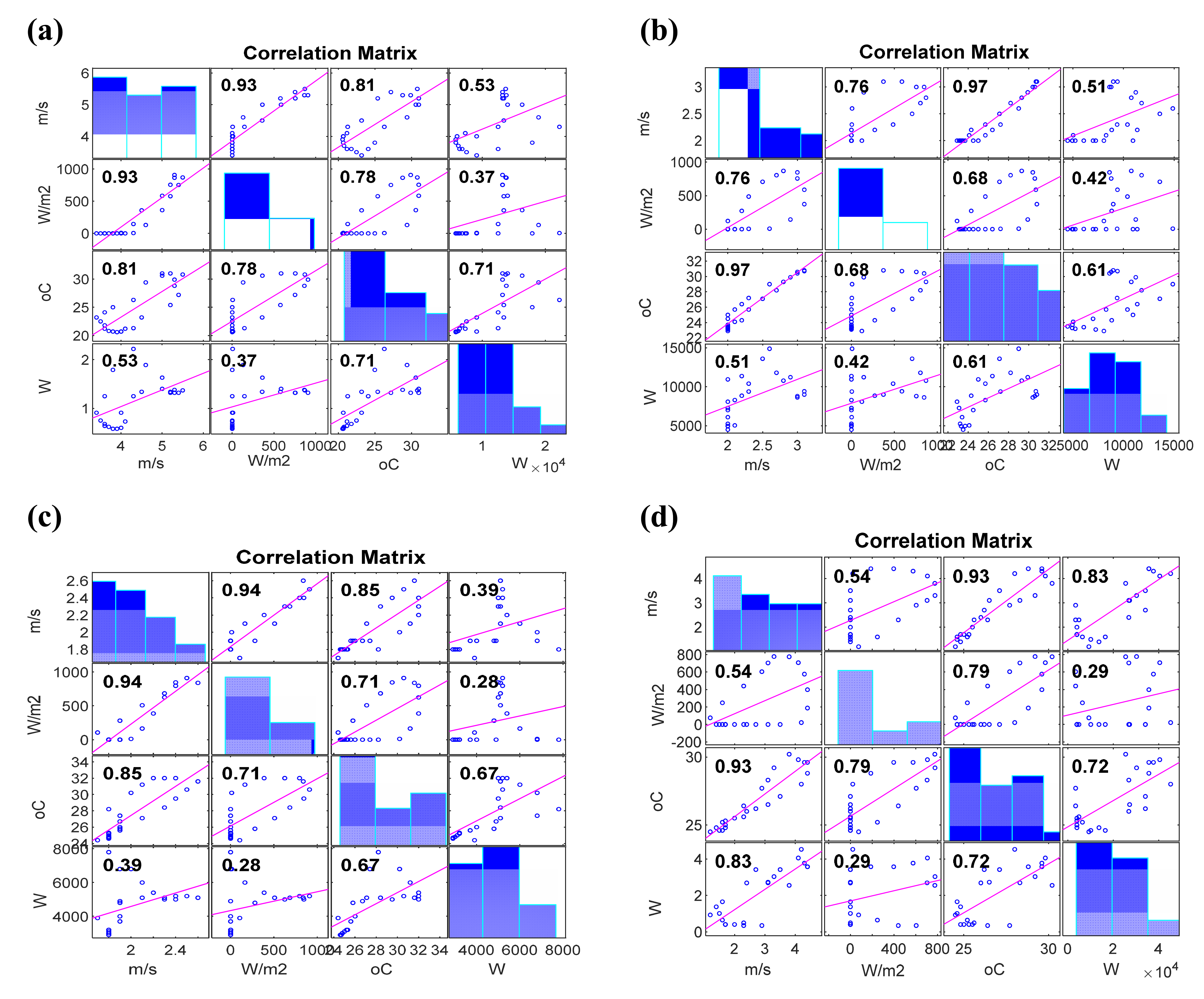
Calibration Phase							Verification Phase
States	Models	R2	MSE	RMSE	R	MAPE	R2	MSE	RMSE	R	MAPE
Kano	SVR-M1	0.6895	0.0150	0.1223	0.8303	1.8064	0.5081	0.0589	0.2427	0.7128	1.8564
	SVR-M2	0.9173	0.0040	0.0631	0.9577	0.8436	0.6789	0.0384	0.1961	0.8240	0.8936
	SVR-M3	0.9678	0.0016	0.0394	0.9838	0.6492	0.9569	0.0052	0.0718	0.9782	0.6992
Abuja	SVR-M1	0.4390	0.0381	0.1951	0.6626	3.4502	0.2739	0.0599	0.2448	0.5234	3.5002
	SVR-M2	0.4554	0.0369	0.1922	0.6748	4.4545	0.3209	0.0560	0.2367	0.5665	4.5045
	SVR-M3	0.7917	0.0141	0.1189	0.8898	1.5837	0.6186	0.0315	0.1774	0.7865	1.6337
Niger	SVR-M1	0.8112	0.0088	0.0937	0.9007	1.8776	0.5230	0.0557	0.2361	0.7232	1.9276
	SVR-M2	0.6297	0.0172	0.1312	0.7936	0.7319	0.6892	0.0363	0.1905	0.8302	0.7819
	SVR-M3	0.9813	0.0009	0.0295	0.9906	1.0518	0.9639	0.0042	0.0649	0.9818	1.1018
Lagos	SVR-M1	0.6167	0.0409	0.2023	0.7853	2.0895	0.6339	0.2238	0.4730	0.7961	2.1395
	SVR-M2	0.7298	0.0288	0.1698	0.8543	2.0959	0.6207	0.0442	0.2104	0.7879	2.1459
	SVR-M3	0.7312	0.0287	0.1694	0.8551	2.6675	0.6274	0.0435	0.2085	0.7921	2.7175

. This table also displays the multi-state performance of the models based on different input variables for both calibration and verification phases. From the results, it can be observed that the predictive modeling approaches achieved different adequacies in accordance with evaluation criteria. Additionally, the overall multi-state results demonstrate that SVR-M3 served as the best simulation in terms of R², MSE, RMSE, R, and MAPE. Although it is difficult to rank the models in accordance with the achieved accuracies, the SVR-M3 approach relatively showed the best prediction accuracy, with Kano and Niger attaining more than 90%, while Abuja displayed more than 79% with regard to the goodness of fit. The comparative visualization of the three model combinations for multi-states is presented in the scatter plots of Figure 7. A scatter plot shows the level of agreement between the observed and predicted loads for the overall goodness of fit. It is obvious from the scatter plot that the SVR-M3 model shows a higher accuracy in comparison to the SVR-M1 and SVR-M2 models.

Further analysis can be conducted using a dimensional radar diagram for the prediction of load demand, which is depicted in Figure 8. It can be observed that SVR-M3 > SVR-M2 > SVR-M1 models were able to capture the best fitting pattern for Kano (R² > 0.9), Abuja, and Lagos (R² > 0.73), while SVR-M3 > SVR-M1 > SVR-M2 models were able to capture this for Niger (R² > 0.97). It is essential to note that the promising ability of SVR-M3 could be attributed to the fact that three variables were engaged in the prediction (temperature, wind, and solar radiation). That means this component includes all useful parameters that have an effective impact on load demand prediction. Similarly, the numerical comparison of multi-states with regard to MSE indicated that SVR-M3 (MSE = 0.0052) is superior to SVR-M1 (MSE = 0.0589), and SVR-M2 (MSE = 0.0384). The predictive error of the best model reduced by 2% on average for Kano. For Abuja, the simulated error of SVR-M3 reduced by 6% on average for both SVR-M1 and SVR-M2, and, lastly, the predictive error of the best model decreased by 14% for Niger and 26% for Lagos.

However, the overall accuracy of Abuja was unsatisfactory and recorded high uncertainty with regard to errors regardless of considering the non-linear relationship between predictors and their corresponding targets. This could be improved by introducing optimization algorithms (PSO and HHO). Basically, it should be taken into consideration that the promising estimations took place during the calibration phase which is primarily employed to effectively calibrate the models based on known input variables and targets. However, the testing step is vital in assessing the performance of a model since it examines the model’s accuracy based on unseen target values. This benefit does not exist in the training set. Therefore, a reliable model should have a stable and balanced performance in both calibration and verification phases. The section of optimization algorithms generally depicted a promising ability with regard to the single model. This is not surprising, as it can be seen in many studies [51,52,53,54,55]. As with the single model, the simulation performance of the metaheuristic algorithms was evaluated using R², MSE, RMSE, R, and MAPE for consistency.

Table 2. Results of SVR-PSO and SVR-HHO for Kano, Abuja, Niger, and Lagos.

Calibration Phase							Verification Phase
States	Models	R2	MSE	RMSE	R	MAPE	R2	MSE	RMSE	R	MAPE
Kano	SVR-PSO	0.9725	0.0013	0.0364	0.9861	0.3751	0.9628	0.0044	0.0667	0.9812	0.4051
Abuja	SVR-PSO	0.8298	0.0115	0.1075	0.9109	0.1480	0.7188	0.0232	0.1523	0.8478	0.1780
Niger	SVR-PSO	0.9813	0.0009	0.0295	0.9906	0.1929	0.9639	0.0042	0.0649	0.9818	0.2229
Lagos	SVR-PSO	0.8701	0.0136	0.1166	0.9328	0.2041	0.7238	0.0322	0.1795	0.8507	0.2341
Kano	SVR-HHO	0.9951	0.0002	0.0154	0.9975	0.1311	0.9872	0.0015	0.0392	0.9936	0.1611
Abuja	SVR-HHO	0.8963	0.0070	0.0839	0.9467	0.1452	0.9755	0.0020	0.0450	0.9877	0.1752
Niger	SVR-HHO	0.9951	0.0002	0.0151	0.9976	0.0599	0.9835	0.0019	0.0439	0.9917	0.0899
Lagos	SVR-HHO	0.9313	0.0080	0.0895	0.9650	0.1817	0.8904	0.0115	0.1071	0.9436	0.2117

presents the results of SVR-PSO and SVR-HHO for both training and verification phases. From Table 2, SVR-HHO has the highest R² values of 0.9951, 0.8963, 0.9951, and 0.9313, the lowest MSE values of 0.0002, 0.0070, 0.0002, and 0.0080, and the lowest MAPE values of 0.1311, 0.1452, 0.0599, and 0.1817, respectively, for Kano, Abuja, Niger, and Lagos. The results prove that SVR-HHO outperformed SVR-PSO for the simulation of load demand at Kano, Abuja, Niger, and Lagos. The predictive ability of HHO over others is consistent with findings from the works of [29,31,56]. The exploratory analysis for the SVR-PSO and SVR-HHO models can also be better understood through the boxplots in Figure 9. As indicated in Figure 9, the computed models that mimic the pattern of the observed values are selected as the best performing model based on the box and whisker evolution criteria. The degree and trend patterns between the measured and computed models show that SVR-HHO > SVR-PSO > SVR-M3 ranked as the best model among all the models considered.

However, considering the other evaluation performance indices, the simulated outcomes justified a high level of superiority of all the metaheuristics algorithms despite the better predictive skill shown by SVR-M3. Figure 10 shows the scatter plots between the observed and predicted values of SVR-PSO and SVR-HHO for Kano, Abuja, Niger, and Lagos. Close agreement between the observed and predicted values was attained in SVR-HHO compared to SVR-PSO. Moreover, the R values of all the models were found to be greater than 0.9, which agrees with conclusions reached by [57,58,59] that R values higher than 0.70 are considered acceptable; thus, the results of all optimization algorithm models are acceptable (see Table 2).

An overall comparison between the best traditional SVR model and the two hybrid SVR algorithms (SVR-HHO and SVR-PSO) is provided using a two-dimensional Taylor diagram, as shown in Figure 11. The Taylor diagram highlights and summarizes several statistical indices such as the correlation coefficient (R), RMSE, and standard deviation between the observed and predicted values [60]. To the best of the authors’ knowledge, this research serves as the first to use this diagram in forecasting load demand. This diagram can highlight the goodness of fit of various models in comparison with one another; therefore, the diagram can be seen as a series of points on a polar plot. A detailed explanation and discussion on the Taylor diagram can be found in [61]. From Figure 11, it can be observed that SVR-HHO achieved better goodness of fit in all four states with the values of R = 0.9975, R = 0.9467, R = 0.9976, and R = 0.9650 for Kano, Abuja, Niger, and Lagos, respectively, in the verification phase. The results lead to the conclusion that for both calibration and verification, SVR-HHO, SVR-PSO, and SVR-M3 are capable of capturing the complex non-linear patterns between the load demand variables.

The simulated results can be better visualized using a time series graph, as presented in Figure 12. From these figures, the optimal predicted load is attributed to the SVR-HHO algorithm in all four states, despite the simultaneous reliability of SVR-PSO.

Despite the availability of large metaheuristic algorithms, none of them can assure a consistent optimal performance in solving different kinds of problems [62,63]. However, recent research on a novel population-based, nature-inspired optimization paradigm (HHO) algorithm showed better effectiveness in discovering optimal solutions for higher and multi-dimensional problems [64,65,66,67]. According to [68,69], the novel HHO optimizer has been checked, through a comparison with other nature-inspired techniques, on 29 benchmark problems and several real-world engineering problems. The statistical results and comparisons show that the HHO algorithm provides very promising and occasionally competitive results compared to well-established metaheuristic techniques such as GA, BBO, GWO, BAT, and FPA.

5.2. Results and Cost Analysis for Optimal Sizing

For finding the optimal sizing, the stand-alone PV/wind/battery HRES was modeled and run in the MATLAB environment. As input, the model used data of solar irradiance, temperature, wind speed, and the forecasted load demand by the novel SVR-HHO, and PSO and GA were used as optimizers. The component parameters are presented in

Table 3. Component parameters.

Component	Specifications
Financial	Interest rate (i) = 5%, system life span (n) = 20 years
PV Panel	PV rated power = 260 W, 𝛼 = −0.25%/°C, Gref = 1000 W/m2, Tref = 25 °C, PVCost = USD 585, CPV-Mtn = USD 21, life span = 20 years
Wind Turbine	Pr = 1 kW, Vci = 2.5 m/s, Vco = 13 m/s, Vr = 11 m/s, WTCost = USD 2312.5, CWT-Mtn = USD 40, life span = 20 years
Battery	Voltage = 12 V, SBat = 2.4 kWh, ȠBC = 85%, ȠBF = 100%, PBat = USD 170, DOD = 0.8, σ = 0.0002, life span = 5 years
Power Conv/Inv	Rated power = 3 kW, ȠInv = 95%, PConv/Inv = USD 2000, life span = 10 years

. The parameter settings of PSO and GA were as follows: PSO: $N=50,$ $c_1=2,$ $c_2=2,$ $\omega =0.9,$ $ite{r}_{max}=100$; GA: $N=50,$ $m=0.25, c=0.7, ite{r}_{max}=100$. PSO and GA attempt to find the optimal number of decision variables. The minimum and maximum values of the decision variables were set to 0 and 10,000, respectively. In the beginning, the charge quantity of each battery was assumed to be 30% of its nominal capacity.

The optimal results obtained by PSO and GA for Kano, Abuja, Niger, and Lagos are shown in

Table 4. Results of optimal sizing for Kano.

Hybrid Systems Algorithms	PV/Wind/Battery		PV/Battery		Wind/Battery
	PSO	GA	PSO	GA	PSO	GA
NPV	51	43	172	175	-	-
NWT	43	47	-	-	40	41
NBat	44	66	44	41	42	42
NConv/Inv	4	4	3	3	3	3
PV cost (USD)	3465.0	2921.50	11,686.0	11,890.0	-	-
WT cost (USD)	9699.1	10,601.0	-	-	9022.40	9248.0
Battery cost (USD)	1727.7	2591.50	1727.70	1609.90	1649.20	1649.20
Conv/Inv cost (USD)	1036.0	1036.0	777.03	777.03	777.03	777.03
Total annual cost (USD)	15,927.8	17,150.0	14,190.73	14,276.93	11,448.63	11,674.23

,

Table 5. Results of optimal sizing for Abuja.

Hybrid Systems Algorithms	PV/Wind/Battery		PV/Battery		Wind/Battery
	PSO	GA	PSO	GA	PSO	GA
NPV	78	54	134	136	-	-
NWT	41	52	-	-	546	546
NBat	73	55	36	36	58	59
NConv/Inv	4	4	3	3	3	3
PV cost (USD)	5299.50	3668.90	9104.20	9240.10	-	-
WT cost (USD)	9248.00	11,729.0	-	-	123,160.0	123,160.0
Battery cost (USD)	2866.40	2159.60	1413.60	1413.60	2277.40	2316.70
Conv/Inv cost (USD)	1036.0	1036.0	777.03	777.03	777.03	777.03
Total annual cost (USD)	18,449.9	18,593.5	11,294.83	11,430.73	126,214.43	126,253.73

,

Table 6. Results of optimal sizing for Niger.

Hybrid Systems Algorithms	PV/Wind/Battery		PV/Battery		Wind/Battery
	PSO	GA	PSO	GA	PSO	GA
NPV	54	49	71	74	-	-
NWT	52	58	-	-	9317	9326
NBat	55	46	26	27	152	174
NConv/Inv	4	4	3	3	3	3
PV cost (USD)	3668.90	3329.20	4823.90	5027.70	-	-
WT cost (USD)	11,729.00	13,083.0	-	-	2,101,600.0	2,103,600.0
Battery cost (USD)	2159.60	1806.20	1020.90	1060.20	5968.40	6832.20
Conv/Inv cost (USD)	1036.0	1036.0	777.03	777.03	777.03	777.03
Total annual cost (USD)	18,593.5	19,254.4	6621.80	6864.93	2,108,345.43	2,111,209.23

and

Table 7. Results of optimal sizing for Lagos.

Hybrid Systems Algorithms	PV/Wind/Battery		PV/Battery		Wind/Battery
	PSO	GA	PSO	GA	PSO	GA
NPV	56	79	299	300	-	-
NWT	42	41	-	-	262	262
NBat	57	42	68	70	41	43
NConv/Inv	4	4	3	3	3	3
PV cost (USD)	3804.70	5367.40	20,315.00	20,383.0	-	-
WT cost (USD)	9473.60	9248.0	-	-	59,097.0	59,097.0
Battery cost (USD)	2238.10	1649.20	2670.10	2748.60	1609.90	1688.40
Conv/Inv cost (USD)	1036.0	1036.0	777.03	777.03	777.03	777.03
Total annual cost (USD)	16,552.4	17,300.6	23,762.13	23,908.63	61,483.93	61,562.43

. Table 4 summarizes the results of optimal sizing for Kano. In this table, the optimal sizes of PV/wind/battery, PV/battery, and wind/battery systems are indicated. From an economic point of view, the wind/battery system is the best system for meeting the load demand requirements of Kano. The total annual cost of the wind/battery system is USD 11,448.63, and the optimal number of decision variables is 40 wind turbines and 42 batteries.

Table 5 shows the optimal number of decision variables and total annual costs of the systems for Abuja. It can be observed that the best system for supplying the load demand is the PV/battery system, with a cost of USD 11,294.83. The optimal sizes of the system components are 134 PV panels and 36 batteries. Table 6 presents the optimal number of each component and total annual costs for the hybrid system in Niger. In this table, the most cost-effective system is the PV/battery system, with the lowest cost of USD 6621.80. The optimal number of system components is 71 PV panels and 26 batteries. Simulation results reveal that is it not economically viable to have a wind/battery system in Niger due to poor wind speeds.

Finally, the results of optimal sizing for Lagos are presented in Table 7. In Lagos, the PV/wind/battery hybrid system is the best system for meeting the load demand requirements. The total annual cost of the hybrid system is USD 16,552.4, and the optimal number of decision variables is 56 PV panels, 42 wind turbines, and 57 batteries. From Table 4, Table 5, Table 6 and Table 7, it can be observed that PSO produces more promising results than GA in all four states.

6. Conclusions

A methodology for multi-state load demand forecasting and optimal sizing of a stand-alone PV/wind/battery hybrid energy system was presented in this paper. A prediction approach based on SVR was used to predict the load demand variability in four different states in Nigeria. Knowing the limitations of traditional SVR, two hybrid SVR algorithms (SVR-HHO, and SVR-PSO) were developed to compare the feasibility of predicting the load demand. Three input attributes, M1, M2, and M3, were defined for the traditional SVR model. SVR-M1, SVR-M2, and SVR-M3 were compared based on input attributes’ sensitivity analysis. SVR-M3 was found to outperform SVR-M1 and SVR-M2 in terms of prediction accuracy. For the hybrid SVR algorithms, there was an increase in performance for both SVR-HHO and SVR-SPO over SVR-M3. SVR-HHO had the highest R² values and the lowest MSE and MAPE values in all four states. The results show that both SVR-HHO and SVR-PSO are capable of predicting multi-state load demands.

For optimal sizing, the PSO algorithm was used based on the predicted load demands by SVR-HHO in all four states to determine the best sizes and combinations of three generation systems (PV/wind/battery, PV/wind, and wind/battery systems), and the results were compared with the results found by GA. The simulation results reveal that, economically, the wind/battery system is the best system for meeting the load requirements of Kano. For Abuja and Niger, the best system for supplying the load demand is the PV/battery system, while the results of optimal sizing for Lagos show that the PV/wind/battery hybrid system is the best system for meeting the load demand requirements.