Study of Creep Mechanical Properties and a Rheological Model of Sandstone under Disturbance Loads
Abstract
:1. Introduction
2. Creep Disturbance Test
2.1. Test Plan
2.2. Test Procedure
- (1)
- Specimen preparation: All samples were taken from the same rock mass, the samples with obvious external defects were removed, and rock samples with the same wave velocity in the wave velocity tester were taken as the sample objects.
- (2)
- Stress application: The stress level of the creep test was determined according to the maximum deviatoric stress of the triaxial compression test, and the initial stress level was 60% of the peak strength from the triaxial test. To facilitate the application of stress, the initial value was selected as an integer value, and the later loads were taken as 70%, 80%, and 90% of the peak strength from the triaxial test.
- (3)
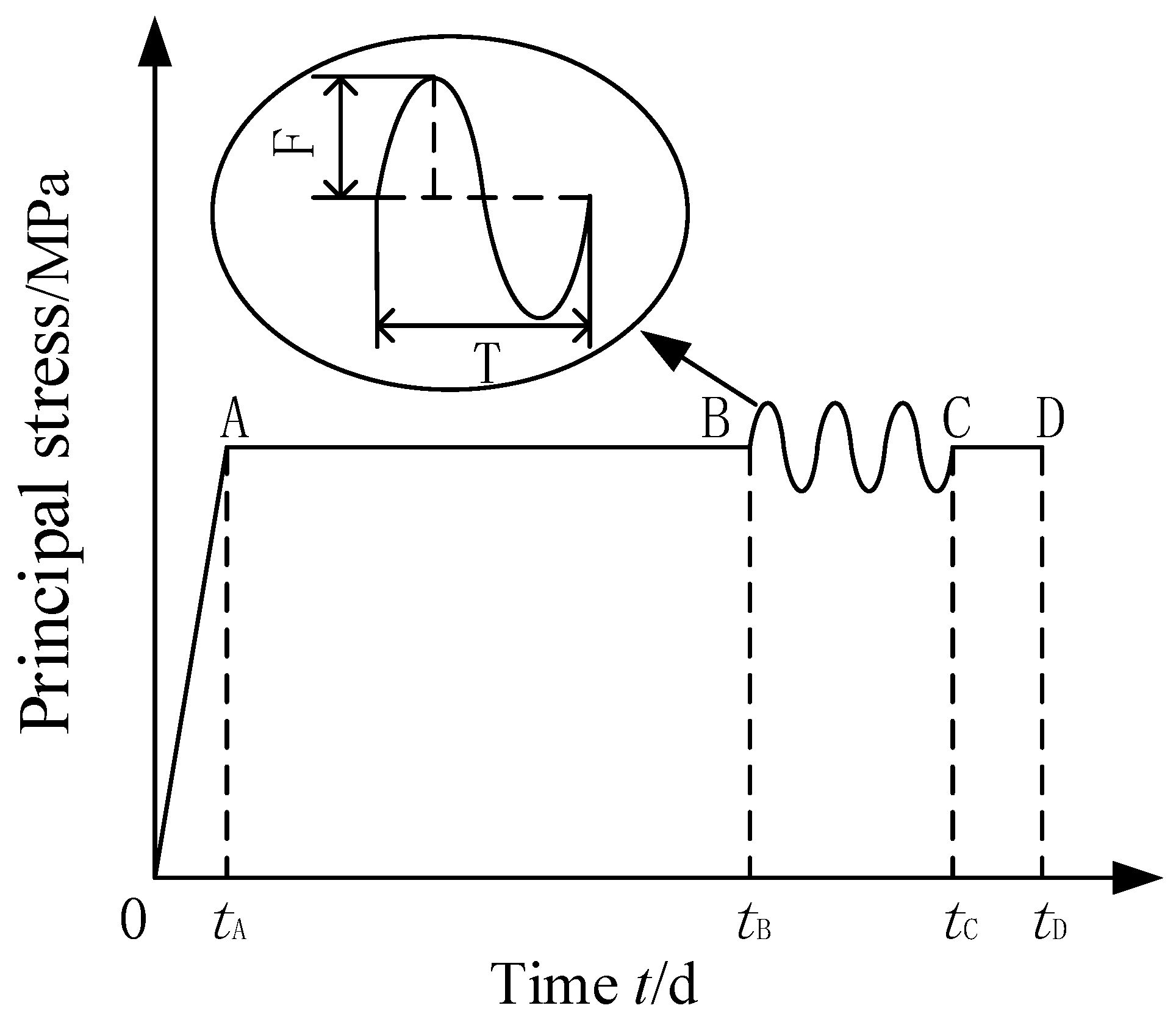
- Disturbance load application: First, the confining pressure was applied to the predetermined value at the loading speed of 500 N/s; next, the axial pressure was applied to the predetermined value at the same loading speed after stabilization, and the disturbance load was then applied by using the load control to increase or decrease the axial stress, as shown in Figure 3. When the radial deformation of rock was less than 0.03 mm/24 h, the next level load was applied, and the above steps were repeated until the specimen was destroyed.
- (4)
- Data recording: After the completion of the test, the confining pressure was first unloaded to zero; then, the axial pressure was unloaded to zero, the hydraulic oil in the pressure chamber was pumped back to the equipment, the pressure chamber was raised, and the rock sample was removed for storage; the test data storage interval was 5 s, and finally, the test data were exported.
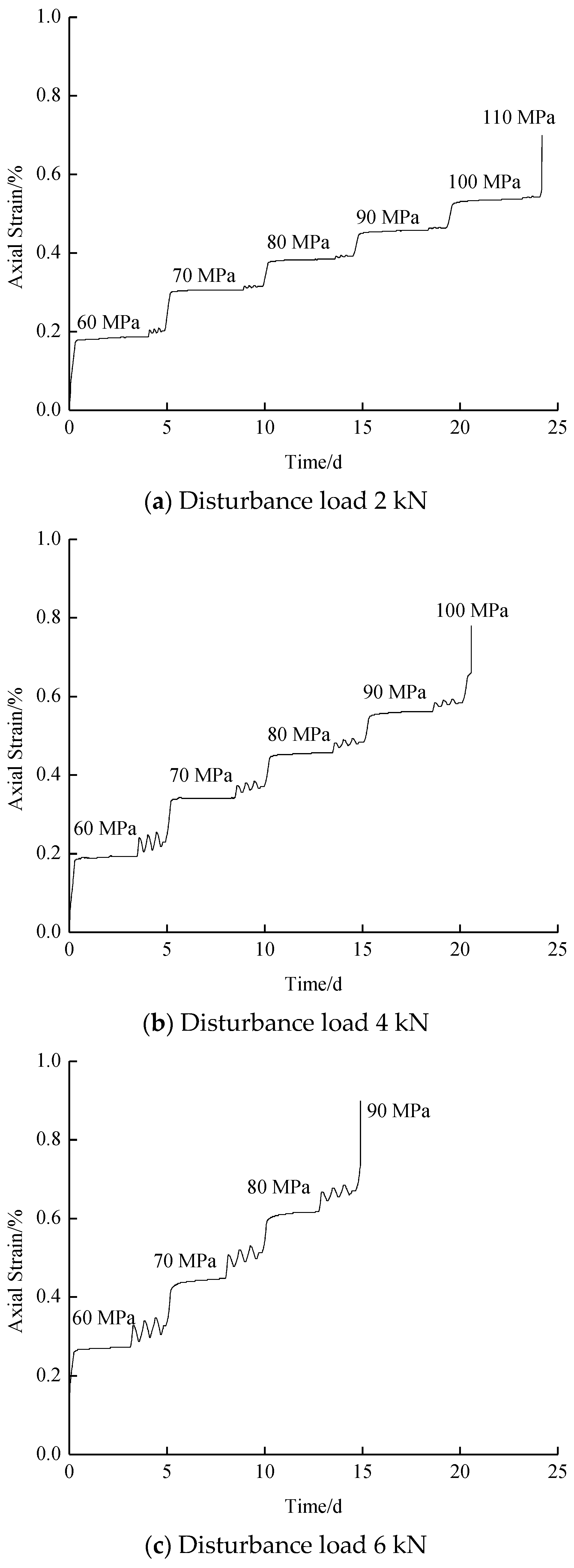
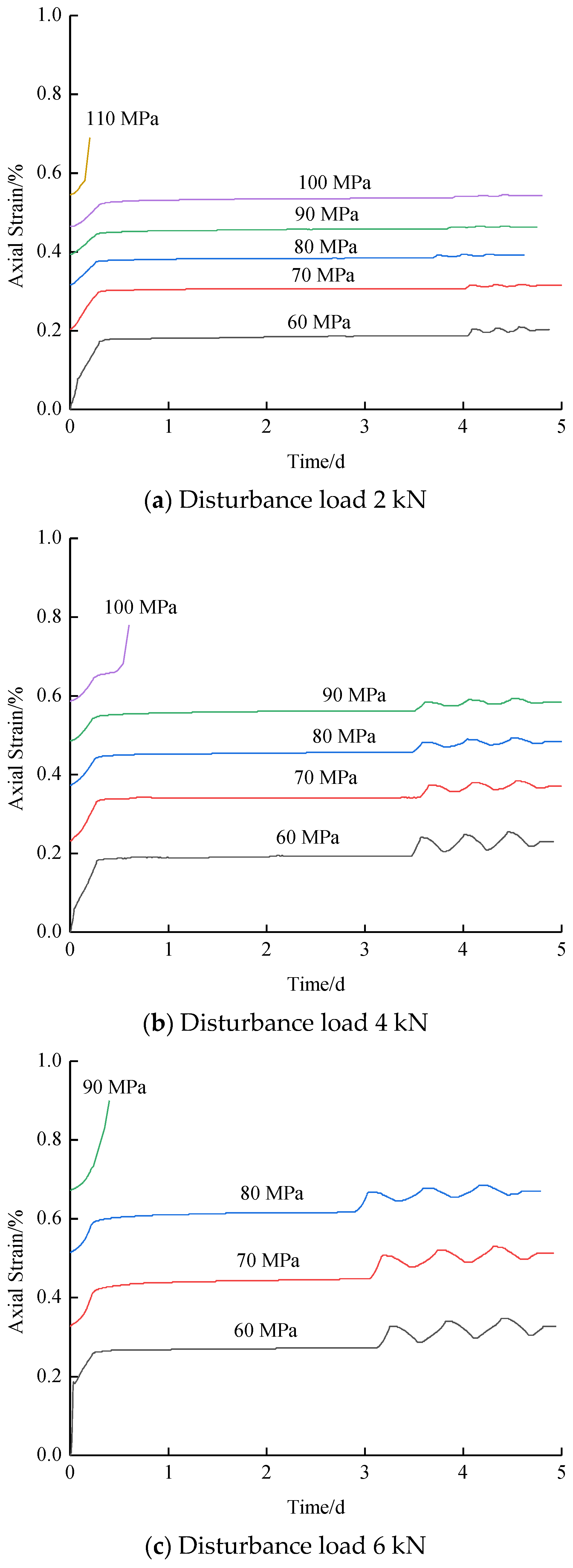
2.3. Test Results
- (1)
- Decay creep stage: This stage is consistent with the attenuation stage in the conventional creep test, which shows that with increasing time, the rock displacement increases gradually, but the creep deformation rate decreases gradually until it reaches 0. The reason is that with the pressure, the density of the interior pores of the specimen changes, and the ability of the specimen to resist deformation gradually increases, which leads to the gradual improvement in the deformation of the specimen, but the deformation rate decreases.
- (2)
- Stable creep stage: The deformation of the specimen is basically consistent with the conventional creep curve, but the difference is that unstable creep deformation occurs at a low stress level due to the addition of the disturbance load. This indicates that an increase in disturbance load can change or even affect the mechanical properties and failure mechanism of the specimen. The reason is that the disturbance load causes some interlaminar dislocation in the stable specimen, which advances the crack initiation and crack propagation time, and creep increment appears at a low stress level.
- (3)
- Creep stage of disturbance: The curve of this stage shows a reversed “V” change; that is, with an increase in disturbance load, it shows a trend of first increasing and then decreasing. At a low stress level, the creep deformation is obvious; that is, the creep increment before and after disturbance is large, but when the stress level increases, the creep increment of disturbance is smaller. At a low stress level, there are many pores in the specimen, and the application of an appropriate disturbance load can cause the specimen to deform greatly. When the specimen is at a high stress level, the proportion of the disturbance load is small, and the influence on the creep deformation of rock is limited. Moreover, when the specimen is subjected to a periodic disturbance load, the specimen has some irreparable deformation compared with the overall deformation, which also indicates that the fracture of the pores inside the specimen is irreversible permanent deformation.
- (4)
- Accelerated creep stage: The deformation characteristics of this stage are basically consistent with conventional creep. Due to the application of the disturbance load in the early stage, the load is stored in the form of elastic energy inside the specimen. When the specimen is at a high stress level, the crack inside the specimen expands rapidly due to the application of elastic energy, which leads to deformation and failure of the specimen. The deformation velocity and degree are higher than those of the conventional creep curve.
3. Analysis of Creep Disturbance Tests
3.1. Disturbance Load Characteristics
3.2. Analysis of Mechanical Properties
- (1)
- When the disturbance load increased from 2 kN to 4 kN and then to 6 kN, the increments were 11.4% and 15.4%, respectively, which indicates that the disturbance load has a certain enhancing effect on the peak strain of rock. The reason is that the increase in disturbance load gradually compacts the pores and cracks in the specimen, so the creep deformation of the specimen increases.
- (2)
- The long-term strength of rock is the strength value of rock resisting failure under long-term load, which produces a creep effect under long-term load, so the creep strength is regarded as the long-term strength of rock. The long-term strength of rock is greatly affected by its structure and internal defects, as well as by the complicated genesis.
- (3)
- When the disturbance load increased from 2 kN to 4 kN, the decrease proportion was 15%, and when the disturbance load increased from 4 kN to 6 kN, the decrease proportion was 27.6%. The reason is that the increase in disturbance load shortens the compaction time of pores and cracks, and the failure time of the specimen decreases gradually.
- (4)
- The elastic modulus of a rock is one of the physical and mechanical properties of the rock and represents the relationship between rock stress and strain. The change in elastic modulus indicates that the disturbance load has a certain impact on the deformation characteristics of the rock and then affects the physical and mechanical properties of the rock.
4. Creep Disturbance Constitutive Model
4.1. Disturbance Damage Function
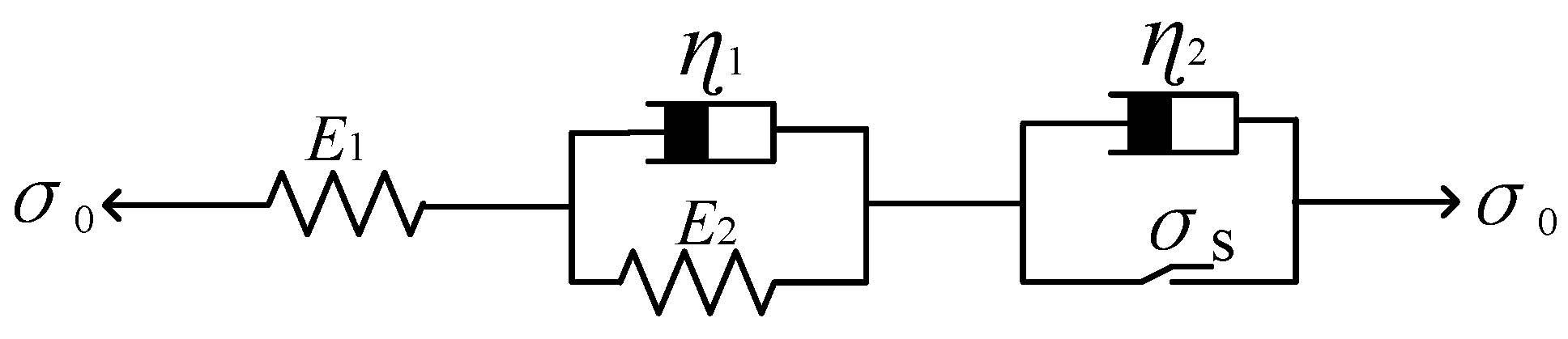
4.2. Establishment of One-Dimensional Creep Model
- (1)
- The creep equation of the elastic element is as follows [20]:
- (2)
- The creep equation of the elastic viscous element is as follows:
- (3)
- The creep equation of the viscoplastic element is as follows:
4.3. Establishment of Triaxial Creep Model
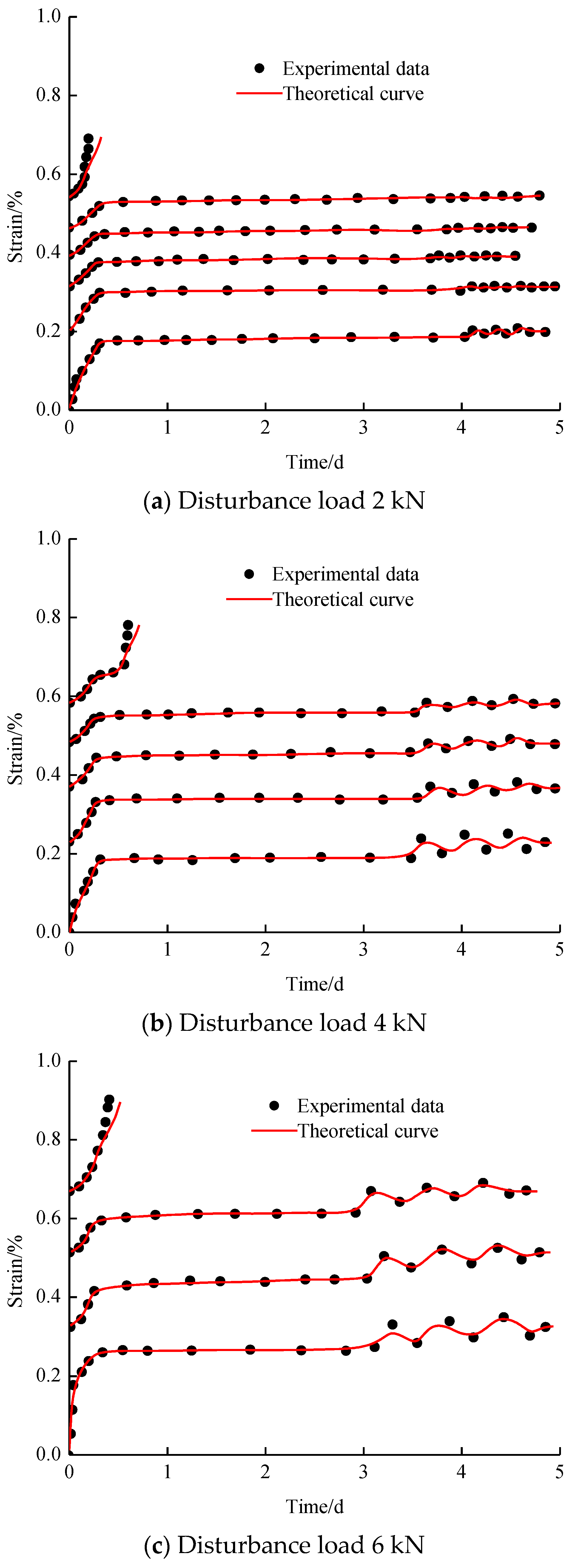
4.4. Parameter Identification and Verification of the Creep Model
5. Conclusions
- (1)
- Compared with the conventional triaxial creep curve, the triaxial creep curves of sandstone under disturbance load are divided into decay creep, steady creep, disturbance creep, and accelerated creep stages, and the increment of disturbance creep varies with different disturbance loads.
- (2)
- With increasing disturbance load, the long-term strength, failure time, and elastic modulus of sandstone show linear decreases, while the peak strain increases.
- (3)
- An acceleration element is introduced into the Nishihara model, and the influence of disturbance load is considered. A constitutive model describing the whole deformation of sandstone under creep disturbance load is established. The accuracy of the model is verified by the test data, which provides a theoretical basis for the stability analysis of rock masses.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Grgic, D. Constitutive modelling of the elastic–plastic, viscoplastic and damage behaviour of hard porous rocks within the unified theory of inelastic flow. Acta Geotech. 2014, 11, 95–126. [Google Scholar] [CrossRef]
- Mishra, V.; Singh, K.N. Microstructural relation of macerals with mineral matter in coals from Ib valley and Umaria, Son-Mahanadi basin, India. Int. J. Coal Sci. Technol. 2017, 4, 191–197. [Google Scholar] [CrossRef] [Green Version]
- Kwon, T.H.; Hong, E.S.; Cho, G.C. Shear behavior of rectangular-shaped asperities in rock joints. KSCE J. Civ. Eng. 2010, 14, 323–332. [Google Scholar] [CrossRef]
- Li, S.; Wang, G.; Wang, S.; Yang, W.; Wang, X. Application of fracture-damage model to anchorage of discontinuous jointed rockmass of excavation and supporting. Yanshilixue Yu Gongcheng Xuebao/Chin. J. Rock Mech. Eng. 2006, 25, 1582–1590. [Google Scholar]
- Ming, Z.G.; Song, X.W.; Rui, M.X.; Yan, L.C. Instability mechanism of high stress rock mass under excavation and unloading induced by disturbance. J. China Coal Soc. 2010, 45, 936–948. [Google Scholar]
- Zhao, T.B.; Tan, Y.L.; Liu, S.S.; Xiao, Y.X. Analysis of rheological properties and control mechanism of anchored rock. Rock Soil Mech. 2012, 33, 1730–1734. [Google Scholar]
- Jiang, P.; Pan, P.Z.; Kun, Z.S. A coupled elasto-viscoplastic damage model based on strain energy theory of rock and application. J. China Coal Soc. 2019, 43, 2967–2979. [Google Scholar]
- Liu, Q.S.; Luo, C.Y.; Peng, X.X.; Liu, H.; Chen, L.; Pan, Y.C. Research on field rheological test and nonlinear fractional derivative creep model of weak rock mass. J. China Coal Soc. 2020, 45, 1348–1356. [Google Scholar]
- Fahimifar, A.; Karami, M. Modifications to an elasto-visco-plastic constitutive model for prediction of creep deformation of rock samples. Soils Found. 2015, 55, 1364–1371. [Google Scholar] [CrossRef] [Green Version]
- Wang, J.G.; Liang, B.; Yang, P.J. Creep experiment and nonlinear disturbance creep model of gneiss under dynamic and static loads. J. China Coal Soc. 2019, 44, 199–205. [Google Scholar]
- Jia, Z.E.; Zhang, J. Damage constitutive model of mudstone creep based on the theory of fractional calculus. Adv. Pet. Explor. Dev. 2015, 10, 83–87. [Google Scholar]
- Khaledi, K.; Mahmoudi, E.; Datcheva, M.; Schanz, T. Stability and serviceability of underground energy storage caverns in rock salt subjected to mechanical cyclic loading. Int. J. Rock Mech. Min. Sci. 2016, 86, 115–131. [Google Scholar] [CrossRef]
- Cao, P.; Wen, Y.; Wang, Y.; Yuan, H.; Yuan, B. Study on nonlinear damage creep constitutive model for high-stress soft rock. Environ. Earth Sci. 2016, 75, 900. [Google Scholar] [CrossRef]
- Xi, D.Y.; Qiu, W.L. Relationship between attenuation of saturated porous rock and porosity and saturation. Oil Geop. Prospect. 1997, 32, 196–201. [Google Scholar]
- Prodan, M.V.; Mileusnić, M.; Arbanas, S.M.; Arbanas, Ž. Influence of weathering processes on the shear strength of siltstones from a flysch rock mass along the northern Adriatic coast of Croatia. Bull. Eng. Geol. Environ. 2016, 76, 695–711. [Google Scholar] [CrossRef]
- Valiulin, S.V.; Onischuk, A.A.; Baklanov, A.M.; Bazhina, A.A.; Paleev, D.Y.; Zamashchikov, V.V.; Korzhavin, A.; Dubtsov, S.N. Effect of coal mine organic aerosol on the methane/air lower explosive limit. Int. J. Coal Sci. Technol. 2020, 7, 778–786. [Google Scholar] [CrossRef] [Green Version]
- Nyoni, B.; Duma, S.; Bolo, L.; Shabangu, S.; Hlangothi, S.P. Co-pyrolysis of South African bituminous coal and Scenedesmus microalgae: Kinetics and synergistic effects study. Int. J. Coal Sci. Technol. 2020, 7, 807–815. [Google Scholar] [CrossRef] [Green Version]
- Hood, M.M.; Eble, C.F.; Hower, J.C.; Dai, S. Geochemistry, petrology, and palynology of the Princess No. 3 coal, Greenup County, Kentucky. Int. J. Coal Sci. Technol. 2020, 7, 633–651. [Google Scholar] [CrossRef] [Green Version]
- Tang, L.; Chen, H.; Sang, H.; Zhang, S.; Zhang, J. Determination of traffic-load-influenced depths in clayey subsoil based on the shakedown concept. Soil Dyn. Earthq. Eng. 2015, 77, 182–191. [Google Scholar] [CrossRef]
- Ajamzadeh, M.; Sarfarazi, V.; Dehghani, H. Evaluation of plow system performance in long-wall mining method using particle flow code. Int. J. Coal Sci. Technol. 2019, 6, 518–535. [Google Scholar] [CrossRef] [Green Version]
- Yang, S.Q.; Xu, W.Y.; Yang, S.L. Investigation on shear rheological mechanical properties of shale in Longtan Hydropower Project. Yantu Lixue 2007, 28, 895–902. [Google Scholar]




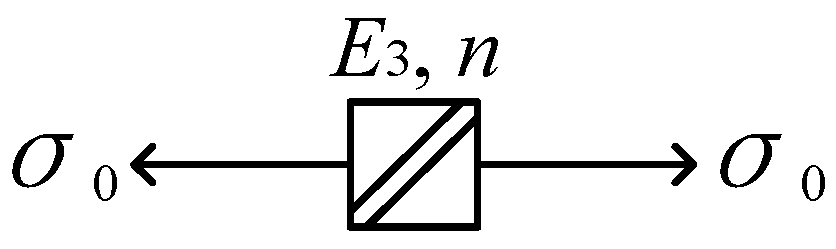

| Dry Density Mg/m3 | Porosity/% | Natural Moisture Content/% | Water Absorption/% | Compressive Strength/MPa | Elastic Modulus/GPa |
|---|---|---|---|---|---|
| 2.51 | 3.1 | 0.84 | 1.4 | 109.56 | 43.5 |
| Disturbance Load/kN | 60/MPa | 70/MPa | 80/MPa | 90/MPa | 100/MPa |
|---|---|---|---|---|---|
| 2 | 0.021 | 0.019 | 0.017 | 0.016 | 0.015 |
| 4 | 0.036 | 0.027 | 0.025 | 0.023 | / |
| 6 | 0.055 | 0.045 | 0.0325 | / | / |
| Disturbance Load/kN | Peak Strain/% | Long-Term Strength/MPa | Destruction Time/d | Elastic Modulus/GPa |
|---|---|---|---|---|
| 2 | 0.7 | 100 | 24.19 | 26.13 |
| 4 | 0.78 | 90 | 20.57 | 33.49 |
| 6 | 0.9 | 80 | 14.90 | 22.76 |
| Parameter | a | b | c | Fitting Parameters |
|---|---|---|---|---|
| First level | 0.011 | 0.462 | −0.066 | 1 |
| Second level | 0.108 | 0.304 | −0.042 | 1 |
| Third level | 0.205 | 0.272 | −0.037 | 1 |
| Fourth level | 0.246 | 0.266 | −0.036 | 1 |
| σ1/MPa | G1/GPa | G2/GPa | K/GPa | η1/GPa·h | η2/GPa·h | G3/GPa | Q | n | R2 |
|---|---|---|---|---|---|---|---|---|---|
| 60 | 1.44 | 47.18 | 3.41 | 0.46 | 2.56 | - | - | - | 0.978 |
| 70 | 2.94 | 73.22 | 4.23 | 0.79 | 3.09 | - | - | - | 0.984 |
| 80 | 3.01 | 60.12 | 5.12 | 0.84 | 3.16 | - | - | - | 0.962 |
| 90 | 4.59 | 46.33 | 6.11 | 0.78 | 2.04 | 2.44 | 1.27 | 1.53 | 0.945 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, X.; Yin, Z. Study of Creep Mechanical Properties and a Rheological Model of Sandstone under Disturbance Loads. Processes 2021, 9, 1291. https://doi.org/10.3390/pr9081291
Li X, Yin Z. Study of Creep Mechanical Properties and a Rheological Model of Sandstone under Disturbance Loads. Processes. 2021; 9(8):1291. https://doi.org/10.3390/pr9081291
Chicago/Turabian StyleLi, Xiaofeng, and Zhixiang Yin. 2021. "Study of Creep Mechanical Properties and a Rheological Model of Sandstone under Disturbance Loads" Processes 9, no. 8: 1291. https://doi.org/10.3390/pr9081291
APA StyleLi, X., & Yin, Z. (2021). Study of Creep Mechanical Properties and a Rheological Model of Sandstone under Disturbance Loads. Processes, 9(8), 1291. https://doi.org/10.3390/pr9081291





