Novel Hopfield Neural Network Model with Election Algorithm for Random 3 Satisfiability
Abstract
:1. Introduction
- (i)
- To formulate a random logical rule that consist of first, second and third-order logical rule namely Random 3 Satisfiability in Hopfield Neural Network.
- (ii)
- To construct a functional Election Algorithm that learns all the logical combination of Random 3 Satisfiability during the learning phase of Hopfield Neural Network.
- (iii)
- To conduct a comprehensive analysis of the Random 3 Satisfiability incorporated with Election Algorithm for both learning and retrieval phase.
2. Random 3 Satisfiability Representation
3. RAN3SAT Representation in Hopfield Neural Network
- (i)
- The variables in are irredundant and if there is such that . Hence all the clauses are independent to each other.
- (ii)
- The no self-connection among all neurons in where and the symmetric property of HNN leads to and is equivalent to all permutation order of such as etc.
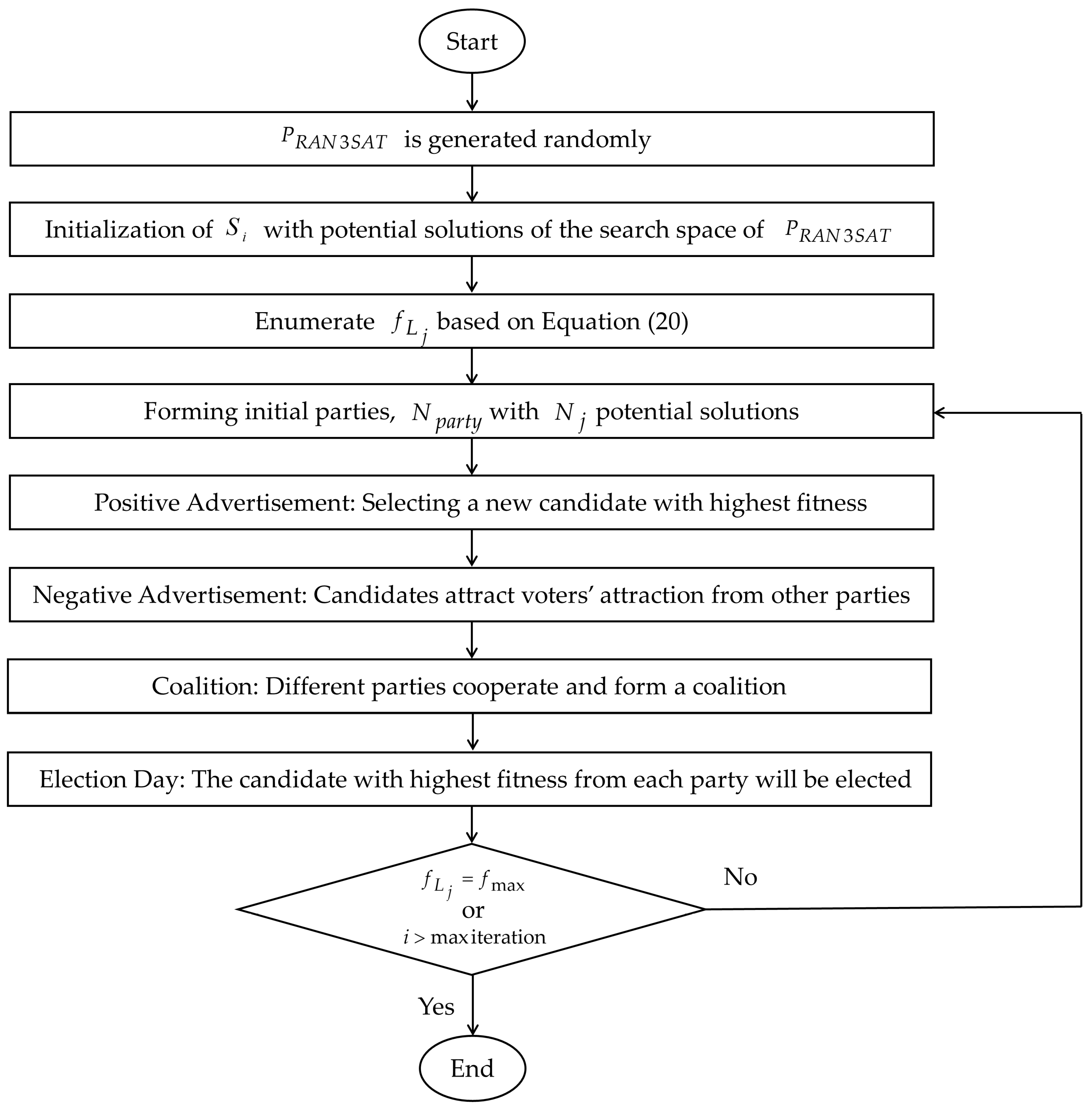
4. Election Algorithm
- 1.
- Stage 1: Initialize Population
- 2.
- Stage 2: Forming Initial Parties
- 3.
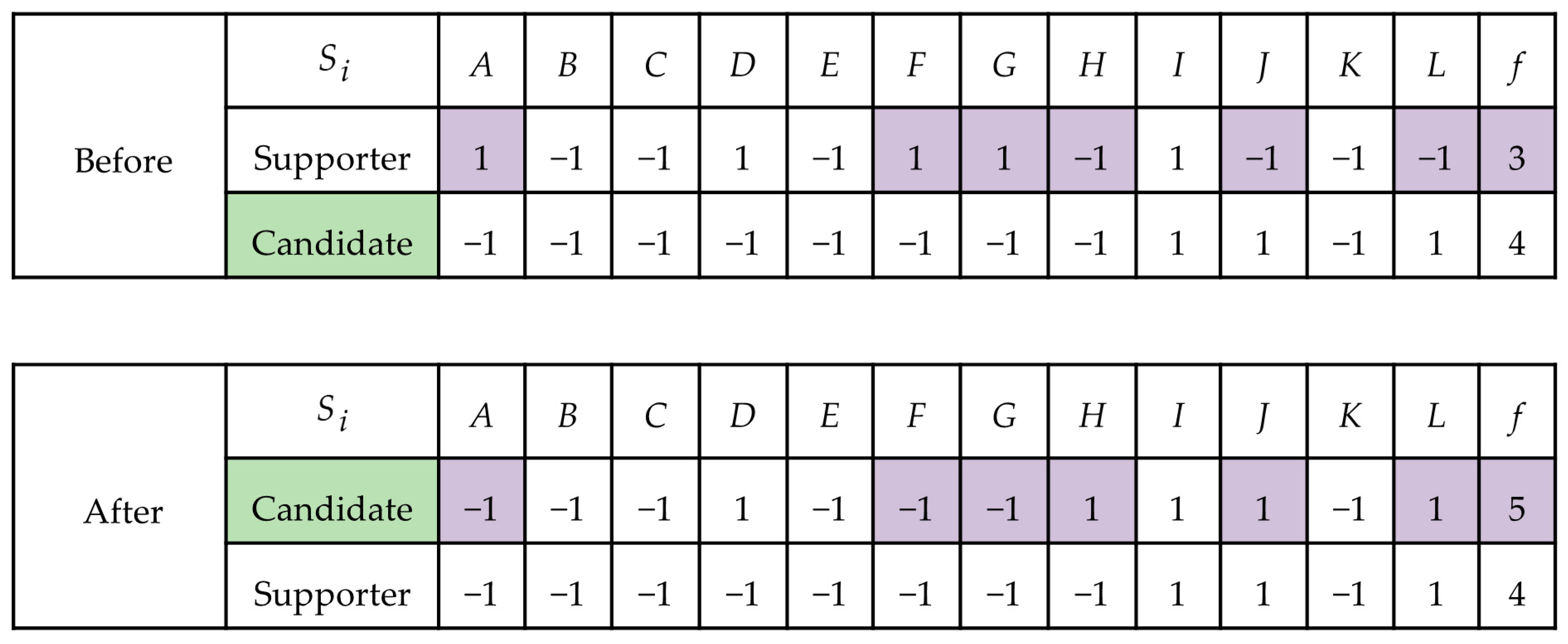
- Stage 3: Advertisement Campaign
- 4.
- Stage 4: The Election Day
| Algorithm 1: Pseudo Code of the Proposed HNN-RAN3SATEA | |
| 1 | Generate initial population |
| 2 | while or |
| 3 | Forming Initial Parties by using Equation (22) |
| 4 | fordo |
| 5 | Calculate the similarity between the voter and the candidate utilizing Equation (23) |
| 6 | end |
| 7 | {Positive Advertisement} |
| 8 | Evaluate the number of voters by using Equation (24) |
| 9 | fordo |
| 10 | Evaluate the reasonable effect from the candidate by using Equation (26) |
| 11 | Update the neuron state according to Equation (25) |
| 12 | if |
| 13 | Assign as a new |
| 14 | Else |
| 15 | Remain |
| 16 | End |
| 17 | {Negative advertisement} |
| 18 | Evaluate the number of voters |
| 19 | fordo |
| 20 | Evaluate the reasonable effect from the candidate by using Equation (29) |
| 21 | Update the neuron state according to Equation (30) |
| 22 | if |
| 23 | Assign as a new |
| 24 | Else |
| 25 | Remain |
| 26 | End |
| 27 | {Coalition} |
| 28 | fordo |
| 29 | Evaluate the reasonable effect from the candidate , by using Equation (29) |
| 30 | Update the neuron state according to Equation (30) |
| 31 | if |
| 32 | Assign as a new |
| 33 | Else |
| 34 | Remain |
| 35 | End |
| 36 | end while |
| 37 | return output the final neuron state |
5. Exhaustive Search (ES)
- 1.
- Step 1: Initialization.
- 2.
- Step 2: Fitness Evaluation.
- 3.
- Step 3: Test the solutions.
6. Summary of Learning and Retrieval Phase of HNN-RAN3SAT
6.1. Learning Phase in HNN-RAN3SAT
- 1.
- Step 1: Convert into CNF type of Boolean Algebra.
- 2.
- Step 2: Assign neuron for each variable in .
- 3.
- Step 3: Initialize the synaptic weights and the neuron state of HNN-RAN3SAT.
- 4.
- Step 4: Define the inconsistency of the logic by taking the negation of .
- 5.
- Step 5: Derive the using Equation (6) that is associated with the defined inconsistencies in Step 4.
- 6.
- Step 6: Obtain the neuron assignments that leads to (using EA and ES), .
- 7.
- Step 7: Map the neuron assignment associated with the optimal synaptic weight. Precalculated synaptic weight can be obtained by comparing with the Final Energy function in Equation (15).
- 8.
- Step 8: Store synaptic weights as a Control Addressable Memory (CAM).
- 9.
- Step 9: Calculate the value of by using Equation (17).
6.2. Retrieval Phase in HNN-RAN3SAT
- 1.
- Step 1: Calculate the local field of each neuron in HNN-RAN3SAT model using Equation (8).
- 2.
- Step 2: Compute the neurons state value by using HTAF [40] and classify the final neuron state based on Equation (9).
- 3.
- Step 3: Calculate the final energy of the HNN-RAN3SAT model using Equation (15).
- 4.
- Step 4: Verify whether the final energy obtained satisfy the condition in Equation (18). If the difference in energy is within the tolerance value, we consider the final neuron state as global minimum solution.
7. Experimental Setup
8. Performance Metric for HNN-RAN3SAT Models
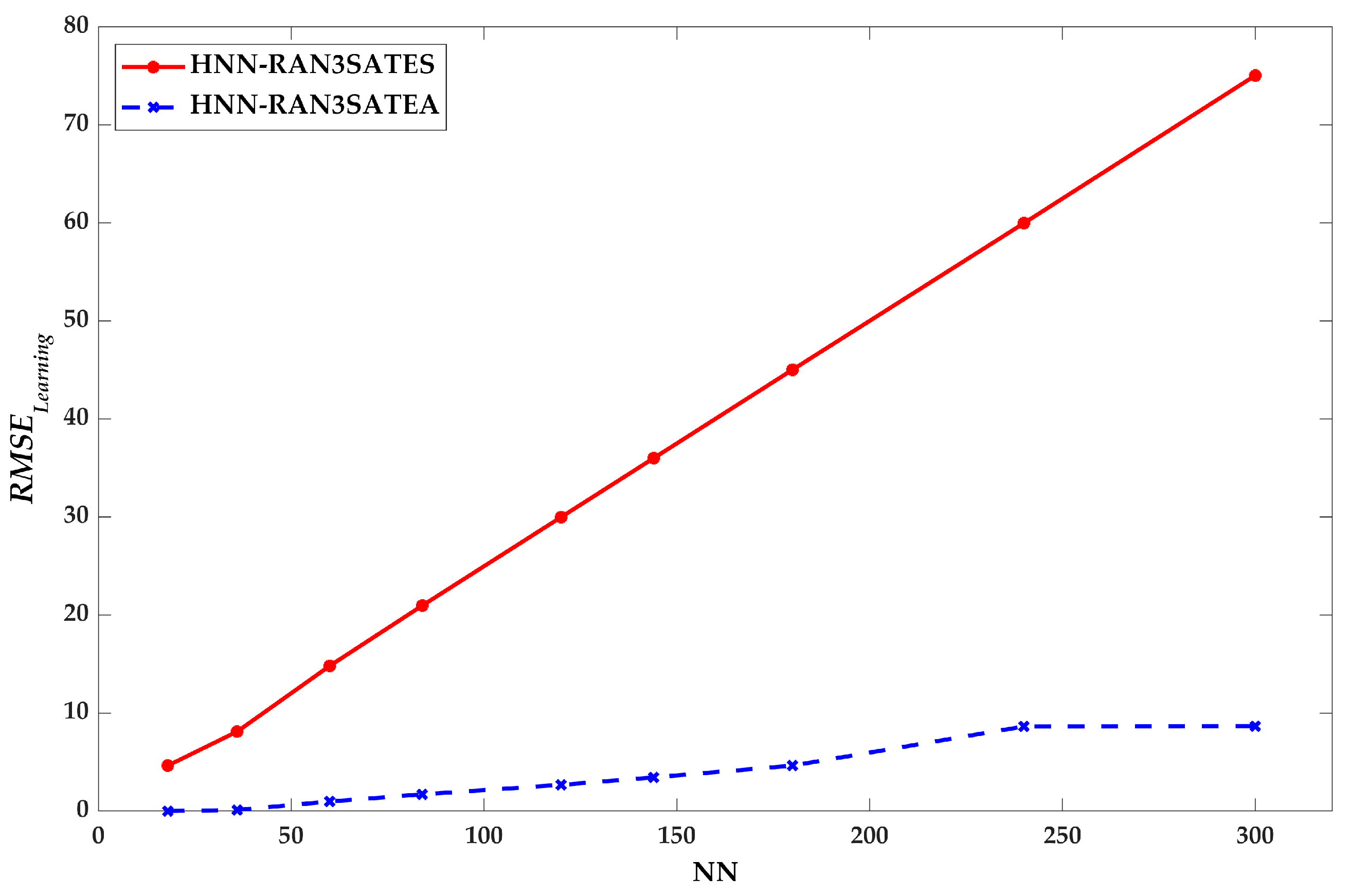
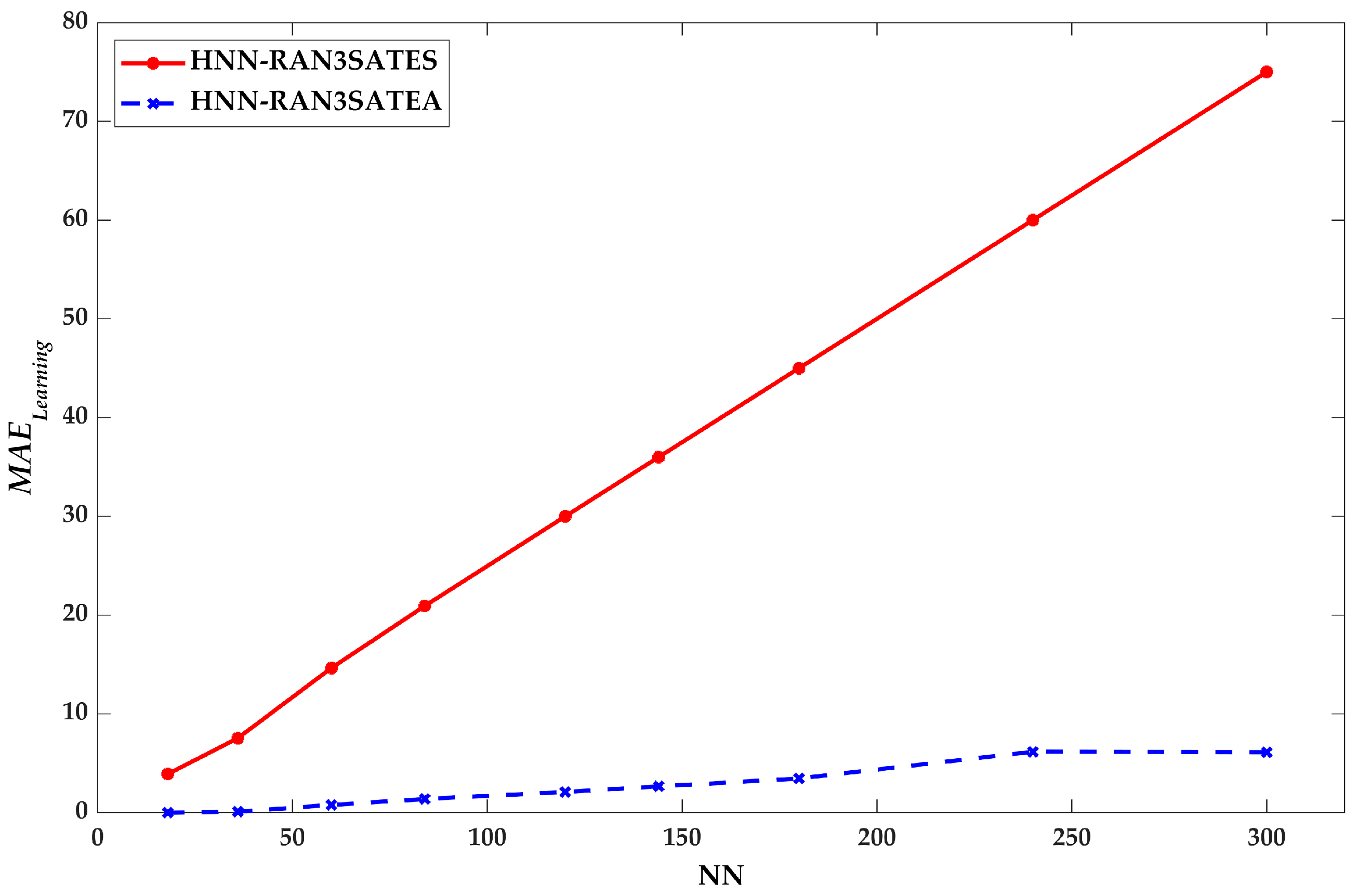
8.1. Root Mean Square Error (RMSE), Mean Absolute Error (MAE), and Mean Absolute Percentage Error (MAPE)
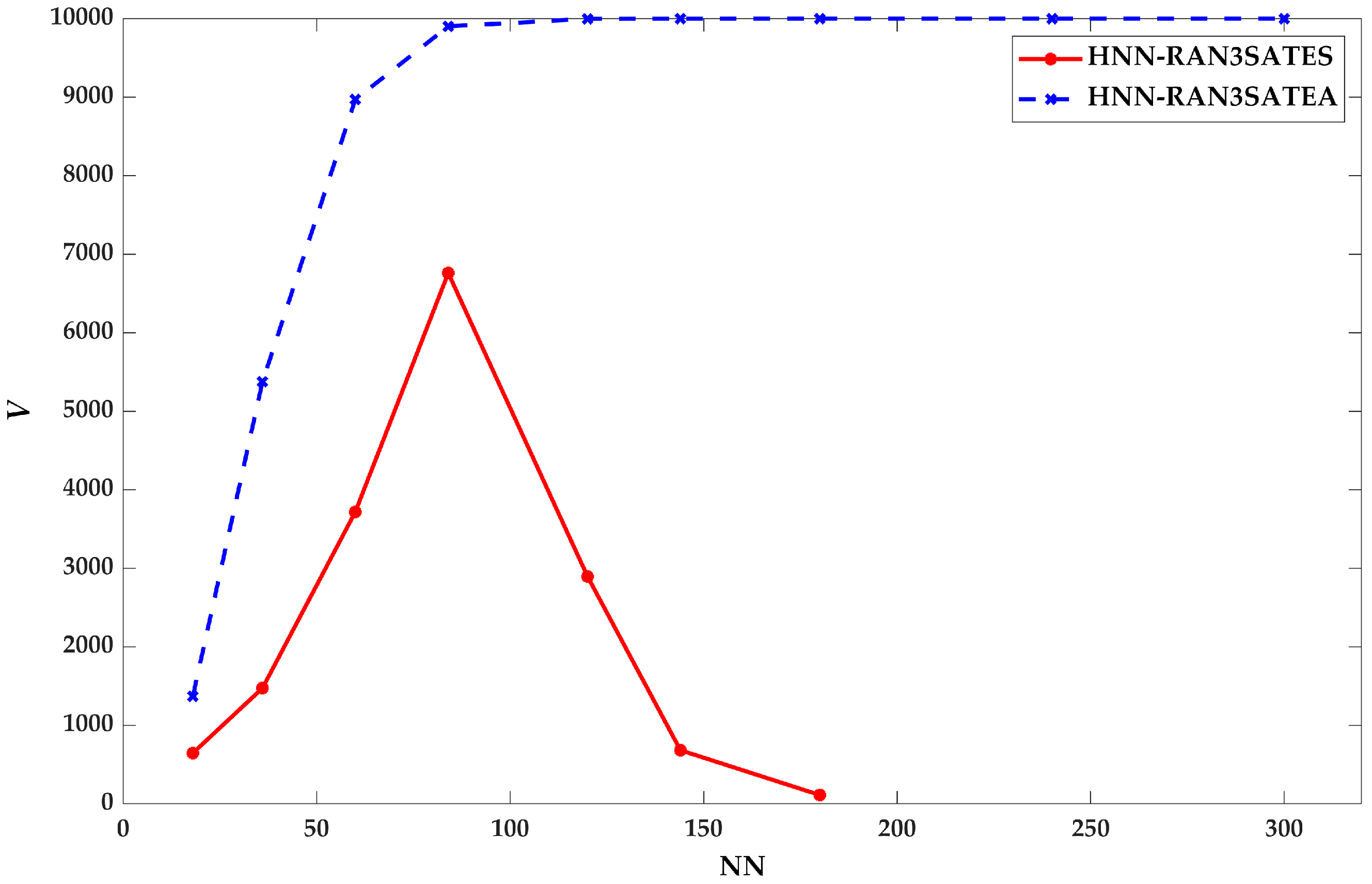
8.2. Global Minima Ratio
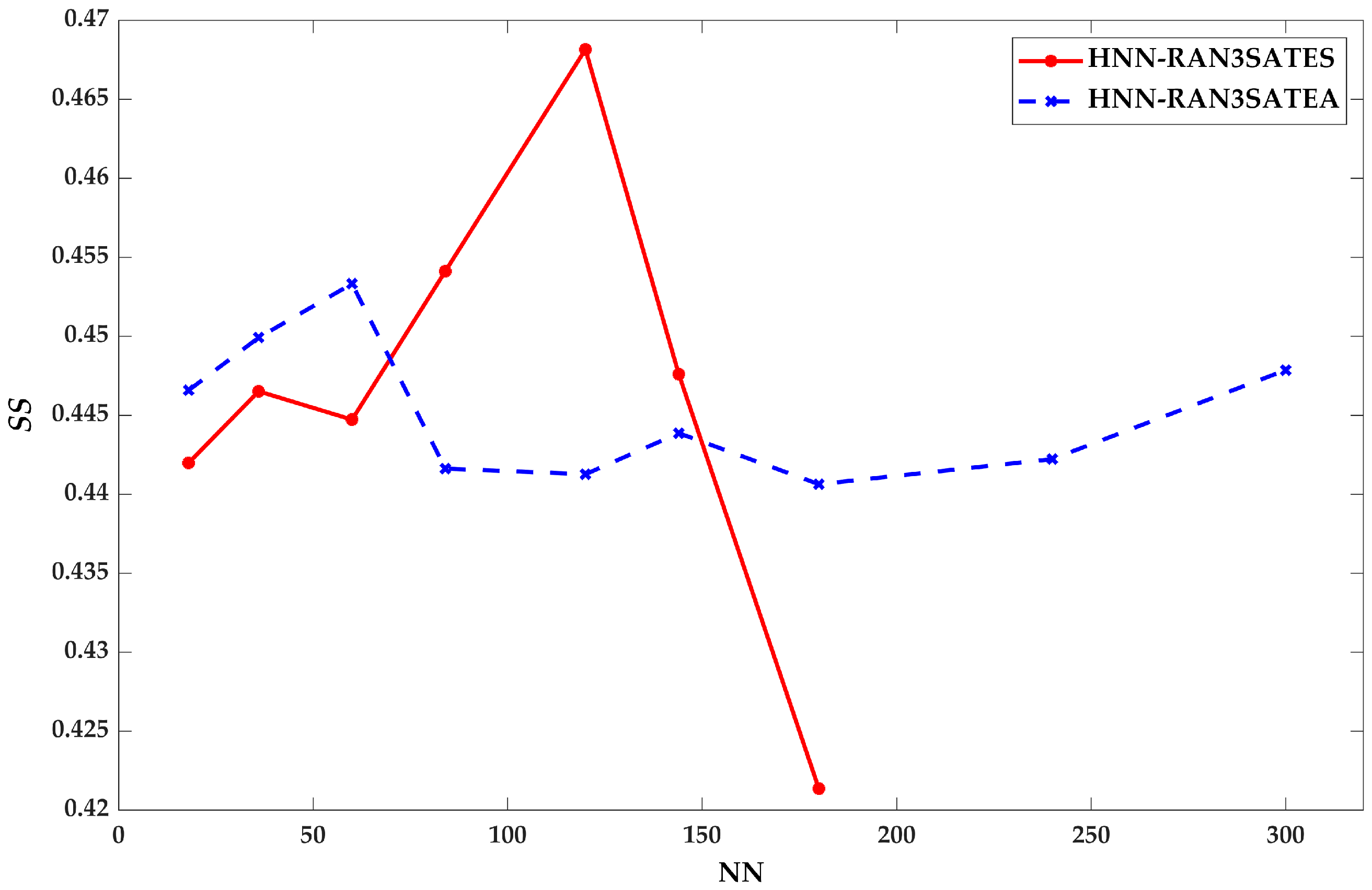
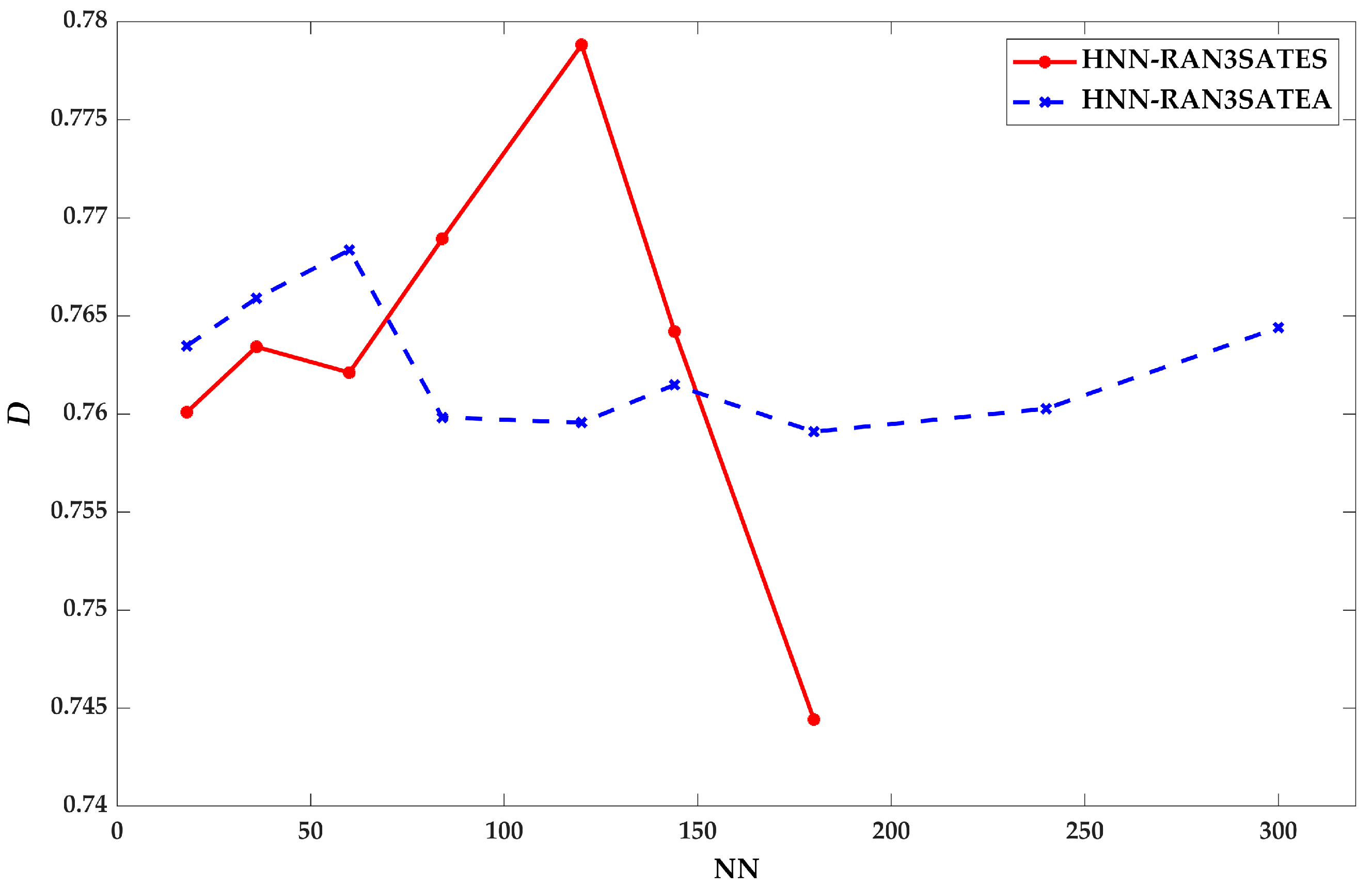
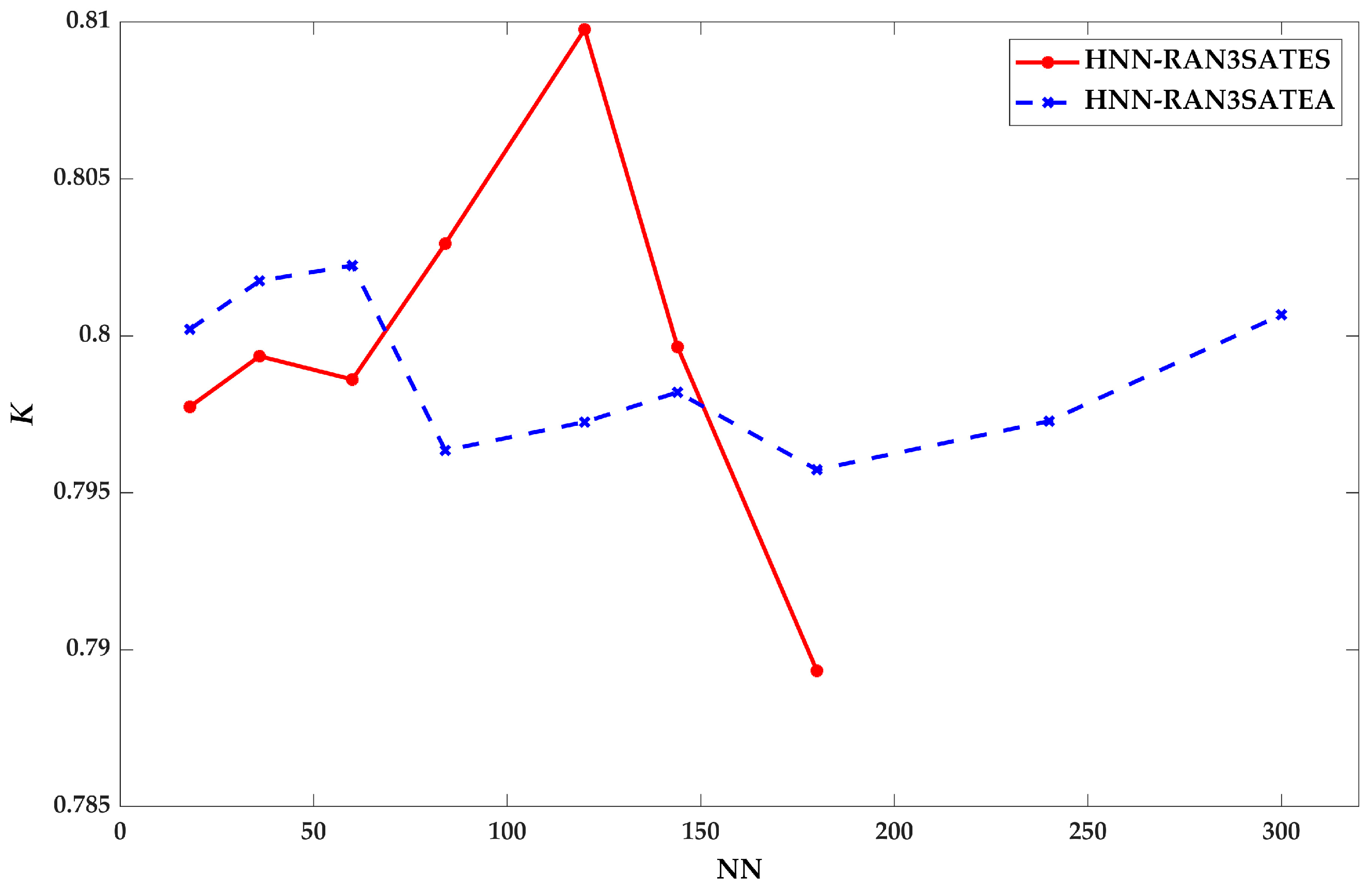
8.3. Similarity Index
9. Result and Discussion
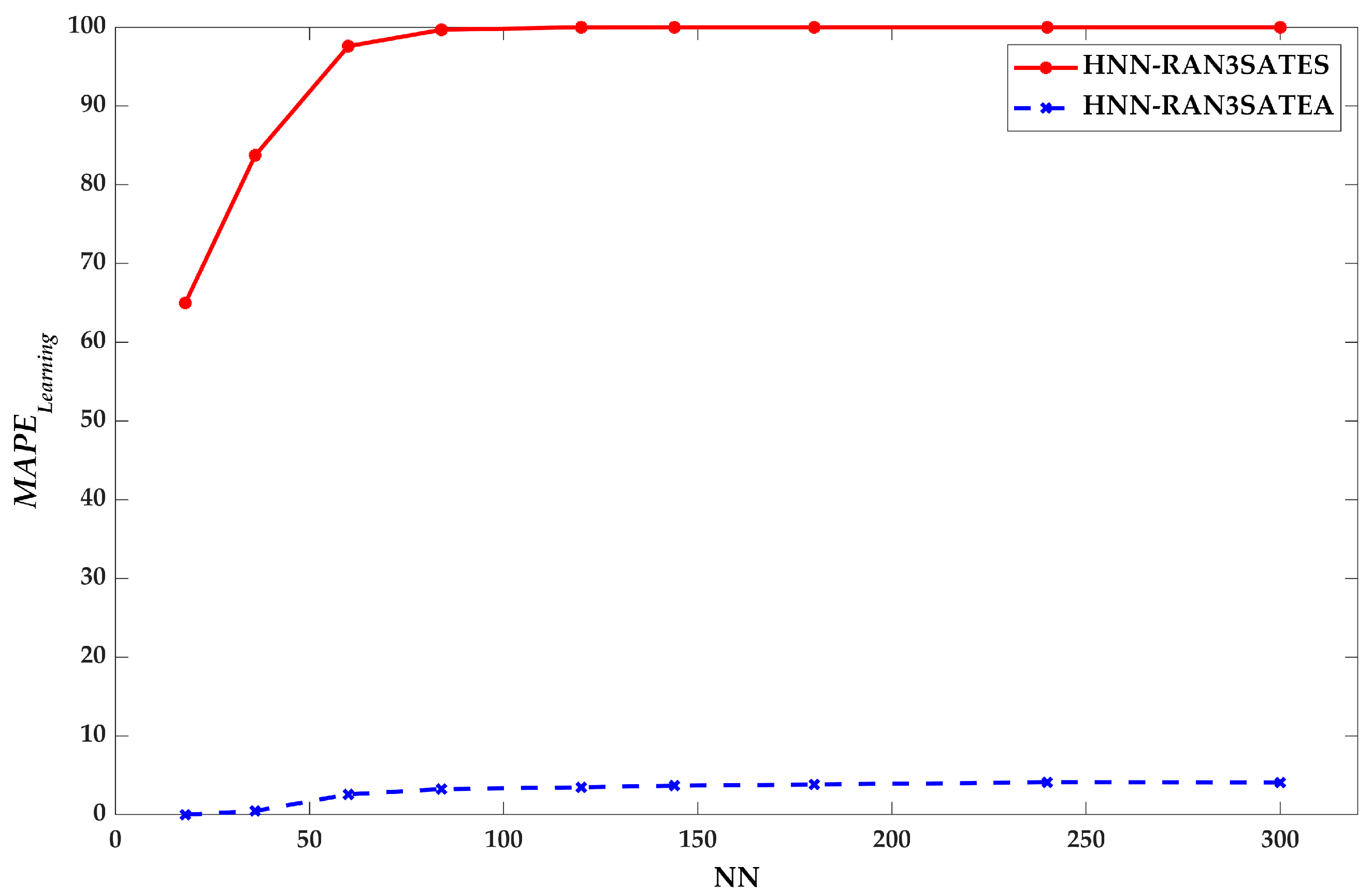
9.1. Learning Phase Performance
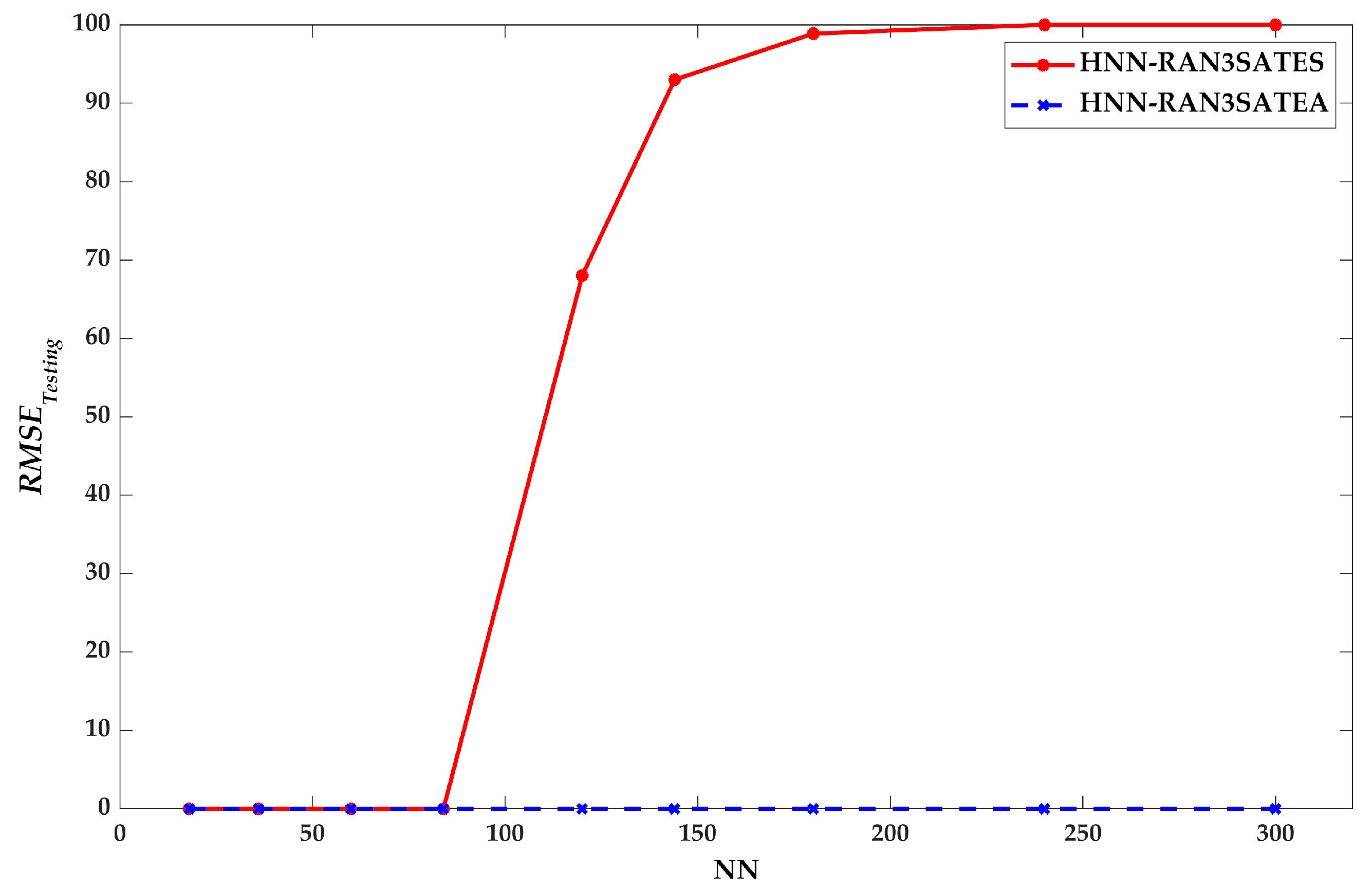
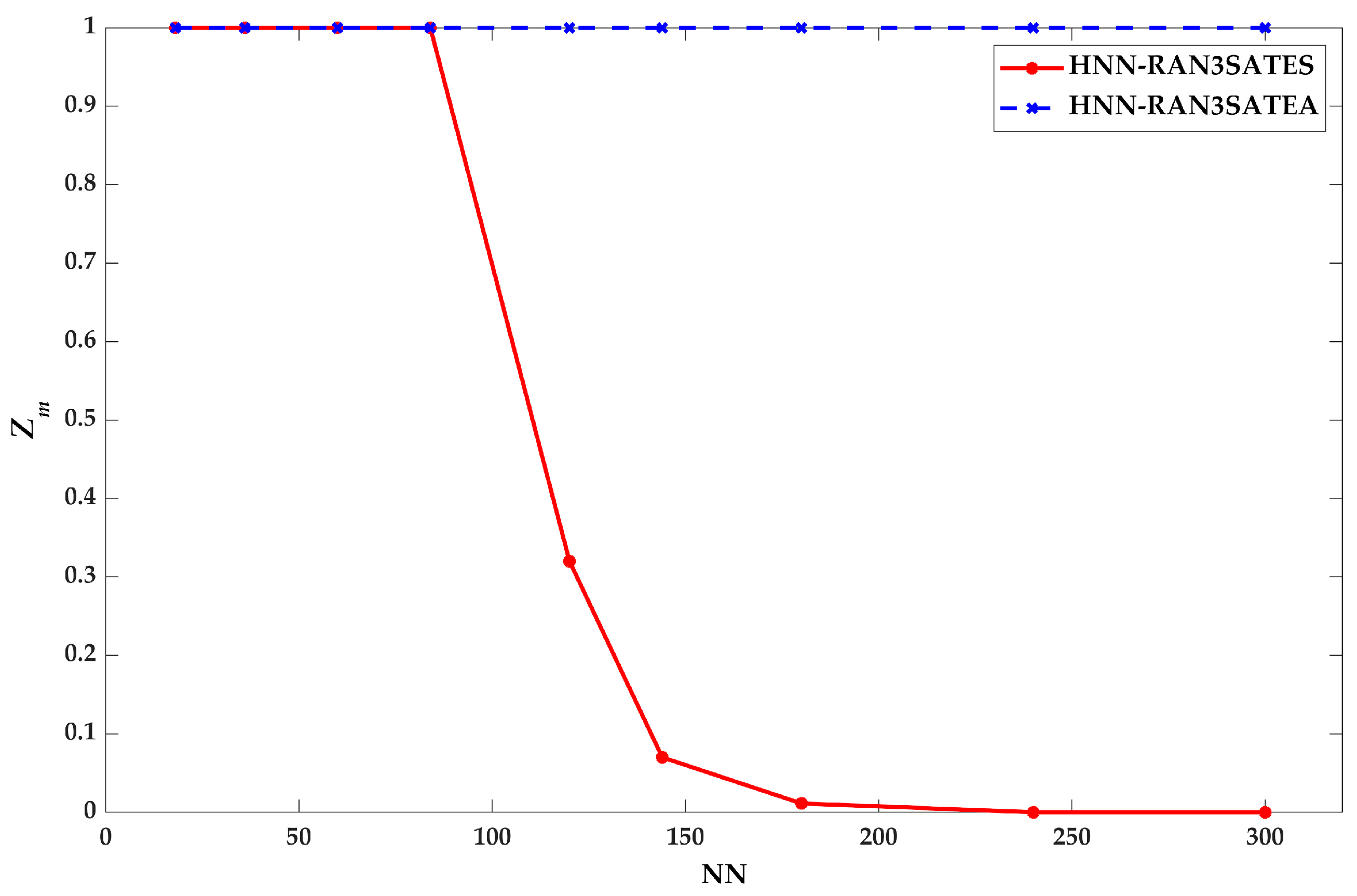
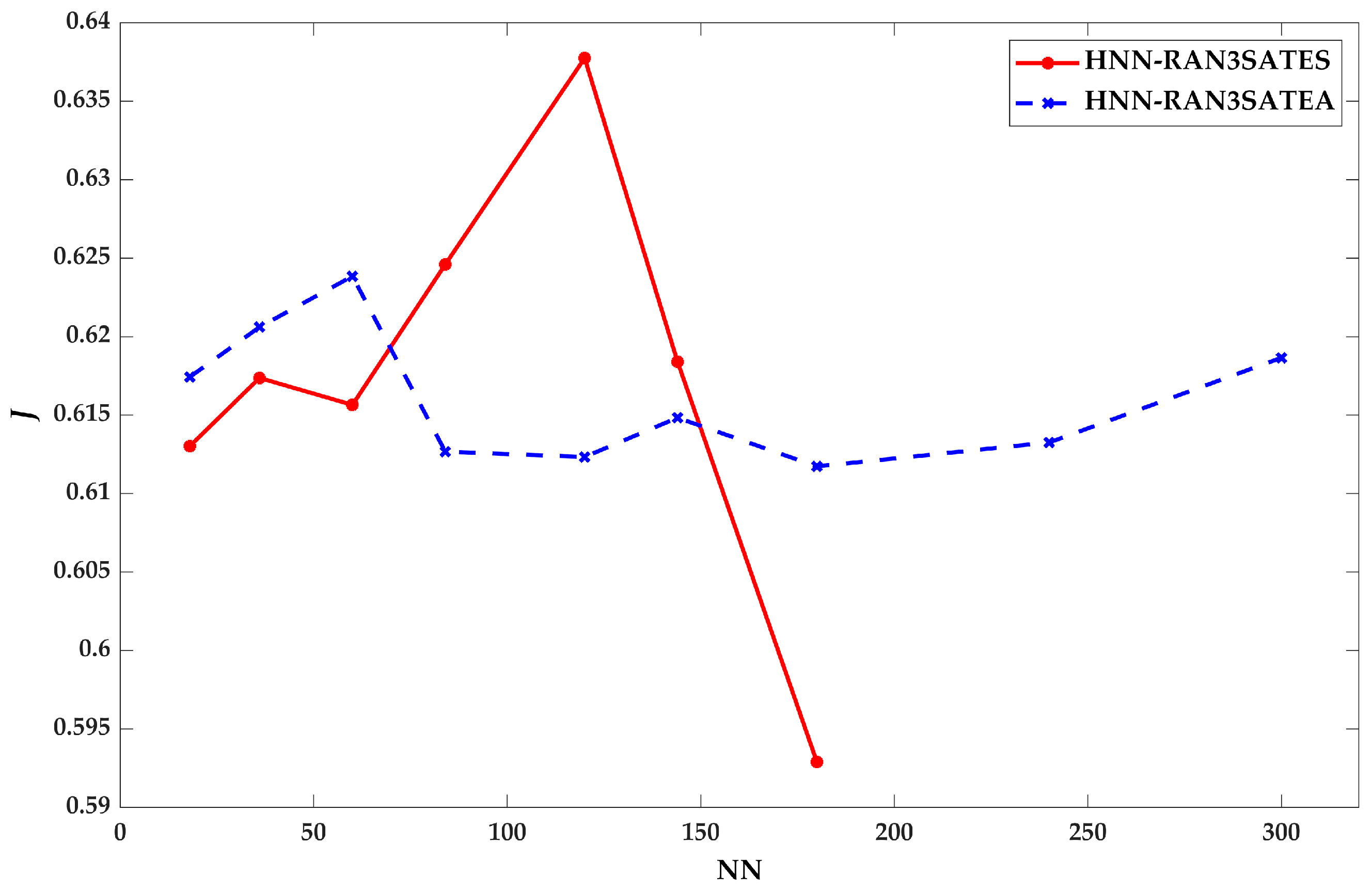
9.2. Retrieval Phase Performance
10. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hopfield, J.J.; Tank, D.W. “Neural” computation of decisions in optimization problems. Biol. Cyber. 1985, 52, 141–152. [Google Scholar]
- Hemanth, D.J.; Anitha, J.; Mittal, M. Diabetic retinopathy diagnosis from retinal images using modified Hopfield neural network. J. Med. Syst. 2018, 42, 1–6. [Google Scholar] [CrossRef]
- Channa, A.; Ifrim, R.C.; Popescu, D.; Popescu, N. A-WEAR Bracelet for detection of hand tremor and bradykinesia in parkinson’s patients. Sensors 2021, 21, 981. [Google Scholar] [CrossRef]
- Channa, A.; Popescu, N.; Ciobanu, V. Wearable solutions for patients with parkinson’s disease and neurocognitive disorder: A systematic review. Sensors 2020, 20, 2713. [Google Scholar] [CrossRef]
- Veerasamy, V.; Wahab, N.I.A.; Ramachandran, R.; Madasamy, B.; Mansoor, M.; Othman, M.L.; Hizam, H. A novel rk4-Hopfield neural network for power flow analysis of power system. Appl. Soft Comput. 2020, 93, 106346. [Google Scholar] [CrossRef]
- Chen, H.; Lian, Q. Poverty/investment slow distribution effect analysis based on Hopfield neural network. Future Gener. Comput. Syst. 2021, 122, 63–68. [Google Scholar] [CrossRef]
- Cook, S.A. The Complexity of Theorem-Proving Procedures. In Proceedings of the Third Annual ACM Symposium on Theory of Computing, New York, NY, USA, 3 May 1971; Association for Computing Machinery: New York, NY, USA, 1971; pp. 151–158. [Google Scholar]
- Fu, H.; Xu, Y.; Wu, G.; Liu, J.; Chen, S.; He, X. Emphasis on the flipping variable: Towards effective local search for hard random satisfiability. Inf. Sci. 2021, 566, 118–139. [Google Scholar] [CrossRef]
- Lagerkvist, V.; Roy, B. Complexity of inverse constraint problems and a dichotomy for the inverse satisfiability problem. J. Comput. Syst. Sci. 2021, 117, 23–39. [Google Scholar] [CrossRef]
- Luo, J.; Hu, M.; Qin, K. Three-way decision with incomplete information based on similarity and satisfiability. Int. J. Approx. Reason. 2020, 120, 151–183. [Google Scholar] [CrossRef]
- Hitzler, P.; Hölldobler, S.; Seda, A.K. Logic programs and connectionist networks. J. Appl. Log. 2004, 2, 245–272. [Google Scholar] [CrossRef] [Green Version]
- Abdullah, W.A.T.W. Logic programming on a neural network. Int. J. Intell. Syst. 1992, 7, 513–519. [Google Scholar] [CrossRef]
- Pinkas, G. Symmetric neural networks and propositional logic satisfiability. Neural Comput. 1991, 3, 282–291. [Google Scholar] [CrossRef] [PubMed]
- Abdullah, W.A.T.W. Logic programming in neural networks. Malays. J. Comput. Sci. 1996, 9, 1–5. [Google Scholar] [CrossRef]
- Hamadneh, N.; Sathasivam, S.; Choon, O.H. Higher order logic programming in radial basis function neural network. Appl. Math. Sci. 2012, 6, 115–127. [Google Scholar]
- Mansor, M.A.; Jamaludin, S.Z.M.; Kasihmuddin, M.S.M.; Alzaeemi, S.A.; Basir, M.F.M.; Sathasivam, S. Systematic Boolean satisfiability programming in radial basis function neural network. Processes 2020, 8, 214. [Google Scholar] [CrossRef] [Green Version]
- Kasihmuddin, M.S.M.; Mansor, M.A.; Sathasivam, S. Discrete Hopfield neural network in restricted maximum k-satisfiability logic programming. Sains Malays. 2018, 47, 1327–1335. [Google Scholar] [CrossRef]
- Kasihmuddin, M.S.M.; Mansor, M.A.; Basir, M.F.M.; Sathasivam, S. Discrete mutation Hopfield neural network in propositional satisfiability. Mathematics 2019, 7, 1133. [Google Scholar] [CrossRef] [Green Version]
- Kasihmuddin, M.S.M.; Mansor, M.A.; Sathasivam, S. Hybrid genetic algorithm in the Hopfield network for logic satisfiability problem. Pertanika J. Sci. Technol. 2017, 25, 139–152. [Google Scholar]
- Mansor, M.A.; Kasihmuddin, M.S.M.; Sathasivam, S. Modified artificial immune system algorithm with Elliot Hopfield neural network for 3-satisfiability programming. J. Inform. Math. Sci. 2019, 11, 81–98. [Google Scholar]
- Sathasivam, S.; Mamat, M.; Kasihmuddin, M.S.M.; Mansor, M.A. Metaheuristics approach for maximum k satisfiability in restricted neural symbolic integration. Pertanika J. Sci. Technol. 2020, 28, 545–564. [Google Scholar]
- Zamri, N.E.; Alway, A.; Mansor, A.; Kasihmuddin, M.S.M.; Sathasivam, S. Modified imperialistic competitive algorithm in Hopfield neural network for boolean three satisfiability logic mining. Pertanika J. Sci. Technol. 2020, 28, 983–1008. [Google Scholar]
- Emami, H.; Derakhshan, F. Election algorithm: A new socio-politically inspired strategy. AI Commun. 2015, 28, 591–603. [Google Scholar] [CrossRef]
- Lv, W.; He, C.; Li, D.; Cheng, S.; Luo, S.; Zhang, X. Election campaign optimization algorithm. Procedia Comput. Sci. 2010, 1, 1377–1386. [Google Scholar] [CrossRef] [Green Version]
- Pourghanbar, M.; Kelarestaghi, M.; Eshghi, F. EVEBO: A New Election Inspired Optimization Algorithm. In Proceedings of the 2015 IEEE Congress on Evolutionary Computation (CEC), Sendai, Japan, 25–28 May 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 916–924. [Google Scholar]
- Emami, H. Chaotic election algorithm. Comput. Inform. 2019, 38, 1444–1478. [Google Scholar] [CrossRef]
- Sathasivam, S.; Mansor, M.A.; Kasihmuddin, M.S.M.; Abubakar, H. Election algorithm for random k satisfiability in the Hopfield neural network. Processes 2020, 8, 568. [Google Scholar] [CrossRef]
- Karim, S.A.; Zamri, N.E.; Alway, A.; Kasihmuddin, M.S.M.; Ismail, A.I.M.; Mansor, M.A.; Hassan, N.F.A. Random satisfiability: A higher-order logical approach in discrete Hopfield Neural Network. IEEE Access 2021, 9, 50831–50845. [Google Scholar]
- Li, C.M.; Xiao, F.; Luo, M.; Manyà, F.; Lü, Z.; Li, Y. Clause vivification by unit propagation in CDCL SAT solvers. Artif. Intell. 2020, 279, 103197. [Google Scholar] [CrossRef] [Green Version]
- Kasihmuddin, M.S.M.; Sathasivam, S.; Mansor, M.A. Hybrid Genetic Algorithm in the Hopfield Network for Maximum 2-Satisfiability Problem. In Proceedings of the 24th National Symposium on Mathematical Sciences: Mathematical Sciences Exploration for the Universal Preservation, Kuala Terengganu, Malaysia, 27–29 September 2016; AIP Publishing: Melville, NY, USA, 2017; p. 050001. [Google Scholar]
- Sathasivam, S. Upgrading logic programming in Hopfield network. Sains Malays. 2010, 39, 115–118. [Google Scholar]
- Alway, A.; Zamri, N.E.; Kasihmuddin, M.S.M.; Mansor, A.; Sathasivam, S. Palm oil trend analysis via logic mining with discrete Hopfield Neural Network. Pertanika J. Sci. Technol. 2020, 28, 967–981. [Google Scholar]
- Jamaludin, S.Z.M.; Kasihmuddin, M.S.M.; Ismail, A.I.M.; Mansor, M.A.; Basir, M.F.M. Energy based logic mining analysis with Hopfield Neural Network for recruitment evaluation. Entropy 2021, 23, 40. [Google Scholar] [CrossRef]
- Abdullah, W.A.T.W. The logic of neural networks. Phys. Lett. A 1993, 176, 202–206. [Google Scholar] [CrossRef]
- Kumar, M.; Kulkarni, A.J. Socio-inspired optimization metaheuristics: A review. In Socio-Culture. Inspired Metaheuristics; Kulkarni, A.J., Singh, P.K., Satapathy, S.C., Kashan, A.H., Tai, K., Eds.; Springer: Singapore, 2019; Volume 828, pp. 241–266. [Google Scholar]
- Blum, C.; Roli, A. Hybrid metaheuristics: An introduction. In Hybrid Metaheuristics; Blum, C., Aguilera, M.J.B., Roli, A., Sampels, M., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; Volume 114, pp. 1–30. [Google Scholar]
- Nievergelt, J. Exhaustive search, combinatorial optimization and enumeration: Exploring the potential of raw computing power. In International Conference on Current Trends in Theory and Practice of Computer Science; Springer: Heidelberg/Berlin, Germany, 2000; pp. 18–35. [Google Scholar]
- Mansor, M.A.; Kasihmuddin, M.S.M.; Sathasivam, S. Robust artificial immune system in the Hopfield network for maximum k-satisfiability. Int. J. Interact. Multimed. Artif. Intell. 2017, 4, 63–71. [Google Scholar] [CrossRef] [Green Version]
- Hopfield, J.J. Neural networks and physical systems with emergent collective computational abilities. Proc. Natl. Acad. Sci. USA 1982, 79, 2554–2558. [Google Scholar] [CrossRef] [Green Version]
- Mansor, M.A.; Sathasivam, S. Performance Analysis of Activation Function in Higher Order Logic Programming. In Proceedings of the 23rd Malaysian National Symposium of Mathematical Sciences (SKSM23), Johor Bahru, Malaysia, 24–26 November 2015; AIP Publishing: Melville, NY, USA, 2016; p. 030007. [Google Scholar]
- Kho, L.C.; Kasihmuddin, M.S.M.; Mansor, M.A. Logic mining in league of legends. Pertanika J. Sci. Technol. 2020, 28, 211–225. [Google Scholar]
- Chai, T.; Draxler, R.R. Root mean square error (RMSE) or mean absolute error (MAE)? Arguments against avoiding RMSE in the literature. Geosci. Model Dev. 2014, 7, 1247–1250. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Kim, H. A new metric of absolute percentage error for intermittent demand forecasts. Int. J. Forecast. 2016, 32, 669–679. [Google Scholar] [CrossRef]
- Myttenaere, A.D.; Golden, B.; Le Grand, B.; Rossi, F. Mean absolute percentage error for regression models. Neurocomputing 2016, 192, 38–48. [Google Scholar] [CrossRef] [Green Version]
- Zamri, N.E.; Mansor, M.A.; Kasihmuddin, M.S.M.; Alway, A.; Jamaludin, S.Z.M.; Alzaeemi, S.A. Amazon employees resources access data extraction via clonal selection algorithm and logic mining approach. Entropy 2020, 22, 596. [Google Scholar] [CrossRef] [PubMed]
- Sathasivam, S.; Mansor, M.A.; Ismail, A.I.M.; Jamaludin, S.Z.M.; Kasihmuddin, M.S.M.; Mamat, M. Novel Random k Satisfiability for k≤ 2 in Hopfield Neural Network. Sains Malays. 2020, 49, 2847–2857. [Google Scholar] [CrossRef]
- Miah, A.S.M.; Rahim, M.A.; Shin, J. Motor-imagery classification using riemannian geometry with median absolute deviation. Electronics 2020, 9, 1584. [Google Scholar] [CrossRef]
- Liu, Y.P.; Li, Z.; Xu, C.; Li, J.; Liang, R. Referable diabetic retinopathy identification from eye fundus images with weighted path for convolutional neural network. Artif. Intel. Med. 2019, 99, 101694. [Google Scholar] [CrossRef] [PubMed]
- Sedik, A.; Iliyasu, A.M.; El-Rahiem, A.; Abdel Samea, M.E.; Abdel-Raheem, A.; Hammad, M.; Peng, J.; El-Samie, F.A.; El-Latif, A.A.A. Deploying machine and deep learning models for efficient data-augmented detection of COVID-19 infections. Viruses 2020, 12, 769. [Google Scholar] [CrossRef] [PubMed]
- Wells, J.R.; Aryal, S.; Ting, K.M. Simple supervised dissimilarity measure: Bolstering iForest-induced similarity with class information without learning. Knowl. Inform. Syst. 2020, 62, 3203–3216. [Google Scholar] [CrossRef]


| Parameter | Parameter Value |
|---|---|
| Neuron combination | 100 |
| Number of Trials | 100 |
| Maximum Number of Iterations | 100,000 |
| Size of population | 120 |
| Number of parties | 4 |
| Positive advertisement rate | 0.5 |
| Negative advertisement rate | 1 |
| Tolerance value | 0.001 |
| Threshold Time | 1 day |
| Activation Function | Hyperbolic Tangent activation function (HTAF) |
| Initialization of neuron states | Random |
| Parameter | Parameter Value |
|---|---|
| Neuron combination | 100 |
| Number of Trials | 100 |
| Maximum Number of Iterations | 100,000 |
| Size of population | 100 |
| Tolerance value | 0.001 |
| Threshold Time | 1 day |
| Similarity Index | The Formula |
|---|---|
| Jaccard | |
| Sokal Sneath | |
| Dice | |
| Kulczynski |
| Parameter | ||
|---|---|---|
| 1 | ||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bazuhair, M.M.; Jamaludin, S.Z.M.; Zamri, N.E.; Kasihmuddin, M.S.M.; Mansor, M.A.; Alway, A.; Karim, S.A. Novel Hopfield Neural Network Model with Election Algorithm for Random 3 Satisfiability. Processes 2021, 9, 1292. https://doi.org/10.3390/pr9081292
Bazuhair MM, Jamaludin SZM, Zamri NE, Kasihmuddin MSM, Mansor MA, Alway A, Karim SA. Novel Hopfield Neural Network Model with Election Algorithm for Random 3 Satisfiability. Processes. 2021; 9(8):1292. https://doi.org/10.3390/pr9081292
Chicago/Turabian StyleBazuhair, Muna Mohammed, Siti Zulaikha Mohd Jamaludin, Nur Ezlin Zamri, Mohd Shareduwan Mohd Kasihmuddin, Mohd. Asyraf Mansor, Alyaa Alway, and Syed Anayet Karim. 2021. "Novel Hopfield Neural Network Model with Election Algorithm for Random 3 Satisfiability" Processes 9, no. 8: 1292. https://doi.org/10.3390/pr9081292
APA StyleBazuhair, M. M., Jamaludin, S. Z. M., Zamri, N. E., Kasihmuddin, M. S. M., Mansor, M. A., Alway, A., & Karim, S. A. (2021). Novel Hopfield Neural Network Model with Election Algorithm for Random 3 Satisfiability. Processes, 9(8), 1292. https://doi.org/10.3390/pr9081292







