Analysis of Channel Vortex and Cavitation Performance of the Francis Turbine under Partial Flow Conditions
Abstract
:1. Introduction
2. Mathematical Formulations and Numerical Method
2.1. LES Method
2.2. WALE Subgrid Scale Model
2.3. Schnerr–Sauer Cavitation Model
2.4. Numerical Examples and Boundary Conditions
3. Results
3.1. Flow Regime of Distributor and Runner
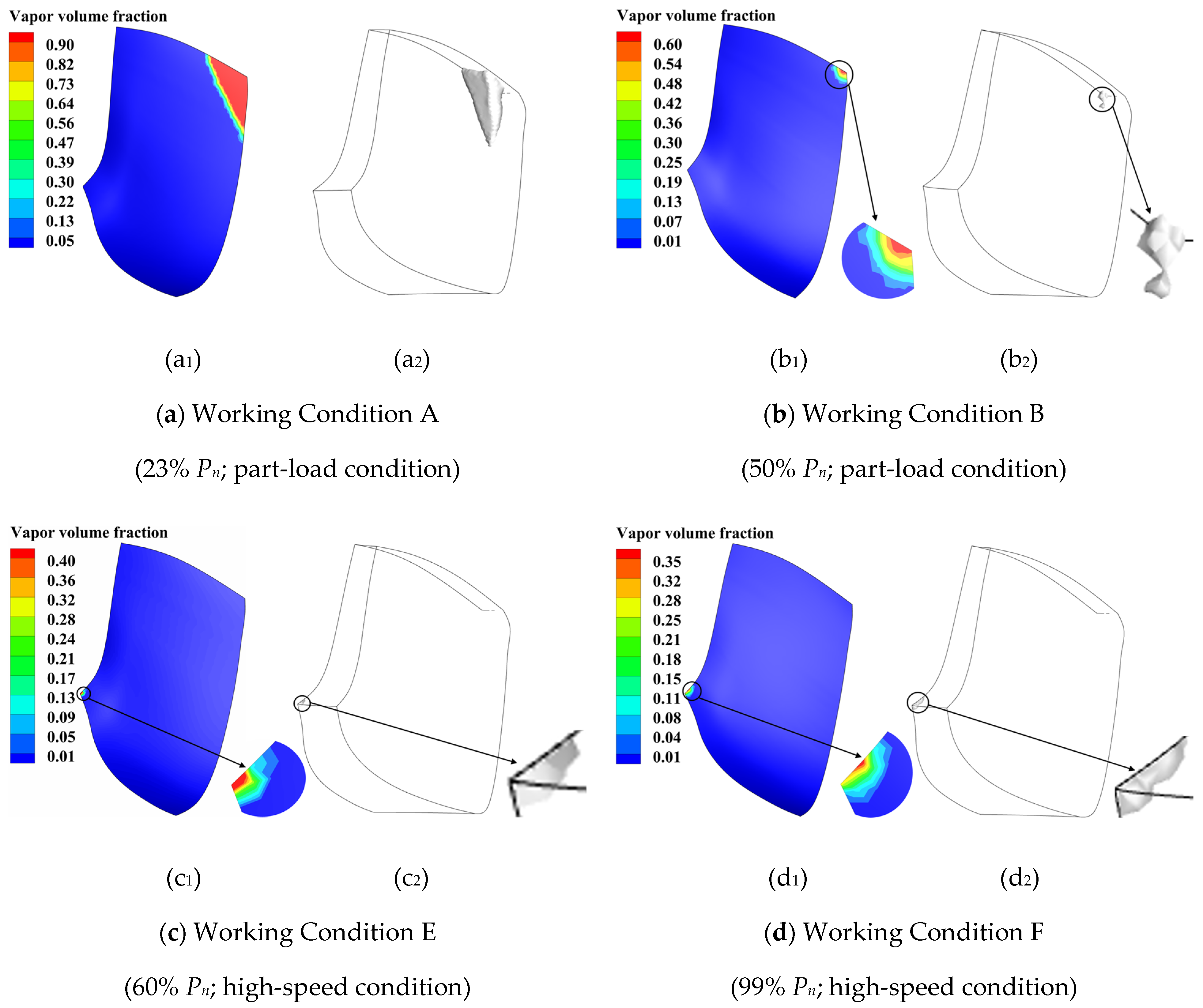
3.2. Analysis of Cavitation around the Runner
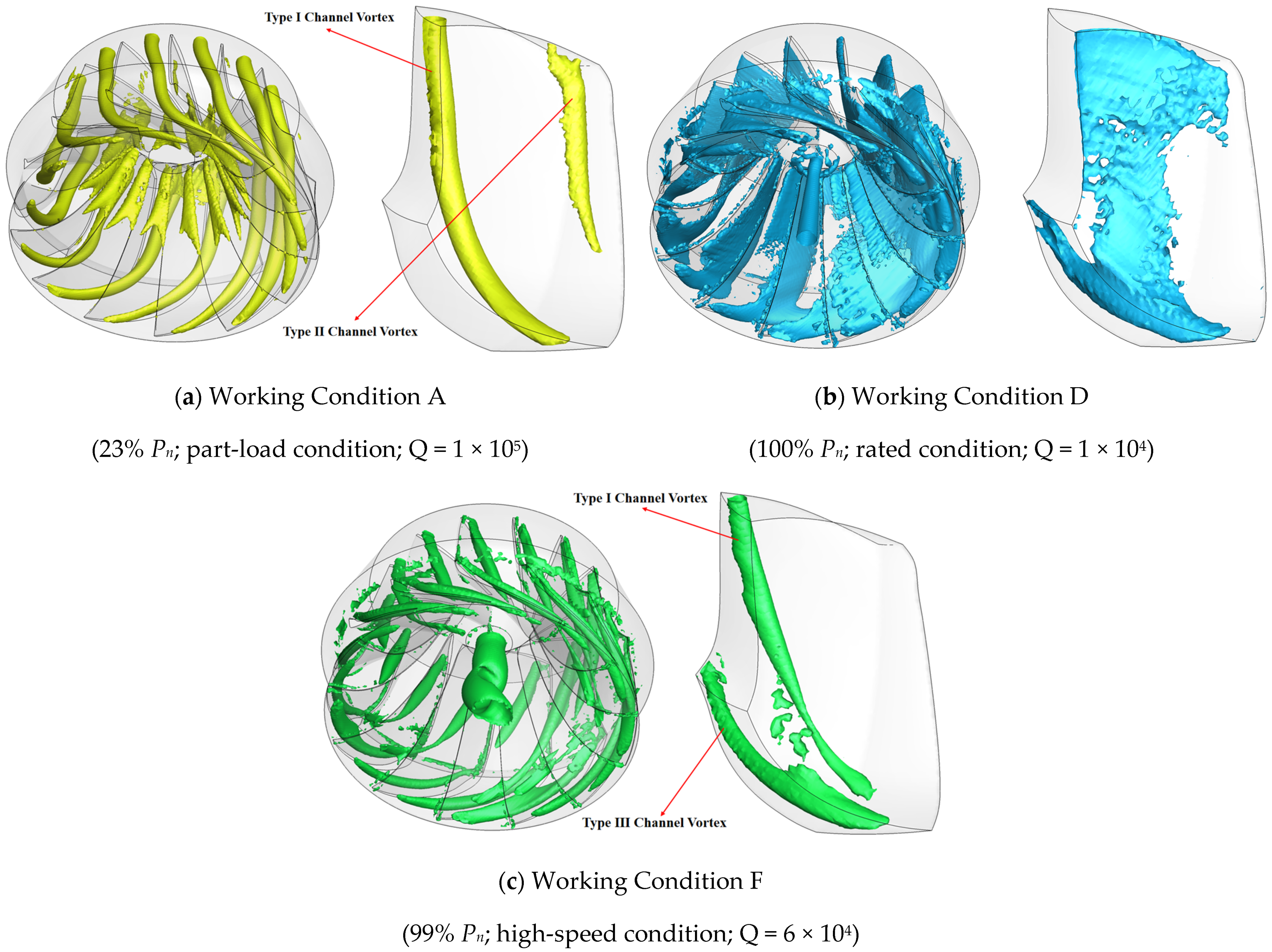
3.3. Analysis of Channel Vortexes around the Runner
4. Conclusions
5. Further Work
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Fluid–structure interaction mechanisms leading to dangerous power swings in Francis turbines at full load. J. Fluids Struct. 2017, 69, 56–71. [Google Scholar] [CrossRef]
- Duan, R. Some Technical Problems of Reversible Pump Turbine and in the Construction of Pumped-storage Power Stations. Water Power 2012, 38, 47–50+83. (In Chinese) [Google Scholar]
- Trivedi, C.; Agnalt, E.; Dahlhaug, O.G. Experimental study of a Francis turbine under variable-speed and discharge conditions. Renew. Energy 2018, 119, 447–458. [Google Scholar] [CrossRef]
- Trivedi, C.; Gandhi, B.; Michel, C.J. Effect of transients on Francis turbine runner life: A review. J. Hydraul. Res. 2013, 51, 121–132. [Google Scholar] [CrossRef]
- Kirschner, O.; Ruprecht, A.; Göde, E.; Riedelbauch, S. Experimental investigation of pressure fluctuations caused by a vortex rope in a draft tube. IOP Conf. Ser. Earth Environ. Sci. 2012, 15, 062059. [Google Scholar] [CrossRef]
- Celebioglu, K.; Altintas, B.; Aradag, S.; Tascioglu, Y. Numerical research of cavitation on Francis turbine runners. Int. J. Hydrog. Energy 2017, 42, 17771–17781. [Google Scholar] [CrossRef]
- Jiang, W.; Chang, J. Cavitation Performance of Hydraulic Turbines in the Three Gorges Reservoir with Consideration of Influence of Total Phosphorus Pollution. J. Fluids Eng. 2016, 138, 081301. [Google Scholar] [CrossRef]
- Goyal, R.; Gandhi, B.K. Review of hydrodynamics instabilities in Francis turbine during off-design and transient operations. Renew. Energy 2018, 116, 697–709. [Google Scholar] [CrossRef]
- Chen, J.X.; Li, G.; Liu, S.; Lu, G.P. The Occurrence and the Influence of the Interblade Wortex on the Hydraulic Turbine Stability. Large Electr. Mach. Hydraul. Turbine 2007, 3, 42–46. (In Chinese) [Google Scholar]
- Escaler, X.; Egusquiza, E.; Farhat, M.; Avellan, F.; Coussirat, M. Detection of cavitation in hydraulic turbines. Mech. Syst. Signal Process. 2004, 20, 983–1007. [Google Scholar] [CrossRef] [Green Version]
- Magnoli, M.V.; Anciger, D.; Maiwald, M. Numerical and experimental investigation of the runner channel vortex in Francis turbines regarding its dynamic flow characteristics and its influence on pressure oscillations. IOP Conf. Ser. Earth Environ. Sci. 2019, 240, 022044. [Google Scholar] [CrossRef]
- Guo, T.; Zhang, L.; Wang, W.; Luo, Z. Rotating Turbulent Flow Simulation with LES and Vreman Subgrid-Scale Models in Complex Geometries. Adv. Mech. Eng. 2014, 6, 1–8. [Google Scholar] [CrossRef]
- Yamamoto, K.; Müller, A.; Favrel, A.; Avellan, F. Experimental evidence of inter-blade cavitation vortex development in Francis turbines at deep part load condition. Exp. Fluids 2017, 58, 142. [Google Scholar] [CrossRef]
- Favrel, A.; Junior JG, P.; Müller, A.; Landry, C.; Yamamoto, K.; Avellan, F. Swirl number based transposition of flow-induced mechanical stresses from reduced scale to full-size Francis turbine runners. J. Fluids Struct. 2020, 94, 102956. [Google Scholar] [CrossRef]
- Yamamoto, K.; Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Flow characteristics and influence associated with inter-blade cavitation vortices at deep part load operations of a Francis turbine. J. Phys. Conf. Ser. 2017, 813, 012029. [Google Scholar] [CrossRef]
- Yamamoto, K.; Müller, A.; Favrel, A.; Landry, C.; Avellan, F. Numerical and experimental evidence of the inter-blade cavitation vortex development at deep part load operation of a Francis turbine. IOP Conf. Ser. Earth Environ. Sci. 2016, 49, 082005. [Google Scholar] [CrossRef]
- Guo, P.; Sun, L.; Luo, X. Flow characteristic investigation into inter-blade vortex for Francis turbine. Trans. Chin. Soc. Agric. Eng. 2019, 35, 43–51. (In Chinese) [Google Scholar]
- Guo, P.C.; Wang, Z.N.; Luo, X.Q.; Wang, Y.L.; Zuo, J.L. Flow characteristics on the blade channel vortex in the Francis turbine. IOP Conf. Ser. Mater. Sci. Eng. 2016, 129, 012038. [Google Scholar] [CrossRef] [Green Version]
- Guo, P.; Wang, Z.; Sun, L.; Luo, X. Characteristic analysis of the efficiency hill chart of Francis turbine for different water heads. Adv. Mech. Eng. 2017, 9, 21–26. [Google Scholar] [CrossRef]
- Liu, D.; Liu, X.; Zhao, Y. Experimental Investigation of Inter-Blade Vortices in a Model Francis Turbine. Chin. J. Mech. Eng. 2017, 30, 854–865. [Google Scholar] [CrossRef]
- Cheng, H.; Zhou, L.; Liang, Q.; Guan, Z.; Liu, D.; Wang, Z.; Kang, W. The investigation of runner blade channel vortices in two different Francis turbine models. Renew. Energy 2020, 156, 201–212. [Google Scholar] [CrossRef]
- Cheng, H.; Zhou, L.; Liang, Q.; Guan, Z.; Liu, D.; Wang, Z.; Kang, W. A method of evaluating the vortex rope strength in draft tube of Francis turbine. Renew. Energy 2020, 152, 770–780. [Google Scholar] [CrossRef]
- Zhou, L.; Liu, M.; Wang, Z.; Liu, D.; Zhao, Y. Numerical simulation of the blade channel vortices in a Francis turbine runner. Eng. Comput. 2017, 34, 364–376. [Google Scholar] [CrossRef]
- Su, W.; Zheng, Z.; Li, X.; Li, F.; Lan, C. Verification of large eddy simulation (LES) applied in Francis hydro-turbine under partial flow conditions. J. Harbin Inst. Technol. 2015, 47, 84–91. (In Chinese) [Google Scholar]
- Trivedi, C.; Dahlhaug, O.G. Interaction between trailing edge wake and vortex rings in a Francis turbine at runaway condition: Compressible large eddy simulation. Phys. Fluids 2018, 30, 075101. [Google Scholar] [CrossRef]
- Trivedi, C. Time-dependent inception of vortex rings in a Francis turbine during load variation: Large eddy simulation and experimental validation. J. Hydraul. Res. 2020, 58, 790–806. [Google Scholar] [CrossRef]
- Trivedi, C.; Iliev, I.; Dahlhaug, O.G.; Markov, Z.; Engstrom, F.; Lysaker, H. Investigation of a Francis turbine during speed variation: Inception of cavitation. Renew. Energy 2020, 166, 147–162. [Google Scholar] [CrossRef]
- Sun, L.; Guo, P.; Luo, X. Numerical investigation of inter-blade cavitation vortex for a Francis turbine at part load conditions. IET Renew. Power Gener. 2021, 15, 1163–1177. [Google Scholar] [CrossRef]
- Shi, G.T.; Xue, Z.C.; Yang, Q.; Liu, Z.K. Effect of Guide Vane Opening on Cavitation Performance of Runner Blade of Francis Turbine. China Rural. Water Hydropower 2021, 3, 163–167. (In Chinese) [Google Scholar]
- Anvari, S.; Taghavifar, H.; Khalilarya, S.; Jafarmadar, S.; Shervani-Tabar, M.T. Numerical simulation of diesel injector nozzle flow and in-cylinder spray evolution. Appl. Math. Model. 2016, 40, 8617–8629. [Google Scholar] [CrossRef]
- Roohi, E.; Pendar, M.R.; Rahimi, A. Simulation of three-dimensional cavitation behind a disk using various turbulence and mass transfer models. Appl. Math. Model. 2016, 40, 542–564. [Google Scholar] [CrossRef]
- Li, M.; Chen, X.; Ruan, X. Investigation of flow structure and heat transfer enhancement in rectangular channels with dimples and protrusions using large eddy simulation. Int. J. Therm. Sci. 2020, 149, 106207. [Google Scholar] [CrossRef]
- Li, L.M.; Wang, Z.D.; Li, X.J.; Wang, Y.P.; Zhu, Z.C. Very Large Eddy Simulation of Cavitation from Inception to Sheet/Cloud Regimes by A Multiscale Model. China Ocean. Eng. 2021, 35, 361–371. [Google Scholar] [CrossRef]
- Nicoud, F.; Ducros, F. Subgrid-Scale Stress Modelling Based on the Square of the Velocity Gradient Tensor. Flow Turbul. Combust. 1999, 62, 183–200. [Google Scholar] [CrossRef]
- Yu, J.Y.; Wang, R.Y.; Chen, F.; Song, Y. A Comparison of the Different Subgrid-Scale Models and Its Application. J. Eng. Thermophys. 2016, 37, 2311–2318. (In Chinese) [Google Scholar]
- Yang, J. Study on Cavitation Flows in Draft Tube of a Francis Turbine. Diploma Thesis, China Agricultural University, Beijing, China, 2013. (In Chinese). [Google Scholar]
- Rayleigh, L., VIII. On the pressure developed in a liquid during the collapse of a spherical cavity. Philos. Mag. 1917, 34, 94–98. [Google Scholar] [CrossRef]
- Susan-Resiga, R.; Dan Ciocan, G.; Anton, I.; Avellan, F. Analysis of the Swirling Flow Downstream a Francis Turbine Runner. J. Fluids Eng. 2006, 128, 177–189. [Google Scholar] [CrossRef]
- Valdes, J.R.; Rodríguez, J.M.; Monge, R.; Peña, J.C.; Pütz, T. Numerical simulation and experimental validation of the cavitating flow through a ball check valve. Energy Convers. Manag. 2014, 78, 776–786. [Google Scholar] [CrossRef]
- Cheng, H.Y.; Bai, X.R.; Long, X.P.; Ji, B.; Peng, X.X.; Farhat, M. Large eddy simulation of the tip-leakage cavitating flow with an insight on how cavitation influences vorticity and turbulence. Appl. Math. Model. 2020, 77 Pt 1, 788–809. [Google Scholar] [CrossRef]
- Wack, J.; Riedelbauch, S. Numerical simulations of the cavitation phenomena in a Francis turbine at deep part load conditions. J. Phys. Conf. Ser. 2015, 656, 012074. [Google Scholar] [CrossRef]
- Wu, Y. (Ed.) Proceedings of the 23th National Congress on Hydrodynamics and 10nd National Conference on Hydrodynamics, Venice, Italy, 8–14 September 2002; China Ocean Press: Beijing, China, 2011. (In Chinese).
- Pan, Z.; Yuan, Q.S. Fundamentals of Cavitation in Pumps; Jiangsu University Press: Zhenjiang, China, 2013. (In Chinese) [Google Scholar]
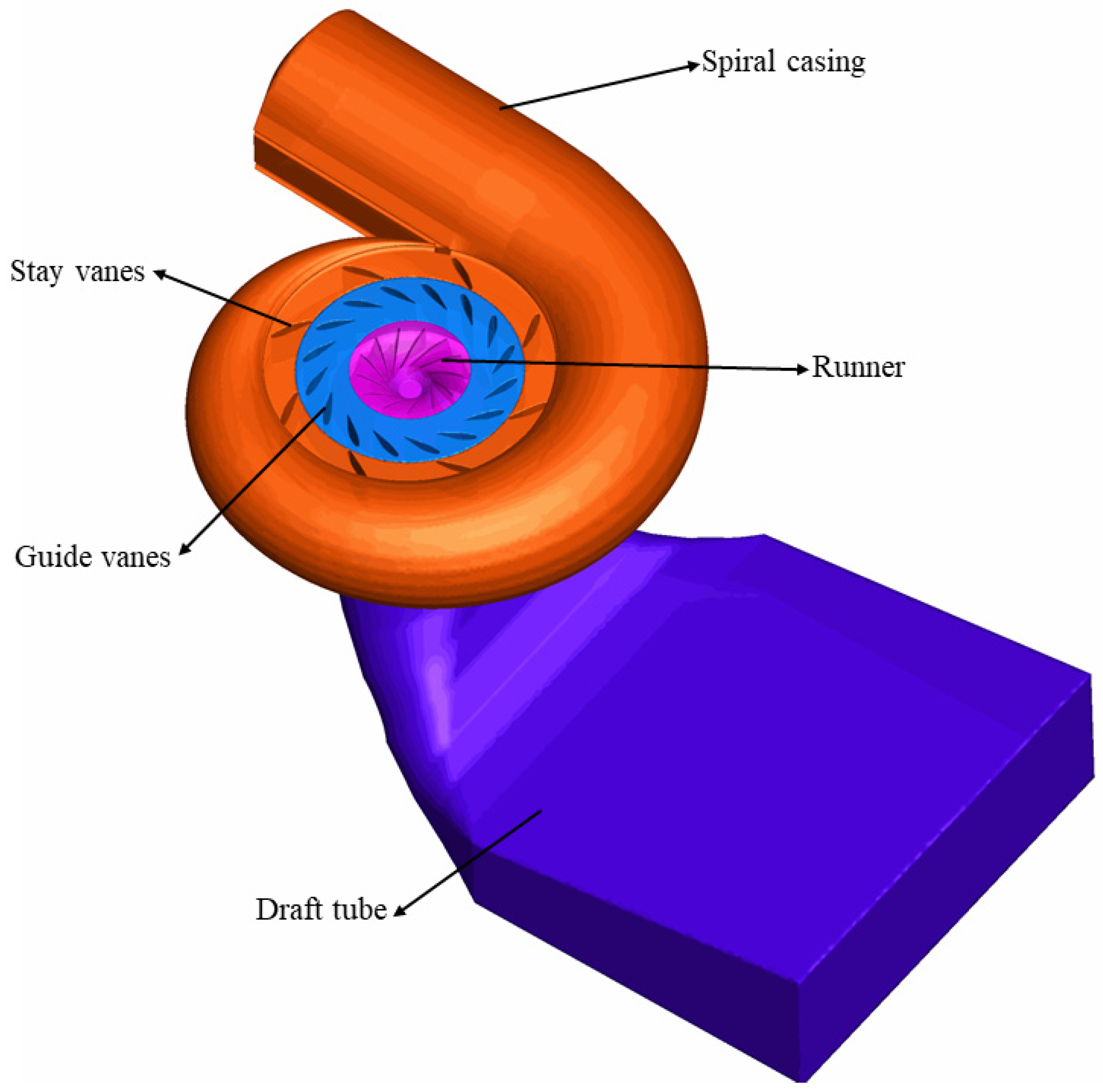











| Condition | α/mm | α% | n11/rpm | Q11/(m3/s) | η | Pn% |
|---|---|---|---|---|---|---|
| A | 16.00 | 33 | 74.94 | 0.36 | 0.72 | 23 |
| B | 26.17 | 54 | 74.94 | 0.65 | 0.86 | 50 |
| C | 32.05 | 65 | 74.94 | 0.83 | 0.91 | 67 |
| D | 48.74 | 100 | 74.94 | 1.22 | 0.91 | 100 |
| E | 32.05 | 65 | 94.37 | 0.79 | 0.86 | 60 |
| F | 48.74 | 100 | 94.37 | 1.23 | 0.91 | 99 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, T.; Zhang, J.; Luo, Z. Analysis of Channel Vortex and Cavitation Performance of the Francis Turbine under Partial Flow Conditions. Processes 2021, 9, 1385. https://doi.org/10.3390/pr9081385
Guo T, Zhang J, Luo Z. Analysis of Channel Vortex and Cavitation Performance of the Francis Turbine under Partial Flow Conditions. Processes. 2021; 9(8):1385. https://doi.org/10.3390/pr9081385
Chicago/Turabian StyleGuo, Tao, Jinming Zhang, and Zhumei Luo. 2021. "Analysis of Channel Vortex and Cavitation Performance of the Francis Turbine under Partial Flow Conditions" Processes 9, no. 8: 1385. https://doi.org/10.3390/pr9081385
APA StyleGuo, T., Zhang, J., & Luo, Z. (2021). Analysis of Channel Vortex and Cavitation Performance of the Francis Turbine under Partial Flow Conditions. Processes, 9(8), 1385. https://doi.org/10.3390/pr9081385






