Photovoltaic Module Fault Detection Based on a Convolutional Neural Network
Abstract
:1. Introduction
2. Architecture of the System
2.1. Photovoltaic Module Fault Signal Capture
2.2. PV Module Defect Construction
2.2.1. Normal PV Module (Type 1)
2.2.2. PV Module Breakage (Type 2)
2.2.3. PV Module Contact Defectiveness (Type 3)
2.2.4. PV Module Diode Failure (Type 4)
3. Proposed Fault Diagnosis Algorithm
3.1. Chaos Synchronization Detection Method
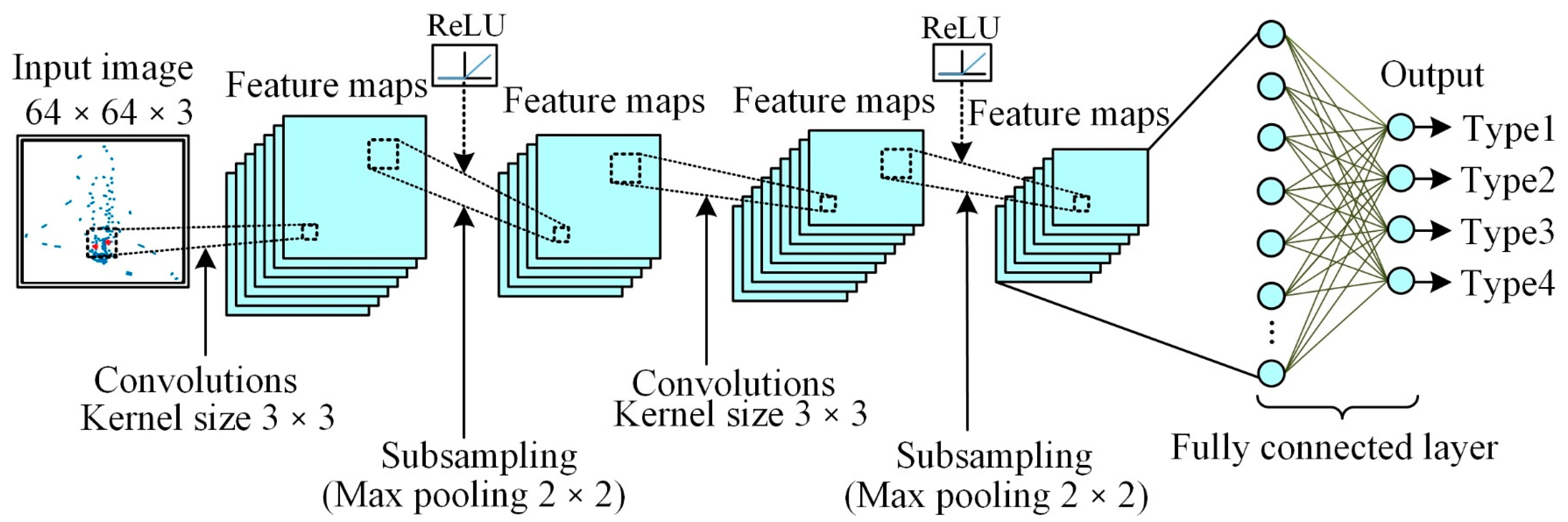
3.2. Convolutional Neural Networks
3.2.1. Convolution Layer
3.2.2. Pooling Layer
3.2.3. Fully-Connected Layer
3.2.4. Activation Layer
4. Results
4.1. Original Signal Captured
4.2. Convolutional Neural Network Recognition Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Mariusz, M.; Jose, I.L.; Haitham, A.R. Solar Photovoltaic and Thermal Energy Systems: Current Technology and Future Trends. Proc. IEEE 2017, 105, 2132–2146. [Google Scholar]
- Jiang, Z.; Michael, K. Changes of solar cell parameters during damp-heat exposure. Prog. Photovolt Res. Appl. 2016, 24, 1346–1358. [Google Scholar]
- Khan, F.; Kim, J.H. Performance Degradation Analysis of c-Si PV Modules Mounted on a Concrete Slab under Hot-Humid Conditions Using Electroluminescence Scanning Technique for Potential Utilization in Future Solar Roadways. Materials 2019, 12, 4047. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Firoz, K.; Seong, H.B. Extraction of diode parameters of silicon solar cells under high illumination conditions. Energy Convers. Manag. 2013, 76, 421–429. [Google Scholar]
- Lorenzo, G.D.; Araneo, R.; Mitolo, M.; Niccolai, A. Review of O&M Practices in PV Plants: Failures, Solutions, Remote Control, and Monitoring Tools. IEEE J. Photovolt. 2020, 10, 914–926. [Google Scholar]
- Skomedal, A.; Deceglie, M.G. Combined Estimation of Degradation and Soiling Losses in Photovoltaic Systems. IEEE J. Photovolt. 2020, 10, 1788–1796. [Google Scholar] [CrossRef]
- Lillo-Bravo, I.; González-Martínez, P.; Larrañeta, M.; Guasumba-Codena, J. Impact of Energy Losses Due to Failures on Photovoltaic Plant Energy Balance. Energies 2018, 11, 363. [Google Scholar] [CrossRef] [Green Version]
- Ogbomo, O. Effect of operating temperature on degradation of solder joints in crystalline silicon photovoltaic modules for improved reliability in hot climates. Sol. Energy 2018, 170, 682–693. [Google Scholar] [CrossRef] [Green Version]
- Caixia, T.; Xu, W. Fault diagnosis of photovoltaic array based on deep belief network optimized by genetic algorithm. Chin. J. Electr. Eng. 2020, 6, 106–114. [Google Scholar]
- Zhehan, Y.; Amir, H.E. Fault Detection for Photovoltaic Systems Based on Multi-Resolution Signal Decomposition and Fuzzy Inference Systems. IEEE Trans. Smart Grid 2017, 8, 1274–1283. [Google Scholar]
- Farkhanda, A.; Azhar, U.H. A Novel Convolutional Neural Network-Based Approach for Fault Classification in Photovoltaic Arrays. IEEE Access 2020, 8, 41889–41904. [Google Scholar]
- Ayobami, S.E.; Cody, L. Finding Faults in PV Systems: Supervised and Unsupervised Dictionary Learning with SSTDR. IEEE Sens. J. 2021, 21, 4855–4865. [Google Scholar]
- Mahmoud, D.; Peter, M. Novel Photovoltaic Hot-Spotting Fault Detection Algorithm. IEEE Trans. Device Mater. Reliab. 2019, 19, 378–386. [Google Scholar]
- Faqih, A.; Kamanditya, B.; Kusumoputro, B. Multi-Step Ahead Prediction of Lorenz’s Chaotic System Using SOM ELM-RBFNN. In Proceedings of the 2018 Internacional Conference on Computer, Information and Telecommunication Systems (IEEE, 2018), Alsace, Colmar, France, 11–13 July 2018; pp. 1–5. [Google Scholar]
- Li, B.; Li, P.; Zhang, L.; Ma, M. Research on islanding detection method for PV module power system based on chaos theory. In Proceedings of the 2008 China International Conference on Electricity Distribution, Guangzhou, China, 10–13 December 2008; pp. 1–5. [Google Scholar]
- Hasegawa, S.; Ueda, Y. I-V Curve Differences Image Classification by CNN for Failure Factor Determination in PV module system. In Proceedings of the 2020 47th IEEE Photovoltaic Specialists Conference (PV moduleSC), Calgary, AB, Canada, 15 June–21 August 2020; pp. 683–688. [Google Scholar]
- Huang, J.; Wai, R.; Gao, W. Newly-Designed Fault Diagnostic Method for Solar Photovoltaic Generation System Based on IV-Curve Measurement. IEEE Access 2019, 7, 70919–70932. [Google Scholar] [CrossRef]
- Khelifa, M.A.; Boukabou, A.; Hammami, N. Data Transmission Based on Chaotic Synchronization System. In Proceedings of the International Conference on Computer Applications Technology, Sousse, Tunisia, 20–22 January 2013; pp. 1–2. [Google Scholar]
- Huang, C.H.; Lin, C.H.; Kuo, C.L. Chaos Synchronization-Based Detector for Power-Quality Disturbances Classification in a Power System. IEEE Trans. Power Deliv. 2010, 26, 944–953. [Google Scholar] [CrossRef]
- Yau, H.T.; Wang, M.H. Chaotic Eye-Based Fault Forecasting Method for Wind Power Systems. IET Renew. Power Gener. 2015, 9, 593–599. [Google Scholar] [CrossRef]
- Liu, R.; Meng, G.; Yang, B.; Sun, C.; Chen, X. Dislocated Time Series Convolutional Neural Architecture: An Intelligent Fault Diagnosis Approach for Electric Machine. IEEE Trans. Ind. Inform. 2017, 13, 1310–1320. [Google Scholar] [CrossRef]
- Sharma, A.K.; Foroosh, H. Slim-CNN: A Light-Weight CNN for Face Attribute Prediction. In Proceedings of the 2020 15th IEEE International Conference on Automatic Face and Gesture Recognition (FG 2020), Buenos Aires, Argentina, 16–20 November 2020; pp. 329–335. [Google Scholar]
- Chen, Y.H.; Fan, C.P.; Chang, R.C.H. Prototype of Low Complexity CNN Hardware Accelerator with FPGA-based PYNQ Platform for Dual-Mode Biometrics Recognition. In Proceedings of the 2020 International SoC Design Conference (ISOCC), Yeosu, Korea, 21–24 October 2020; pp. 189–190. [Google Scholar]
- Wang, M.H.; Lu, S.D.; Liao, R.M. Fault Diagnosis for Power Cables Based on Convolutional Neural Network with Chaotic System and Discrete Wavelet Transform. IEEE Trans. Power Deliv. 2021, 1. [Google Scholar] [CrossRef]
- Lau, M.M.; Lim Hann, K. Review of Adaptive Activation Function in Deep Neural Network. In Proceedings of the 2018 IEEE-EMBS Conference on Biomedical Engineering and Sciences (IECBES), Sarawak, Malaysia, 3–6 December 2018; pp. 686–690. [Google Scholar]
- Wang, Y.; Li, Y.; Rong, X. The Influence of the Activation Function in a Convolution Neural Network Model of Facial Expression Recognition. Appl. Sci. 2020, 10, 1897. [Google Scholar] [CrossRef] [Green Version]


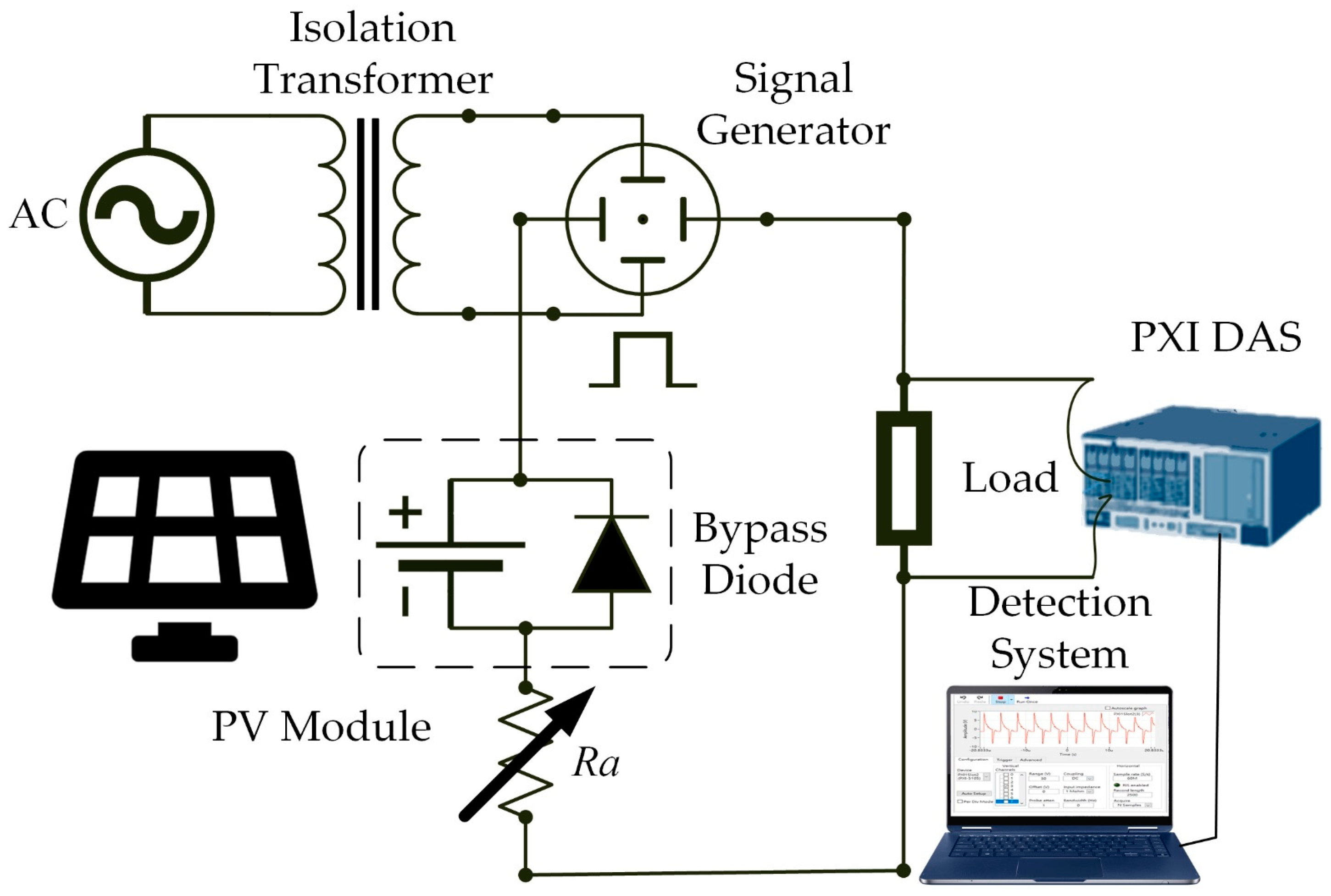

















| Work Style | PV Module Defect Construction |
|---|---|
| (Off-line) | normal PV module (Type1) |
| PV module breakage (Type2) | |
| PV module contact defectiveness (Type3) | |
| PV module bypass diode failure (Type4) |
| Algorithm | Epoch | Training Rate (%) | Accuracy Rate (%) | Training Time (s) | Ranking |
|---|---|---|---|---|---|
| CNN + Lorenz | 50 | 100 | 99.5 | 9 | 1 |
| CNN + Lorenz | 50 | 100 | 98 | 9 | 2 |
| ENN + Lorenz | 100 | 97.2 | 86.75 | 0.154 | 3 |
| ENN + Lorenz | 100 | 95.5 | 83.25 | 0.146 | 4 |
| ENN + Lorenz | 100 | 95.25 | 80.25 | 0.143 | 5 |
| CNN + Lorenz | 50 | 100 | 74 | 9 | 6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lu, S.-D.; Wang, M.-H.; Wei, S.-E.; Liu, H.-D.; Wu, C.-C. Photovoltaic Module Fault Detection Based on a Convolutional Neural Network. Processes 2021, 9, 1635. https://doi.org/10.3390/pr9091635
Lu S-D, Wang M-H, Wei S-E, Liu H-D, Wu C-C. Photovoltaic Module Fault Detection Based on a Convolutional Neural Network. Processes. 2021; 9(9):1635. https://doi.org/10.3390/pr9091635
Chicago/Turabian StyleLu, Shiue-Der, Meng-Hui Wang, Shao-En Wei, Hwa-Dong Liu, and Chia-Chun Wu. 2021. "Photovoltaic Module Fault Detection Based on a Convolutional Neural Network" Processes 9, no. 9: 1635. https://doi.org/10.3390/pr9091635
APA StyleLu, S.-D., Wang, M.-H., Wei, S.-E., Liu, H.-D., & Wu, C.-C. (2021). Photovoltaic Module Fault Detection Based on a Convolutional Neural Network. Processes, 9(9), 1635. https://doi.org/10.3390/pr9091635








