The Long-Term Mitigating Effect of Horizontal Ground-Source Heat Exchangers on Permafrost Thaw Settlement
Abstract
:1. Introduction
2. Materials and Methods
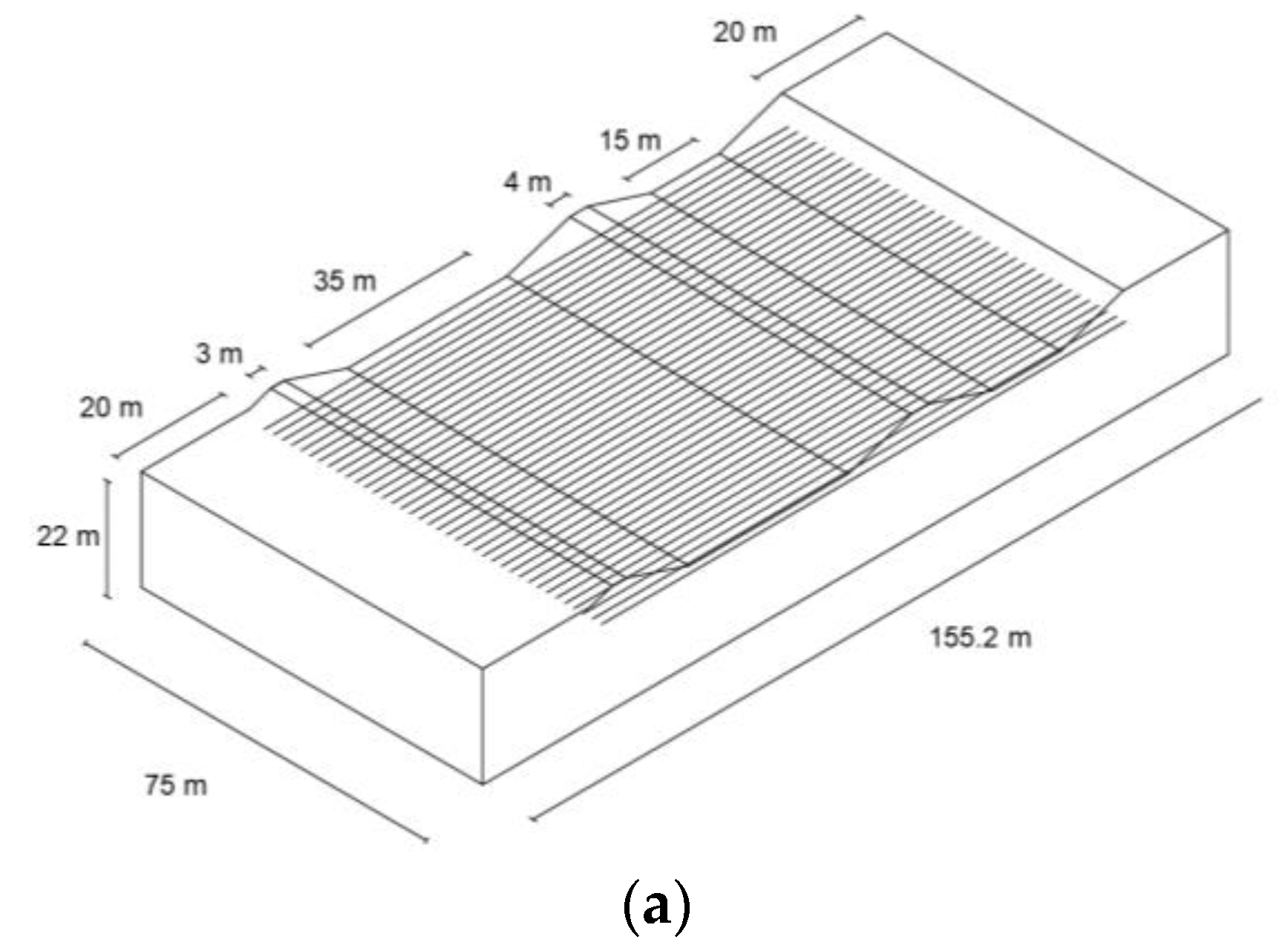
2.1. Study Area
2.2. Specification and Conceptual Model of the Proposed GSHE System
2.3. Governing Equations
2.3.1. Heat Transfer within Degrading Permafrost during Freeze–Thaw Cycle
Conductive Heat Transfer Considering Pore Water Phase Change
2.3.2. Mechanical Behavior of the Soil during Freeze–Thaw Cycles
Kinematic Formulation
Constitutive Model
Non-Isothermal Heat Transfer from Pipe Flow
Convective Heat Flux
2.4. Numerical Modeling
2.4.1. Soil Properties
2.4.2. Mesh Sensitivity Analysis
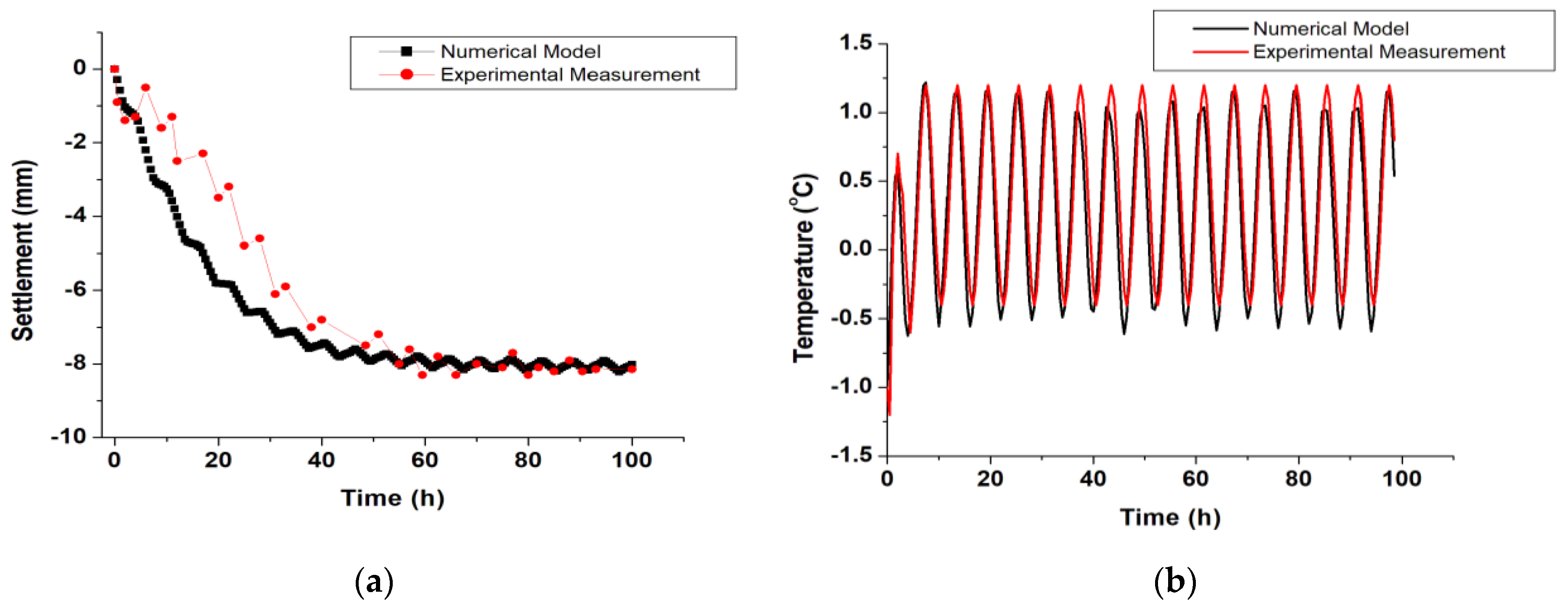
2.5. Model Validation
3. Results and Discussion
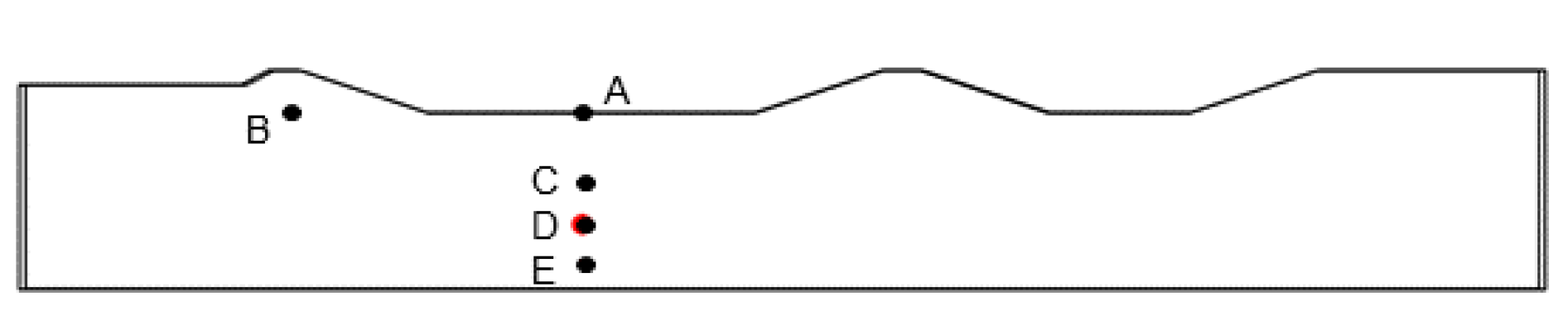
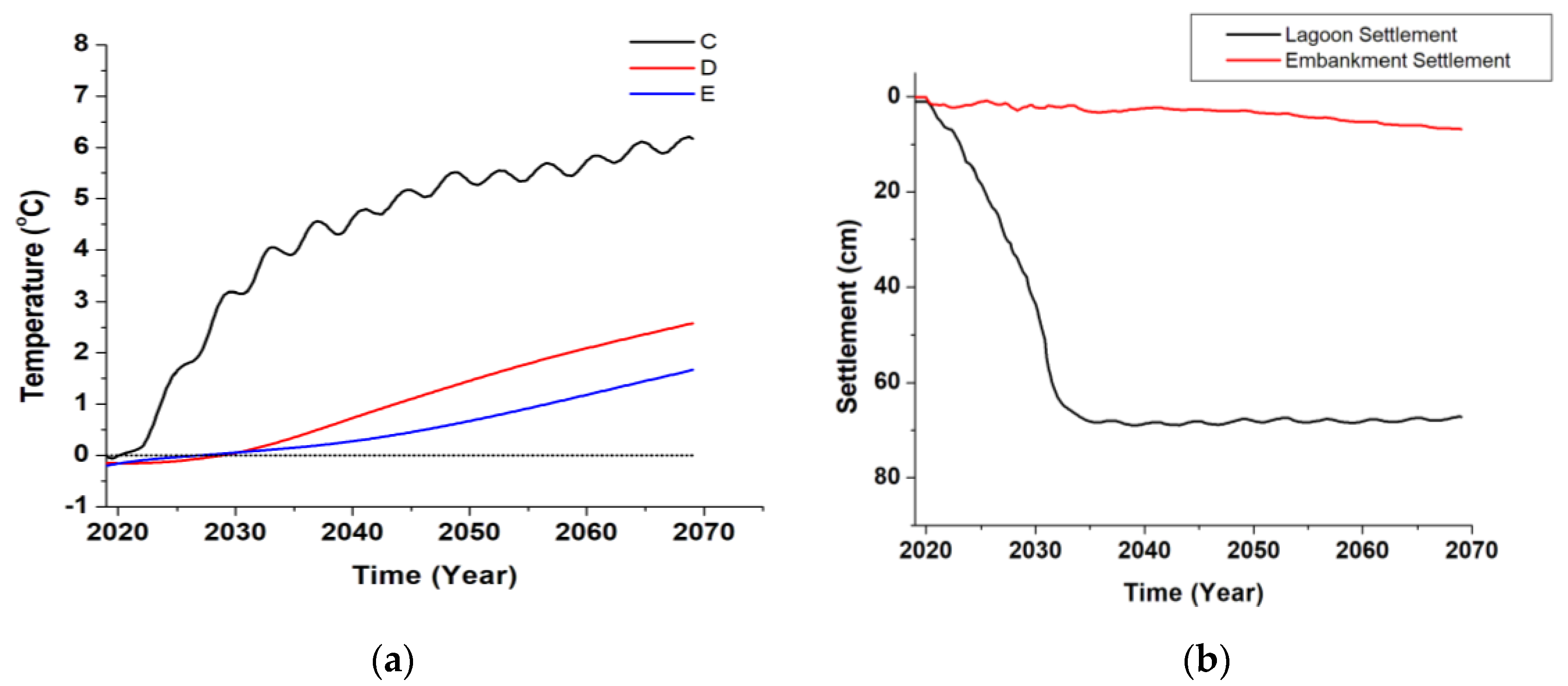
3.1. Thaw Settlement Due to the Lagoon Heat Flux and Climatic Conditions without Embedded GHSE System
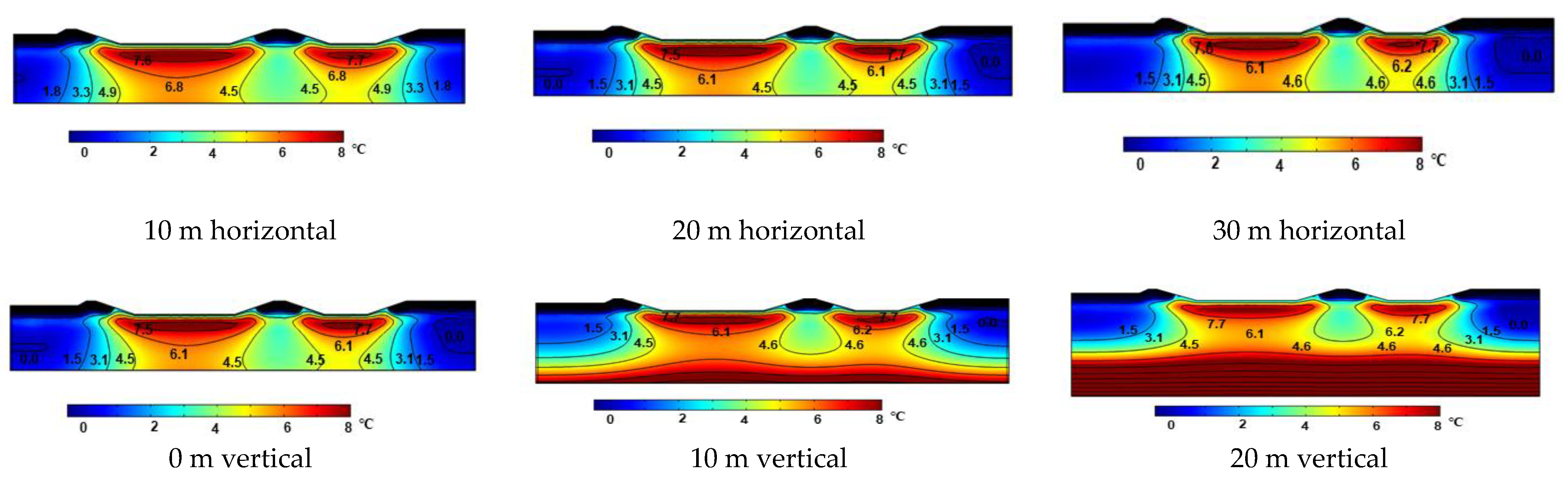
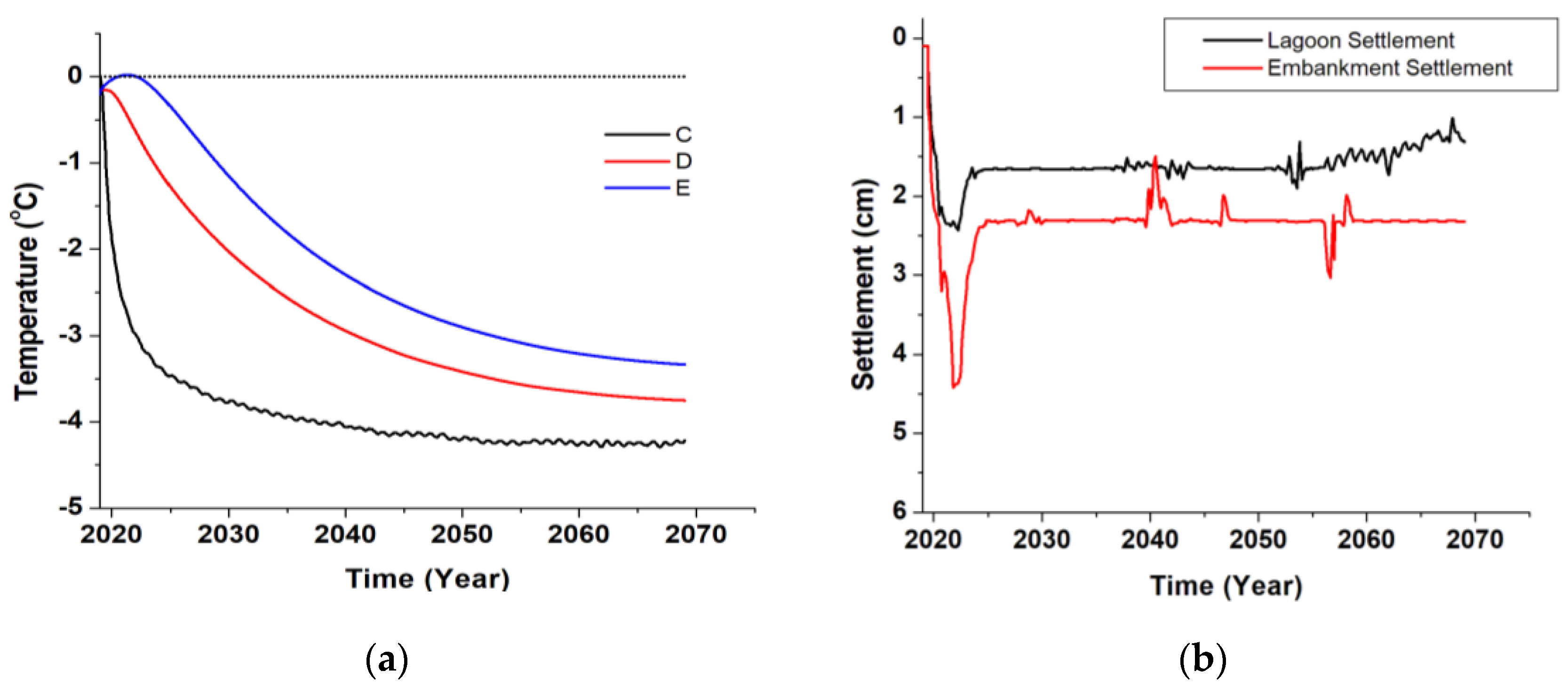
3.2. Effect of Horizontal GSHE System on Permafrost Preservation
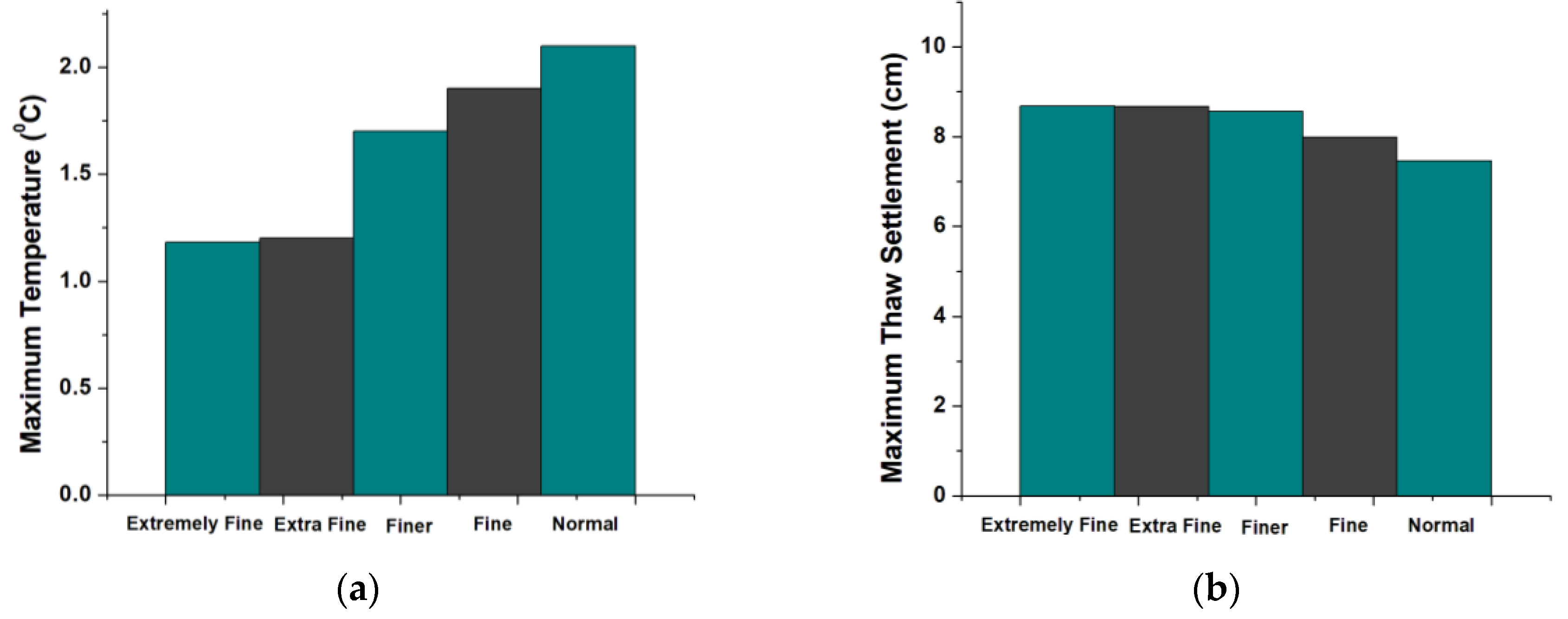
3.3. Effect of Operational Parameters of the Horizontal GSHE System on the Heat Extraction Power and Thaw Settlement
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Subcommittee, P. Glossary of permafrost and related ground-ice terms. In Associate Committee on Geotechnical Research; National Research Council of Canada: Ottawa, ON, Canada, 1988; p. 156. [Google Scholar]
- GISTEMP Team. G. S. T. A. G., version 4. NASA Goddard Institute for Space Studies. Available online: https://data.giss.nasa.gov/gistemp/ (accessed on 25 January 2021).
- Zhang, Y.; Michalowski, R.L. Thermal-hydro-mechanical analysis of frost heave and thaw settlement. J. Geotech. Geoenviron. Eng. 2015, 141, 04015027. [Google Scholar] [CrossRef]
- Morgenstern, N.T.; Nixon, J. One-dimensional consolidation of thawing soils. Can. Geotech. J. 1971, 8, 558–565. [Google Scholar] [CrossRef]
- Dumais, S.; Konrad, J.-M. One-dimensional large-strain thaw consolidation using nonlinear effective stress–void ratio–hydraulic conductivity relationships. Can. Geotech. J. 2018, 55, 414–426. [Google Scholar] [CrossRef] [Green Version]
- Foriero, A.; Ladanyi, B. FEM assessment of large-strain thaw consolidation. J. Geotech. Eng. 1995, 121, 126–138. [Google Scholar] [CrossRef]
- Doré, G.; Niu, F.; Brooks, H. Adaptation methods for transportation infrastructure built on degrading permafrost. Permafr. Periglac. Process. 2016, 27, 352–364. [Google Scholar] [CrossRef]
- Jiao, B.; Qiu, L.; Zhang, X.; Zhang, Y. Investigation on the effect of filling ratio on the steady-state heat transfer performance of a vertical two-phase closed thermosyphon. Appl. Therm. Eng. 2008, 28, 1417–1426. [Google Scholar] [CrossRef]
- Chen, L.; Yu, W.; Lu, Y.; Liu, W. Numerical simulation on the performance of thermosyphon adopted to mitigate thaw settlement of embankment in sandy permafrost zone. Appl. Therm. Eng. 2018, 128, 1624–1633. [Google Scholar] [CrossRef]
- Fontaine, P.-O.; Marcotte, D.; Pasquier, P.; Thibodeau, D. Modeling of horizontal geoexchange systems for building heating and permafrost stabilization. Geothermics 2011, 40, 211–220. [Google Scholar] [CrossRef]
- Sinclair, R.; Kenton, T. Ross River Wastewater Treatment System, Ross River, Yukon; Final Design Report; KGS Group: Winnipeg, MB, USA, 2014. [Google Scholar]
- Tetra Tech EBA. Geothermal Evaluation-Proposed Wastewater Disposal Facilities; Tetra Tech EBA: Ross River, YT, Canada, 2014. [Google Scholar]
- Fatolahzadeh Gheysari, A.; Holländer, H.M.; Maghoul, P.; Shalaby, A. Sustainability, climate resiliency, and mitigation capacity of geothermal heat pump systems in cold regions. Geothermics 2021, 91, 101979. [Google Scholar] [CrossRef]
- Konrad, J.-M. Hydraulic conductivity changes of a low-plasticity till subjected to freeze–thaw cycles. Géotechnique 2010, 60, 679–690. [Google Scholar] [CrossRef]
- Dacquay, C.; Holländer, H.M.; Kavgic, M.; Maghoul, P.; Liu, H.; Fujii, H. Evaluation of an integrated sewage pipe with ground heat exchanger for long-term efficiency estimation. Geothermics 2020, 86, 101796. [Google Scholar] [CrossRef] [Green Version]
- Bergman, T.L.; Lavine, A.; Incropera, F.P.; Dewitt, D.P. Fundamentals of Heat and Mass Transfer; John Wiley Sons: New York, NY, USA, 2017. [Google Scholar]
- Saaly, M.; Sinclair, R.; Kurz, D.; Maghoul, P.; Holländer, H.; Gheisari, A.F. Assessment of a Closed-Loop Geothermal System for Seasonal Freeze-Back Stabilization of Permafrost. GeoVirtual 2020. Available online: https://geovirtual2020.ca/wp-content/files/343.pdf (accessed on 15 July 2021).
- Liu, H.; Maghoul, P.; Shalaby, A.; Bahari, A. Thermo-hydro-mechanical modeling of frost heave using the theory of poroelasticity for frost-susceptible soils in double-barrel culvert sites. Transp. Geotech. 2019, 20, 100251. [Google Scholar] [CrossRef]
- Wang, S.; Qi, J.; Yin, Z.; Zhang, J.; Ma, W. A simple rheological element based creep model for frozen soils. Cold Reg. Sci. Technol. 2014, 106, 47–54. [Google Scholar] [CrossRef]



| Material | Thermal Conductivity (W/(m. K)) | Mass Heat Capacity (J/kg. K) | Density (kg/m3) |
|---|---|---|---|
| Sandy Gravel | 2.3 | 1255 | 2300 |
| Clayey Silt | 1.25 | 942 | 1900 |
| Water | 0.56 | 4188 | 1000 |
| Ice | 2.2 | 2093 | 917 |
| Coolant | 0.41 | 4250 | 955 |
| Property | Value |
|---|---|
| Latent heat of water (Lf) (kJ/kg) | 334 |
| Phase change temperature (Tpc) (°C) | 0 |
| Upward heat flux (W/m2) | 0.075 |
| HDPE pipe wall thickness (mm) | 2 |
| HDPE pipe wall thermal conductivity (W/(m. K)) | 0.46 |
| Operational Parameter | Value | Heat Extraction 1 (MW·h) | Final Thaw Settlement (cm) | |
|---|---|---|---|---|
| Lagoon | Embankment | |||
| Fluid Temperature (°C) | −1 | 328 | 5.1 | 7.4 |
| −5 | 573 | 2.2 | 2.4 | |
| −10 | 954 | −0.5 (Heave) | 3.5 | |
| −15 | 1339 | −1.9 (Heave) | 2.3 | |
| Fluid Velocity (m/s) | 0.2 | 547 | 2.5 | 28.9 |
| 0.4 | 573 | 2.2 | 2.4 | |
| 0.6 | 565 | 2.4 | 9.8 | |
| Burial Depth (m) | 1.5 | 573 | 2.2 | 2.4 |
| 2.5 | 387 | 2.1 | 16.3 | |
| 3.5 | 336 | 2.2 | 10.9 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fatollahzadeh Gheisari, A.; Maghoul, P.; Holländer, H.M.; Kenyon, R.; Sinclair, R.; Saaly, M. The Long-Term Mitigating Effect of Horizontal Ground-Source Heat Exchangers on Permafrost Thaw Settlement. Processes 2021, 9, 1636. https://doi.org/10.3390/pr9091636
Fatollahzadeh Gheisari A, Maghoul P, Holländer HM, Kenyon R, Sinclair R, Saaly M. The Long-Term Mitigating Effect of Horizontal Ground-Source Heat Exchangers on Permafrost Thaw Settlement. Processes. 2021; 9(9):1636. https://doi.org/10.3390/pr9091636
Chicago/Turabian StyleFatollahzadeh Gheisari, Amir, Pooneh Maghoul, Hartmut M. Holländer, Rob Kenyon, Rob Sinclair, and Maryam Saaly. 2021. "The Long-Term Mitigating Effect of Horizontal Ground-Source Heat Exchangers on Permafrost Thaw Settlement" Processes 9, no. 9: 1636. https://doi.org/10.3390/pr9091636
APA StyleFatollahzadeh Gheisari, A., Maghoul, P., Holländer, H. M., Kenyon, R., Sinclair, R., & Saaly, M. (2021). The Long-Term Mitigating Effect of Horizontal Ground-Source Heat Exchangers on Permafrost Thaw Settlement. Processes, 9(9), 1636. https://doi.org/10.3390/pr9091636





