Research on Feedback-Linearized Sliding Mode Control of Direct-Drive Volume Control Electro-Hydraulic Servo System
Abstract
1. Introduction
2. Principle of the DDVC Electro-Hydraulic Servo System
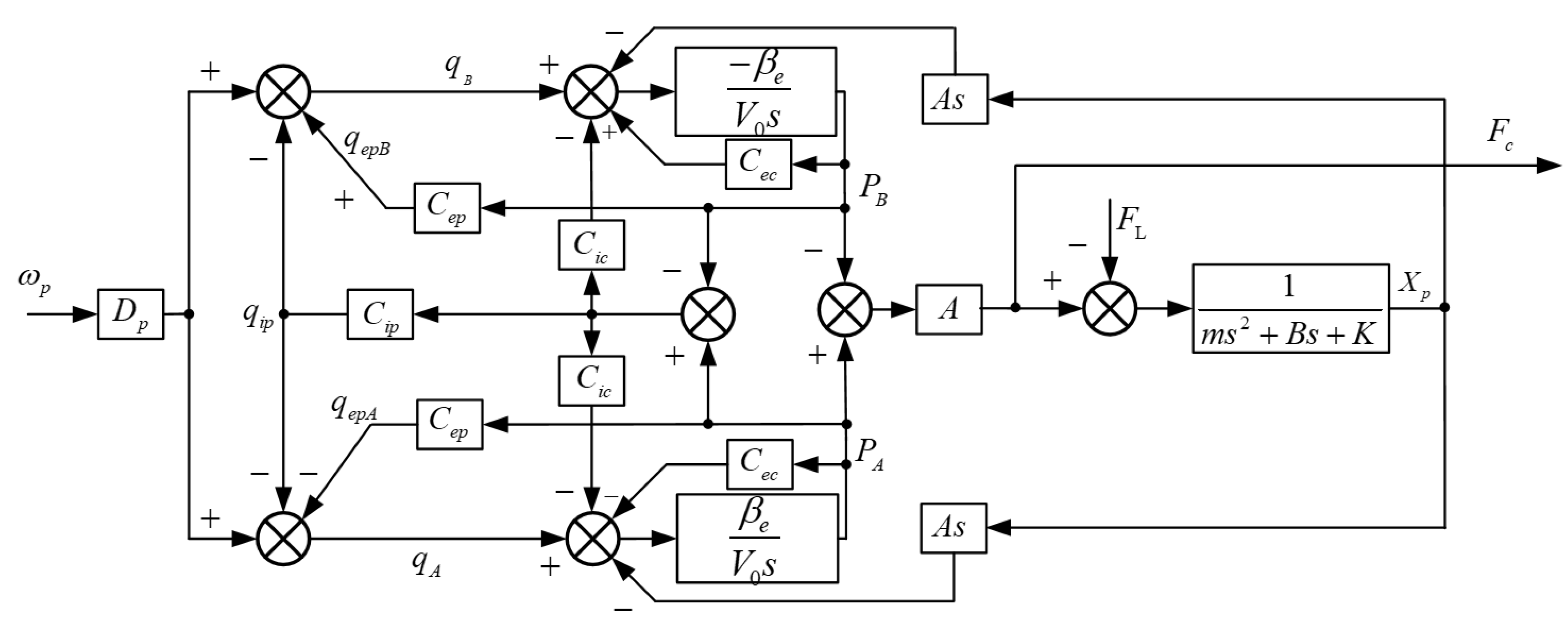
3. Nonlinear Mathematical Model of the DDVC Electro-Hydraulic Servo System
3.1. Servo Motor Control Unit
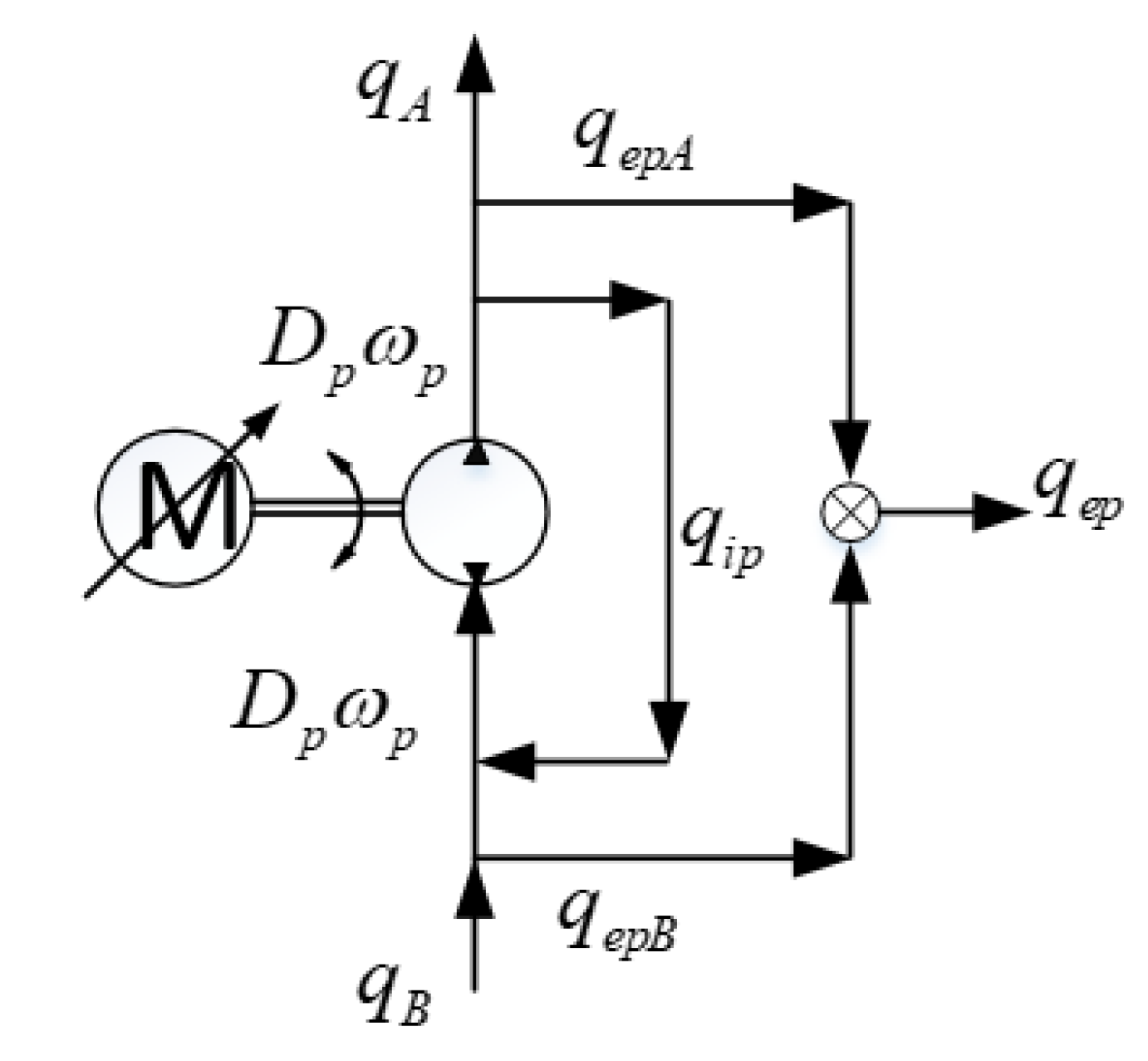
3.2. Fixed-Displacement Radial Piston Pump
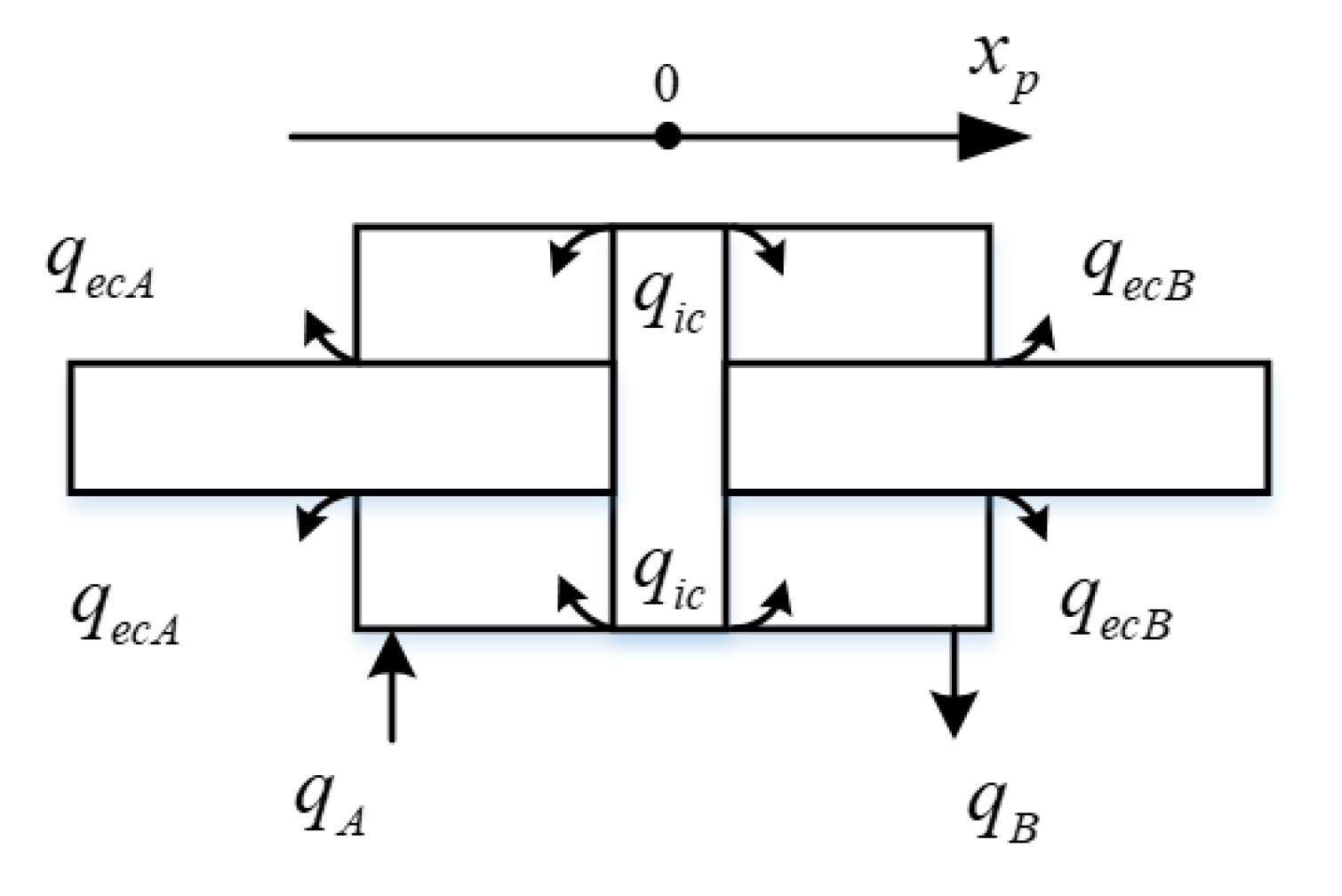
3.3. Double-Acting Symmetrical Hydraulic Cylinder
4. Feedback Linearization of Nonlinear Models
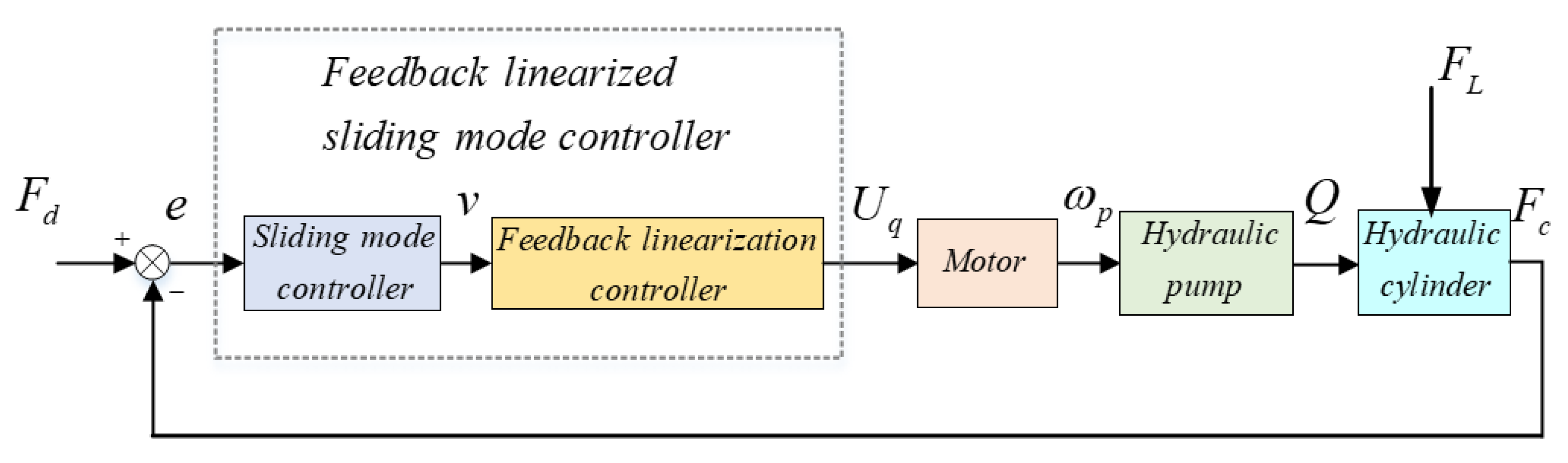
5. Sliding Mode Controller Design
6. Experimental Study
6.1. Electro-Hydraulic Servo System Test Bench Design
6.2. Experiment Content and Result Analysis
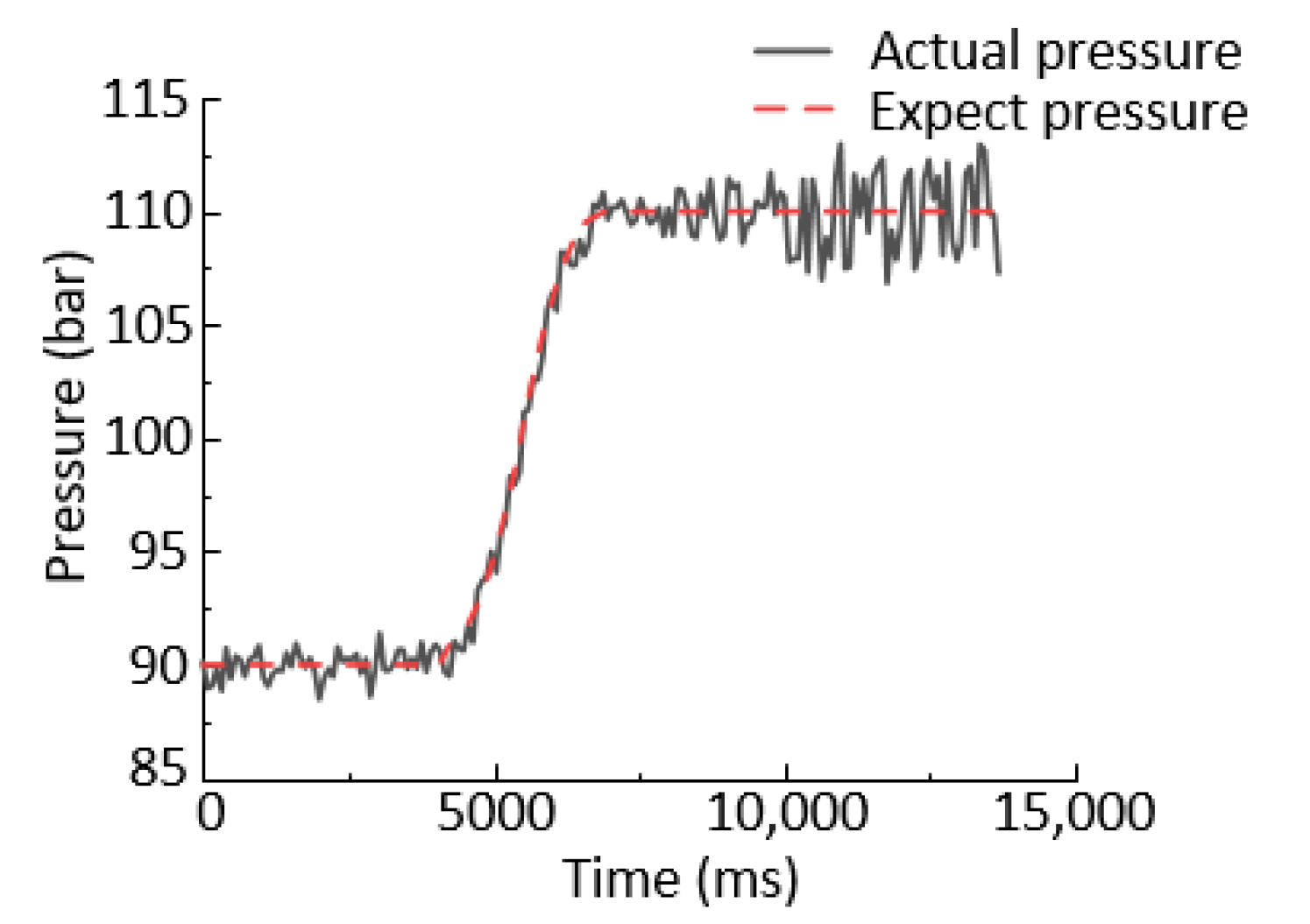
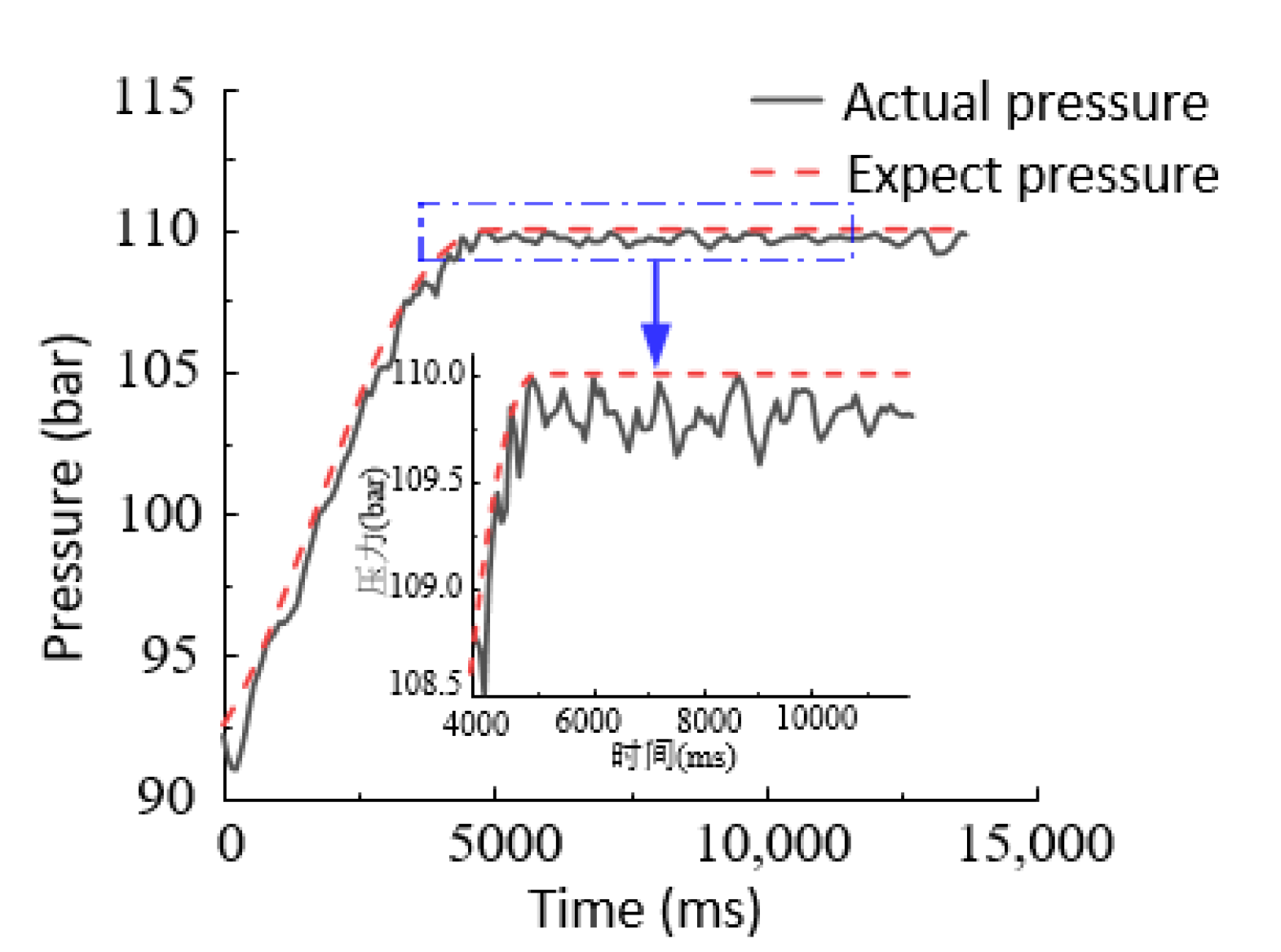
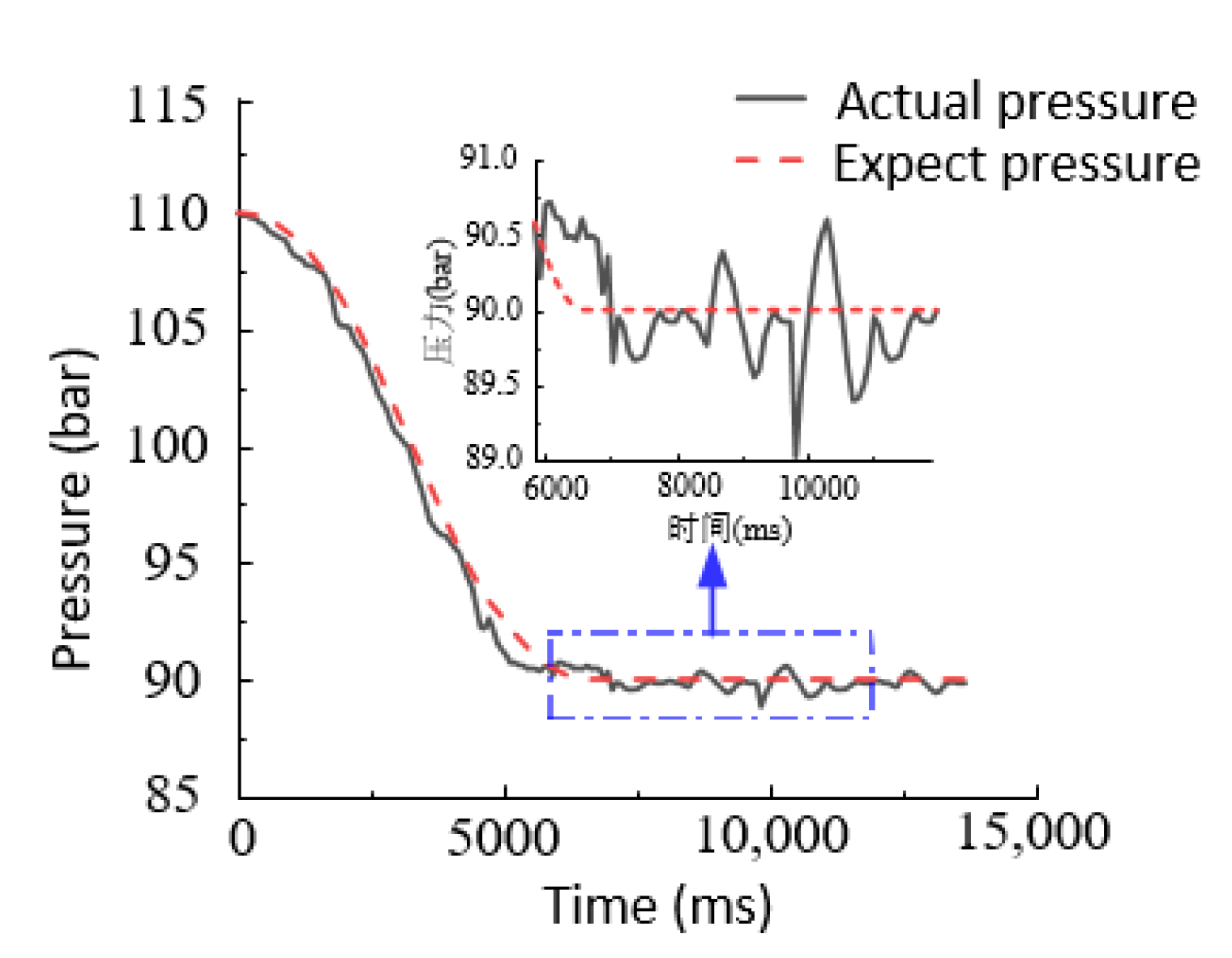
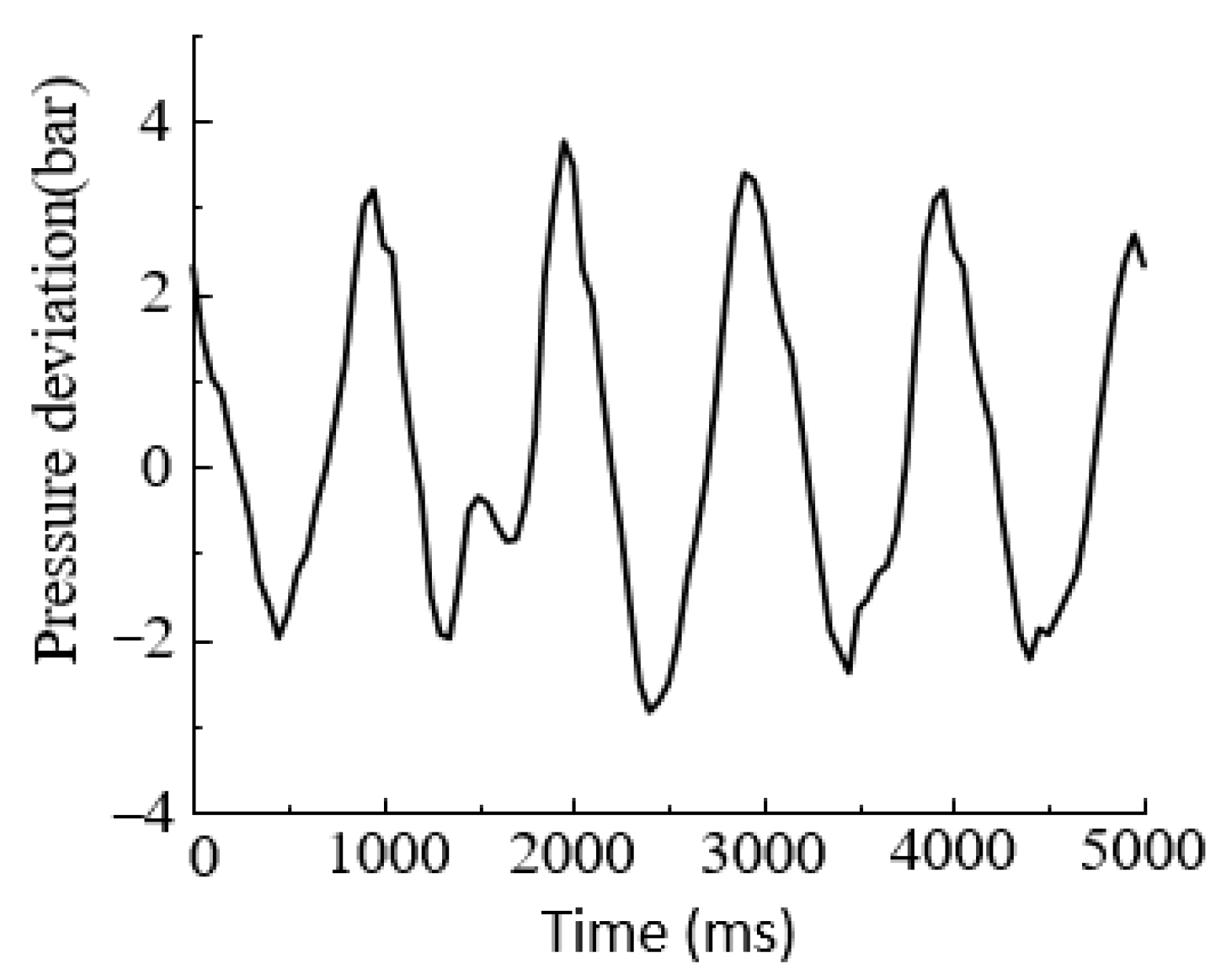
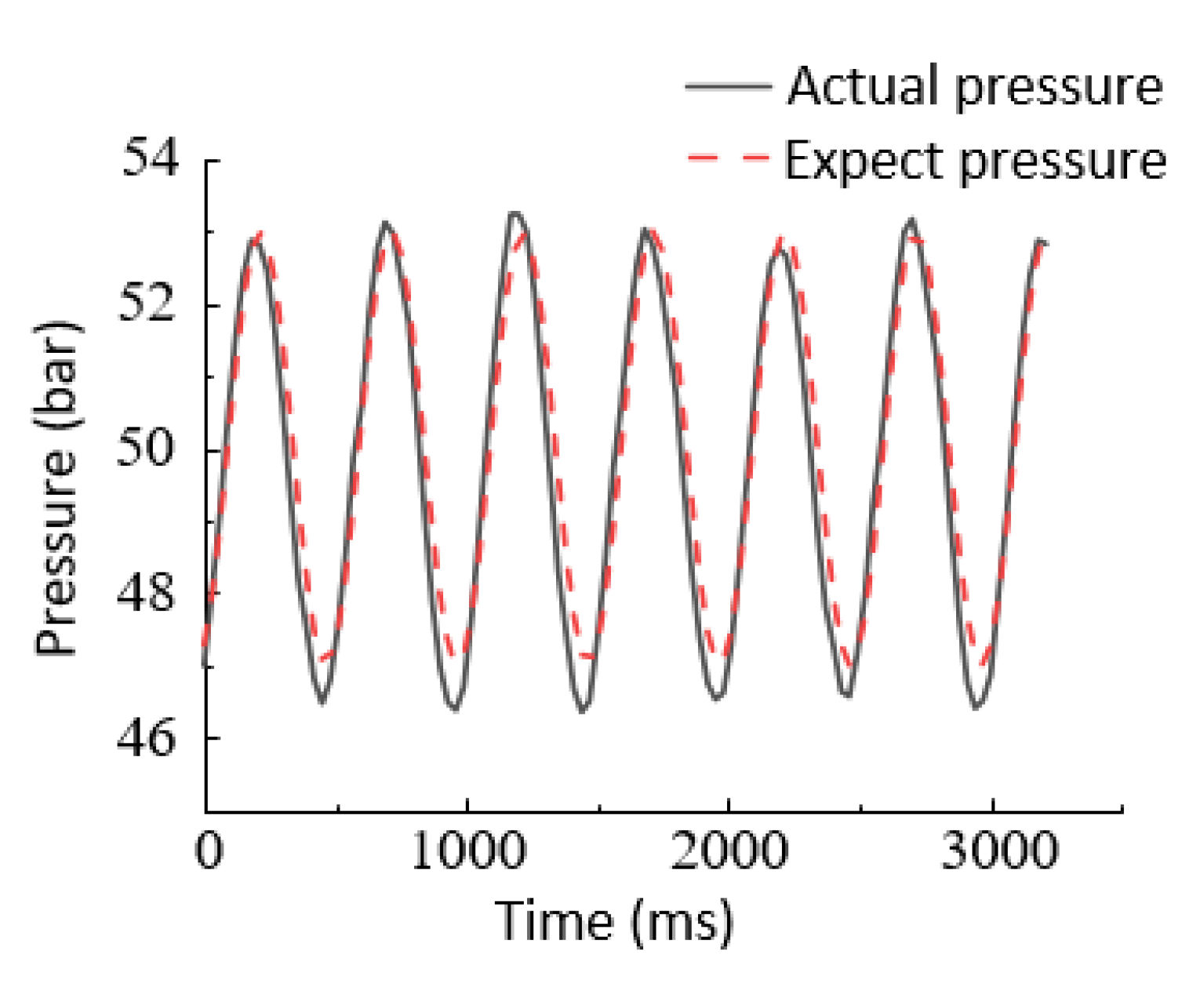
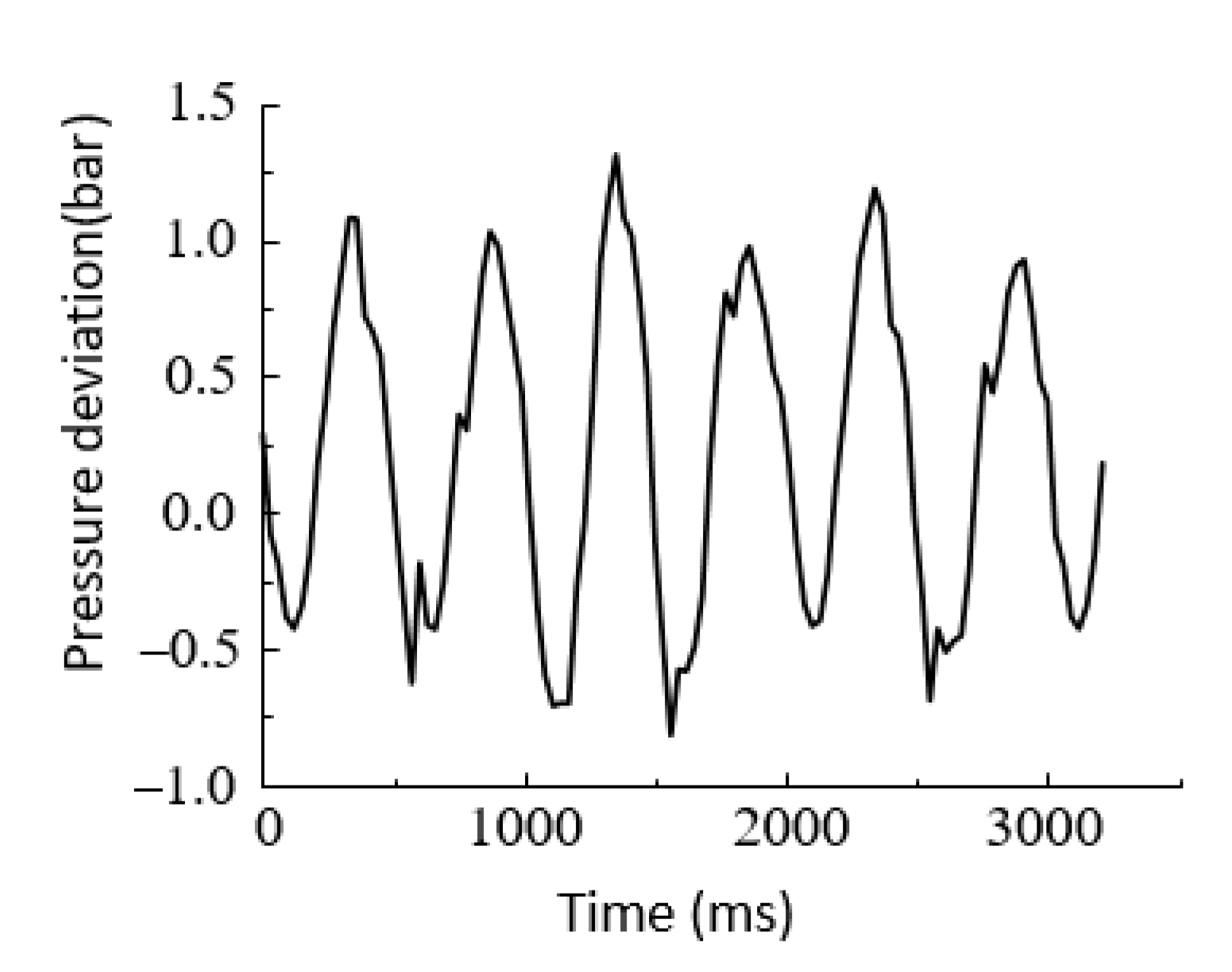
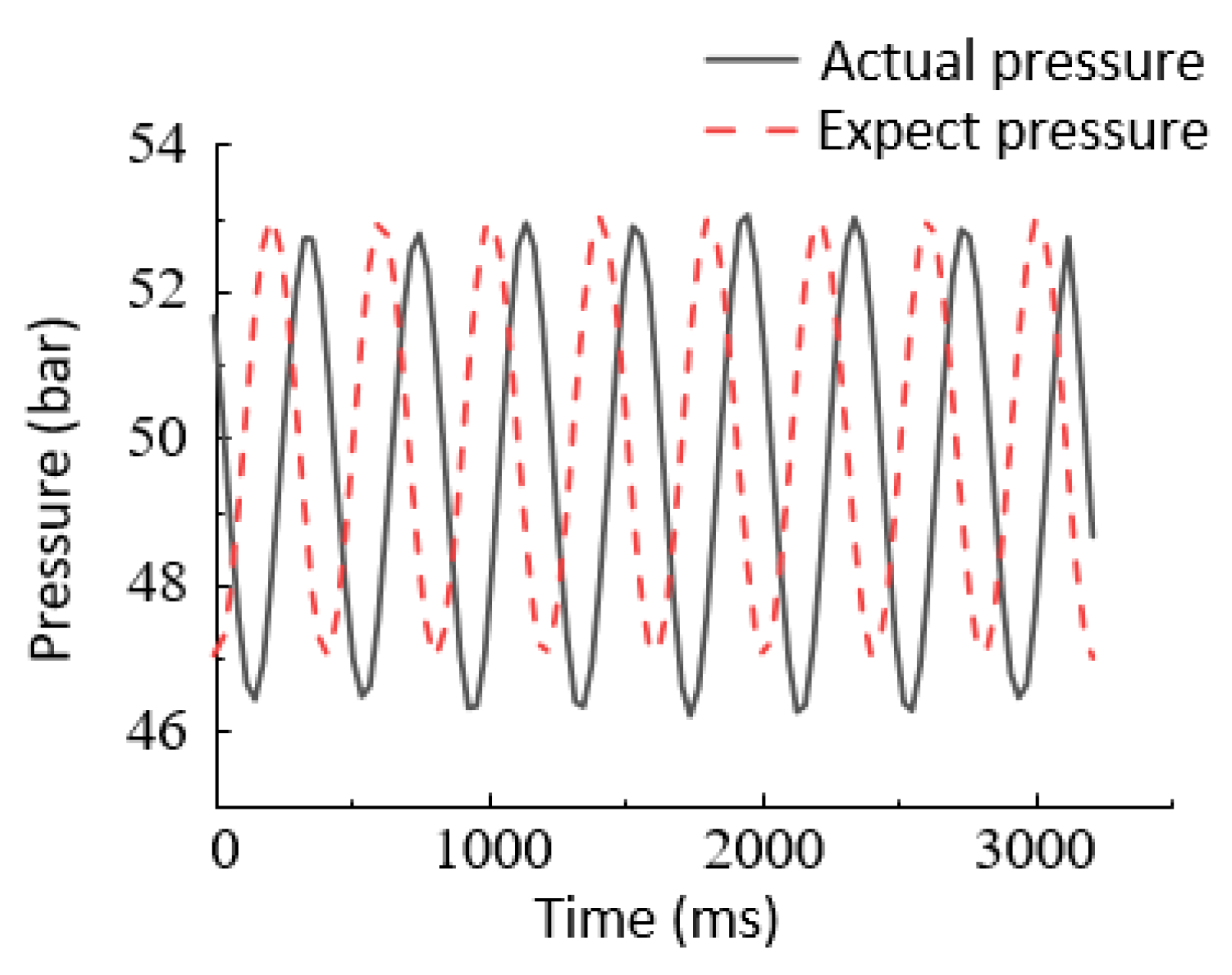
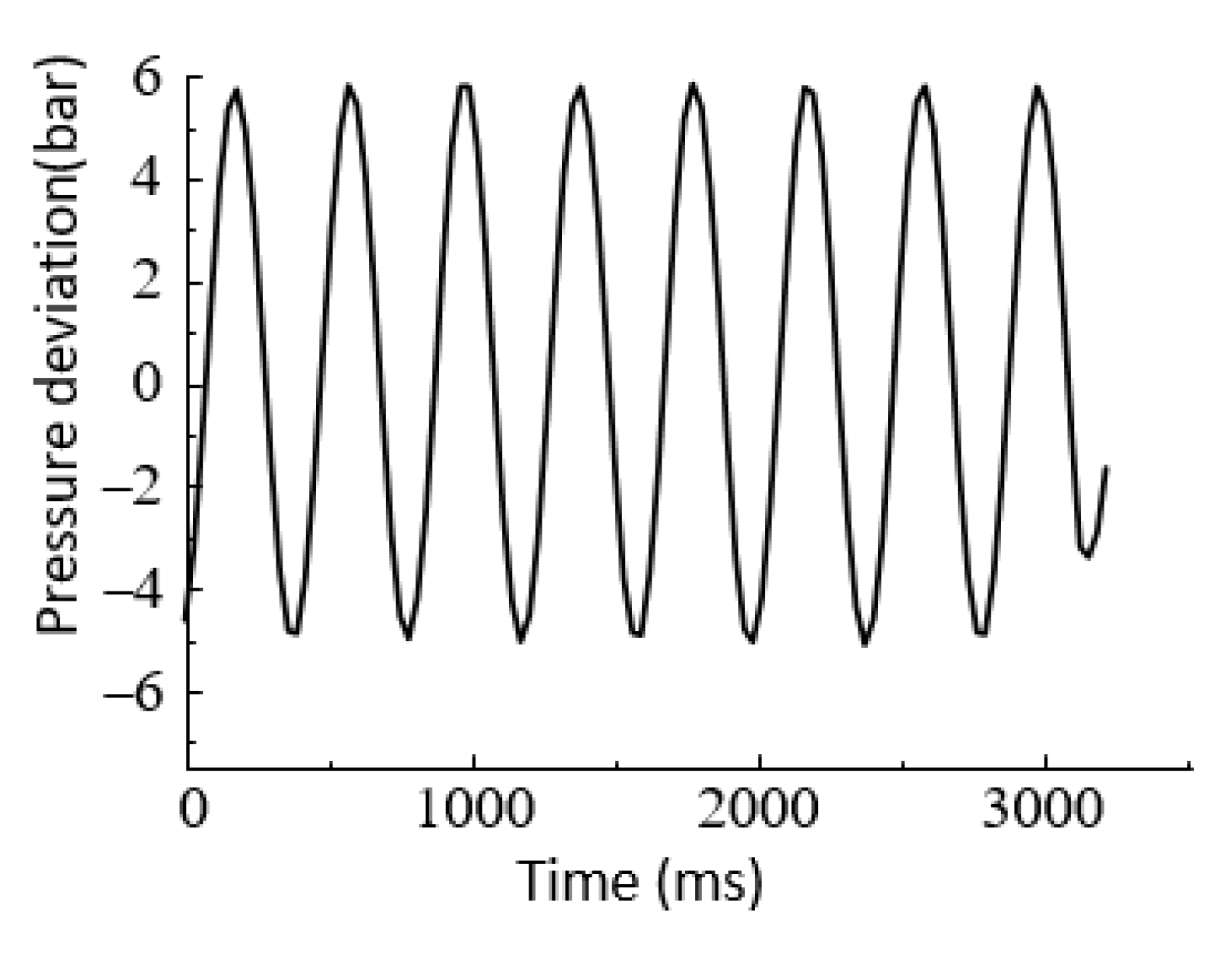
6.2.1. Step Signal Response Experiment
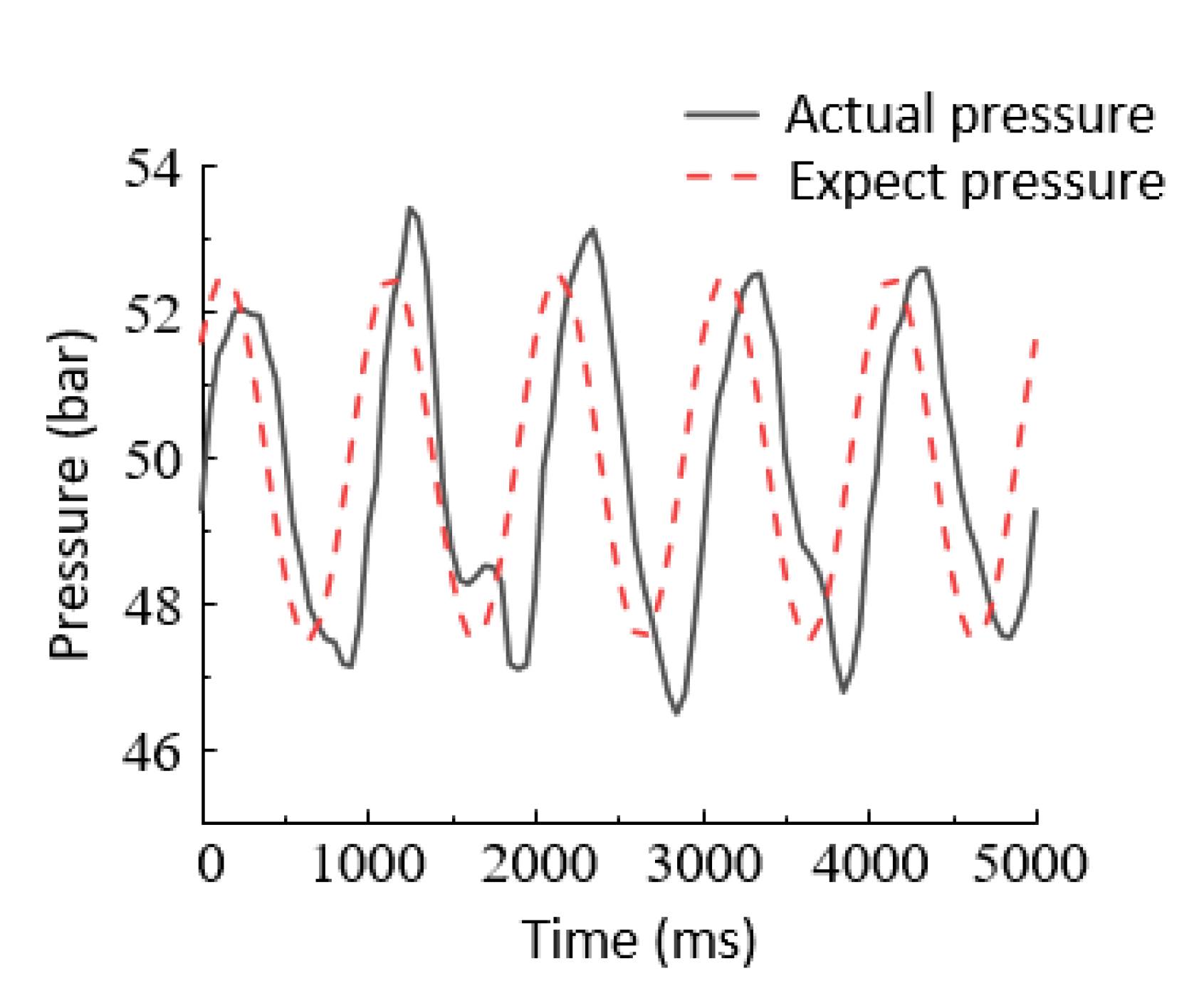
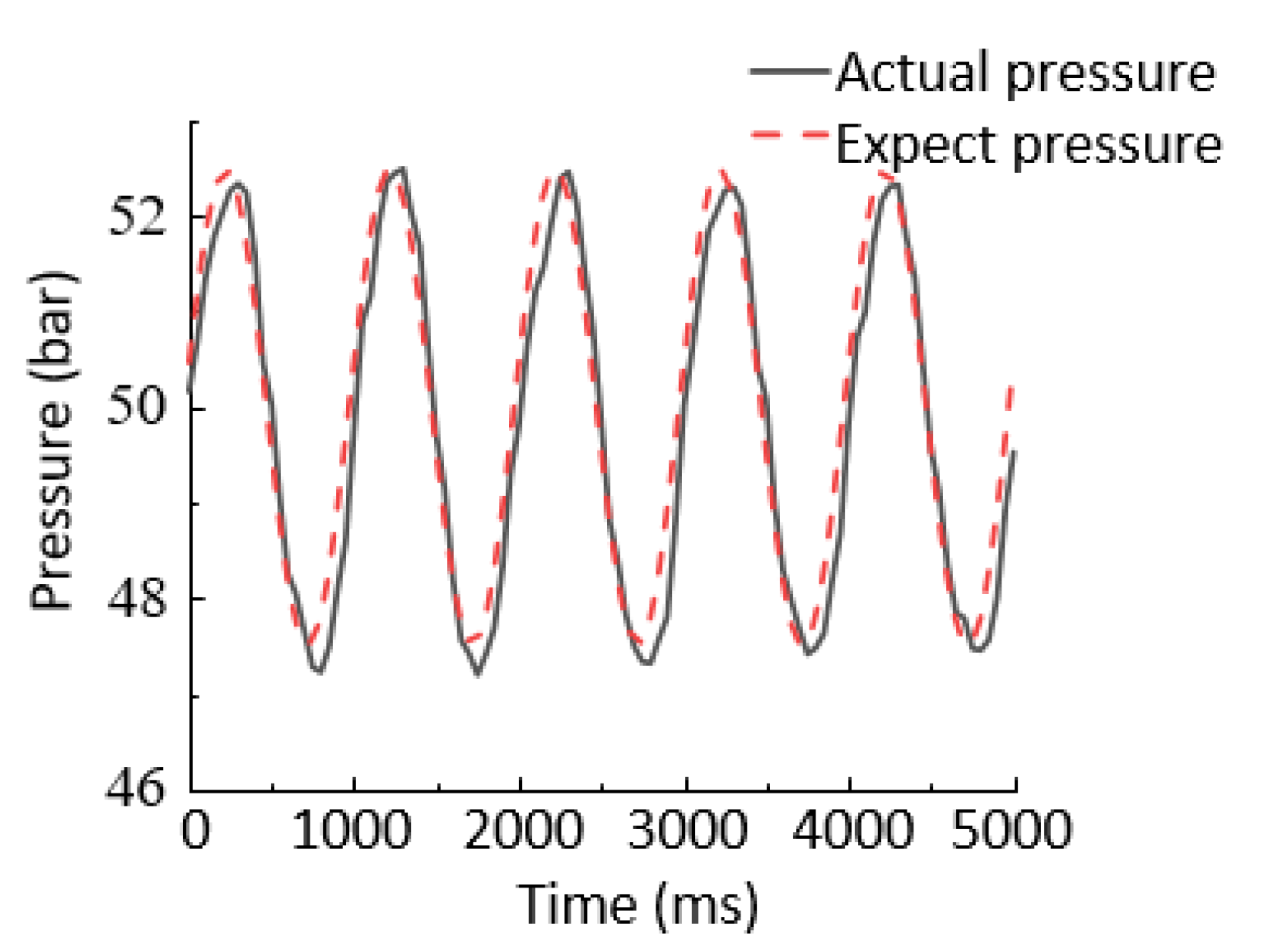
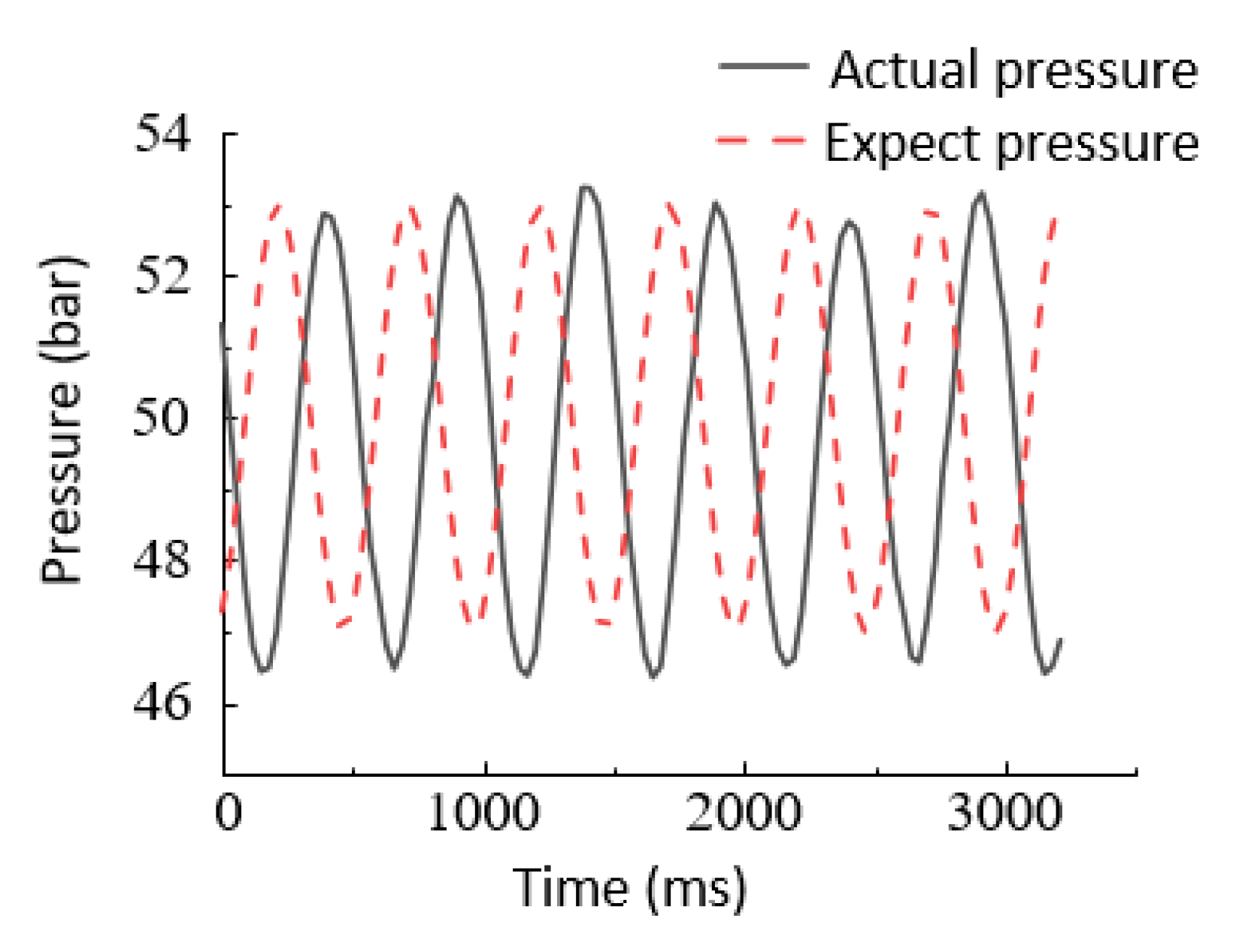
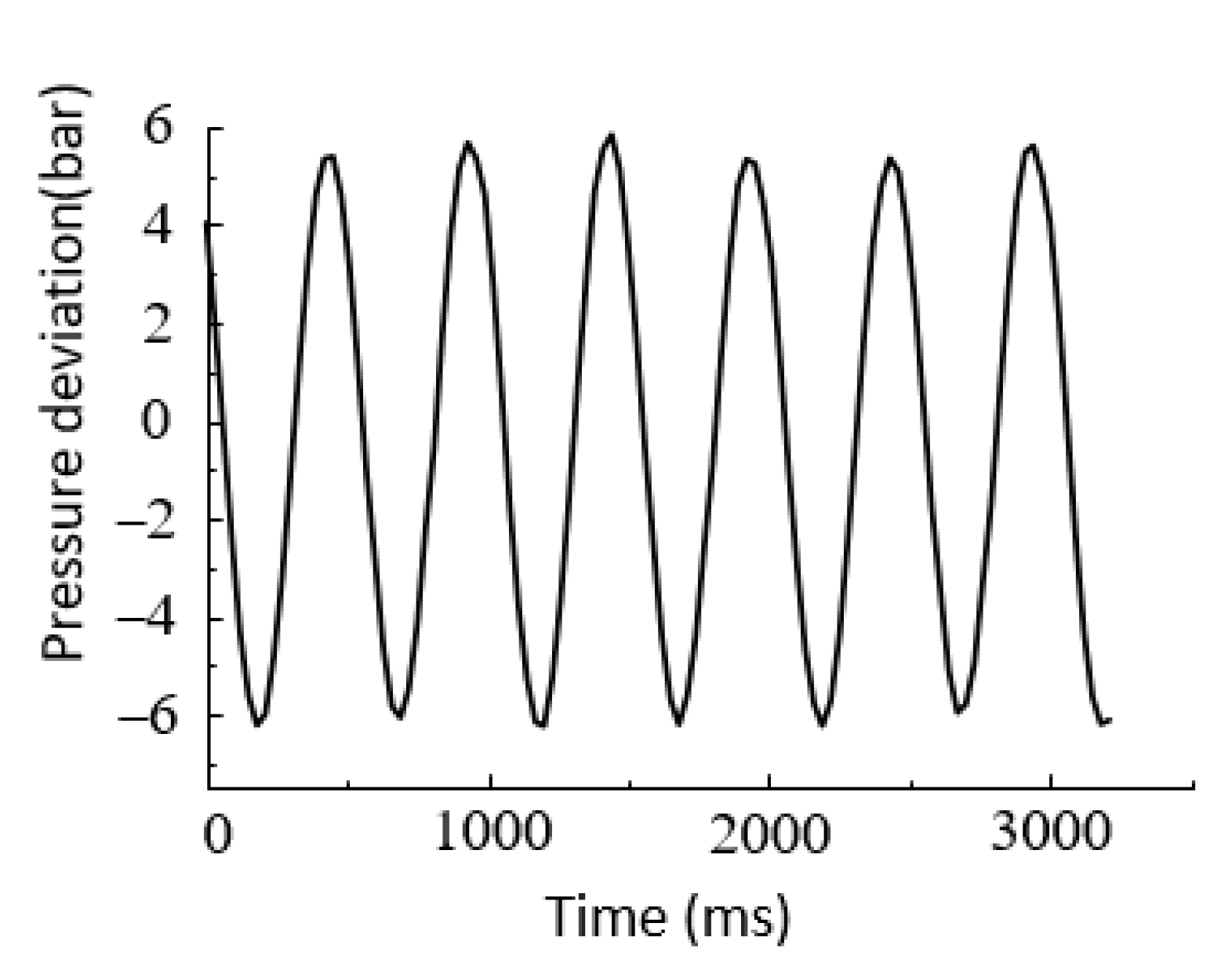
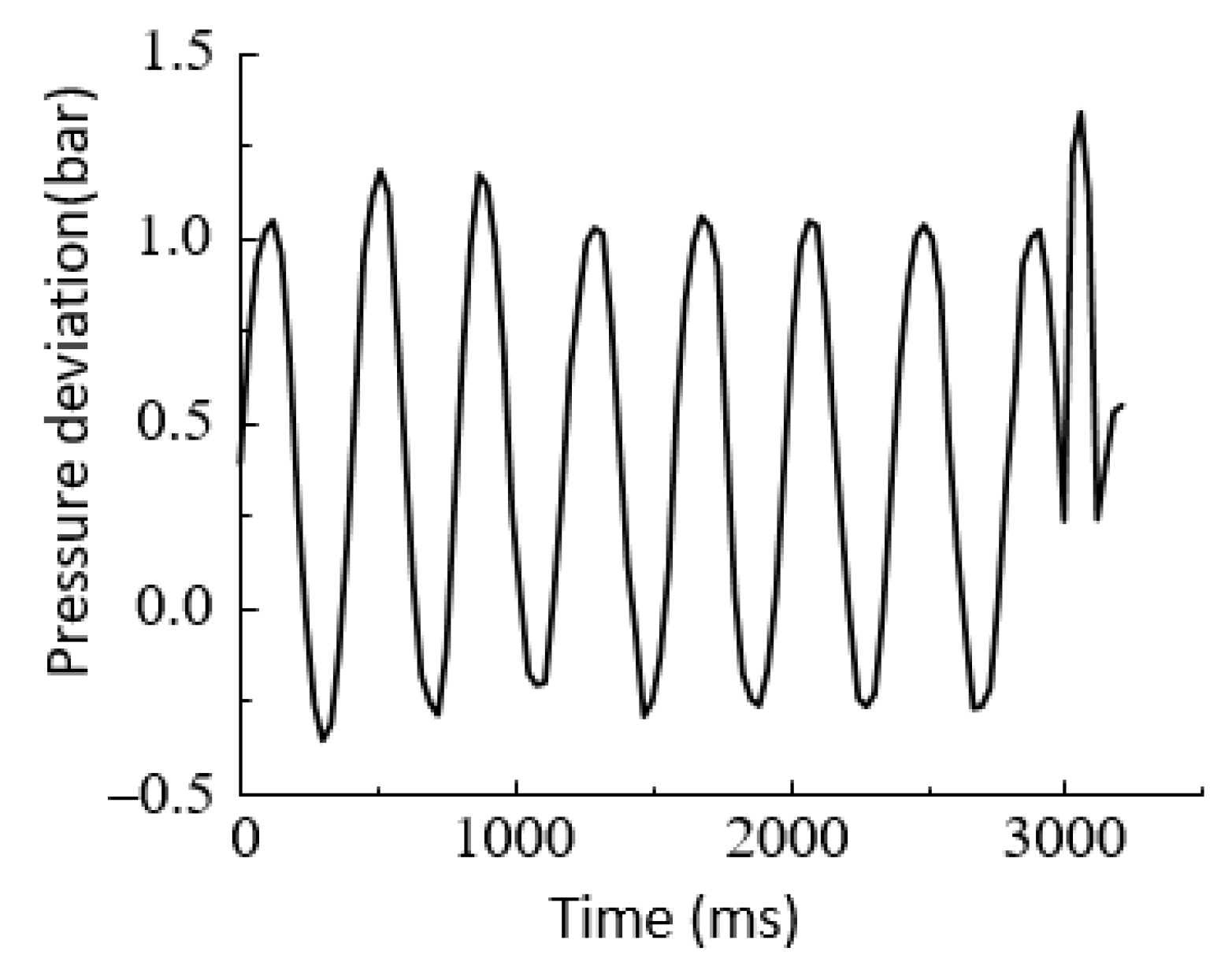
6.2.2. Sinusoidal Response Experiments
7. Conclusions
- (1)
- The mathematical model of the DDVC electro-hydraulic servo system was established, and the pressure output transfer function of the system was deduced.
- (2)
- Considering the nonlinearity of the system, a feedback-linearized sliding mode control strategy was proposed to deal with the nonlinear components of the system and convert the dynamic performance of the nonlinear system to linear characteristics to optimize the control performance of the system. The linearized sliding mode control strategy was applied to the DDVC system for high-precision pressure control.
- (3)
- The experimental analysis shows that the proposed controller can effectively improve the pressure output accuracy of the electro-hydraulic servo pressure control system and improve the dynamic response characteristics of the system compared with the PID controller. However, some idealized models of the system are simplified. To improve the nonlinear accuracy of the system, the nonlinear model can be further refined.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bo, W.; Yunxiao, H.; Long, Q.; Xiangyu, W.; Lei, G.; Bin, Z. Research on characteristics of electro hydraulic servo system controlled by separate cavity independent variable speed pump. J. Mech. Eng. 2020, 56, 235–243. [Google Scholar] [CrossRef]
- Penghui, Z. Research on Position Control of Transferable Vane Electro-Hydraulic Servo Closed Pump Control System. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2020. [Google Scholar]
- Bing, Y. Study on Thermal Balance of Direct-Drive Volumetric Control Electro-Hydraulic Servo System. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2020. [Google Scholar]
- Helbig, A. Injection moulding machine with electric-hydrostatic drives. In Proceedings of the 3. International Fluid Power Conference (3. IFK), Aachen, Germany, 5–6 March 2002; pp. 67–82. [Google Scholar]
- Sedrak, D. Closed-loop electronic valuing and the application of variable voltage variable frequency in hydraulics. Elev. World 1999, 47, 66–72. [Google Scholar]
- Lee, S.R.; Hong, Y.S. A dual EHA system for the improvement of position control performance via active load compensation. Int. J. Precis. Eng. Manuf. 2017, 18, 937–944. [Google Scholar] [CrossRef]
- Ahn, K.K.; Nam, C.; Jin, M. Adaptive backstepping control of an electro-hydraulic actuator. IEEE ASME Trans. Mechatron. 2014, 19, 987–995. [Google Scholar] [CrossRef]
- Zhen, Z.; Haijun, L.; Xiaoyan, Q.; Zhen, Z. Robust feedback linearization control of electro-hydraulic position servo system. Mach. Tools Hydraul. 2016, 44, 148–152. [Google Scholar]
- Juni, H. Development and application of electro-hydraulic servo system. Mach. Tool Hydraul. 2012, 40, 15–18. [Google Scholar]
- Ruidong, L. Analysis and Compensation Method for Position and Force Control Characteristics of Electrohydrostatic System. Master’s Thesis, Yanshan University, Qinhuangdao, China, 2020. [Google Scholar]
- Song, B.; Lee, D.; Park, S.Y.; Baek, Y.S. Design and performance of nonlinear control for an electro-hydraulic actuator considering a wearable robot. Processes 2019, 7, 389. [Google Scholar] [CrossRef]
- Helian, B.; Chen, Z.; Yao, B. Precision motion control of a servomotor-pump direct-drive electrohydraulic system with a nonlinear pump flow mapping. IEEE Trans. Ind. Electron. 2020, 67, 8638–8648. [Google Scholar] [CrossRef]
- Kim, J.H.; Hong, Y.S. Robust internal-loop compensation of pump velocity controller for precise force control of an electro-hydrostatic actuator. J. Drive Control 2018, 15, 55–60. [Google Scholar]
- Kim, J.H.; Hong, Y.S. Improvement of back drivability of a force-controlled EHA by introducing bypass flow control. Int. J. Precis. Eng. Manuf. 2020, 21, 819–830. [Google Scholar] [CrossRef]
- Komsta, J.; Adamy, J.; Antoszkiewicz, P. Input-output linearization and integral sliding mode disturbance compensation for electro-hydraulic drives. In Proceedings of the 2010 11th International Workshop on Variable Structure Systems (VSS), Mexico City, Mexico, 26–28 June 2010; pp. 446–451. [Google Scholar] [CrossRef]
- Koch, S.; Reichhartinger, M. Observer-based sliding mode control of hydraulic cylinders in the presence of unknown load forces. e i Elektrotechnik Inf. 2016, 133, 253–260. [Google Scholar] [CrossRef][Green Version]
- Huang, J.; An, H.; Ma, H.; Wei, Q.; Wang, J. Electro-hydraulic servo force control of foot robot based on feedback linearization sliding mode control. In Proceedings of the 2018 13th World Congress on Intelligent Control and Automation (WCICA), Changsha, China, 4–8 July2018; pp. 1441–1445. [Google Scholar]
- Lu, X.; Wei, H.; Zhuoping, Y.; Haocheng, L. Accurate hydraulic pressure control of master cylinder of integrated electronic hydraulic braking system considering key nonlinear characteristics. J. Mech. Eng. 2019, 55, 117–126. [Google Scholar] [CrossRef]
- Kou, F.; Du, J.; Wang, Z.; Li, D.; Xu, J. Nonlinear modeling and coordinate optimization of a semi-active energy regenerative suspension with an electro-hydraulic actuator. Algorithms 2018, 11, 12. [Google Scholar] [CrossRef]
- Zhu, Y.; Tang, S.; Wang, C.; Jiang, W.; Zhao, J.; Li, G. Absolute stability condition derivation for position closed-loop system in hydraulic automatic gauge control. Processes 2019, 7, 766. [Google Scholar] [CrossRef]
- Wang, C. Hydraulic Control System; China Machine Press: Beijing, China, 2012; pp. 41–42. [Google Scholar]
- Zhang, Z.; Li, H.; Zhu, D. EHA feedback linearization optimal sliding mode surface double fuzzy sliding mode control. J. Beijing Univ. Aeronaut. Astronaut. 2016, 42, 1398–1405. [Google Scholar]






| Parameter | Physical Meaning | Value |
|---|---|---|
| ((m3/s)/Pa) | Internal leakage coefficient of pump | 1 × 10−13 |
| Cep ((m3/s)/Pa) | External leakage coefficient of pump | 1 × 10−13 |
| D (mL/r) | pump delivery | 0.8 |
| (kW) | Rated power of pump | 1 |
| Pm (MPa) | Maximum working pressure of pump | 21 |
| Cic ((m3/s)/Pa) | Internal leakage coefficient of hydraulic cylinder | 1 × 10−13 |
| (N/(m/s)) | Damping coefficient of piston | 150 |
| Gas polytropic coefficient | 1.3 | |
| (N) | Sliding static friction | 25 |
| Fc (N) | Sliding Coulomb friction | 15 |
| (mL) | Initial volume of one side of hydraulic cylinder | 450 |
| (N/m2) | Oil elastic modulus | 6.5 × 108 |
| (cm2) | Effective area of piston | 71 |
| (Kg) | Load conversion quality | 2000 |
| (mL) | Initial gas volume of accumulator | 200 |
| Pai (MPa) | Initial pressure of accumulator | 3 |
| (mL) | Initial oil volume of accumulator | 200 |
| (V) | Rated voltage of servo motor | 220 |
| (kW) | Rated power of servo motor | 1 |
| (r/min) | Rated speed of servo motor | 3000 |
| (N·m) | Servo motor torque | 3.18 |
| (kg·m2) | Moment of inertia of servo motor | 2.65 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, G.; Jia, P.; Yan, G.; Liu, H.; Chen, W.; Jia, C.; Ai, C. Research on Feedback-Linearized Sliding Mode Control of Direct-Drive Volume Control Electro-Hydraulic Servo System. Processes 2021, 9, 1676. https://doi.org/10.3390/pr9091676
Chen G, Jia P, Yan G, Liu H, Chen W, Jia C, Ai C. Research on Feedback-Linearized Sliding Mode Control of Direct-Drive Volume Control Electro-Hydraulic Servo System. Processes. 2021; 9(9):1676. https://doi.org/10.3390/pr9091676
Chicago/Turabian StyleChen, Gexin, Pengshuo Jia, Guishan Yan, Huilong Liu, Wenbin Chen, Chunyu Jia, and Chao Ai. 2021. "Research on Feedback-Linearized Sliding Mode Control of Direct-Drive Volume Control Electro-Hydraulic Servo System" Processes 9, no. 9: 1676. https://doi.org/10.3390/pr9091676
APA StyleChen, G., Jia, P., Yan, G., Liu, H., Chen, W., Jia, C., & Ai, C. (2021). Research on Feedback-Linearized Sliding Mode Control of Direct-Drive Volume Control Electro-Hydraulic Servo System. Processes, 9(9), 1676. https://doi.org/10.3390/pr9091676





