Applying the Swept Rule for Solving Two-Dimensional Partial Differential Equations on Heterogeneous Architectures

Abstract

The partial differential equations describing compressible fluid flows can be notoriously difficult to resolve on a pragmatic scale and often require the use of high-performance computing systems and/or accelerators. However, these systems face scaling issues such as latency, the fixed cost of communicating information between devices in the system. The swept rule is a technique designed to minimize these costs by obtaining a solution to unsteady equations at as many possible spatial locations and times prior to communicating. In this study, we implemented and tested the swept rule for solving two-dimensional problems on heterogeneous computing systems across two distinct systems and three key parameters: problem size, GPU block size, and work distribution. Our solver showed a speedup range of 0.22–2.69 for the heat diffusion equation and 0.52–1.46 for the compressible Euler equations. We can conclude from this study that the swept rule offers both potential for speedups and slowdowns and that care should be taken when designing such a solver to maximize benefits. These results can help make decisions to maximize these benefits and inform designs.

1. Introduction

Unsteady partial differential equations (PDEs) are used to model many important phenomena in science and engineering. Among these, fluid dynamics and heat transfer can be notoriously difficult to solve on pragmatic scales. These problems often require using distributed memory computing systems to obtain a solution with practical grid resolution or scale in a reasonable time frame. In this regard, the CFD 2030 Vision report expresses several challenges in fluid dynamics that require “orders of magnitude improvement” in simulation capabilities [1].

Advancing the solution at any point in a fluid dynamics grid inherently depends on the neighboring points in each spatial dimension. Solving large problems on distributed computing systems relies on domain decomposition, which assigns regions of the simulation domain to different compute nodes/processors. The dependence on neighboring states requires communication between computing nodes to transfer data associated with the boundary locations. Traditionally, this happens after each time step, when boundary information is needed to advance the solution further. Each of these communication events incur a minimum cost regardless of the amount of information communicated—this is network latency. In contrast, bandwidth is the variable cost associated with the amount of data transferred.

Achieving the goals outlined in the CFD 2030 Vision report requires focusing on solvers that effectively use heterogeneous HPC systems. High latency costs are a substantial barrier in achieving these goals [1], and advancements here have been slower than other performance aspects [2]. Latency is a bottleneck in the system that can limit the performance regardless of the architecture.

Graphics processing units (GPUs) are powerful tools for scientific computing because they are well suited for parallel applications and large quantities of simultaneous calculations. Modern computing clusters often have GPUs in addition to CPUs because of their potential to accelerate simulations and, similar to CPUs, they perform best when communication is minimized. These modern clusters are often referred to as heterogeneous systems or systems with multiple processor types—CPUs and GPUs, in this case [3,4]. Ideally, a heterogeneous application will minimize communication between the GPU and CPU, which effectively minimizes latency costs. Minimizing latency in high-performance computing is one of the barriers to exascale computing that requires the implementation of novel techniques to improve [5].

This study presents our implementation and testing of a two-dimensional heterogeneous solver for unsteady partial differential equations that employs a technique to help overcome network latency: the swept rule [6]. The swept rule is a latency reduction technique that focuses on obtaining a solution to unsteady PDEs at as many possible locations and times prior to communicating with other computing nodes (ranks). In this article, we first discuss related work, distinguish our work from prior swept studies, and provide more motivation in Section 2. Next, we describe implementation details, objectives, study parameters, design decisions, methods, and tests in Section 3, and follow with results, discussion, and conclusions in Section 4, Section 5 and Section 6.

2. Related Work

Surmounting network latency costs has been approached in many ways; the most closely related to this work include prior swept rule studies, which involve multiple dimensions and architectures but not the combination of the two [6,7,8,9]. Parallel-in-time methods are similar cost reduction techniques, but they differ in the sense that they iteratively parallelize the temporal direction, whereas the swept rule minimizes communication [10]. There are many examples of parallel-in-time methods, which are all variations of the core concept [11,12,13,14,15,16]. For example, Parareal is one of the more popular parallel-in-time methods; it works by iterating over a series of coarse and fine grids with initial guesses to parallelize the problem [12]. However, there are some stability concerns with Parareal that are addressed by local time integrators [13]. These methods have the same goal but achieve that goal differently. Similarly, techniques that strive for higher cache locality aim to reduce communication costs, but they achieve it differently. These methods focus on improving cache locality and management, i.e., having the information readily available in memory that is quickly accessed [17,18,19,20]. These differ from the swept rule in that they optimize communication rather than avoid it.

Communication-avoidance techniques involve overlapping parts or redundant operations. Our GPU implementation of the swept rule particularly blurs this difference because it solves an extra block to avoid intranode communication but no extra blocks are solved for internode communication. The swept rule also differs because it particularly focuses on solving PDEs. Many communication avoidance algorithms tend to focus on linear algebra [21,22,23,24,25]. Finally, the DiamondTorre algorithm is designed to improve bandwidth costs of simulations and fully realize parallelism on GPUs by achieving high levels of data localization [26].

The swept rule was originally developed by Alhubail and Wang [6], who presented a one-dimensional CPU-only swept PDE solver and tested it by solving the Kuramoto–Sivashinsky equation and the compressible Euler equations. They showed in both cases that a number of integrations can be performed during the time of a communication. Their analysis showed that applying the swept rule accelerates time integration on distributed computing systems [6]. Alhubail et al. [7] followed this work with a two-dimensional CPU only swept PDE solver that reported speedups of up to three times compared to classical methods when solving the wave and Euler equations. These studies differ from our study most prominently by the dimensionality and intended architecture.

Magee et al. created a one-dimensional GPU swept solver and a one-dimensional heterogeneous solver and applied both to solving the compressible Euler equations [8,9]. They concluded that their shared memory approach typically performs better than alternative approaches, but did not obtain speedup for all cases in either study. Varying performance results were attributed to greater usage of lower-level memory, which can limit the benefits of the swept rule depending on the problem [8]. Our current study extends upon the swept rule for heterogeneous architectures, but it differs in the dimensionality. Our implementation also attempts to use and extend some of the implementation strategies that showed promise in the aforementioned studies.

The effect of added dimensionality on performance is a pragmatic interest and can be considered from multiple perspectives. The primary goal is speeding up simulations requiring high-performance computing by reducing network latency. The swept rule is motivated by reducing the time to obtain solutions of problems involving complicated phenomena frequently requiring the use of high-performance computing systems. While many simplifications exist to reduce the dimensionality of fluid dynamics problems, most realistic problems are three-dimensional. Our solver is a step toward more realistic simulations by considering two spatial dimensions, which can provide insight into multidimensional performance and constraints. This insight can offer the chance to optimize system usage and promote faster design and prototype of thermal fluid systems.

In the event that computation time is not the primary concern, available resources or resource costs are important considerations. The ability to execute a simulation on a high-performance computing system depends on access to such systems. Pay-per-use systems such as Amazon AWS, Microsoft Azure, and Google Cloud offer cloud computing time. However, pricing models for university-managed clusters remain ambiguous, making determination of cost challenging on the user’s end [27]. In the case of Amazon EC2, simulation time can be purchased at different hourly rates depending on the application. We generated an estimate using Amazon’s pricing tool with a two-node configuration (g4dn.xlarge instances) that yielded a monthly “on-demand” cost of $928.46 [28]. Purchasing such time quickly becomes expensive for applications that require large numbers of computing hours or larger hardware configurations. Network latency contributes substantially to this cost as it is aggrandized in applications requiring a great amount of communication because each communication event takes a finite amount of time regardless of the data size.

Furthermore, it is possible to obtain and show performance benefits on smaller systems. This claim is supported by findings from Magee et al., who showed speedup on a workstation with a single GPU and CPU [8]. While this is not the primary focus, an optimized solver would require less computing resources and more practical applications could potentially be solved on smaller, less costly computing clusters. Hopefully, it is clear at this point that latency reduction is important in high-performance computing and scientific applications as this is the intention of this work.

3. Materials and Methods

3.1. Implementation & Objectives

We call our implementation of the two-dimensional swept rule PySweep [29]. It consists of two core solvers: Swept and Standard. Swept minimizes communication during the simulation via the swept rule. Standard is a traditional solver that communicates as is necessary to complete a timestep, and serves as a baseline to the swept rule. Both solvers use the same decomposition, process handling, and work allocation code so that a performance comparison between them fairly represents swept rule performance. However, Swept does require additional calculations prior to solving that are penalties of this swept rule implementation.

We implemented PySweep using Python and CUDA; the parallelism relies primarily on mpi4py [30] and pycuda [31]. Each process spawned by MPI is capable of managing a GPU and a CPU process, e.g., 20 processes can handle up to 20 GPUs and 20 CPU processes. Consequently, the aforementioned implementation allowed us to meet the objectives of this study on the swept rule, which include understanding:

• its performance on distributed heterogeneous computing systems,
• its performance with simple and complex numerical problems on heterogeneous systems,
• the impact of different computing hardware on its performance, and 
• the impact of input parameters on its performance.

3.2. Introduction to the Swept Rule

The swept rule is an abstract concept that is difficult to grasp without thorough introduction, so we first describe the idea as a general process and then examine for one-dimensional problems. Once the process is outlined and parameters are understood, we will move into the details for two dimensions. Figure 1 shows high-level solution processes for the Standard solver and Swept solver. In Figure 1b, the swept process starts with preprocessing, where each node is given instructions about what it is solving. Each node then initially solves as many time steps as it can before needing boundary information. Communication between nodes then allows the nodes to solve the remainder of those time steps. This process repeats until the desired solution time is reached.

More specifically, the swept algorithm works by solving as many spatial points of a time step as it can for a given subdomain and repeating this for subsequent time steps until information is required from neighboring nodes or hardware. This leaves the solution in a state with several incomplete time steps. Communication is then necessary to continue and fill in the incomplete time steps. This process repeats in various forms until the entire solution space has been completed to a desired time level.

The standard process in Figure 1a demonstrates the traditional way of solving unsteady PDEs using domain decomposition. Following any necessary preprocessing, the standard process begins by advancing one time step and then communicating boundary information. The standard process repeats these steps—advance one step, then communicate the boundaries—until reaching the desired solution time. In the example shown in Figure 1 for three timesteps, the standard process communicates twice while the swept process communicates once. Reducing these communication events is the core idea behind the swept rule.

Figure 2 demonstrates the swept rule in one dimension on two nodes with a three-point stencil, as well as some of the controllable parameters in a given simulation. The black boxes in Figure 2 represent the block size that is a fixed parameter throughout any single simulation—in this case, it is 12. The block size is a metric used to describe decomposition on GPUs. Another parameter, array size, is then the combination of all of the black boxes or the total number of spatial points. We discuss these parameters in more detail in Section 3.3.

In Figure 2a, we show how the swept rule starts from a set of spatial points and progresses in time until it cannot. Once it reaches that point, the highlighted points in Figure 2b are required by neighboring nodes to fill the voids (valleys between the triangles). The next computation shown in Figure 2c then uses those communicated points to fill the voids and build on top of the completed solution. Again, we reach a point where neighboring nodes require information and the highlighted points in Figure 2d must be communicated. This continues until a desired time level is reached with the benefit of bundling all of the highlighted points in Figure 2b,d into a single communication.

3.3. Parameters & Testing

In Section 3.2, we introduced the swept rule from a high-level perspective. Now, we take a step back to discuss the parameters that we can vary. GPUs execute code on a “block-wise” basis, i.e., they solve all the points of a given three-dimensional block simultaneously. We refer to the dimensions of these blocks as block size or b, which is a single integer that represents the x and y dimensions. The z dimension of the block was always unity because the solver is two-dimensional. The block size is a parameter of interest because it affects the performance of the swept rule by limiting the number of steps between communications. It also provides a natural basis for decomposing the data: using multiples of the block size makes splitting the data among nodes and processors convenient because the GPU already requires it.

The swept solution process restricts the block size, b, to the range $(2n,b_{max}]$ where $b_{max}$ is the maximum block size allowed by the hardware and n is the maximum number of points on either side of any point j used to calculate derivatives. We then define the maximum number of time steps that can be taken before communication is necessary as k:

$$k=\frac{b_{max}}{2n}-1.$$

(1)

Consequently, we restrict the block size to being square ($x=y$) because the block’s shortest dimension limits the number of time steps before communication.

Blocks provide a natural unit for describing the amount of work, e.g., a $16\times 16$ array has four $8\times 8$ blocks to solve. As such, the workload of each GPU and CPU is determined by the GPU share, s, on a blockwise basis:

$$s=\frac{G}{W}=1-\frac{C}{W}.$$

(2)

where G, C, and W represent the number of GPU blocks, CPU blocks, and total blocks, respectively. A share of $s=1$ corresponds to the GPU handling 100% of the work. This parameter is of interest because it directly impacts the performance of the solvers.

In our implementation, the share does not account for the number of GPU or CPU cores available but simply divides the given input array based on the number of blocks in the x direction, e.g., if the array contains 10 blocks and $s=0.5$ then five blocks will be allocated as GPU work and the remainder as CPU work. These portions of work would then be divided among available resources of each type.

Array size is another parameter of interest because it demonstrates how performance scales with problem size. We restricted array size to be evenly divisible by the block size for ease of decomposition. We also only considered square arrays, so array size is represented by a single number of points in the x and y directions. Finally, array sizes were chosen as multiples of the largest block size used across all the tested sizes (32); this can result in unemployed processes if there are not enough blocks. Potential for unemployed processes is, however, consistent across solvers and still provides a valuable comparison.

The numerical scheme used to solve a problem directly affects the performance of the swept rule as it limits the number of steps that can be taken in time before communication. As such, the aforementioned parameters were applied to solving the unsteady heat diffusion equation and the unsteady compressible Euler equations as in prior swept rule studies [6,7,8,9]. The heat diffusion equation was applied to a temperature distribution on a flat plate and solved using the forward Euler method in time and a three-point finite difference in each spatial direction. The compressible Euler equations were applied to the isentropic Euler vortex problem and solved using a second-order Runge–Kutta in time and a five-point finite volume method in each spatial direction with a minmod flux limiter and Roe-approximate Riemann solver [32,33]. Appendix B and Appendix C provide further detail on these methods and associated problems.

We selected hardware for testing based on the available resources at Oregon State University to analyze performance differences of the swept rule on differing hardware. We used two hardware sets, each containing two nodes with each node using 16 CPU cores and one GPU during testing. These sets were tested separately with 32 processes spawned by MPI. The first two nodes each have Tesla V100-DGXS-32GB GPUs and Intel E5-2698v4 CPUs, and the second two nodes each have GeForce GTX 1080 Ti GPUs and Intel Skylake Silver 4114 CPUs. We used each of these hardware sets to solve both the heat diffusion equation and the compressible Euler equations. Section 4 present the performance data that we collected.

We also performed a scalability study on the two solvers to better understand the performance results obtained. Accordingly, weak scalability was considered over up to four nodes. Each node was given approximately two million spatial points and solved both problems for 500 time steps. This test used a share of 90% and block size of 16.

3.4. Swept Solution Process

To recap, the swept rule is a latency reduction technique that obtains a solution to unsteady PDEs at as many possible locations and times prior to communicating boundary information. The algorithm works by solving as many spatial points of a time step as it can for a given subdomain and repeating this for subsequent time steps until information is required from neighboring nodes/subdomains. This leaves the solution in a state with several incomplete time steps. Communication is then necessary to continue and fill in the incomplete time steps. This process repeats in various forms until the entire solution space has been completed to a desired time. To aid understanding, we refer to the two primary actions of the code as “communication” and “calculation”.

Communication refers to events when the code transfers data to other processes. Node-based rank communication between the CPU and GPUs happens via the use of shared memory, a capability implemented in MPICH-3 or later [34]. Internode communication is performed with typical MPI constructs such as send and receive. A shared GPU memory approach implemented by Magee et al. showed some benefit [8]; this concept led to the idea of using shared memory on each node for node communication and primary processes for internode communication.

Calculation refers to the code advancing the solution in time. The specifics of CPU and GPU calculation depend on the particular phase of the simulation. In general, the GPU calculation proceeds by copying the allocated section of the shared array to GPU memory and launching the appropriate kernel; GPUs solve on a per-block basis, so decomposition of the given subdomain is a natural consequence. The CPU calculation begins by disseminating predetermined blocks among the available processes. Each block is a portion of the shared memory that each process can modify.

Four distinct phases occur during the swept solution process. In the code, we refer to them as Up-Pyramid, Bridge (X or Y), Octahedron, and Down-Pyramid, and continue that convention here. These names match the shapes produced during the solution procedure, if visualizing the solution’s progression in three dimensions $(x,y,t)$; later figures demonstrate this for a general case. To summarize the progression of swept phases, the Up-Pyramid is calculated once; the Bridge and Octahedron phases are then repeated until the simulation reaches a value greater than or equal to that of the desired final time. Finally, the Down-Pyramid executes to fill in the remaining portion of the solution.

Figure 3 shows the first phase of calculation: the Up-Pyramid (top left). We used a dynamic programming approach on the CPU portion to calculate the Up-Pyramid in lieu of conditional statements. Specifically, the indices to develop the Up-Pyramid are stored in a set that is accessed as needed. The GPU portion implements a conditional statement to accomplish this same task because its speed typically dwarfs that of the CPU. Optimizing the code should consider a dynamic programming approach for the GPU version, such as that implemented on the CPU. In both cases, conditional or dynamic, the code removes $2n$ points from each boundary after every time step. If the time scheme requires multiple intermediate time steps, these points are removed after each intermediate step. The initial boundaries of the Up-Pyramid are the given block size and the final boundaries are $2n$ using a variation of Equation (1).

The next phase in the process is the Bridge, which occurs independently in each dimension. The solution procedure for Bridge on the CPU and GPU follows the same paradigm as the Up-Pyramid but twice as many bridges are formed because there is one in each direction. Bridge formed in a given direction is labeled as such, e.g., the Bridge that forms parallel to the y-axis as time progresses is the Y-Bridge. The initial boundaries of each Bridge are determined from n and b. Each Bridge grows by $2n$ from these initial boundaries in the reference dimension and shrinks by $2n$ in the other dimension, which allows the appropriate calculation points to be determined conditionally or prior to calculation.

Depending on the decomposition strategy, a large portion of the Bridges can occur prior to internode communication. In this implementation, the Y-Bridge—shown in Figure 3 (top right)—occurs prior to the first communication. The first internode communication then follows by shifting nodal data $b/2$ points in the positive x direction. Any data that exceeds the boundaries of its respective shared array is communicated to the appropriate adjacent node. Figure 3 (bottom left) demonstrates this process. The shift in data allows previously determined sets and blocks to be used in the upcoming calculation phases so the X-Bridge proceeds directly after the communication as shown in Figure 3 (bottom right).

The first three phases in the swept solution process demonstrated in Figure 3 are followed by the Octahedron phase shown in Figure 4 (top left). This phase is a superposition of the Down-Pyramid and Up-Pyramid. The Down-Pyramid—shown in Figure 4 (bottom right)—begins with boundaries that are $2n$ wide and expand by $2n$ on each boundary with every passing time step. This start is a natural consequence of removing these points during the Up-Pyramid phase. The Down-Pyramid completes upon reaching the top of the previous Up-Pyramid or Octahedron when the upward portion of Octahedron phase begins. The entire Octahedron is calculated in the same fashion as the Up-Pyramid on both CPUs and GPUs. While the steps are described separately for clarity, they occur in a single calculation step without communication between ranks.

The Octahedron always precedes the Y-Bridge, Communicate, X-Bridge sequence. However, the communication varies in direction as the shift and communication of data is always the opposite of the former communication. We repeated this series of events as many times as was necessary to reach the final desired time of each simulation. The final phase is the aforementioned Down-Pyramid, which occurs only once at the end of the simulation. Figure 4 shows the ending sequence—minus the communication—in its entirety.

The shapes that we presented previously are generalizations for understanding and will vary based on the situation. The specific shape that forms during each phase is a function of the spatial stencil, time scheme chosen to solve a given problem, and block size. As previously determined in Section 3.3, the maximum number of steps based on block size is k. A communication, therefore, must be made after k steps for each phase, with the exception of Octahedron, which communicates after $2k$ steps.

The final number of time steps taken by a swept simulation is determined by the number of Octahedron phases ($2k$ time steps) that most accurately capture the specified number of time steps. This is a consequence of the swept rule: the exact number of steps is not always achievable in some cases because the simulation only stops after the completion of a phase. These phases occur on both the GPU and CPU with respect to the given share. Between each calculation step, a communication step occurs that consists of shared memory data management and writing to disk.

The shared memory data management of the communication step as well as the writing to disk involve a couple of nuances worth mentioning. It includes shifting the data, which is a strategy implemented for handling boundary blocks in the array. PySweep was implemented with periodic boundary conditions based on the targeted test problems. The boundary blocks of the array form half of the shape it would normally form in the direction orthogonal to the boundary (e.g., during the Octahedron phase on the boundary where $x=0$, only half the Octahedron will be formed in the x direction). As expected, the corner will form a fourth of the respective shape. In lieu of added logic for handling these varying shapes, we implemented a data shifting strategy that allows the majority of the same functions and kernels to be used. The boundary points are able to be solved as if they were in the center of a block with this strategy. This strategy comes at the expense of moving the data in memory.

PySweep writes to disk during every communication as it is the ideal time. The code uses parallel HDF5 (h5py) so that each rank can write its data to disk independently of other ranks [35]. The size of the shared memory array is $2k$ spaces in time plus the number of intermediate steps of the time scheme so that the intermediate steps of the scheme may be used for future steps if necessary. The appropriate fully solved steps are written to disk. The data is then moved down in the time dimension of the array so that the next phase can be calculated in the existing space. This step requires writing to disk because some of the larger simulations exceed the available device memory. Though frequently writing to disk is expensive, and a production solver would not do this, both solvers performed this consistently and so it should not impact comparisons.

The solver has a few restrictions based on architecture and implementation which have been previously described. It is currently implemented for periodic boundary conditions but can be modified to suit other conditions using the same strategy. The solver is also capable of handling given CPU functions and GPU kernels so that it may be used for any desired application that falls within the guidelines presented here. In this condition, we found it suitable for this study.

4. Results

Here, we present the results of applying PySweep to the heat transfer and compressible flow problems introduced in Section 3. When solving these problems, we varied the following parameters to assess performance: array size, block size, share, and hardware. Array sizes of [320, 480, 640, 800, 960, 1120] were used to make the total number of points span a couple orders of magnitude. Block sizes of [8, 12, 16, 20, 24, 32] were used based on hardware constraints. Share was varied from 0 to 100% at intervals of 10%. Based on the initial results, we ran a weak scalability study with a share of 90% and block size of 16. Along with these parameters, we advanced each problem 500 time steps.

4.1. Heat Diffusion Equation

We solved the heat diffusion equation numerically using the forward Euler method and a three-point central difference in space. We verified it against an analytical solution developed for the two-dimensional heat diffusion equation with periodic boundary conditions. Appendix B describes the problem formulation and verification in detail. Our performance metrics of choice for the swept rule are speedup, S, and time per timestep, T, as a function of array size, block size, and share:

$$S=\frac{T_{\mathrm{standard}}}{T_{\mathrm{swept}}},$$

(3)

where $T_i$ is with respect to simulation type i. Figure 5 and Figure 6 show speedup results produced from our tests for the two sets of hardware described in Section 3.3. The time-per-timestep results unanimously occur at a share of 100% across both sets of hardware. So, we also include Figure 7 that compares optimal cases between Swept and Standard. The full set of results are available in Appendix A.

Figure 5 shows a range of 0.22–2.69. The performance of the swept rule diminishes as the array size increases. The largest areas of performance increases generally occur above a share of 50% and along the block size of 12–20. The majority of best cases lie between 90–100% share and the 12–20 block size range. The worst-performing cases lay close to the optimal cases: between 90–100% share but outside the block size limits 12–20.

Figure 6 shows different trends than Figure 5 with a speedup range of 0.78–1.31. Performance again diminishes as array size increases; it is better with lower shares in the case of this hardware, and it is somewhat consistent across different block sizes. The best case for a given array size tends to occur at or below a 50% share and between block sizes 12–24. The worst case for a given array size tends to occur between 80–100% share and between block sizes of 20–32 with a couple occurrences on the upper limit.

The speedup contours are a convenient way to view variation with parameters and identify areas of performance benefit. However, a given solver would be tuned to where it performs optimally and compared with others in that manner. To dive further into this, Figure 7 shows the optimal cases of time per timestep, where Swept performs closely to Standard but only better in a few cases. Figure 7b shows the time-per-timestep results of the first hardware set. The optimal cases of Swept for this hardware generally occur between a block size of 8–12. Likewise, Standard optimal cases occur consistently at a block size of 20. Figure 7a shows the same result for the second hardware set where a block size of 8 being the apparent best choice for both solvers.

4.2. Compressible Euler Equations

We solved the Euler equations using a second-order Runge–Kutta scheme in time and a five-point central difference in space with a minmod flux limiter and Roe-approximate Riemann solver, which we verified against the analytical solution to the isentropic Euler vortex as described in Appendix C. We performed the same tests here as in Section 4.1. Figure 8 and Figure 9 show performance results produced by these simulations.

Figure 8 shows that the Swept solver consistently performs slower than Standard with a range of 0.52–1.46. Similar to the heat equation, performance declines with increasing array size but there is benefit in some cases. The best case for a given array size tends to occur above approximately 90% share but there is no clear block size trend. The worst case for a given array size tends to occur at 100% share, but, likewise, a block size trend is unclear. However, in the three largest array sizes, they always occur at 100% share with a block size of 8.

Figure 9 shows that the Swept solver is consistently slower than Standard with a range of 0.36–1.41. Similar to the other configurations, performance consistently declines with increasing array size. Most best cases occur below approximately 50% share with a block size between 12–24. The majority of the worst cases occur at 100% share on the block size limits of 8 and 32.

In the case of time per timestep, all optimal cases again occur at a share of 100%. The Swept solver has most of these occurrences between block sizes of 16–24 for the both hardware sets while Standard skews toward higher block sizes (20–32) for Intel E5-2698v4 CPUs and Tesla V100-DGXS-32GB GPUs. We again consider the optimal cases over given array sizes in Figure 10, which shows that Swept generally performs worse with a one-to-one comparison of the optimal cases. Results are aligned with Standard at lower array sizes but quickly become worse.

4.3. Weak Scalability

The results above raised some questions about performance. For example, does latency reduction of the swept rule outweigh the overhead of a more complicated process? To better isolate the latency and overhead of the method, we performed a weak scaling study with a share of 90% and block size of 16 for the two equations over 500 hundred time steps. Figure 11 shows results, where the Standard solver performs better in both cases. This suggests that implementation overhead may dominate the simulation cost, so latency improvements are less noticeable.

5. Discussion

From the heat diffusion results, there is an overall range of speedup from 0.22–2.69 for the first hardware set and 0.78–1.31 for the second. However, the limits of speedup are outliers. These speedups are lower in comparison to the one-dimensional heterogeneous version, which reported 1.9 to 23 times speedup [9], and the one-dimensional GPU version, which reported 2 to 9 times speedup for similar applications [8]. There are no clear trends in speedup, but we can explore other results to help understand what is happening.

Specifically, time per timestep results show that the best cases consistently occur for both solvers at 100% share. In these cases, the block sizes of Swept skew toward sizes of 8–12 for best performance, while Standard prefers block sizes of 20–24. This difference occurs due to the overhead of the swept rule. The smallest block sizes experience less overhead in exchange for less latency reduction. 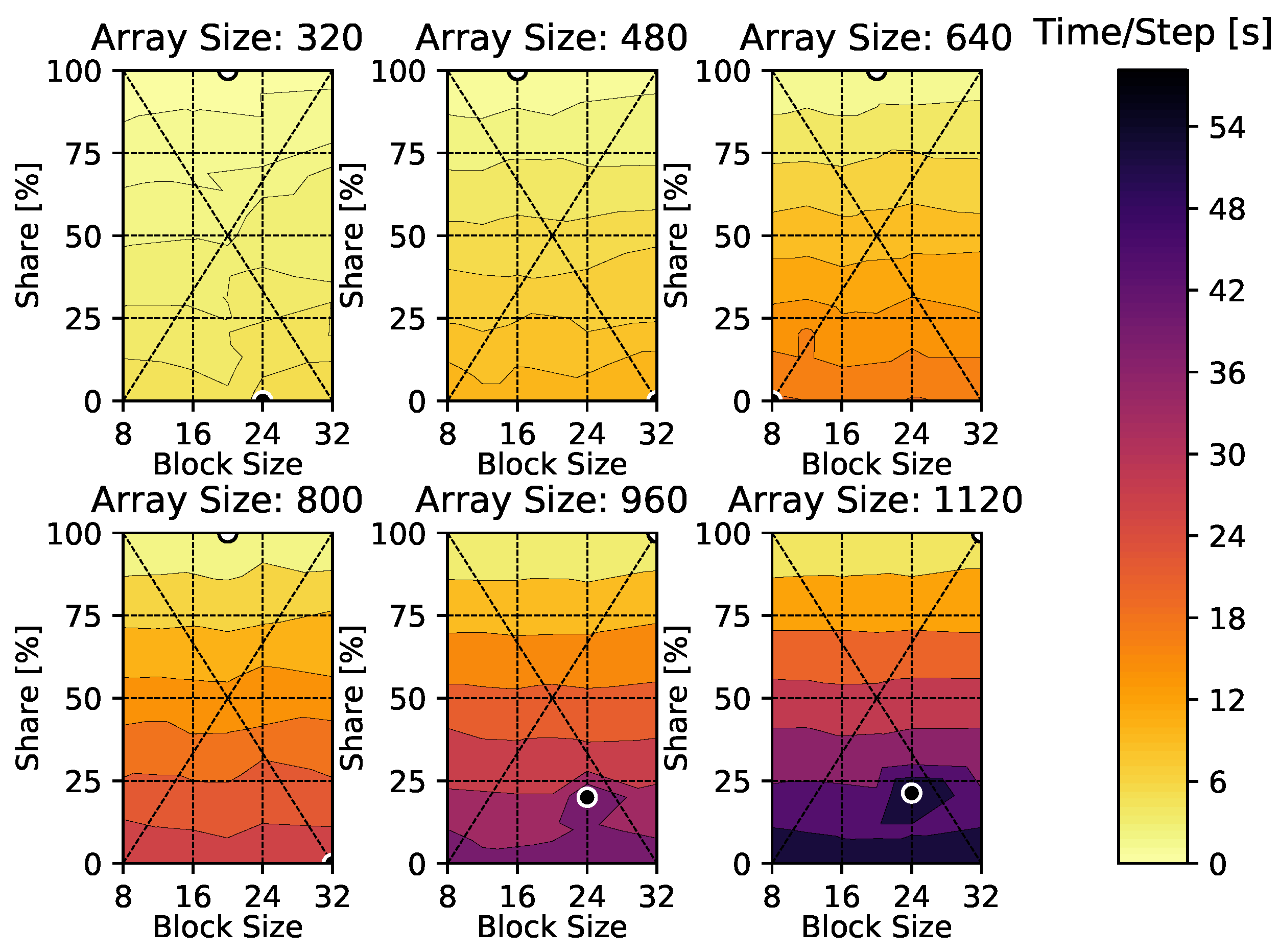Overhead losses mitigate benefits in latency costs, but as seen in the optimal case comparison (Figure 7), the swept rule can offer speedup for the heat diffusion equation on a per-time-step basis for both sets of hardware. However, improvements deteriorate with increasing array size and would require further optimizations to maintain.

For the Euler equations, the swept rule achieves an overall speedup range of 0.52–1.46 for the first set of hardware and 0.36–1.41 for the second. These speedups agree with values reported in other studies. The two-dimensional CPU version reported a speedup of at most 4 [7], the one-dimensional GPU version reported 0.53–0.83 [8], and the one-dimensional heterogeneous version reported 1.1–2.0 [9]. Similar to the heat diffusion equation, optimal and worst-case scenario speed ups appear to be randomly scattered over the contours.

Again, we look to the time-per-time-step results to realize any performance benefits. The optimal cases occur at a share of 100% but the block sizes for the Swept and Standard both have more moderate values of 16–24, due to higher bandwidth costs. The heat diffusion equation only uses one state variable compared with the four variables required for the Euler equations. With smaller block sizes, bandwidth plays a larger role in our implementation. When transferring data, we use less logic for organizing the data, which leads to sending half of the current shape from the boundaries. So, the extra bandwidth costs of state variables play a larger role and the balance is now between latency reduction, overhead, and bandwidth. Lower latency and bandwidth occurs when block size is increased but overhead costs also increase, which skews the optimal cases to greater block sizes.

Numerical complexity degrades swept rule performance across all studies of the method. On GPUs, it contributes to greater thread divergence, which the swept rule compounds. Thread vacancy is another a problem encountered and amplified on both CPUs and GPUs. More complicated schemes will take longer per time step, leading to threads being vacant for longer periods of time. So, optimal cases will balance this vacancy with latency improvements. Despite these costs compounding with extra bandwidth costs in our implementation, we realized some improvements over the traditional solver. However, performance testing to determine optimal parameters becomes especially important in cases where increased costs are associated to ensure speedup.

The scalability results also help us to understand the swept rule’s performance. Figure 11 shows that our implementation generally scales worse for both problems. The Standard performance has a shallower slope in Figure 11a, which again supports the idea that swept overhead outweighs benefits of latency reduction. The solvers exhibit similar slopes in Figure 11b, but Swept has a higher starting point so the benefits are less apparent. The decrease in slopes between Figure 11a and Figure 11b is consistent with the increase in block sizes between the two problems and supports the idea that latency is reduced. Unfortunately, overhead expenses of Swept outweigh savings in latency reduction and performance gains over Standard are not realized.

Specific problems aside, bandwidth plays a significant role in the performance comparison of the solvers. While latency is reduced, the performance declines with increasing array size because Swept moves more data both between nodes and on the nodes. Again, the bandwidth effect is exacerbated by the Euler equations having more data; this is apparent in both the contours and scalability results. In Figure 11, the Swept curve is separated completely from the Standard curve in Figure 11b, but this does not occur in Figure 11a—this is the added overhead.

Other causes of poor performance could be preprocessing overhead that the Swept solver undergoes but the Standard solver does not. PySweep determines and stores the appropriate blocks for communication prior to the simulation to avoid conditionals with the intention of boosting GPU performance. This process was parallelized as much as possible but there are some serial parts which undoubtedly reduce the performance of the algorithm.

Finally, the fastest option is typically the most desired outcome when it comes to high-performance computing applications. While in some cases a GPU share of less than 100% yield faster results, this is not one of those cases. Figure 12 demonstrates that the clock time only increases as share decreases. This same effect occurs in all of the time-per-time-step figures in Appendix A. We did not present figures for clock time in other cases because they show the same result: 100% leads to the lowest clock time. However, the optimal configuration is useful if simulation requires data greater than the limit of the GPU(s).

6. Conclusions

In this study, we examined the performance of a two-dimensional swept rule solver on heterogeneous architectures. We tested our implementation over a range of GPU work shares, block sizes, and array sizes with two hardware configurations each containing two nodes. Our goal was to understand how the method performs based on these configurations.

We found that using GPUs alone, with no CPU contribution, provides the best possible performance for the swept rule in these examples. This results from the GPU having to wait on the CPU and remaining idle for some amount of time in the process, if sharing work. Swept rule performance depends on the problem solved, so the block size and share should be tuned to obtain the optimal performance based on the problem. GPUs are typically much more powerful, but CPUs can be useful in more problems requiring complex logic. Our study suggests that block sizes between 16–24 and a GPU share of 100% are a good place to start for fastest run time. However, it could be advantageous to explore share values of a few percentage points below 100%, depending on the problem.

Next, we found that hardware can affect swept rule performance. The swept rule does show differing performance characteristics between different hardware combinations, but the major trends hold. However, the precise combination of performance parameters leading to optimal performance does vary between the hardware sets, and this should be considered when tuning for a given a simulation. Hardware-based performance differences also varied by the problem.

Overall, we conclude from this study that the performance of two-dimensional swept rule depends on the implementation, problem, and computing hardware. Speedup can be achieved, but care should be taken when designing and implementing a solver. Finally, any practical use of the swept rule requires tuning input parameters to achieve optimal performance and, in some cases, speedup at all over a traditional decomposition.