On the Performance of Intelligent Reconfigurable Surfaces for 6G Indoor Visible Light Communications Systems
Abstract
:1. Introduction
- Site Survey and Analysis: Identify areas with poor LoS or Non-LoS conditions where the VLC system performance is degraded. These could be areas with obstacles or signal blocks.
- IRS Placement and Configuration: Determine suitable locations to install IRS panels. These locations should enable optimal reflection of VLC signals towards the receiver. Furthermore, it is necessary to configure the IRS panels according to the specific environment.
- Adaptive Adjustment: Use real-time channel information to adaptively adjust the IRS configuration. This could involve dynamic phase shifting to counteract changing obstacles or interferences.
- System Integration: Integrate the IRS system with the VLC infrastructure. This includes connecting IRS control mechanisms to the VLC transmitter and receiver.
- Indoor Environments: Environments with walls, partitions, and other obstacles can experience significant signal degradation. IRS can reflect signals around these obstacles, enhancing coverage.
- Large Public Spaces: Areas like shopping malls, airports, and convention centers often have challenging signal propagation due to their size and architectural features. IRS can help overcome these challenges.
- Smart Cities: In urban environments with tall buildings and signal interference, IRS can be strategically deployed to improve signal coverage and connectivity.
- Underground Areas: Basements, parking lots, and tunnels often have poor signal penetration. IRS can redirect signals to improve communication.
- We present an in-depth analysis of the behavior of an optical signal in a VLC system assisted by an IRS on metasurfaces.
- We obtain mathematical expressions of the LoS and Non-LoS channel components, including the effect of the reflection of the optical signal in the IRS and obstacles and obstacles that can cause shadowing.
- We evaluated the VLC system in terms of relevant metrics for wireless communication systems, such as the Channel Impulse Response (CIR) and the Bit Error Rate (BER).
Related Works
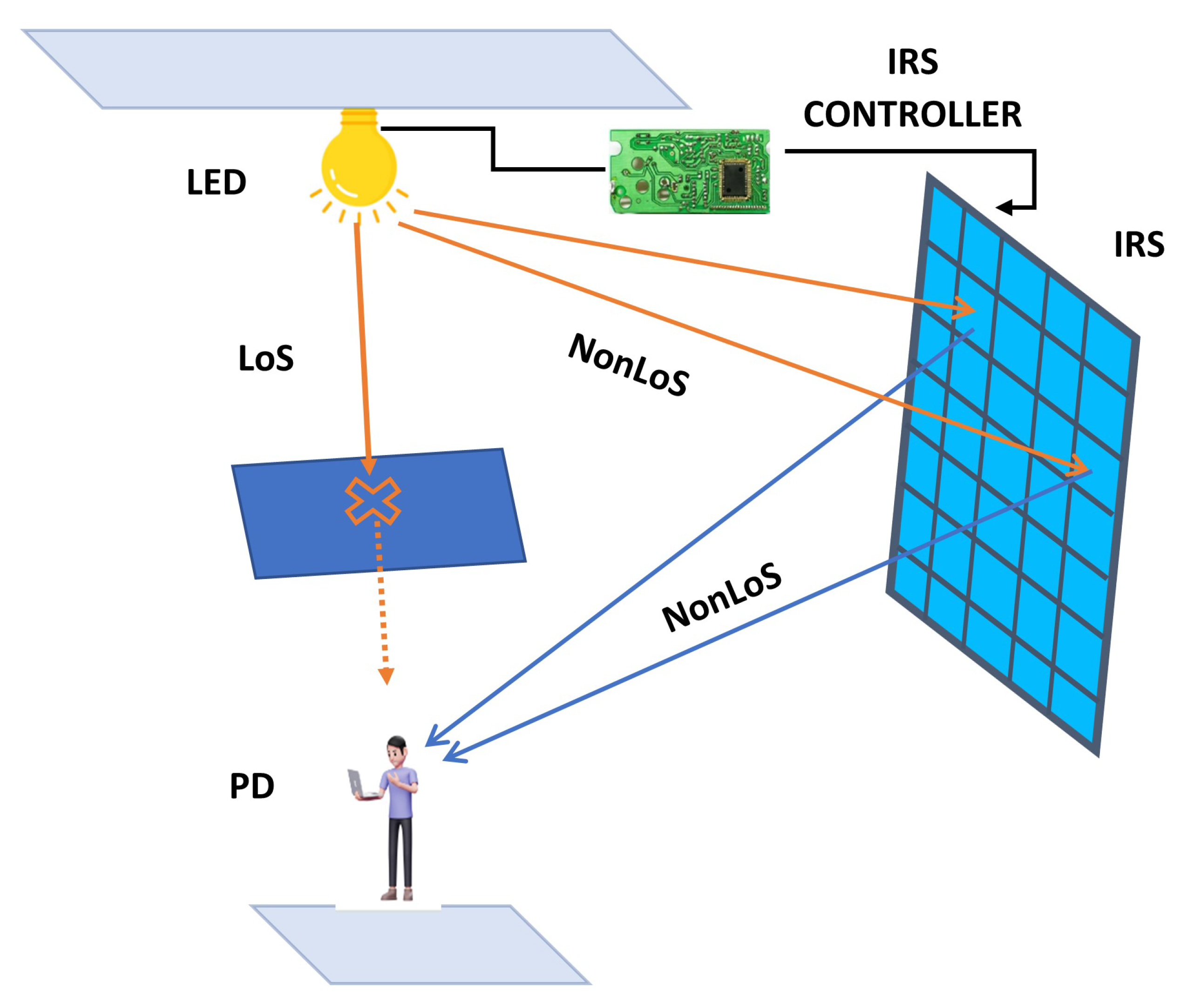
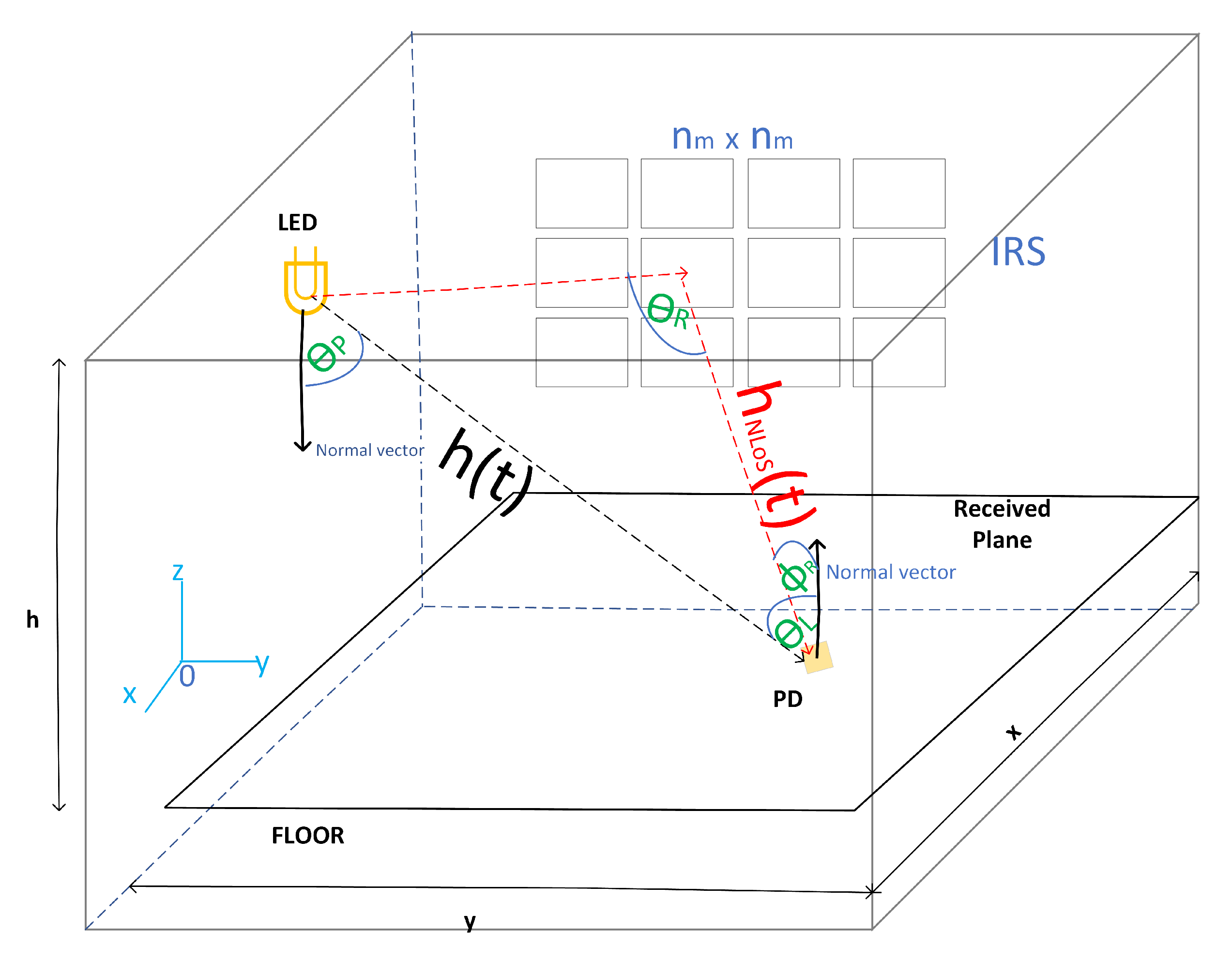
2. System Model
3. Intelligent Reconfigurable Surface Model
- Reflective elements must have thicknesses much higher than the penetration depths of the metal used. To avoid polarization sensitivity, IRS is constructed without birefringent or dichroic materials.
- The dimensions of the IRS must be much larger than the wavelength of visible light. Therefore, we adopt as in [9] a macroscopic model for each IRS, which allows us to consider them as equivalent anomalous reflective rectangular blocks. This approach makes it possible to harness and direct most of the incident light in a direction imposed by the generalized law of reflection. In addition, it implies the dependence of only two variables, and of the IRS.
- The function of for each IRS patch is adjusted so that the incident light beam from the LED strikes and reflects off the center of the reflector.
- We have adjusted the duration of the symbol in the transmitter to avoid intersymbol interference.
- IRS is perfectly smooth, so that nonspecular reflections can be neglected.
- The IRS phase gradient is smooth for all directions found on the surface.
- Data are transported on a white light beam to avoid reflection spectral dependencies.
3.1. IRS Incidence and Radiance Angles
3.2. Reflective Channel Component
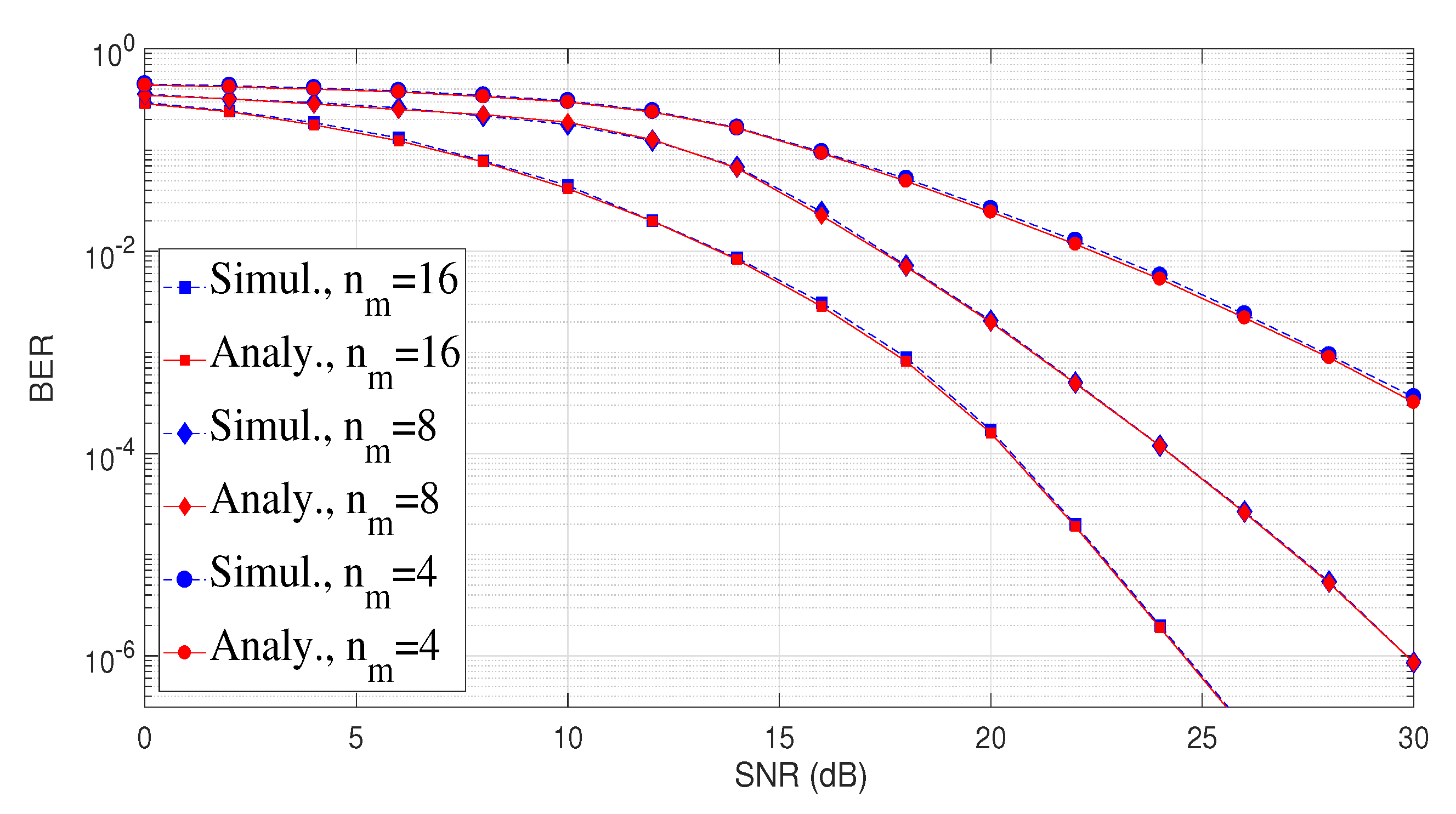
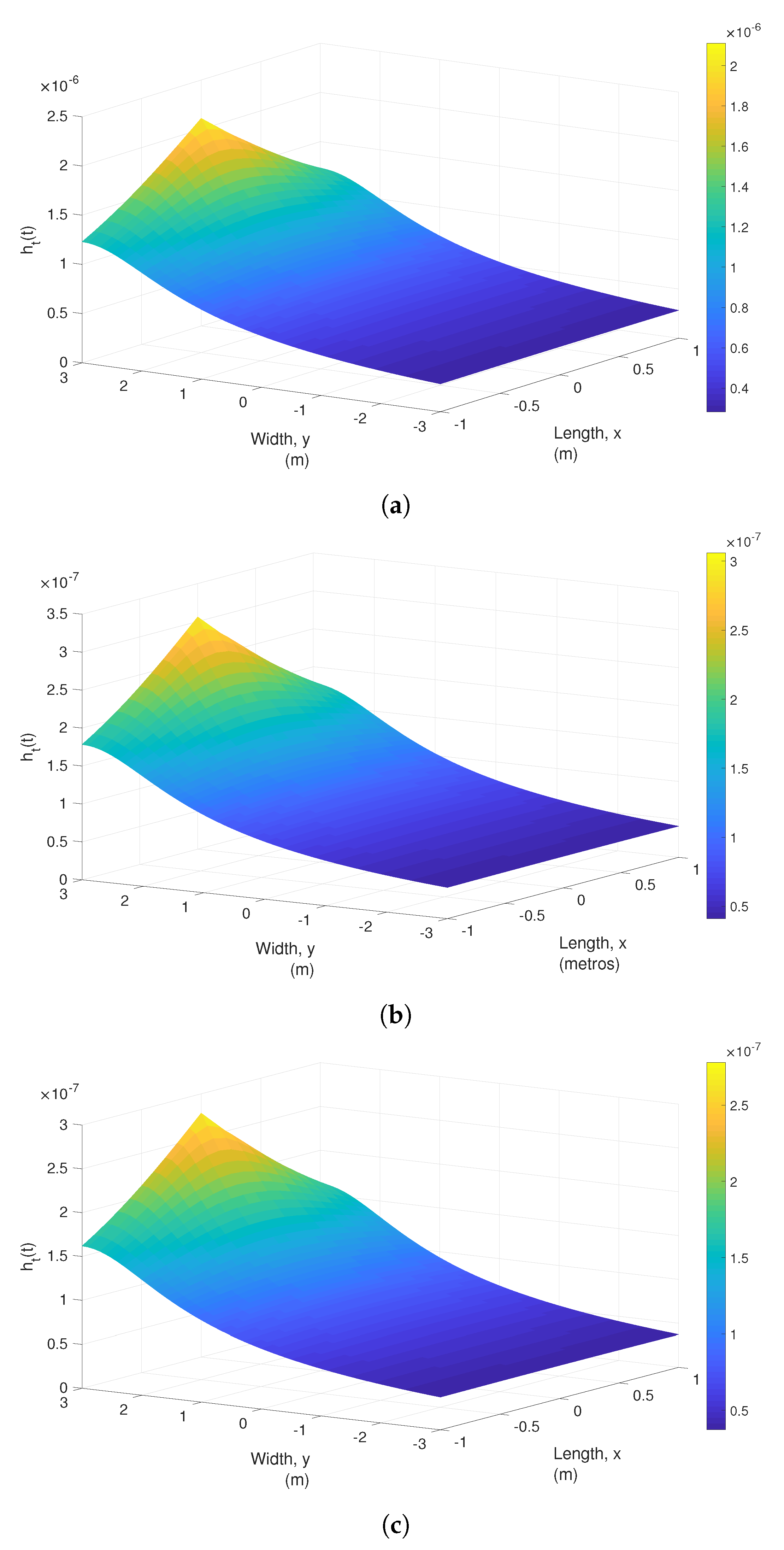
4. Simulation Results and Discussion
4.1. Bit Error Rate of the System
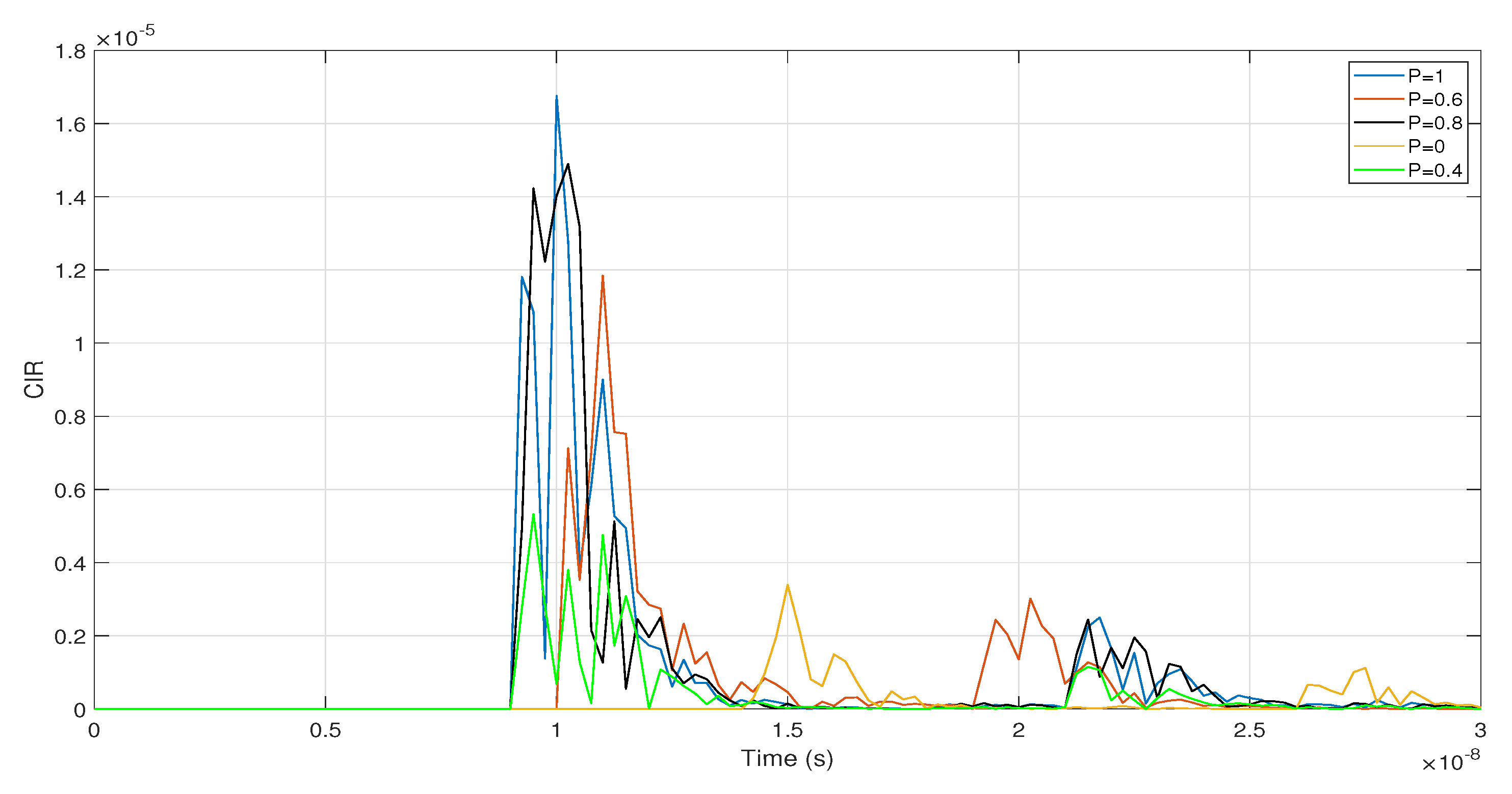
4.2. Channel Impulse Response of the VLC System
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BER | Bit Error Rate |
| CIR | Channel Impulse Response |
| CSI | Channel State Information |
| DD | Direct Detection |
| FoV | Field-of-View |
| FSO | Free Space Optical |
| IM | Intensity Modulation |
| IRS | Intelligent Reconfigurable Surfaces |
| LED | Light-Emitting Diode |
| LoS | Line-of-Sight |
| Non-LoS | Non-Line of Sight |
| OOK | ON-OFF Keying |
| PD | Photo-Diode |
| RF | Radio Frequency |
| SINR | Signal to Interference plus-Noise-Ratio |
| SLM | Spatial Light Modulator |
| SNR | Signal-to-Noise-Ratio |
| SISO | Single Input Single Output |
| VLC | Visible Light Communication |
| V2V | Vehicle to Vehicle |
References
- De Alwis, C.; Kalla, A.; Pham, Q.V.; Kumar, P.; Dev, K.; Hwang, W.J.; Liyanage, M. Survey on 6G frontiers: Trends, applications, requirements, technologies and future research. IEEE Open J. Commun. Soc. 2021, 2, 836–886. [Google Scholar] [CrossRef]
- Porambage, P.; Gür, G.; Osorio, D.P.M.; Liyanage, M.; Gurtov, A.; Ylianttila, M. The roadmap to 6G security and privacy. IEEE Open J. Commun. Soc. 2021, 2, 1094–1122. [Google Scholar] [CrossRef]
- Aboagye, S.; Ndjiongue, A.R.; Ngatched, T.M.; Dobre, O.A.; Poor, H.V. RIS-assisted visible light communication systems: A tutorial. IEEE Commun. Surv. Tutor. 2022, 25, 251–288. [Google Scholar] [CrossRef]
- Sun, S.; Wang, T.; Yang, F.; Song, J.; Han, Z. Intelligent reflecting surface-aided visible light communications: Potentials and challenges. IEEE Veh. Technol. Mag. 2021, 17, 47–56. [Google Scholar] [CrossRef]
- Zhu, X.; Wang, C.X.; Huang, J.; Chen, M.; Haas, H. A Novel 3D Non-Stationary Channel Model for 6G Indoor Visible Light Communication Systems. IEEE Trans. Wirel. Commun. 2022, 21, 8292–8307. [Google Scholar] [CrossRef]
- Ndjiongue, A.R.; Ngatched, T.M.; Dobre, O.A.; Haas, H. Toward the use of re-configurable intelligent surfaces in VLC systems: Beam steering. IEEE Wirel. Commun. 2021, 28, 156–162. [Google Scholar] [CrossRef]
- Román Cañizares, M.; Palacios Játiva, P.; Azurdia-Meza, C.A.; Montejo-Sánchez, S.; Céspedes, S. Impact of diversity combining schemes in a multi-cell VLC system with angle diversity receivers. Photonic Netw. Commun. 2022, 43, 13–22. [Google Scholar] [CrossRef]
- Abumarshoud, H.; Mohjazi, L.; Dobre, O.A.; Di Renzo, M.; Imran, M.A.; Haas, H. LiFi through reconfigurable intelligent surfaces: A new frontier for 6G? arXiv 2021, arXiv:2104.02390. [Google Scholar] [CrossRef]
- Abdelhady, A.M.; Salem, A.K.S.; Amin, O.; Shihada, B.; Alouini, M.S. Visible light communications via intelligent reflecting surfaces: Metasurfaces vs mirror arrays. IEEE Open J. Commun. Soc. 2020, 2, 1–20. [Google Scholar] [CrossRef]
- Shafique, T.; Tabassum, H.; Hossain, E. Stochastic geometry analysis of IRS-assisted downlink cellular networks. IEEE Trans. Commun. 2022, 70, 1442–1456. [Google Scholar] [CrossRef]
- Zhou, X.; Yan, S.; Wu, Q.; Shu, F.; Ng, D.W.K. Intelligent reflecting surface (IRS)-aided covert wireless communications with delay constraint. IEEE Trans. Wirel. Commun. 2021, 21, 532–547. [Google Scholar] [CrossRef]
- Najafi, M.; Schmauss, B.; Schober, R. Intelligent reflecting surfaces for free space optical communication systems. IEEE Trans. Commun. 2021, 69, 6134–6151. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, Y.J.A.; Shi, Y.; Yan, W.; Liu, H. Reconfigurable-intelligent-surface empowered wireless communications: Challenges and opportunities. IEEE Wirel. Commun. 2021, 28, 136–143. [Google Scholar] [CrossRef]
- Wu, Q.; Zhang, S.; Zheng, B.; You, C.; Zhang, R. Intelligent reflecting surface-aided wireless communications: A tutorial. IEEE Trans. Commun. 2021, 69, 3313–3351. [Google Scholar] [CrossRef]
- Arfaoui, M.A.; Ghrayeb, A.; Assi, C. Integration of IRS in Indoor VLC Systems: Challenges, Potential and Promising Solutions. arXiv 2021, arXiv:2101.05927. [Google Scholar]
- Nemati, A.; Wang, Q.; Hong, M.; Teng, J. Tunable and reconfigurable metasurfaces and metadevices. Opto-Electron. Adv. 2018, 1, 180009. [Google Scholar] [CrossRef]
- Sun, S.; Yang, F.; Song, J.; Zhang, R. Intelligent reflecting surface for MIMO VLC: Joint design of surface configuration and transceiver signal processing. IEEE Trans. Wirel. Commun. 2023, 22, 5785–5799. [Google Scholar] [CrossRef]
- Valagiannopoulos, C.; Tsiftsis, T.A.; Kovanis, V. Metasurface-enabled interference mitigation in visible light communication architectures. J. Opt. 2019, 21, 115702. [Google Scholar] [CrossRef]
- Mohsan, S.A.H.; Khan, M.A.; Amjad, H. Hybrid FSO/RF networks: A review of practical constraints, applications and challenges. Opt. Switch. Netw. 2023, 47, 100697. [Google Scholar] [CrossRef]
- Stefanovic, C.; Morales-Céspedes, M.; Armada, A.G. Performance analysis of RIS-assisted FSO communications over Fisher–Snedecor F turbulence channels. Appl. Sci. 2021, 11, 10149. [Google Scholar] [CrossRef]
- Gomez, A.; Shi, K.; Quintana, C.; Sato, M.; Faulkner, G.; Thomsen, B.C.; O’Brien, D. Beyond 100-Gb/s Indoor Wide Field-of-View Optical Wireless Communications. IEEE Photonics Technol. Lett. 2015, 27, 367–370. [Google Scholar] [CrossRef]
- Jian, Y.H.; Wang, C.C.; Chow, C.W.; Gunawan, W.H.; Wei, T.C.; Liu, Y.; Yeh, C.H. Optical Beam Steerable Orthogonal Frequency Division Multiplexing (OFDM) Non-Orthogonal Multiple Access (NOMA) Visible Light Communication Using Spatial-Light Modulator Based Reconfigurable Intelligent Surface. IEEE Photonics J. 2023, 15, 1–8. [Google Scholar] [CrossRef]
- Palacios Játiva, P.; Azurdia-Meza, C.A.; Sánchez, I.; Zabala-Blanco, D.; Dehghan Firoozabadi, A.; Soto, I.; Seguel, F. An Enhanced VLC Channel Model for Underground Mining Environments Considering a 3D Dust Particle Distribution Model. Sensors 2022, 22, 2483. [Google Scholar] [CrossRef] [PubMed]
- Játiva, P.P.; Azurdia-Meza, C.A.; Sánchez, I.; Seguel, F.; Zabala-Blanco, D.; Firoozabadi, A.D.; Gutiérrez, C.A.; Soto, I. A VLC Channel Model for Underground Mining Environments with Scattering and Shadowing. IEEE Access 2020, 8, 185445–185464. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Popoola, W.; Rajbhandari, S. Optical Wireless Communications: System and Channel Modelling with Matlab®; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Palacios Játiva, P.; Román Cañizares, M.; Azurdia-Meza, C.A.; Zabala-Blanco, D.; Dehghan Firoozabadi, A.; Seguel, F.; Montejo-Sánchez, S.; Soto, I. Interference mitigation for visible light communications in underground mines using angle diversity receivers. Sensors 2020, 20, 367. [Google Scholar] [CrossRef]
- Becerra, R.; Azurdia-Meza, C.A.; Palacios Játiva, P.; Soto, I.; Sandoval, J.; Ijaz, M.; Carrera, D.F. A Wavelength-Dependent Visible Light Communication Channel Model for Underground Environments and Its Performance Using a Color-Shift Keying Modulation Scheme. Electronics 2023, 12, 577. [Google Scholar] [CrossRef]
- Xiang, Y.; Zhang, M.; Kavehrad, M.; Chowdhury, M.S.; Liu, M.; Wu, J.; Tang, X. Human shadowing effect on indoor visible light communications channel characteristics. Opt. Eng. 2014, 53, 86113. [Google Scholar] [CrossRef]
- Játiva, P.P.; Azurdia-Meza, C.A.; Cañizares, M.R.; Sánchez, I.; Seguel, F.; Zabala-Blanco, D.; Carrera, D.F. Performance analysis of IEEE 802.15. 7-based visible light communication systems in underground mine environments. Photonic Netw. Commun. 2022, 43, 23–33. [Google Scholar] [CrossRef]
- Jativa, P.P.; Azurdia-Meza, C.A.; Zabala-Blanco, D.; Gutiérrez, C.A.; Sanchez, I.; Castillo-Soria, F.R.; Seguel, F. Bit Error Probability of VLC Systems in Underground Mining Channels with Imperfect CSI. AEU-Int. J. Electron. Commun. 2022, 145, 154101. [Google Scholar] [CrossRef]
| System Model Parameters | Values | References |
|---|---|---|
| Average output optical power | 20 W | [9,24,26] |
| Band-pass filter of transmission | 1 | [24,26] |
| Dimensions (w × l × h) | (3 × 6 × 3) m | |
| Gain of the optical filter | 1 | [24,26] |
| LED position (x, y, z) | (0, 3, 2) m | |
| LED semi-angle at half power | [24,26] | |
| Modulation | OOK | [24,26] |
| Modulation bandwidth | 50 MHz | [24,26] |
| Modulation index | 0.3 | [24,26] |
| Number of PDs | 1 | |
| Open-loop voltage gain | 10 | [24,26] |
| Optical filter bandwidth | 340 nm to 694.3 nm | [30] |
| Optical filter center wavelength | 340 ± 2 nm | [30] |
| Optical filter full width half max | 10 ± 2 nm | [30] |
| Phase discontinuity () | [−] | |
| PD physical area | 1 cm | [24,26] |
| PD FoV | 60 | [24,26] |
| Refractive index | 1.5 | [24,26] |
| Reflection coefficient | 0.8 | [24,26] |
| Responsivity | 0.53 A/W | [24,26] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cañizares, M.R.; Játiva, P.P.; Guaña-Moya, J.; Villegas-Ch, W.; Azurdia-Meza, C. On the Performance of Intelligent Reconfigurable Surfaces for 6G Indoor Visible Light Communications Systems. Photonics 2023, 10, 1117. https://doi.org/10.3390/photonics10101117
Cañizares MR, Játiva PP, Guaña-Moya J, Villegas-Ch W, Azurdia-Meza C. On the Performance of Intelligent Reconfigurable Surfaces for 6G Indoor Visible Light Communications Systems. Photonics. 2023; 10(10):1117. https://doi.org/10.3390/photonics10101117
Chicago/Turabian StyleCañizares, Milton Román, Pablo Palacios Játiva, Javier Guaña-Moya, William Villegas-Ch, and Cesar Azurdia-Meza. 2023. "On the Performance of Intelligent Reconfigurable Surfaces for 6G Indoor Visible Light Communications Systems" Photonics 10, no. 10: 1117. https://doi.org/10.3390/photonics10101117
APA StyleCañizares, M. R., Játiva, P. P., Guaña-Moya, J., Villegas-Ch, W., & Azurdia-Meza, C. (2023). On the Performance of Intelligent Reconfigurable Surfaces for 6G Indoor Visible Light Communications Systems. Photonics, 10(10), 1117. https://doi.org/10.3390/photonics10101117








