Stable Acoustic Pulling in Two-Dimensional Phononic Crystal Waveguides Based on Mode Manipulation
Abstract
:1. Introduction
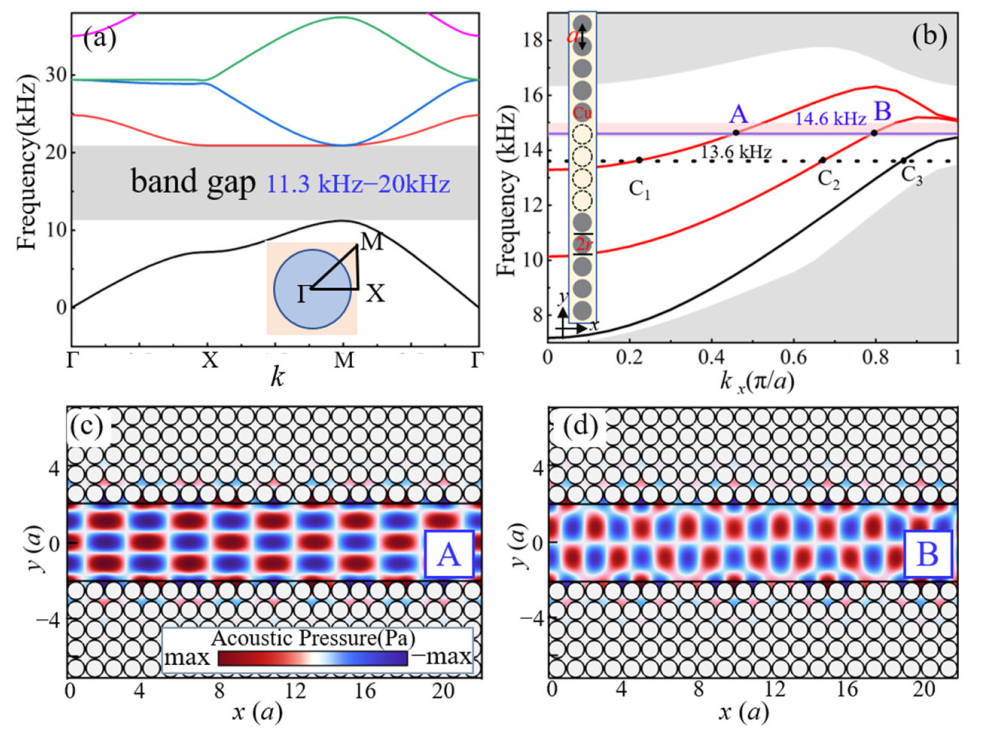
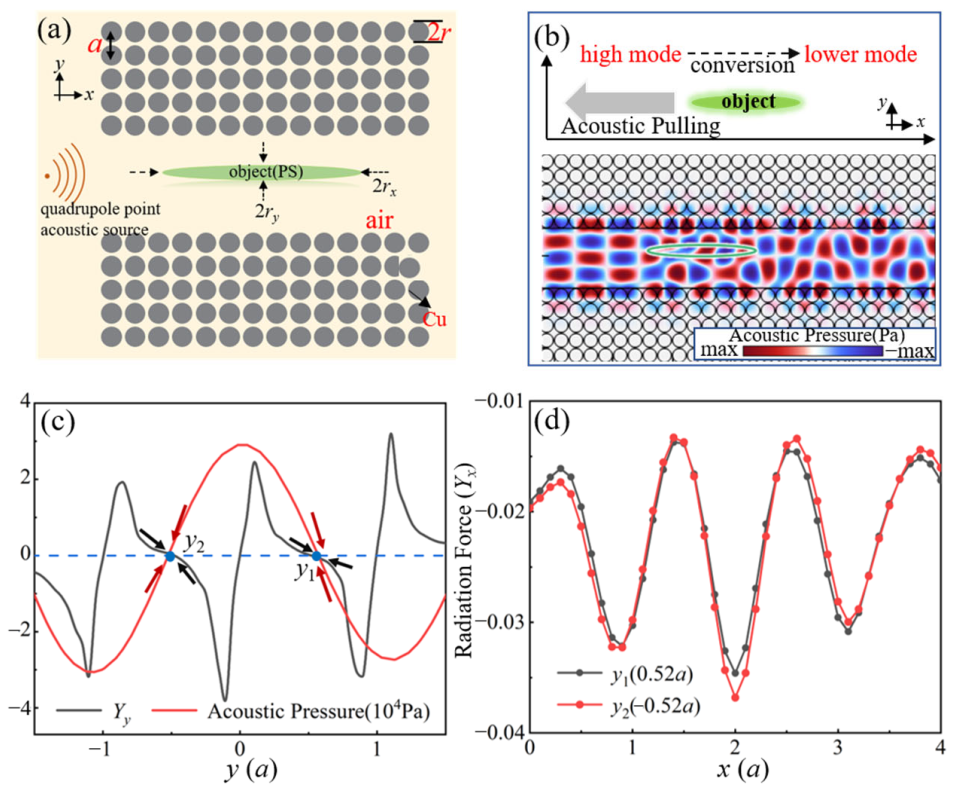
2. The Model
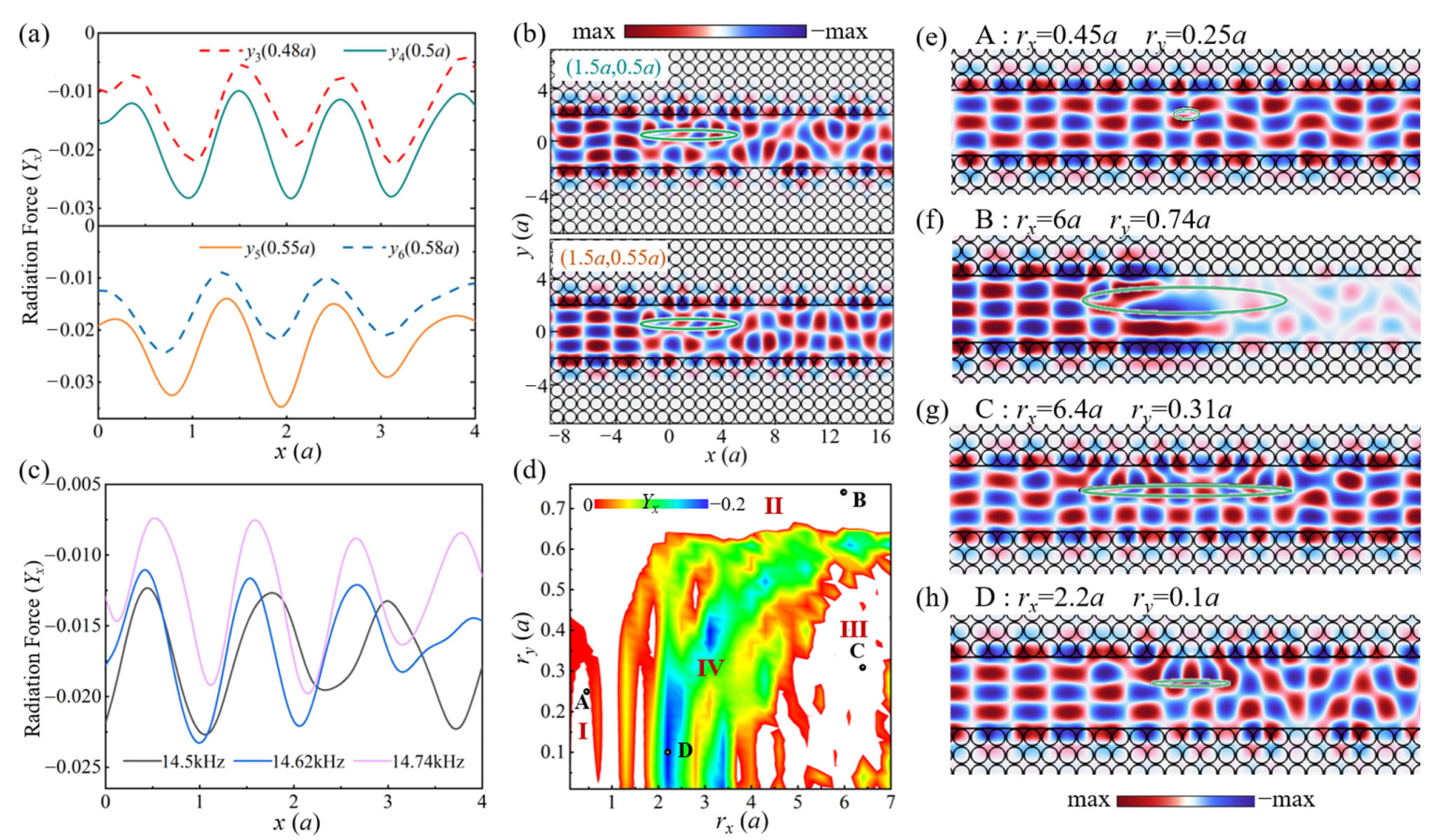
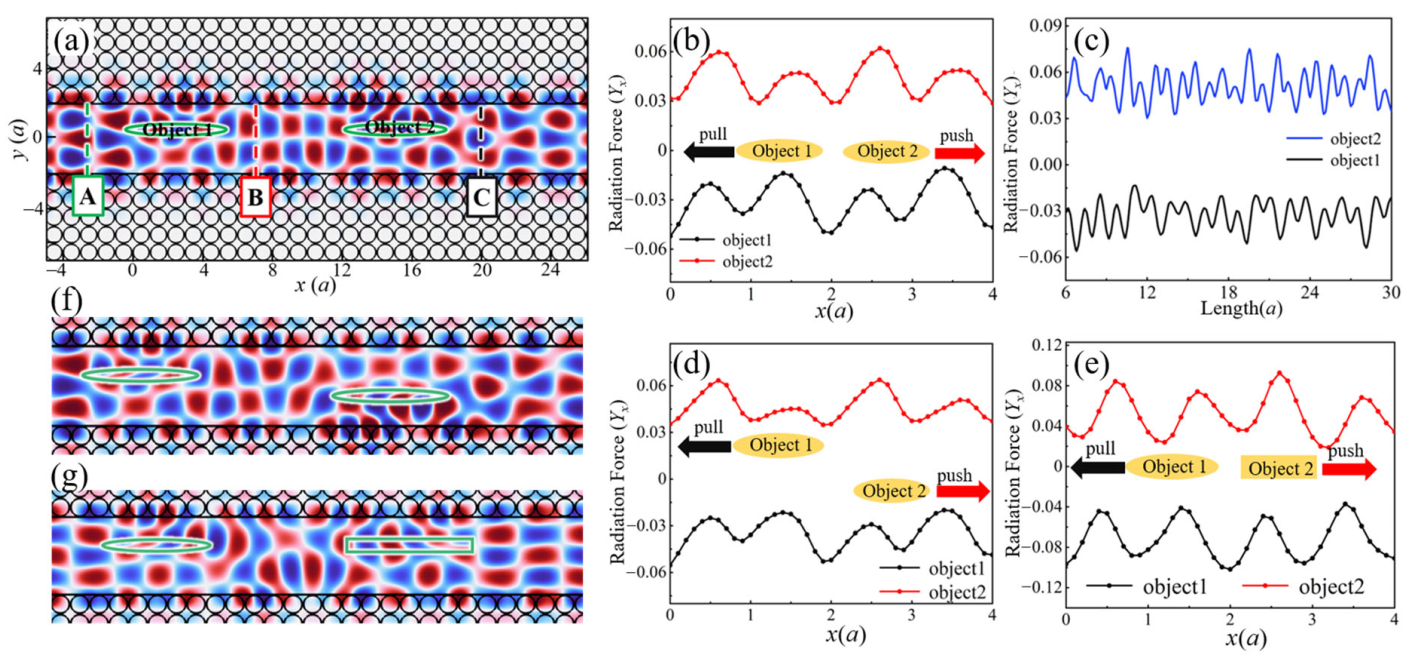
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Khandurina, J.; Guttman, A. Bioanalysis in Microfluidic Devices. J. Chromatogr. A 2002, 943, 159–183. [Google Scholar] [CrossRef] [PubMed]
- Ozcelik, A.; Rufo, J.; Guo, F.; Gu, Y.; Li, P.; Lata, J.; Huang, T.J. Acoustic Tweezers for the Life Sciences. Nat. Methods 2018, 15, 1021–1028. [Google Scholar] [CrossRef] [PubMed]
- Chen, Z.; Segev, M. Highlighting Photonics: Looking into the next Decade. eLight 2021, 1, 2. [Google Scholar] [CrossRef]
- Cook, L.J.; Mazilu, D.A.; Mazilu, I.; Simpson, B.M.; Schwen, E.M.; Kim, V.O.; Seredinski, A.M. Cooperative Sequential-Adsorption Model in Two Dimensions with Experimental Applications for Ionic Self-Assembly of Nanoparticles. Phys. Rev. E 2014, 89, 062411. [Google Scholar] [CrossRef] [PubMed]
- Ashkin, A. Optical Trapping and Manipulation of Neutral Particles Using Lasers. Proc. Natl. Acad. Sci. USA 1997, 94, 4853–4860. [Google Scholar] [CrossRef] [PubMed]
- Kishimoto, T.; Masui, K.; Minoshima, W.; Hosokawa, C. Recent Advances in Optical Manipulation of Cells and Molecules for Biological Science. J. Photochem. Photobiol. C Photochem. Rev. 2022, 53, 100554. [Google Scholar] [CrossRef]
- Zhong, M.-C.; Wei, X.-B.; Zhou, J.-H.; Wang, Z.-Q.; Li, Y.-M. Trapping Red Blood Cells in Living Animals Using Optical Tweezers. Nat. Commun. 2013, 4, 1768. [Google Scholar] [CrossRef]
- Jonáš, A.; Zemánek, P. Light at Work: The Use of Optical Forces for Particle Manipulation, Sorting, and Analysis. Electrophoresis 2008, 29, 4813–4851. [Google Scholar] [CrossRef]
- Wen, F.; Zhang, X.; Ye, H.; Wang, W.; Wang, H.; Zhang, Y.; Dai, Z.; Qiu, C.-W. Efficient and Tunable Photoinduced Honeycomb Lattice in an Atomic Ensemble. Laser Photonics Rev. 2018, 12, 1800050. [Google Scholar] [CrossRef]
- Blázquez-Castro, A. Optical Tweezers: Phototoxicity and Thermal Stress in Cells and Biomolecules. Micromachines 2019, 10, 507. [Google Scholar] [CrossRef]
- Yu, P.; Liu, Y.; Zhao, Q.; Wang, Z.; Li, Y.-M.; Gong, L. Reducing Photodamage in Optical Trapping of Individual Cells in Living Zebrafish. Appl. Phys. Express 2020, 13, 032008. [Google Scholar] [CrossRef]
- Foo, J.-J.; Liu, K.-K.; Chan, V. Thermal Effect on a Viscously Deformed Liposome in a Laser Trap. Ann. Biomed. Eng. 2003, 31, 354–362. [Google Scholar] [CrossRef] [PubMed]
- Shan, X.; Wang, F.; Wang, D.; Wen, S.; Chen, C.; Di, X.; Nie, P.; Liao, J.; Liu, Y.; Ding, L.; et al. Optical Tweezers beyond Refractive Index Mismatch Using Highly Doped Upconversion Nanoparticles. Nat. Nanotechnol. 2021, 16, 531–537. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Zhang, Y.; Zhang, S.; Adam, A.J.L.; Min, C.; Urbach, H.P.; Yuan, X. Nonlinear Optical Trapping Effect with Reverse Saturable Absorption. Adv. Photonics 2023, 5, 046006. [Google Scholar] [CrossRef]
- Zhang, P.; Rufo, J.; Chen, C.; Xia, J.; Tian, Z.; Zhang, L.; Hao, N.; Zhong, Z.; Gu, Y.; Chakrabarty, K.; et al. Acoustoelectronic Nanotweezers Enable Dynamic and Large-Scale Control of Nanomaterials. Nat. Commun. 2021, 12, 3844. [Google Scholar] [CrossRef] [PubMed]
- Wiklund, M. Acoustofluidics 12: Biocompatibility and Cell Viability in Microfluidic Acoustic Resonators. Lab. Chip 2012, 12, 2018–2028. [Google Scholar] [CrossRef] [PubMed]
- Hultström, J.; Manneberg, O.; Dopf, K.; Hertz, H.M.; Brismar, H.; Wiklund, M. Proliferation and Viability of Adherent Cells Manipulated by Standing-Wave Ultrasound in a Microfluidic Chip. Ultrasound Med. Biol. 2007, 33, 145–151. [Google Scholar] [CrossRef]
- Mohanty, S.; Khalil, I.S.M.; Misra, S. Contactless Acoustic Micro/Nano Manipulation: A Paradigm for next Generation Applications in Life Sciences. Proc. R. Soc. Math. Phys. Eng. Sci. 2020, 476, 20200621. [Google Scholar] [CrossRef]
- Zhu, H.; Zhang, P.; Zhong, Z.; Xia, J.; Rich, J.; Mai, J.; Su, X.; Tian, Z.; Bachman, H.; Rufo, J.; et al. Acoustohydrodynamic Tweezers via Spatial Arrangement of Streaming Vortices. Sci. Adv. 2021, 7, eabc7885. [Google Scholar] [CrossRef]
- Wu, M.; Ouyang, Y.; Wang, Z.; Zhang, R.; Huang, P.-H.; Chen, C.; Li, H.; Li, P.; Quinn, D.; Dao, M.; et al. Isolation of Exosomes from Whole Blood by Integrating Acoustics and Microfluidics. Proc. Natl. Acad. Sci. USA 2017, 114, 10584–10589. [Google Scholar] [CrossRef]
- Lakshmanan, A.; Jin, Z.; Nety, S.P.; Sawyer, D.P.; Lee-Gosselin, A.; Malounda, D.; Swift, M.B.; Maresca, D.; Shapiro, M.G. Acoustic Biosensors for Ultrasound Imaging of Enzyme Activity. Nat. Chem. Biol. 2020, 16, 988–996. [Google Scholar] [CrossRef] [PubMed]
- Dholakia, K.; Drinkwater, B.W.; Ritsch-Marte, M. Comparing Acoustic and Optical Forces for Biomedical Research. Nat. Rev. Phys. 2020, 2, 480–491. [Google Scholar] [CrossRef]
- Husseini, G.A.; Pitt, W.G.; Martins, A.M. Ultrasonically Triggered Drug Delivery: Breaking the Barrier. Colloids Surf. B Biointerfaces 2014, 123, 364–386. [Google Scholar] [CrossRef]
- Basha, S.A.; Salkho, N.; Dalibalta, S.; Husseini, G.A. Liposomes in Active, Passive and Acoustically-Triggered Drug Delivery. Mini Rev. Med. Chem. 2019, 19, 961–969. [Google Scholar] [CrossRef] [PubMed]
- Moradi Kashkooli, F.; Jakhmola, A.; Hornsby, T.K.; Tavakkoli, J.; Kolios, M.C. Ultrasound-Mediated Nano Drug Delivery for Treating Cancer: Fundamental Physics to Future Directions. J. Control. Release 2023, 355, 552–578. [Google Scholar] [CrossRef]
- Ding, X.; Lin, S.-C.S.; Kiraly, B.; Yue, H.; Li, S.; Chiang, I.-K.; Shi, J.; Benkovic, S.J.; Huang, T.J. On-Chip Manipulation of Single Microparticles, Cells, and Organisms Using Surface Acoustic Waves. Proc. Natl. Acad. Sci. USA 2012, 109, 11105–11109. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Yang, Y.; Liu, D.; Wang, Y.; Lu, M.; Zhang, Q.; Huang, J.; Li, Y.; Ma, T.; Yan, F.; et al. In-Vivo Programmable Acoustic Manipulation of Genetically Engineered Bacteria. Nat. Commun. 2023, 14, 3297. [Google Scholar] [CrossRef] [PubMed]
- Kolesnik, K.; Xu, M.; Lee, P.V.S.; Rajagopal, V.; Collins, D.J. Unconventional Acoustic Approaches for Localized and Designed Micromanipulation. Lab. Chip 2021, 21, 2837–2856. [Google Scholar] [CrossRef]
- Baudoin, M.; Thomas, J.-L.; Sahely, R.A.; Gerbedoen, J.-C.; Gong, Z.; Sivery, A.; Matar, O.B.; Smagin, N.; Favreau, P.; Vlandas, A. Spatially Selective Manipulation of Cells with Single-Beam Acoustical Tweezers. Nat. Commun. 2020, 11, 4244. [Google Scholar] [CrossRef]
- Terquem, A. KUNDT ET O. LEHMANN.—Ueber longitudinale Schwingungen and Klangfiguren in cylindrischen Flüssigkeitssaülen (Sur les vibrations longitudinales et les figures acoustiques dans les colonnes de liquides cylindriques); Annales de Poggendorff, t. CLIII, p. 1, 1874. J. Phys. Theor. Appl. 1876, 5, 159–161. [Google Scholar] [CrossRef]
- Meng, L.; Cai, F.; Chen, J.; Niu, L.; Li, Y.; Wu, J.; Zheng, H. Precise and Programmable Manipulation of Microbubbles by Two-Dimensional Standing Surface Acoustic Waves. Appl. Phys. Lett. 2012, 100, 173701. [Google Scholar] [CrossRef]
- Tang, Q.; Liu, P.; Guo, X.; Zhou, S.; Dong, Y. 2D Acoustofluidic Patterns in an Ultrasonic Chamber Modulated by Phononic Crystal Structures. Microfluid. Nanofluidics 2020, 24, 91. [Google Scholar] [CrossRef]
- Démoré, C.E.M.; Dahl, P.M.; Yang, Z.; Glynne-Jones, P.; Melzer, A.; Cochran, S.; MacDonald, M.P.; Spalding, G.C. Acoustic Tractor Beam. Phys. Rev. Lett. 2014, 112, 174302. [Google Scholar] [CrossRef] [PubMed]
- Baresch, D.; Thomas, J.-L.; Marchiano, R. Observation of a Single-Beam Gradient Force Acoustical Trap for Elastic Particles: Acoustical Tweezers. Phys. Rev. Lett. 2016, 116, 024301. [Google Scholar] [CrossRef] [PubMed]
- Mitri, F.G. Acoustical Pulling Force on Rigid Spheroids in Single Bessel Vortex Tractor Beams. Europhys. Lett. 2015, 112, 34002. [Google Scholar] [CrossRef]
- Fan, X.-D.; Zhang, L. Trapping Force of Acoustical Bessel Beams on a Sphere and Stable Tractor Beams. Phys. Rev. Appl. 2019, 11, 014055. [Google Scholar] [CrossRef]
- Xu, S.; Qiu, C.; Liu, Z. Transversally Stable Acoustic Pulling Force Produced by Two Crossed Plane Waves. Europhys. Lett. 2012, 99, 44003. [Google Scholar] [CrossRef]
- Meng, Y.; Li, X.; Liang, Z.; Ng, J.; Li, J. Acoustic Pulling with a Single Incident Plane Wave. Phys. Rev. Appl. 2020, 14, 014089. [Google Scholar] [CrossRef]
- Kushwaha, M.S.; Halevi, P.; Dobrzynski, L.; Djafari-Rouhani, B. Acoustic Band Structure of Periodic Elastic Composites. Phys. Rev. Lett. 1993, 71, 2022–2025. [Google Scholar] [CrossRef]
- Walker, E.L.; Jin, Y.; Reyes, D.; Neogi, A. Sub-Wavelength Lateral Detection of Tissue-Approximating Masses Using an Ultrasonic Metamaterial Lens. Nat. Commun. 2020, 11, 5967. [Google Scholar] [CrossRef]
- Kaya, O.A.; Cicek, A.; Ulug, B. Self-Collimated Slow Sound in Sonic Crystals. J. Phys. Appl. Phys. 2012, 45, 365101. [Google Scholar] [CrossRef]
- Jin, Y.; Walker, E.; Choi, T.-Y.; Neogi, A.; Krokhin, A. Simultaneous Negative Reflection and Refraction and Reverse-Incident Right-Angle Collimation of Sound in a Solid-Fluid Phononic Crystal. J. Acoust. Soc. Am. 2022, 151, 2723–2731. [Google Scholar] [CrossRef] [PubMed]
- Pennec, Y.; Vasseur, J.O.; Djafari-Rouhani, B.; Dobrzyński, L.; Deymier, P.A. Two-Dimensional Phononic Crystals: Examples and Applications. Surf. Sci. Rep. 2010, 65, 229–291. [Google Scholar] [CrossRef]
- Zhu, T.; Novitsky, A.; Cao, Y.; Mahdy, M.R.C.; Wang, L.; Sun, F.; Jiang, Z.; Ding, W. Mode Conversion Enables Optical Pulling Force in Photonic Crystal Waveguides. Appl. Phys. Lett. 2017, 111, 061105. [Google Scholar] [CrossRef]
- Korozlu, N.; Biçer, A.; Sayarcan, D.; Adem Kaya, O.; Cicek, A. Acoustic Sorting of Airborne Particles by a Phononic Crystal Waveguide. Ultrasonics 2022, 124, 106777. [Google Scholar] [CrossRef] [PubMed]
- Lighthill, M.J.; Newman, M.H.A. On Sound Generated Aerodynamically I. General Theory. Proc. R. Soc. Lond. Ser. Math. Phys. Sci. 1997, 211, 564–587. [Google Scholar] [CrossRef]
- Brillouin, L. Les tensions de radiation; Leur interprétation en mécanique classique et en relativité. J. Phys. Radium 1925, 6, 337–353. [Google Scholar] [CrossRef]
- Brillouin, L.; Brennan, R.O. Tensors in Mechanics and Elasticity. J. Appl. Mech. 1965, 32, 238. [Google Scholar] [CrossRef]
- Faridi, M.A.; Ramachandraiah, H.; Iranmanesh, I.; Grishenkov, D.; Wiklund, M.; Russom, A. MicroBubble Activated Acoustic Cell Sorting. Biomed. Microdevices 2017, 19, 23. [Google Scholar] [CrossRef]
- Ciampa, F.; Mankar, A.; Marini, A. Phononic Crystal Waveguide Transducers for Nonlinear Elastic Wave Sensing. Sci. Rep. 2017, 7, 14712. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gao, Y.; Cao, Y.; Zhu, T.; Tang, D.; Shi, B.; Li, H.; Gao, W.; Zhang, Y.; Jia, Q.; Li, X.; et al. Stable Acoustic Pulling in Two-Dimensional Phononic Crystal Waveguides Based on Mode Manipulation. Photonics 2023, 10, 1325. https://doi.org/10.3390/photonics10121325
Gao Y, Cao Y, Zhu T, Tang D, Shi B, Li H, Gao W, Zhang Y, Jia Q, Li X, et al. Stable Acoustic Pulling in Two-Dimensional Phononic Crystal Waveguides Based on Mode Manipulation. Photonics. 2023; 10(12):1325. https://doi.org/10.3390/photonics10121325
Chicago/Turabian StyleGao, Yanyu, Yongyin Cao, Tongtong Zhu, Donghua Tang, Bojian Shi, Hang Li, Wenya Gao, Yanxia Zhang, Qi Jia, Xiaoxin Li, and et al. 2023. "Stable Acoustic Pulling in Two-Dimensional Phononic Crystal Waveguides Based on Mode Manipulation" Photonics 10, no. 12: 1325. https://doi.org/10.3390/photonics10121325
APA StyleGao, Y., Cao, Y., Zhu, T., Tang, D., Shi, B., Li, H., Gao, W., Zhang, Y., Jia, Q., Li, X., Feng, R., Sun, F., & Ding, W. (2023). Stable Acoustic Pulling in Two-Dimensional Phononic Crystal Waveguides Based on Mode Manipulation. Photonics, 10(12), 1325. https://doi.org/10.3390/photonics10121325




