1. Introduction
In recent years, reflective differential interference contrast (DIC) digital microscopy system has been widely used in precision processing and inspection fields, such as the observation of conductive particles in thin-film transistor liquid crystal displays [
1], the measurement of martensite microstructures, and the classification of individual dielectric nanoparticles [
2,
3]. DIC microscopy system can be used for qualitative or quantitative measurements of samples [
4,
5,
6,
7], as well as for reflective surface assessment [
8] and optical profiling [
9].
As one of the main 3D morphological tools available for microsurface inspection, differential interference contrast microscopy [
10] can transform small phase or optical path length variations on the object surface into light intensity, i.e., the phase or optical path length variations on the object surface are transformed into intensity variations due to the interference of light from two closely separated points on the object surface. It shows the subtle bumps on the sample surface with strong light intensity and interference color variations. The images captured by the DIC microscopy system have a distinctive shadow effect and a strong three-dimensional relief.
Studying the Nomarski prism is of utmost importance as it serves a critical function in differential interference contrast microscopy. Numerous researchers have conducted meticulous studies on the design theory of Nomarski prisms and engaged in DIC microscopy [
11,
12,
13,
14,
15,
16,
17,
18,
19,
20]. Early studies proposed simplified mathematical theoretical models for DIC imaging, such as the DIC imaging model constructed based on differential methods [
21,
22]. These studies provided a good research basis and reference value for accurate models in later research. However, these imaging models did not take into account the phase difference produced by the light in the Nomarski prism itself, so they were only suitable for qualitative observation of the sample and could not be used for quantitative measurements.
In order to use the differential interference contrast microscopy for quantitative measurements, the phase change due to the Nomarski prism must be calculated. The above theoretical study only calculated the phase change for the half of the light path, i.e., the linearly polarized light incident to the prism and out to the intersection of the two linearly polarized beams, and did not take into account the light incident to the Nomarski prism, reflected from the sample surface and then returned to the Nomarski prism, and the outgoing process. Hartman [
23] makes an approximation to the phase change caused by the Nomarski prism and does not obtain an exact solution. In this paper, the theoretical calculation of the phase difference arising during the passage of the incident light through the prism to the horizontal viewing plane and back to the prism is investigated based on the incident light perpendicular to the plane of apparent splitting, covering the entire light path and obtaining an algebraic solution.
In addition, previous theoretical studies of differential interference contrast microscopy systems have been dominated by single wavelength analysis. Practical differential interference contrast microscopy systems usually use a composite light source containing multiple wavelengths, such as white light, rather than a monochromatic source. The standard wavelengths d (656 nm), F (587 nm), and C (486 nm) are taken as examples to analyze the relationship between the interference color change of the observation surface under the superposition of different wavelengths and the prism wedge angle when the prism moves.
The research content of this paper includes three parts. In
Section 2, we derive an expression between the prism parameters based on a geometric model of incident light perpendicular to the plane of apparent splitting and then derive the relationship between the optical path difference produced by the light in the prism as it is incident to the prism and reflected the prism through the image plane and the position of the incident light. In
Section 3, we discuss the effect of different prism wedge angles on the interference color when the prism is moved at the same distance under a superposition of light intensities of multiple wavelengths. We briefly draw a conclusion in
Section 4.
2. Methods
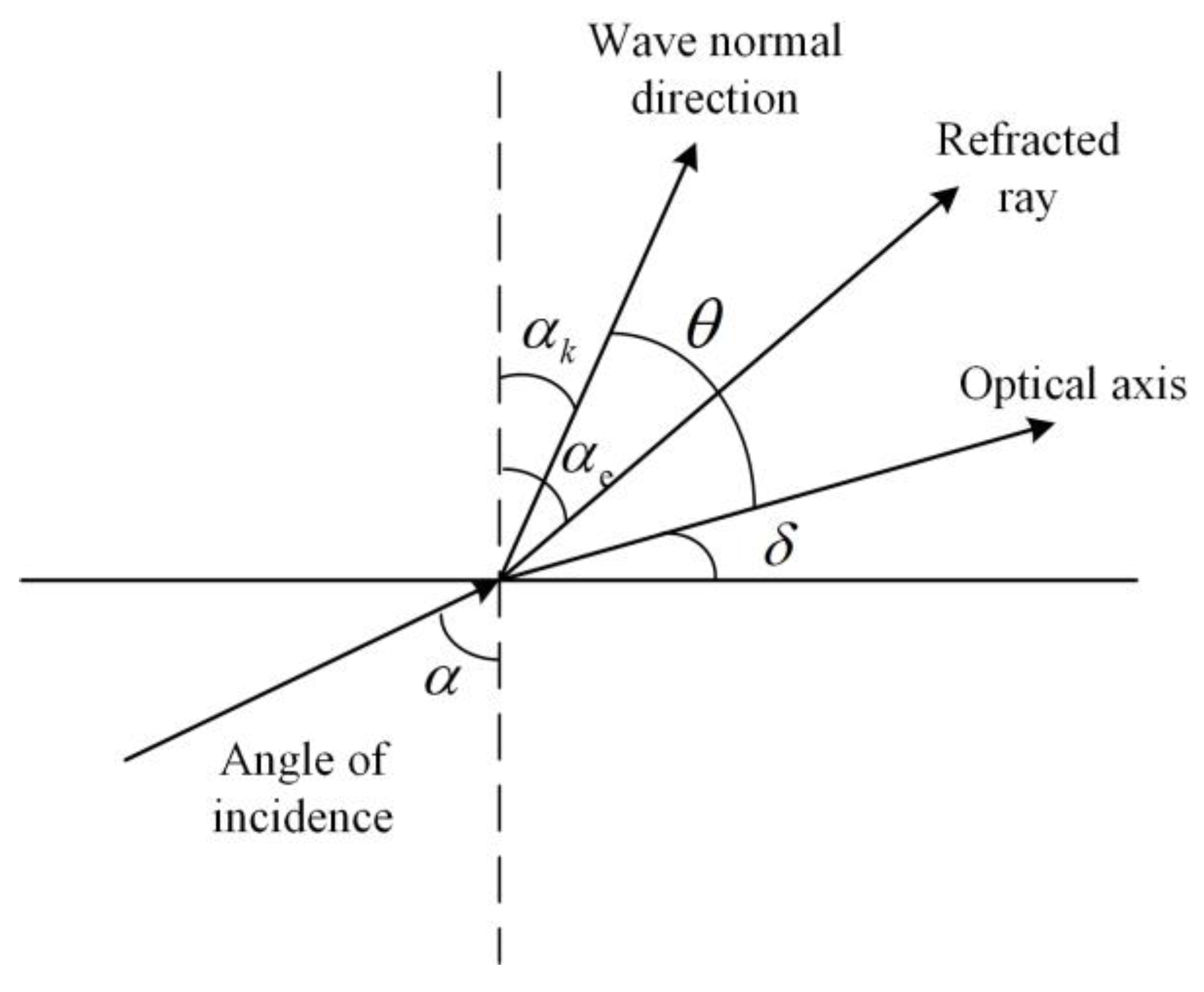
Figure 1 shows a diagram of the incidence plane of a Nomarski prism with a wedge angle of
, the thickness of the prism
d,
the angle between the crystal axis of the first crystal and the lower surface (axially orthogonal), and the optical axis of the second crystal perpendicular to the incidence plane, which divides the optical system into zones 1, 2, 3 and 4. Assuming that the linearly polarized light is incident on the prism at an angle of incidence
,
is the angle of separation between the ordinary(
o) and extraordinary(
e) rays, where the principal refractive index of the ordinary ray is
, and the principal refractive index of the extraordinary ray is
.
First, we discuss the component of light whose vibrational direction is perpendicular to the incident surface—ray
o in zone 2 and ray
e in zone 3, and we can then obtain the exit angle
, and the subscript
oe indicates that the component of polarized light changes from ray
o (zone 2) to ray
e (zone 3). We call it ray
oe.
Then, we focus on the light component, whose vibrational direction is parallel to the incident surface, ray
e in zone 2 and ray
o in zone 3, and we can then obtain the exit angle
, and the subscript
eo indicates that the component of polarized light changes from ray
e (zone 2) to ray
o (zone 3). We call it ray
eo.
where, in Equation (2)
where
is the angle between the direction normal to the ray
e light in zone 2 and the crystal optical axis.
The detailed derivation process of Equations (1) and (2) is shown in
Appendix A.
Therefore, the beam splitting angle
after the two beams exit through the prism is
The right-angle coordinate system is shown in
Figure 1, and
represents the angle between the ray intersection plane and the positive direction of the
y-axis. Let the coordinates of the incident point be
, the coordinates of rays
o and
e on the second dividing plane are
and
, respectively; the coordinates of rays
oe and
eo on the third dividing plane are
and
, respectively; the two beams intersect at the point
.
The geometric path of light in zone 2 is
where
is the refraction angle of ray
o in zone 2; then, the coordinates of point
as
Similarly, the coordinates of point
can be found as
where
is the angle of incidence at the junction of zone 3 and zone 4, and the geometric path of ray
e in zone 2 is
where
is the refraction angle of ray
e in zone 2; then, the coordinates of point
as
Similarly, the coordinates of point
can be found as
where
is the angle of incidence at the junction of zone 3 and zone 4, and the final two outgoing beams are determined by the following set of equations:
Solving the coordinates of the intersection point of the two beams in Equation (11), we can obtain the following:
The distance between the upper surface of the prism and the intersecting surface of the outgoing ray is .
The two polarized beams of light pass through the Nomarski prism and produce an optical path difference. The optical path of ray
oe is
The optical path of ray
eo is
Thus, the optical path difference between the two linearly polarized beams is
In reflective differential interference contrast microscopy systems, as shown in
Figure 2, light incident into the Nomarski prism gathers through the objective lens to the middle image plane, and then it reflects to the prism through the middle image plane and leaves the prism. The optical path difference mainly comes from the process of incidence and refraction of light in the prism.
As shown in
Figure 2, the light incident from point
into the Nomarski prism converges to the middle image plane through the objective lens and then reflects to the prism through the middle image plane and leaves the prism from point
. In the whole process, Fermat’s principle states that the actual path of a light ray between two points gives optical path length a stationary value. Since the family of rays from
to
are all actual paths, they all have the same optical path length. So, there is no optical path difference between the rays
and
. The main optical path difference comes from two parts: the light incident into the prism, which refracted through the prism and reached the ray intersection plane, and the reflected light from the ray intersection plane to the prism, which emerges through the prism. Firstly, the optical path difference generated by the process of light incident from point
to the prism and reaching the ray intersection plane through prism refraction can be calculated using Equation (15). Because the optical path difference
caused by an incident on the Nomarski prism has a linear relationship with the incident coordinates
x, when the incident coordinate
is known, the coordinate
of the reflected light on the prism can be calculated by geometric relation in
Figure 2. We next calculate the optical path difference. When the prism moves horizontally along the ray intersection plane directly to the prism with the dotted line in
Figure 2, the position of the incident light relative to the optical axis does not change because the optical axis of the system does not change, but the position relative to the prism surface changes, so the optical path difference also changes.
As shown in
Figure 1,
is the extension line of the incident light, and the incident point
is set. The expression of the extension line of the incident ray can be obtained in the coordinate system based on a prism:
where
represents the slope and
represents the intercept of the incident ray.
Because the plane of intersection of the ray of the Nomarski prism in the differential interference contrast microscope coincides with the rear focal plane of the objective lens, we need to make the incident ray extend perpendicular to the plane of intersection of ray:
The ray direction satisfying the above formula is the optical axis direction of the differential interference contrast optical system so that we can find the linear expression of the plane of intersection of rays:
where
is the slope of the line between P′ and I′, and
is the value at which the line intersects the positive
y-axis.
By connecting (17) and (19), the intersection coordinate
can be obtained as
From the coordinates of
and
, the offset
, represented by
, can be obtained from the geometric relationship in
Figure 2.
We take the wedge angle
, the optical axis inclination angle
, and the prism thickness of the Nomarski prism as 2 mm; the optimized parameters are the light incidence angle
and the plane distance between the upper surface of the prism and the ray
D = 25.9643 mm. By substituting the above data into Equations (15) and (21), the offset
generated by different incident light positions passing through the prism can be obtained, as shown in
Figure 3.
As can be seen from
Figure 3,
has a linear relationship with
x. That is, the offset generated by each incident point through the prism (the difference between the incident ray extension line and its intersection point on the plane of intersection of ray) can be determined using Equation (21).
Figure 2 shows that, when the Nomarski prism is placed at an angle (for the purpose of parallel coincidence between the ray intersection plane and the objective lens), light incident into the prism passes through the objective lens to the viewing surface and then reflects from the viewing surface to the prism and out. In
Figure 2,
corresponds to the incident light, and
corresponds to the light emitted through the prism after reflection, with the following relation expression:
where
,
, and
are the values in the
x-y coordinate system;
,
, and
are the values in the
u-v coordinate system. According to the geometric relation in
Figure 2 Because
, we have,
As can be seen from Equation (21), in the
x-y coordinate system, each
x value corresponds to a
, and the relationship between them is linear, so
can be simplified into the following relation:
From Equations (25) and (26), we can calculate the value of
x in the
x-y coordinate system when the ray returns.
When
and
values are known, the corresponding optical path difference can be determined by substituting in the equation. Then, the optical path difference generated during the whole process of light incident into the Nomarski prism and exiting is
The function expression of the change in light intensity of the observed surface along with the phase is as follows [
24].
For an ideal optical system, we have
. Therefore, Equation (30) can be further simplified as
Similarly, we take the Nomarski prism with wedge angle
, optical axis inclination
, and prism thickness of 2 mm, and from Equation (28), we can obtain the relationship between the optical path difference
generated during the whole process of light incident to the Nomarski prism and outgoing and the light incident coordinate
, as shown in
Figure 4.
is linearly related to
.
3. Simulation Results and Analysis
In the use of differential interference contrast (DIC) microscopy systems, it is necessary to adjust the position of the Normaski prism in the direction perpendicular to the optical axis to introduce a suitable optical path difference to obtain the best sample image. We found that the adjustment of the prism position brings about a change in the interference color. A specific analysis is presented below.
Assume that the prism length is 20 mm, and the thickness is
d. As shown in
Figure 5, the point where the intersecting prisms meet is considered the origin of coordinates in the absolute coordinate system. Half of the thickness is used as the center of the prism. If the prism wedge angle is
, then the prism center transverse coordinate is
, and the prism is located at [
− 10,
+ 10], as shown in the gray area in
Figure 5; if the prism wedge angle is
, then the prism center transverse coordinate is
, and the prism is located at [
− 10,
+ 10], as shown in the green area in
Figure 5 With the prism center as the initial position, it moves no further than the length of the prism itself, i.e., [−10 mm, 10 mm]. Therefore, we now use relative coordinates instead of absolute coordinates. Let the prism center be the zero point in relative coordinates, then its moving range is [−10 mm, 10 mm], as shown in
Figure 6.
Based on the above theory, three wavelengths of red light (
nm), yellow-orange light (
nm), and blue light (
nm) in white light were selected. At the same time, the angle of the optical axis in the Nomarski prism was
, the thickness of the prism was 2 mm, and the wedge angle
was 0.2°, 0.45°, 0.75°, and 0.95°, respectively. As shown in
Figure 6, the horizontal coordinates indicate the position of the prism in the
x-y coordinate system shown in
Figure 2, and the difference between different coordinate values indicates the prism moves to the distance, and the vertical coordinates indicate the light intensity, where it can be seen from the comparison of (a), (b), (c) and (d) that the light intensity changes for more periods when the prism wedge angle is larger, and the prism moves the same distance.
As shown in
Figure 7a, when the wedge angle
, the prism moves from left to right, i.e., from −10 mm to 10 mm, and the interference color changes in the order of “red-cyan-green-black-rose-green-blue-violet.” As shown in
Figure 7b–d, the interference color changes faster as the wedge angle becomes larger when the prisms move the same distance. Taking the change from red to rose red as an example when the wedge angle
is 0.2°, 0.45°, 0.75°, and 0.95°, the required moving distance is about 4.8 mm, 2.2 mm, 1.4 mm, and 1 mm, respectively. The larger the wedge angle, the shorter the moving distance required to change the same color. In other words, the larger the wedge angle is, the faster the interference color changes, provided that the same distance is moved. The results suggest that the prism wedge angle should be made as small as possible in the actual design of Nomarski. Otherwise, when the prism moves a tiny distance, it will produce multiple color changes in the observation screen, and it is not easy to find the best prism position for imaging.