Sb-Based Low-Noise Avalanche Photodiodes
Abstract
:1. Introduction
2. Materials and Methods
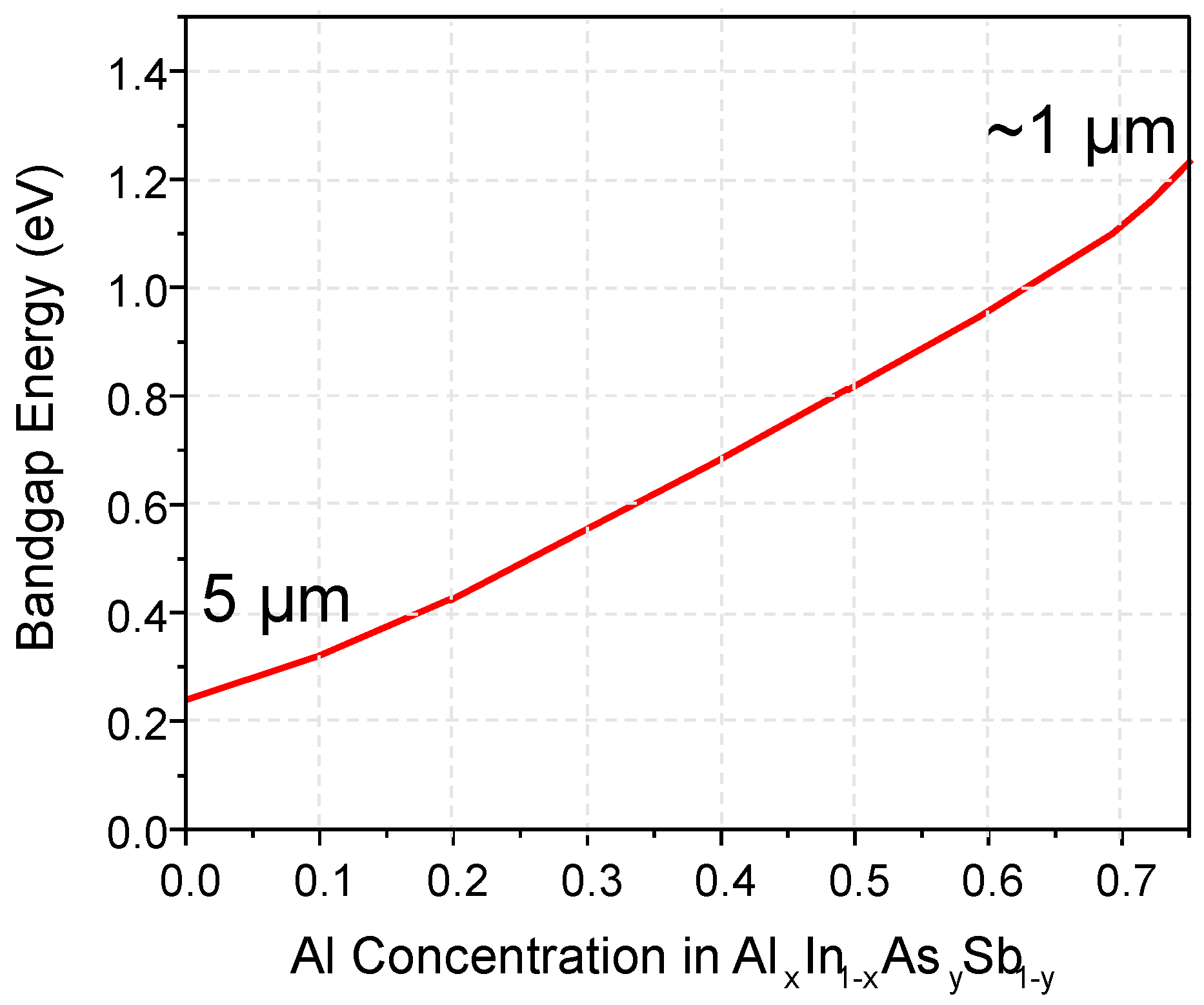
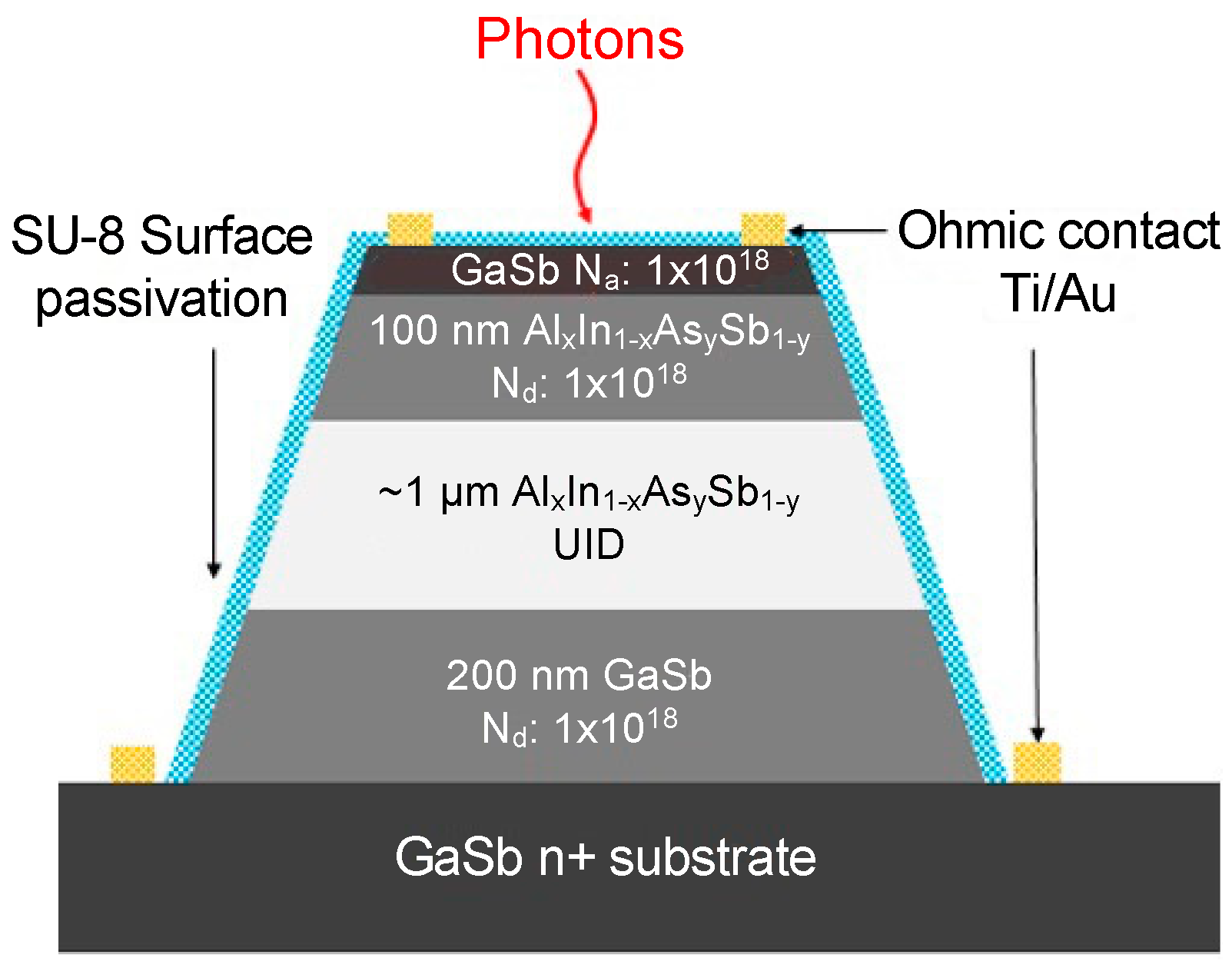
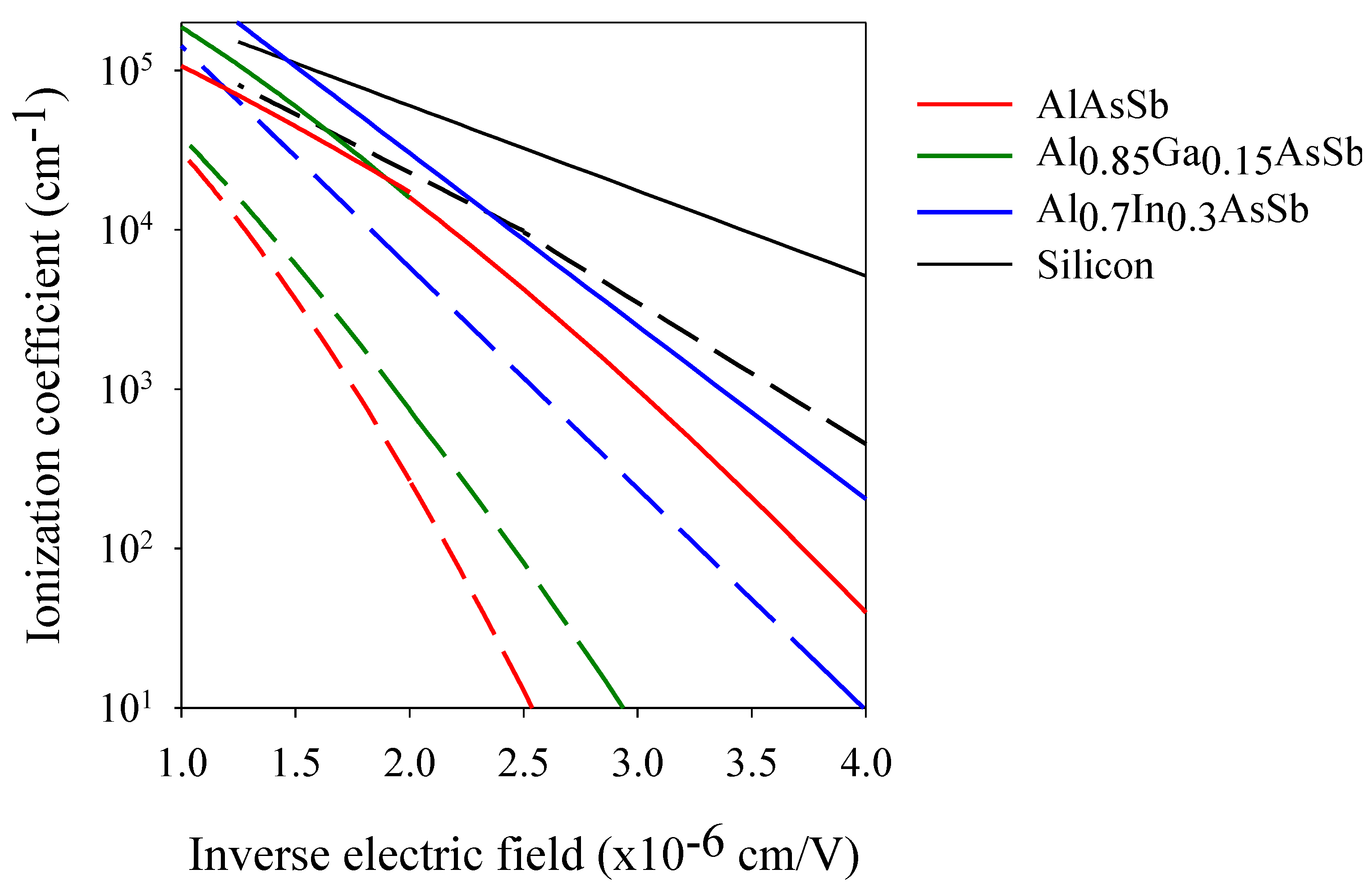
2.1. AlxIn1-xAsySb1-y on GaSb Substrate
2.2. AlxGa1-xAs0.56Sb0.44 on InP Substrate
3. Results
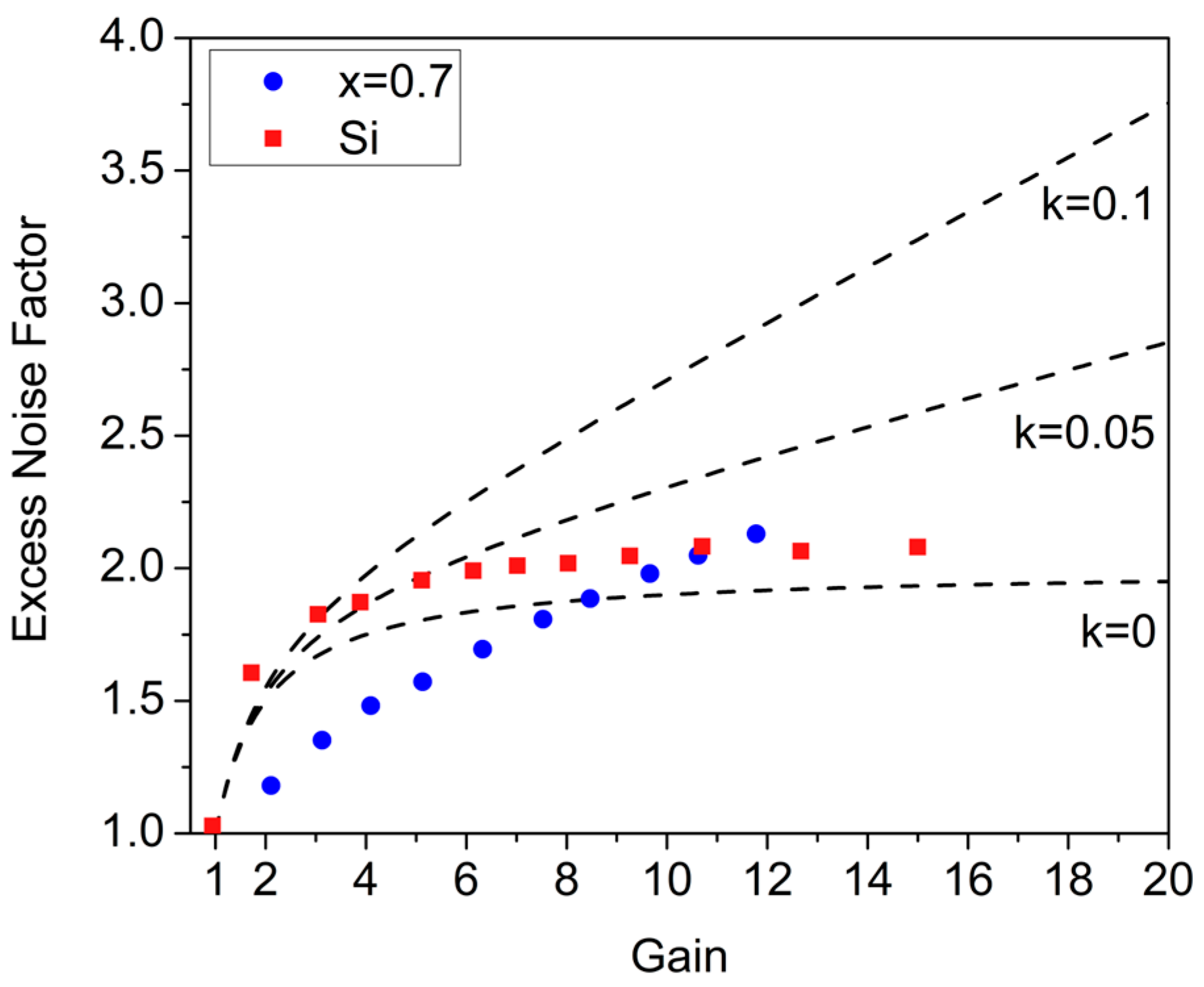
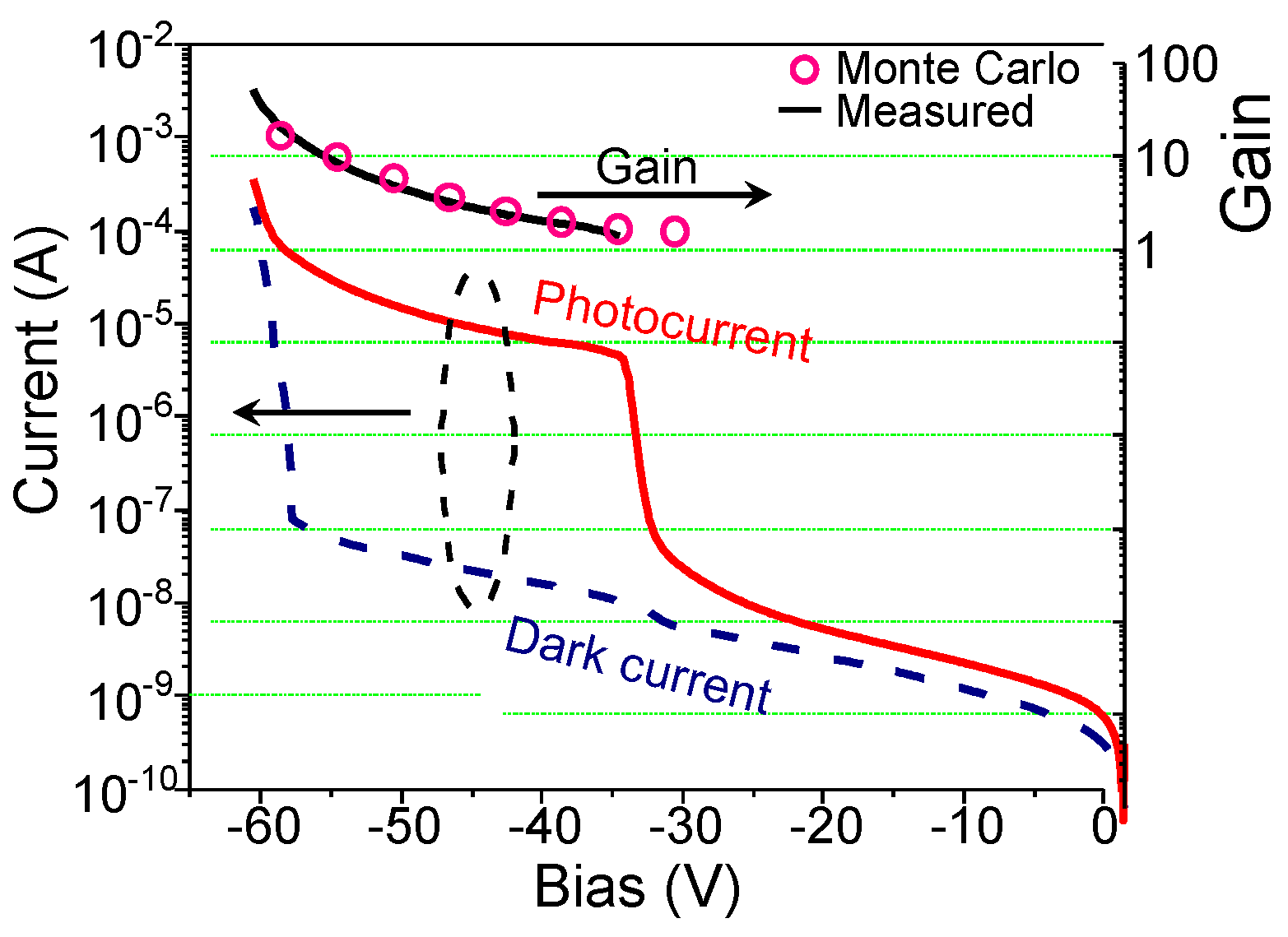
3.1. AlxIn1-xAsySb1-y p-i-n Structure APDs
3.2. AlxIn1-xAsySb1-y Separate Absorption, Charge, and Multiplication APDs
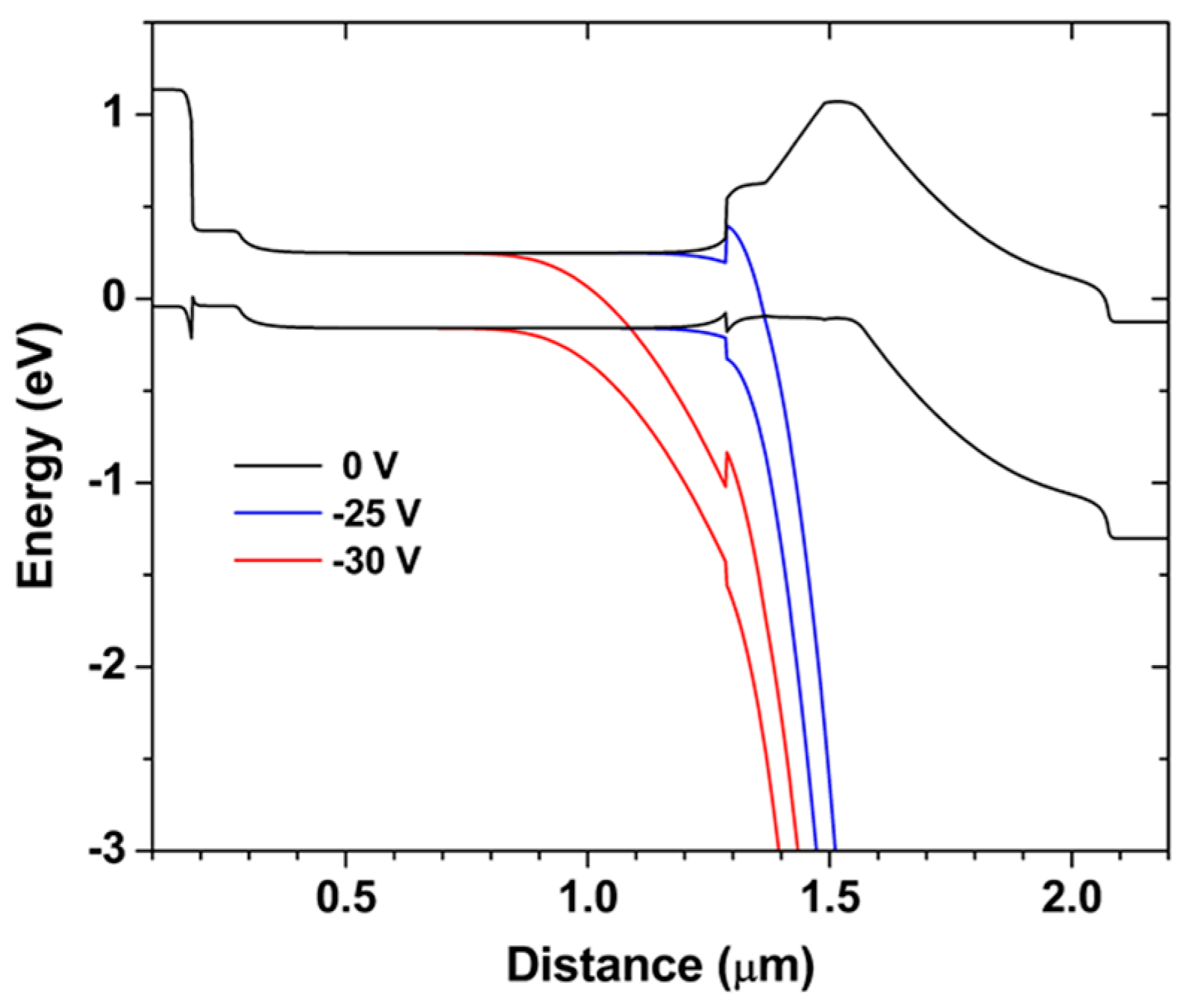
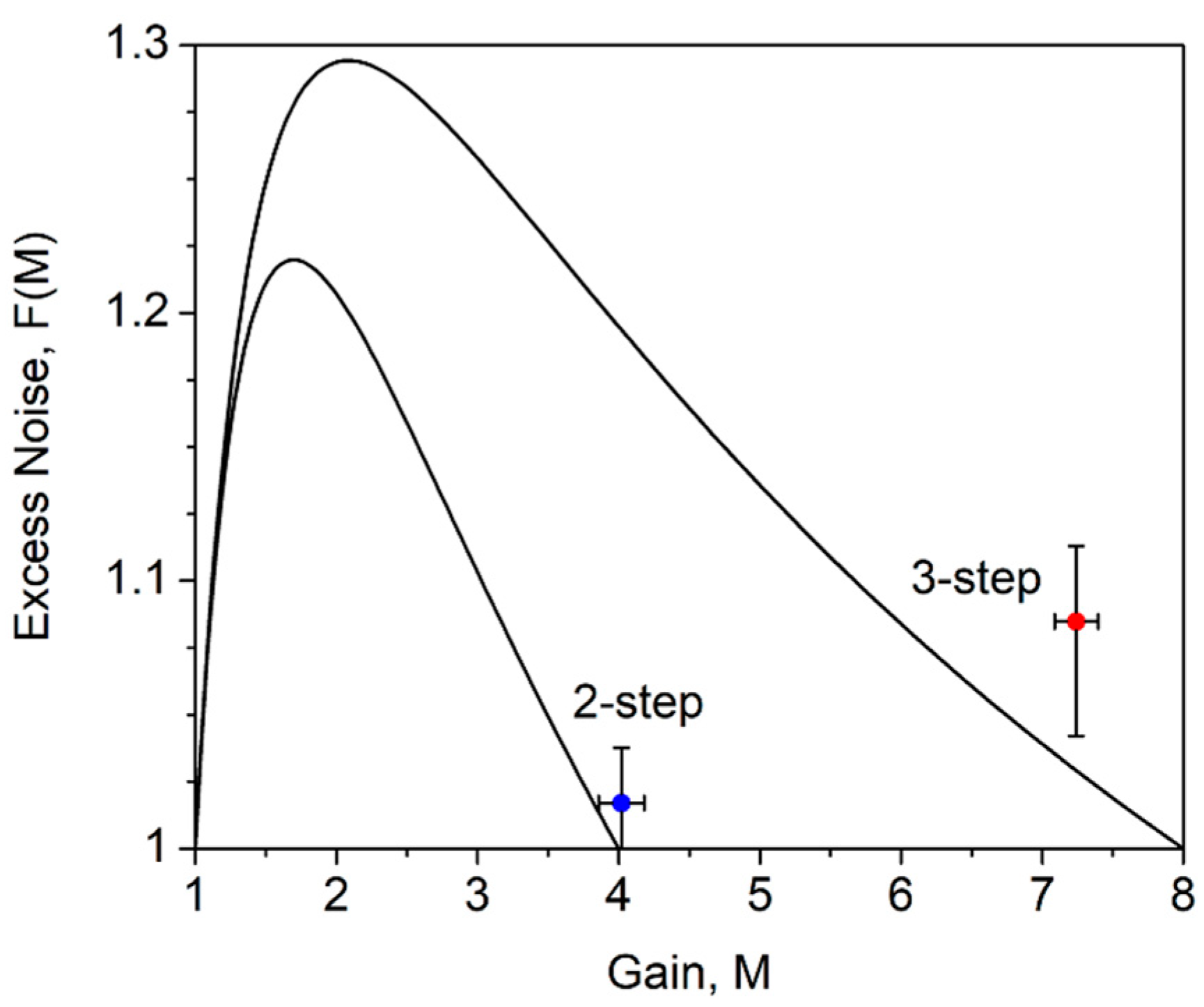
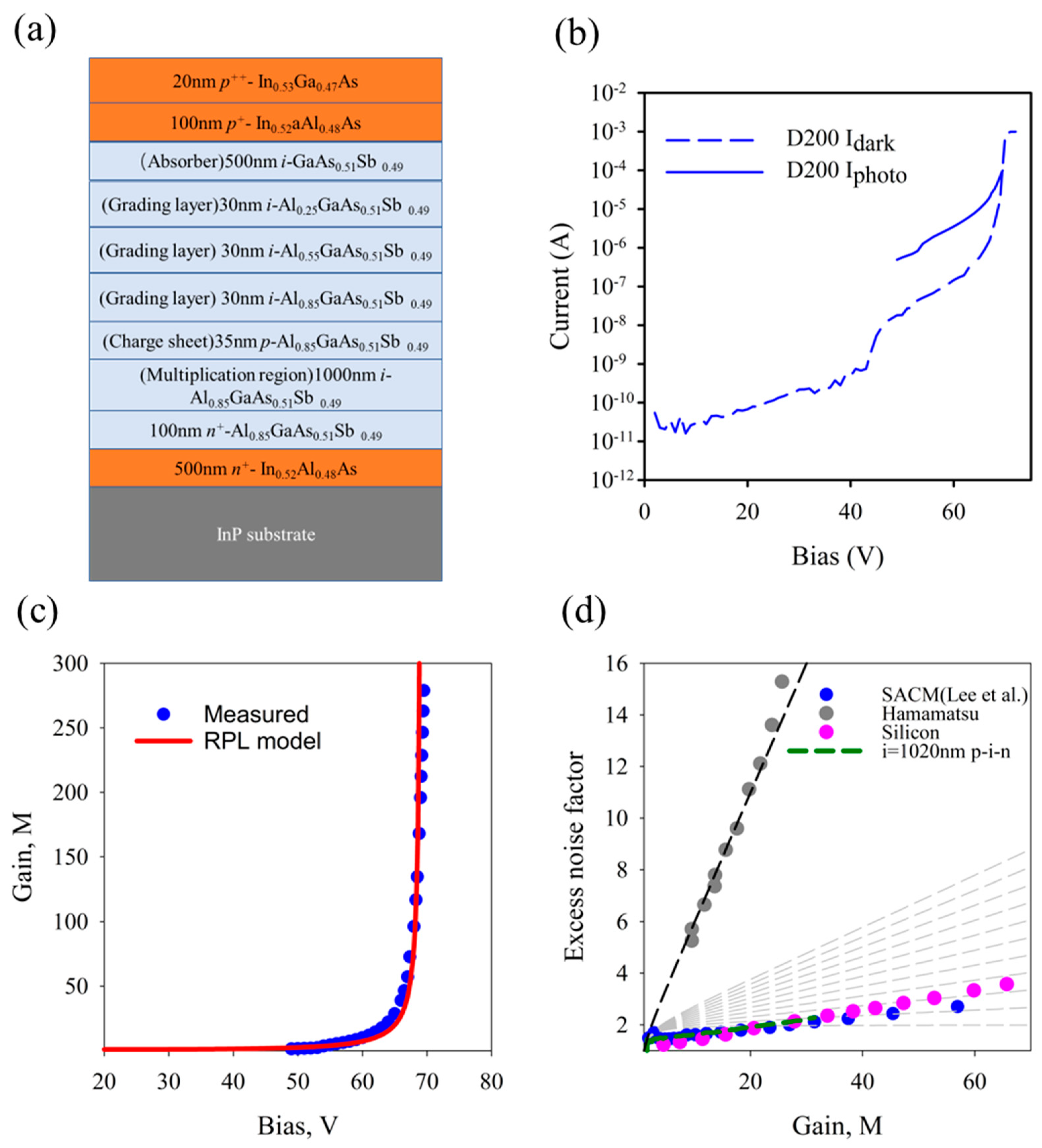
3.3. Staircase APDs
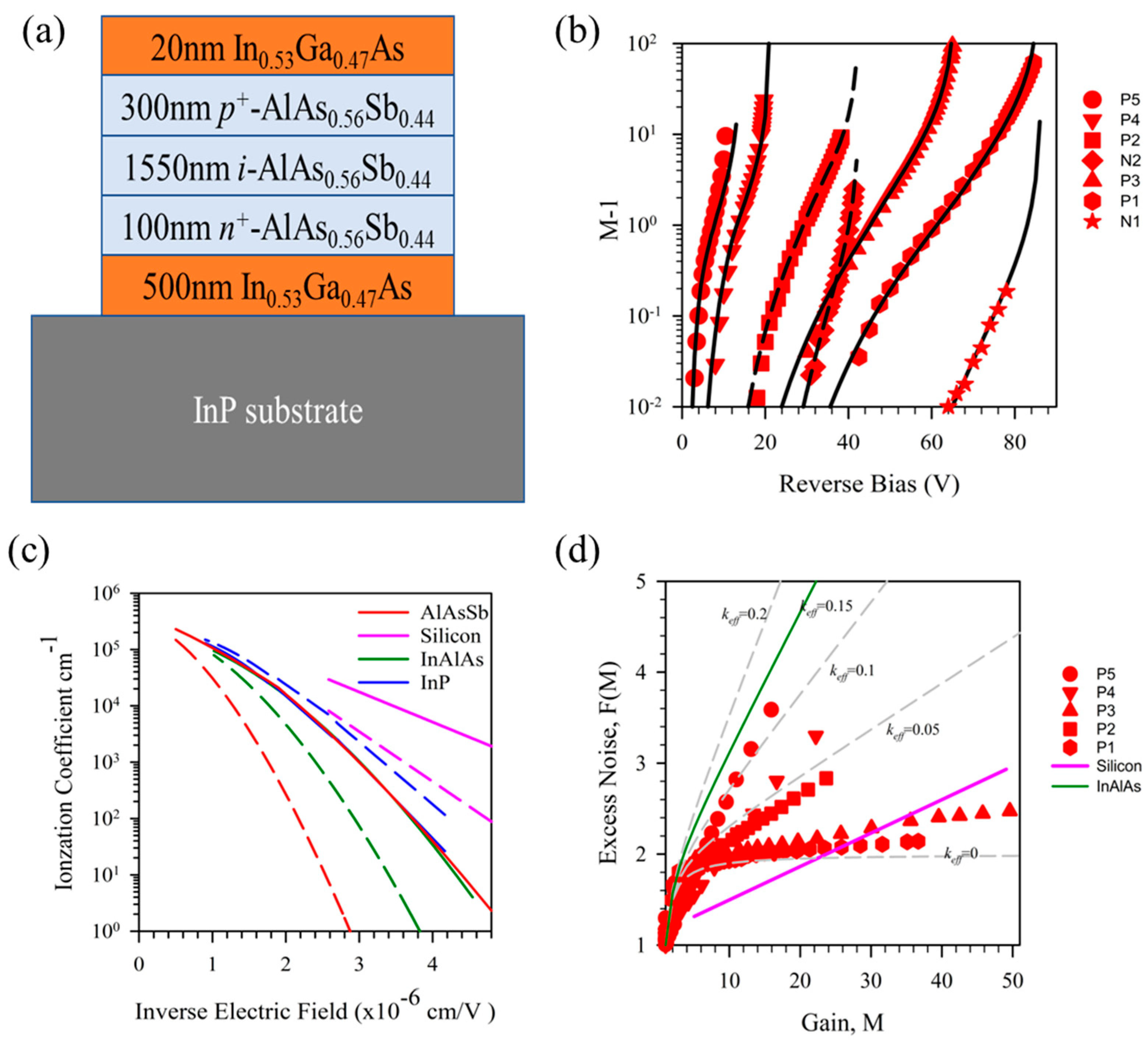
3.4. AlxGa1-xAs0.56Sb0.44 p-i-n and n-i-p Structure APDs
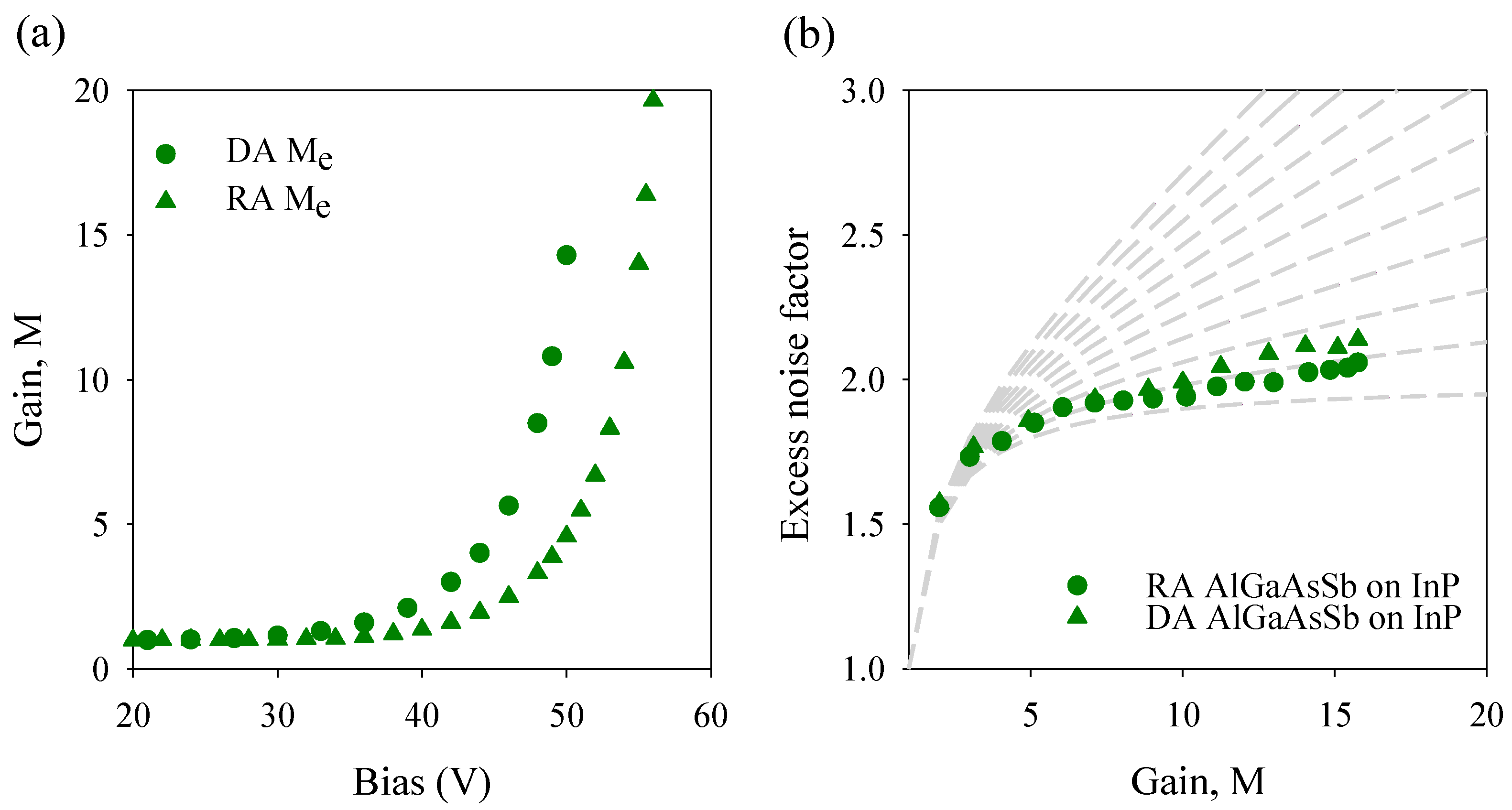
3.5. AlxGa1-xAs0.56Sb0.44 Separate Absorption, Charge, and Multiplication APDs
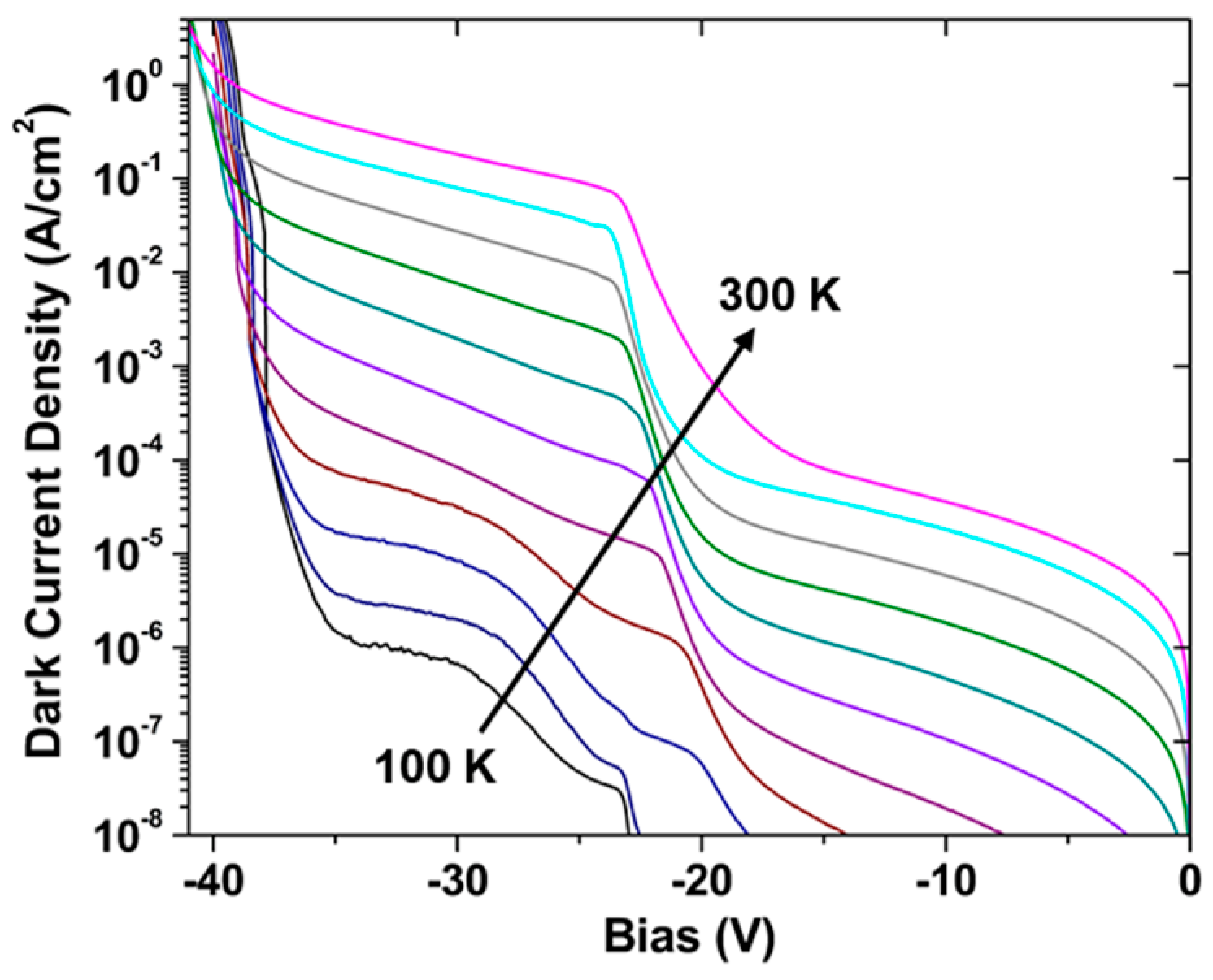
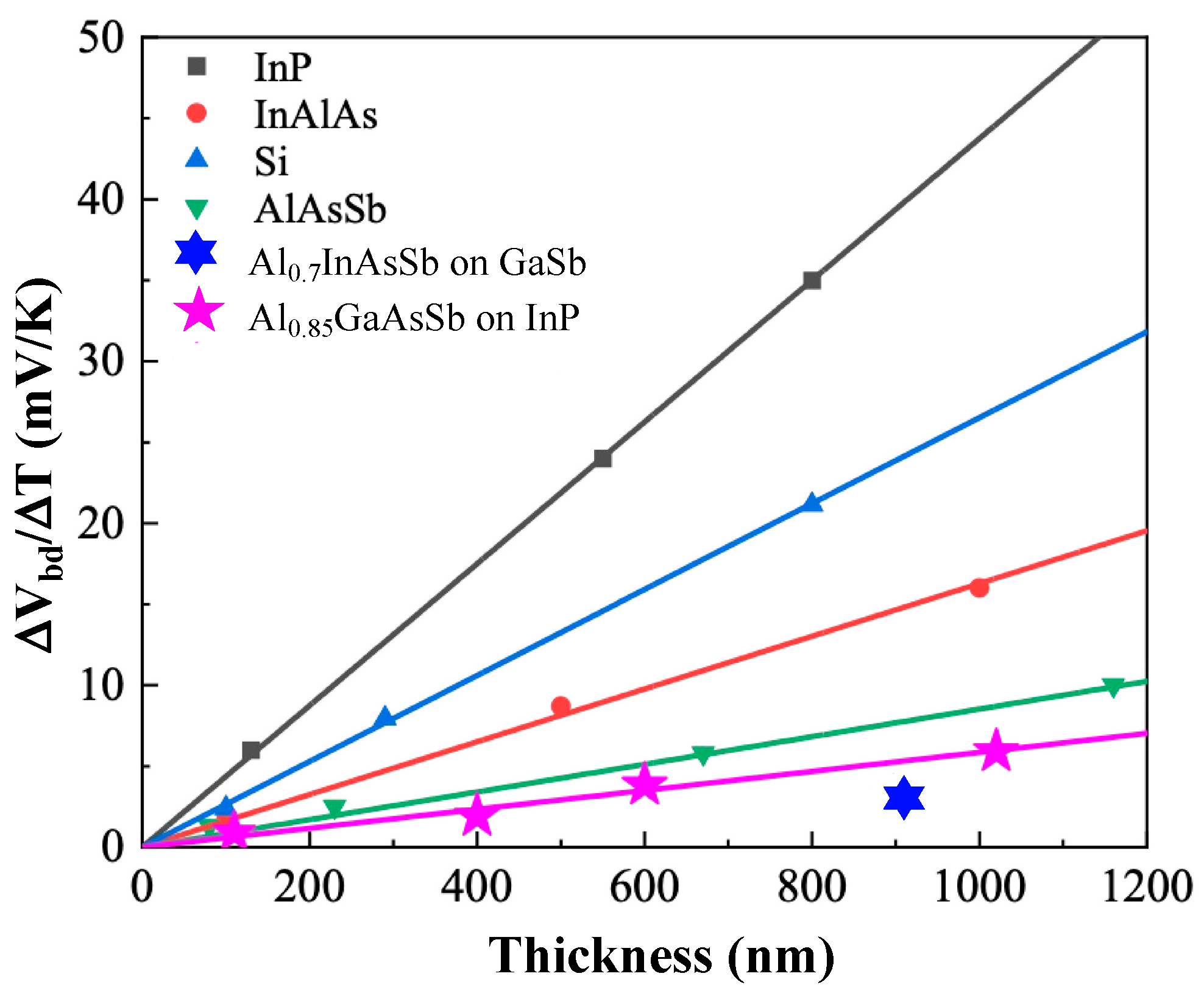
3.6. Temperature Variation of Breakdown Voltage
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Campbell, J.C. Advances in photodetectors. In Optical Fiber Telecommunications V; Kaminow, I., Li, T., Willner, A.E., Eds.; Elsevier: Amsterdam, The Netherlands, 2008; Volume A, pp. 221–268. [Google Scholar]
- Huang, Z.; Li, C.; Liang, D.; Yu, K.; Santori, C.; Fiorentino, M.; Sorin, W.; Palermo, S.; Beausoleil, R.G. 25 Gbps low-voltage waveguide Si–Ge avalanche photodiode. Optica 2016, 3, 793–798. [Google Scholar] [CrossRef]
- Lecomte, R.; Martel, C.; Carrier, C. Status of BGO-avalanche photodiode detectors for spectroscopic and timing measurements. Nucl. Instrum. Methods Phys. Res. Sect. Accel. Spectrometers Detect. Assoc. Equip. 1989, 278, 585–597. [Google Scholar] [CrossRef]
- Dunai, D.; Zoletnik, S.; Sárközi, J.; Field, A.R. Avalanche photodiode based detector for beam emission spectroscopy. Rev. Sci. Instrum. 2010, 81, 103503. [Google Scholar] [CrossRef] [Green Version]
- Albota, M.A.; Heinrichs, R.M.; Kocher, D.G.; Fouche, D.G.; Player, B.E.; O’Brien, M.E.; Aull, B.F.; Zayhowski, J.J.; Mooney, J.; Willard, B.C.; et al. Three-dimensional imaging laser radar with a photon-counting avalanche photodiode array and microchip laser. Appl. Opt. 2002, 41, 7671–7678. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Brian, F.; Aull, B.F.; Duerr, E.K.; Frechette, J.P.; McIntosh, K.A.; Schuette, D.R.; Younger, R.D. Large-Format Geiger-Mode Avalanche Photodiode Arrays and Readout Circuits. IEEE J. Sel. Top. Quantum. Electron. 2018, 24, 1–10. [Google Scholar]
- Hugi, A.; Villares, G.; Blaser, S.; Liu, H.C.; Faist, J. Mid-infrared frequency comb based on a quantum cascade laser. Nature 2021, 492, 229–233. [Google Scholar] [CrossRef]
- Villares, G.; Hugi, A.; Blaser, S.; Faist, J. Dual-comb spectroscopy based on quantum-cascade-laser frequency combs. Nat. Commun. 2014, 5, 5192. [Google Scholar] [CrossRef] [Green Version]
- Jiang, X.; Itzler, M.; O’Donnell, K.; Entwistle, M.; Owens, M.; Slomkowski, K.; Rangwala, S. InP-Based Single-Photon Detectors and Geiger-Mode APD Arrays for Quantum Communications Applications. IEEE J. Sel. Top. Quantum Electron. 2015, 21, 5–16. [Google Scholar] [CrossRef]
- Kardynał, B.E.; Yuan, Z.L.; Shields, A.J. An avalanche-photodiode-based photon-number-resolving detector. Nat. Photonics 2008, 2, 425–428. [Google Scholar] [CrossRef] [Green Version]
- McIntyre, R.J. Multiplication noise in uniform avalanche diodes. IEEE Trans. Electron. Dev. 1966, 13, 154–158. [Google Scholar] [CrossRef]
- Vaughn, L.G.; Dawson, L.R.; Pease, E.A.; Lester, L.F.; Xu, H.; Jiang, Y.; Gray, A.L. Type I mid-infrared MQW lasers using AlInAsSb barriers and InAsSb wells. Proc. SPIE 2005, 5722, 307–318. [Google Scholar]
- Maddox, S.J.; Bank, S.R. Broadly Tunable AlInAsSb Digital Alloys Grown on GaSb. ACS Cryst. Growth Des. 2016, 16, 3582–3586. [Google Scholar] [CrossRef]
- Yi, X.; Xie, S.; Liang, B.; Lim, L.W.; Zhou, X.; Debnath, M.C.; Huffaker, D.L.; Tan, C.H.; David, J.P.R. Demonstration of large ionization coefficient ratio in AlAs0.56Sb0.44 lattice matched to InP. Sci. Rep. 2018, 8, 8–13. [Google Scholar] [CrossRef] [PubMed]
- Yi, X.; Xie, S.; Liang, B.; Lim, L.W.; Cheong, J.S.; Debnath, M.C.; Huffaker, D.L.; Tan, C.H.; David, J.P.R. Extremely low excess noise and high sensitivity AlAs0.56Sb0.44 avalanche photodiodes. Nat. Photonics 2019, 13, 683–686. [Google Scholar] [CrossRef]
- Lee, S.; Kodati, S.H.; Guo, B.; Jones, A.H.; Schwartz, M.; Winslow, M.; Grein, C.H.; Ronningen, T.J.; Campbell, J.C.; Krishna, S. Low noise Al0.85Ga0.15As0.56Sb0.44 avalanche photodiodes on InP substrates. Appl. Phys. Lett. 2021, 118, 081106. [Google Scholar] [CrossRef]
- Lee, S.; Guo, B.; Kodati, S.H.; Jung, H.; Schwartz, M.; Jones, A.H.; Winslow, M.; Grein, C.H.; Ronningen, T.J.; Campbell, J.C.; et al. Random alloy thick AlGaAsSb avalanche photodiodes on InP substrates. Appl. Phys. Lett. 2022, 120, 071101. [Google Scholar] [CrossRef]
- Ren, M.; Maddox, S.J.; Woodson, M.E.; Chen, Y.; Bank, S.R.; Campbell, J.C. Characteristics of AlxIn1−xAsySb1−y (x: 0.3–0.7) avalanche photodiodes. IEEE J. Light. Tech. 2017, 35, 2380–2384. [Google Scholar] [CrossRef]
- Woods, M.H.; Johnson, W.C.; Lampert, M.A. Use of a Schottky barrier to measure impact ionization coefficients in semiconductors. Solid-State Electron. 1973, 16, 381–394. [Google Scholar] [CrossRef]
- Kodati, S.H.; Lee, S.; Guo, B.; Jones, A.H.; Schwartz, M.; Winslow, M.; Pfiester, N.A.; Grein, C.H.; Ronningen, T.J.; Campbell, J.C.; et al. AlInAsSb avalanche photodiodes on InP substrates. Appl. Phys. Lett. 2012, 118, 091101. [Google Scholar] [CrossRef]
- Ahmed, S.Z.; Tan, Y.; Zheng, J.; Campbell, J.C.; Ghosh, A.W. Atomistic Transport Modeling, Design Principles, and Empirical Rules for Low-Noise III-V Digital-Alloy Avalanche Photodiodes. Phys. Rev. Appl. 2022, 17, 034044. [Google Scholar] [CrossRef]
- Kang, Y.; Liu, H.-D.; Morse, M.; Paniccia, M.J.; Zadka, M.; Litski, S.; Sarid, G.; Pauchard, A.; Kuo, Y.-H.; Chen, H.-W.; et al. Epitaxially-Grown Ge/Si Avalanche Photodiodes for 1.3 mm Light Detection. Nat. Photonics 2009, 3, 59. [Google Scholar] [CrossRef]
- Huang, M.; Cai, P.; Wang, L.; Shi, T.; Chen, W.; Li, S.; Hou, G.; Hong, C.; Pan, D. Development of Si photonics technology: Ge/Si avalanche photodiode for PON applications. In Proceedings of the Optical Fiber Communication Conference, San Francisco, CA, USA, 9–13 March 2014. [Google Scholar]
- Nada, M.; Muramoto, Y.; Yokoyama, H.; Toshimatsu, T.; Matsuzaki, H. High-speed avalanche photodiodes for 100-Gb/s systems and beyond. In Proceedings of the European Conference on Optical Communications, Cannes, France, 21–25 September 2014. [Google Scholar]
- Jones, A.H.; March, S.D.; Bank, S.R.; Campbell, J.C. AlInAsSb/GaSb Separate Absorption, Charge, and Multiplication Avalanche Photodiodes for 2-μm Applications. Nat. Photonics 2020, 14, 559–563. [Google Scholar] [CrossRef]
- Zheng, J.; Jones, A.H.; Tan, Y.; Rockwell, A.K.; March, S.; Ahmed, S.Z.; Dukes, C.A.; Ghosh, A.W.; Bank, S.R.; Campbell, J.C. Characterization of band offsets in AlxIn1−xAsySb1−y alloys with varying Al composition. Appl. Phys. Lett. 2019, 115, 122105. [Google Scholar] [CrossRef]
- Jones, A.H.; March, S.D.; Dadey, A.A.; Muhowski, A.J.; Bank, S.R.; Campbell, J.C. AlInAsSb Separate Absorption, Charge, and Multiplication Avalanche Photodiodes for Mid-Infrared Detection. IEEE J. Quantum. Electron. 2022, 58, 4500306. [Google Scholar] [CrossRef]
- Maddox, S.J.; Sun, W.; Lu, Z.; Nair, H.P.; Campbell, J.C.; Bank, S.R. Enhanced low-noise gain from InAs avalanche photodiodes with reduced dark current and background doping. Appl. Phys. Lett. 2012, 101, 151124. [Google Scholar] [CrossRef] [Green Version]
- Ker, P.J.; Marshall, A.R.J.; Krysa, A.B.; David, J.P.R.; Tan, C.H. Temperature Dependence of Leakage Current in InAs Avalanche Photodiodes. IEEE J. Quantum. Electron. 2011, 47, 1123–1128. [Google Scholar] [CrossRef]
- Dadey, A.A.; McArthur, J.A.; Kamboj, A.; Bank, S.R.; Wasserman, D.; Campbell, J.C. High-gain low-excess-noise MWIR detection with a 3.5-μm cutoff AlInAsSb-based separate absorption, charge, and multiplication avalanche photodiode. APL Photonics 2023, 8, 036101. [Google Scholar] [CrossRef]
- Rothman, J.; Perrais, G.; Destefanis, G.; Baylet, J.; Castelein, P.; Chamonal, J.-P. High performance characteristics in pin MW HgCdTe e-APDs. Proc. SPIE 2007, 6542, 475–484. [Google Scholar]
- Singh, A.; Srivastav, V.; Pal, R. HgCdTe avalanche photodiodes: A review. Opt. Laser Tech. 2011, 43, 1358. [Google Scholar] [CrossRef]
- Sun, W.; Lu, Z.; Zheng, X.; Campbell, J.C.; Maddox, S.J.; Nair, H.P.; Bank, S.R. High gain InAs avalanche photodiodes. IEEE J. Quantum. Electron. 2013, 49, 154–161. [Google Scholar] [CrossRef] [Green Version]
- Marshall, R.J.; Tan, C.H.; Steer, M.J.; David, J.P.R. Extremely Low Excess Noise in InAs Electron Avalanche Photodiodes. IEEE Photon. Technol. Lett. 2009, 21, 866–868. [Google Scholar] [CrossRef] [Green Version]
- Huang, J.; Zhao, C.; Zhao, C.; Nie, B.; Xie, S.; Kwan, D.C.M.; Meng, X.; Zhang, Y.; Huffaker, D.L.; Ma, W. High-performance mid-wavelength InAs avalanche photodiode using AlAs0.13Sb0.87 as the multiplication layer. Photon. Res. 2020, 8, 755–759. [Google Scholar] [CrossRef]
- Capasso, F.; Tsang, W.T.; Williams, G.F. Staircase solid-state photomultipliers and avalanche photodiodes with enhanced ionization rates ratio. IEEE Trans. Electron. Dev. 1983, 30, 381–390. [Google Scholar] [CrossRef]
- March, S.D.; Jones, A.H.; Campbell, J.C.; Bank, S.R. Multistep staircase avalanche photodiodes with extremely low noise and deterministic amplification. Nat. Photonics 2021, 15, 468–474. [Google Scholar] [CrossRef]
- Xie, S.; Tan, C.H. AlAsSb avalanche photodiodes with a Sub-mV/K temperature coefficient of breakdown voltage. IEEE J. Quantum. Electron. 2011, 47, 1391–1395. [Google Scholar]
- Xie, J.; Xie, S.; Tozer, R.C.; Tan, C.H. Excess noise characteristics of thin AlAsSb APDs. IEEE Trans. Electron. Dev. 2012, 59, 1475–1479. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, S.; David, J.P.R.; Ng, J.S.; Tan, C.H. Avalanche Breakdown Characteristics of Al1−xGaxAs0.56Sb0.44 Quaternary Alloys. IEEE Photon. Technol. Lett. 2016, 28, 2495–2498. [Google Scholar] [CrossRef] [Green Version]
- Lau, K.S.; Ng, B.K.; Li, K.F.; Tan, C.H. Excess noise measurement in avalanche photodiodes using a transimpedance amplifier front-end. Meas. Sci. Technol. 2016, 17, 1941–1946. [Google Scholar] [CrossRef]
- Taylor-Mew, J.; Shulyak, V.; White, B.; Tan, C.H.; Ng, J.S. Low Excess Noise of Al0.85Ga0.15As0.56Sb0.44Avalanche Photodiode from Pure Electron Injection. IEEE Photonics Technol. Lett. 2021, 33, 1155–1158. [Google Scholar] [CrossRef]
- Tan, C.H.; Xie, S.; Xie, J. Low Noise Avalanche Photodiodes Incorporating a 40 nm AlAsSb Avalanche Region. IEEE J. Quantum. Electron. 2012, 48, 36–41. [Google Scholar] [CrossRef]
- Xie, S.; Zhou, X.; Zhang, S.; Thomson, D.J.; Chen, X.; Reed, G.T.; Ng, J.S.; Tan, C.H. InGaAs/AlGaAsSb avalanche photodiode with high gain-bandwidth product. Opt. Exp. 2016, 24, 24242. [Google Scholar] [CrossRef]
- Lee, S.; Jin, X.; Jung, H.; Lewis, H.; Liu, Y.; Guo, B.; Kodati, S.H.; Schwartz, M.; Grein, C.; Ronningen, T.J.; et al. High Gain, Low Noise, Room Temperature 1550 nm GaAsSb/AlGaAsSb Avalanche Photodiodes. Optica 2022, 10, 147–154. [Google Scholar] [CrossRef]
- Cao, Y.; Blain, T.; Taylor-Mew, J.D.; Li, L.; Ng, J.S.; Tan, C.H. Extremely low excess noise avalanche photodiode with GaAsSb absorption region and AlGaAsSb avalanche region. Appl. Phys. Lett. 2023, 122, 51103. [Google Scholar] [CrossRef]
- Jones, A.H.; Yuan, Y.; Ren, M.; Woodson, M.; Maddox, S.; Bank, S.; Campbell, J.C. AlxIn1−xAsySb1−y photodiodes with low avalanche breakdown temperature dependenc. Opt. Express 2017, 25, 24340–24345. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Tan, L.J.J.; Ong, D.S.G.; Ng, J.-S.; Hing Tan, C.H.; Jones, S.K.; Qian, Y.; David, J.P.R. Temperature dependence of avalanche breakdown in InP and InAlAs. IEEE J. Quantum Electron. 2010, 46, 1153–1157. [Google Scholar] [CrossRef]
- Massey, D.J.; David, J.P.R.; Rees, G.J. Temperature dependence of impact ionization in submicrometer silicon devices. IEEE Trans. Electron Devices 2006, 53, 2328–2334. [Google Scholar] [CrossRef]
- Guo, B.; Ahmed, S.Z.; Xue, X.; Rockwell, A.K.; Ha, J.; Lee, S.; Liang, B.; Jones, A.H.; McArthur, J.A.; Kodati, S.H.; et al. Temperature Dependence of Avalanche Breakdown of AlGaAsSb and AlInAsSb Avalanche Photodiodes. IEEE J. Light. Technol. 2022, 40, 5934–5942. [Google Scholar] [CrossRef]
- Jin, X.; Xie, S.; Liang, B.; Yi, X.; Lewis, H.; Lim, L.W.; Liu, Y.; Ng, B.K.; Huffaker, D.L.; Tan, C.H.; et al. Temperature Dependence of the Impact Ionization Coefficients in AlAsSb Lattice Matched to InP. IEEE J. Sel. Top. Quantum. Electron. 2022, 28, 3801208. [Google Scholar] [CrossRef]
- Cao, Y.; Osman, T.; Clarke, E.; Patil, P.K.; Ng, J.S.; Tan, C.H. A GaAsSb/AlGaAsSb Avalanche Photodiode With a Very Small Temperature Coefficient of Breakdown Voltage. IEEE J. Light. Tech. 2022, 14, 4709–4713. [Google Scholar] [CrossRef]
- Yuan, Y.; Zheng, J.; Rockwell, A.K.; March, S.D.; Bank, S.R.; Campbell, J.C. AlInAsSb Impact Ionization Coefficients. IEEE Photon. Tech. Lett. 2019, 31, 315–318. [Google Scholar] [CrossRef]
- Guo, B.; Jin, X.; Lee, S.; Ahmed, S.Z.; Jones, A.H.; Xue, X.; Liang, B.; Lewis, H.; Kodati, S.; Chen, D.; et al. Impact ionization coefficients of digital alloy and random alloy Al0.85Ga0.15As0.56Sb0.44 in a wide electric field range. IEEE J. Light. Tech. 2022, 40, 4758–4764. [Google Scholar] [CrossRef]
- Liu, Y.; Yi, X.; Bailey, N.J.; Zhou, Z.; Rockett, T.B.O.; Lim, L.W.; Tan, C.H.; Richards, R.D.; David, J.P.R. Valence band engineering of GaAsBi for low noise avalanche photodiodes. Nature Comm. 2021, 12, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Ong, D.S.; Tan, A.H.; Choo, K.Y.; Yeoh, K.H.; David, J.P.R. Weibull-Fréchet random path length model for avalanche gain and noise in photodiodes. J. Phys. D. Appl. Phys. 2022, 55, 065105. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Campbell, J.C.; David, J.P.R.; Bank, S.R. Sb-Based Low-Noise Avalanche Photodiodes. Photonics 2023, 10, 715. https://doi.org/10.3390/photonics10070715
Campbell JC, David JPR, Bank SR. Sb-Based Low-Noise Avalanche Photodiodes. Photonics. 2023; 10(7):715. https://doi.org/10.3390/photonics10070715
Chicago/Turabian StyleCampbell, Joe C., John P. R. David, and Seth R. Bank. 2023. "Sb-Based Low-Noise Avalanche Photodiodes" Photonics 10, no. 7: 715. https://doi.org/10.3390/photonics10070715
APA StyleCampbell, J. C., David, J. P. R., & Bank, S. R. (2023). Sb-Based Low-Noise Avalanche Photodiodes. Photonics, 10(7), 715. https://doi.org/10.3390/photonics10070715





