Multiplexing Perfect Optical Vortex for Holographic Data Storage
Abstract
:1. Introduction
2. Materials and Methods
3. Results
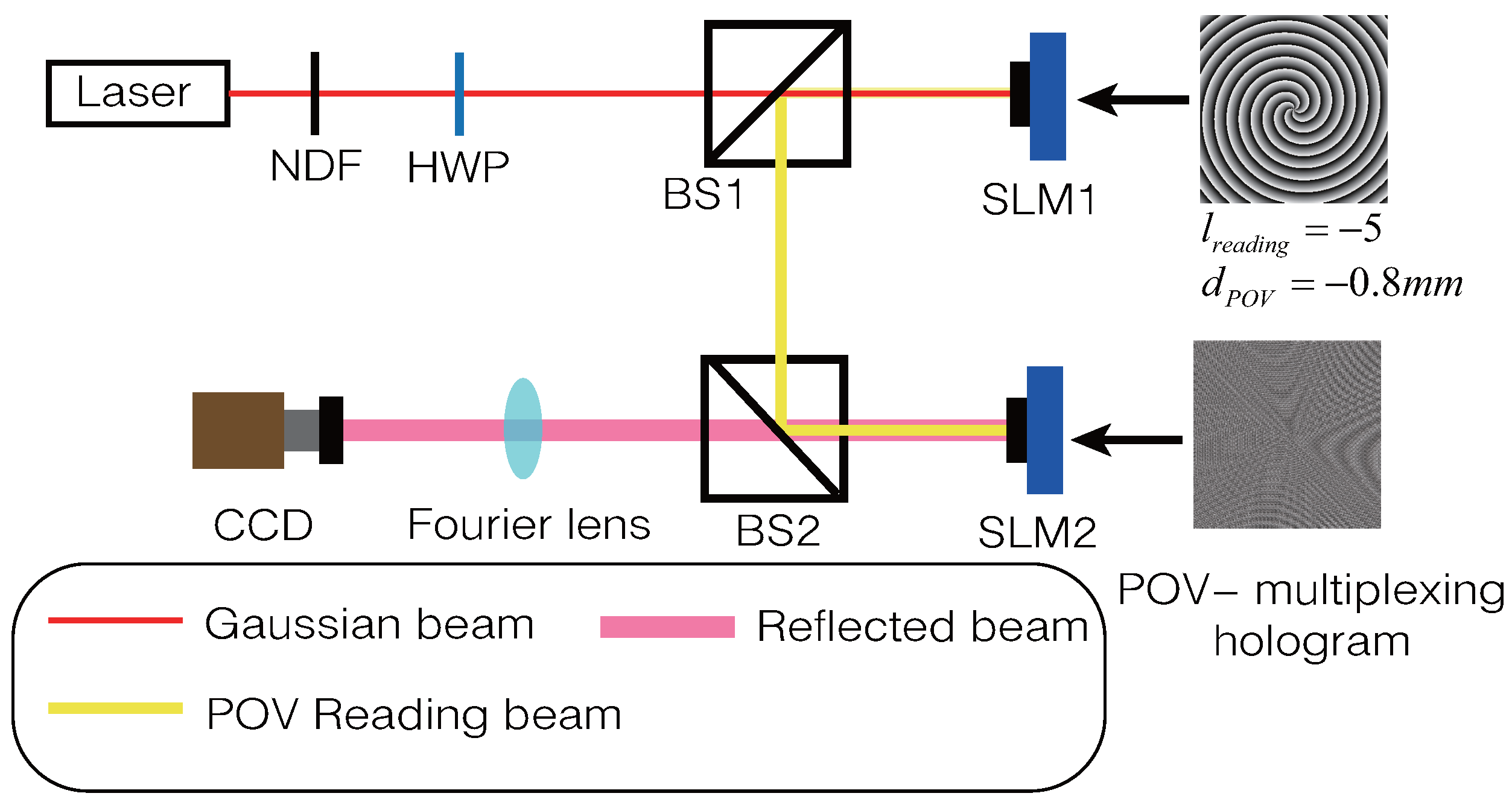
3.1. Optical Setup
3.2. Experimental Reconstructed Process in Holographic Data Storage
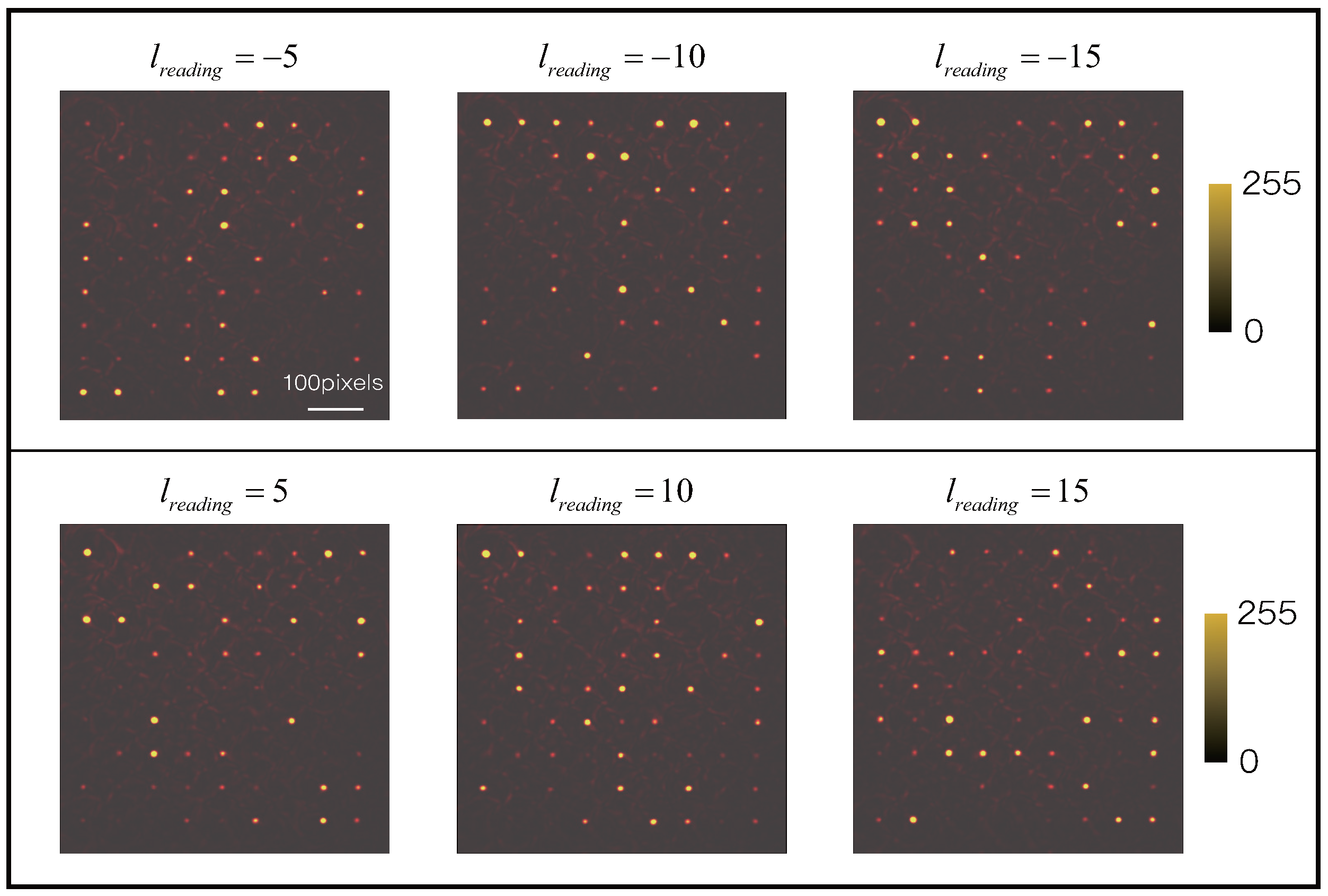
3.3. Experimental Multiplexing Process in Holographic Data Storage
4. Discussion
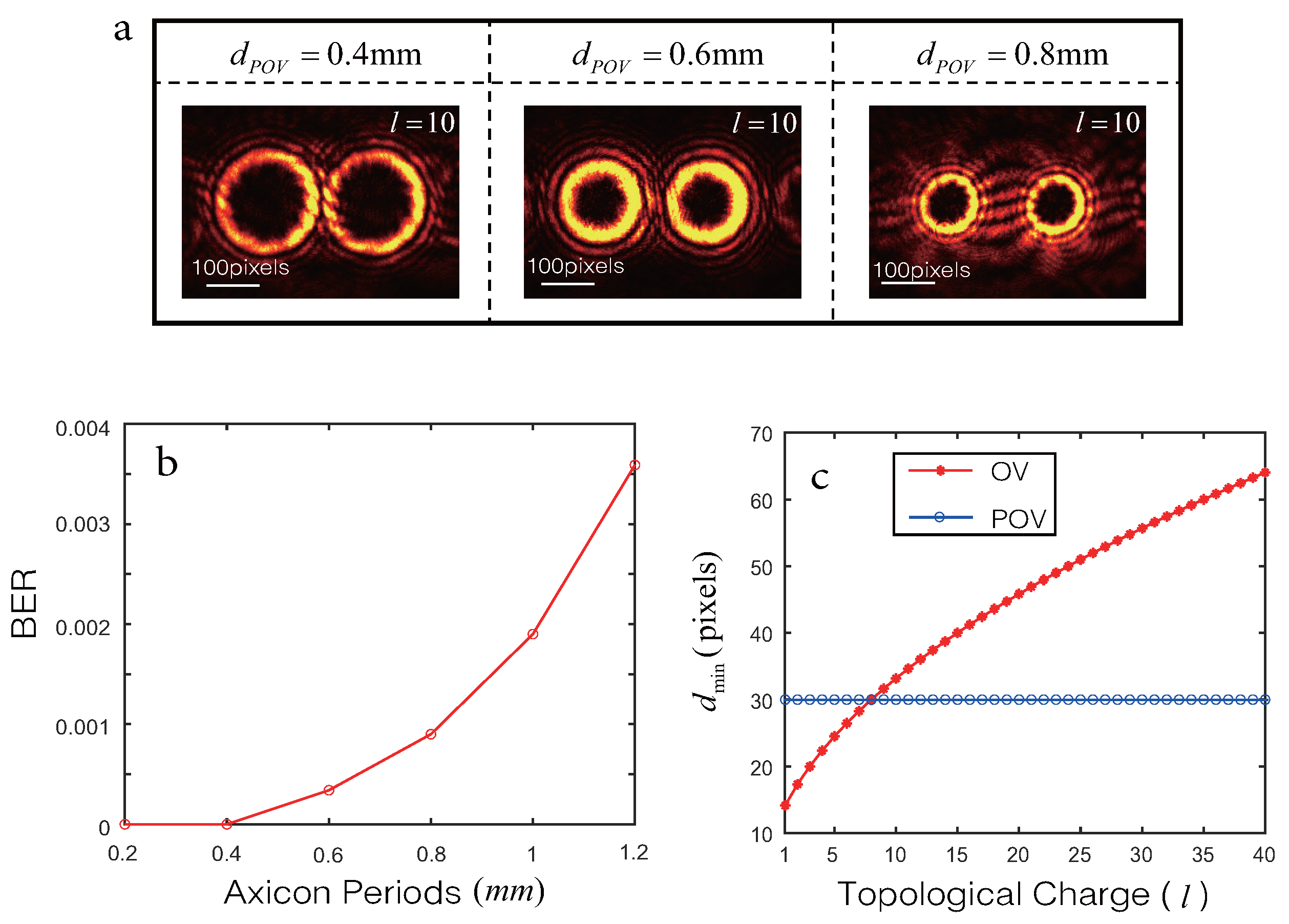
4.1. Effect of Axicon Periods on Reconstructed Data Quality and BER
4.2. Effect of Multiplexing Number on BER
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Psaltis, D.; Burr, G.W. Holographic Data Storage. Computer 1998, 31, 52–60. [Google Scholar] [CrossRef]
- Hao, J.; Lin, X.; Lin, Y.; Song, H.; Chen, R.; Chen, M.; Wang, K.; Tan, X. Lensless phase retrieval based on deep learning used in holographic data storage. Opt. Lett. 2021, 46, 4168–4171. [Google Scholar] [CrossRef]
- Bunsen, M.; Tateyama, S. Detection method for the complex amplitude of a signal beam with intensity and phase modulation using the transport of intensity equation for holographic data storage. Opt. Express 2019, 27, 24029–24042. [Google Scholar] [CrossRef]
- Hao, J.; Lin, X.; Chen, R.; Lin, Y.; Liu, H.; Song, H.; Lin, D.; Tan, X. Phase retrieval combined with the deep learning denoising method in holographic data storage. Opt. Contin. 2022, 1, 51–62. [Google Scholar] [CrossRef]
- Hong, J.; Li, J.; Chu, D. Efficient dynamic control method of light polarization using single phase-only liquid crystal on silicon spatial light modulators for optical data storage. Appl. Opt. 2021, 61, B34–B42. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.; Beijersbergen, M.W.; Spreeuw, R.J.C.; Woerdman, J.P. Orbital angular momentum of light and the transformation of Laguerre-Gaussian laser modes. Phys. Rev. A At. Mol. Opt. Phys. 1992, 45, 8185–8189. [Google Scholar] [CrossRef] [PubMed]
- Ren, Y.; Wang, C.; Liu, T.; Wang, Z.; Yin, C.; Qiu, S.; Li, Z.; Wu, H. Polygonal shaping and multi-singularity manipulation of optical vortices via high-order cross-phase. Opt. Express 2020, 28, 26257–26266. [Google Scholar] [CrossRef]
- Zou, L.; Wang, L.; Zhao, S. Turbulence mitigation scheme based on spatial diversity in orbital-angular-momentum multiplexed system. Opt. Commun. 2017, 400, 123–127. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, L.; Ji, J.; Zhao, S. Real-time measurement of dynamic micro-displacement and direction using light’s orbital angular momentum. Appl. Phys. Lett. 2022, 120, 251104. [Google Scholar] [CrossRef]
- Zhang, Z.; Cen, L.; Wang, F.; Zhao, Y. Tiny velocity measurement using rotating petal-like mode of orbital angular momentum. Opt. Lett. 2021, 46, 4805–4808. [Google Scholar] [CrossRef]
- Deng, D.; Zhao, H.; Ni, J.; Li, Y.; Qiu, C.-W. A phase-to-intensity strategy of angular velocity measurement based on photonic orbital angular momentum. Nanophotonics 2021, 11, 865–872. [Google Scholar] [CrossRef]
- Zhu, J.; Wang, L.; Zhao, S. Orbital Angular Momentum Multiplexing Holography for Data Storage. IEEE Photonics Technol. Lett. 2023, 35, 179–182. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, X.; Xiong, R.; Ma, X.; Yuan, H.; Li, L.; Jiang, X. Flexible Image Reconstruction in the Orbital Angular Momentum Holography with Binarized Airy Lens. Photonics 2022, 9, 460. [Google Scholar] [CrossRef]
- Wang, F.; Zhang, X.; Xiong, R.; Ma, X.; Li, L.; Jiang, X. Depth multiplexing in an orbital angular momentum holography based on random phase encoding. Opt. Express 2022, 30, 31863–31871. [Google Scholar] [CrossRef]
- Zhang, N.; Xiong, B.; Zhang, X.; Yuan, X. Holographic Encryption Applications Using Composite Orbital Angular Momentum Beams. Photonics 2022, 9, 605. [Google Scholar] [CrossRef]
- Ren, H.; Fang, X.; Jang, J.; Bürger, J.; Rho, J.; Maier, S.A. Complex-amplitude metasurface-based orbital angular momentum holography in momentum space. Nat. Nanotechnol. 2020, 15, 948–955. [Google Scholar] [CrossRef]
- Guo, M.; Le, W.; Wang, C.; Rui, G.; Zhu, Z.; He, J.; Gu, B. Generation, Topological Charge, and Orbital Angular Momentum of Off-Axis Double Vortex Beams. Photonics 2023, 10, 368. [Google Scholar] [CrossRef]
- Khonina, S.N.; Kharitonov, S.I.; Volotovskiy, S.G.; Soifer, V.A. Caustics of Non-Paraxial Perfect Optical Vortices Generated by Toroidal Vortex Lenses. Photonics 2021, 8, 259. [Google Scholar] [CrossRef]
- Shi, Z.; Wan, Z.; Zhan, Z.; Liu, K.; Liu, Q.; Fu, X. Super-resolution orbital angular momentum holography. Nat. Commun. 2023, 14, 1869. [Google Scholar] [CrossRef]
- Wang, H.; Fu, S.; Gao, C. Tailoring a complex perfect optical vortex array with multiple selective degrees of freedom. Opt. Express 2021, 29, 10811–10824. [Google Scholar] [CrossRef]
- Ostrovsky, A.S.; Rickenstorff-Parrao, C.; Arrizón, V. Generation of the “perfect” optical vortex using a liquid-crystal spatial light modulator. Opt. Lett. 2013, 38, 534–536. [Google Scholar] [CrossRef] [PubMed]
- Kotlyar, V.V.; Kovalev, A.A.; Porfirev, A.P. Optimal phase element for generating a perfect optical vortex. JOSA A 2016, 33, 2376–2384. [Google Scholar] [CrossRef] [PubMed]
- Kumar, P.; Nishchal, N.K.; Alfalou, A. Controllable Optical Vortex Array for Image Encoding. IEEE Photonics Technol. Lett. 2022, 34, 521–524. [Google Scholar] [CrossRef]
- Fu, S.; Wang, T.; Gao, C. Perfect optical vortex array with controllable diffraction order and topological charge. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2016, 33, 1836–1842. [Google Scholar] [CrossRef]
- Yang, D.; Lin, J.; Chen, C.; Li, C.X.; Hao, J.; Lv, B.; Zhou, K.; Wang, Y.; Jin, P. Multiwavelength high-order optical vortex detection and demultiplexing coding using a metasurface. Adv. Photonics Nexus 2022, 1, 016005. [Google Scholar] [CrossRef]
- Li, Z.; Rukhlenko, I.D.; Zhu, W. Microwave metasurface hologram for holographic imaging and its data encryption applications. J. Opt. 2022, 24, 113001. [Google Scholar] [CrossRef]
- Sahin, F.E.; Yilmaz, M. High Concentration Photovoltaics (HCPV) with Diffractive Secondary Optical Elements. Photonics 2019, 6, 68. [Google Scholar] [CrossRef] [Green Version]
- Kim, D.C.; Hermerschmidt, A.; Dyachenko, P.N.; Scharf, T. Inverse design and demonstration of high-performance wide-angle diffractive optical elements. Opt. Express 2020, 28, 22321–22333. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, J.; Zou, F.; Wang, L.; Lu, X.; Zhao, S. Multiplexing Perfect Optical Vortex for Holographic Data Storage. Photonics 2023, 10, 720. https://doi.org/10.3390/photonics10070720
Zhu J, Zou F, Wang L, Lu X, Zhao S. Multiplexing Perfect Optical Vortex for Holographic Data Storage. Photonics. 2023; 10(7):720. https://doi.org/10.3390/photonics10070720
Chicago/Turabian StyleZhu, Jialong, Fucheng Zou, Le Wang, Xiaodong Lu, and Shengmei Zhao. 2023. "Multiplexing Perfect Optical Vortex for Holographic Data Storage" Photonics 10, no. 7: 720. https://doi.org/10.3390/photonics10070720
APA StyleZhu, J., Zou, F., Wang, L., Lu, X., & Zhao, S. (2023). Multiplexing Perfect Optical Vortex for Holographic Data Storage. Photonics, 10(7), 720. https://doi.org/10.3390/photonics10070720




