Twisted Silica Few-Mode Hollow GeO2-Doped Ring-Core Microstructured Optical Fiber
Abstract
:1. Introduction
- -
- -
- -
- -
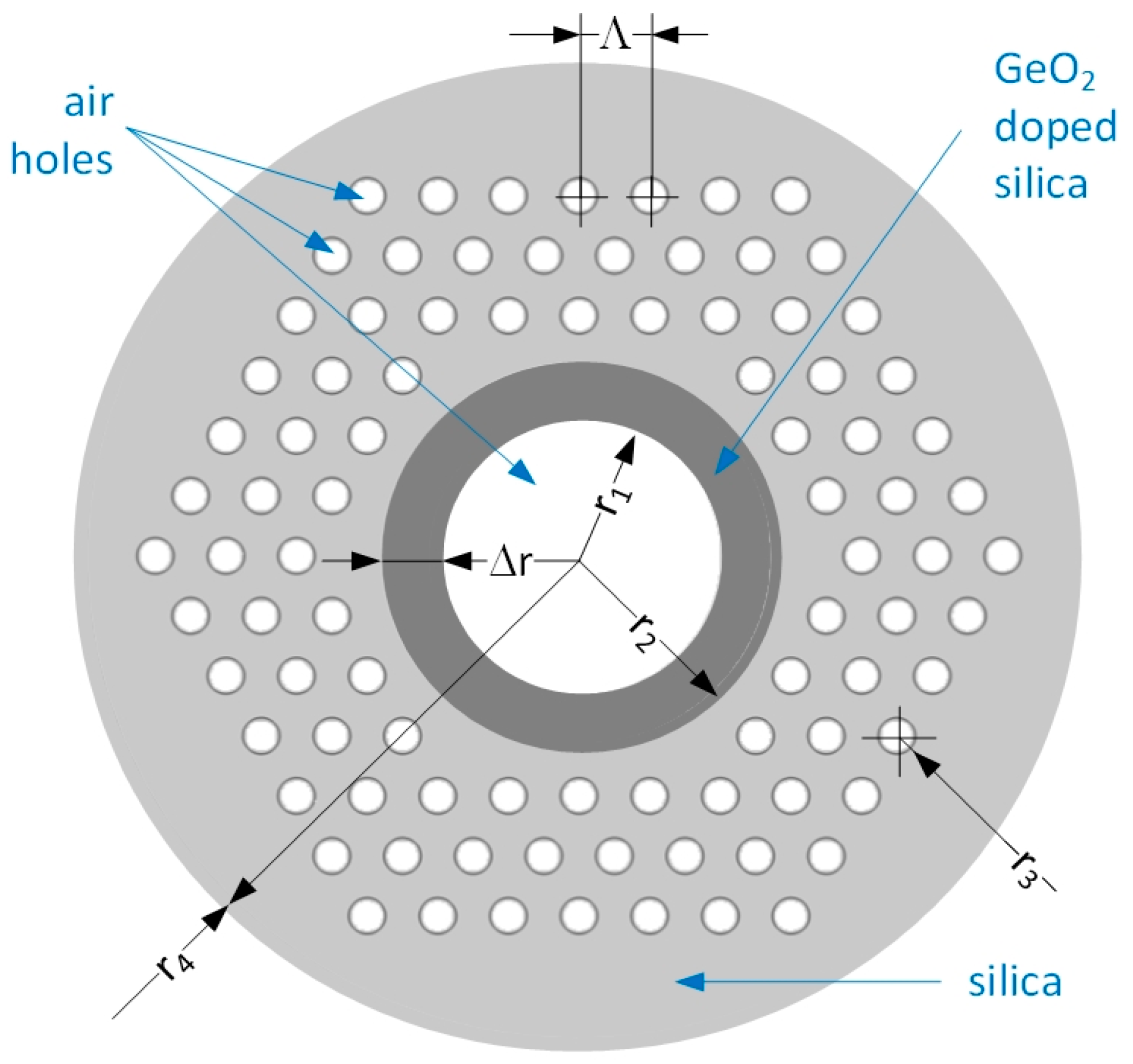
2. Fiber Design
- -
- Mesh: sequence-type physics—controlled mesh; element size—extra fine; maximum mesh element size control parameter—from study;
- -
- Simulation: physics—electromagnetic waves; frequency domain—(ewfd); study—mode analysis;
- -
- Study: effective mode—index; mode analysis frequency—c/λ; mode solver—ARPACK; mode search method—manual; desired number of modes—64; search for modes around—refractive index of ring core (20.5% GeO2-doped silica);
- -
- Computation: number of degrees of freedom solved—384,935; solution time—348 s (5 min, 48 s); physical memory—4.45 Gb; virtual memory—5.02 Gb.
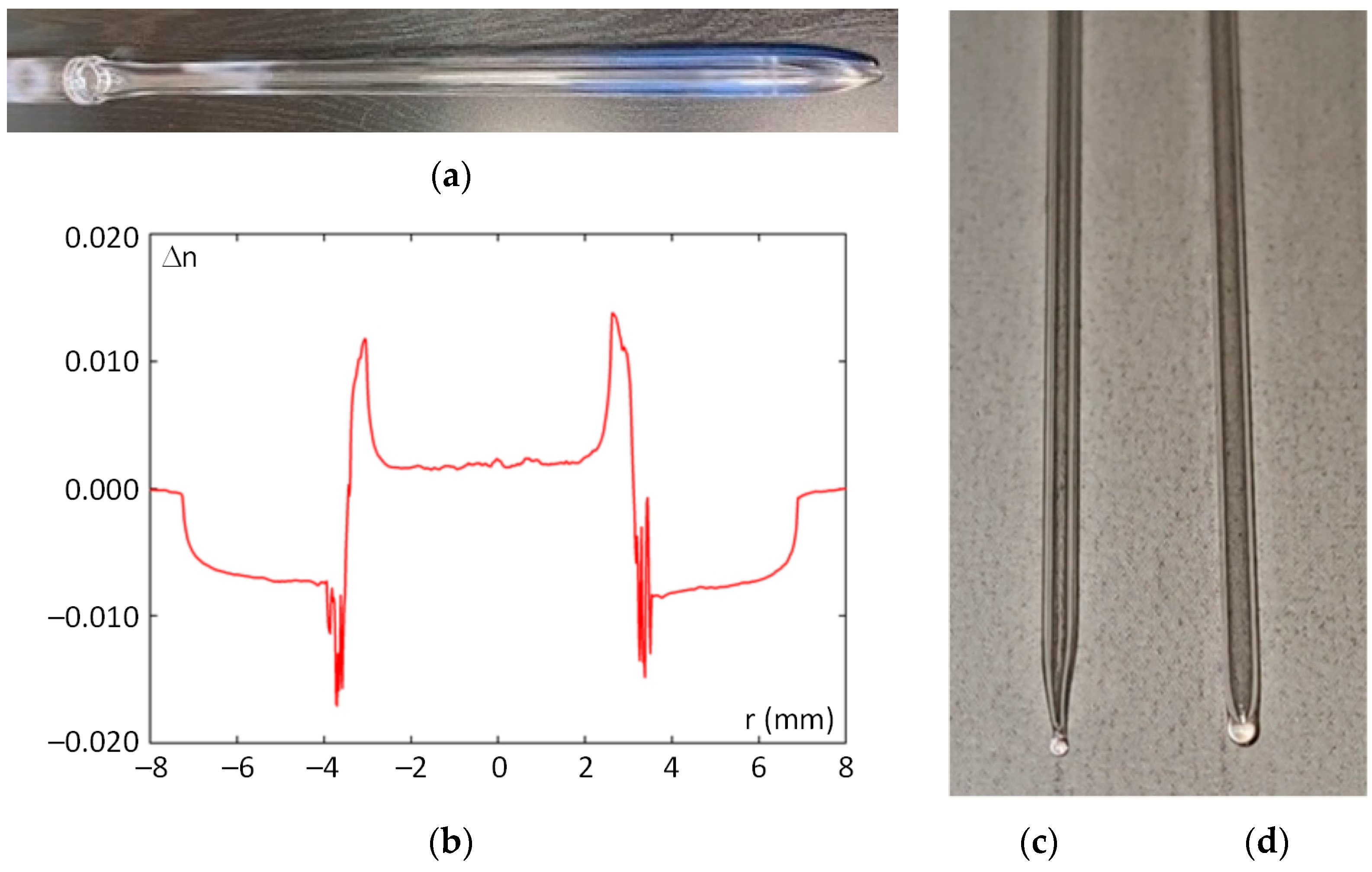
3. Fabrication of GeO2-Doped Supporting Tubes—Preforms of Hollow Ring Core
- Flushing the supporting tube in distilled water with further drying under normal conditions;
- Installing the supporting tube in the chucks of the MCVD station.
- Supplying SF6 gas to the inside of the tube for the chemical etching of the distorted near-surface quartz layers;
- Depositing the phosphor–silicate quartz layers to prevent the diffusion of OH-groups from the supporting tube to the germane–silicate quartz layers;
- Depositing germane–silicate quartz layers for an improvement in the refractive index and material photosensitivity by the formation of germanium oxygen-deficient centers.
- -
- Delivering the rate and concentration of gas mixture/reagents (in particular, GeCl4 in vapor–gas mixture to prevent bubbles, which leads to further cracks in the fabrication of the supporting element).
- -
- Oxygen torch movement speed and its flame temperature.
- -
- Number of torch passes.
- -
- Dried oxygen flow rate (in mm3 per minute (mm3/min)), going through the bubbler systems with GeCl4 and SiCl4, during torch passes.
- -
- Ratio between the numbers of phosphor–silicate quartz layers (4…9) and germane–silicate quartz layers (20…55).
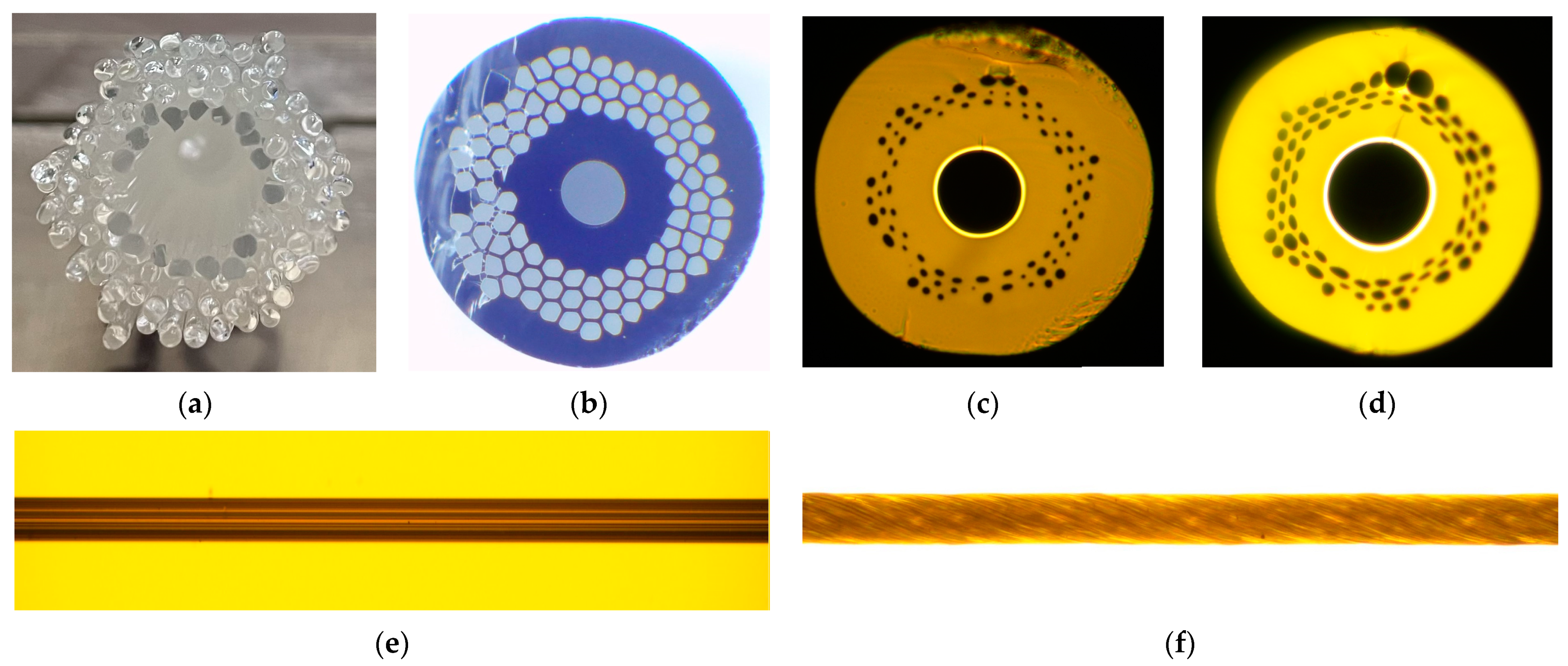
4. Fabrication of Silica Microstructured Optical Fibers with Improved Induced Twisting
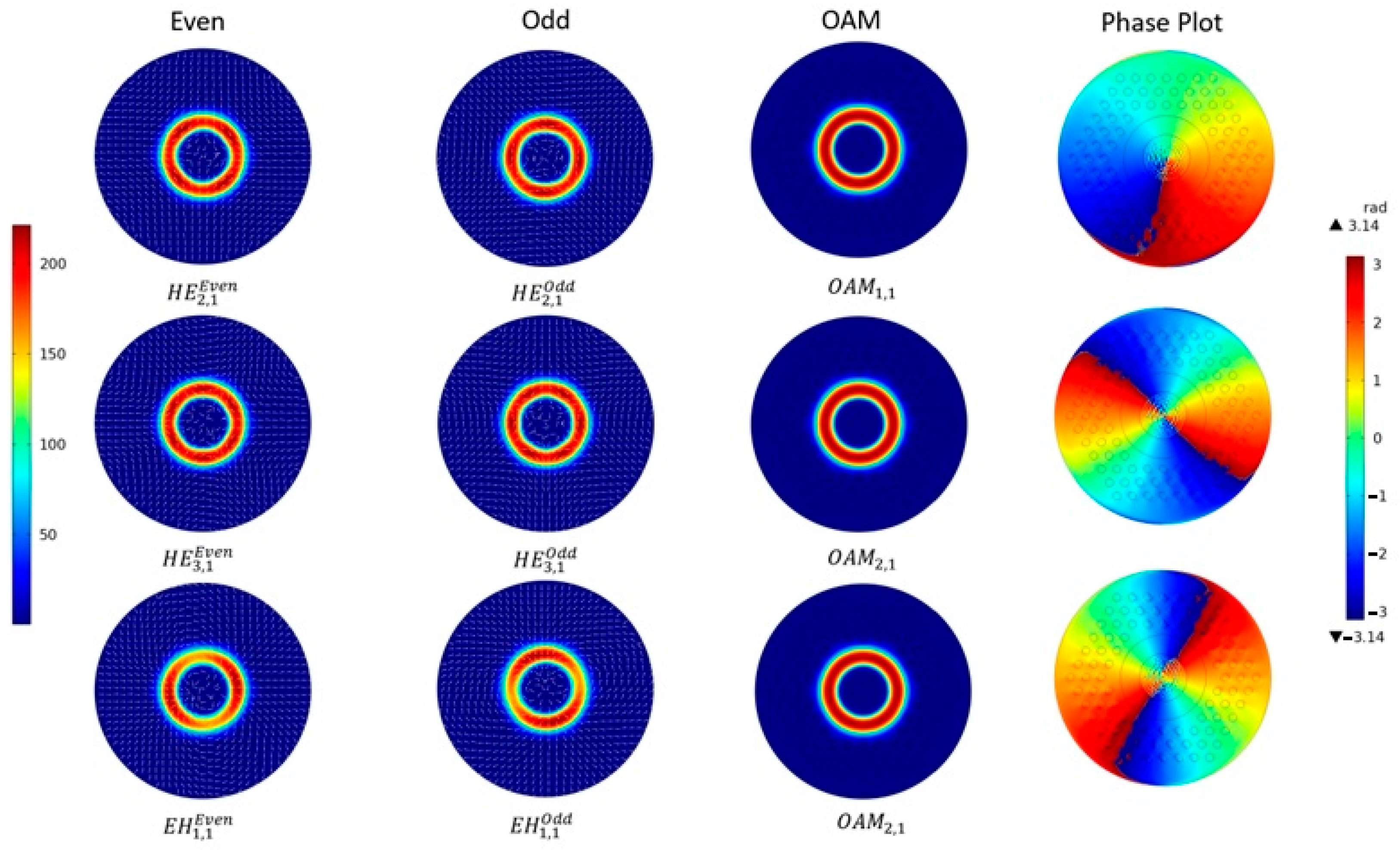
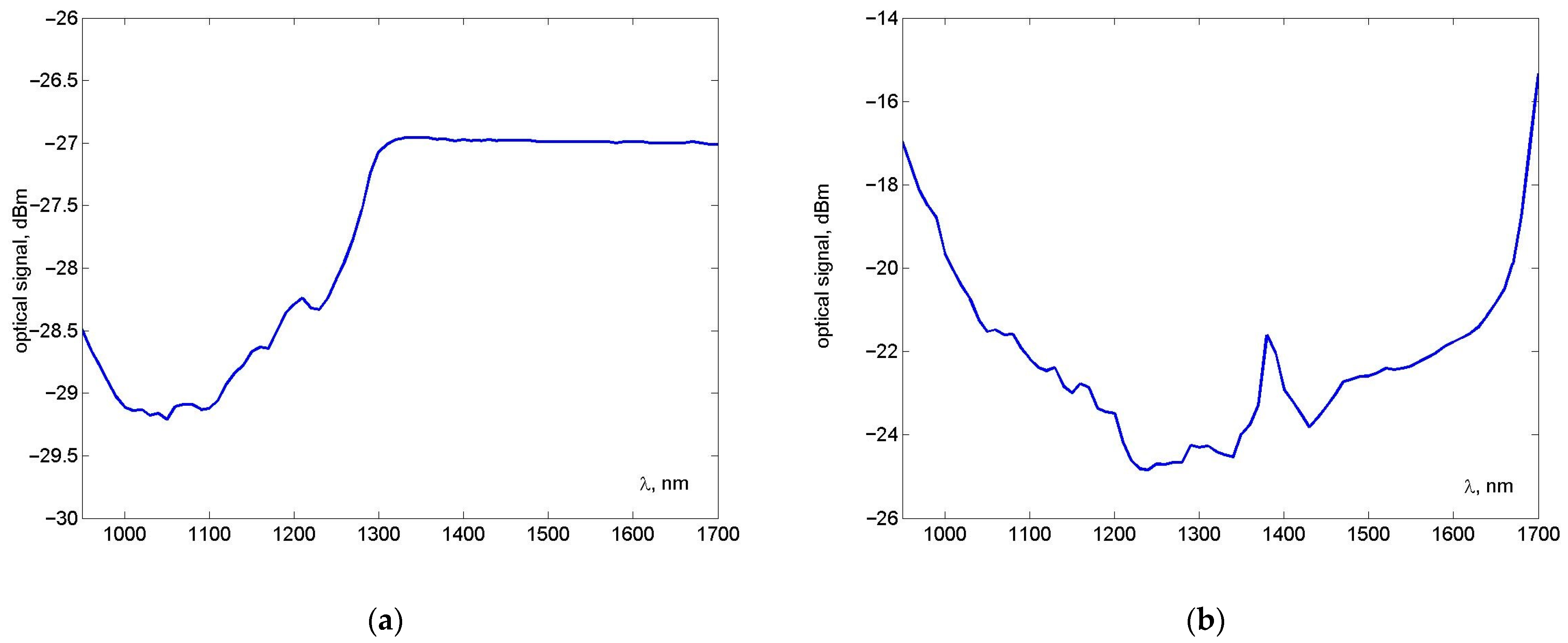
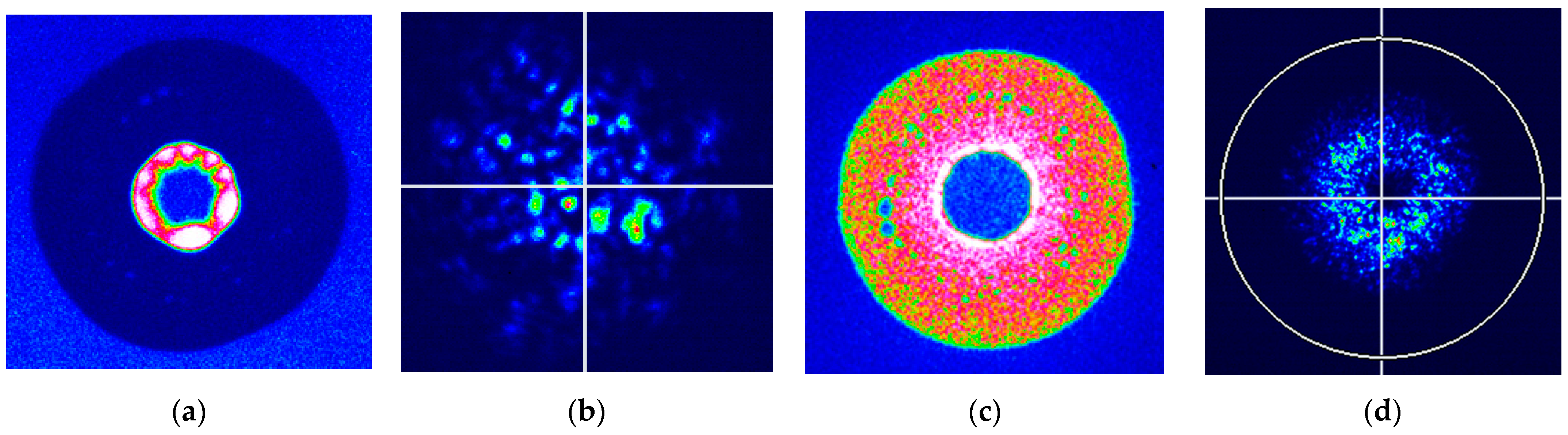
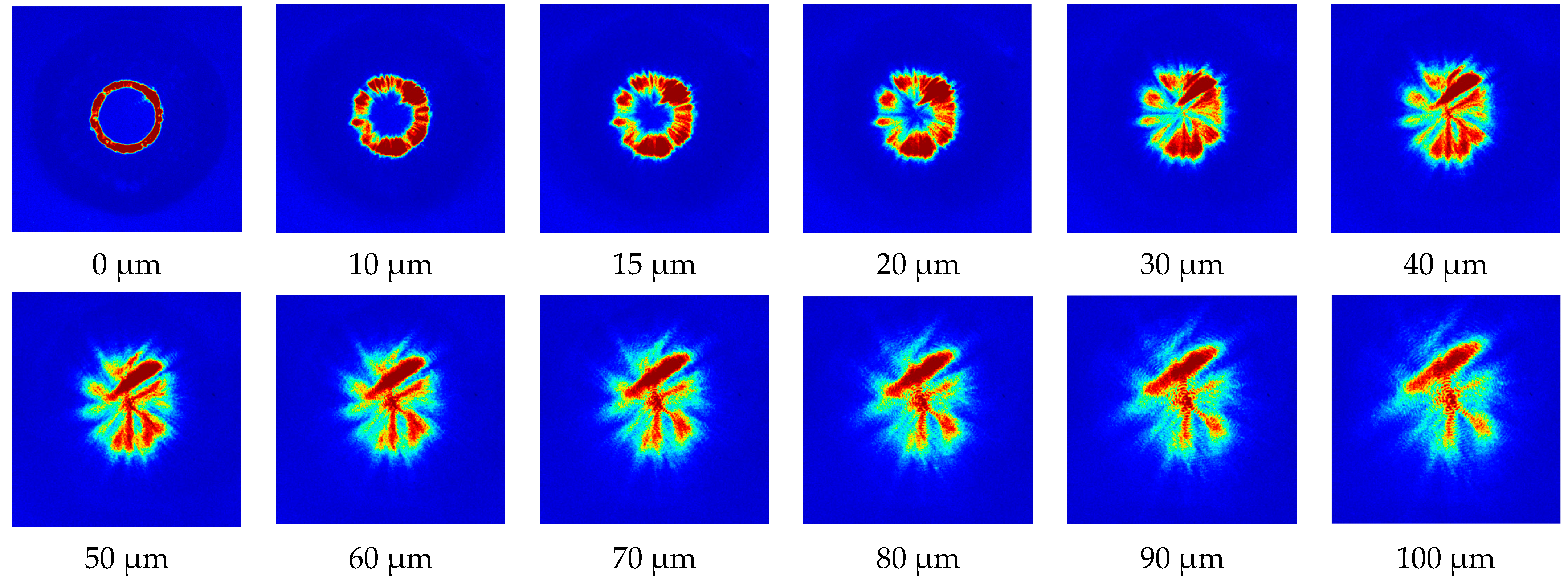
5. Twisted Silica Few-Mode Hollow GeO2-Doped Ring-Core Microstructure Optical Fiber: Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rusch, L.A.; Rad, M.; Allahverdyan, K.; Fazal, I.; Bernier, E. Carrying data on the orbital angular momentum of light. IEEE Commun. Mag. 2018, 56, 219–224. [Google Scholar] [CrossRef] [Green Version]
- Ma, M.; Lian, Y.; Wang, Y.; Lu, Z. Generation, transmission and application of orbital momentum in optical fiber: A review. Front. Phys. 2021, 9, 703. [Google Scholar] [CrossRef]
- Wang, Z.; Tu, J.; Gao, S.; Li, Z.; Yu, C.; Lu, C. Transmission and generation of orbital angular momentum modes in optical fibers. Photonics 2021, 8, 246. [Google Scholar] [CrossRef]
- Choi, S.; Oh, K.; Shin, W.; Park, C.S.; Paek, U.C.; Park, K.J.; Chung, Y.C.; Kim, G.Y.; Lee, Y.G. Novel mode converter based on hollow optical fiber for Gigabit LAN communication. IEEE Photonics Technol. Lett. 2002, 14, 248–250. [Google Scholar] [CrossRef]
- Oh, K.; Choi, S.; Shin, W. Applications of hollow core fibers. In Proceedings of the 16th Annual Meeting of the IEEE Lasers and Electro-Optics Society (LEOS), Tucson, AZ, USA, 27–28 October 2003; pp. 905–906. [Google Scholar]
- Choi, S.; Shin, W.; Oh, K. Higher-order mode dispersion compensation technique based on mode converter using hollow optical fiber. In Proceedings of the Optical Fiber Communication Conference (OFC), Anaheim, CA, USA, 17 March 2002; pp. 177–178. [Google Scholar]
- Yue, Y.; Yan, Y.; Ahmed, N.; Yang, J.-Y.; Zhang, L.; Ren, Y.; Huang, H.; Birnbaum, K.; Erkmen, B.I.; Dolinar, S.; et al. Mode properties and propagation effects of optical orbital angular momentum (OAM) modes in a ring fiber. IEEE Photonics J. 2012, 4, 535–543. [Google Scholar]
- Yan, H.; Zhang, E.; Duan, K. Free-space propagation of guided optical vortices excited in an annular core fiber. Opt. Express 2012, 20, 17904–17915. [Google Scholar] [CrossRef]
- Ramachandran, S.; Kristensen, P. Optical vortices in fiber. Nanophotonics 2013, 2, 455–474. [Google Scholar] [CrossRef]
- Brunet, C.; Ung, B.; Wang, L.; Messaddeq, Y.; LaRochelle, S.; Rusch, L.A. Design of a family of ring-core fibers for OAM transmission studies. Opt. Express 2015, 23, 10553–10563. [Google Scholar] [CrossRef]
- Zhang, X.; Chen, S.; Wang, J. Weakly guiding graded-index ring-core fiber supporting 16-channel long distance mode division multiplexing systems based on OAM modes with low MIMO-DSP complexity. Opt. Express 2022, 30, 35828–35839. [Google Scholar] [CrossRef]
- Yang, J.; Wang, Y.; Fang, Y.; Geng, W.; Zhao, W.; Bao, C.; Ren, Y.; Wang, Z.; Liu, Y.; Pan, Z.; et al. Over-two-octave supercontinuum generation of light-carrying orbital angular momentum in Germania-doped ring-core fiber. Sensors 2022, 22, 6699. [Google Scholar] [CrossRef]
- Geng, W.; Fang, Y.; Wang, Y.; Bao, C.; Wang, Z.; Liu, Y.; Huang, H.; Ren, Y.; Pan, Z.; Yuie, Y. Highly dispersive Germanium-doped coupled ring-core fiber for vortex modes. IEEE J. Light. Technol. 2022, 40, 2144–2150. [Google Scholar] [CrossRef]
- Al-Zahrani, F.A.; Kabir, M.A. Ring-core photonic crystal fiber of terahertz orbital angular momentum modes with excellence guiding properties in optical fiber communication. Photonics 2021, 8, 122. [Google Scholar] [CrossRef]
- Al-Zahrani, F.A.; Hassan, M.M. Enhancement of OAM and LP modes based on double guided ring fiber for high capacity optical communication. Alex. Eng. J. 2021, 60, 5065–5076. [Google Scholar] [CrossRef]
- Zhou, G.; Zhou, G.; Chen, C.; Xu, M.-N.; Xia, C.; Hou, Z. Design and analysis of a microstructure ring fiber for orbital angular momentum transmission. IEEE Photonics J. 2016, 8, 1–12. [Google Scholar] [CrossRef]
- Tian, W.; Zhang, H.; Zhang, X.; Xi, L.; Zhang, W.; Tang, X. A circular photonic crystal fiber supporting 26 OAM modes. Opt. Fiber Technol. 2016, 30, 184–189. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, X.; Li, H.; Deng, Y.; Xi, L.; Tang, X.; Zhang, W. The orbital angular momentum modes supporting fibers based on the photonic crystal fiber structure. Crystals 2017, 7, 286. [Google Scholar] [CrossRef] [Green Version]
- Bai, X.; Chen, H.; Yang, H. Design of a circular photonic crystal fiber with square air-holes for orbital angular momentum modes transmission. Optics 2018, 158, 1266–1274. [Google Scholar] [CrossRef]
- Xu, M.; Zhou, G.; Chen, C.; Zhou, G.; Sheng, Z.; Hou, Z.; Xia, C. A novel micro-structured fiber for OAM mode and LP mode simultaneous transmission. J. Opt. 2018, 47, 428–436. [Google Scholar] [CrossRef]
- Debord, B.; Amrani, F.; Vincetti, L.; Gérôme, F.; Benabid, F. Hollow-core fiber technology: The rising of “gas photonics”. Fibers 2018, 7, 16. [Google Scholar] [CrossRef] [Green Version]
- Huang, W.; You, Y.; Song, B.-B.; Chen, S.-Y. A photonic crystal fiber for supporting 30 orbital angular momentum modes with low dispersion. Optoelectron. Lett. 2020, 16, 34–39. [Google Scholar] [CrossRef]
- Ke, X.; Wang, S. Design of photonic crystal fiber capable of carrying multle orbital angular momentum modes transmission. Opt. Photonics J. 2020, 10, 49–63. [Google Scholar] [CrossRef] [Green Version]
- Hong, S.; Lee, Y.S.; Choi, H.; Quan, C.; Li, Y.; Kim, S.; Oh, K. Hollow silica photonic crystal fiber guiding 101 orbital angular momentum modes without phase distortion in C + L band. IEEE J. Light. Technol. 2020, 38, 1010–1018. [Google Scholar] [CrossRef]
- Hassan, M.M.; Kabir, M.A.; Hossain, M.N.; Nguyen, T.K.; Paul, B.K. Numerical analysis of circular core shaped photonic crystal fiber for orbital angular momentum with efficient transmission. Appl. Phys. B Lasers Opt. 2020, 126, 145. [Google Scholar] [CrossRef]
- Zhao, L.; Zhao, H.; Xu, Z.; Liang, R. A Design of novel photonic crystal fiber with low and flattened dispersion for supporting 84 orbital angular momentum modes. Commun. Theor. Phys. 2021, 73, 085501. [Google Scholar] [CrossRef]
- Rjeb, A.; Fathallah, H.; Chebaane, S.; Machhout, M. Design of novel circular lattice photonic crystal fiber suitable for transporting 48 OAM modes. Optoelectron. Lett. 2021, 17, 501–506. [Google Scholar] [CrossRef]
- Liu, C.; Fu, H.; Hu, C.; Zhou, L.; Shi, Y.; Lv, J.; Yang, L.; Chu, P.K. Optimization of photonic crystal fibers for transmission of orbital angular momentum modes. Opt. Quantum Electron. 2021, 53, 639. [Google Scholar] [CrossRef]
- Li, J.; Li, H.; Wang, Z. Application of hollow-core photonic crystal fibers in gas Raman lasers operating at 1.7 µm. Crystal 2021, 11, 121. [Google Scholar] [CrossRef]
- Fu, H.; Shi, Y.; Yi, Z.; Liu, C.; Song, X.; Lv, J.; Yang, L. Effects of air holes in the cladding of photonic crystal fibers on dispersion and confinement loss of orbital angular momentum modes. Opt. Quantum Electron. 2022, 54, 353. [Google Scholar] [CrossRef]
- Sun, Y.; Lu, W.; Liu, Q.; Lv, J.; Tai, S.; Han, M.; Chu, P.K.; Liu, C. A large effective mode area photonic crystal fiber supporting 134 OAM modes. J. Opt. 2023, 2023, 1–10. [Google Scholar] [CrossRef]
- Belardi, W. Design and properties of hollow antiresonant fibers for the visible and near infrared spectral range. IEEE J. Light. Technol. 2015, 33, 4497–4503. [Google Scholar] [CrossRef] [Green Version]
- Bufetov, I.A.; Kosolapov, A.F.; Pryamikov, A.D.; Gladyshev, A.V.; Kolyadin, A.N.; Krylov, A.A.; Yatsenko, Y.P.; Biriukov, A.S. Revolver hollow core optical fibers. Fibers 2018, 6, 39. [Google Scholar] [CrossRef] [Green Version]
- Chafer, M.; Osório, J.H.; Amrani, F.; Delahaye, F.; Maurel, M.; Debord, B.; Gérôme, F.; Benabid, F. 1 km hollow-core fiber with loss at the silica Rayleigh limit in the green spectral region. IEEE Photonics Technol. Lett. 2019, 31, 685–688. [Google Scholar] [CrossRef]
- Sakr, H.; Chen, Y.; Jasion, G.T.; Bradley, T.D.; Hayes, J.R.; Mulvad, H.C.H.; Davidson, I.A.; Fokoua, N.; Poletti, F. Hollow core optical fibres with comparable attenuation to silica fibres between 600 and 1100 nm. Nature 2020, 11, 6030. [Google Scholar] [CrossRef]
- Pierscinski, K.; Stepniewski, G.; Klimczak, M.; Sobczak, G.; Dobrakowski, D.; Pierscinska, D.; Pysz, D.; Bugajski, M.; Buczynski, R. Butt-coupling of 4.5 μm quantum cascade lasers to silica hollow core anti-resonant fibers. IEEE J. Light. Technol. 2021, 39, 3284–3290. [Google Scholar] [CrossRef]
- Tsiminis, G.; Rowland, K.J.; Schartner, E.P.; Spooner, N.A.; Monro, T.M.; Ebendorff-Heidepriem, H. Single-ring hollow core optical fibers made by glass billet extrusion for Raman sensing. Opt. Express 2016, 24, 5911–5917. [Google Scholar] [CrossRef]
- Tu, J.; Gao, S.; Wang, Z.; Liu, Z.; Li, W.; Du, C.; Liu, W.; Li, Z.; Yu, C.; Tam, H.; et al. Bend-insensitive grapefruit-type holey ring-core fiber for weakly-coupled OAM mode division multiplexing transmission. IEEE J. Light. Technol. 2020, 38, 4497–4503. [Google Scholar] [CrossRef]
- Cubillas, A.M.; Jiang, X.; Euser, T.G.; Taccardi, N.; Etzold, B.J.M.; Wasserscheid, P.; Russell, P.S.J. Photochemistry in a soft-glass single-ring hollow-core photonic crystal fibre. R. Soc. Chem. Anal. 2017, 142, 925–929. [Google Scholar] [CrossRef] [Green Version]
- Huang, S.-H.; Ma, Q.-C.; Chen, W.-C.; Liu, H.-Z.; Xing, X.-B.; Cui, H.; Luo, Z.-C.; Xu, W.-C.; Luo, A.-P. Microstructure ring fiber for supporting higher-order orbital angular momentum modes with flattened dispersion in broad waveband. Appl. Phys. B Lasers Opt. 2019, 125, 197. [Google Scholar] [CrossRef]
- Ma, Q.; Luo, A.P.; Hong, W. Numerical study of photonic crystal fiber supporting 180 orbital angular momentum modes with high mode quality and flat dispersion. IEEE J. Light. Technol. 2021, 39, 2971–2979. [Google Scholar] [CrossRef]
- Fu, H.; Liu, C.; Yi, Z.; Song, X.; Li, X.; Zeng, Y.; Wang, J.; Lv, J.; Yang, L.; Chu, P.-K. A new technique to optimize the properties of photonic crystal fibers supporting transmission of multiple orbital angular momentum. J. Opt. 2023, 52, 307–316. [Google Scholar] [CrossRef]
- Wang, Y.; Zhao, W.; Geng, W.; Fang, Y.; Bao, C.; Wang, Z.; Zhang, H.; Ren, Y.; Wang, Z.-Y.; Pan, Z.; et al. Air-core ring fiber guiding > 400 radially fundamental OAM modes across S + C + L bands. IEEE Access 2021, 9, 75617–75625. [Google Scholar] [CrossRef]
- Wang, Y.; Lu, Y.; Bao, C.; Geng, W.; Fang, Y.; Mao, B.; Wang, Z.; Liu, Y.; Huang, H.; Ren, Y.; et al. Hollow ring-core photonic crystal fiber with > 500 OAM modes over 360-nm communication bandwidth. IEEE Access 2021, 9, 66999–67005. [Google Scholar] [CrossRef]
- Wang, Y.; Bao, C.; Geng, W.; Lu, Y.; Fang, Y.; Mao, B.; Liu, Y.; Liu, B.; Huang, H.; Ren, Y.; et al. Air-core ring fiber with >1000 radially fundamental OAM modes across O + E + S + C + L bands. IEEE Access 2020, 8, 68280–68287. [Google Scholar] [CrossRef]
- Gregg, P.; Kristensen, P.; Golowich, E.; Olsen, J.O.; Steinvurzel, P.; Ramachandran, S. Stable transmission of 12 OAM states in air-core fiber. In Proceedings of the Conference on Lasers and Electro-Optics (CLEO), San Jose, CA, USA, 9–14 June 2013; pp. CTu2K.2-1–CTu2K.2-2. [Google Scholar]
- Gregg, P.; Kristensen, P.; Ramachandran, S. Conservation of orbital angular momentum in air-core optical fibers. Optica 2015, 2, 267–270. [Google Scholar] [CrossRef] [Green Version]
- Kang, Q.; Gregg, P.; Jung, Y.; Lim, E.L.; Alam, S.; Ramachandran, S.; Richardson, D.J. Amplification of 12 OAM States in an Air-Core EDF. In Proceedings of the Optical Fiber Communication Conference (OFC), Los Angeles, CA, USA, 22–26 March 2015; pp. Tu3C.2-1–Tu3C.2-3. [Google Scholar]
- Gregg, P.; Kristensen, P.; Ramachandran, S. 13.4 km OAM state propagation by recirculating fiber loop. Opt. Express 2016, 24, 18938–18947. [Google Scholar] [CrossRef]
- Gregg, P.; Kristensen, P.; Rubano, A.; Golowich, S.; Marrucci, L.; Ramachandran, S. Enhanced spin orbit interaction of light in highly confining optical fibers for mode division multiplexing. Nat. Commun. 2019, 10, 4707. [Google Scholar] [CrossRef] [Green Version]
- Bozinovic, N.; Yue, Y.; Ren, Y.; Tur, M.; Kristensen, P.; Huang, H.; Willner, A.E.; Ramachandran, S. Terabit-scale orbital angular momentum mode division multiplexing in fibers. Science 2013, 340, 1545–1548. [Google Scholar] [CrossRef] [Green Version]
- Brunet, C.; Vaity, P.; Messaddeq, Y.; LaRochelle, S.; Rush, L.A. Design, fabrication and validation of an OAM fiber supporting 36 states. Opt. Express 2014, 22, 26117–26127. [Google Scholar] [CrossRef]
- Rush, L.A.; Larochelle, S. Fiber transmission demonstrations in vector mode space division multiplexing. Front. Optoelectron. 2018, 11, 155–162. [Google Scholar] [CrossRef] [Green Version]
- Tu, J.; Liu, Z.; Gao, S.; Wang, Z.; Zhang, J.; Zhang, B.; Li, J.; Liu, W.; Tam, H.; Li, Z.; et al. Ring-core fiber with negative curvature structure supporting orbital angular momentum modes. Opt. Express 2019, 27, 20358–20372. [Google Scholar] [CrossRef]
- Wen, Q.; Shecheng, G.; Ting, L.; Hong, J.; Yinlan, R.; Zhenwei, X.; Chuanwu, Y.; Xiaocong, Y. Transmission of orbital angular momentum modes in grapefruit-type microstructure. Chin. J. Lasers 2017, 44, 406002. [Google Scholar]
- Xi, X.M.; Wong, G.K.L.; Weiss, T.; Russell, P.S.J. Measuring mechanical strain and twist using helical photonic crystal fiber. Opt. Lett. 2013, 38, 5401–5404. [Google Scholar] [CrossRef]
- Napiorkowski, M.; Zolnacz, K.; Statkiewicz-Barabach, G.; Bernas, M.; Kiczor, A.; Mergo, P.; Urbanczyk, W. Twist induced mode confinement in partially open ring of holes. IEEE J. Light. Technol. 2020, 38, 1372–1381. [Google Scholar] [CrossRef]
- Zhang, M.; Zhang, L.; Chen, O.; Bai, G.; Li, S. A designed twist sensor based on the SPR effect in the thin-gold-film-coated helical microstructured optical fibers. Sensors 2022, 22, 5668. [Google Scholar] [CrossRef]
- Bohnert, K.; Gabus, P.; Kostovic, J.; Brandle, H. Optical fiber sensors for the electric power industry. Opt. Lasers Eng. 2005, 43, 511–526. [Google Scholar] [CrossRef]
- Weiss, T.; Wong, G.K.L.; Biancalana, F.; Barnett, S.M.; Xi, X.M.; Russell, P.S.J. Topological Zeeman effect and circular birefringence in twisted photonic crystal fibers. J. Opt. Soc. Am. B 2013, 30, 2921–2927. [Google Scholar] [CrossRef] [Green Version]
- Xi, X.M.; Weiss, T.; Wong, G.K.L.; Biancalana, F.; Barnett, S.M.; Padgett, M.J.; Russell, P.S.J. Optical activity in twisted solid-core photonic crystal fibers. Phys. Rev. Lett. 2013, 110, 143903. [Google Scholar] [CrossRef] [Green Version]
- Wong, G.K.L.; Xi, X.M.; Frosz, M.H.; Russell, P.S.J. Enhanced optical activity and circular dichroism in twisted photonic crystal fiber. Opt. Lett. 2015, 40, 4639–4642. [Google Scholar] [CrossRef]
- Alexeyev, C.N.; Lapin, B.P.; Milione, G.; Yavorsky, M.A. Optical activity in multihelicoidal optical fibers. Phys. Rev. A 2015, 92, 033809. [Google Scholar] [CrossRef]
- Alexeyev, C.N.; Lapin, B.P.; Milione, G.; Yavorsky, M.A. Resonance optical activity in multihelicoidal optical fibers. Opt. Lett. 2016, 41, 962–965. [Google Scholar] [CrossRef]
- Napiórkowski, M.; Urbanczyk, W. The effect of coupling between core and cladding modes in twisted microstructured optical fibers. In Micro-Structured and Specialty Optical Fibres V; SPIE: Bellingham, WA, USA, 2018; Volume 10681, pp. 84–90. [Google Scholar]
- Ma, X.; Zhu, C.; Hu, I.-N.; Kaplan, A.; Galvanauskas, A. Single-mode chirally-coupled-core fibers with larger than 50 μm diameter cores. Opt. Express 2014, 22, 9206–9219. [Google Scholar] [CrossRef] [PubMed]
- Wong, G.K.L.; Kang, M.S.; Lee, H.W.; Biancalana, F.; Conti, C.; Weiss, T.; Russell, P.S.J. Excitation of orbital angular momentum resonances in helically twisted photonic crystal fiber. Science 2012, 337, 446–449. [Google Scholar] [CrossRef]
- Barshak, E.V.; Alexeyev, C.N.; Lapin, B.P.; Yavorsky, M.A. Twisted anisotropic fibers for robust orbital-angular-momentum-based information transmission. Phys. Rev. A 2015, 91, 033833. [Google Scholar] [CrossRef]
- Chattopadhyay, R.; Biswas, T.; Bhadra, S.K. Light propagation at Dirac point in twisted photonic crystal. In Proceedings of the 13th International Conference on Fiber Optics and Photonics, Kanpur, India, 4–8 December 2016. [Google Scholar]
- Cui, Y.; Ye, J.; Li, Y.; Dai, P.; Qu, S. Vortex chirality-dependent filtering in helically twisted single-ring photonic crystal fibers. Opt. Express 2019, 27, 20816–20823. [Google Scholar] [CrossRef] [PubMed]
- Vigneswaran, D.; Rajan, M.S.M.; Biswas, B.; Grover, A.; Ahmed, K.; Paul, B.K. Numerical investigation of spiral photonic crystal fiber (S-PCF) with supporting high order OAM modes propagation for space division multiplexing applications. Opt. Quantum Electron. 2021, 53, 78. [Google Scholar] [CrossRef]
- Russel, P.S.J.; Beravat, R.; Wong, G.K.L. Helically twisted photonic crystal fibres. Philos. Trans. A R. Soc. 2017, 375, 20150440. [Google Scholar] [CrossRef] [Green Version]
- Xi, X.M.; Wong, C.K.L.; Frosz, M.H.; Babic, F.; Ahmed, G.; Jiang, X.; Euser, T.G.; Russel, P.S.J. Orbital-angular-momentum-preserving helical Bloch modes in twisted photonic crystal fiber. Optica 2014, 1, 165–169. [Google Scholar] [CrossRef]
- Stefani, A.; Kuhlmey, B.T.; Fleming, S. Orbital angular momentum modes by twisting of a hollow core antiresonant fiber. In Proceedings of the European Conference on Lasers and Electro-Optics and European Quantum Electronics Conference (CLEO/Europe-EQEC), Munich, Germany, 25–29 June 2017. [Google Scholar]
- Stefani, A.; Fleming, S.C.; Kuhlmey, B.T. Terahertz orbital angular momentum modes with flexible twisted hollow core antiresonant fiber. APL Photonics 2018, 3, 051708. [Google Scholar] [CrossRef] [Green Version]
- Fu, C.; Liu, S.; Wang, Y.; Bai, Z.; He, J.; Liao, C.; Zhang, C.; Zhang, F.; Yu, B.; Gao, S.; et al. High-order orbital angular momentum mode generator based on twisted photonic crystal fiber. Opt. Lett. 2018, 43, 1786–1789. [Google Scholar] [CrossRef] [Green Version]
- Zhou, G.; Liu, J.; Xia, C.; Hou, Z.; Li, B. Orbital-angular-momentum-amplifying helical vector modes in Yb3+-doped three-core twisted microstructure fiber. Opt. Express 2020, 28, 21110–221119. [Google Scholar]
- Tandje, A.; Yammine, J.; Dossou, M.; Bouwmans, G.; Baudelle, K.; Vianou, A.; Andresen, E.R.; Bigot, L. Ring-core photonic crystal fiber for propagation of OAM modes. Opt. Lett. 2019, 44, 1611–1614. [Google Scholar] [CrossRef]
- Zhang, H.; Fang, S.; Wang, J.; Feng, H.; Li, H.; Wan, D.; Zhang, X.; Xi, L. A hybrid cladding ring-core photonic crystal Fibers for OAM transmission with weak spin–orbit coupling and strong bending resistance. Photonics 2023, 10, 352. [Google Scholar] [CrossRef]
- Adams, M.J. An Introduction to Optical Waveguides; John Wiley & Sons Ltd.: New York, NY, USA, 1981; ISBN 9780471279693. [Google Scholar]
- Binh, L.N. Design Guidelines for Ultra-Broadmand Dispersion-Flattened Optical Fibers with Segmented-Core Index Profile; Technical Report MECSE-14-2003; Monash University: Clayton, Australia, 2003. [Google Scholar]
- Fleming, J.W. Dispersion in GeO2-SiO2 glasses. Appl. Opt. 1984, 23, 4486–4493. [Google Scholar] [CrossRef]
- Burdin, V.A. Methods for computation of Sellmeier coefficients for dispersion analysis of silica optical fibers. Infocommun. Technol. 2006, 4, 30–34. [Google Scholar]
- Bourdine, A.V.; Burdin, V.A.; Demidov, V.V.; Dukelskii, K.V.; Gizatulin, A.R.; Khokhlov, A.V.; Meshkov, I.K.; Sultanov, A.K.; Ter-Nersesyants, E.V.; Ustinov, S.V.; et al. Design of vortex optical fibers for RoF systems: Part II: Pilot samples of chiral microstructured optical fibers. In Optical Technologies for Telecommunications 2019; SPIE: Bellingham, WA, USA, 2020; Volume 11516, pp. 522–528. [Google Scholar]
- Bourdine, A.V.; Barashkin, A.Y.; Burdin, V.A.; Dashkov, M.V.; Demidov, V.V.; Dukelskii, K.V.; Evtushenko, A.S.; Ismail, Y.; Khokhlov, A.V.; Kuznetsov, A.A.; et al. Twisted silica microstructured optical fiber with equiangular spiral six-ray geometry. Fibers 2021, 9, 27. [Google Scholar] [CrossRef]
- Bourdine, A.V.; Demidov, V.V.; Kuznetsov, A.A.; Vasilets, A.A.; Ter-Nersesyants, E.V.; Khokhlov, A.V.; Matrosova, A.S.; Pchelkin, G.A.; Dashkov, M.V.; Zaitseva, E.S.; et al. Twisted few-mode optical fiber with improved height of quasi-step refractive index profile. Sensors 2021, 22, 3124. [Google Scholar] [CrossRef]
- Bourdine, A.V.; Dashkov, M.V.; Kuznetsov, A.A.; Demidov, V.V.; Evtushenko, A.S.; Barashkin, A.Y.; Ter-Nersesyants, E.V.; Vasilets, A.A.; Morozov, O.G.; Burdin, V.A.; et al. Pulse and spectral responses of laser-excited twisted silica few-mode optical fiber with improved height of quasi-step refractive index profile. In Optical Technologies for Telecommunications 2021; SPIE: Bellingham, WA, USA, 2021; Volume 12295, pp. 51–61. [Google Scholar]
- Bourdine, A.V.; Barashkin, A.Y.; Burdin, V.A.; Dashkov, M.V.; Demidov, V.V.; Khokhlov, A.V.; Ter-Nersesyants, E.V.; Matrosova, A.S.; Pchelkin, G.A.; Dukelskii, K.V.; et al. Researches of parameters of chiral few-mode optical fiber pilot sample with improved height of step refractive index profile. Proc. Telecommun. Univ. 2021, 7, 37–49. [Google Scholar] [CrossRef]
- Pchelkin, G.A.; Demidov, V.A.; Ter-Nersesyants, E.V.; Khokhlov, A.V.; Bourdine, A.V.; Matrosova, A.S.; Dukelskii, K.V.; Davydov, V.V.; Podoprigora, A.N.; Pilipova, V.M.; et al. Study of the characteristics of few-mode microstructured optical fibers with 6 cores, made of highly doped GeO2 silica and induced chirality. In Proceedings of the IEEE 2022 International Conference on Electrical Engineering and Photonics (EExPolytech-2022), St. Petersburg, Russia, 20–21 October 2022. [Google Scholar]
- Bourdine, A.V.; Demidov, V.A.; Dukelskii, K.V.; Khokhlov, A.V.; Ter-Nersesyants, E.V.; Bureev, S.V.; Matrosova, A.S.; Pchelkin, G.A.; Kuznetsov, A.A.; Morozov, O.G.; et al. Six-core GeO2-doped silica microstructured optical fiber with induced chirality. Fibers 2023, 11, 28. [Google Scholar] [CrossRef]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bourdine, A.V.; Demidov, V.V.; Ter-Nersesyants, E.V.; Pchelkin, G.A.; Shurupov, D.N.; Khokhlov, A.V.; Matrosova, A.S.; Kashin, A.I.; Bureev, S.V.; Dashkov, M.V.; et al. Twisted Silica Few-Mode Hollow GeO2-Doped Ring-Core Microstructured Optical Fiber. Photonics 2023, 10, 846. https://doi.org/10.3390/photonics10070846
Bourdine AV, Demidov VV, Ter-Nersesyants EV, Pchelkin GA, Shurupov DN, Khokhlov AV, Matrosova AS, Kashin AI, Bureev SV, Dashkov MV, et al. Twisted Silica Few-Mode Hollow GeO2-Doped Ring-Core Microstructured Optical Fiber. Photonics. 2023; 10(7):846. https://doi.org/10.3390/photonics10070846
Chicago/Turabian StyleBourdine, Anton V., Vladimir V. Demidov, Egishe V. Ter-Nersesyants, Grigori A. Pchelkin, Dmitriy N. Shurupov, Alexander V. Khokhlov, Alexandra S. Matrosova, Andrey I. Kashin, Sergei V. Bureev, Michael V. Dashkov, and et al. 2023. "Twisted Silica Few-Mode Hollow GeO2-Doped Ring-Core Microstructured Optical Fiber" Photonics 10, no. 7: 846. https://doi.org/10.3390/photonics10070846
APA StyleBourdine, A. V., Demidov, V. V., Ter-Nersesyants, E. V., Pchelkin, G. A., Shurupov, D. N., Khokhlov, A. V., Matrosova, A. S., Kashin, A. I., Bureev, S. V., Dashkov, M. V., Evtushenko, A. S., Zaitseva, E. S., Gizatulin, A. R., Meshkov, I. K., Dyavangoudar, A. A., Saharia, A., Tiwari, M., Vasilets, A. A., Elagin, V. S., ... Dukelskii, K. V. (2023). Twisted Silica Few-Mode Hollow GeO2-Doped Ring-Core Microstructured Optical Fiber. Photonics, 10(7), 846. https://doi.org/10.3390/photonics10070846






