Investigation of Hybrid Remote Fiber Optic Sensing Solutions for Railway Applications
Abstract
1. Introduction
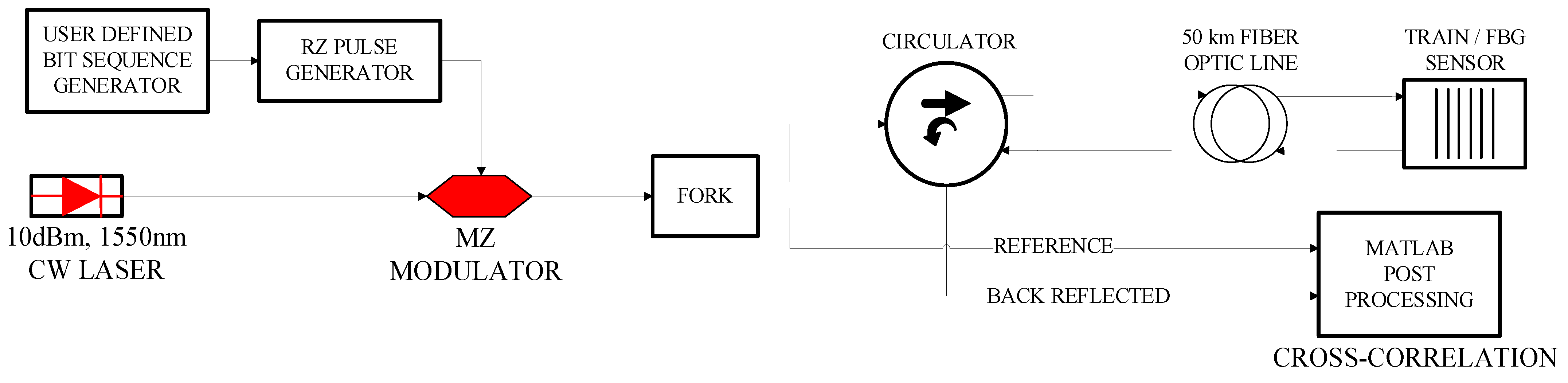
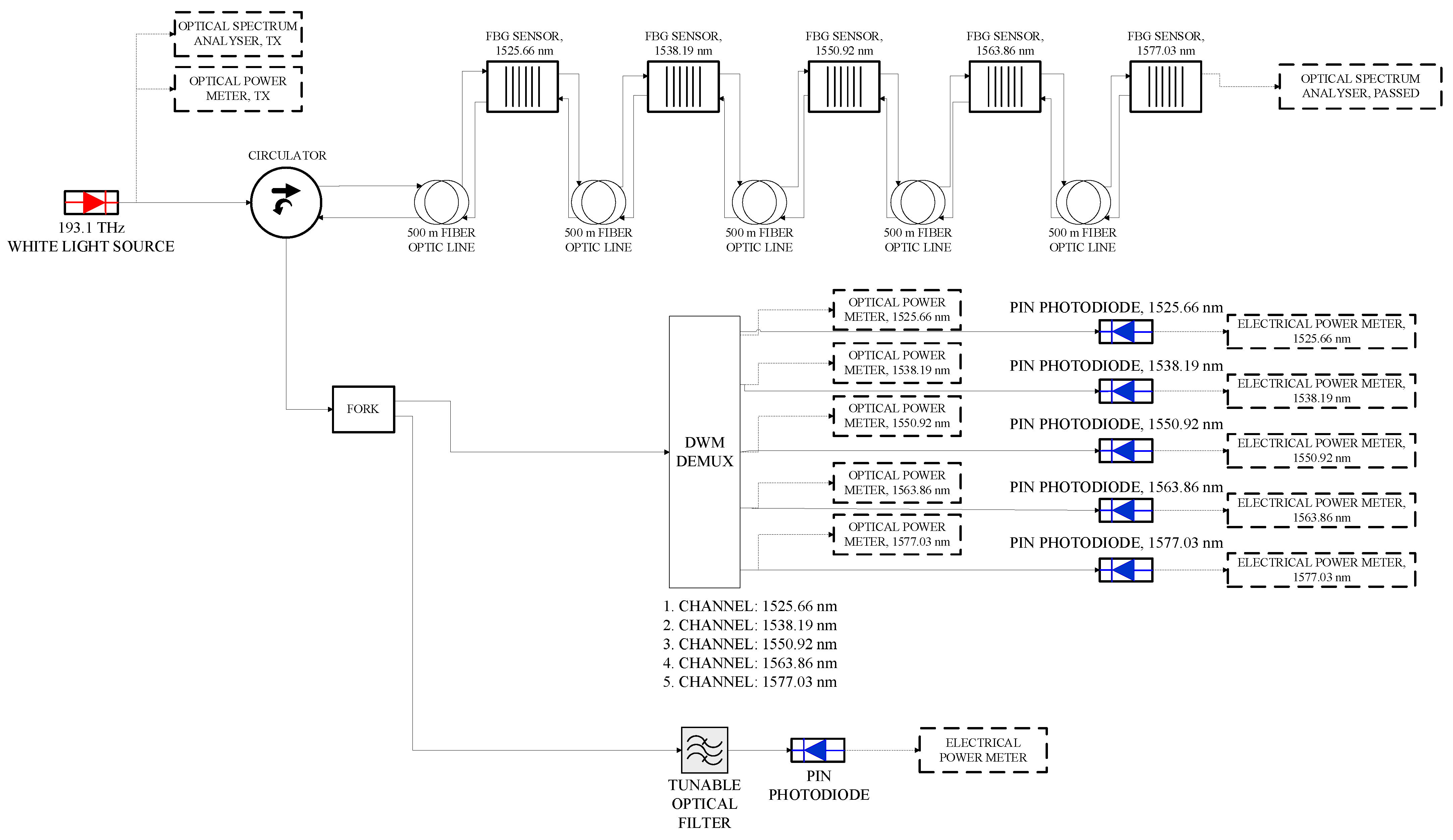
2. Investigated Sensing System
3. Train-Resistant Forces
4. General Setup and Base Design
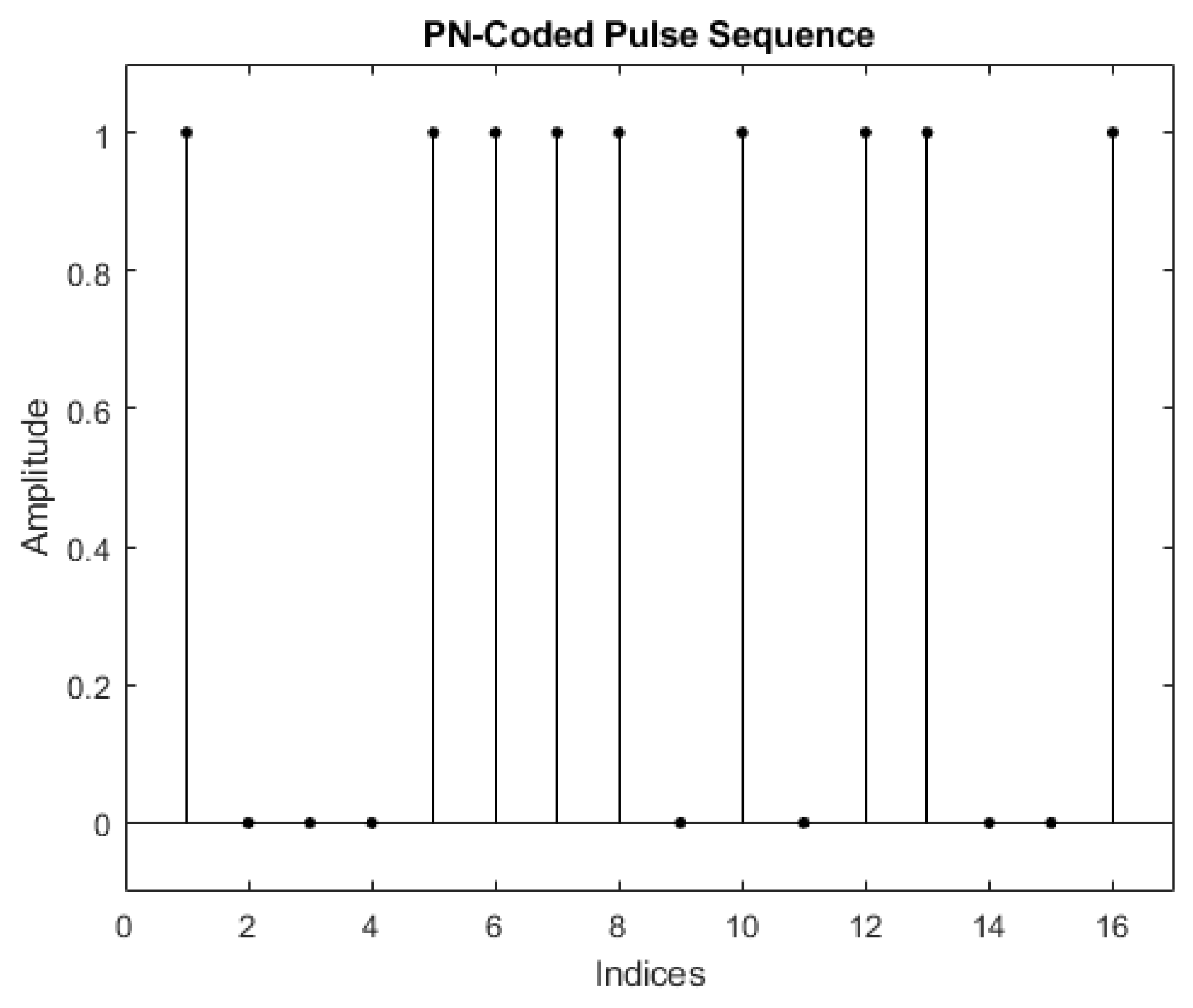
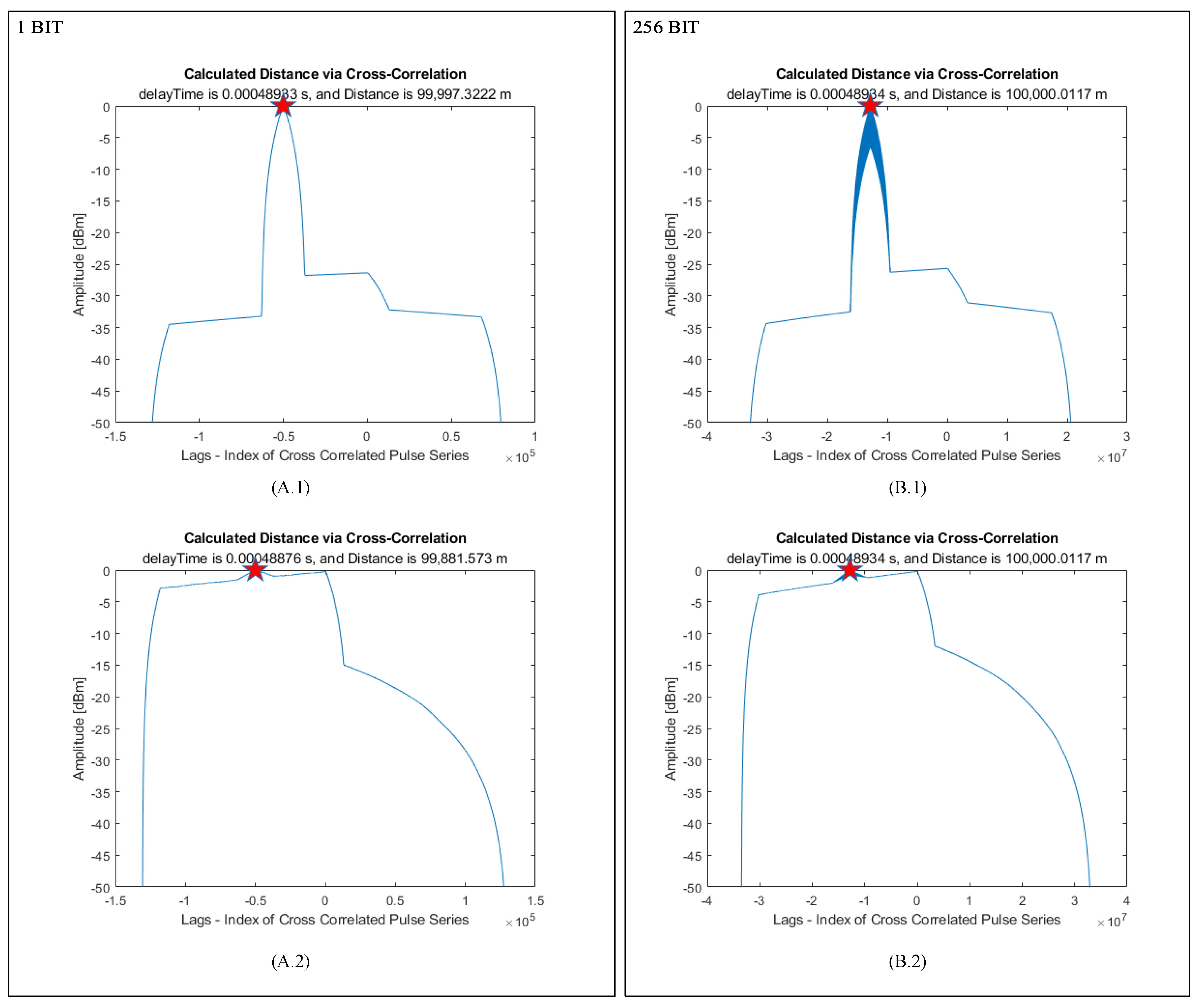
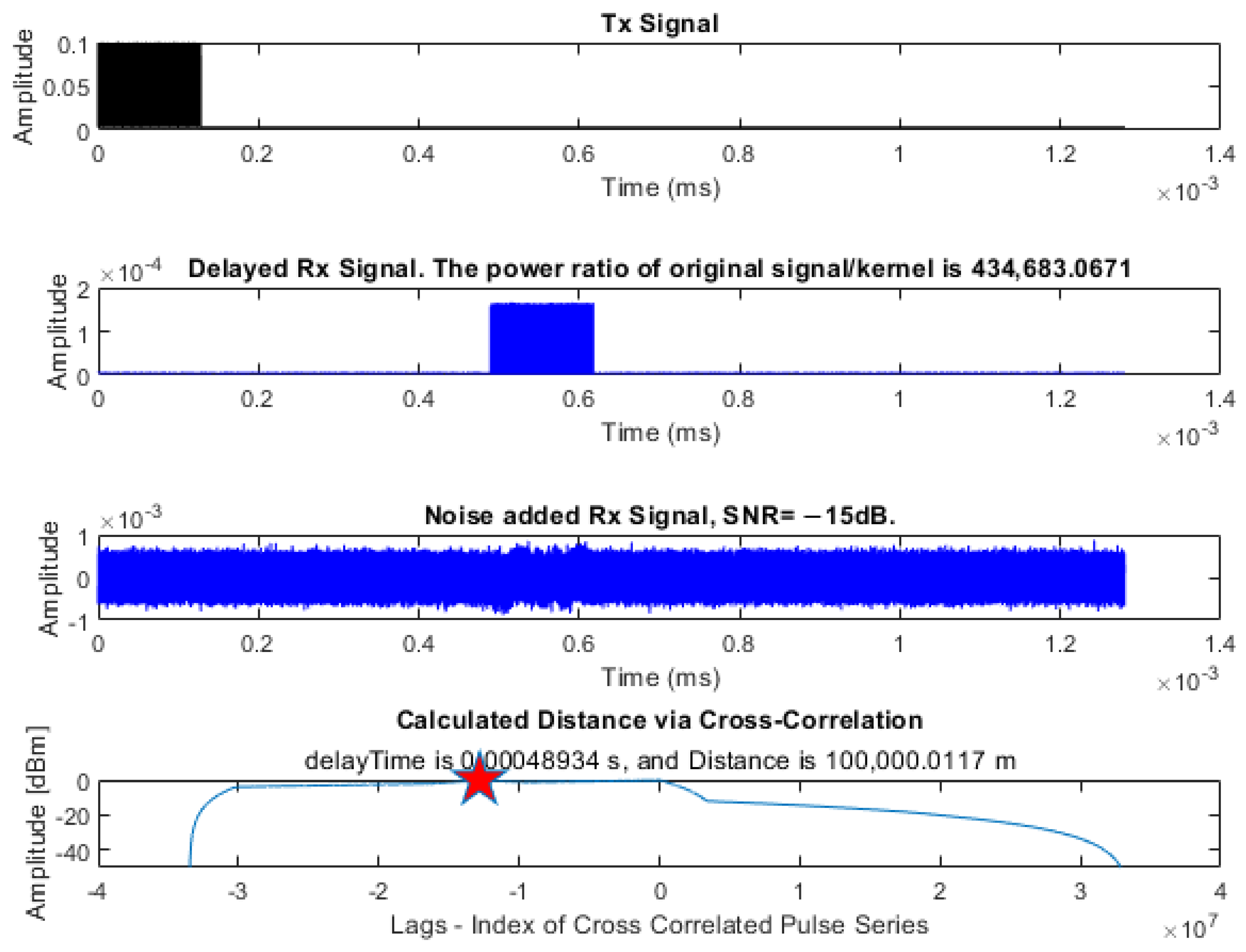
5. Transmitted Pulse Coding
6. Train Speed Detection Mechanism Using Bragg Shifting
7. FBG Sensing Design
General Layout of the FBG Design
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Barnoski, M.K.; Jensen, S.M. Fiber waveguides: A novel technique for investigating attenuation characteristics. Appl. Opt. 1976, 15, 2112–2115. [Google Scholar] [CrossRef] [PubMed]
- Barnoski, M.K.; Rourke, M.D.; Jensen, S.M.; Melville, R.T. Optical time domain reflectometer. Appl. Opt. 1977, 16, 2375–2379. [Google Scholar] [CrossRef] [PubMed]
- Personick, S.D. Photon probe—An optical time-domain reflectometer. Bell Syst. Tech. J. 1977, 56, 355. [Google Scholar] [CrossRef]
- Agrawal, P. Fiber-Optic Communication Systems, 3rd ed.; John Wiley & Sons: Hoboken, NJ, USA, 2012; pp. 57–58. [Google Scholar]
- Asawa, C.K.; Taylor, H.F. Propagation of light trapped within a set of lowest-order modes of graded-index multi-mode fiber undergoing bending. Appl. Opt. 2000, 39, 2029–2037. [Google Scholar] [CrossRef] [PubMed]
- Asawa, C.K.; Yao, S.-K. Microbending of Optical Fibers for Remote Force Measurement. U.S. Patent No. 4,412,979, 3 March 1983. [Google Scholar]
- Asawa, C.K.; Yao, S.K.; Stearns, R.C.; Mota, N.L.; Downs, J.W. High-sensitivity fibre-optic strain sensors for measuring structural distortion. Electron. Lett. 1982, 18, 362–364. [Google Scholar] [CrossRef]
- Yao, S.K.; Asawa, C.K. Microbending Fiber Optic Sensing; 1983 Technical Symposium East; SPIE: Bellingham, WA, USA, 1983; pp. 9–13. [Google Scholar]
- Griffiths, R.W. Structural Monitoring System Using Fiber Optics. U.S. Patent No. 4,654,520, 31 March 1987. [Google Scholar]
- Experimental Data Provided by Vendor OptiSystem Software under the Governmentally Funded Project NSERC/Card1 538408-18; OptiSystem: Nowy Sącz, Poland, 2019.
- Hartog, A.H. An Introduction to Distributed Optical Fibre Sensors; CRC Press: Boca Raton, FL, USA, 2017; pp. 6–38. [Google Scholar]
- Zan, M.S.D.; Elgaud, M.M.; Bakar, A.A.A. Coding the Optical Pulse in TDM-FBG Sensors with Hybrid Simplex-and Golay Codes for SNR Improvement. In Proceedings of the 2019 24th OptoElectronics and Communications Conference (OECC) and 2019 International Conference on Photonics in Switching and Computing (PSC), Fukuoka, Japan, 7–11 July 2019; pp. 1–3. [Google Scholar] [CrossRef]
- Ito, F.; Fan, X.; Koshikiya, Y. Long-range coherent OFDR with light source phase noise compensation. J. Light. Technol. 2012, 30, 1015–1024. [Google Scholar] [CrossRef]
- Geng, J.; Spiegelberg, C.; Shibin, J. Narrow linewidth fiber laser for 100-km optical frequency domain reflectometry. IEEE Photon. Technol. Lett. 2005, 17, 1827–1829. [Google Scholar] [CrossRef]
- Xiong, J.; Wang, Z.; Wu, Y.; Wu, H.; Rao, Y. Long-distance distributed acoustic sensing utilizing negative frequency band. Opt. Express 2020, 28, 35844–35856. [Google Scholar] [CrossRef] [PubMed]
- He, Z.; Liu, Q. Optical Fiber Distributed Acoustic Sensors: A Review. J. Light. Technol. 2021, 39, 3671–3686. [Google Scholar] [CrossRef]
- Sun, Y.; Li, H.; Fan, C.; Yan, B.; Chen, J.; Yan, Z.; Sun, Q. Review of a Specialty Fiber for Distributed Acoustic Sensing Technology. Photonics 2022, 9, 277. [Google Scholar] [CrossRef]
- IEEE Std 1698-2009; IEEE Guide for the Calculation of Braking Distances for Rail Transit Vehicles. IEEE: New York, NY, USA, 2009; pp. 1–41. [CrossRef]
- Izadi, T.; Abouali, O.; Mehrabian, M.A.; Salmanzadeh, M. Investigation of the effects of different parameters on the generated pressure waves inside the tunnels. SN Appl. Sci. 2020, 2, 1406. [Google Scholar] [CrossRef]
- Werneck, M.; Allil, R.; Ribeiro, B.; de Nazaré, F. A Guide to Fiber Bragg Grating Sensors; Intec Open Science: London, UK, 2013. [Google Scholar] [CrossRef]
- FS.COM Community. CWDM/DWDM ITU Channels Guide. FS.COM News. Available online: https://community.fs.com/news/cwdmdwdm-itu-channels-guide.html (accessed on 22 June 2023).
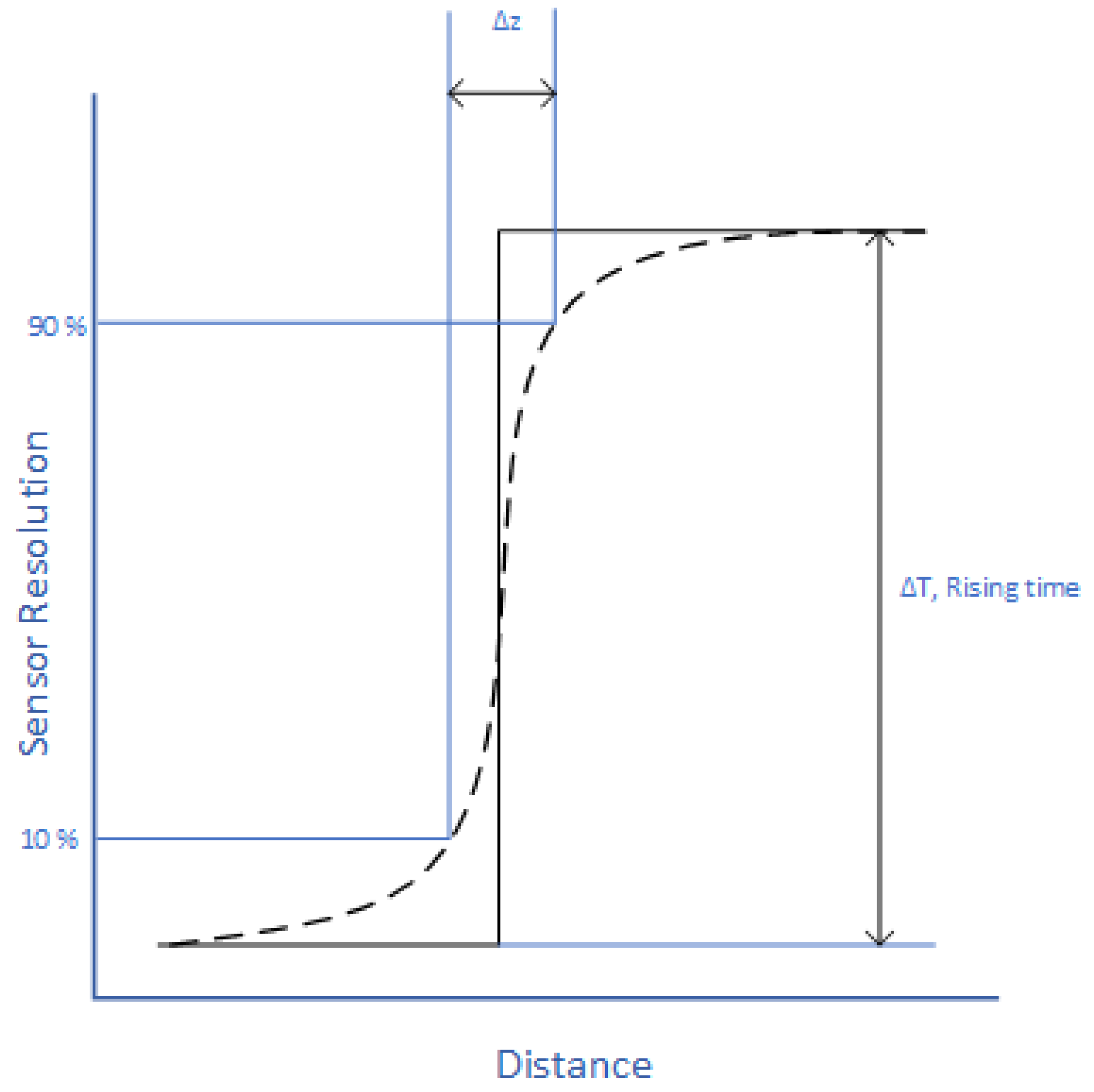
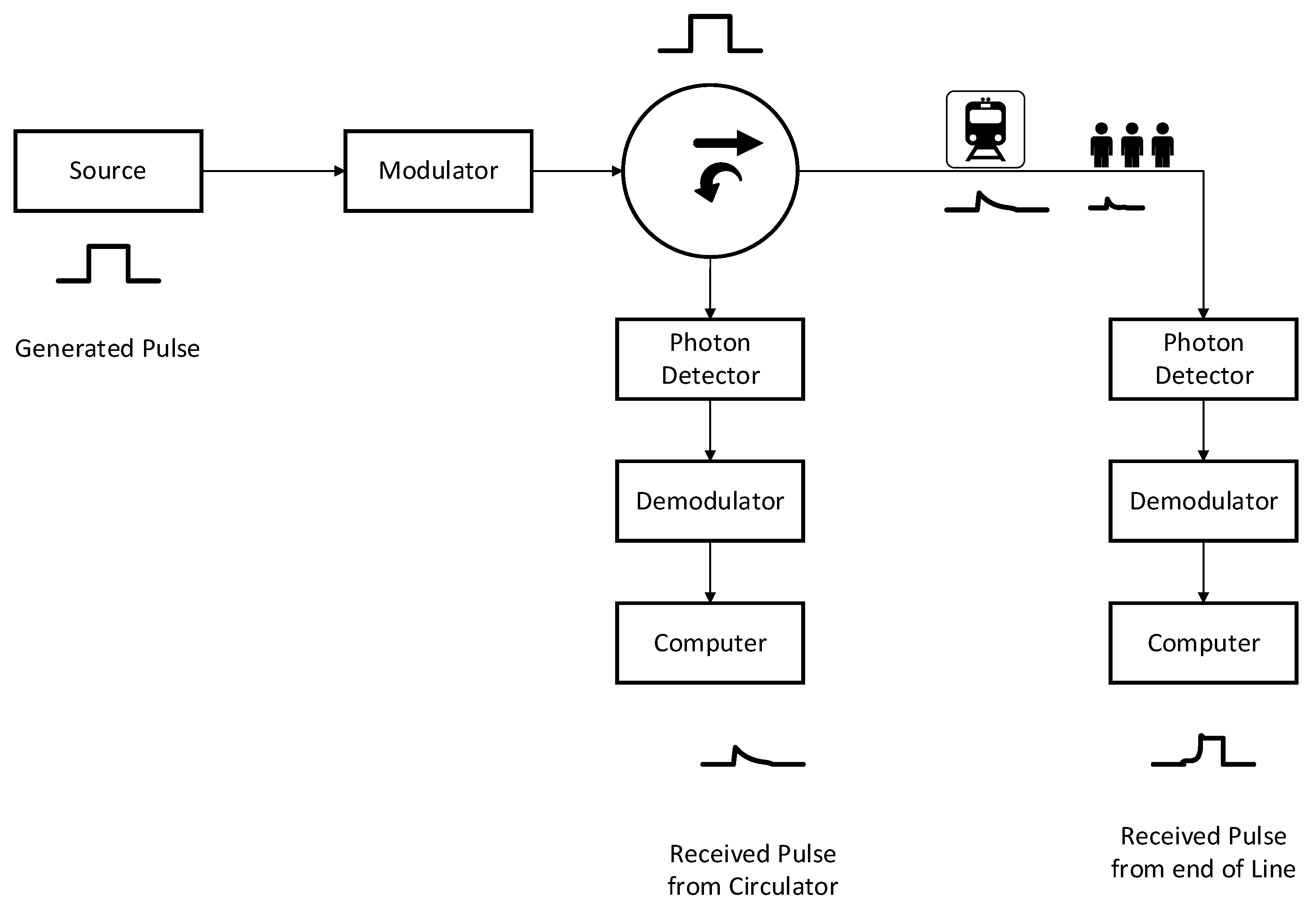
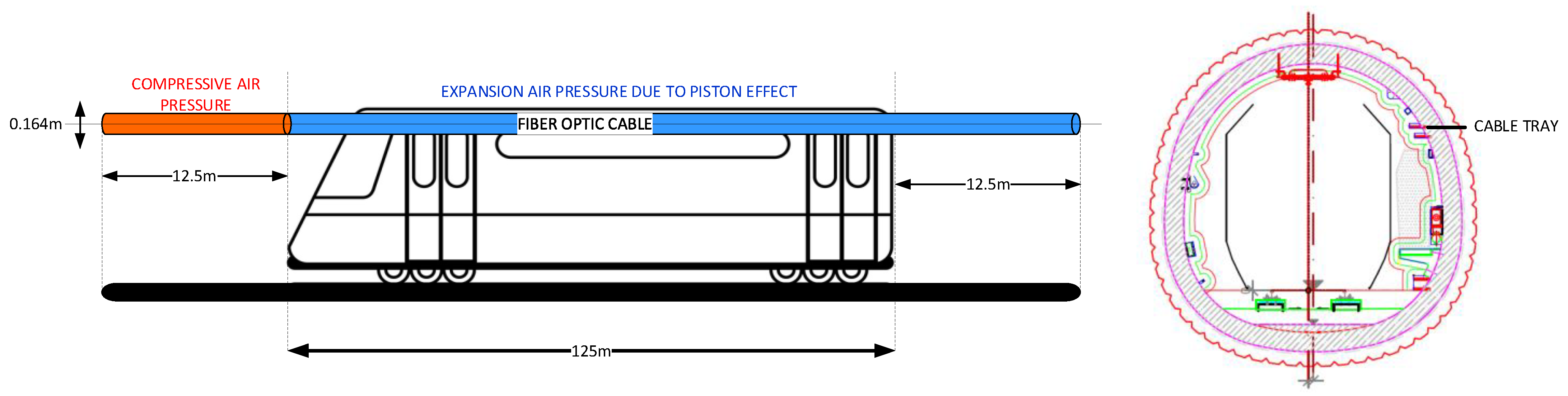

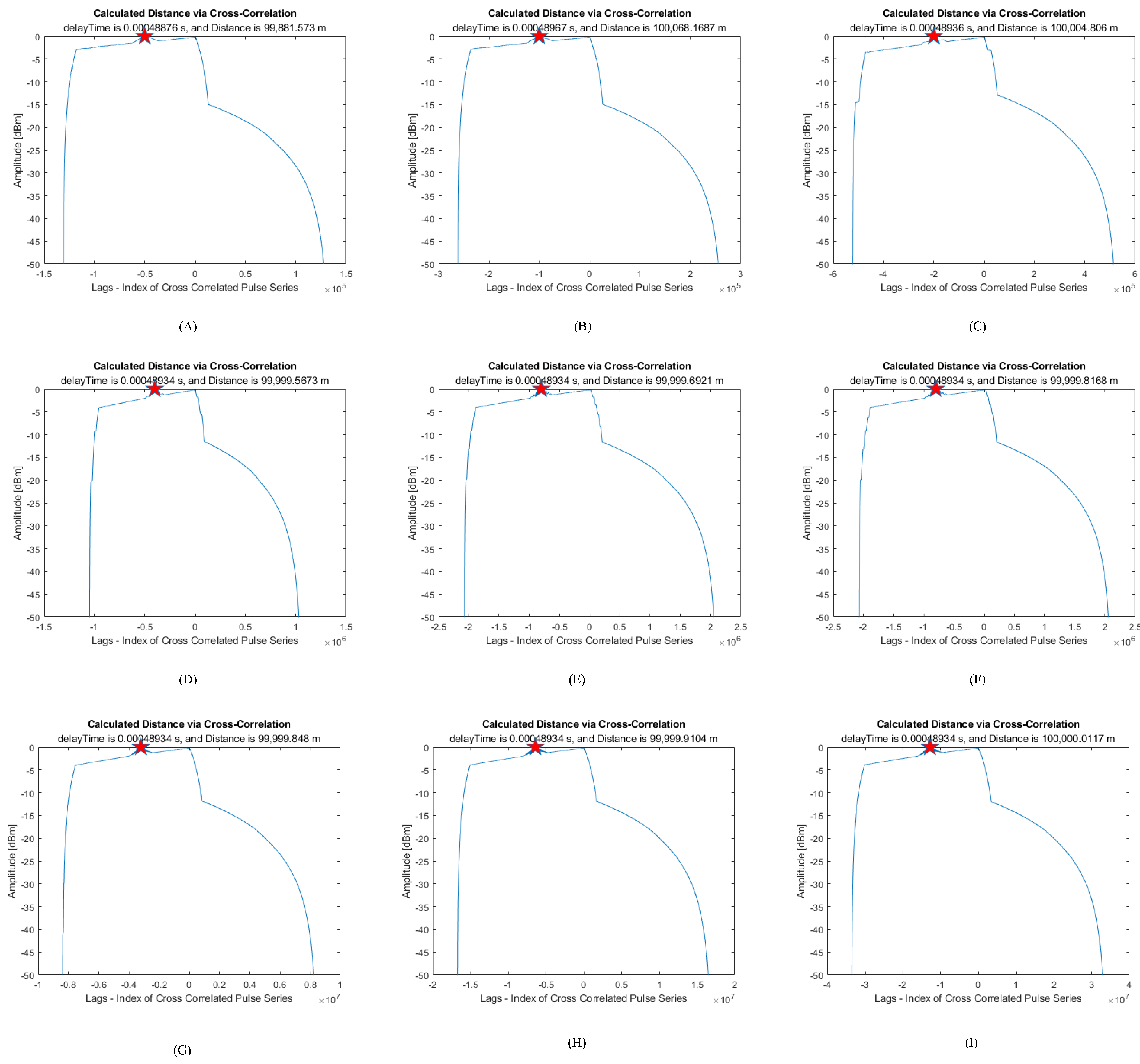
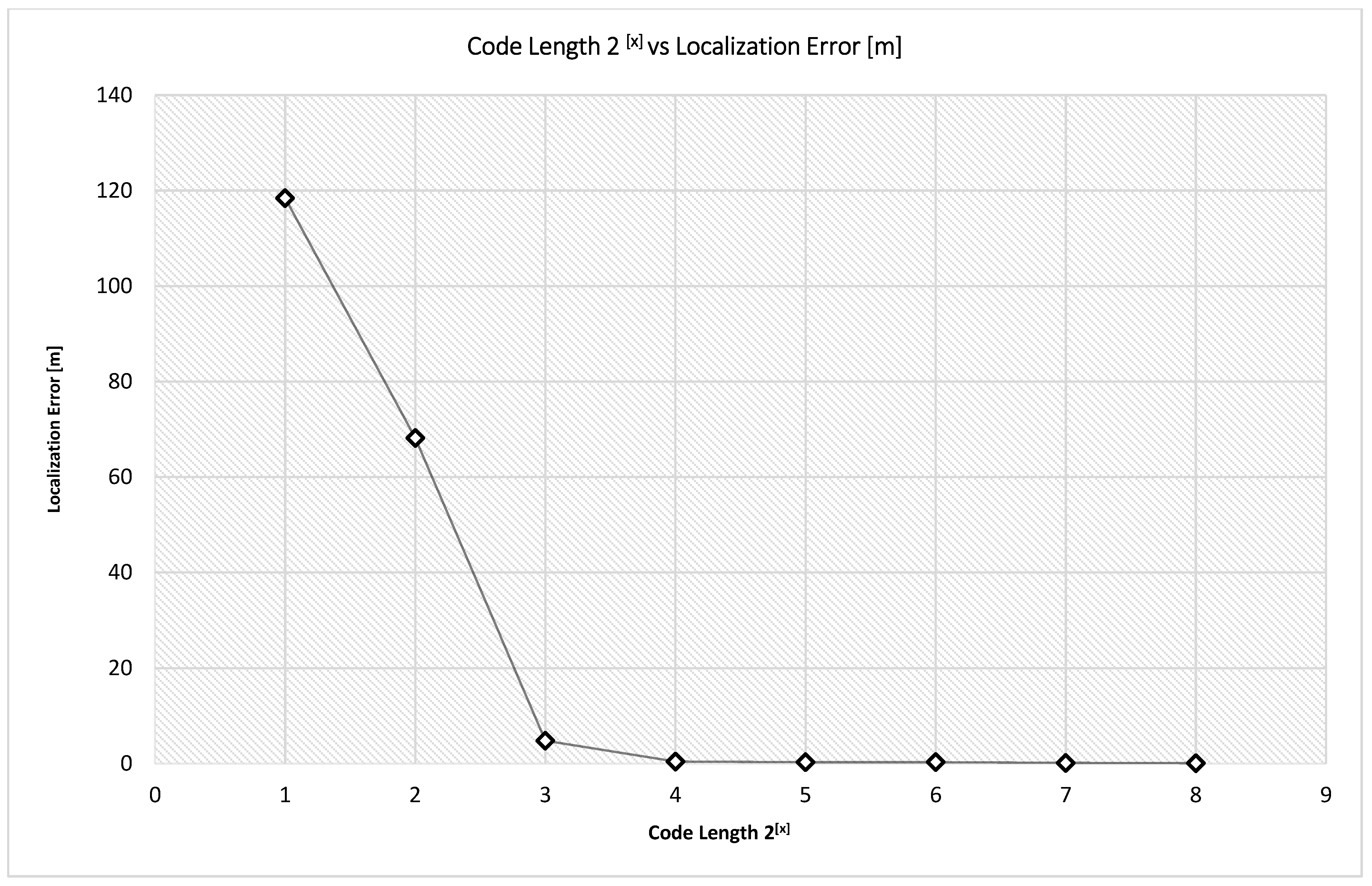
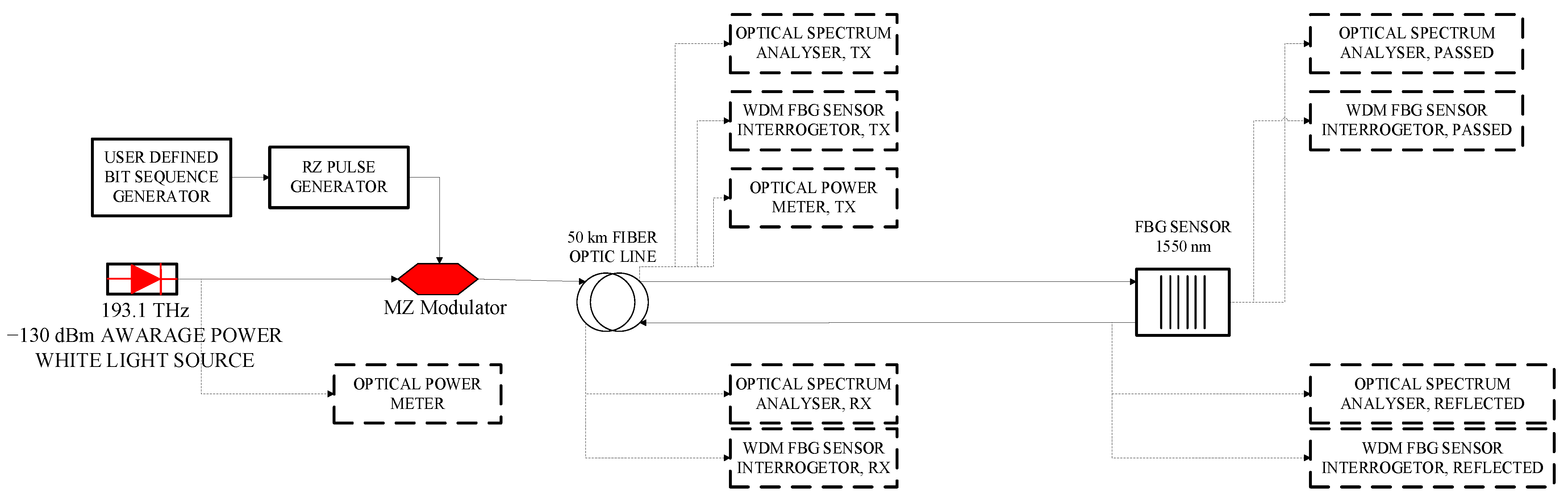
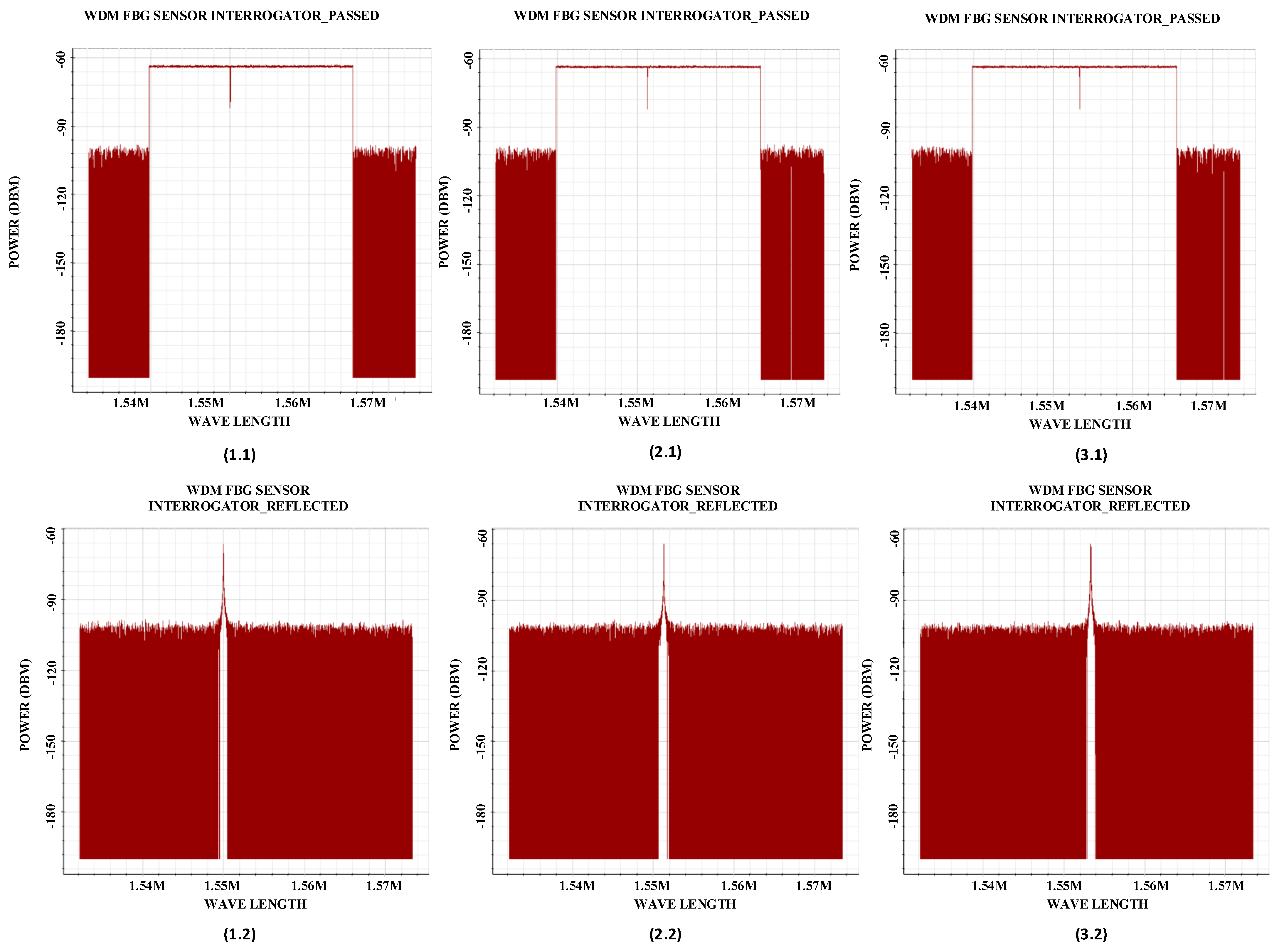


| Tain Speed (km/h) | Air Resistant Force (F(R_Air) (N)) |
|---|---|
| 20 | 353 |
| 50 | 2205 |
| 80 | 5646 |
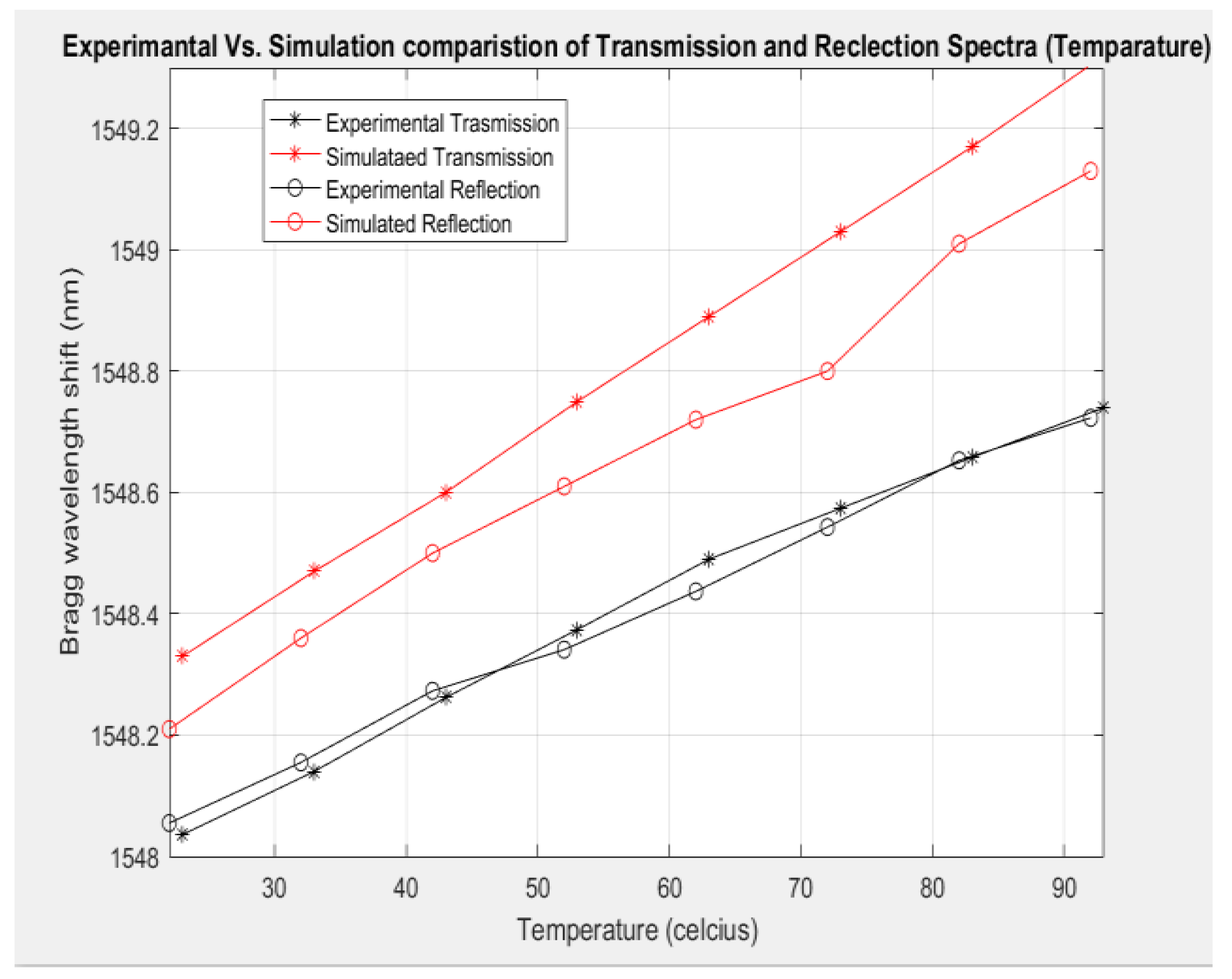
| Parameter | Set Value | Bragg Wavelength (nm) | Set Value | Bragg Wavelength (nm) |
|---|---|---|---|---|
| Experimental Temperature (Transmission) | 23 | 1548.036 | 93 | 1548.74 |
| Simulated Temperature (Transmission) | 20 | 1548.11494 | 100 | 1549.07486 |
| Simulated Proposed System Temperature (Transmission) | 23 | 1548.33 | 93 | 1549.32 |
| Experimental Temperature (Reflection) | 22 | 1548.055 | 92 | 1548.723 |
| Simulated Temperature (Transmission) | 20 | 1548.000028 | 100 | 1549.154909 |
| Simulated Temperature Proposed System (Reflection) | 22 | 1548.21 | 92 | 1549.131549 |
| Experimental Strain (Reflection) | 0.001176 | 1548.62 | 0.011765 | 1560.262 |
| Simulated Strain (Reflection) | 0.002 | 1550.5169 | 0.012 | 1563.291 |
| Simulated Strain Proposed System (Reflection) | 0.001176 | 1548.41 | 0.011765 | 1562.19 |
| Measurand | Accuracy (RMSE)% |
|---|---|
| Temperature (Transmission) | 0.429 |
| Temperature (Reflection) | 0.28 |
| Strain (Reflection) | 1.39 |
| Name | Value | Units |
|---|---|---|
| Bit rate | 1.00 × 104 | bit/s |
| Time window | 0.0008 | s |
| Sample rate | 1.31 × 109 | Hz |
| Sequence length | 8 | bits |
| Samples per bit | 131,072 | |
| Guard Bits | 0 | |
| Symbol rate | 2000 | symbols/s |
| Number of samples | 1,048,576 | |
| Refractive Index | 1.467 | |
| Speed of Light in Space | 299,792 | m/µs |
| Fiber length | 50 | km |
| Laser Power | 10 | dBm |
| Laser wavelength | 1550 | nm |
| Train Velocity (km/h) | Duration to Pass 12.5 m (s) | Air Force (N) | Strain Over Cable (Pa) | Shifted Center Wavelength (nm) | Reflected Power (dBm) |
|---|---|---|---|---|---|
| 80 | 0.56 | 5646 | 2754 | 3.33 | −66.2 |
| 70 | 0.64 | 4322 | 2108 | 2.56 | −66.2 |
| 60 | 0.75 | 3176 | 1549 | 1.88 | −66.37 |
| 50 | 0.90 | 2205 | 1076 | 1.3 | −66.21 |
| 40 | 1.13 | 1411 | 688 | 0.84 | −66.38 |
| 30 | 1.50 | 794 | 387 | 0.46 | −66.35 |
| 20 | 2.25 | 353 | 172 | 0.21 | −66.38 |
| 10 | 4.50 | 88 | 43 | 0.05 | −66.16 |
| 0 | NA | 0 | 0 | 0 | −66.44 |
| Frequency | Wavelength |
|---|---|
| GHz | nm |
| 190.1 | 1577.03 |
| 191.7 | 1563.86 |
| 193.3 | 1550.92 |
| 194.9 | 1538.19 |
| 196.5 | 1525.66 |
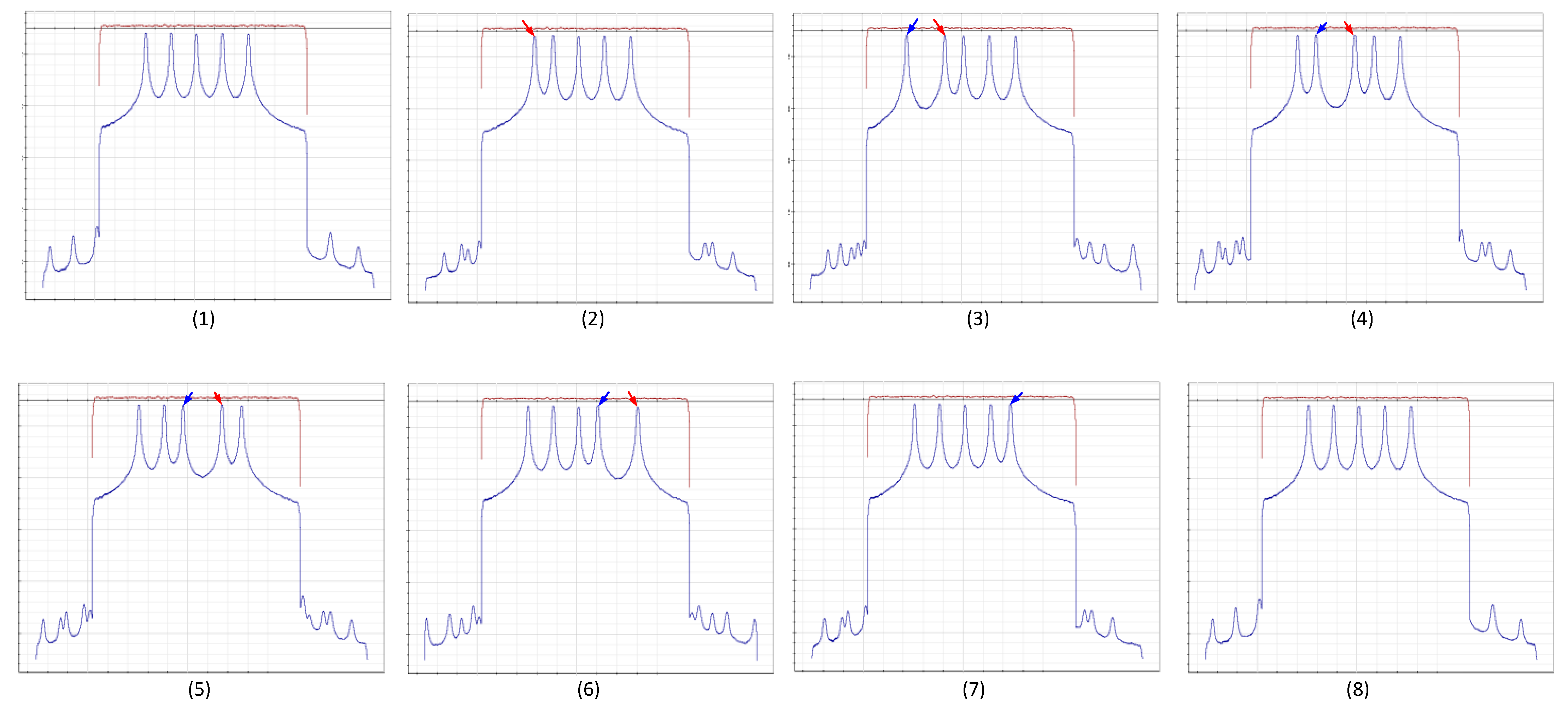
| Iteration | Air Pressure (Mpa), 1525.66 nm | Air Pressure (Mpa), 1538.19 nm | Air Pressure (Mpa), 1550.92 nm | Air Pressure (Mpa), 1563.86 nm | Air Pressure (Mpa), 1577.03 nm |
|---|---|---|---|---|---|
| 1 | 0.002754 | 0 | 0 | 0 | 0 |
| 2 | −0.002754 | 0.002754 | 0 | 0 | 0 |
| 3 | 0 | −0.002754 | 0.002754 | 0 | 0 |
| 4 | 0 | 0 | −0.002754 | 0.002754 | 0 |
| 5 | 0 | 0 | 0 | −0.002754 | 0.002754 |
| 6 | 0 | 0 | 0 | 0 | −0.002754 |
| Total Power of Photodiodes | |||||
|---|---|---|---|---|---|
| Iteration | PIN 1525.66 nm | PIN 1538.19 nm | PIN 1550.92 nm | PIN 1563.86 nm | PIN 1577.03 nm |
| 1 | −2.2272 | −2.2345 | −2.2039 | −2.1348 | −2.1332 |
| 2 | −24.963 | −2.2364 | −2.2054 | −2.1359 | −2.1316 |
| 3 | −24.953 | −24.653 | −2.2046 | −2.1341 | −2.1335 |
| 4 | −2.2256 | −24.811 | −24.436 | −2.1267 | −2.1323 |
| 5 | −2.2276 | −2.2343 | −24.442 | −24.005 | −2.127 |
| 6 | −2.2288 | −2.2342 | −2.2024 | −24.528 | −24.391 |
| 7 | −2.2275 | −2.2347 | −2.2043 | −2.1364 | −24.417 |
| 8 | −2.2272 | −2.2345 | −2.2039 | −2.1348 | −2.1332 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boynukalin, S.; Paker, S.; Atieh, A. Investigation of Hybrid Remote Fiber Optic Sensing Solutions for Railway Applications. Photonics 2023, 10, 864. https://doi.org/10.3390/photonics10080864
Boynukalin S, Paker S, Atieh A. Investigation of Hybrid Remote Fiber Optic Sensing Solutions for Railway Applications. Photonics. 2023; 10(8):864. https://doi.org/10.3390/photonics10080864
Chicago/Turabian StyleBoynukalin, Serhat, Selçuk Paker, and Ahmad Atieh. 2023. "Investigation of Hybrid Remote Fiber Optic Sensing Solutions for Railway Applications" Photonics 10, no. 8: 864. https://doi.org/10.3390/photonics10080864
APA StyleBoynukalin, S., Paker, S., & Atieh, A. (2023). Investigation of Hybrid Remote Fiber Optic Sensing Solutions for Railway Applications. Photonics, 10(8), 864. https://doi.org/10.3390/photonics10080864







