Fresnel Lens Array-Based Phase Mask Location Method for Adjustable Multi-Pass Cavity

Abstract

The modulation accuracy of Multi-Plane Light Conversion (MPLC) mainly depends on the positioning accuracy of the phase mask on the Spatial Light Modulator (SLM). To improve positioning accuracy, the impact of phase mask shift on modulation accuracy is investigated, and a position method is proposed. In order to investigate the influence of phase mask offset on the input light conversion effect, a convolution transmission model for the adjustable multi-pass cavity is established. Then, the positioning process for the phase masks is analyzed and simulated, and a method of positioning the phase masks is presented. This method reduces the positioning time and increases the positioning accuracy to 8 μm. Finally, experiments are performed to verify the feasibility of the method. Experimental results show that the similarity of the adjustable multi-pass cavity positioned by this method can reach 93.44%.

1. Introduction

MPLC is a rapidly evolving free-space technology in the field of optics. It enables precise control of light fields through multiple phase modulations and spatial transmissions within a multi-pass cavity [1]. MPLC offers notable advantages, including compact size and high conversion accuracy, making it suitable for various research applications. It has found applications in diverse areas such as mode multiplexing and de-multiplexing [2,3,4,5], beam encryption [6], and laser communication [7,8,9]. And it will play an important role in the application of mechanical learning [10] and optical nanoprinting [11] in the future.

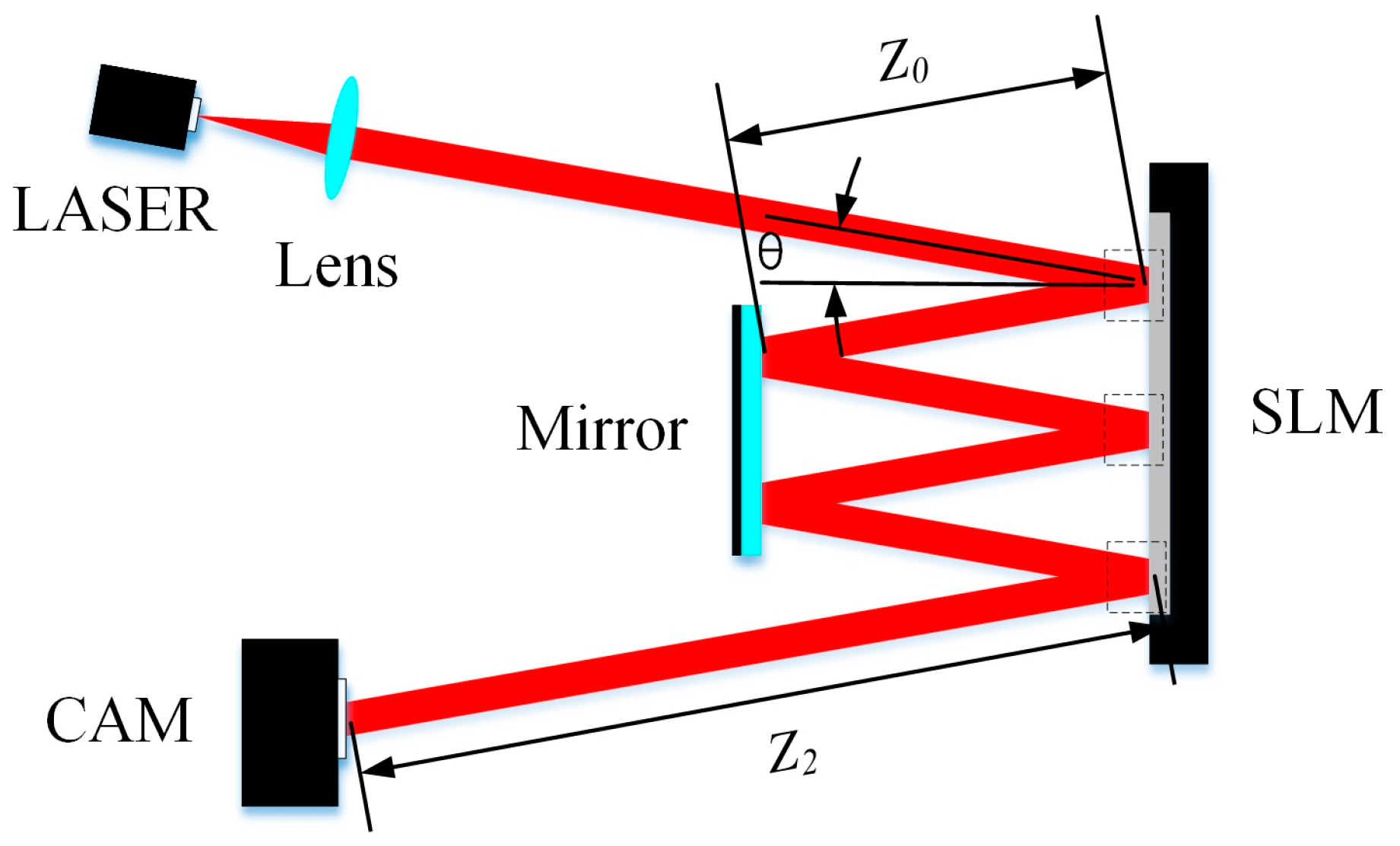
The core component of MPLC is a multi-pass cavity consisting of a phase control element and a mirror. Within this cavity, the beam undergoes phase modulation and spatial transmission. In specific laser communication applications such as adaptive optics, mode multiplexing, and system aberration correction, achieving adjustable phase control in MPLC is crucial. To facilitate this, the phase-only Liquid Crystal Spatial Light Modulator (LC-SLM) is employed as the phase element within the multi-pass cavity. Consequently, it becomes essential not only to position the LC-SLM accurately but also to adjust the loading position of the phase mask on the LC-SLM. Precise determination of the location of incident light on the LC-SLM and loading of the pre-designed phase mask at the corresponding location are vital steps for achieving accurate phase control.

Guillaume L. proposed the use of blazed gratings to adjust the unregulated multi-pass cavity with high accuracy [12,13,14]. The phase element of this multi-pass cavity is a phase plate, which cannot adjust flexibly. However, this method requires additional devices, such as an optical circulator and power meter, in the input optical path for measurement. Moreover, due to the small grating period, implementing it on the LC-SLM is challenging. After our investigation, we did not find any literature concentrating on the location method for the phase mask of an adjustable multi-pass cavity assembly. Direct assembly without a specific method leads to issues such as difficult assembly, slow installation, and uncontrollable adjustment accuracy; therefore, determining the precise location of the incident light on the LC-SLM is problematic.

The utilization of Fresnel lenses for alignment purposes has a longstanding history, dating back to the 1960s, when they were employed in large systems [15]. By imaging the incident light beam onto a detector through the Fresnel lens, accurate optical alignment over long distances can be achieved by analyzing the position of the imaged light spot. In recent years, several papers have focused on the utilization of loading Fresnel lenses onto SLM. In these papers, Fresnel lenses realize various techniques, including SLM calibration [16], beam shaping [17], and imaging with flexible variations of defocusing distance [18].

In this paper, we propose an adjustable multi-pass cavity phase mask location method based on Fresnel lenses loaded onto the phase masks to position the phase masks rapidly and accurately. Firstly, loading a Fresnel lens array on the SLM to locate the first phase mask Secondly, other phase masks are located by Fresnel lenses with appropriate focal lengths. Thirdly, evaluating the beam conversion effect of the multi-pass cavity In the simulation analysis and experimental verification, the position of the phase mask loaded onto the SLM can be determined within an accuracy of one unit (8 μm), which is the pixel size of the liquid crystal screen in this paper. This accuracy satisfies the requirement for an adjustable multi-pass cavity. In addition, this method increases the adjustment speed by reducing some procedures in the adjustment process. It took about two hours to complete the process, from the initial setting up of the adjustable multi-pass cavity to the phase mask positioning.

The outline of this paper follows. The transmission model is established, and the influence of phase mask shift is simulated in Section 2. In Section 3, we present an innovative approach to locating the phase masks and validating them by simulation. In Section 4, we provide a detailed explanation of the phase mask positioning process along with the corresponding experimental results. Conclusions are drawn in Section 5.

2. Multi-Pass Cavity Transmission Model and Effect of Phase Mask Shift

2.1. Multi-Pass Cavity and Its Transmission Model

In this part, we establish a theoretical model to describe the beam transmission in a multi-pass cavity, which will serve as the basis for subsequent simulation analysis.

The design parameters and component configuration of the adjustable multi-pass cavity are depicted in Figure 1. Subsequently, a transmission model is established to analyze and comprehend the variation of the light field as it propagates through the cavity.

The transmission of the incident beam within the multi-pass cavity comprises both free-space transmission and phase modulation through the phase mask. This combination enables the conversion of the light field through staggered space transmission and phase manipulation.

The free space transmission component is achieved through the convolution operation, while the phase modulation component is implemented by adding the phase distribution formula, which is shown in Equation (1) and Figure 2.

$$A_i\left(x,y\right)=A_{i-1}\left(x,y\right)e^{j{\phi }_i}\ast h_i(i=1,2,\dots ,s)$$

(1)

where $s$ is the total number of the phase masks loaded on the SLM, $A_i\left(x,y\right)$ is the light field distribution before the ith phase mask, ${\phi }_i$ is the phase modulation by the ith phase mask, $h_i$ is the impulse response of the ith spatial transmission shown in Equation (2).

$$h_i\left(x,y\right)=\frac{1}{j\lambda z_i}exp(jk{z}_i)exp\left[j\frac{k}{2z_i}\left(x^2+y^2\right)\right] (i=1,2,\dots ,s)$$

(2)

The wavelength of the incident beam is $\lambda$, $k$ is the wavenumber of the incident beam, $z_i$ is the transmission distance of ith spatial transmission. When transmitting in a multi-pass cavity, the transmission distance $z_1$ to $z_{s-1}$ is $2Z_0$, $z_s$ is $Z_2$.

In order to apply MPLC technology to improve the coupling efficiency of intersatellite laser communication in the future, the input light for the laser communication receiver employed in intersatellite communication serves as the incident beam of the MPLC. Given the long-distance propagation of the beam, the Gaussian mode field of the receiving beam is approximated as a plane wave. Therefore, we utilize a plane wave $a_0\left(x,y\right)=1$ as the incident beam for the MPLC.

The complex amplitude expression of the incident beam $A_0(x,y)$ is expressed as Equation (3).

$$A_0(x,y)=a_0(x,y)·[rect(\frac{x}{d_x})rect(\frac{y}{d_y})]·[e^{ikxsin(\theta )}·e^{iky\sin (\psi )}]$$

(3)

$A_0(x,y)$ is made up of three parts. The first part $a_0(x,y)$ is the input plane wave. The second part with two rectangular functions expresses the diaphragm limitations imposed by the shape and size of the phase mask. The third part with two natural exponential functions describes the orientation of the input plane wave, angles θ and φ quantify the angle of inclination in the X and Y directions.

After the modulation of phase masks on SLM and spatial transmissions, the expression of the final output beam is shown in Equation (4).

$$A_s(x,y)=\underset{A_{s-1}}{\underbrace{\{\underset{A_2}{\underbrace{[\underset{A_1}{\underbrace{(A_0{e}^{j{\phi }_1}\ast h_1)}}{e}^{j{\phi }_2}\ast h_2]}}\dots \}}}{e}^{j{\phi }_s}\ast h_s$$

(4)

The complex amplitude distribution of the output light field with various phase masks on SLM can be calculated by using the multi-cavity beam transmission model.

2.2. Effect of Phase Mask Shift

In this section, we investigate the impact of the phase mask shift on the output light spot by analyzing the transmission model of the beam in the multi-pass cavity.

To assess the conversion capability of the adjustable multi-pass cavity, the concept of similarity is introduced as an evaluation index. This parameter quantifies the ability of the multi-pass cavity to convert the light field by calculating the similarity between the complex amplitudes of the actual output beam and the ideal output beam [19]. Equation (5) describes how to calculate the similarity; the formula considers both the intensity and phase factors and is appropriately normalized.

$$\eta =\frac{\left|{\displaystyle \iint A_S{}^{*}\times A_S{}^{\prime }}\right|}{{\displaystyle \iint {\left|A_S\right|}^2\times {\displaystyle \iint {\left|A_s{}^{\prime }\right|}^2}}}$$

(5)

$A_s(x,y)$ is mentioned in Equation (4). The ideal output complex amplitude is expressed as Equation (6). We want the ideal output ${{ A}_s}^{\prime }(x,y)$ to be a Gaussian optical field that corresponds to a single-mode fiber equivalent propagates to the mode field on the surface of the coupling element. In this way, the theory upper limit of coupling efficiency can increase from 81.45% to 100%, and the value of coupling efficiency is square to the similarity value [20]. So, the target of our location method is to reach 90.25% similarity.

$$A_s{}^{\prime }\left(x,y\right)=U_0{e}^{-(\frac{x^2+y^2}{{\omega }_0})}$$

(6)

$U_0$ represents the amplitude. ${\omega }_0$ represents the waist radius of the fundamental mode Gaussian beam, which depends on the single-mode fiber used as well as the coupling element.

Phase mask shift refers to the situation where the position of the phase mask is displaced in the X and Y directions while keeping the input beam transmission static. In our simulation model, we perform cuts and shifts on the positions of the phase masks and fill a zero phase part, while keeping the position of the stop fixed. The example of contrast before and after phase mask shift is shown in Figure 3.

The phase mask shift changes the distribution of the nth phase mask ${\phi }_n$, the generated phase mask ${\varphi }_n\left(x,y\right)$ is shown in Equation (7); and the final output beam is shown in Equation (8).

$${\varphi }_n\left(x,y\right)={\phi }_n(x-x_0,y-y_0)$$

(7)

$$A_s\left(x,y\right)=\{[(A_n{e}^{j{\phi }_n}\ast h_n)e^{j{\varphi }_{n+1}}\ast h_{n+1}]\cdots \}{e}^{j{\phi }_s}\ast h_s$$

(8)

where $x_0$ and $y_0$ are shifts in the positive direction of the X-axis and Y-axis of the phase mask, if $x_0$ and $y_0$ are negative, it represents the shift in the negative direction of the X-axis and Y-axis, respectively.

Based on the simulation model parameters presented in

Table 1. The universal simulation parameters and multi-pass cavity simulation parameters.

Parameter Name	Symbol	Value
wavelength	λ	632.8 nm
incidence angle	θ and φ	θ = 5°; φ = 0
middle transmission distance 1	$Z_0$	29.836 mm
output transmission distance 2	$Z_2$	177 mm
waist of output beam	${\omega }_0$	300 μm

¹ The transmission distance between phase masks on SLM and mirror. ² The transmission distance between the last phase mask on SLM and receiving plane on camera.

and

Table 2. The phase mask simulation parameters.

Parameter Name	Symbol	Value
gray level		256 (2π) 1
unit size		8 μm
phase mask size	$d_x$ and $d_y$	300 units × 300 units
number of phase masks		3

¹ The 256 gray levels here refer to the division of 0–2π into 256 steps.

, we use the wavefront matching algorithm to calculate the transmission phase mask of the multi-pass cavity [21], which converts the plane wave to Gaussian light with a beam waist radius of 300 μm. It is crucial to accurately determine the universal parameters and multi-pass cavity parameters. These parameters play a pivotal role in generating the evaluation phase screen used in our analysis.

The conversion of a plane wave to Gaussian light through three-phase masks achieves a similarity of over 99%, satisfying the requirements of our simulation. Less phase masking will lead to a decrease in similarity. While increasing the number of phase masks would prolong the simulation time, the improvement in similarity is minuscule. Taking all factors into consideration, we opt to analyze the system using a model consisting of three phase masks. The ideal grayscale image of the plane wave to Gaussian light in three-phase masks loaded onto SLM is shown in Figure 4.

Furthermore, the distance and angle parameters utilized in the current experiment are measured using reliable methods such as displacement transducers and autocollimators.

By incorporating the adjusted phase masks into Equation (8), a series of complex amplitude outputs are obtained through calculation. In this way, the effects of phase mask shift are investigated using similarity. Figure 5 presents the results of the simulation.

During the phase modulation process that converts a plane wave to a Gaussian beam, when the position of any phase mask shifts, even a slight movement of only one unit will lead to a reduction in similarity of less than 40%. The results reveal that the similarity metric is highly sensitive to the phase mask offset. Consequently, it becomes imperative to ensure the precise positioning of each phase mask to achieve accurate results.

In this section, the similarity is introduced as an evaluation parameter to assess positioning accuracy, and a convolution transmission model for the adjustable multi-pass cavity is established and used to investigate the influence of phase mask offset on the input light conversion effect. In conclusion, similarity is sensitive to the position shift of the phase mask, and it is important to accurately locate each phase mask. The position of the first phase mask is utilized as a reference to accurately locate other phase masks within one unit. Therefore, the location of the first-phase mask is crucial.

3. The Simulation of Fresnel Lens Array-Based Location Method

When positioning and adjusting the first phase mask, it can be achieved either directly by shifting or by utilizing a single Fresnel lens loading on the SLM. However, this process generates additional grayscale images to determine the adjustment direction, which increases the complexity and reduces the speed of mounting, and it is difficult to ensure positioning accuracy in this way. To address these challenges, we propose a novel design using a Fresnel lens array to replace the single Fresnel lens. This innovative approach offers the advantage of directly determining both the adjustment direction and the number of units to be adjusted through a single image acquisition and calculation, streamlining the installation process significantly.

Due to the limited focal length and phase mask size used in the simulation, the phase mask of the Fresnel lens array is composed of 2 × 2 small phase masks of Fresnel lenses, whose expression Ψ is expressed in matrix form as shown in Equation (9).

$$\psi =\left[\begin{array}{cc}{\phi }_f{}^{\prime }& {\phi }_f{}^{\prime }\\ {\phi }_f{}^{\prime }& {\phi }_f{}^{\prime }\end{array}\right]$$

(9)

Each ${{\phi }_f}^{\prime }$ represents the phase expression of the Fresnel lens shown in Equation (10)

$${\phi }_f{}^{\prime }=\frac{k}{2f}\left(x^2+y^2\right)$$

(10)

f is the focus distance of the Fresnel lens. In this part of the simulation, the focal length of the Fresnel lens f is 296.344 mm. The size of the complete Fresnel lens array is 400 units × 400 units, while each individual Fresnel lens measures 200 units × 200 units.

The Fresnel lens array needs to be loaded onto the SLM via the generated grayscale image, such as in Figure 6.

The size of the incident plane wave is 300 units × 300 units, and the transmission plane has a size of 1400 units × 1400 units. The dimensions of the incident light and phase mask are constrained by the rectangle function.

The simulation transmission process is divided into two main parts. Firstly, the incident tilted light is directed onto the phase mask-loaded Fresnel lens array, where it undergoes modulation. Secondly, the modulated beam transmits to the receiving focal plane. The transmission process is shown in Figure 7, and the simulation output beam is expressed as $A_1(x,y)$ in Equation (11).

$$A_1\left(x,y\right)=\left\{\left[e^{j\psi }·rect(\frac{x-x_0}{400})rect(\frac{y-y_0}{400})\right]·\left[e^{ikxsin(\theta )}·rect(\frac{x}{300})rect(\frac{y}{300})\right]\right\}\ast h_f$$

(11)

Ψ represents the phase distribution of the Fresnel lens array, $x_0$ and $y_0$ represent the number of units moved by the Fresnel lens array in the horizontal and vertical directions, which correspond to the X and Y axis directions in this section. This part represents the modulation performed by the Fresnel lens array on the phase mask. The next part represents tilted incident plane waves. $h_f$ represents the impulse response of the transmission process as shown in Equation (12).

$$h_f\left(x,y\right)=\frac{1}{j\lambda f}exp(jkf)exp\left[j\frac{k}{2f}\left(x^2+y^2\right)\right]$$

(12)

The intensity is defined as the energy of each unit, and the intensity of the output beam can be calculated as ${\left|A_1(x,y)\right|}^2$. The beam intensity distribution is 1400 units × 1400 units. According to the position of the output beam in the receiving plane, the intercepted image of 400 units × 400 units is shown in Figure 8, and divided into four 200 units × 200 units parts numbered 1–4.

When the values of $x_0$ and $y_0$ in Equation (13) are nonzero, the phase mask featuring the Fresnel lens array distribution is positioned off-center from the inclined incident beam center. As a result, the output beam experiences an offset, and the beam intensity distribution also changes. According to the results, the offset in the X and Y directions has partial symmetry; therefore, the X direction shift is analyzed here as an example.

When the offset of the Fresnel lens array changes from 200 units in the negative direction of the X-axis to 200 units in the positive direction of the X-axis, the curve can be further divided into five distinct parts.

When the offset of the Fresnel lens array is over 150 units in the negative direction of the X-axis and part of the right half of the Fresnel lens array intersects with the incident plane wave and undergoes modulation, the maximum intensity of parts 3 and 4 is proportional to the intersection size. Between 150 units and 50 units in the negative direction of the X-axis, the right half of the Fresnel lens array completely intersects with the incident plane wave, resulting in the maximum intensity of parts 3 and 4 in the output beam remaining at its peak value. When the offset ranges from 50 units in the negative direction of the X-axis to 150 units in the positive direction of the X-axis, the part of the intersection where the right half of the Fresnel lens array intersects with the incident plane wave drops off, resulting in a gradual decrease in the maximum intensity for parts 3 and 4 of the output beam. In a similar way, the intersection part, where the left half of the Fresnel lens array intersects with the incident plane wave, and the maximum intensity for parts 1 and 2 have a symmetry change with the right half, and parts 3 and 4 have a zero offset. These are shown in Figure 9.

Using the analysis method described above, we divide the analog output beam generated at each offset into four regions based on Figure 8. Subsequently, we calculate the maximum intensity of each region.

In each offset direction, we analyze the behavior of the output beam based on the changes in the maximum intensity of the spot. The four parts of the output beam can be divided into two groups, and each group exhibits the same offset curve.

We respectively simulated and investigated the impact of shifts in the Fresnel lens array in the X and Y directions, ranging from 200 units in the negative position to 200 units in the positive position, on the maximum light intensity of the four sections of the output beam. The results of this simulation are presented in the curve depicted in Figure 10.

When the Fresnel lens array intersects with the plane wave, the number of offset units on the two axes can be directly determined by analyzing the curve in the figure based on the maximum intensity values of the four regions. Subsequently, the position of the first phase mask can be directly determined.

From the position of the first-phase mask, the positions of the second and third-phase masks can be determined by the Fresnel lens. Although the Fresnel lens array can also be used in this procedure, it serves the same purpose as a single Fresnel lens with a more complex process.

In order to accurately determine the positions of the second and third phase masks, Fresnel lenses with focal lengths of $z_2+4z_0$, $z_2+2z_0$ and $z_2$ are individually loaded onto the first, second, and third phase masks. The centers of the resulting light spots on the receiving plane should align perfectly by adjusting the position of the second and third phase masks. The specific equivalent transmission scenario is depicted in the accompanying Figure 11.

The proposed method, which utilizes a Fresnel lens array as a phase mask adjustment technique, offers a significant advantage in terms of location speed. By utilizing a camera image and simple calculations, it allows for the direct determination of the direction and magnitude of the first phase mask displacement on the SLM. This method eliminates the need for time-consuming phase mask scanning during the positioning process. Moreover, this method ensures accurate positioning at the single-unit level of all three phase masks.

4. Experiment and Discussion

4.1. Fresnel Lens-Based Location Process for Phase Masks

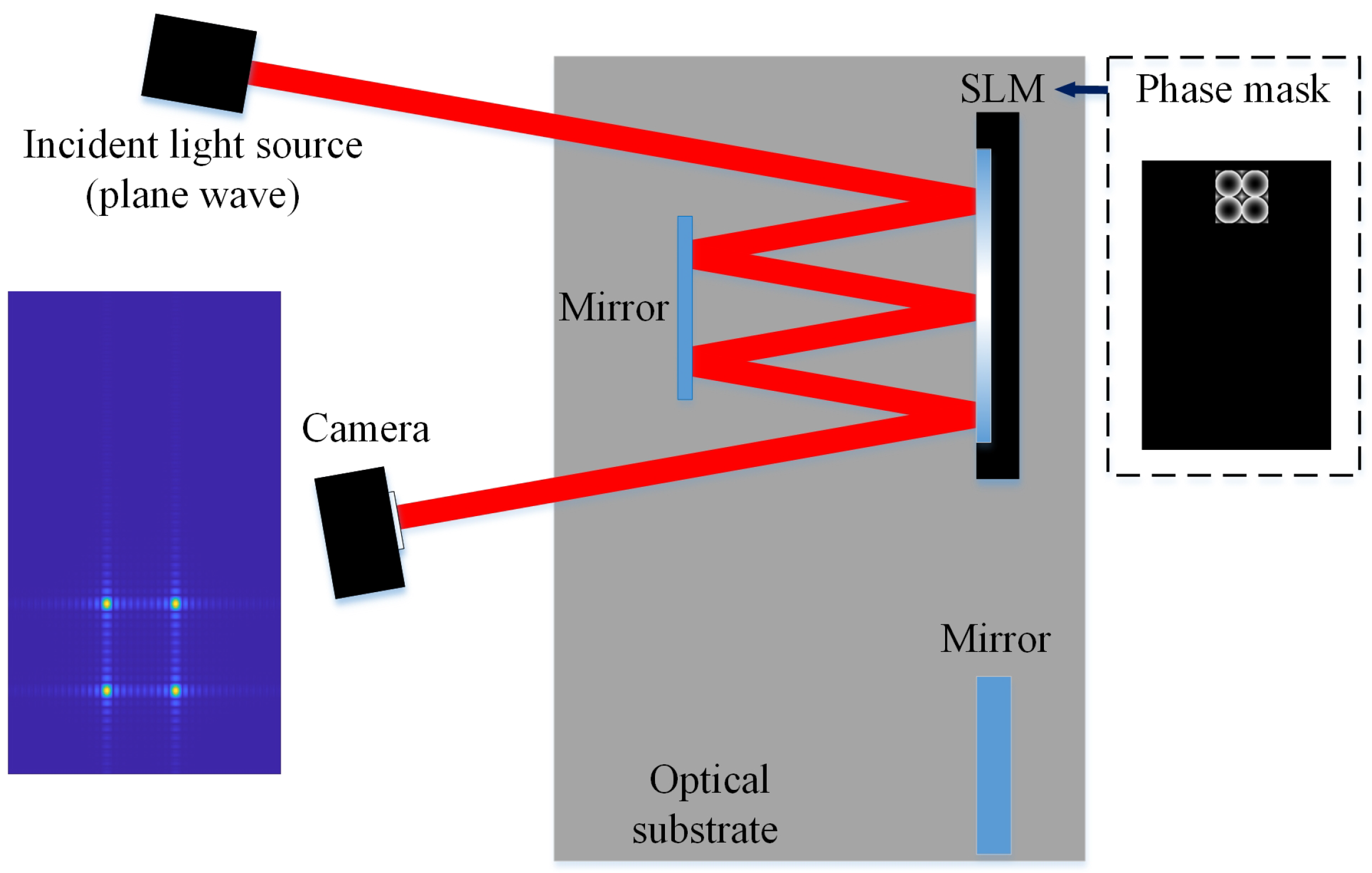
In this section, a positioning process that utilizes a Fresnel lens array loaded on SLM is provided for accurate placement of the adjustable multi-pass cavity phase mask. The following steps were implemented:

Firstly, an interferometer is used to detect fringes to ensure parallel alignment between the mirror and SLM within the multi-pass cavity. Simultaneously, the distance between the mirror and SLM is determined using a displacement transducer. The moving angle of the optical substrate is determined using an autocollimator. This process ensures that the incident beam is directed at a specified angle, facilitating precise alignment. The schematic diagram of the first step is shown in Figure 12.

Secondly, the alignment process involves the utilization of a Fresnel lens array loaded on the SLM. The incident light source uses an interferometer to add an aperture to generate a plane wave of a specified size. The incident plane wave is directed towards the camera target surface after applying the phase mask consisting of a Fresnel lens array onto the SLM. The displacement transducer is used to position the camera in a specified position. By utilizing camera software, the maximum intensity of the four parts is extracted from the received image. The obtained results are then utilized to calculate the required adjustment direction and amount. Subsequently, the system loads the calculated phase mask. The alignment process is considered complete when the maximum intensity of the four parts becomes equal, indicating the successful alignment of the first phase mask. The schematic diagram of the second step is shown in Figure 13.

Thirdly, a focal length corresponding Fresnel lens is introduced at the location of the first phase mask, causing the incident plane waves to converge on the camera as they pass through the Fresnel lens. The position of the resulting spot is recorded. Subsequently, the focal lengths of the Fresnel lenses of the second and third phase masks are generated and adjusted. The transverse and longitudinal positions of the output light spot are modified to achieve the recorded position, and the loading positions of the second and third phase masks are recorded at this stage. The schematic diagram of the third step is shown in Figure 14.

Finally, the three phase masks corresponding to the plane wave converted to Gaussian light are loaded at their respective positions. The output light is then fitted with a Gaussian distribution, and the similarity between the actual and ideal Gaussian beams is calculated to validate the effectiveness of the proposed method. The schematic diagram of the last step is shown in Figure 15.

The accuracy of the positioning method based on Fresnel lenses depends on the unit size of the SLM and the pixel size of the camera. The unit size of the SLM determines the precision achievable during phase modulation adjustment, while the pixel size of the camera determines the accuracy of data acquisition, including image acquisition and spot positioning. To maximize the adjustment accuracy, it is essential that the pixel size of the camera be smaller than the unit size of the SLM.

4.2. Experiment and Results

The experimental device in Figure 16 was constructed to verify the Fresnel lens-based location method. The position of the multi-pass cavity phase mask is determined by the aforementioned position steps. The key experimental parameters are listed in

Table 3. The key parameters in the experiment.

Parameter Type	Parameter Name	Value
Universal parameter	Wavelength	632.8 nm
	Incidence angle	θ = 5°; φ = 0
Multi-pass cavity parameter	Transmission distance between phase masks	59.677 mm
	Output transmission distance	177 mm
	Phase mask size	300 units × 300 units
	Number of phase masks	3
	Mirror size	12.7 mm × 12.7 mm
	Mirror reflectance	>99%

,

Table 4. The parameters of SLM (PLUTO NIR-015, Holoeye Photonics AG, Berlin/Heidelberg, Germany).

Parameter Name	Value
Wavelength range	600 nm–1100 nm
Active area	15.36 mm × 8.64 mm
Resolution (nominal)	1920 × 1080
Unit size	8 μm
Gray level	256 (2π)
Image frame rate	60 Hz

and

Table 5. The parameters of the camera (acA3800-14 μm, Basler, Germany).

Parameter Name	Value
Sensor Type	CMOS
Resolution	3840 pix × 2748 pix
Pixel size	1.67 μm × 1.67 μm
Frame rate	14 fps
Dynamic range (typical)	54 dB

. Ultimately, the positioning of phase masks is successfully finished.

Errors in angle parameters and distance parameters directly impact the conversion phase masks, leading to a reduction in the similarity value. Therefore, ensuring the precise adjustment of key parameters is important for the modulation of plane waves into Gaussian light. The accuracy of the displacement transducer used in this paper is 1 μm, and the accuracy of the autocollimator is 0.1 minute.

At each step of the Fresnel lens-based location method for phase mask in the MPLC adjustable multi-pass cavity, the corresponding spot images are obtained to show the positioning process.

The results of positioning the first phase mask through the Fresnel lens array are shown in Figure 17. All four light spots have the same maximum intensity value, which corresponds to the gray value of 132 in this figure. It indicates that the first phase mask has been positioned accurately.

In order to position the second and third phase masks accurately, we utilized the Fresnel lens in combination with relevant calculations. Specifically, each of the three-phase masks was loaded into its respective Fresnel lens, ensuring correct alignment. All images are presented in Figure 18. The centroid coordinates of the three spots are (830,898), (829,898), and (828,898). The centroid distances between the three spots are only two pixels of the camera, which is equivalent to 0.41 units of SLM. It means that this step shifts the three-phase masks to the optimal position by less than one unit.

At last, three-phase masks are loaded to convert the plane wave into a corresponding Gaussian beam with a waist radius of 300 μm. The received cropped image and its distribution are shown in Figure 19.

The fitting analysis is used to fit the spot image with a Gaussian shape. The waist radius of the spot is then determined as 313 μm based on the fitted Gaussian function. By employing Equation (4), we compare the image with an ideal Gaussian beam possessing a waist radius of 300 μm, yielding a similarity value of 93.44%, more than the target of 90.25%.

This section presents the specific experimental steps and the results of phase mask positioning experiments. The adjustable multi-pass cavity is initially installed using an interferometer, a displacement sensor, and an autocollimator. The positioning method based on the Fresnel lens array is then employed to precisely position the three-phase masks. Subsequently, the phase masks are loaded to evaluate the multi-pass cavity, and the similarity is calculated based on the output spot image. The experimental results demonstrate that the achieved similarity reaches 93.44%. These results validate the effectiveness of the method. Compared with the traditional positioning method, this method simplifies the procedure for scanning the phase masks on SLM, enhances the positioning speed, reduces the entire location process time to about two hours, and improves positioning accuracy within a single unit. The experimental results substantiate the advantages of this method in practical applications.

4.3. Discussion

We successfully positioned the MPLC phase mask based on the positioning method discussed above using the available experimental setup. The effectiveness of this positioning method is validated through the waist radius measurement and similarity calculation of the spot beam. However, it is important to acknowledge that certain factors, such as the diffraction caused by the diaphragm, the polarizer aberration, and the residual correction of SLM inherent aberration, will introduce deformations to the outgoing beam. These deformations affect the accuracy of the beam waist radius measurement and similarity calculation, leading to inaccurate positioning of the phase masks. Therefore, these factors require attention in simulations and experiments. In future studies, we will attempt various conversion phase masks and incident light sources to investigate the applicability of our method. By adjusting the parameters and corresponding simulations, the optimization method can be adapted to different application scenarios, and the range of applications of the method is broadened. Furthermore, we intend to use this method to maintain the accuracy of the adjustable MPLC equipment. In this way, the service life of adjustable MPLC equipment on the terminal can be extended.

5. Conclusions

This paper proposes a novel phase mask positioning method utilizing a combination of Fresnel lens arrays and single Fresnel lenses on the SLM. Firstly, we introduce similarity as an evaluation parameter to assess positioning accuracy and simulate the effect of phase mask offset on similarity, which shows the necessity of accurate location. Secondly, the simulation of our method is accomplished. We use the Fresnel lens array to locate the first phase mask, and single Fresnel lenses with appropriate focal lengths are used to position the remaining phase masks. The simulation results show that all phase masks are shifted by less than one unit to the optimal location. The evaluation phase masks that convert a plane wave to Gaussian light through three phase masks are loaded to calculate the similarity. The similarity results show that the positioning method is feasible in this case. Finally, an experimental scheme is designed to verify the correctness of the positioning method proposed. The experimental results demonstrate that the offset of three-phase masks is 0.41 units and the similarity of the output beam to the ideal beam reaches 93.44%, fulfilling the requirement of improving coupling efficiency in laser communication applications employing adjustable multi-pass cavities. Compared to the traditional positioning method, our method reduces the number of steps involved, improves the positioning speed, reduces the entire location process time to about two hours, and achieves accurate phase mask positioning.