Continuous-Variable Measurement-Device-Independent Quantum Key Distribution in the Terahertz Band

Abstract

We have introduced, for the first time, a protocol for Continuous-Variable Measurement-Device-Independent Quantum Key Distribution (CV-MDI-QKD) in the terahertz (THz) frequency band. We have conducted a secret key rate analysis against collective attacks. The proposed THz CV-MDI-QKD is immune to all detector attacks, significantly enhancing the security assurance of practical THz CVQKD implementations. Furthermore, we investigated the impact of finite key length (the finite-size effect) and finite reconciliation efficiency on the performance of practical THz CV-MDI-QKD systems. Our findings reveal that by employing a large number of keys or signals and optimizing the modulation variance, the detrimental effects arising from the finite-size effect and suboptimal reconciliation efficiency can be notably mitigated. These insights play a crucial role in advancing the feasibility of THz CVQKD technology towards practical applications.

1. Introduction

Quantum key distribution (QKD) enables the establishment of theoretically unconditionally secure keys between legitimate communicating parties, Alice and Bob [1,2], even in the presence of an eavesdropper (Eve) on the channel. Due to the substantial demand for secure communication, the development of quantum key distribution has rapidly progressed and entered practical stages [3,4]. QKD can be implemented using continuous-variable quantum systems (such as optical field quadratures) or discrete variable systems (such as discrete polarization or phase of light), known as CVQKD and DVQKD [5,6,7,8], respectively. Notably, the CVQKD protocol represented by GG02 does not require single-photon sources or detectors, making it compatible with existing optical communication devices and thus highly practical [9,10].

CVQKD has achieved significant progress in both theory and experiments [11,12,13,14,15,16]. In the theory of CVQKD, Ghorai S. et al. established a lower bound on the asymptotic secret key rate of CVQKD with a discrete modulation of coherent states in 2019 [11]. In 2019, Lin J. et al. analyzed the security of discrete-modulation protocols against collective attacks in the asymptotic limit [12]. In 2021, Liu W. B. et al. proposed a homodyne detection protocol using the quadrature phase shift keying technique which enhances excess noise tolerance to a high level [13]. In 2023, Kanitschar F. et al. presented a composable finite-size security proof against independently and identically distributed collective attacks for a general Discrete-Modulated CVQKD protocol [14]. And in an experiment, Zhang Y. et al. reported two different field tests of a CVQKD system through commercial fiber networks in Xi’an and Guangzhou over distances of 30.02 km (12.48 dB) and 49.85 km (11.62 dB) in 2019 [15]. In 2020, Zhang Y. et al. reported a 202.81 km optical fiber CVQKD experiment [16].

Terahertz (THz) waves generally refer to electromagnetic waves with frequencies ranging from 0.1 THz (wavelength 3000 μm) to 10 THz (wavelength 30 μm) [17,18,19]. Compared to free-space optical communication, THz waves are less affected by atmospheric conditions such as dust, smoke, fog, and turbulence [20,21,22,23,24], making THz QKD a subject of extensive scientific interest [25,26,27,28,29,30,31,32,33,34]. Due to the immature development of single-photon detectors in the THz range [35], THz CVQKD holds more promise for experimental verification compared to THz DVQKD [25,26]. Currently, there has been substantial research on THz CVQKD in both ground-based atmospheric environments [36] and space environments [37]. THz CVQKD achieves transmission distances of up to 200 m in ground-based atmospheric environments [38] and several hundred kilometers in space [39].

Although THz CVQKD is theoretically unconditionally secure, the imperfections in experimental devices, resulting in a mismatch between actual devices and ideal models, lead to gaps between practical THz CVQKD systems and ideal protocols. This exposes the security of practical THz QKD systems to significant challenges, as Eve can exploit the gaps between devices and theoretical models to launch attacks on the protocol. Among these attacks, attacks on detectors play a major role, including local oscillator attacks, wavelength attacks, detector blinding attacks [40,41,42,43,44], and so on. To address the security vulnerabilities of detectors of the practical THz CVQKD, inspired by optical-waveband measurement-device-independent (MDI) QKD [45,46,47,48,49], we introduce THz CV-MDI-QKD. MDI-QKD is a protocol immune to detector attacks, where Alice and Bob send unrelated quantum states to an untrusted third party, Charlie. Charlie measures the received quantum states and discloses the measurement results. Alice and Bob process their respective data based on the disclosed measurement results to obtain secure keys [48,49].

However, due to the unique characteristics of the THz range, where THz QKD key rates are significantly affected by noise photons generated by environmental temperature [27,28], the analysis results of the THz band are significantly different from those of the optical band. This paper presents the first theoretical analysis of THz CV-MDI-QKD and thoroughly investigates the relationship between the protocol’s key rate and transmission distance. Considering the finite-size effect in practical QKD systems is essential, as the number of keys (signals) sent by the practical system is finite, while theoretical analysis assumes infinite key length. The limited signal number leads to biases in estimating channel transmittance and excess noise between legitimate communicating parties in the practical QKD system, resulting in an overestimation of secure key rates and causing security vulnerabilities [50,51,52,53]. The solution involves estimating the channel transmittance and excess noise under adverse conditions for the practical THz CV-MDI-QKD system, in order to prevent the overestimation of secure key rates. We analyze the relationship between the THz CV-MDI-QKD key rate and transmission distance under the finite-size effect, aligning our analysis more closely with the operational state of the THz CV-MDI-QKD protocol. Additionally, due to the impact of limited reconciliation efficiency ($\beta <1$), the maximum secure transmission distance of THz CV-MDI-QKD keys decreases. Fortunately, we demonstrate that selecting optimal modulation variances can enhance both key rates and transmission distances.

In conclusion, this paper emphasizes the enhancement of security and practicality in THz CVQKD systems. Our proposed THz CV-MDI-QKD protocol addresses detector vulnerabilities in THz CVQKD. We also study optimal modulation variances in THz CV-MDI-QKD, which partially resolve the decrease in key transmission distance caused by finite reconciliation efficiency in practical THz CV-MDI-QKD systems. Our work contributes to advancing THz QKD towards practical applications.

2. THz Continuous-Variable Measurement-Device-Independent QKD Protocol

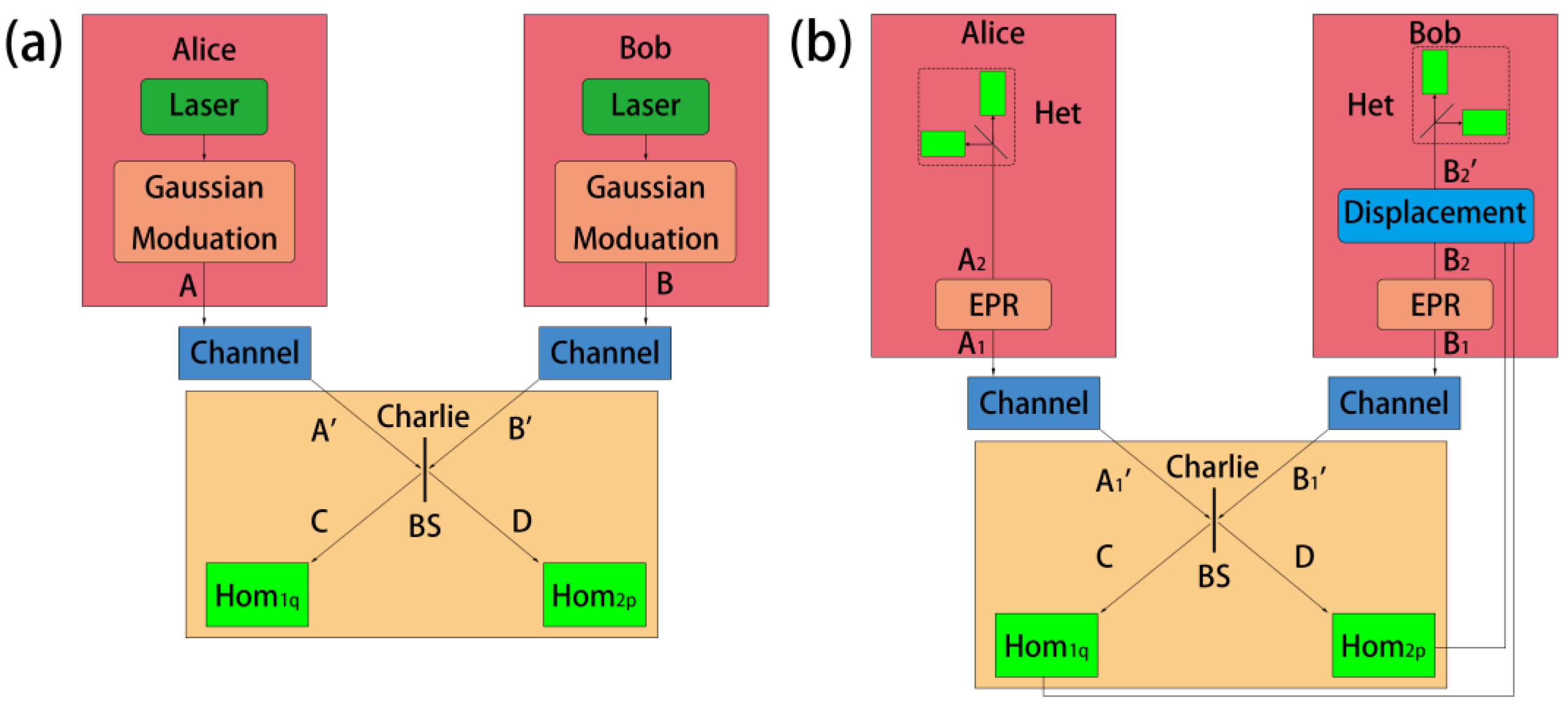
2.1. Basic Principles of THz CV-MDI-QKD

The prepare-and-measure (PM) model of THz CV-MDI-QKD is illustrated in Figure 1a. The protocol proceeds as follows: Alice (Bob) prepares $N$ Gaussian coherent states $|q_A+i{p}_A>$ ($|q_B+i{p}_B>$), where $q_A$ ($q_B$) and $p_A$ ($p_B$) are Gaussian distributions with modulation variances $V_{AS}$ ($V_{BS}$), and sends them through the quantum channel to Charlie. The state $|q_A+i{p}_A>$ is denoted as A, and the state $|q_B+i{p}_B>$ is denoted as B. The channel lengths are $L_{AC}$ (for Alice to Charlie) and $L_{BC}$ (for Bob to Charlie).

Upon receiving the coherent states from Alice and Bob, Charlie employs a 50:50 beam splitter (BS) to interfere with the received Gaussian states $A^{\prime }$ and $B^{\prime }$, creating two output modes, $C$ and $D$. Charlie then measures both the $q$-quadrature of mode $C$ and the $p$-quadrature of mode $D$ using homodyne detections (Hom) and subsequently announces the measurement results {$Q_C$, $P_D$} to Alice and Bob. Following this, Bob applies a displacement operation to his data, $Q_B=q_B+s{Q}_C$, $P_B=p_B-s{P}_D$, based on Charlie’s announced measurement results. In quantum optics, the displacement operator can shift a coherent state from one position in phase space to another, thereby obtaining another coherent state. Specifically, a coherent state is typically defined as a state obtained by applying the corresponding displacement operator to the quantum vacuum state. The amplification coefficient $s$ in the PM scheme is described as follows:

$$s=\frac{g}{\sqrt{\frac{V_B-V_0}{V_B+V_0}}},$$

(1)

where the variable $g$ represents the gain of the displacement. Meanwhile, Alice retains her data unchanged: $Q_A=q_A$, $P_A=p_A$.

When Alice and Bob gather sufficient correlated data, they perform parameter estimation through the public channel. Subsequently, through steps such as data reconciliation and privacy amplification, Alice and Bob can share a secure key.

As shown in Figure 1b, the entanglement-based (EB) model of CV-MDI-QKD is as follows: Alice (Bob) prepares $N$ entangled two-mode squeezed states (EPR states) with modulation variances $V_A$ ($V_B$). Keeping one mode $A_2$ ($B_2$), Alice (Bob) sends the other mode $A_1$ ($B_1$) to a third party, Charlie. Subsequently, Charlie combines two received modes ${A_1}^{\prime }$ and ${B_1}^{\prime }$ using a 50:50 BS and measures the $q$-quadrature of mode $C$ and the $p$-quadrature of mode $D$ with homodyne detections, publicly announcing the measurement results {$Q_C$, $P_D$} to Alice and Bob through classical channels.

Subsequently, Alice directly performs heterodyne detections on the retained mode $A_2$ to obtain the data {$Q_A$, $P_A$}. Bob applies a displacement operation $\widehat{D}\left(\beta \right)$ to mode $B_2$ and obtains ${\widehat{\rho }}_{{B_2}^{\prime }}=\widehat{D}\left(\beta \right){\widehat{\rho }}_{B_2}{\widehat{D}}^{†}\left(\beta \right)$, where ${\widehat{\rho }}_{B_2}$ represents the density matrix of mode $B_2$, $\beta =g(Q_C+i{P}_D)$. Then, Bob performs heterodyne detections to mode ${B_2}^{\prime }$ and obtains the data {$Q_B$, $P_B$}. Finally, Alice and Bob perform parameter estimation, data reconciliation, and privacy amplification on the measured data, ultimately sharing a secure key.

It has been proven that the PM model of CV-MDI-QKD is equivalent to the EB model of CV-MDI-QKD [48]. In quantum communication, the PM model is experimentally feasible, while the EB model is commonly used for theoretical analysis and security proofs. Therefore, for the security analysis of THz CV-MDI-QKD, we employ the EB model. In fact, if Bob’s EPR state preparation and displacement operation are untrusted, the EB scheme of CV-MDI-QKD is essentially equivalent to coherent-state-based one-way CVQKD with heterodyne detections [48,53].

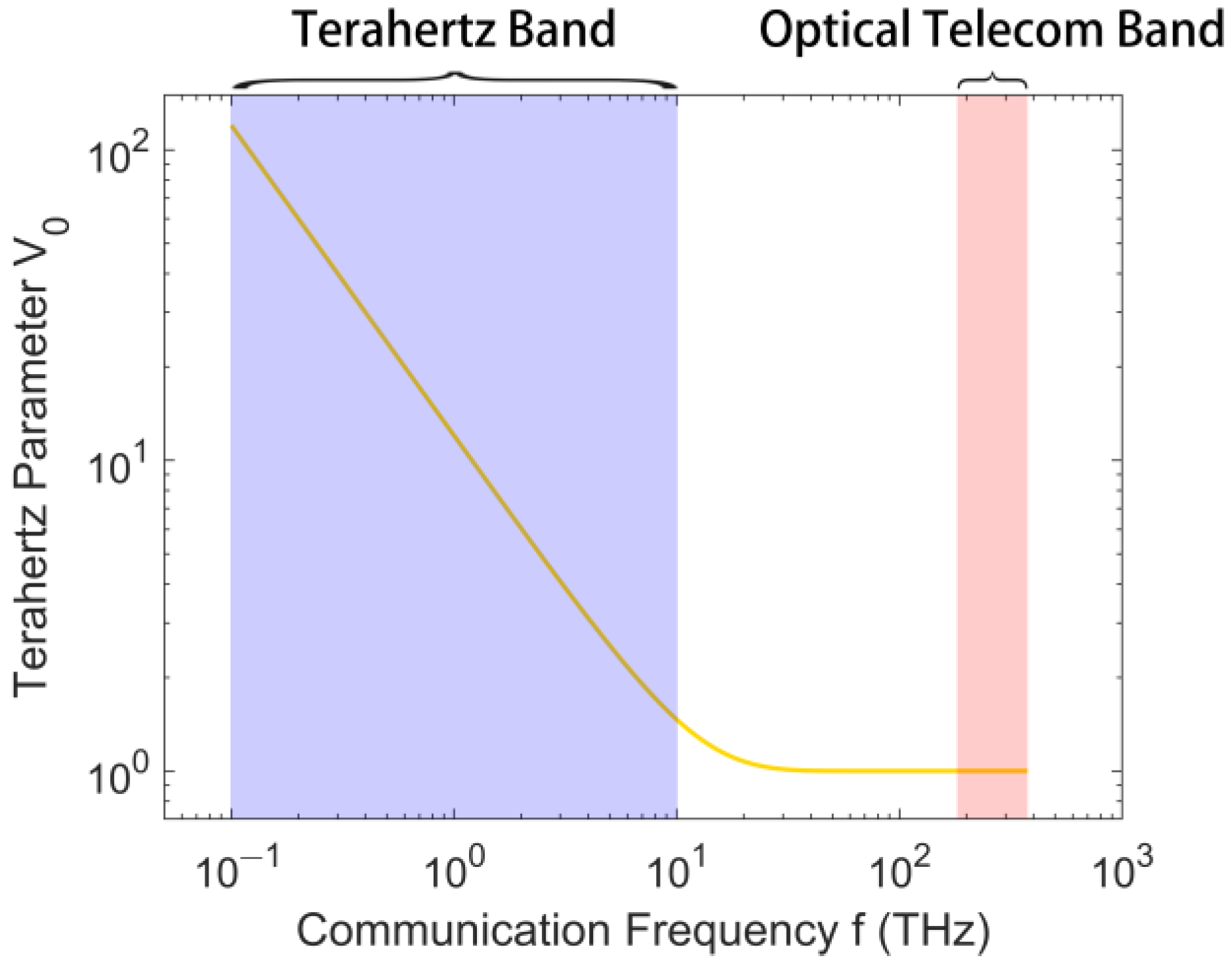
2.2. Terahertz Parameter

The key distinction between THz QKD and standard QKD lies in the fact that THz QKD cannot neglect the impact of thermal photon noise caused by environmental temperature. According to the blackbody radiation formula, the average number of noise photons $\overline{n}$ generated by temperature is:

$$\overline{n}=\frac{1}{e^{hf/k\tau }-1},$$

(2)

where $h$ represents the Planck constant, $\tau$ stands for temperature, $k$ denotes the Boltzmann constant, and $f$ represents communication frequency. It can be observed that, at the same temperature, a lower frequency $f$ corresponds to a larger $\overline{n}$. For instance, at a temperature of 288 K, with $f=300$ GHz, $\overline{n}$ is 19.5; for $f=1$ THz, $\overline{n}$ is 5.5; and for $f=193.5$ THz (wavelength of 1550 nm), $\overline{n}$ is ${10}^{-14}$.

The thermal noise variance $V_0$, which is called the ‘terahertz parameter’ [38], can be described using $\overline{n}$:

$$V_0=2\overline{n}+1.$$

(3)

The THz parameter $V_0$ plays a significant role in THz CV-MDI-QKD. When Alice (Bob) prepares coherent states $|q_A+i{p}_A>$ ($|q_B+i{p}_B>$), the modulation variance is $V_{AS}(V_{BS}$), but in reality, the overall variance of the coherent state is $V_A=V_{AS}+V_0(V_B=V_{BS}+V_0$). This is because environmental thermal noise photons introduce additional quantum shot noise on the modulated coherent state [28].

In the visible light range or near-infrared range (1550 nm), $\overline{n}$ is extremely small, and the parameter $V_0$ is assumed to be 1 SNU (Standard Noise Unit). Therefore, in optical research papers of CVQKD, the value of $V_0$ is usually set to 1 [48,54]. However, in the THz range, due to the non-negligible value of $\overline{n}$, $V_0$ in THz CVQKD is greater than 1. Therefore, special attention is required for this parameter, and it will severely impact the secure key rate of THz CV-MDI-QKD.

To provide a clearer illustration of how the THz parameter $V_0$ changes with frequency $f$ at room temperature (288 K), we have plotted Figure 2. It can be seen that in the optical range (the typical optical QKD band ranges from 800 nm to 1650 nm), $V_0$ approaches 1, while for the Thz band with lower frequencies, the numerical values of $V_0$ are larger than 1. A larger $V_0$ represents higher thermal photon noise, providing Eve with more opportunities to conceal her activities [27].

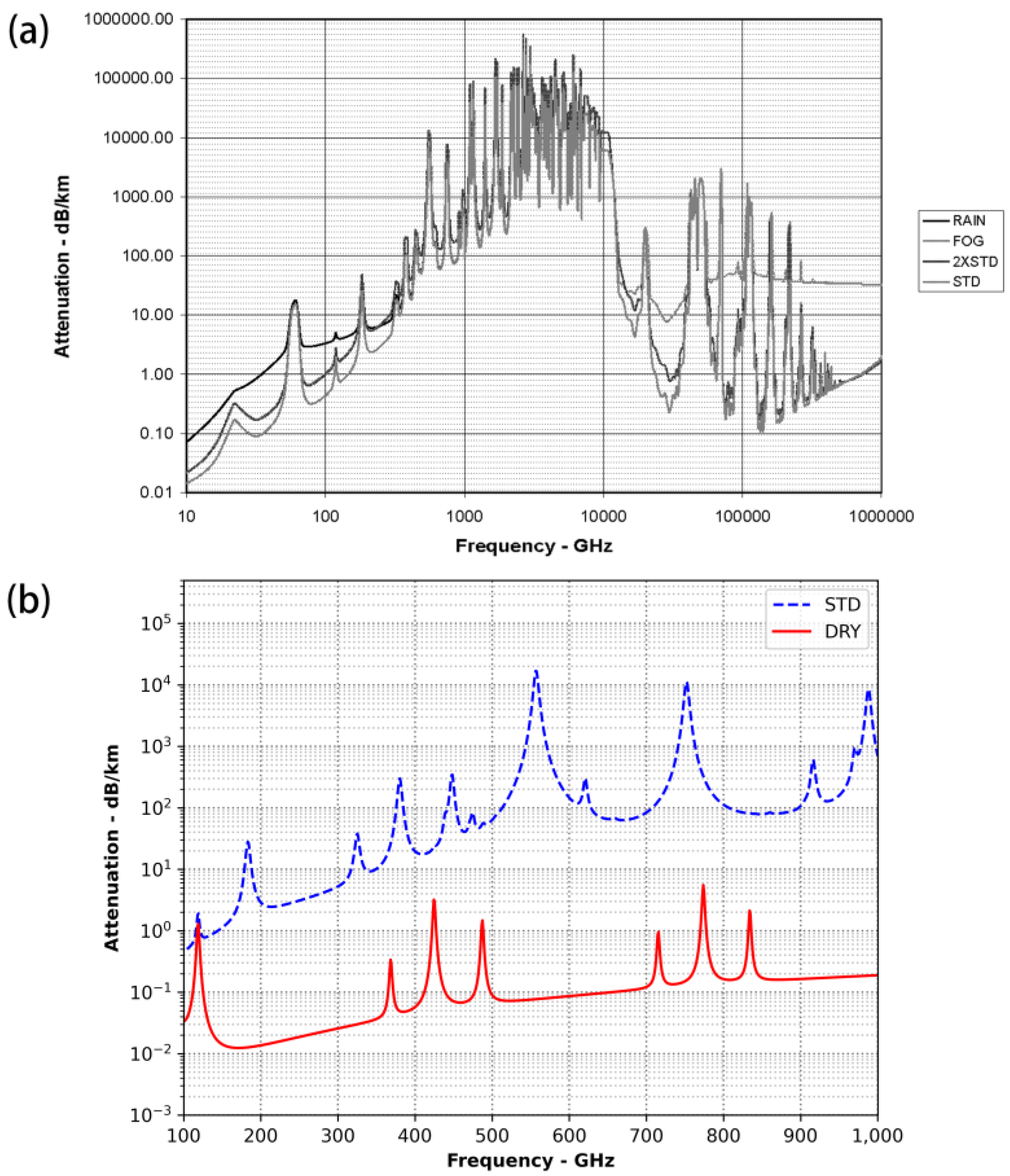
2.3. Channel Analysis for THz CV-MDI-QKD

The path loss experienced by the THz wave in the atmospheric environment is primarily due to three factors [55,56,57]: free-space path loss ($L_{FS}$), atmospheric molecular absorption loss ($L_{AL}$), and miscellaneous loss ($L_{ML}$). The miscellaneous loss is caused by the reflection and scattering of matter along the path and can usually be neglected in THz CVQKD. The free-space path loss ($L_{FS}$) can be expressed as:

$$L_{FS}=20lg\left(\frac{4\pi d}{\lambda }\right)-G_{TX}-G_{RX},$$

(4)

where $G_{TX}$ and $G_{RX}$ represent the gains of the transmitter and receiver antennas, respectively, and $\lambda$ is the wavelength. It can be observed that we can compensate for the signal loss caused by free-space path loss by adjusting the gains of the transmitting and receiving antennas. Consequently, in this paper, we will focus on the impact of atmospheric molecular absorption loss on THz CV-MDI-QKD systems.

The channel characteristics of THz CV-MDI-QKD are determined by the channel transmittance function $T$ and the channel excess noise $\xi$. The channel transmittance function $T$ is given by:

$$T=10^{-\frac{\alpha L}{10}},$$

(5)

where $\alpha$ represents the channel’s attenuation coefficient, with its primary contribution being atmospheric absorption loss, and $L$ denotes the transmission distance. In atmospheric channels, different frequencies are associated with distinct $\alpha$ values. Figure 3 provides the attenuation coefficients of electromagnetic waves at different frequencies under various atmospheric conditions.

This paper primarily focuses on the atmospheric attenuation coefficients corresponding to different THz frequencies under standard conditions. In this paper, we analyzed frequencies of 200 GHz (0.2 THz), 900 GHz (0.9 THz), and 10 THz, corresponding to $\alpha$ values of 1.2 dB/km, 100 dB/km, and 1000 dB/km, respectively [38]. Also, we analyzed 30 THz corresponding to $\alpha$ of 50 dB/km, which is often considered in extended THz QKD research [38].

In the THz CVQKD protocol, the noise in the channel from Alice to Charlie is represented as ${\chi }_1$:

$${\chi }_1=\left(1-T_1\right)/T_1+{\xi }_1,$$

(6)

where $T_1$ and ${\xi }_1$ are the transmittance and channel excess noise of the channel from Alice to Charlie, respectively.

Similarly, the noise in the channel from Bob to Charlie is represented as ${\chi }_2$, while $T_2$ and ${\xi }_2$ are the transmittance and excess noise of the channel from Bob to Charlie, respectively. In this paper, both ${\xi }_1$ and ${\xi }_2$ are set to 0.002.

It is important to note that the total channel of the THz CV-MDI-QKD system includes both the channel from Alice to Charlie ($L_{AC}$) and the channel from Bob to Charlie ($L_{BC}$). Upon the work of Li Z. Y. et al. in 2014 [48], the equivalent transmittance of the protocol channel needs to be calculated:

$$T=\frac{T_1}{2}{g}^2.$$

(7)

Additionally, the equivalent excess noise of the total channel in the THz frequency range is denoted as ${\xi }^{\prime }$:

$${\xi }^{\prime }=1+\frac{1}{T_1}\left[T_2\left({\chi }_2-1\right)+T_1{\chi }_1\right]+\frac{1}{T_1}{\left(\frac{\sqrt{2}}{g}\sqrt{V_B-V_0}-\sqrt{T_2}\sqrt{V_B+V_0}\right)}^2.$$

(8)

It should be noted that the THz parameter $V_0$ significantly affects ${\xi }^{\prime }$, yielding a different form of Equation (8) from that in the optical band [48].

To minimize the above equivalent excess noise, it is easy to derive the value of $g$ as:

$$g=\sqrt{\frac{2}{T_2}}\sqrt{\frac{V_B-V_0}{V_B+V_0}}.$$

(9)

According to Equation (9), the equivalent excess noise ${\xi }^{\prime }$ is given by:

$${\xi }^{\prime }={\xi }_1+\frac{1}{T_1}\left[T_2\left({\xi }_2-2\right)+2\right].$$

(10)

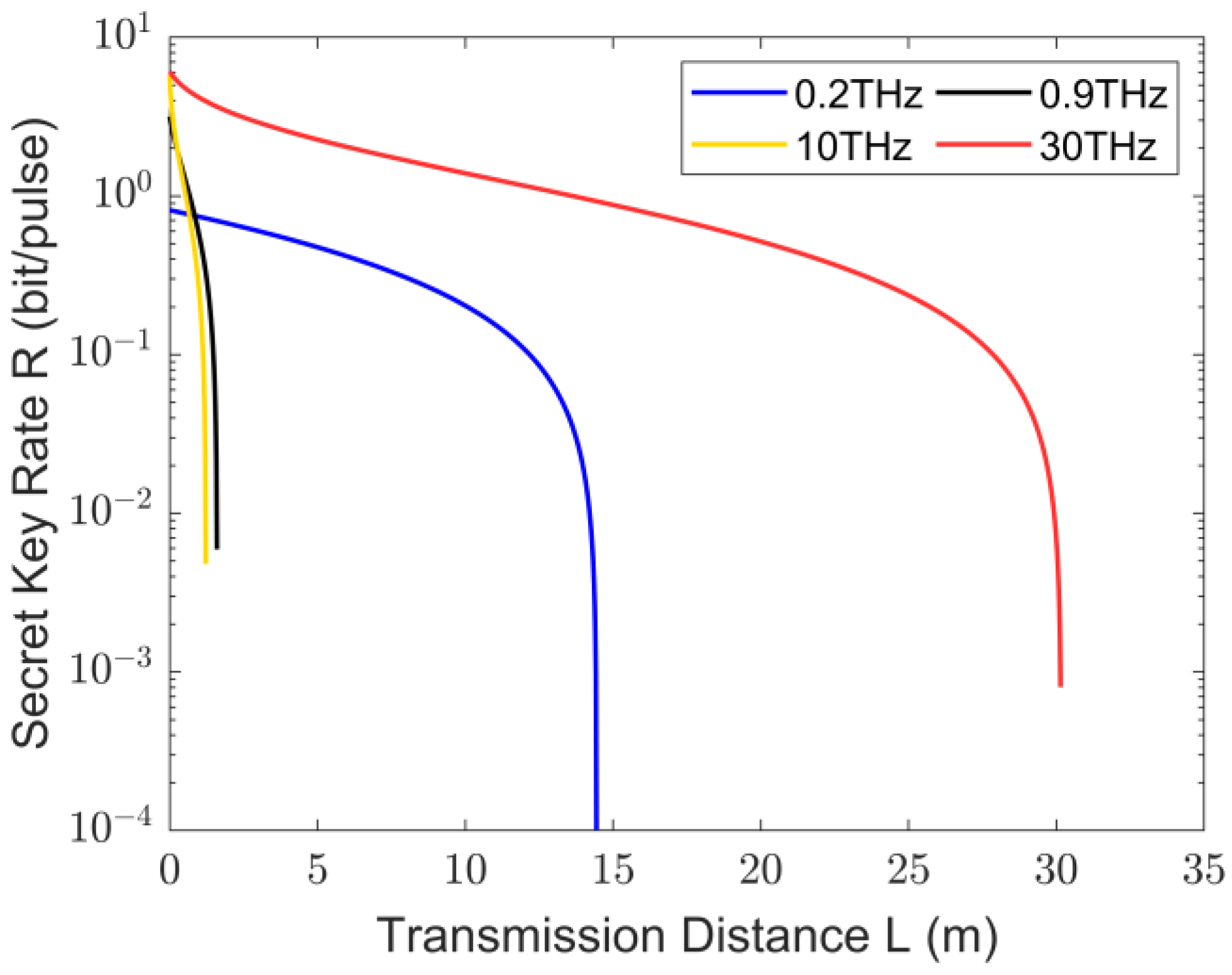
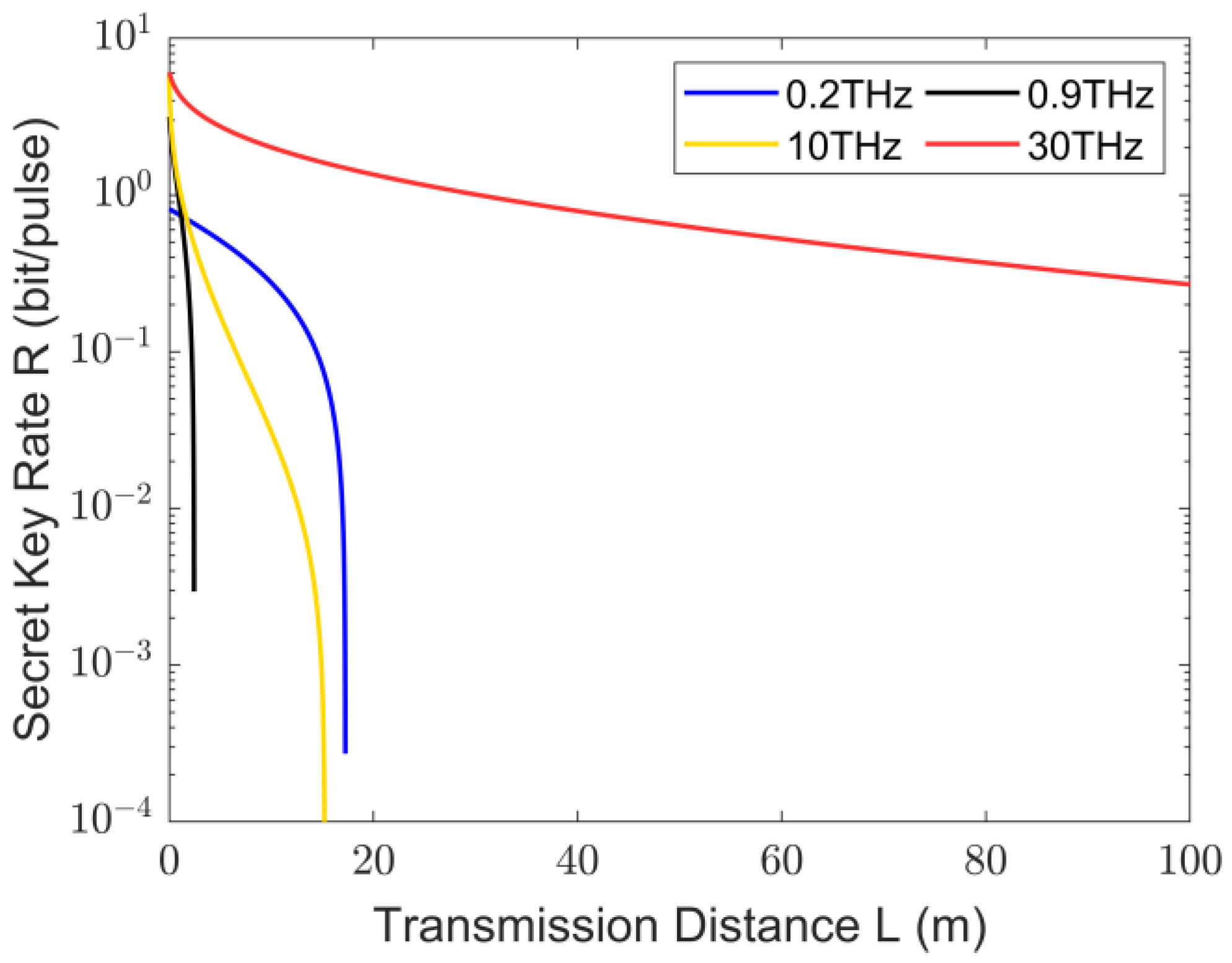
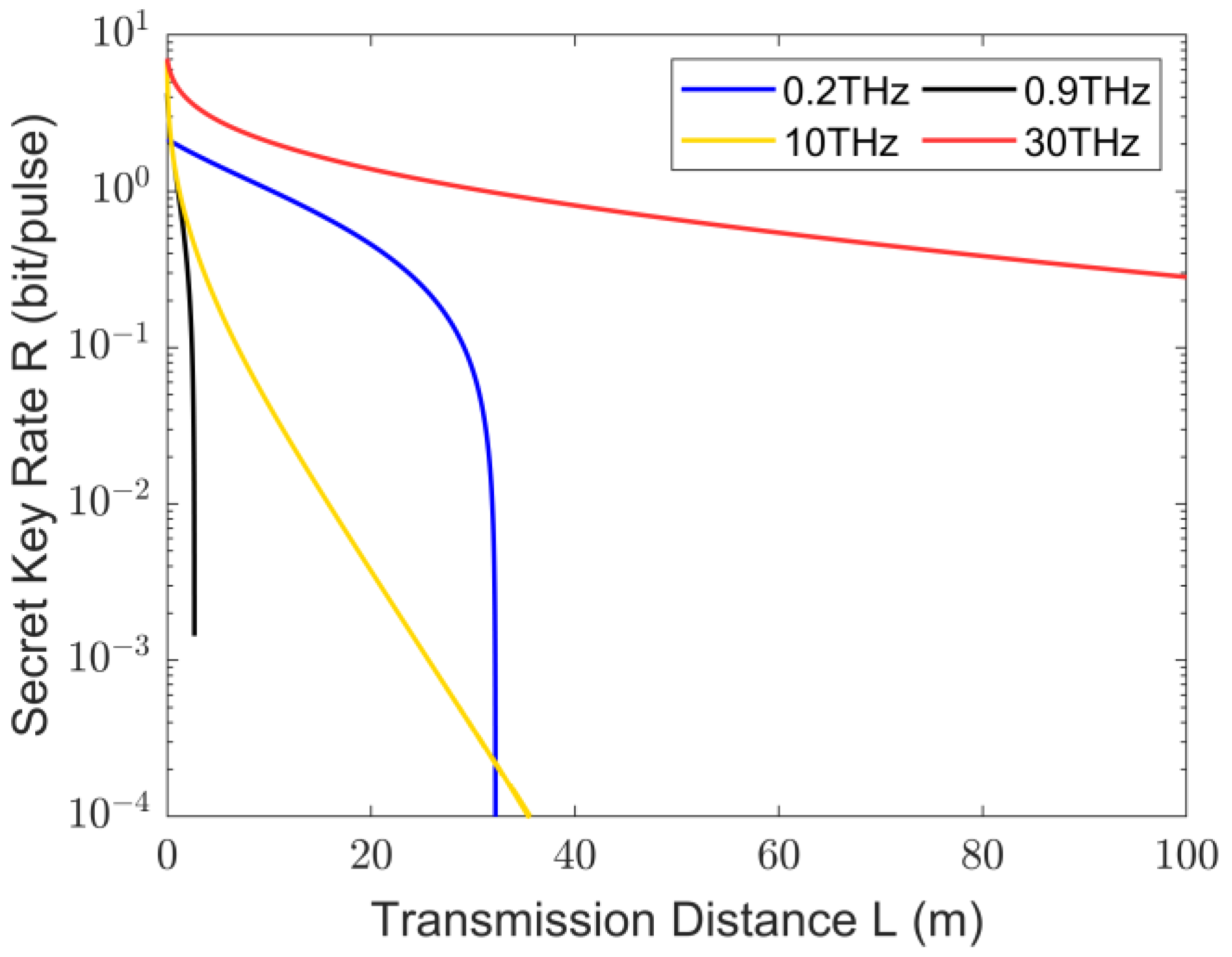
3. Analysis of Secure Key Rates for THz CV-MDI-QKD

Based on the EB model, we analyzed the relationship between the secure key rate and distance of THz CV-MDI-QKD under Gaussian collective attacks [61,62,63]. In the EB model, it is assumed that the channels from Alice to Charlie and from Bob to Charlie are subjected to two independent entanglement-cloning attacks. Charlie conducts the standard CV entanglement swapping process as required by the EB model. Therefore, the formula for the secure key rate of THz CV-MDI-QKD under Gaussian collective attacks is given by [54]:

$$R=\beta I\left(A:B\right)-S\left(B:E\right),$$

(11)

where $I(A:B)$ represents the mutual information between Alice and Bob, $\beta$ is the reconciliation efficiency in the post-processing, and $S(B:E)$ stands for the von Neumann entropy between Bob and Eve.

Next, we will analyze the specific forms of each term in Equation (11). It is worth noting that the THz parameter $V_0$ will significantly impact the two terms in Equation (11).

In the first part of Equation (11), the mutual information between Alice and Bob in THz CV-MDI-QKD is given by [28,48,53]:

$$I\left(A:B\right)={\mathit{log}}_2\left[\frac{T\left(V_A+\chi \right)+1}{T\left(V_0+\chi \right)+1}\right].$$

(12)

According to Williamson’s theorem [64], von Neumann entropy $S(B:E)$ is given by:

$$S\left(B:E\right)=G\left[\left({\lambda }_1-1\right)/2\right]+G\left[\left({\lambda }_2-1\right)/2\right]-G\left[\left({\lambda }_3-1\right)/2\right],$$

(13)

where $G\left(X\right)=\left(x+1\right){\mathit{log}}_2\left(x+1\right)-x{\mathit{log}}_{2}x$.

Specifically, in the first two terms of Equation (13), ${\lambda }_1$ and ${\lambda }_2$ are the symplectic eigenvalues of the covariance matrix ${\gamma }_{A_1{B_1}^{\prime }}$ between Alice and Bob [48]. The matrix ${\gamma }_{A_1{B_1}^{\prime }}$ is defined as:

$${\gamma }_{A_1{B_1}^{\prime }}=\left(\begin{array}{cc}aI& c{\delta }_z\\ c{\delta }_z& bI\end{array}\right),$$

(14)

where the symplectic eigenvalues ${\lambda }_1$ and ${\lambda }_2$ are:

$${\lambda }_{1,2}=\sqrt{\frac{1}{2}\left[a\pm \sqrt{a^2-4b^2}\right]}.$$

(15)

The values of the matrix elements in Equations (14) and (15) are as follows:

$$I=\left(\begin{array}{cc}1& 0\\ 0& 1\end{array}\right)\hspace{1em}{\delta }_z=\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right),$$

(16)

$$a=V_A=V_{AS}+V_0,$$

(17)

$$b=T\left(V_A+\chi \right)=t^2\left(V_{AS}+V_0-1\right)+{\delta }^2,$$

(18)

$$c=\sqrt{T\left({V_A}^2-1\right)}=t\sqrt{{\left(V_{AS}+V_0\right)}^2-1},$$

(19)

where the definitions of the channel transmittance coefficient $t$ and the variance of channel excess noise ${\delta }^2$ are given by:

$$t=\sqrt{T},$$

(20)

$${\delta }^2=1+T{\xi }^{\prime }.$$

(21)

For the eigenvalues ${\lambda }_3$ in Equation (13), considering the essence of the EB model of THz CV-MDI-QKD and its equivalence to coherent-state-based heterodyne detection CVQKD [48,53], we can derive:

$${\lambda }_3=a-c^2/\left(b+1\right).$$

(22)

Combining Equations (11)–(13), (15) and (22), we can calculate the secure key rate for THz CV-MDI-QKD.

Finally, it can be observed that in previous optical QKD research [48,54], all the $V_0$ mentioned above were directly replaced with the number 1, resulting in significant distinctions with THz QKD. In conclusion, the THz QKD and optical QKD theories have significant differences because of the THz parameter $V_0$.

As depicted in Figure 4, we show the secure key rates $R$ of THz CV-MDI-QKD with the transmission distance $L$ at different THz frequencies. In this case, we consider the scenario where both channels have equal lengths, i.e., $L_{AC}=L_{BC}$, resulting in a total channel length of $L=L_{AC}+L_{BC}$. The reconciliation efficiency $\beta$ is set to 1, and the modulation variances $V_{AS}=V_{BS}=\mathrm{100,000}$.

Another important scenario arises when Charlie’s interferometric measurement setup is placed adjacent to Bob’s. In this case, $L_{BC}=0$, indicating that the total channel length is $L=L_{AC}$. The key rates and transmission distances for different THz frequencies of CV-MDI-QKD in this case are shown in Figure 5.

Comparing Figure 4 and Figure 5 reveals that the transmission distance of THz CV-MDI-QKD is significantly longer when Charlie’s interferometric measurement setup is placed adjacent to Bob than that in the case of equal-length channels. In practical applications, this asymmetric arrangement of THz CV-MDI-QKD can be leveraged to enhance the key rate and secure the transmission distance.

To illustrate the differences between THz CVQKD and THz CV-MDI-QKD, we present the key rates and transmission distances of THz CVQKD in Figure 6. Considering the equivalence of MDI-QKD and the coherent-state heterodyne detection CVQKD (with reverse reconciliation) [48], we selected the reverse reconciliation coherent-state heterodyne detection THz CVQKD for comparison.

The important parameters for them are the same: $L_{BC}=0$; the reconciliation efficiency $\beta =1$; the modulation variance $V_{AS}=V_{BS}=\mathrm{100,000}$; and frequencies of 0.2 THz, 0.9 THz, 10 THz, and 30 THz.

By comparing Figure 5 and Figure 6, we can conclude that THz CV-MDI-QKD offers lower distance but higher security, whereas THz CVQKD provides greater distance at the cost of lower practical security. This is due to the design of the MDI protocol; the communication between Charlie and Bob inevitably introduces extra quantum noise, resulting in a reduction in the secure key rate.

4. The Finite-Size Effect and Suboptimal Reconciliation Efficiency for THz CV-MDI-QKD

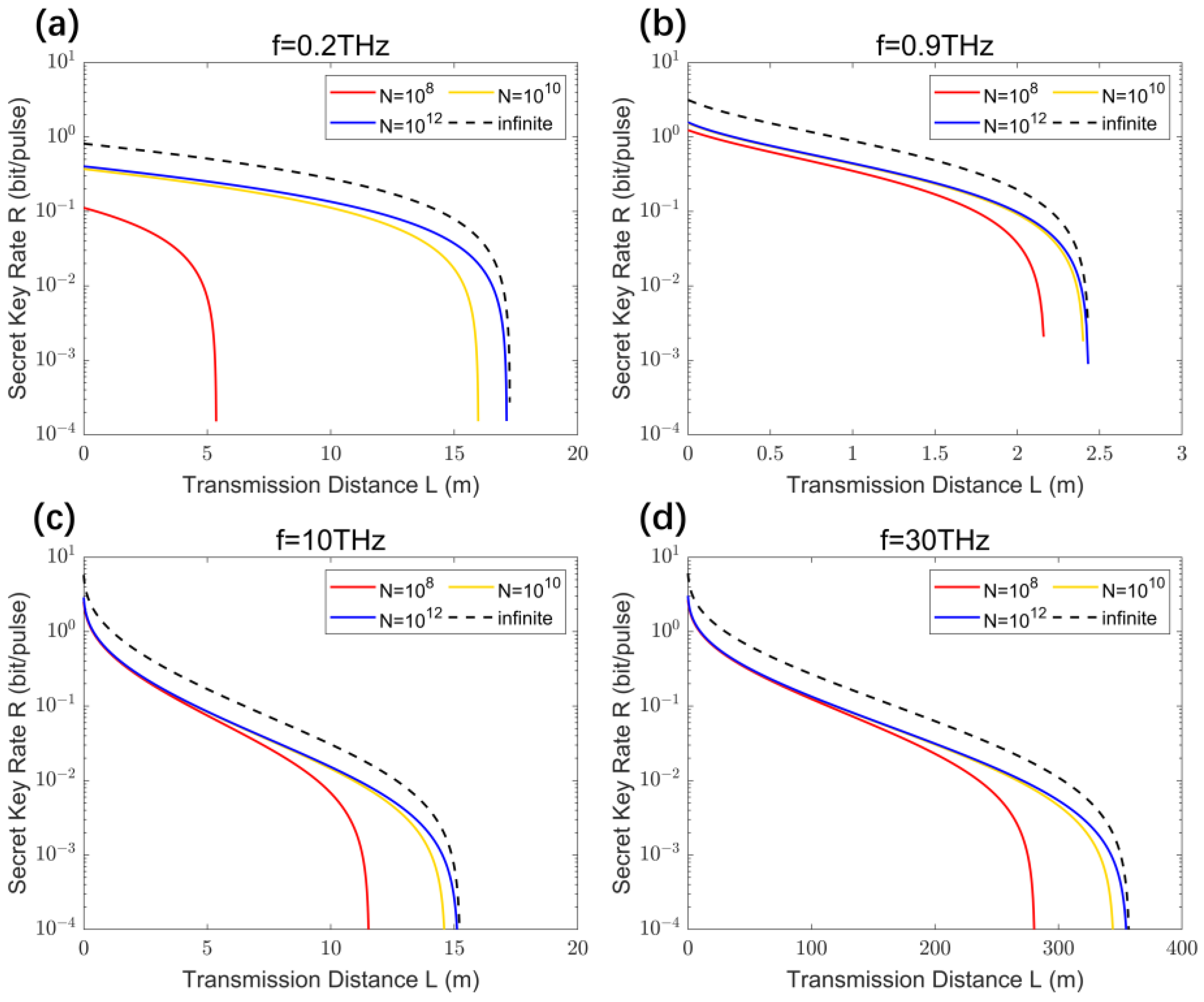
4.1. Impact of the Finite-Size Effect

The preceding section analyzed the theoretical model and theoretical transmission efficiency of THz CV-MDI-QKD under collective Gaussian attacks, assuming an infinite amount of data. However, in practical QKD systems, the number of transmitted keys and the amount of data employed by both Alice and Bob for parameter estimation are finite. To bring the analysis of the THz CV-MDI-QKD protocol closer to practical scenarios, in this section, we delve into the discussion of the relationship between key rate and transmission distance in THz CV-MDI-QKD under the finite-size effect [50]:

$$R=\frac{n}{N}\left[\beta I\left(A:B\right)-S_{{ϵ}_{PE}}\left(B:E\right)-\Delta \left(n\right)\right],$$

(23)

where $N$ represents the total length of data exchanged between the communicating parties; $n=N-m$, where $m$ signifies the data length used for estimating the parameters $t$ and ${\delta }^2$ mentioned earlier. In this study, $m$ is set to be half of $N$. Actually, the values of $N$ and $m$ are always finite. Consequently, the estimation of $t$ and ${\delta }^2$ through limited samples is not accurate, leading to incorrect assessments of the amount of information Eve can potentially intercept, resulting in security vulnerabilities.

Therefore, it is necessary to adjust the conditional entropy $S(B:E)$ in Equation (11) to $S_{{ϵ}_{PE}}(B:E)$, which, considers the probability of errors occurring during the parameter estimation process. The ${ϵ}_{PE}$ is the failure probability of parameter estimation, with ${ϵ}_{PE}$ taking ${10}^{-10}$. The adjustment approach involves estimating parameter $t$ with a minimum value assumption and estimating parameter ${\delta }^2$ with a maximum value assumption, thus correcting the impact of the finite-size effect on the key rate.

Specifically, it is necessary to adjust Equations (20) and (21) by substituting $t$ with $t_{min}$ and ${\delta }^2$ with, respectively:

$$t_{\mathit{min}}=\sqrt{T}-Z_{{ϵ}_{PE}/2}\sqrt{\frac{{\delta }^2}{{mV}_{AS}}},$$

(24)

$${\delta }_{\mathit{max}}^2=1+T{\xi }^{\prime }+Z_{{ϵ}_{PE}/2}\frac{\sqrt{2}{\delta }^2}{\sqrt{m}},$$

(25)

where $Z_{{ϵ}_{PE}/2}$ is $2-erf\left(0.5Z_{{ϵ}_{PE}/2}\right)={ϵ}_{PE}$, and when ${ϵ}_{PE}$ takes ${10}^{-10}$, its value is about 6.5.

And the third part of Equation (23) $\Delta \left(n\right)$ is related to the security of private key amplification:

$$\Delta \left(n\right)=\left(2{\mathit{dimH}}_X+3\right)\sqrt{\frac{{\mathit{log}}_2\left(2/\overline{ϵ}\right)}{n}}+\frac{2}{n}{\mathit{log}}_2\frac{1}{{ϵ}_{\mathit{PA}}},$$

(26)

Among them, $H_x$ represents the Hilbert space corresponding to the variable $x$ used in the original key, and the value of $dim{H}_x$ is 2.

The post-processing procedure of THz CV-MDI-QKD comprises three stages, namely parameter estimation, data reconciliation, and privacy amplification. The global security parameters for these three stages are defined as follows:

$$ϵ={ϵ}_{PE}+{ϵ}_{EC}+\overline{ϵ}+{ϵ}_{PA},$$

(27)

Among them, ${ϵ}_{PE}$ is the failure probability of parameter estimation, ${ϵ}_{EC}$ represents the probability of data reconciliation failures, $\overline{ϵ}$ is a smoothing parameter, and ${ϵ}_{PA}$ represents the failure probability of the privacy amplification procedure. The post-processing procedure is essentially a data processing step and is unrelated to the wavelength in the communication process. Therefore, when discussing the finite-size effects of CVQKD [41,50] and THz CVQKD [30], optimized parameters can be applied. In this paper, ${ϵ}_{PE}$, ${ϵ}_{EC}$, $\overline{ϵ}$, and ${ϵ}_{PA}$ are all taken as ${10}^{-10}$, which is consistent with other related works.

The relationship between the key rate and distance of THz CV-MDI-QKD under the finite-size effect calculated according to Equation (23) is shown in Figure 7. For the convenience of comparison, we set the important parameters in Figure 7 to be consistent with Figure 5, namely $L_{BC}=0$ (Charlie’s measuring equipment is placed at Bob’s end), modulation variance $V_{AS}=V_{BS}=100000$, and coordination efficiency $\beta =1$. We investigated the relationship between the CV-MDI-QKD key rate and transmission distance under four different THz frequencies (values of 0.2 THz, 0.9 THz, 10 THz, and 30 THz, respectively) at different data lengths.

From Figure 7, it can be seen that due to the finite-size effect, the secure key rate of the system decreases compared to the case where $N$ is infinite, as shown by the black dashed line (as shown in Figure 5). Therefore, the finite-size effect cannot be ignored in THz CV-MDI-QKD. Of course, it can also be seen that when the $N$ value reaches ${10}^{12}$, the protocol key rate and the farthest transmission distance are close to the infinite data length, which is also the reason why many QKD experimental systems have key lengths ranging from ${10}^{12}$ to ${10}^{14}$ [4,16].

4.2. Impacts of the Reconciliation Efficiency

The previous discussion was based on the case of the reconciliation efficiency $\beta =1$. Considering that the reconciliation efficiency of the practical QKD system is generally less than 1, we set the reconciliation efficiency $\beta =0.96$ in Figure 8, and the secure key rate of THz CV-MDI-QKD under the finite-size effect varies with signal number $N$ and transmission distance $L$. The important parameters are the same as in Figure 7, except for the reconciliation efficiency.

Comparing Figure 7 and Figure 8, it can be seen that when $\beta$ is less than 1, the secure key rate $R$ and transmission distance $L$ of THz CV-MDI-QKD are reduced regardless of whether the finite-size effect is considered. Therefore, improving the reconciliation efficiency is of great significance for practical THz CV-MDI-QKD systems.

Please note that in Figure 8a, the red curve’s disappearance signifies that under conditions of limited reconciliation efficiency and a room-temperature atmospheric environment, and taking finite-size effects into account for $N={10}^8$, achieving secure 0.2 THz CV-MDI-QKD becomes unattainable. This is primarily due to the substantial influence of statistical errors on parameters like channel transmittance and excess noise when the data length is insufficient. Fortunately, when the data length is scaled up to $N={10}^{10}$, the 0.2 THz CV-MDI-QKD protocol can operate effectively and facilitate secure key transmission, as illustrated by the yellow curve in Figure 8a.

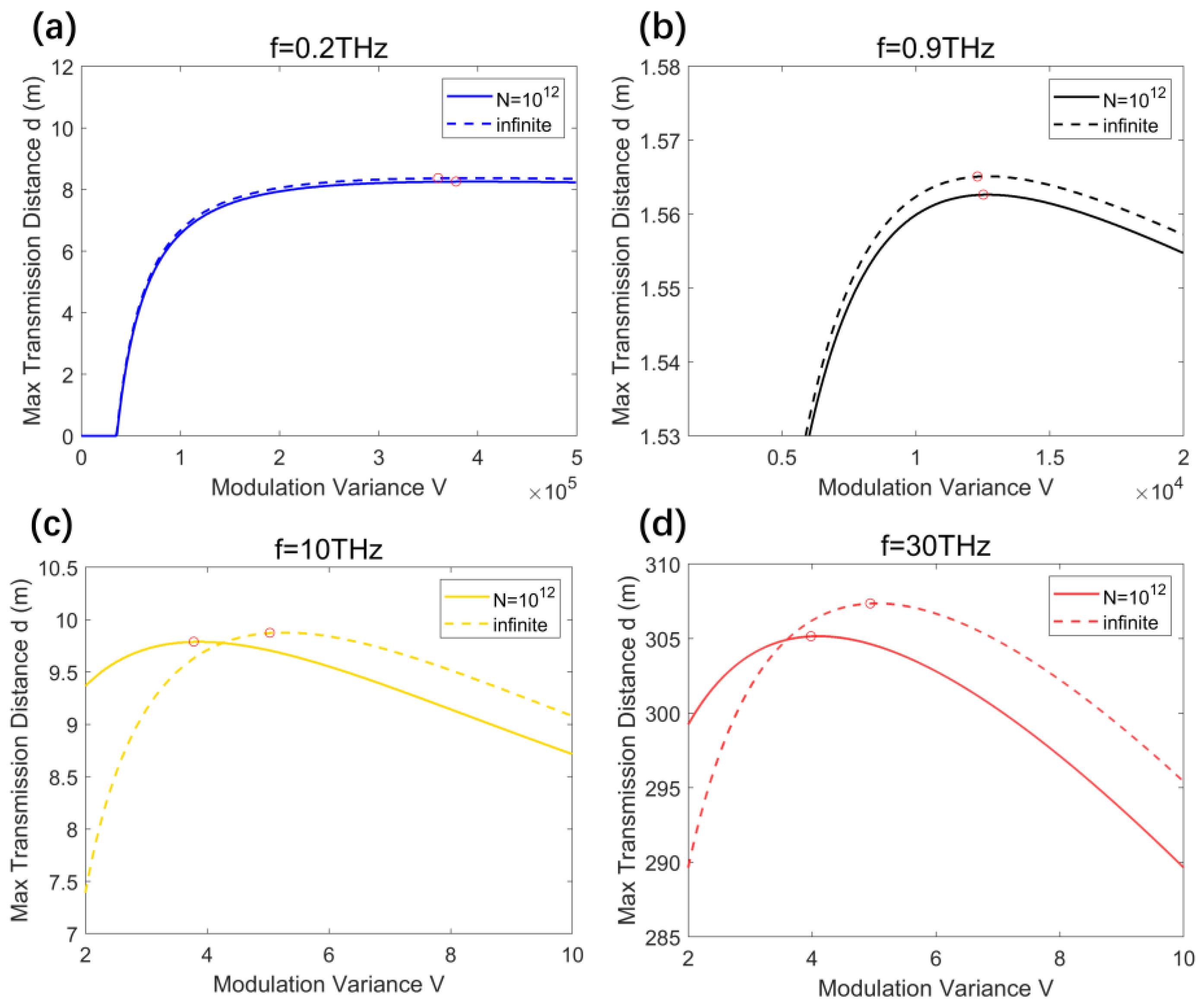
4.3. Optimal Modulation Variances

Although many studies have improved the reconciliation efficiency $\beta$, the efficiency in practical CVQKD systems still remains below 1 [4,65]. To address the issue of suboptimal reconciliation efficiency $\beta$ causing a decrease in key rate and transmission distance in THz CV-MDI-QKD, we investigated the relationship between modulation variances and transmission distances. In CVQKD experiments, the values of $V_{AS}$ and $V_{BS}$ can be adjusted according to practical considerations [16,66]. In THz CVQKD, when $\beta =1$, larger values of modulation variance for both Alice and Bob lead to higher key rates. Therefore, we set the default modulation variance to 100,000 in the case of $\beta =1$.

However, when the reconciliation efficiency is less than 1, larger modulation variances do not necessarily yield better results. Referring to Equation (23), we studied the impact of different modulation variance values on the farthest secure transmission distance under the conditions of $N={10}^{12}$ and $N$ approaching infinity, with $L_{BC}=0$ and modulation variance values ${V=V}_{AS}=V_{BS}$. As shown in Figure 9, each subgraph displays the farthest transmission distances changes with different modulation variances for different THz frequencies, with the red circles indicating the extremum points of the respective curves. The farthest transmission distance refers to the distance at which the protocol’s key rate becomes zero, signifying that beyond this distance, the THz CV-MDI-QKD protocol will be unable to generate a secure key.

Based on Figure 9, we determined the optimal modulation variances for different THz frequencies at $N={10}^{12}$ and when $N$ approaches infinity. We selected the optimal modulation variances and default modulation variances for various THz frequencies to depict the relationship between the secure key rate and transmission distance, as shown in Figure 10. The solid lines represent the comparison of key rate variation with transmission distance between the default and optimal modulation variance conditions when $N={10}^{12}$. Correspondingly, the dashed lines represent the comparison of key rate variation with transmission distance between the default and optimal modulation variance conditions when $N$ approaches infinity.

For practical THz QKD systems, achieving $V_{AS}$($V_{BS}$) values exceeding 10,000 in experimental implementations is challenging. Therefore, when considering scenarios at 0.2 THz and 0.9 THz, the choice of modulation variance must take into account the constraints of practical conditions.

By comparing the variations in key rates under these two conditions, it can be observed that THz CV-MDI-QKD with the optimal modulation variance achieves a greater maximum transmission distance. As depicted in Figure 10a,b, employing the optimal modulation variances has a positive impact on extending the maximum transmission distance for frequencies of 0.2 THz and 0.9 THz. From Figure 10c,d, it is evident that using the optimal modulation variances significantly improves the extension of the maximum transmission distance for frequencies of 10 THz and 30 THz.

Additionally, in Figure 10, the maximum transmission distances achieved after optimizing the modulation variances align with the optimization outcomes obtained by selecting the optimal modulation variances for different THz frequencies, as shown in Figure 9. From the analysis in this section, it is apparent that careful planning is necessary when determining the modulation variance for practical THz CV-MDI-QKD systems.

4.4. Low-Temperature THz CV-MDI-QKD

The theoretical analysis of CVQKD is primarily based on large modulation variances ($V_S=\mathrm{100,000}$ [41,48], $V_S=1000$ [30]). The practical modulation variances reported in CVQKD experimental work are typically around 40 [67,68,69]. Based on the previous analysis, it is evident that the optimal modulation variances for 0.2 THz and 0.9 THz CV-MDI-QKD are much greater than 100, making experimental implementation quite challenging. This situation can be addressed through cryogenic methods.

Figure 11 illustrates that even when not using the optimal modulation variances, and instead using typical modulation variances, the asymmetric scheme of THz CV-MDI-QKD can transmit over several meters. At a temperature of 18.6 K, the optimal modulation variance for 0.2 THz CV-MDI-QKD is 481. As shown in Figure 11a, when the modulation variance ($V$) is set to 30 and $N={10}^{12}$, a transmission distance of 15 m can be achieved. At a temperature of 77 K, the optimal modulation variance for 0.9 THz CV-MDI-QKD is 364. As depicted in Figure 11b, with a modulation variance of 30 ($V=30$) and when $N={10}^{12}$, a transmission distance of 2 m is attainable.

5. Discussion

We investigated the relationship between the key rate and transmission distance of THz CV-MDI-QKD at four different THz frequencies in atmospheric environments. We found that in the asymmetric configuration (with Charlie’s detection setup placed adjacent to Bob’s end), the protocol achieves longer key transmission distances.

Considering the finite-size effect in practical THz CV-MDI-QKD systems, we studied the impact of different numbers of signals on the key rate. Furthermore, in the context of practical THz CV-MDI-QKD systems, the issue of reconciliation efficiency being less than 1 greatly affects the key rate and transmission distance. We have demonstrated that by searching for the optimal modulation variance, the protocol’s transmission distance can be significantly extended.

It is worth noting that the THz CV-MDI-QKD proposed here primarily addresses vulnerabilities in the detection equipment. Addressing deficiencies at the source end can be achieved through the CV source-device-independent (SDI) QKD protocol [70]. However, the THz CV-SDI-QKD protocol frequency range still requires further research and exploration.

5.1. Compared with Optical QKD

Optical QKD has seen rapid development [9,10,48], and THz QKD has also garnered significant attention from researchers [35,38,39]. In comparison to optical QKD, THz waves exhibit a reduced susceptibility to atmospheric factors, such as dust, smoke, fog, and turbulence (scintillation) [20,21,22,23,24]. These atmospheric conditions pose challenges for optical QKD but can be effectively addressed by THz QKD, thereby enhancing the reliability of secure communication systems. It is worth noting that THz QKD faces its own challenges, as it is more sensitive to environmental noise photons and experiences significant atmospheric attenuation. Therefore, THz QKD is better suited for short-distance secure communication scenarios.

In addition, the space environment offers unique advantages for THz QKD, as it is free from atmospheric losses and features lower temperatures, enabling long-distance THz QKD over hundreds of kilometers [39].

5.2. Experimental Implementation of THz CV-MDI-QKD

This paper primarily focuses on a theoretical analysis and numerical simulation for the THz CV-MDI-QKD. The required experimental instruments for THz CV-MDI-QKD are similar to those for THz CVQKD (as outlined in ref. [30]). Of course, the arrangement of these experimental instruments should adhere to the PM model, as depicted in Figure 1. These instruments mainly include THz light sources, THz detectors, as well as THz intensity and phase modulators.

The advancement of THz CV-MDI-QKD experimental systems requires several key aspects of work:

• Advances in the main components of THz QKD, which encompass THz light sources, THz detectors, and THz intensity and phase modulators, are expected to significantly promote the development of THz QKD technology.
• The maturity of THz single-photon detectors will greatly advance THz DVQKD, as the majority of current research, including our work, has been focused on THz CVQKD.
• Developments in THz optical waveguides, akin to how optical fiber advancements have greatly promoted optical QKD, can lead to significant improvements in THz wired channel QKD by reducing losses. This can help circumvent issues associated with wireless channel attenuation and obstacles.

6. Conclusions

In conclusion, we propose THz CV-MDI-QKD to address challenges faced by THz QKD in real-world applications, including detector attacks, the finite-size effect, and suboptimal reconciliation efficiency. We also provide insights into the relationship between the secure key rate and transmission distance for THz CV-MDI-QKD under the optimal modulation variance. Our work contributes to the practical implementation of THz QKD systems.