Dissipation-Induced Photon Blockade in the Anti-Jaynes–Cummings Model
Abstract
1. Introduction
2. Model and Theoretical Analysis
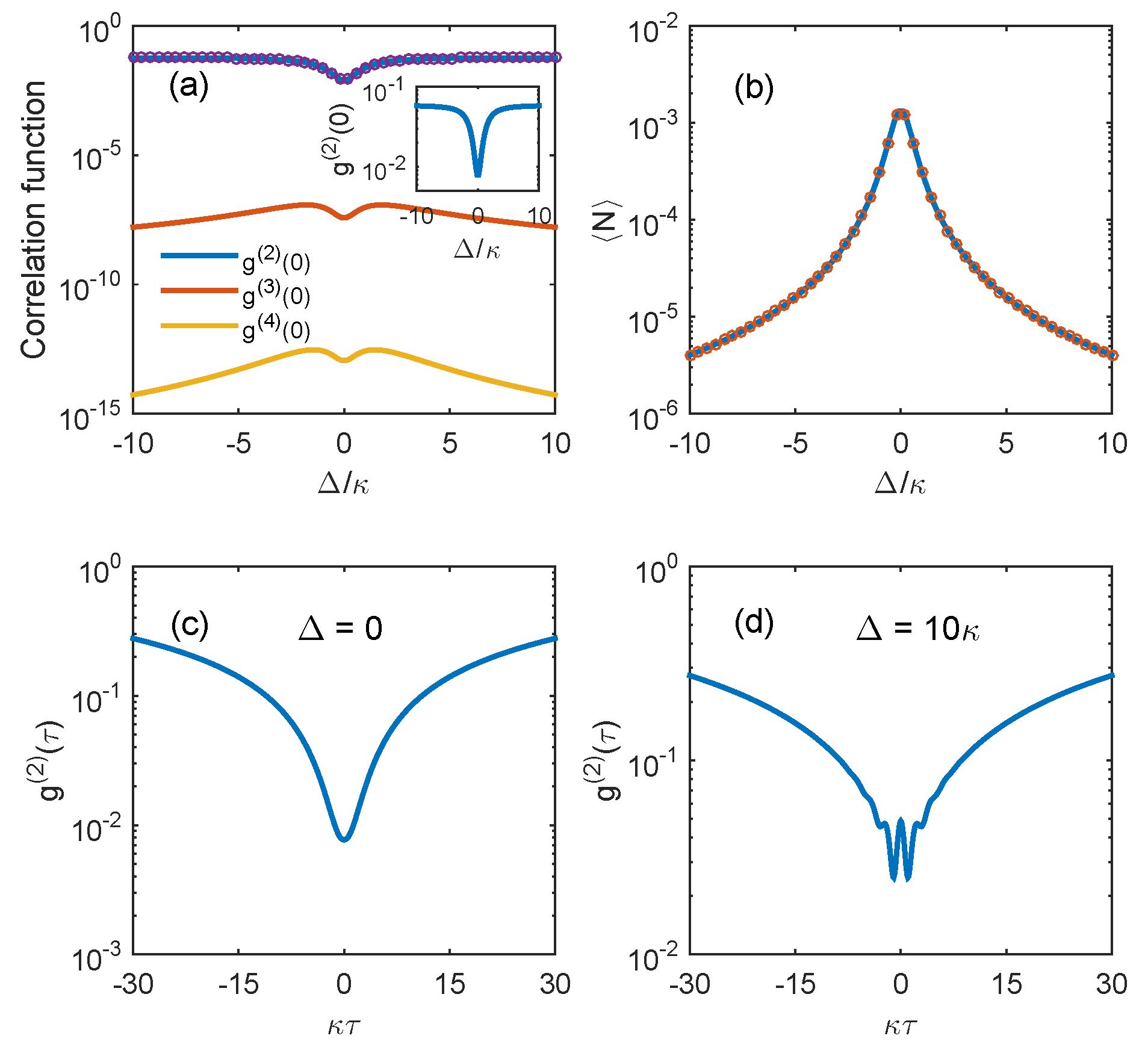
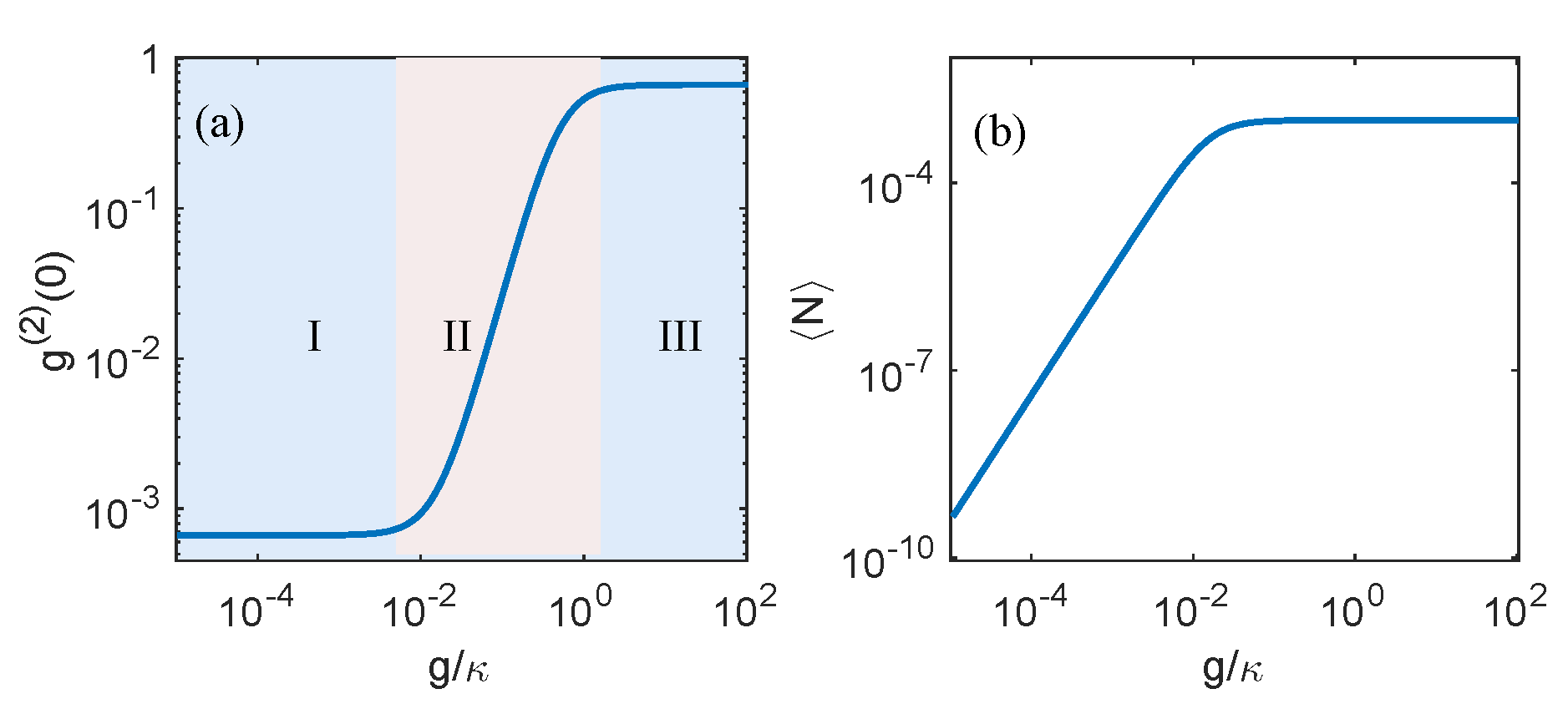
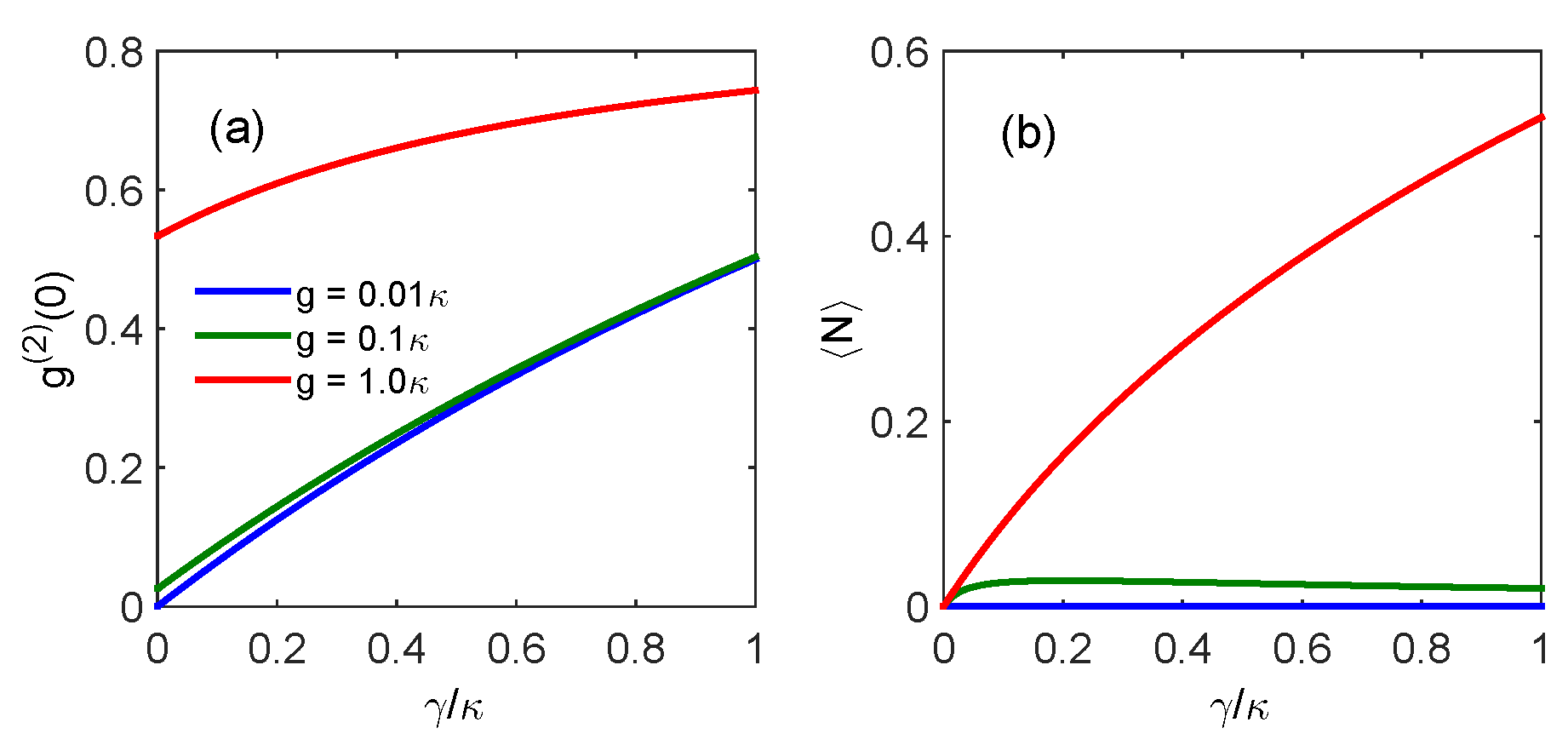
3. Quantum Statistical Properties in the Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Scarani, V.; Bechmann-Pasquinucci, H.; Cerf, N.J.; Dusek, M.; Lutkenhaus, N.; Peev, M. The security of practical quantum key distribution. Rev. Mod. Phys. 2009, 81, 1301. [Google Scholar] [CrossRef]
- Knill, E.; Laflamme, R.; Milburn, G.J. A scheme for efficient quantum computation with linear optics. Nature 2001, 409, 46. [Google Scholar] [CrossRef] [PubMed]
- Kok, P.; Munro, W.J.; Nemoto, K.; Ralph, T.C.; Dowling, J.P.; Milburn, G.J. Linear optical quantum computing with photonic qubits. Rev. Mod. Phys. 2007, 79, 135. [Google Scholar] [CrossRef]
- Ladd, T.D.; Jelezko, F.; Laflamme, R.; Nakamura, Y.; Monroe, C.; O’Brien, J.L. Quantum computers. Nature 2010, 464, 45. [Google Scholar] [CrossRef] [PubMed]
- Yao, P.; Rao, V.S.C.M.; Hughes, S. On chip single photon sources using planar photonic crystals and single quantum dots. Laser Photon. Rev. 2009, 4, 499. [Google Scholar] [CrossRef]
- Pironio, S.; Acín, A.; Brunner, N.; Gisin, N.; Massar, S.; Scarani, V. Device-independent quantum key distribution secure against collective attacks. New J. Phys. 2009, 11, 045021. [Google Scholar] [CrossRef]
- Gisin, N.; Thew, R. Quantum communication. Nat. Photonics 2007, 1, 165–171. [Google Scholar] [CrossRef]
- Pezze, L.; Smerzi, A. Mach-Zehnder interferometry at the Heisenberg limit with coherent and squeezed-vacuum light. Phys. Rev. Lett. 2008, 100, 073601. [Google Scholar] [CrossRef] [PubMed]
- Bennerr, C.H.; Brassard, G.; Crépeau, C.; Jozsa, R.; Peres, A.; Wootters, W.K. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels. Phys. Rev. Lett. 1993, 70, 1895. [Google Scholar]
- Ding, X.; He, Y.; Duan, Z.-C.; Gregersen, N.; Chen, M.-C.; Unsleber, S.; Maier, S.; Schneider, C.; Kamp, M.; Hofling, S.; et al. On-demand single photons with high extraction efficiency and near-unity indistinguishability from a resonantly driven quantum dot in a micropillar. Phys. Rev. Lett. 2016, 116, 020401. [Google Scholar] [CrossRef] [PubMed]
- Qi, R.; Yu, X.-L.; Li, Z.B.; Liu, W.M. Non-Abelian Josephson Effect between Two F = 2 Spinor Bose-Einstein Condensates in Double Optical Traps. Phys. Rev. Lett. 2009, 102, 185301. [Google Scholar] [CrossRef] [PubMed]
- Ji, A.-C.; Sun, Q.; Xie, X.C.; Liu, W.M. Josephson Effect for Photons in Two Weakly Linked Microcavities. Phys. Rev. Lett. 2009, 102, 023602. [Google Scholar] [CrossRef] [PubMed]
- Ji, A.-C.; Xie, X.C.; Liu, W.M. Quantum Magnetic Dynamics of Polarized Light in Arrays of Microcavities. Phys. Rev. Lett. 2007, 99, 183602. [Google Scholar] [CrossRef] [PubMed]
- Carusotto, I.; Ciuti, C. Quantum fluids of light. Rev. Mod. Phys. 2013, 85, 299. [Google Scholar] [CrossRef]
- Carmichael, H.J. Photon antibunching and squeezing for a single atom in a resonant cavity. Phys. Rev. Lett. 1985, 55, 2790. [Google Scholar] [CrossRef] [PubMed]
- Faraon, A.; Fushman, I.; Englund, D.; Stoltz, N.; Petroff, P.; Vuckovic, J. Coherent generation of non-classical light on a chip via photon-induced tunnelling and blockade. Nat. Phys. 2008, 4, 859. [Google Scholar] [CrossRef]
- Tang, J.; Geng, W.D.; Xu, X.L. Quantum interference induced photon blockade in a coupled single quantum dot-cavity system. Sci. Rep. 2015, 5, 9252. [Google Scholar] [CrossRef] [PubMed]
- Majumdar, A.; Bajcsy, M.; Rundquist, A.; Vuvckovic, J. Loss-enabled sub-Poissonian light generation in a bimodal nanocavity. Phys. Rev. Lett. 2012, 108, 183601. [Google Scholar] [CrossRef] [PubMed]
- Verger, A.; Ciuti, C.; Carusotto, I. Polariton quantum blockade in a photonic dot. Phys. Rev. B 2006, 73, 193306. [Google Scholar] [CrossRef]
- Majumdar, A.; Gerace, D. Single-photon blockade in doubly resonant nanocavities with second-order nonlinearity. Phys. Rev. B 2013, 87, 235319. [Google Scholar] [CrossRef]
- Ferretti, S.; Gerace, D. Single-photon nonlinear optics with Kerr-type nanostructured materials. Phys. Rev. B 2012, 85, 033303. [Google Scholar] [CrossRef]
- Imamoglu, A.; Schmidt, H.; Woods, G.; Deutsch, M. Strongly interacting photons in a nonlinear cavity. Phys. Rev. Lett. 1997, 79, 1467. [Google Scholar] [CrossRef]
- Hoffman, A.J.; Srinivasan, S.J.; Schmidt, S.; Spietz, L.; Aumentado, J.; Tureci, H.E.; Houck, A.A. Dispersive photon blockade in a superconducting circuit. Phys. Rev. Lett. 2011, 107, 053602. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.X.; Xu, X.W.; Miranowicz, A.; Nori, F. From blockade to transparency: Controllable photon transmission through a circuit-QED system. Phys. Rev. A 2014, 89, 043818. [Google Scholar] [CrossRef]
- Miranowicz, A.; Bajer, J.; Paprzycka, M.; Liu, Y.X.; Zagoskin, A.M.; Nori, F. State-dependent photon blockade via quantum-reservoir engineering. Phys. Rev. A 2014, 90, 033831. [Google Scholar] [CrossRef]
- Xu, X.W.; Li, Y.J.; Liu, Y.X. Photon-induced tunneling in optomechanical systems. Phys. Rev. A 2013, 87, 025803. [Google Scholar] [CrossRef]
- Rabl, P. Photon blockade effect in optomechanical systems. Phys. Rev. Lett. 2011, 107, 063601. [Google Scholar] [CrossRef] [PubMed]
- Liao, J.Q.; Nori, F. Photon blockade in quadratically coupled optomechanical systems. Phys. Rev. A 2013, 88, 023853. [Google Scholar] [CrossRef]
- Bamba, M.; Imamoglu, A.; Carusotto, I.; Ciuti, C. Origin of strong photon antibunching in weakly nonlinear photonic molecules. Phys. Rev. A 2011, 83, 021802. [Google Scholar] [CrossRef]
- Flayac, H.; Savona, V. Unconventional photon blockade. Phys. Rev. A. 2017, 96, 053810. [Google Scholar] [CrossRef]
- Zhang, W.; Yu, Z.Y.; Liu, Y.M.; Peng, Y.W. Optimal photon antibunching in a quantum-dotCbimodal-cavity system. Phys. Rev. A 2014, 89, 043832. [Google Scholar] [CrossRef]
- Liang, X.Y.; Duan, Z.L.; Guo, Q.; Liu, C.J.; Guan, S.G.; Ren, Y. Antibunching effect of photons in a two-level emitter-cavity system. Phys. Rev. A 2019, 100, 063834. [Google Scholar] [CrossRef]
- Zhou, Y.H.; Shen, H.Z.; Yi, X.X. Unconventional photon blockade with second-order nonlinearity. Phys. Rev. A 2015, 92, 023838. [Google Scholar] [CrossRef]
- Sarma, B.; Sarma, A.K. Quantum-interference-assisted photon blockade in a cavity via parametric interactions. Phys. Rev. A 2017, 96, 053827. [Google Scholar] [CrossRef]
- Birnbaum, K.M.; Boca, A.; Miller, R.; Boozer, A.D.; Northup, T.E.; Kimble, H.J. Photon blockade in an optical cavity with one trapped atom. Nature 2005, 436, 87. [Google Scholar] [CrossRef] [PubMed]
- Reinhard, A.; Volz, T.; Winger, M.; Badolato, A.; Hennessy, K.J.; Hu, E.L.; Imamoglu, A. Strongly correlated photons on a chip. Nat. Photonics 2012, 6, 93–96. [Google Scholar] [CrossRef]
- Volz, T.; Reinhard, A.; Winger, M.; Badolato, A.; Hennessy, K.J.; Hu, E.L.; Imamoglu, A. Ultrafast all-optical switching by single photons. Nat. Photonics 2012, 6, 605–609. [Google Scholar] [CrossRef]
- Snijders, H.J.; Frey, J.A.; Norman, J.; Flayac, H.; Savona, V.; Gossard, A.C.; Bowers, J.E.; van Exter, M.P.; Bouwmeester, D.; Lofler, W. Observation of the unconventional photon blockade. Phys. Rev. Lett. 2018, 121, 043601. [Google Scholar] [CrossRef] [PubMed]
- Vaneph, C.; Morvan, A.; Aiello, G.; Fechant, M.; Aprili, M.; Gabelli, J.; Esteve, J. Observation of the unconventional photon blockade in the microwave domain. Phys. Rev. Lett. 2018, 121, 043602. [Google Scholar] [CrossRef]
- Zhang, H.L.; Duan, Z.-L. Photon blockade in the Jaynes-Cummings model with two-photon dissipation. Opt. Express 2023, 31, 22580–22593. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Tang, J.-S.; Xia, K.Y. Nonlinear dissipation-induced photon blockade. Phys. Rev. A 2022, 106, 063707. [Google Scholar] [CrossRef]
- Huang, Y.-C.; Kumar, P. Antibunched emission of photon pairs via quantum zeno blockade. Phys. Rev. Lett. 2012, 108, 030502. [Google Scholar] [CrossRef] [PubMed]
- Sun, Y.-Z.; Huang, Y.-P.; Kumar, P. Photonic nonlinearities via quantum zeno blockade. Phys. Rev. Lett. 2013, 110, 223901. [Google Scholar] [CrossRef] [PubMed]
- Qiang, W.-C.; Sun, G.-H.; Dong, Q.; Camacho-Nieto, O.; Dong, S.-H. Concurrence of three JaynesCCummings systems. Quantum Inf. Process 2018, 17, 90. [Google Scholar] [CrossRef]
- Jaynes, E.T.; Cummings, F.W. Comparison of quantum and semiclassical radiation theories with application to the beam maser. Proc. IEEE 1963, 51, 89. [Google Scholar] [CrossRef]
- Del Valle, E.; Laussy, F.P.; Tejedor, C. Luminescence spectra of quantum dots in microcavities. II. Fermions. Phys. Rev. B 2009, 79, 235326. [Google Scholar] [CrossRef]
- Huang, J.-F.; Liao, J.-Q.; Tian, L.; Kuang, L.-M. Manipulating counter-rotating interactions in the quantum Rabi model via modulation of the transition frequency of the two-level system. Phys. Rev. A 2017, 96, 043849. [Google Scholar] [CrossRef]
- Dodonov, A.V. Photon creation from vacuum and interactions engineering in nonstationary circuit QED. J. Phys. Conf. Ser. 2009, 161, 012029. [Google Scholar] [CrossRef]
- Liberato, S.D.; Gerace, D.; Carusotto, I.; Ciuti, C. Extracavity quantum vacuum radiation from a single qubit. Phys. Rev. A 2009, 80, 053810. [Google Scholar] [CrossRef]
- Werlang, T.; Dodonov, A.V.; Duzzioni, E.I.; Villas-Boas, C.J. Rabi model beyond the rotating-wave approximation: Generation of photons from vacuum through decoherence. Phys. Rev. A 2008, 78, 053805. [Google Scholar] [CrossRef]
- Mayero, C. Photon statistics and quantum field entropy in the anti-jaynes-cummings model: A comparison with the jaynes-cummings interaction. Quantum Inf. Process. 2023, 22, 182. [Google Scholar] [CrossRef]
- Xue, F.; Zhong, L.; Li, Y.; Sun, C.P. Analogue of cavity quantum electrodynamics for coupling between spin and a nanomechanical resonator: Dynamic squeezing and coherent manipulations. Phys. Rev. B 2007, 75, 033407. [Google Scholar] [CrossRef]
- Felicetti, S.; Sabin, C.; Fuentes, I.; Lamata, L.; Romero, G.; Solano, E. Relativistic motion with superconducting qubits. Phys. Rev. B 2015, 92, 064501. [Google Scholar] [CrossRef]
- Tian, L. Circuit QED and sudden phase switching in a superconducting qubit array. Phys. Rev. Lett. 2010, 105, 167001. [Google Scholar] [CrossRef] [PubMed]
- Yin, Y.; Chen, Y.; Sank, D.; O’Malley, P.J.J.; White, T.C.; Barends, R.; Kelly, J.; Lucero, E.; Mariantoni, M.; Megrant, A.; et al. Catch and release of microwave photon states. Phys. Rev. Lett. 2013, 110, 107001. [Google Scholar] [CrossRef] [PubMed]
- Zou, X.T.; Mandel, L. Photon-antibunching and sub-Poissonian photon statistics. Phys. Rev. A 1990, 41, 475. [Google Scholar] [CrossRef] [PubMed]
- Veloso, D.S.; Dodonov, A.V. Prospects for observing dynamical and anti-dynamical Casimir effects in circuit QED due to fast modulation of qubit parameters. J. Phys. B 2015, 48, 165503. [Google Scholar] [CrossRef]
- Dodonov, A.V.; Valente, D.; Werlang, T. Antidynamical Casimir effect as a resource for work extraction. Phys. Rev. A 2017, 96, 012501. [Google Scholar] [CrossRef]
- Gardiner, C.; Zoller, P. Quantum Noise; Springer: Berlin/Heidelberg, Germany, 2004. [Google Scholar]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, B.; Li, C.; Fan, B.; Duan, Z. Dissipation-Induced Photon Blockade in the Anti-Jaynes–Cummings Model. Photonics 2024, 11, 369. https://doi.org/10.3390/photonics11040369
Huang B, Li C, Fan B, Duan Z. Dissipation-Induced Photon Blockade in the Anti-Jaynes–Cummings Model. Photonics. 2024; 11(4):369. https://doi.org/10.3390/photonics11040369
Chicago/Turabian StyleHuang, Biao, Cuicui Li, Bixuan Fan, and Zhenglu Duan. 2024. "Dissipation-Induced Photon Blockade in the Anti-Jaynes–Cummings Model" Photonics 11, no. 4: 369. https://doi.org/10.3390/photonics11040369
APA StyleHuang, B., Li, C., Fan, B., & Duan, Z. (2024). Dissipation-Induced Photon Blockade in the Anti-Jaynes–Cummings Model. Photonics, 11(4), 369. https://doi.org/10.3390/photonics11040369




