Emerging Techniques for Nonlinear Optical Spectroscopy of Disordered and Highly Scattering Materials
Abstract
1. Introduction
2. Nonlinear Optical Characterization Techniques
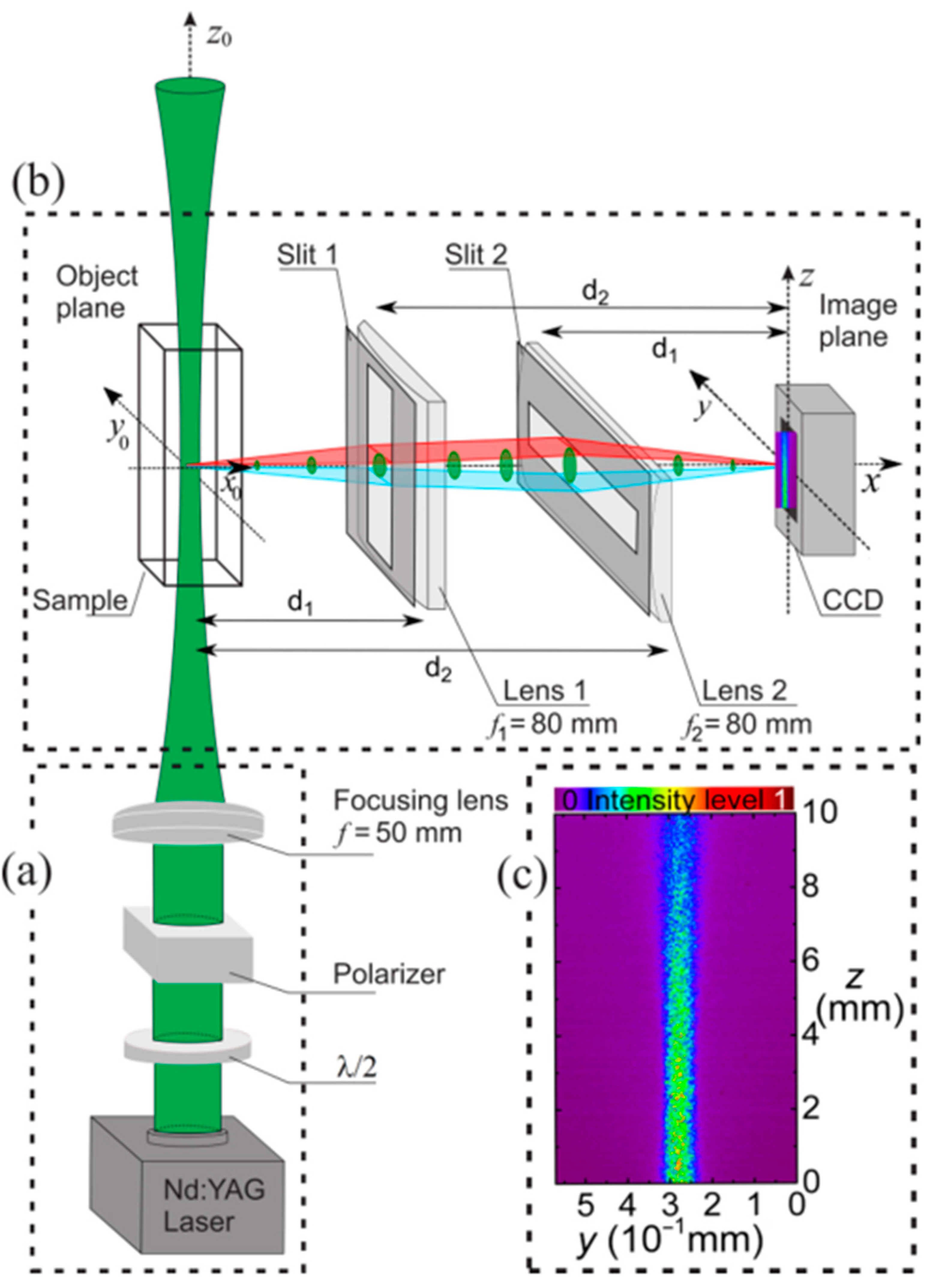
2.1. Scattered Light Imaging Method (SLIM)
2.1.1. Principles of the Method and Experimental Details
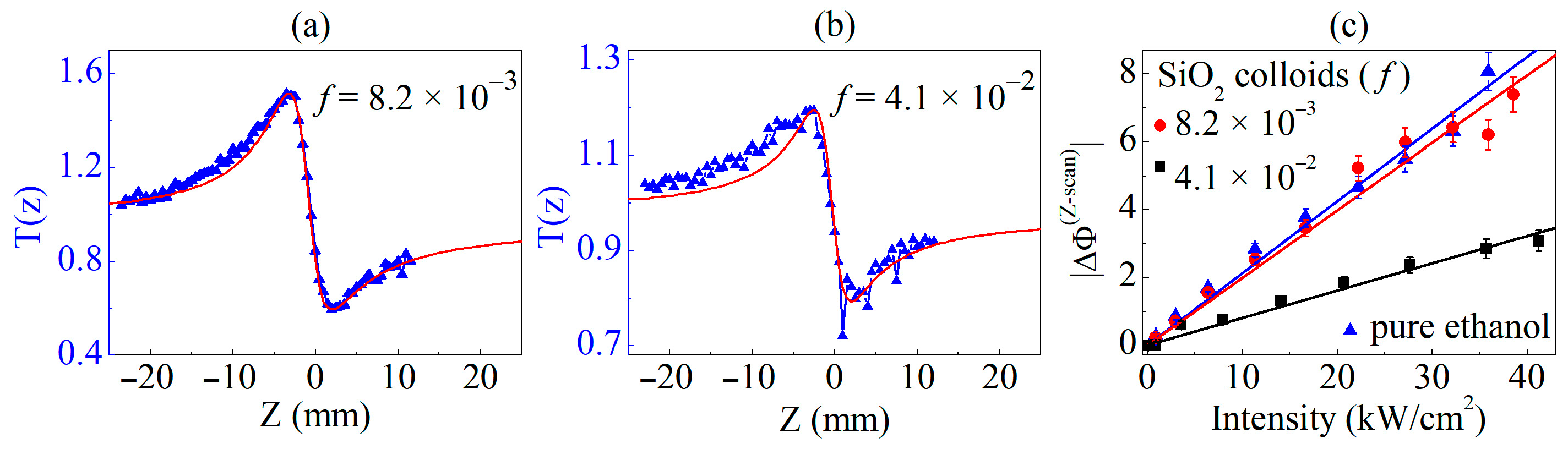
2.1.2. Nonlinear Characterization of Turbid Colloids
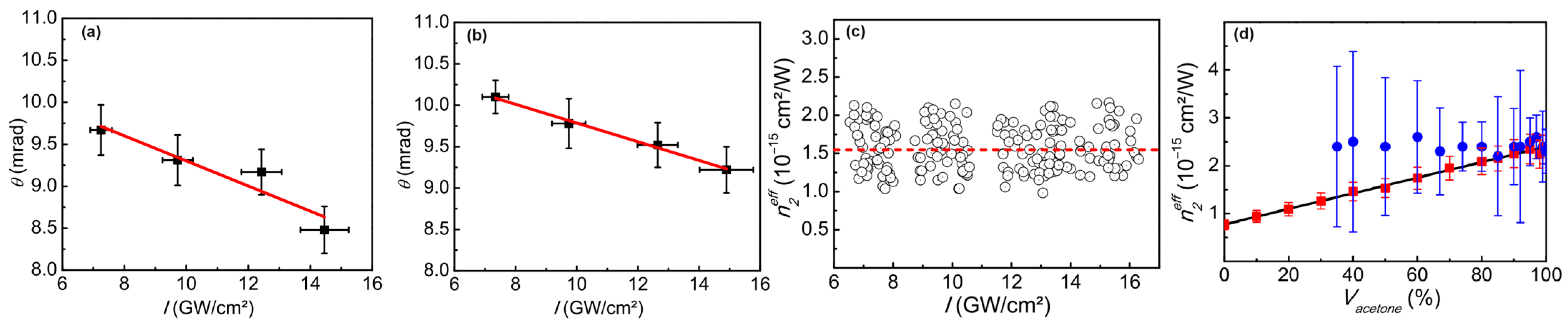
2.2. Intensity Correlation Scan (IC-Scan)
2.2.1. Principles of the Method and Experimental Details
2.2.2. Nonlinear Characterization of Turbid Colloids
2.3. Reflection Intensity Correlation Scan (RICO-Scan)
2.3.1. Principles of the Method and Experimental Details
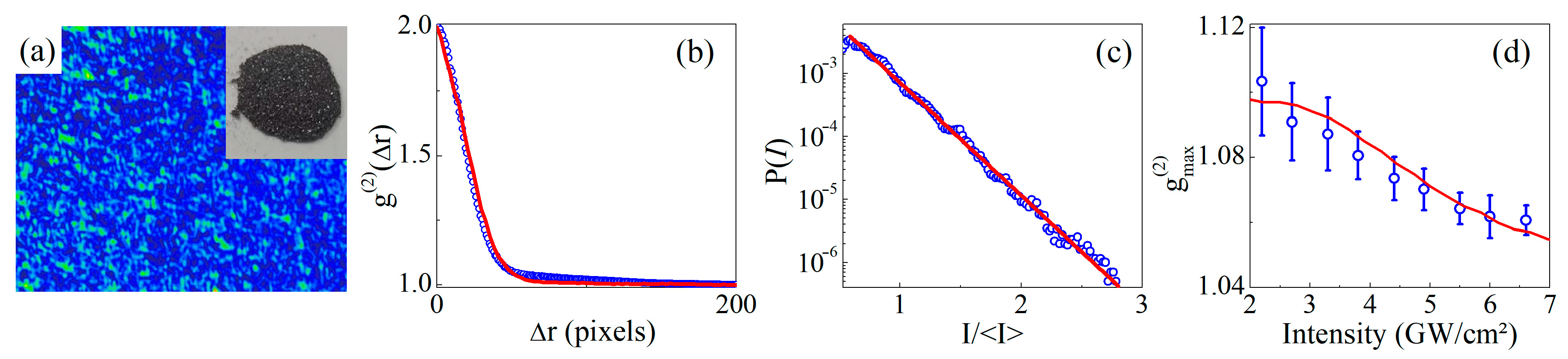
2.3.2. Nonlinear Characterization of Rough Surfaces
2.3.3. Nonlinear Characterization of Powder Media
3. Summary and Final Remarks
Funding
Acknowledgments
Conflicts of Interest
References
- Noginov, M.A. Solid-State Random Lasers; Springer: New York, NY, USA, 2005. [Google Scholar]
- Gomes, A.S.L.; Moura, A.L.; de Araújo, C.B.; Raposo, E.P. Recent advances and applications of Random Lasers and Random Fiber Lasers. Prog. Quantum Electron. 2021, 78, 100343. [Google Scholar] [CrossRef]
- Gomes, A.S.L.; Moura, A.L.; de Araújo, C.B.; Raposo, E.P. Lévy Statistics and Spin Glass Behavior in Random Lasers; Jenny Stanford Publishing Pte. Ltd.: Singapore, 2023. [Google Scholar]
- Zvyagin, A.I.; Chevychelova, T.A.; Chirkov, K.S.; Smirnov, M.S.; Ovchinnikov, O.V. Size dependence of nonlinear optical properties of PbS QDs, passivated with thioglycolic acid. Optik 2023, 272, 170276. [Google Scholar] [CrossRef]
- Perez, N.; Chambers, J.; Chen, Z.; Bezryadina, A. Nonlinear self-trapping and guiding of light at different wavelengths with sheep blood. Opt. Lett. 2021, 46, 629–632. [Google Scholar] [CrossRef]
- Reyna, A.S.; de Araújo, C.B. High-order optical nonlinearities in plasmonic nanocomposites—A review. Adv. Opt. Photonics 2017, 9, 720–774. [Google Scholar] [CrossRef]
- von Sun, M.; Mu, X.; Li, R. Linear and Nonlinear Optical Spectroscopy and Microscopy; Progress in Optical Science and Photonics; Springer: Singapore, 2024. [Google Scholar]
- Ranasinghesagara, J.C.; Potma, E.O.; Venugopalan, V. Modeling nonlinear optical microscopy in scattering media, part I. Propagation from lens to focal volume–tutorial. J. Opt. Am. Soc. A 2023, 40, 867–882. [Google Scholar]
- Parodi, V.; Jacchetti, E.; Osellame, R.; Cerullo, G.; Polli, D.; Raimondi, M.T. Nonlinear Optical Microscopy: From Fundamentals to Applications in Live Bioimaging. Front. Bioeng. Biotechnol. 2020, 8, 585363. [Google Scholar] [CrossRef]
- Sheik-Bahae, M.; Said, A.A.; Wei, T.-H.; Hagan, D.J.; van Stryland, E.W. Sensitive measurement of optical nonlinearities using a single beam. IEEE J. Quantum Electron. 1990, 26, 760–769. [Google Scholar] [CrossRef]
- de Araújo, C.B.; Gomes, A.S.L.; Boudebs, G. Techniques for nonlinear optical characterization of materials: A review. Rep. Prog. Phys. 2016, 79, 036401. [Google Scholar] [CrossRef] [PubMed]
- Boudebs, G.; Besse, V.; Cassagne, C.; Leblond, H.; de Araújo, C.B. Nonlinear characterization of materials using the D4σ method inside a Z-scan 4f-system. Opt. Lett. 2013, 38, 2206–2208. [Google Scholar] [CrossRef]
- Prylepa, A.; Reitböck, C.; Cobet, M.; Jesacher, A.; Jin, X.; Adelung, R.; Schatzl-Linder, M.; Luckeneder, G.; Stellnberger, K.H.; Steck, T.; et al. Material characterization with methods of nonlinear optics. J. Phys. D Appl. Phys. 2018, 51, 043001. [Google Scholar] [CrossRef]
- Verbiest, T.; Clays, K.; Rodriguez, V. Second-Order Nonlinear Optical Characterization Techniques: An Introduction; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Ahmed, M.S.; Biswas, C.; Miranda, P.B.; Raavi, S.S.K. Nonlinear optical techniques for characterization of organic electronic and photonic devices. Eur. Phys. J. Spec. Top. 2022, 231, 695–711. [Google Scholar] [CrossRef]
- Jorge, K.C.; Riva, R.; Rodrigues, N.A.S.; Sakamoto, J.M.S.; Destro, M.G. Scattered Light Imaging Method (SLIM) for Characterization of Arbitrary Laser Beam Intensity Profiles. Appl. Opt. 2014, 53, 4555–4564. [Google Scholar] [CrossRef]
- Amaral, A.M.; Jorge, K.C.; de Araújo, C.B.; Menezes, L.d.S. Toward single-shot characterization of nonlinear optical refraction, absorption, and scattering of turbid media. Phys. Rev. A 2020, 102, 033503. [Google Scholar] [CrossRef]
- Jorge, K.C.; Amaral, A.M.; Reyna, A.S.; Menezes, L.d.S.; de Araújo, C.B. Observation and Analysis of Nonlinear Scattering Using the Scattered Light Imaging Method. Phys. Rev. A 2022, 105, 063520. [Google Scholar] [CrossRef]
- Jorge, K.C.; García, H.A.; Amaral, A.M.; Reyna, A.S.; Menezes, L.d.S.; de Araújo, C.B. Measurements of the Nonlinear Refractive Index in Scattering Media Using the Scattered Light Imaging Method—SLIM. Opt. Express 2015, 23, 19512–19521. [Google Scholar] [CrossRef]
- Crispim, M.J.B.; Pereira, C.C.S.; Oliveira, N.T.C.; Chevrollier, M.; de Oliveira, R.A.; Martins, W.S.; Reyna, A.S. Intensity correlation scan (IC-scan) technique to characterize the optical nonlinearity of scattering media. Sci. Rep. 2023, 13, 7239. [Google Scholar]
- Oliveira, N.T.C.; Vieira, A.M.; de Araújo, C.B.; Martins, W.S.; de Oliveira, R.A.; Reyna, A.S. Light Disorder as a Degree of Randomness to Improve the Performance of Random Lasers. Phys. Rev. Appl. 2021, 15, 064062. [Google Scholar] [CrossRef]
- Bezerra, G.S.; Ocas, L.R.; Kumada, D.K.; Martins, W.S.; Kassab, L.R.P.; Reyna, A.S. Influence of plasmonic and thermo-optical effects of silver nanoparticles on near-infrared optical thermometry in Nd3+-doped TeO2–ZnO glasses. J. Lumin. 2024, 265, 120222. [Google Scholar] [CrossRef]
- Joudrier, V.; Bourdon, P.; Hache, F.; Flytzanis, C. Nonlinear Light Scattering in a Two-Component Medium: Optical Limiting Application. Appl. Phys. B Lasers Opt. 1998, 67, 627–632. [Google Scholar] [CrossRef]
- Lasers and Laser-Related Equipment—Test Methods for Laser Beam Widths, Divergence Angles and Beam Propagation Ratios; International Organization for Standardization: Geneve, Switzerland, 2021.
- Liberman, V.; Sworin, M.; Kingsborough, R.P.; Geurtsen, G.P.; Rothschild, M. Nonlinear Bleaching, Absorption, and Scattering of 532-nm-Irradiated Plasmonic Nanoparticles. J. Appl. Phys. 2013, 113, 053107. [Google Scholar] [CrossRef]
- Gould, T.; Wang, Q.; Pfefer, T.J. Optical-Thermal Light-Tissue Interactions During Photoacoustic Breast Imaging. Biomed. Opt. Express 2014, 5, 832–847. [Google Scholar] [CrossRef] [PubMed]
- Vlasov, S.N.; Petrishchev, V.A.; Talanov, V.I. Averaged Description of Wave Beams in Linear and Nonlinear Media (the Method of Moments). Radiophys. Quantum Electron. 1971, 14, 1062–1070. [Google Scholar] [CrossRef]
- Porras, M.A.; Alda, J.; Bernabeu, E. Nonlinear Propagation and Transformation of Arbitrary Laser Beams by Means of the Generalized ABCD Formalism. Appl. Opt. 1993, 32, 5885–5892. [Google Scholar] [CrossRef] [PubMed]
- Agrawal, G.P. Nonlinear Fiber Optics; Academic Press: New York, NY, USA, 2001. [Google Scholar]
- Siegman, A.E. Defining the Effective Radius of Curvature for a Nonideal Optical Beam. IEEE J. Quantum Electron. 1991, 27, 1146–1148. [Google Scholar] [CrossRef]
- Hughes, S.; Burder, J.M.; Spruce, G.; Wherrett, B.S. Fast Fourier transform technique for efficient simulation of Z-scan measurements. J. Opt. Soc. Am. B 1995, 12, 1888–1893. [Google Scholar] [CrossRef]
- Bezerra, G.S.; Reyna, A.S.; de Araújo, C.B. Nonlinear optical characterization of opaque and scattering media: From rough surfaces to powder materials. In Proceedings of the Digest of the Autum Meeting of the Brazilian Physical Society, Florianopolis, Brazil, 19–23 May 2024. [Google Scholar]



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Reyna, A.S.; Amaral, A.M.; de Araújo, C.B. Emerging Techniques for Nonlinear Optical Spectroscopy of Disordered and Highly Scattering Materials. Photonics 2024, 11, 650. https://doi.org/10.3390/photonics11070650
Reyna AS, Amaral AM, de Araújo CB. Emerging Techniques for Nonlinear Optical Spectroscopy of Disordered and Highly Scattering Materials. Photonics. 2024; 11(7):650. https://doi.org/10.3390/photonics11070650
Chicago/Turabian StyleReyna, Albert S., Anderson M. Amaral, and Cid B. de Araújo. 2024. "Emerging Techniques for Nonlinear Optical Spectroscopy of Disordered and Highly Scattering Materials" Photonics 11, no. 7: 650. https://doi.org/10.3390/photonics11070650
APA StyleReyna, A. S., Amaral, A. M., & de Araújo, C. B. (2024). Emerging Techniques for Nonlinear Optical Spectroscopy of Disordered and Highly Scattering Materials. Photonics, 11(7), 650. https://doi.org/10.3390/photonics11070650






