Structured Optical Toroidal Vortices with Rotational Symmetry
Abstract
:1. Introduction
2. Mathematical Description of Toroidal Vortices
3. Results
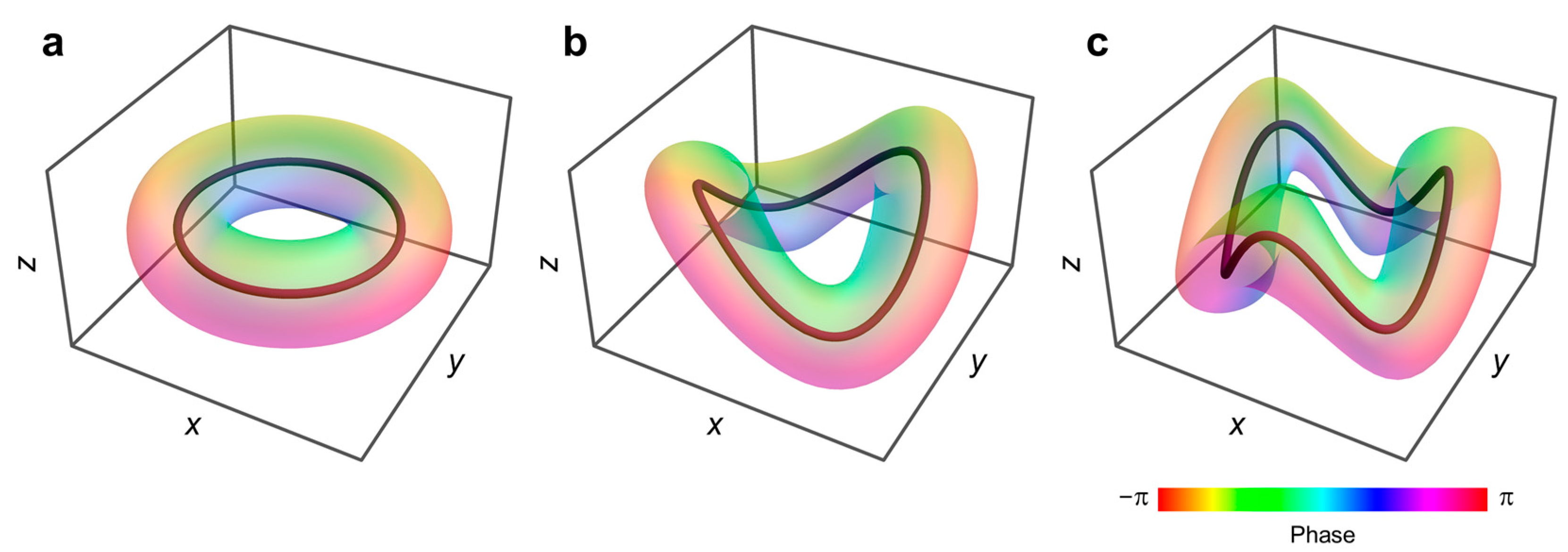
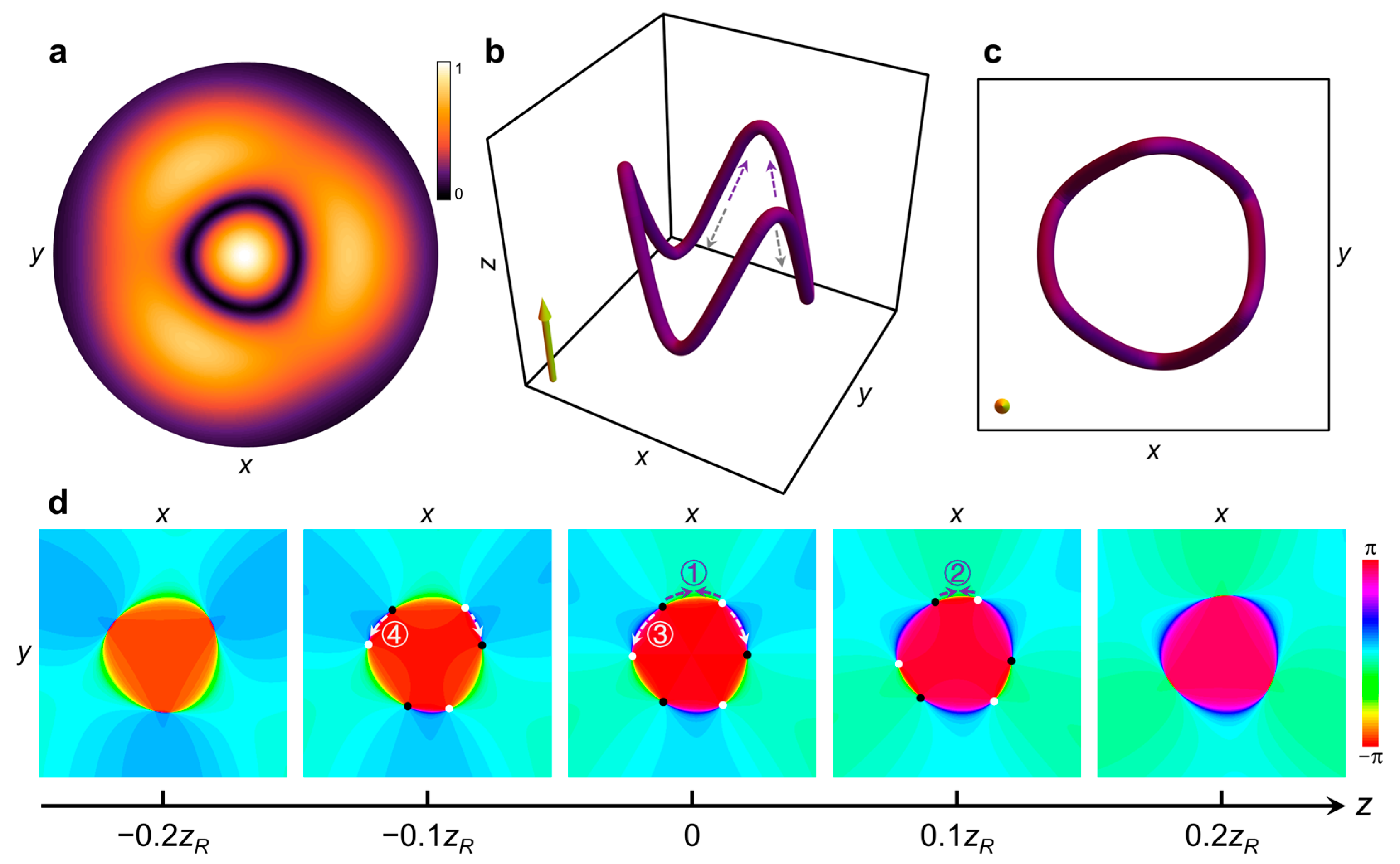
3.1. Optical Paraxial Toroidal Vortices
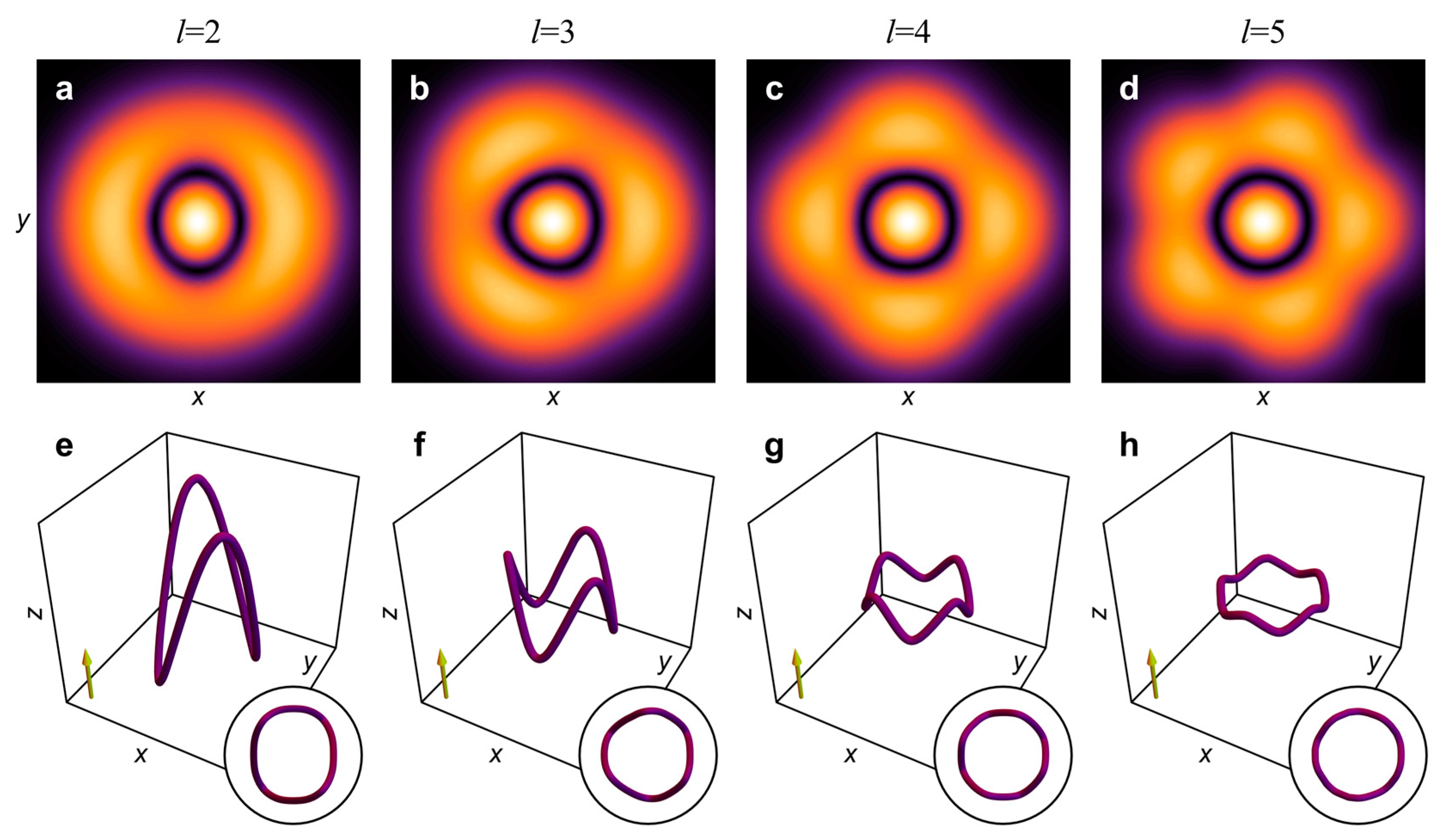
3.2. Optical Structured Toroidal Vortices with l-Fold Symmetry
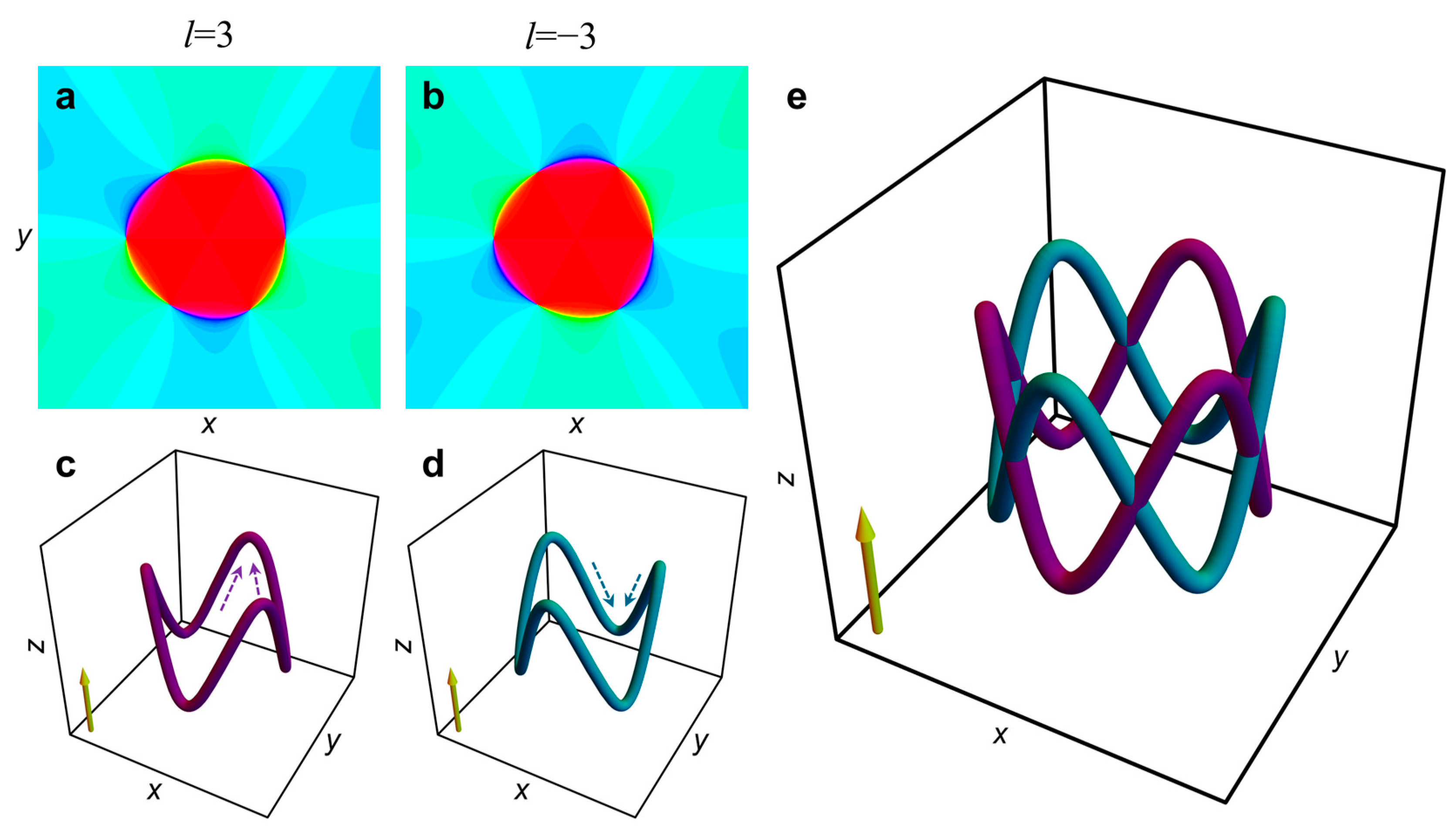
3.3. Optical Structured Toroidal Vortices with Opposite Topological Charge
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Akhmetov, D.G. Vortex Rings; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Lee, J.S.; Park, S.J.; Lee, J.H.; Weon, B.M.; Fezzaa, K.; Je, J.H. Origin and dynamics of vortex rings in drop splashing. Nat. Commun. 2015, 6, 8187. [Google Scholar] [CrossRef] [PubMed]
- Matsuzawa, T.; Mitchell, N.P.; Perrard, S.; Irvine, W.T.M. Creation of an isolated turbulent blob fed by vortex rings. Nat. Phys. 2023, 19, 1193–1200. [Google Scholar] [CrossRef]
- Kleckner, D.; Irvine, W.T.M. Creation and dynamics of knotted vortices. Nat. Phys. 2013, 9, 253–258. [Google Scholar] [CrossRef]
- Ruostekoski, J.; Anglin, J.R. Creating Vortex Rings and Three-Dimensional Skyrmions in Bose-Einstein Condensates. Phys. Rev. Lett. 2001, 86, 3934–3937. [Google Scholar] [CrossRef]
- Kauffman, L.H. Knots and Physics, 3rd ed.; World Scientific Publishing: Singapore, 2001. [Google Scholar]
- Tai, J.-S.B.; Smalyukh, I.I. Three-dimensional crystals of adaptive knots. Science 2019, 365, 1449–1453. [Google Scholar] [CrossRef]
- Zheng, F.; Kiselev, N.S.; Rybakov, F.N.; Yang, L.; Shi, W.; Blügel, S.; Dunin-Borkowski, R.E. Hopfion rings in a cubic chiral magnet. Nature 2023, 623, 718–723. [Google Scholar] [CrossRef]
- Dennis, M.R.; King, R.P.; Jack, B.; O’Holleran, K.; Padgett, M.J. Isolated optical vortex knots. Nat. Phys. 2010, 6, 118–121. [Google Scholar] [CrossRef]
- Zhong, J.; Liu, S.; Guo, X.; Li, P.; Wei, B.; Han, L.; Qi, S.; Zhao, J. Observation of optical vortex knots and links associated with topological charge. Opt. Express 2021, 29, 38849–38857. [Google Scholar] [CrossRef]
- Zhang, H.; Zhang, W.; Liao, Y.; Zhou, X.; Li, J.; Hu, G.; Zhang, X. Creation of acoustic vortex knots. Nat. Commun. 2020, 11, 3956. [Google Scholar] [CrossRef]
- Hall, D.S.; Ray, M.W.; Tiurev, K.; Ruokokoski, E.; Gheorghe, A.H.; Möttönen, M. Tying quantum knots. Nat. Phys. 2016, 12, 478–483. [Google Scholar] [CrossRef]
- Ricca, R.L.; Liu, X. Knotted Fields; Springer Nature: Berlin/Heidelberg, Germany, 2024; Volume 2344. [Google Scholar]
- Larocque, H.; D’Errico, A.; Ferrer-Garcia, M.F.; Carmi, A.; Cohen, E.; Karimi, E. Optical framed knots as information carriers. Nat. Commun. 2020, 11, 5119. [Google Scholar] [CrossRef] [PubMed]
- Zhan, Q. Spatiotemporal sculpturing of light: A tutorial. Adv. Opt. Photon. 2024, 16, 163–228. [Google Scholar] [CrossRef]
- He, C.; Shen, Y.; Forbes, A. Towards higher-dimensional structured light. Light Sci. Appl. 2022, 11, 205. [Google Scholar] [CrossRef]
- Cardano, F.; Marrucci, L. Smoke rings of light. Nat. Photonics 2022, 16, 476–477. [Google Scholar] [CrossRef]
- Wan, C.; Cao, Q.; Chen, J.; Chong, A.; Zhan, Q. Toroidal vortices of light. Nat. Photonics 2022, 16, 519–522. [Google Scholar] [CrossRef]
- Zdagkas, A.; McDonnell, C.; Deng, J.; Shen, Y.; Li, G.; Ellenbogen, T.; Papasimakis, N.; Zheludev, N.I. Observation of toroidal pulses of light. Nat. Photonics 2022, 16, 523–528. [Google Scholar] [CrossRef]
- Wang, R.; Ying, B.; Shi, S.; Wang, J.; Wang, B.-Z.; Liang, M.; Shen, Y. Hybrid electromagnetic toroidal vortices. Sci. Adv. 2025, 11, eads4797. [Google Scholar] [CrossRef]
- Zhong, J.; Teng, H.; Zhan, Q. Toroidal phase topologies within paraxial laser beams. Commun. Phys. 2024, 7, 285. [Google Scholar] [CrossRef]
- Wan, C.; Shen, Y.; Chong, A.; Zhan, Q. Scalar optical hopfions. eLight 2022, 2, 22. [Google Scholar] [CrossRef]
- Zhong, J.; Wan, C.; Zhan, Q. Optical Twisted Phase Strips. ACS Photonics 2023, 10, 3384–3389. [Google Scholar] [CrossRef]
- Sugic, D.; Droop, R.; Otte, E.; Ehrmanntraut, D.; Nori, F.; Ruostekoski, J.; Denz, C.; Dennis, M.R. Particle-like topologies in light. Nat. Commun. 2021, 12, 6785. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.; Liu, Y.; Yu, A.-Z.; Cao, H.; Hu, W.; Qiao, W.; Chen, L.-S.; Lu, Y.-Q. Observation of Chiral Symmetry Breaking in Toroidal Vortices of Light. Phys. Rev. Lett. 2024, 132, 153801. [Google Scholar] [CrossRef]
- Sutcliffe, P.M.; Winfree, A.T. Stability of knots in excitable media. Phys. Rev. E 2003, 68, 016218. [Google Scholar] [CrossRef] [PubMed]
- Mendoza-Hernández, J.; Arroyo-Carrasco, M.L.; Iturbe-Castillo, M.D.; Chávez-Cerda, S. Laguerre-Gauss beams versus Bessel beams showdown: Peer comparison. Opt. Lett. 2015, 40, 3739–3742. [Google Scholar] [CrossRef] [PubMed]
- Ehrmanntraut, D.; Droop, R.; Sugic, D.; Otte, E.; Dennis, M.R.; Denz, C. Optical second-order skyrmionic hopfion. Optica 2023, 10, 725–731. [Google Scholar] [CrossRef]
- Kong, L.-J.; Zhang, W.; Li, P.; Guo, X.; Zhang, J.; Zhang, F.; Zhao, J.; Zhang, X. High capacity topological coding based on nested vortex knots and links. Nat. Commun. 2022, 13, 2705. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhong, J.; Zhan, Q. Structured Optical Toroidal Vortices with Rotational Symmetry. Photonics 2025, 12, 288. https://doi.org/10.3390/photonics12030288
Zhong J, Zhan Q. Structured Optical Toroidal Vortices with Rotational Symmetry. Photonics. 2025; 12(3):288. https://doi.org/10.3390/photonics12030288
Chicago/Turabian StyleZhong, Jinzhan, and Qiwen Zhan. 2025. "Structured Optical Toroidal Vortices with Rotational Symmetry" Photonics 12, no. 3: 288. https://doi.org/10.3390/photonics12030288
APA StyleZhong, J., & Zhan, Q. (2025). Structured Optical Toroidal Vortices with Rotational Symmetry. Photonics, 12(3), 288. https://doi.org/10.3390/photonics12030288




