Comprehensive Optical Inter-Satellite Communication Model for Low Earth Orbit Constellations: Analyzing Transmission Power Requirements
Abstract
:1. Introduction
Motivation and Related Work
2. Constellation Model
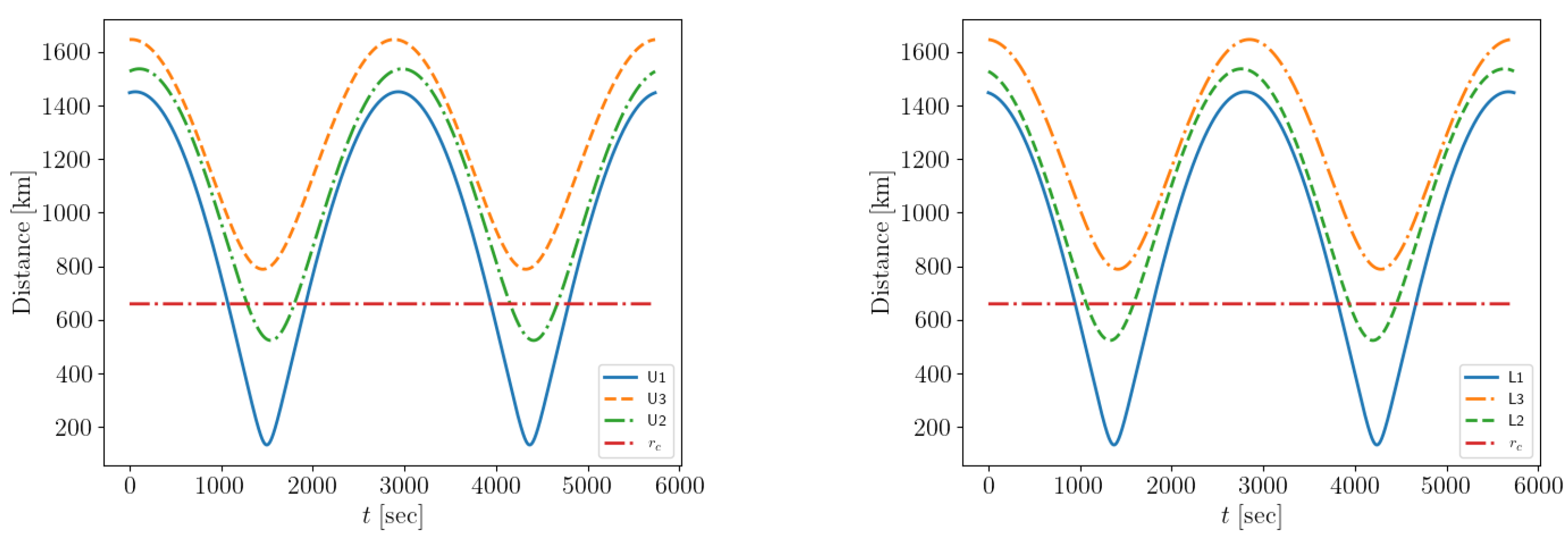
2.1. Constellation Dynamics
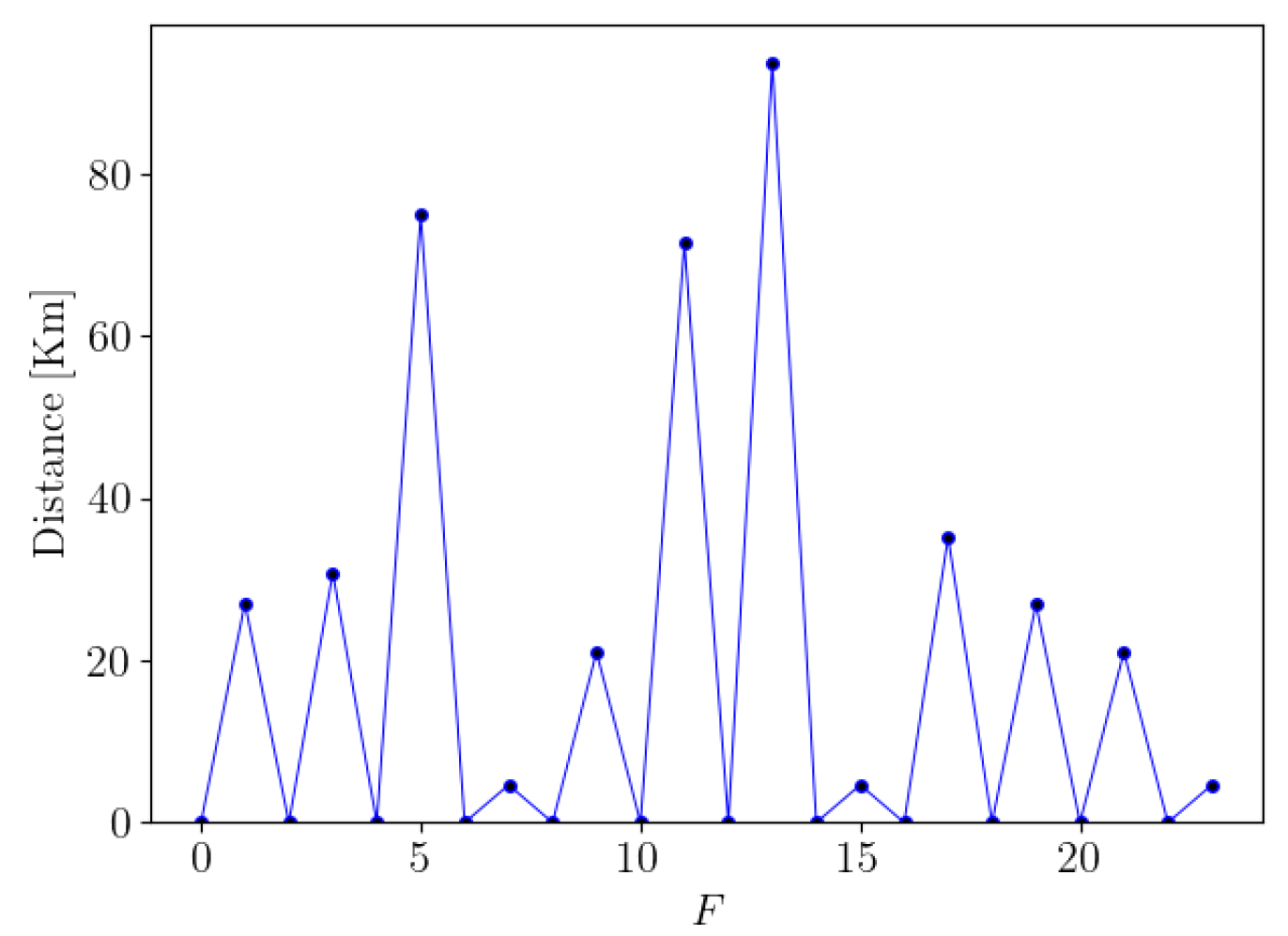
2.2. Collision Avoidance
2.3. Connectivity Requirements
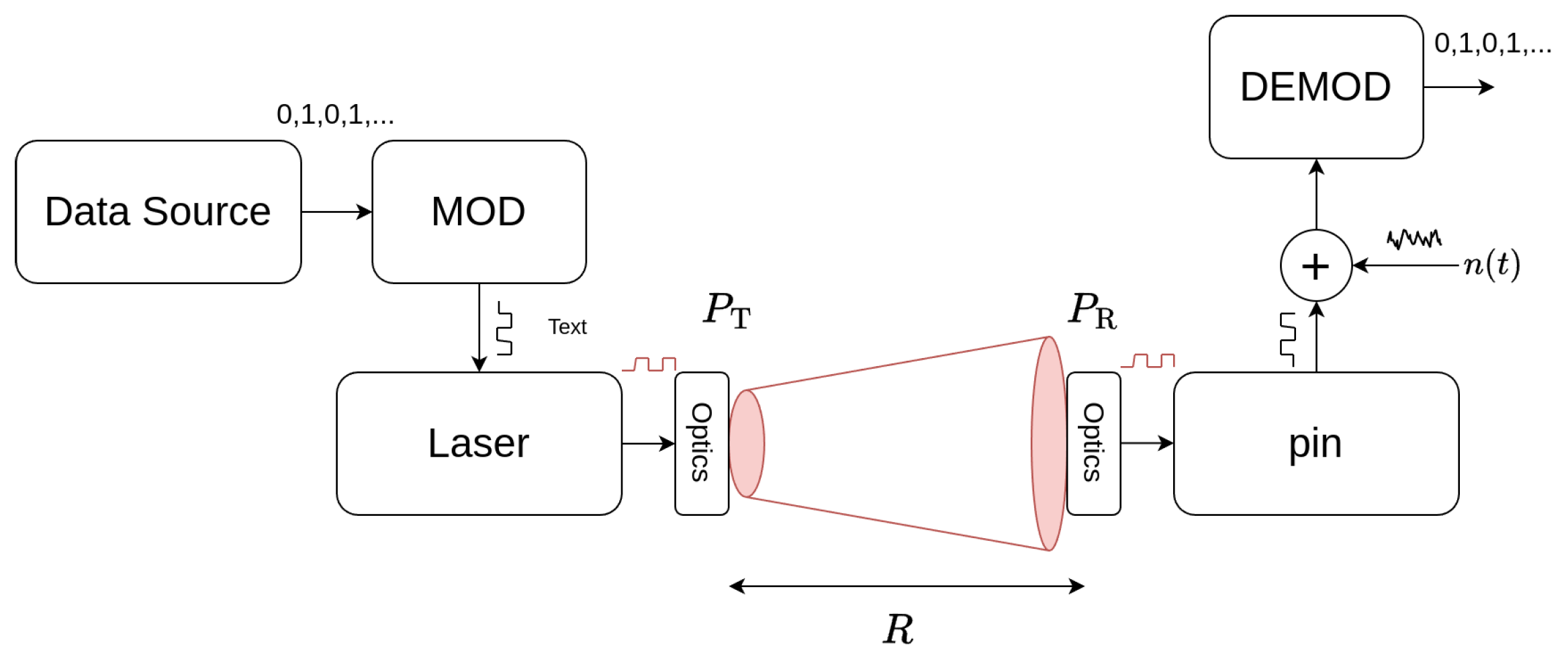
3. Link Model
3.1. Link Budget
3.2. Bit Error Rate
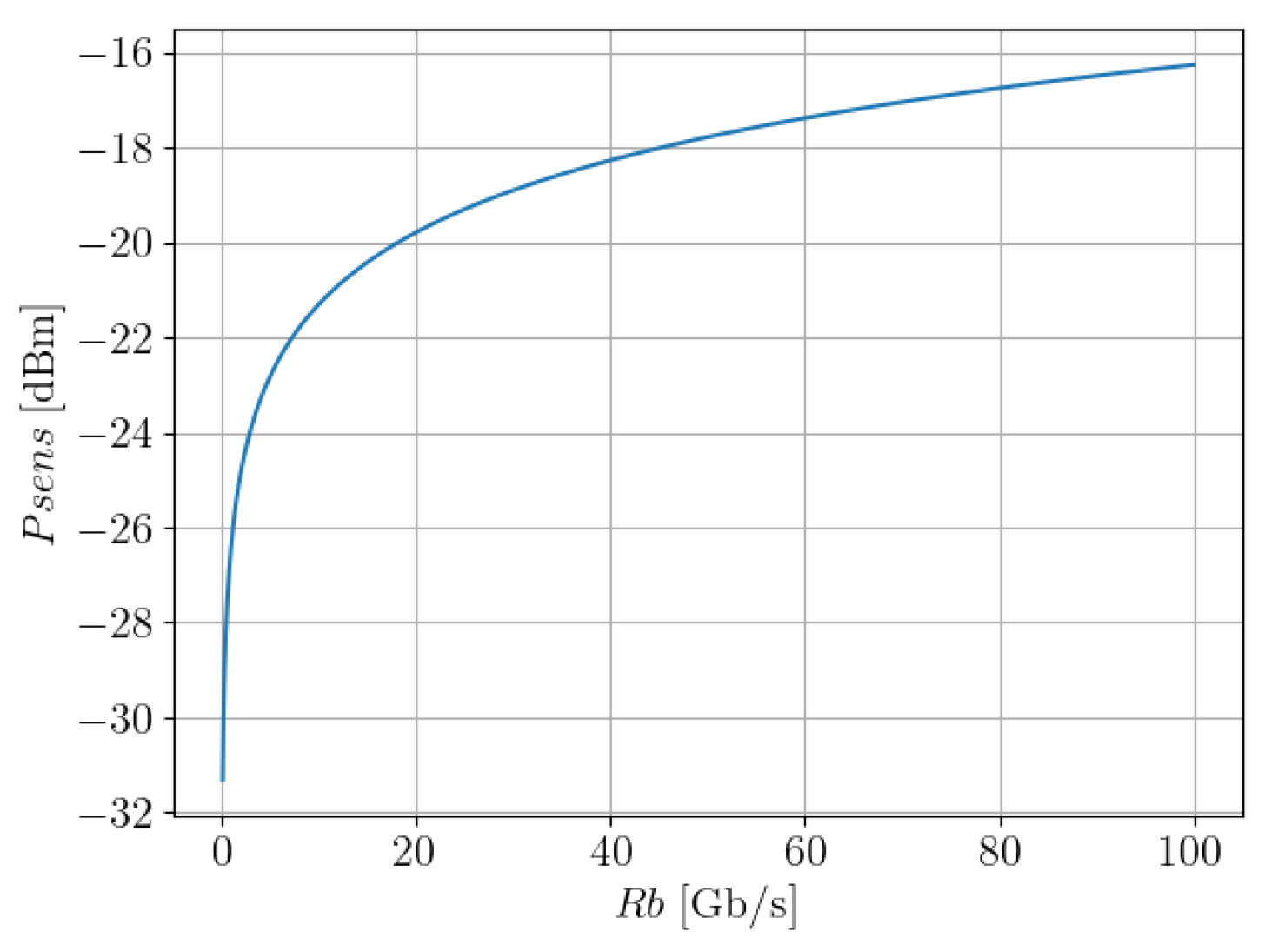
3.3. Receiver Sensitivity
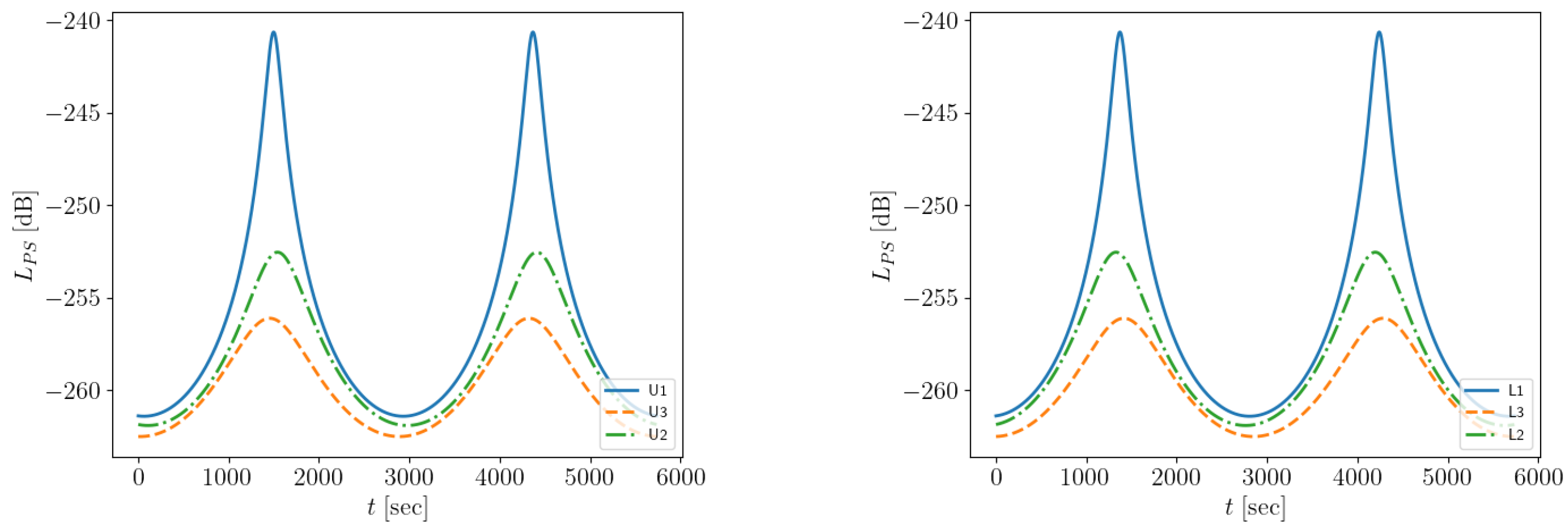
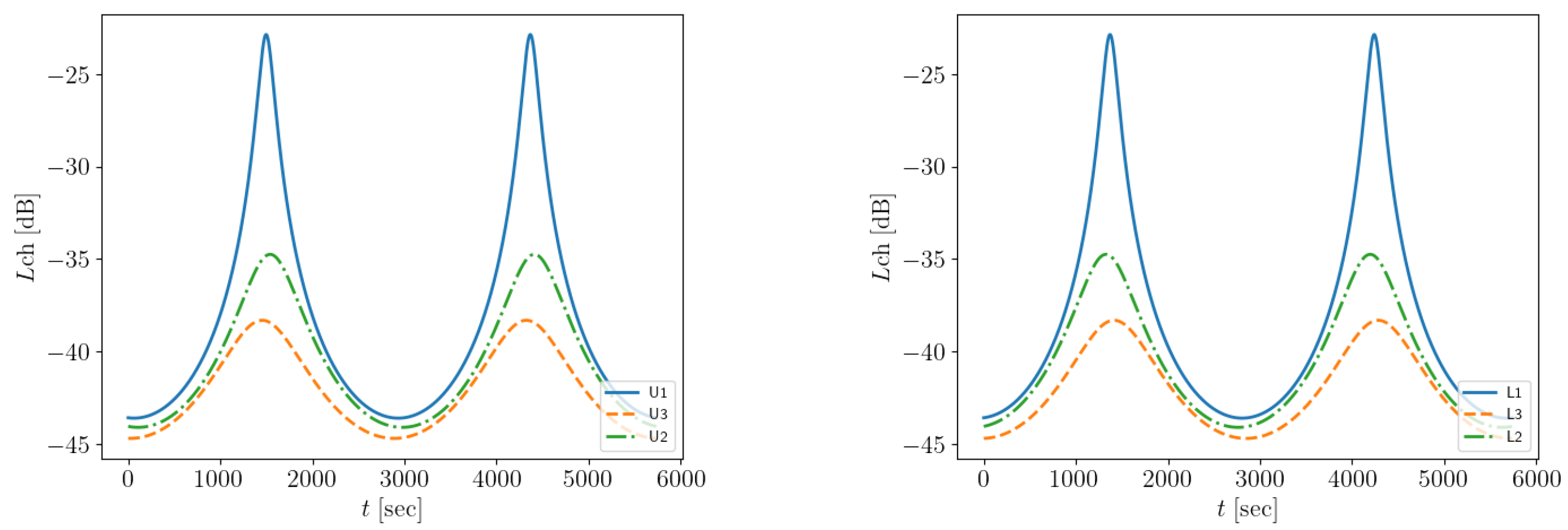
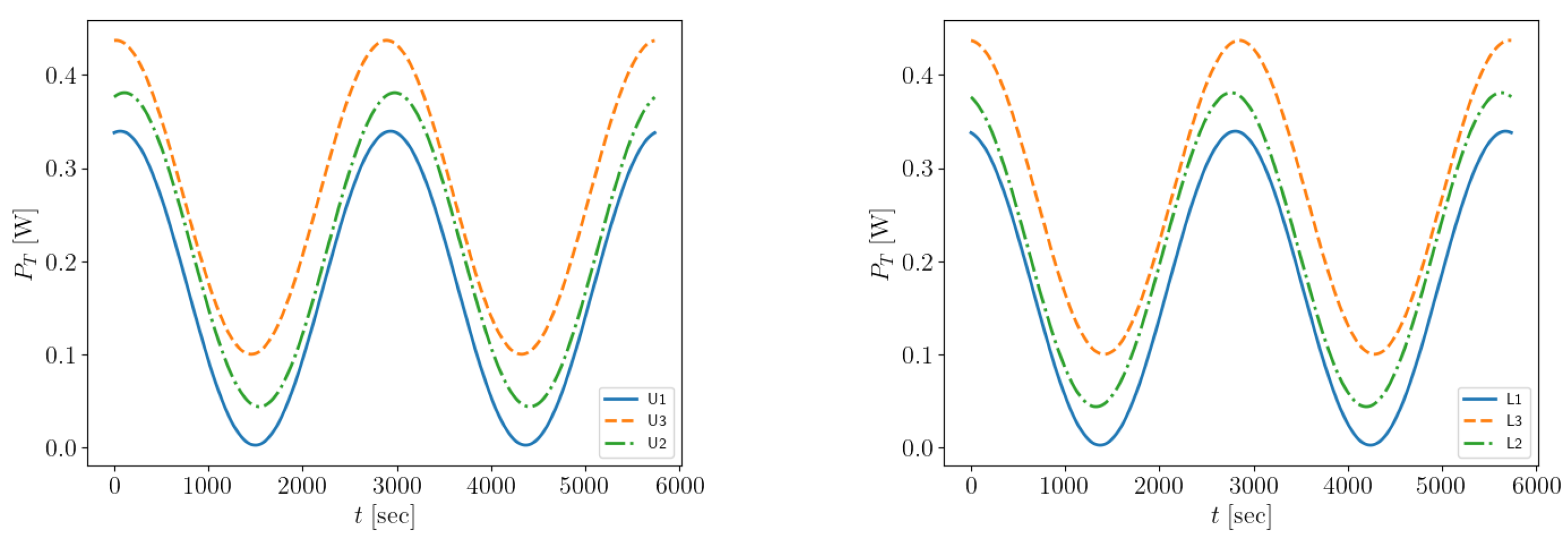
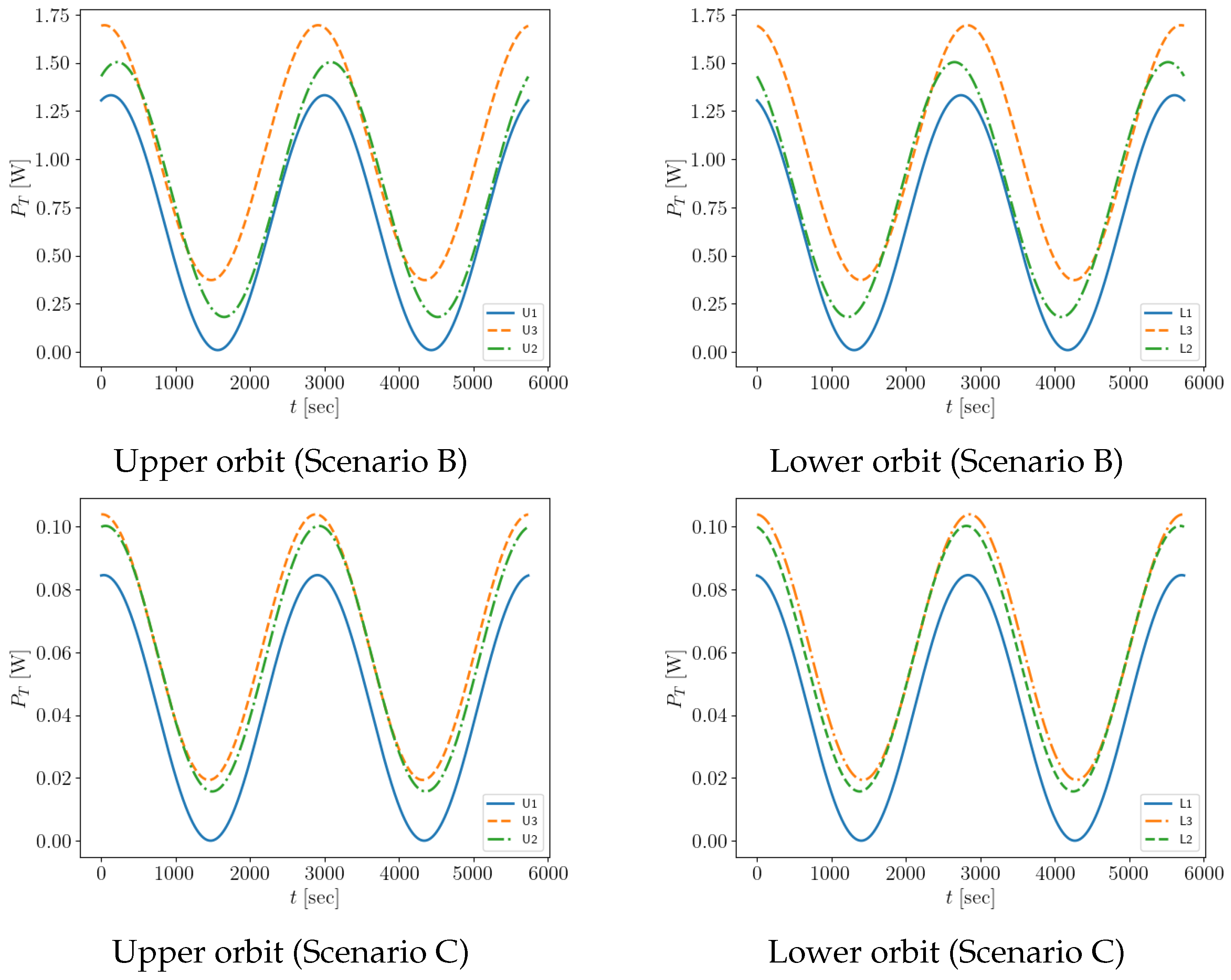
4. Results
4.1. Scenario A
4.2. Alternative Scenarios
5. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A. Pyminisat Module Implementation
References
- Carrizo, C.; Knapek, M.; Horwath, J.; Gonzalez, D.D.; Cornwell, P. Optical inter-satellite link terminals for next generation satellite constellations. In Proceedings of the Free-Space Laser Communications XXXII, San Francisco, CA, USA, 1–6 February 2020; SPIE: Bellingham, WA, USA, 2020; Volume 11272, pp. 8–18. [Google Scholar]
- Kemih, K.; Yaiche, Y.; Benslama, M. Optimization of Transmitter Aperture by Genetic Algorithm in Optical Satellite. World Acad. Sci. Eng. Technol. Int. J. Electr. Comput. Energetic Electron. Commun. Eng. 2007, 1, 1261–1267. [Google Scholar]
- Kim, G.N.; Park, S.Y.; Seong, S.; Choi, J.Y.; Han, S.K.; Kim, Y.E.; Choi, S.; Lee, J.; Lee, S.; Ryu, H.G.; et al. Design of Novel Laser Crosslink Systems Using Nanosatellites in Formation Flying: The VISION. Aerospace 2022, 9, 423. [Google Scholar] [CrossRef]
- Zhu, Q.; Tao, H.; Cao, Y.; Li, X. Laser inter-satellite link visibility and topology optimization for mega constellation. Electronics 2022, 11, 2232. [Google Scholar] [CrossRef]
- Liang, J.; Chaudhry, A.U.; Erdogan, E.; Yanikomeroglu, H. Link Budget Analysis for Free-Space Optical Satellite Networks. In Proceedings of the 2022 IEEE 23rd International Symposium on a World of Wireless, Mobile and Multimedia Networks (WoWMoM), Belfast, UK, 14–17 June 2022; pp. 471–476. [Google Scholar]
- Liang, J.; Chaudhry, A.U.; Erdogan, E.; Yanikomeroglu, H.; Kurt, G.K.; Hu, P.; Ahmed, K.; Martel, S. Free-Space Optical (FSO) Satellite Networks Performance Analysis: Transmission Power, Latency, and Outage Probability. IEEE Open J. Veh. Technol. 2024, 5, 244–261. [Google Scholar] [CrossRef]
- Space Exploration Holdings, LLC. SpaceX Non-Geostationary Satellite System, Attachment A, Technical Information to Supplement Schedule S; FCC: Washington, DC, USA, 2018; Available online: https://fcc.report/IBFS/SAT-MOD-20181108-00083/1569860.pdf (accessed on 6 December 2023).
- Carrasco-Casado, A.; Biswas, A.; Fields, R.; Grefenstette, B.; Harrison, F.; Sburlan, S.; Toyoshima, M. Optical communication on CubeSats—Enabling the next era in space science. In Proceedings of the 2017 IEEE International Conference on Space Optical Systems and Applications (ICSOS), Naha, Japan, 14–16 November 2017; pp. 46–52. [Google Scholar] [CrossRef]
- Goorjian, P.M. Free-space optical communication for spacecraft and satellites, including cubesats in low earth orbit (LEO). In Proceedings of the Photonic Networks and Devices, Burlingame, CA, USA, 29 July–1 August 2019; Optica Publishing Group: Washington, DC, USA, 2019; p. paper NeM2D.4. [Google Scholar]
- Saathof, R.; Crowcombe, W.; Kuiper, S.; van der Valk, N.; Pettazzi, F.; de Lange, D.; Kerkhof, P.; van Riel, M.; de Man, H.; Truyens, N.; et al. Optical satellite communication space terminal technology at TNO. In Proceedings of the International Conference on Space Optics—ICSO 2018, Chania, Greece, 9–12 October 2018; Sodnik, Z., Karafolas, N., Cugny, B., Eds.; International Society for Optics and Photonics, SPIE: Bellingham, WA, USA, 2019; Volume 11180, p. 111800K. [Google Scholar] [CrossRef]
- Benzi, E.; Troendle, D.C.; Shurmer, I.; James, M.; Lutzer, M.; Kuhlmann, S. Optical inter-satellite communication: The Alphasat and Sentinel-1A in-orbit experience. In Proceedings of the 14th International Conference on Space Operations, Daejeon, Republic of Korea, 16–20 May 2016; p. 2389. [Google Scholar]
- Li, L.; Zhang, X.; Zhang, J.; Xu, C.; Jin, Y. Advanced space laser communication technology on cubesats. ZTE Commun. 2021, 18, 45–54. [Google Scholar]
- Schmidt, C.; Rödiger, B.; Rosano, J.; Papadopoulos, C.; Hahn, M.T.; Moll, F.; Fuchs, C. DLR’s Optical Communication Terminals for CubeSats. In Proceedings of the 2022 IEEE International Conference on Space Optical Systems and Applications (ICSOS), Kyoto, Japan, 28–31 March 2022; pp. 175–180. [Google Scholar] [CrossRef]
- Velazco, J.; Boyraz, O. High data rate inter-satellite omnidirectional optical communicator. In Proceedings of the 32 Annual AIAA/USU Conference on Small Satellites, Logan, UT, USA, 4–9 August 2018. [Google Scholar]
- Zaman, I.U.; Velazco, J.E.; Boyraz, O. Omnidirectional optical crosslinks for CubeSats: Transmitter optimization. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 4556–4566. [Google Scholar] [CrossRef] [PubMed]
- Saeed, N.; Almorad, H.; Dahrouj, H.; Al-Naffouri, T.Y.; Shamma, J.S.; Alouini, M.S. Point-to-Point Communication in Integrated Satellite-Aerial 6G Networks: State-of-the-Art and Future Challenges. IEEE Open J. Commun. Soc. 2021, 2, 1505–1525. [Google Scholar] [CrossRef]
- Chaudhry, A.U.; Yanikomeroglu, H. Free Space Optics for Next-Generation Satellite Networks. IEEE Consum. Electron. Mag. 2021, 10, 21–31. [Google Scholar] [CrossRef]
- Liang, J.; Chaudhry, A.U.; Yanikomeroglu, H. Phasing parameter analysis for satellite collision avoidance in starlink and kuiper constellations. In Proceedings of the 2021 IEEE 4th 5G world forum (5GWF), Montreal, QC, Canada, 13–15 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 493–498. [Google Scholar]
- Chaudhry, A.U.; Yanikomeroglu, H. Laser Intersatellite Links in a Starlink Constellation: A Classification and Analysis. IEEE Veh. Technol. Mag. 2021, 16, 48–56. [Google Scholar] [CrossRef]
- Chaudhry, A.U.; Yanikomeroglu, H. Temporary laser inter-satellite links in free-space optical satellite networks. IEEE Open J. Commun. Soc. 2022, 3, 1413–1427. [Google Scholar] [CrossRef]
- Liang, J.; Chaudhry, A.U.; Chinneck, J.W.; Yanikomeroglu, H.; Kurt, G.K.; Hu, P.; Ahmed, K.; Martel, S. Latency Versus Transmission Power Trade-Off in Free-Space Optical (FSO) Satellite Networks with Multiple Inter-Continental Connections. IEEE Open J. Commun. Soc. 2023, 4, 3014–3029. [Google Scholar] [CrossRef]
- Handley, M. Delay is Not an Option: Low Latency Routing in Space. In Proceedings of the 17th ACM Workshop on Hot Topics in Networks, Redmond, WA, USA, 15–16 November 2018; HotNets ’18. pp. 85–91. [Google Scholar] [CrossRef]
- Perlot, N.; Sofieva, V.F. Qualifying optical inter-satellite links for atmospheric occultations. In Proceedings of the International Conference on Space Optical Systems, Tokyo, Japan, 9–12 November 2009. [Google Scholar]
- Walker, J.G. Satellite constellations. J. Br. Interplanet. Soc. 1984, 37, 559. [Google Scholar]
- Wenzel, H.; Klehr, A.; Braun, M.; Bugge, F.; Erbert, G.; Fricke, J.; Knauer, A.; Ressel, P.; Sumpf, B.; Weyers, M.; et al. Design and realization of high-power DFB lasers. In Proceedings of the Physics and Applications of Optoelectronic Devices, Philadelphia, PA, USA, 25–28 October 2004; SPIE: Bellingham, WA, USA, 2004; Volume 5594, pp. 110–123. [Google Scholar]
- McDowell, J.C. The low earth orbit satellite population and impacts of the SpaceX Starlink constellation. Astrophys. J. Lett. 2020, 892, L36. [Google Scholar] [CrossRef]
- Kotake, H.; Abe, Y.; Fuse, T.; Kubooka, T.; Toyoshima, M. Adaptive optical satellite network architecture. In Proceedings of the International Conference on Space Optics—ICSO 2020, Online, 30 March–2 April 2021; SPIE: Bellingham, WA, USA, 2021; Volume 11852, pp. 685–693. [Google Scholar]
- Gioulis, M.; Kamalakis, T. Pyminisat: A Python Package for Simulating Optical Intersatellite Links in a Minisat Constellation. 2024. Available online: https://github.com/thomaskamalakis/pyminisat (accessed on 22 April 2024).
- Curtis, H.D. Orbital Mechanics for Engineering Students, 7th ed.; Elsevier Butterworth Heinemann: Oxford, UK, 2005. [Google Scholar]
- Sumathi, K.; Balasaraswathi, M.; Boopathi, C.; Singh, M.; Malhotra, J.; Dhasarathan, V. Design of 3.84 Tbps hybrid WDM–PDM based inter-satellite optical wireless communication (IsOWC) system using spectral efficient orthogonal modulation scheme. J. Ambient Intell. Humaniz. Comput. 2020, 11, 4167–4175. [Google Scholar] [CrossRef]
- Chaudhary, S.; Chaudhary, N.; Sharma, S.; Choudhary, B. High speed inter-satellite communication system by incorporating hybrid polarization-wavelength division multiplexing scheme. J. Opt. Commun. 2017, 39, 87–92. [Google Scholar] [CrossRef]
- Betti, S.; Carrozzo, V.; Parca, G. Optical Intersatellite hybrid network links based on WDM technology. In Proceedings of the 2008 10th Anniversary International Conference on Transparent Optical Networks, Athens, Greece, 22–26 June 2008; IEEE: Piscataway, NJ, USA, 2008; Volume 4, pp. 209–212. [Google Scholar]
- Horst, Y.; Bitachon, B.I.; Kulmer, L.; Brun, J.; Blatter, T.; Conan, J.M.; Montmerle-Bonnefois, A.; Montri, J.; Sorrente, B.; Lim, C.B.; et al. Tbit/s line-rate satellite feeder links enabled by coherent modulation and full-adaptive optics. Light. Sci. Appl. 2023, 12, 153. [Google Scholar] [CrossRef]
- Ramaswami, R.; Sivarajan, K.N.; Sasaki, G.H. Optical Networks, A Practical Perspective, 3rd ed.; Elsevier: Amsterdam, The Netherlands, 2010. [Google Scholar]
- Vieira, I.P.; Pita, T.C.; Mello, D.A.A. Modulation and Signal Processing for LEO-LEO Optical Inter-Satellite Links. IEEE Access 2023, 11, 63598–63611. [Google Scholar] [CrossRef]
- Brashears, T.R. Achieving 99% link uptime on a fleet of 100G space laser inter-satellite links in LEO. In Proceedings of the Free-Space Laser Communications XXXVI, San Francisco, CA, USA, 27 January–1 February 2024; SPIE: Bellingham, WA, USA, 2024; Volume 12877, p. 1287702. [Google Scholar]
- Kato, W.; Kawamoto, Y.; Kato, N.; Ariyoshi, M.; Sugyo, K.; Funada, J. Stable and Efficient Inter-Satellite Optical Wireless Communications Through Connection of Intersecting Orbits. In Proceedings of the 2024 IEEE 99th Vehicular Technology Conference (VTC2024-Spring), Singapore, 24–27 June 2024; IEEE: Piscataway, NJ, USA, 2024; pp. 1–5. [Google Scholar]
- Zhu, Y.; Xu, G.; Gao, M.; Chu, H.; Song, Z. Average bit-error rate analysis of an inter-satellite optical communication system under the effect of perturbations. Opt. Express 2024, 32, 36796–36810. [Google Scholar] [CrossRef]
- Stampoulidis, L.; Osman, A.; Sourikopoulos, I.; Winzer, G.; Zimmermann, L.; Dorward, W.; Rodrigo, A.S.; Chiesa, M.; Rotta, D.; Maho, A.; et al. H2020-SPACE-ORIONAS Miniaturized optical transceivers for high-speed optical inter-satellite links. arXiv 2022, arXiv:2210.17304. [Google Scholar]
- Rödiger, B.; Fuchs, C.; Nonay, J.R.; Jung, W.; Schmidt, C. Miniaturized optical Intersatellite communication terminal–CubeISL. In Proceedings of the 2021 IEEE International Conference on Communications Workshops (ICC Workshops), Montreal, QC, Canada, 14–23 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–5. [Google Scholar]
- Edmunds, J.; Thipparapu, N.; Kechagias, M.; Hall, K.; Donnot, A.; Kean, P.; Kehayas, E.; Welch, M. Designing transmit optical amplifiers for the current roll out of optical communication constellations. In Proceedings of the International Conference on Space Optics—ICSO 2022, Dubrovnik, Croatia, 3–7 October 2022; SPIE: Bellingham, WA, USA, 2023; Volume 12777, pp. 1497–1504. [Google Scholar]
- Carrasco-Casado, A.; Shiratama, K.; Kolev, D.; Trinh, P.V.; Ishola, F.; Fuse, T.; Toyoshima, M. Development and space-qualification of a miniaturized CubeSat’s 2-W EDFA for space laser communications. Electronics 2022, 11, 2468. [Google Scholar] [CrossRef]
- Morthier, G.; Roelkens, G.; Baets, R. Optical versus RF free-space signal transmission: A comparison of optical and RF receivers based on noise equivalent power and signal-to-noise ratio. IEEE J. Sel. Top. Quantum Electron. 2021, 28, 1–8. [Google Scholar] [CrossRef]






| Parameter | Symbol | Value |
|---|---|---|
| Number of orbits | 24 | |
| Number of satellites per orbit | 66 | |
| Total number of satellites | N | 1584 |
| Altitude | a | 550 km |
| Distance from Earth’s center | r | 6921 km |
| Orbital period | T | 5730.11 s |
| Angular momentum | h | 52,523.60 /s |
| Inclination | i | 53° |
| Optimal phasing parameter | F | 13 |
| Parameter | Symbol | Units | Value |
|---|---|---|---|
| Laser wavelength | nm | 1550 | |
| Transmitter optical efficiency | 0.8 | ||
| Receiver optical efficiency | 0.8 | ||
| Data rate | Gbps | 1–100 | |
| Receiver telescope diameter | mm | 80 | |
| Transmitter pointing error | μrad | 1 | |
| Receiver pointing error | μrad | 1 | |
| Full transmitting divergence angle | μrad | 4 | |
| Target BER | |||
| Extinction ratio | dB | 20 | |
| Quantum efficiency | 1 | ||
| Amplifier noise figure | dB | 3 | |
| Load resistor | 100 | ||
| Temperature in Kelvin | K | 300 | |
| Link margin | dB | 3 |
| Parameters | A | B | C |
|---|---|---|---|
| 66 | 33 | 132 | |
| 24 | 12 | 48 | |
| N | 1584 | 396 | 6336 |
| i | 53° | 53° | 53° |
| a [Km] | 550 | 550 | 550 |
| F | 13 | 6 | 19 |
| [Km] | 659.3 | 1317.1 | 329.7 |
| [Km] | |||
| [Km] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gioulis, M.; Kamalakis, T.; Alexandropoulos, D. Comprehensive Optical Inter-Satellite Communication Model for Low Earth Orbit Constellations: Analyzing Transmission Power Requirements. Photonics 2025, 12, 392. https://doi.org/10.3390/photonics12040392
Gioulis M, Kamalakis T, Alexandropoulos D. Comprehensive Optical Inter-Satellite Communication Model for Low Earth Orbit Constellations: Analyzing Transmission Power Requirements. Photonics. 2025; 12(4):392. https://doi.org/10.3390/photonics12040392
Chicago/Turabian StyleGioulis, Michail, Thomas Kamalakis, and Dimitris Alexandropoulos. 2025. "Comprehensive Optical Inter-Satellite Communication Model for Low Earth Orbit Constellations: Analyzing Transmission Power Requirements" Photonics 12, no. 4: 392. https://doi.org/10.3390/photonics12040392
APA StyleGioulis, M., Kamalakis, T., & Alexandropoulos, D. (2025). Comprehensive Optical Inter-Satellite Communication Model for Low Earth Orbit Constellations: Analyzing Transmission Power Requirements. Photonics, 12(4), 392. https://doi.org/10.3390/photonics12040392





