Metasurface-Refractive Hybrid Lens Modeling with Vector Field Physical Optics
Abstract
:1. Introduction
2. Formalism
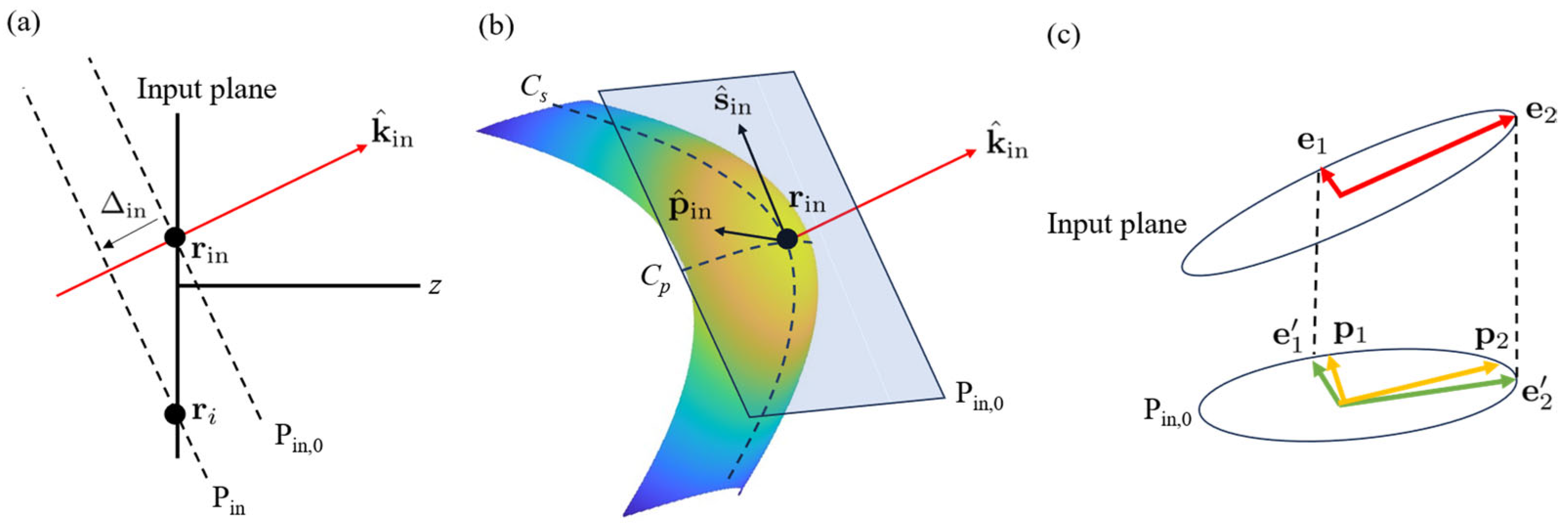
2.1. Properties of Vector Fields
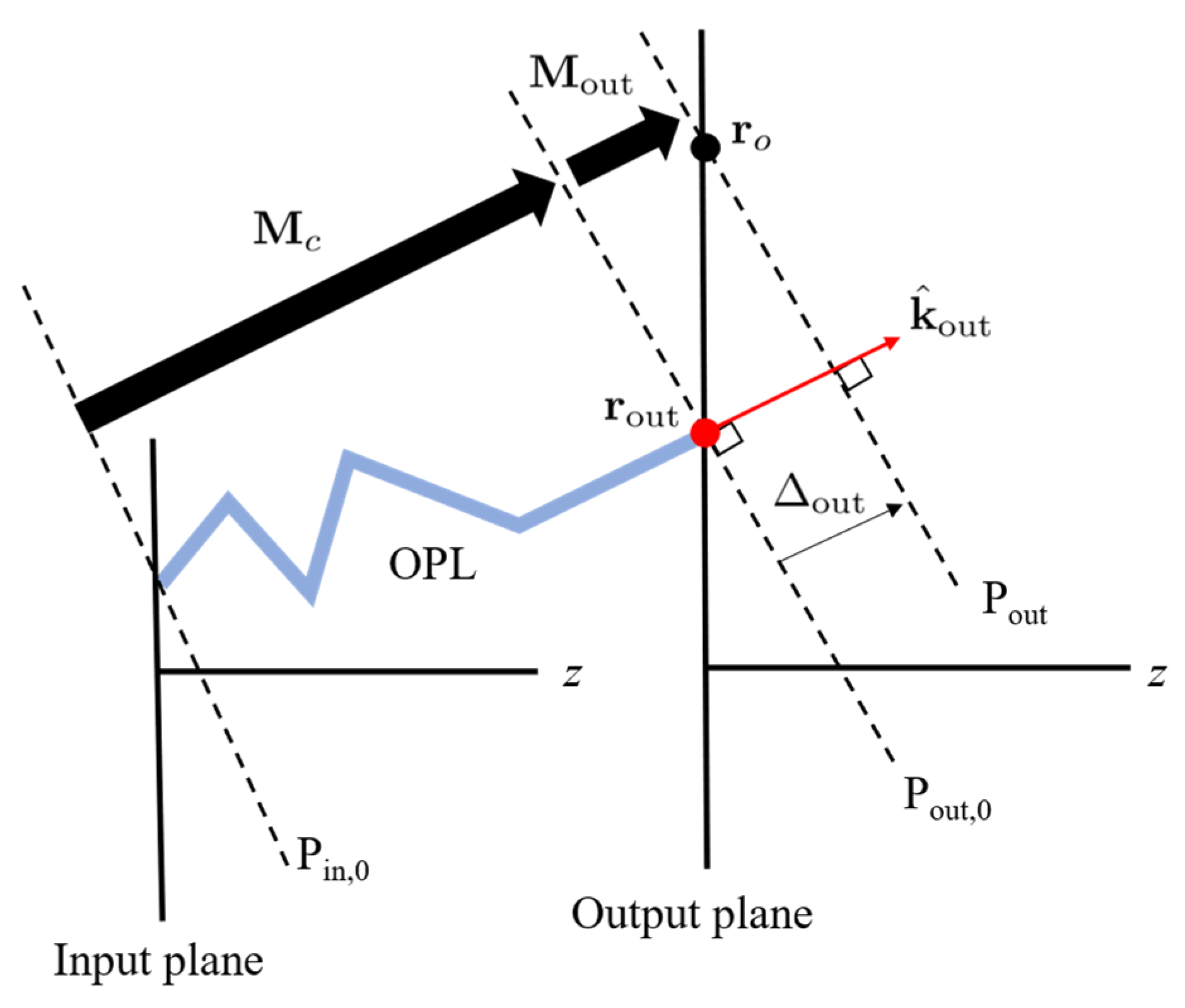
2.2. Propagation in Free Space
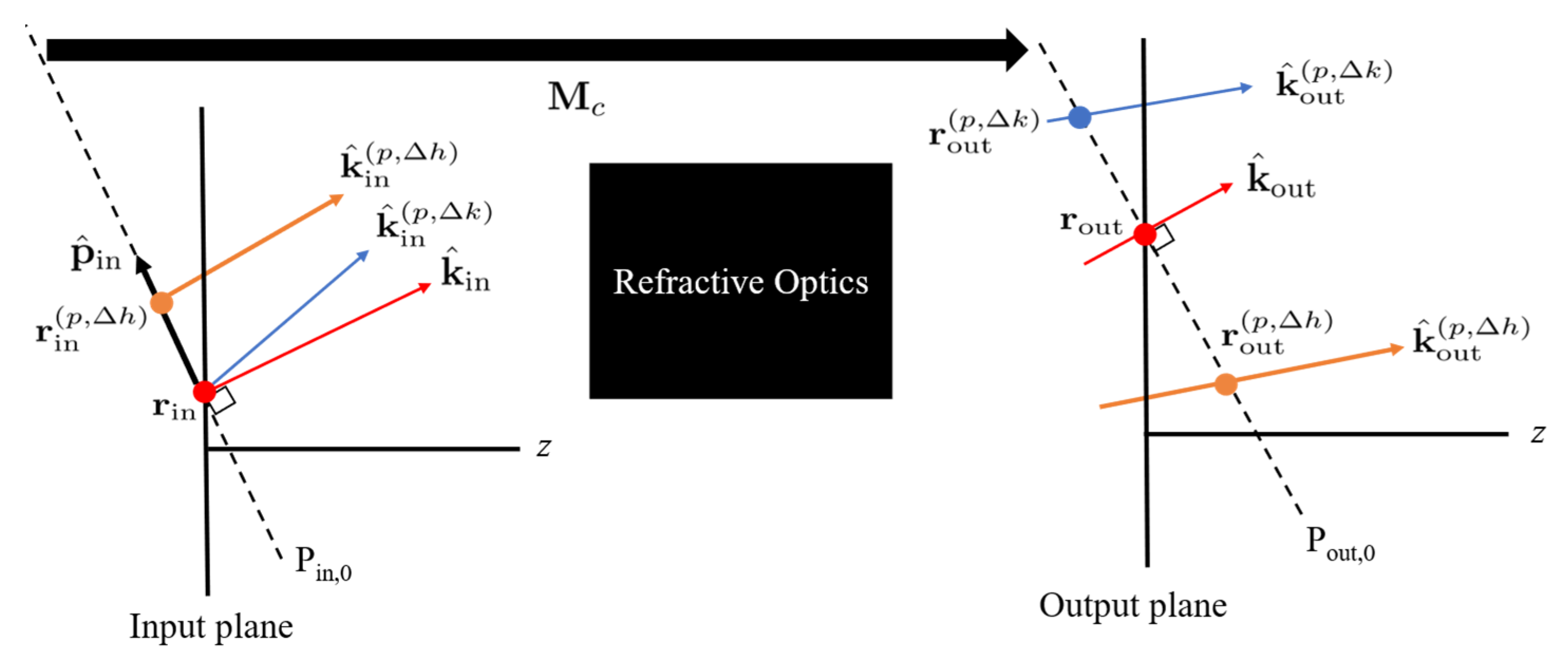
2.3. Propagation Through Refractive Optics
2.3.1. Gaussian Beam Decomposition
2.3.2. Gaussian Beam Propagation
2.3.3. Gaussian Beam Superposition
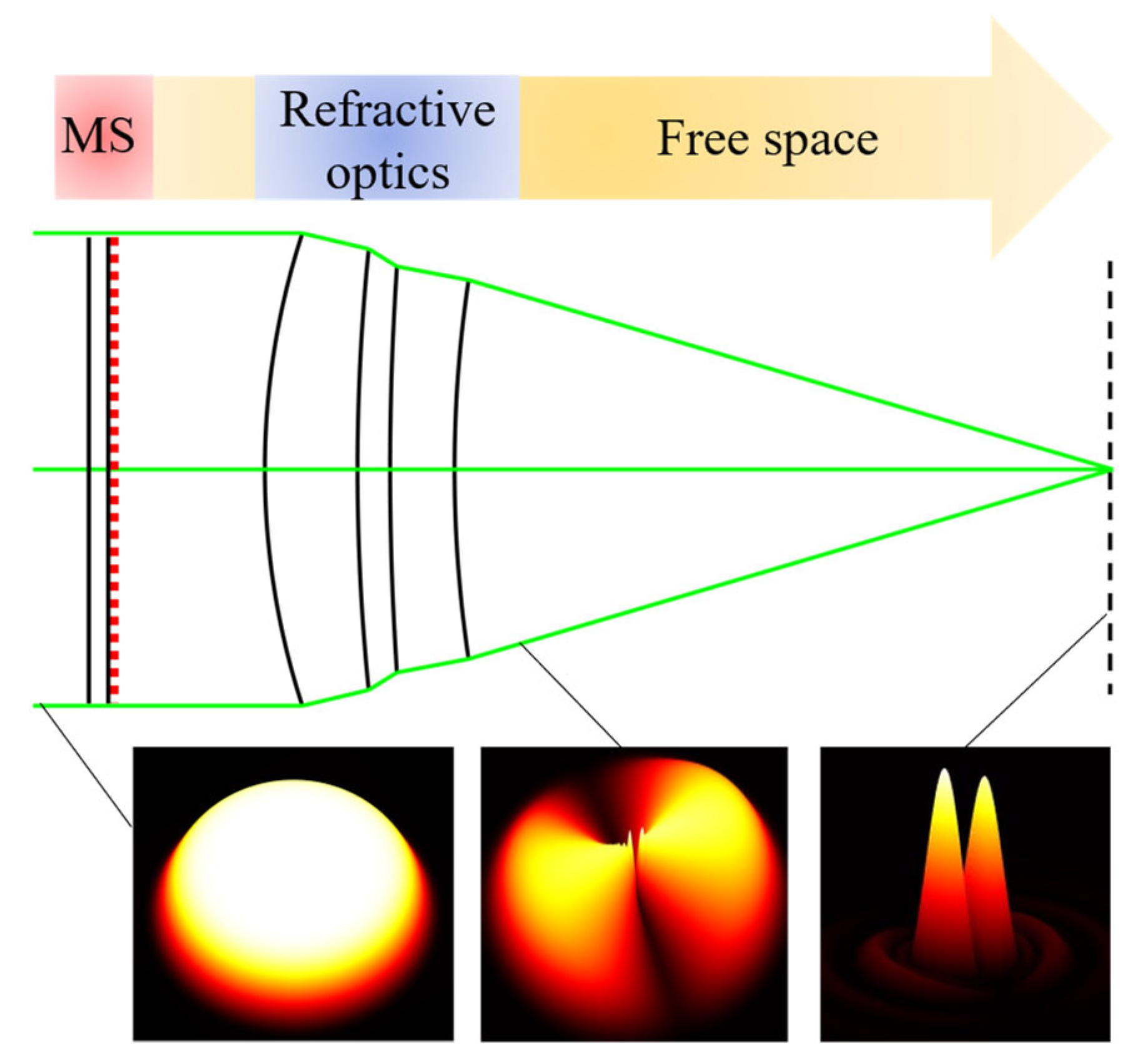
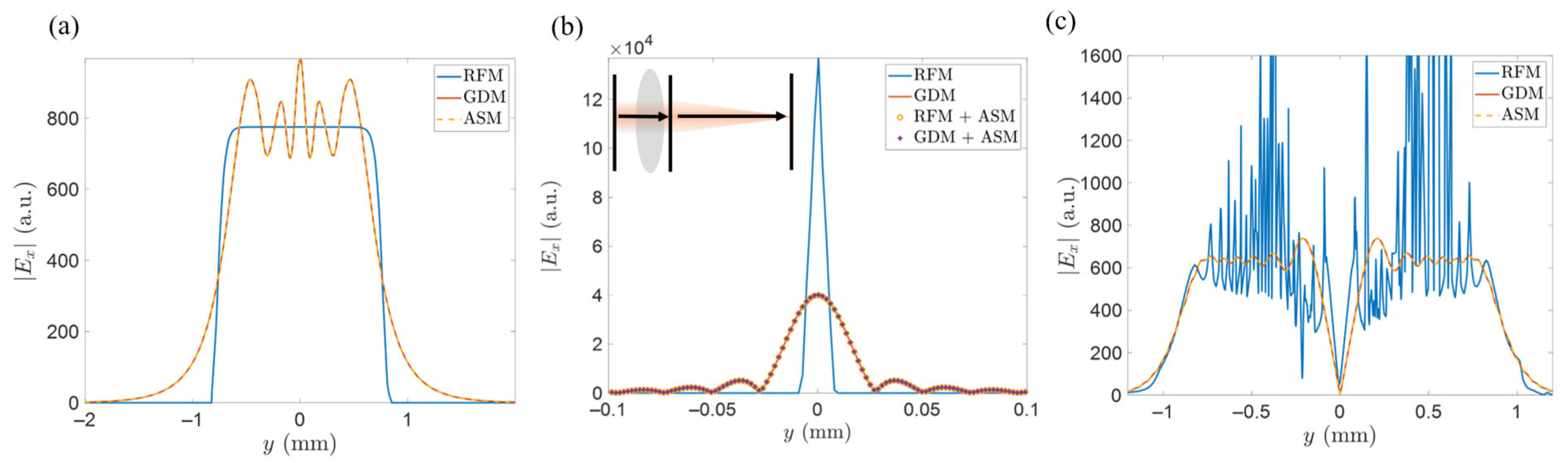
2.4. Comparison to Ray-Field Method
2.5. Propagation Through Metasurfaces
3. Design Examples
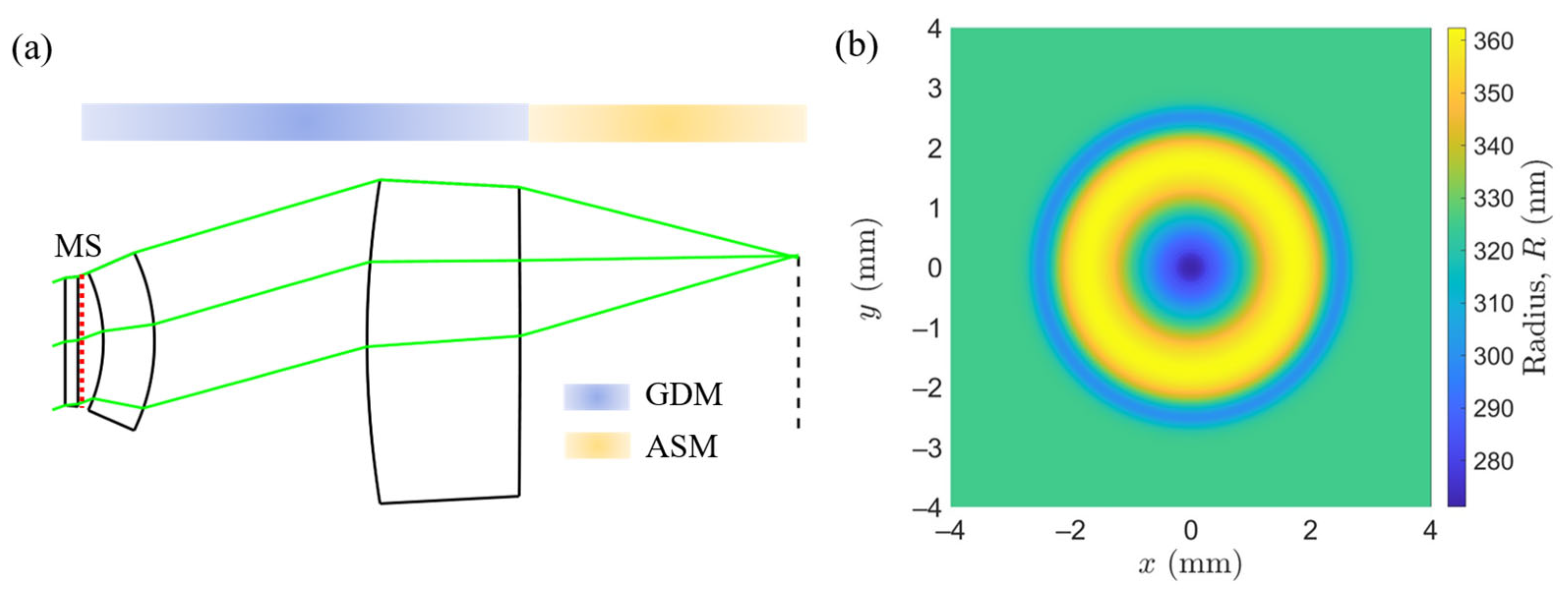
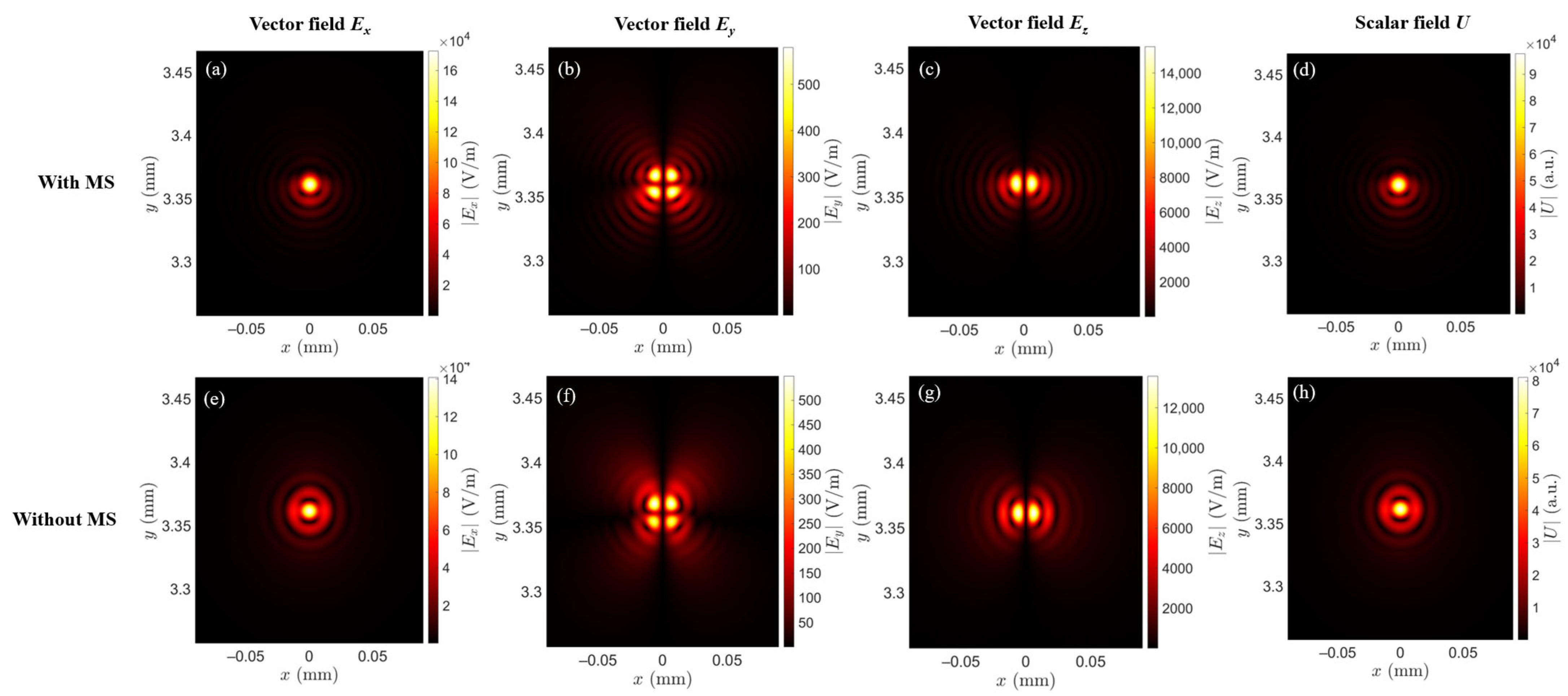
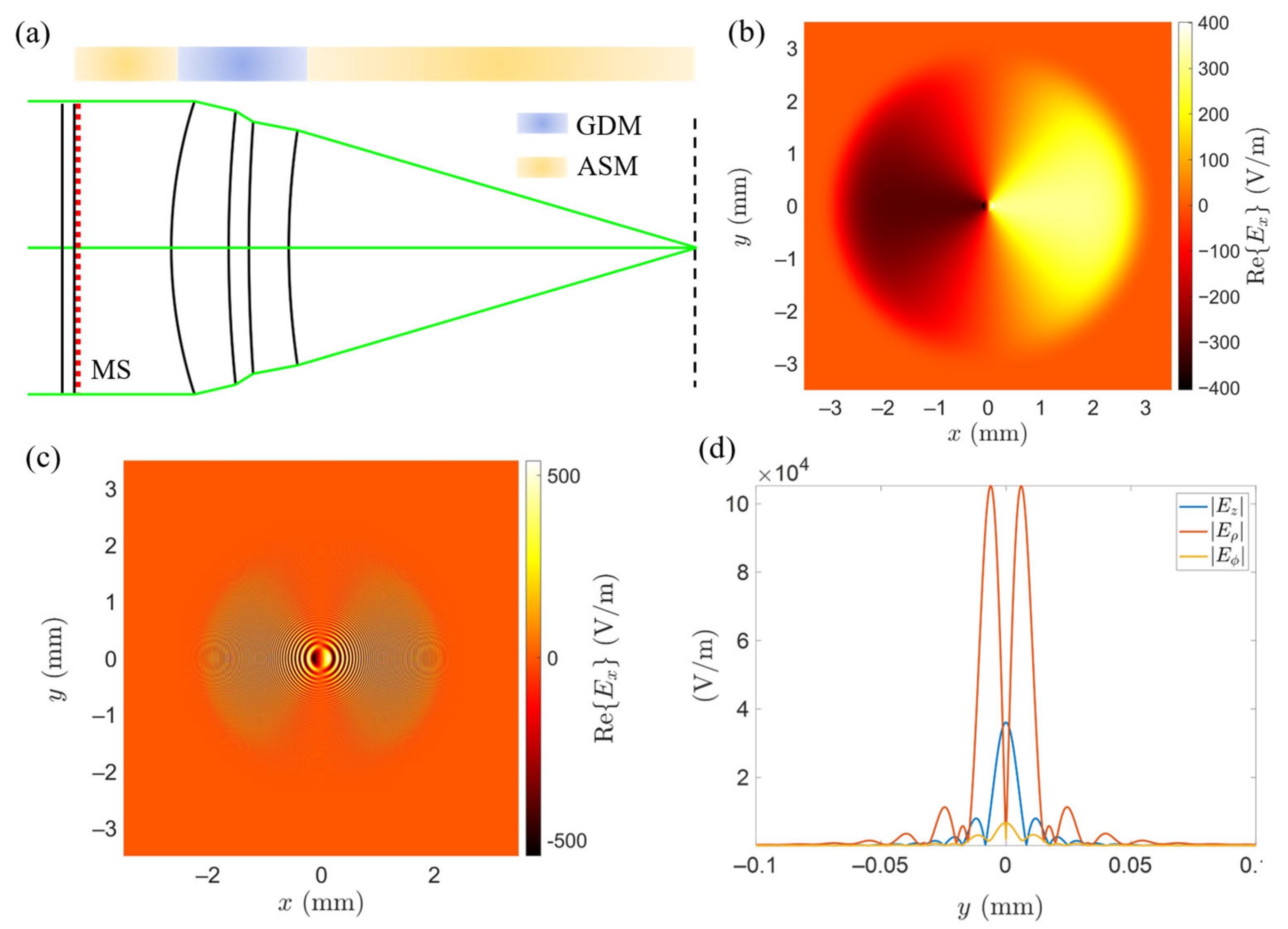
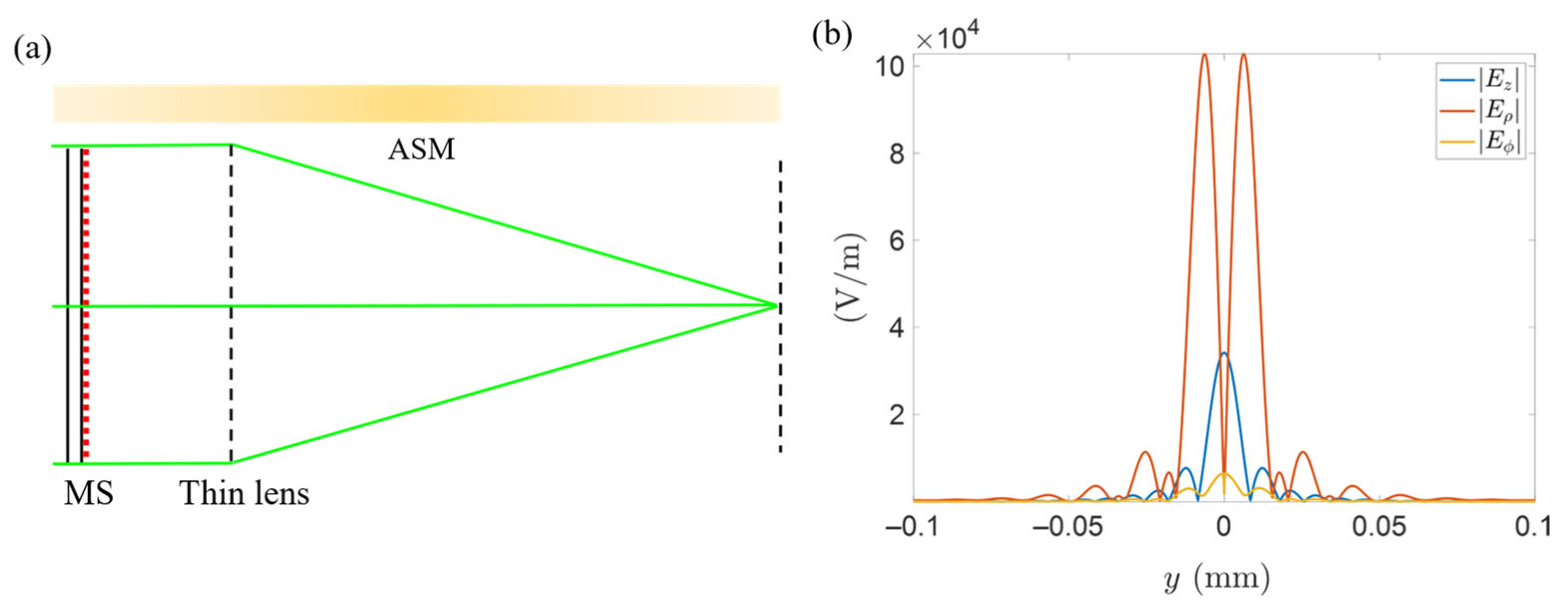
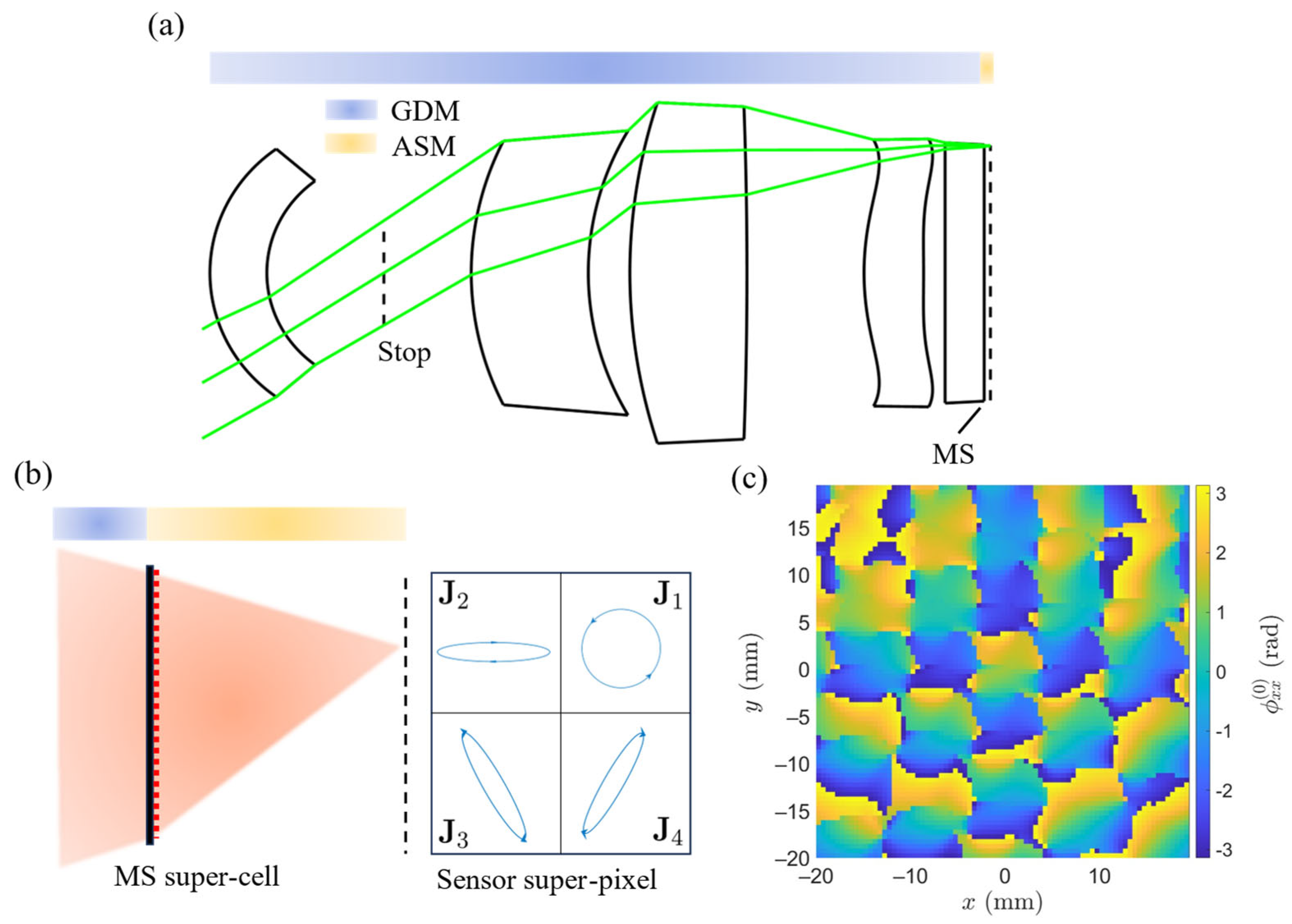
3.1. Hybrid Lens with Aberration-Correcting Metasurface
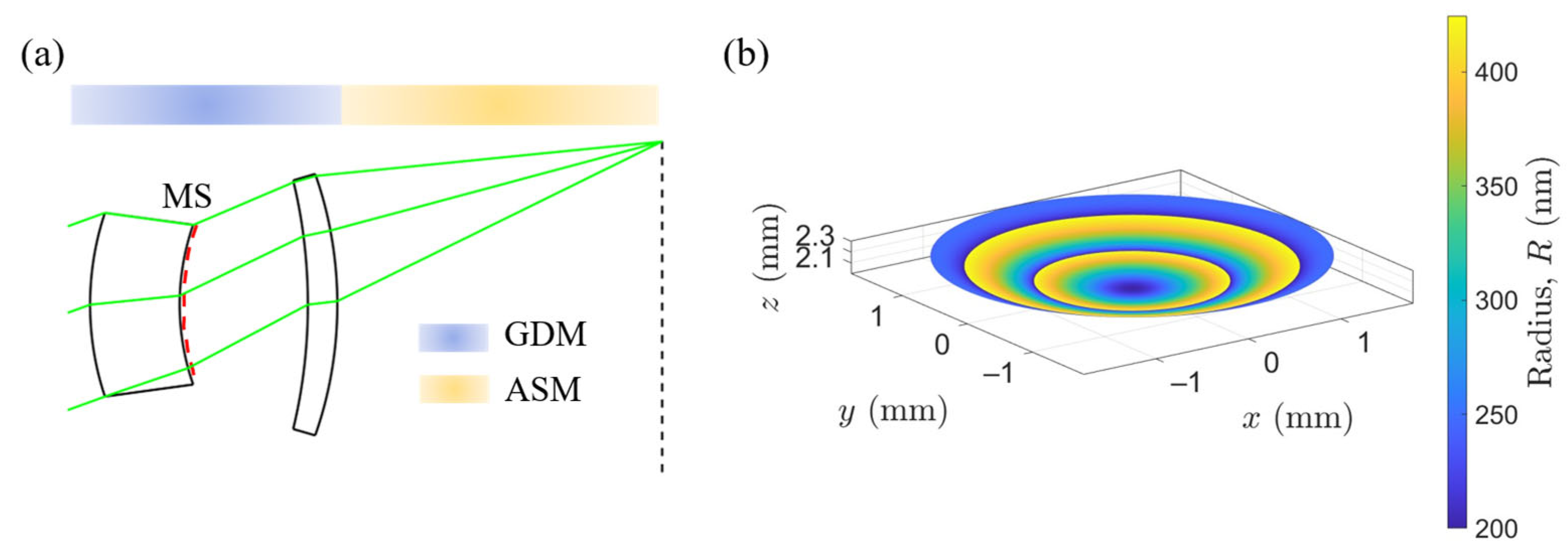
3.2. Hybrid Lens with a Curved Metasurface
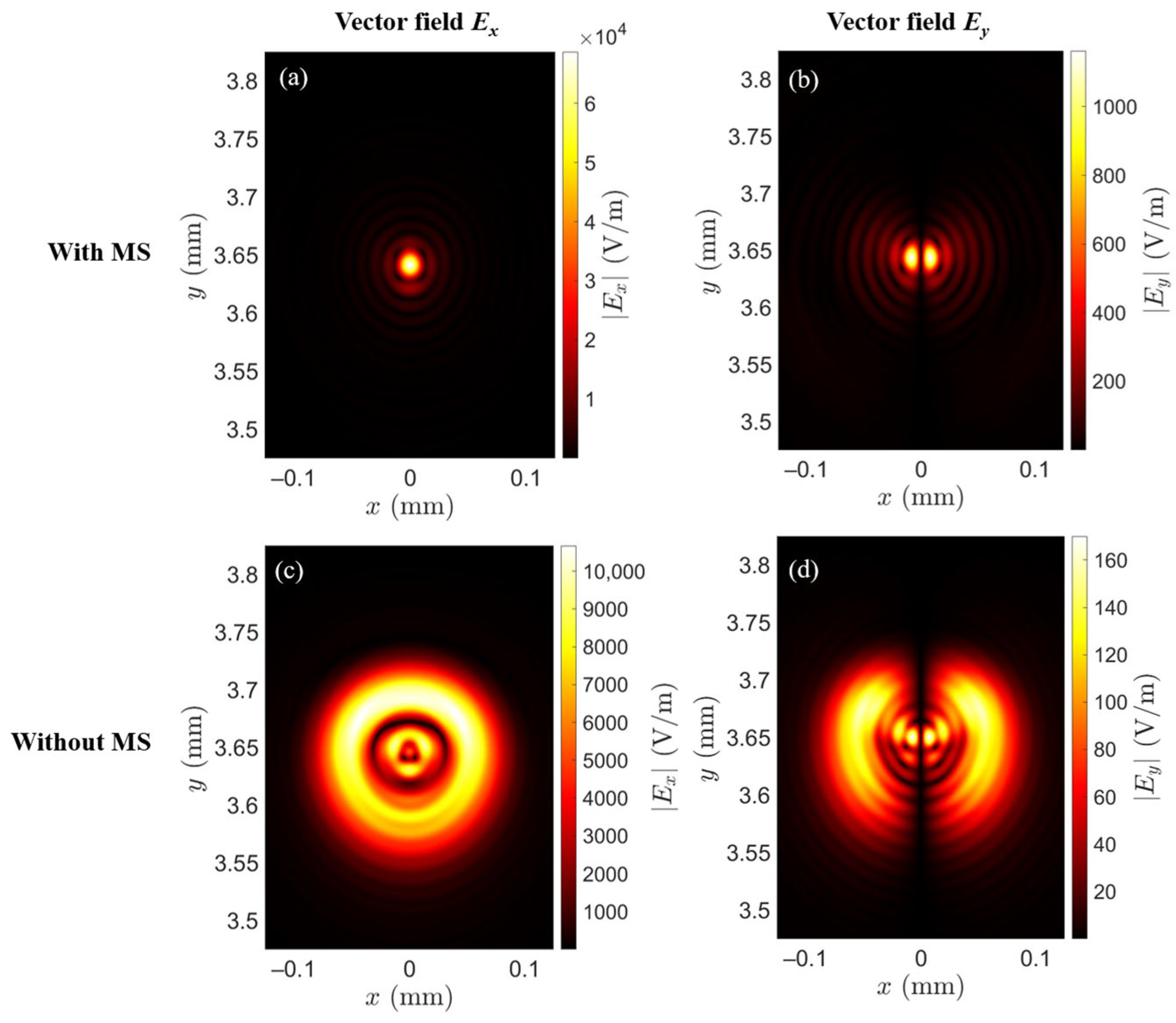
3.3. Focusing a Cylindrical Radially-Polarized Beam
3.4. Adjoint Gradient Optimization
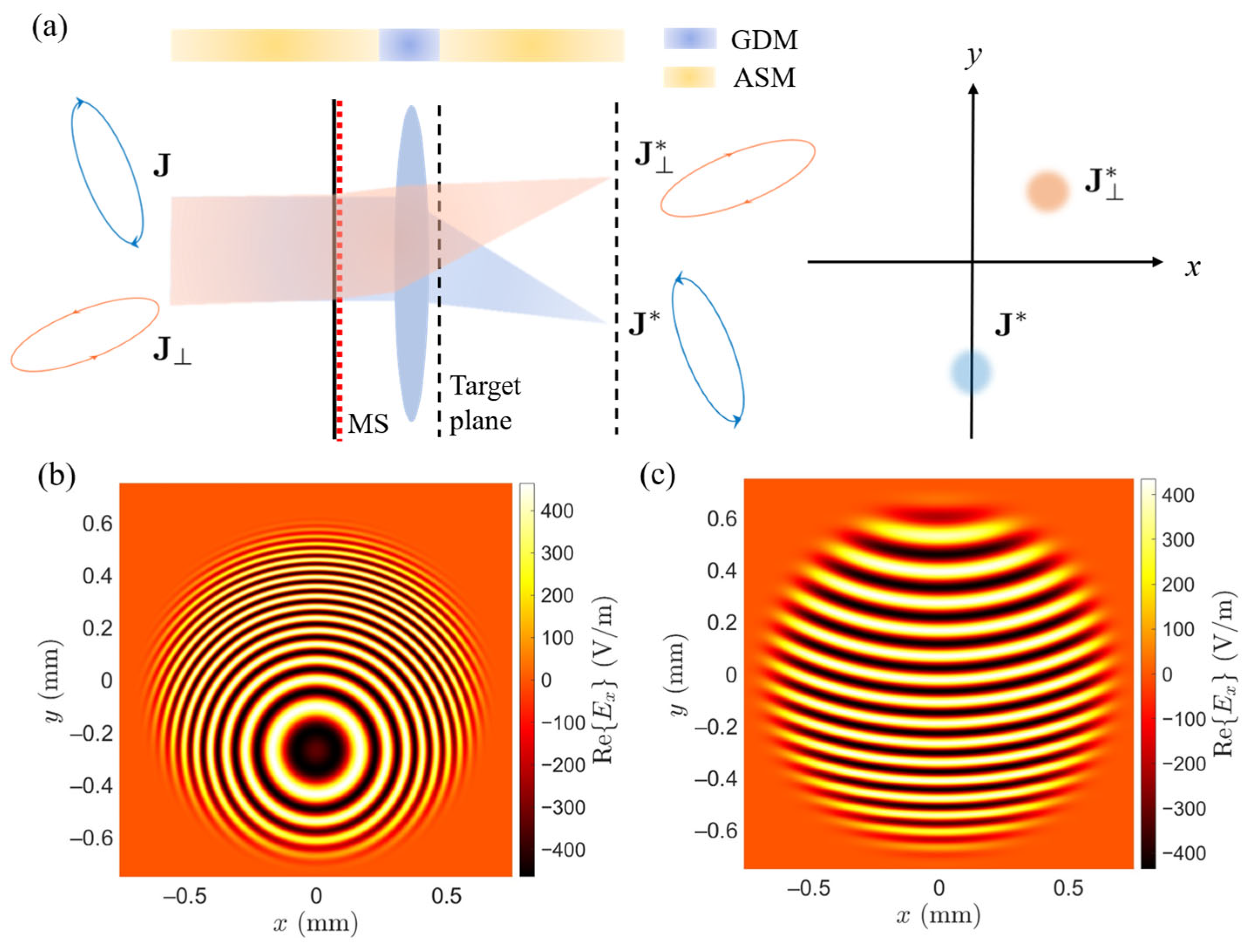
3.5. Full-Stokes Polarization Sensing
4. Discussions
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Safaei, A.; Vázquez-Guardado, A.; Franklin, D.; Leuenberger, M.N.; Chanda, D. High Efficiency Broadband Mid-infrared Flat Lens. Adv. Optical Mater. 2018, 6, 1800216. [Google Scholar] [CrossRef]
- Chen, W.-T.; Zhu, A.Y.; Sisler, J.; Bharwani, Z.; Capasso, F. A Broadband Achromatic Polarization-insensitive Metalens Consisting of Anisotropic Nanostructures. Nat. Commun. 2019, 10, 355. [Google Scholar] [CrossRef] [PubMed]
- Shrestha, S.; Overvig, A.C.; Lu, M.; Stein, A.; Yu, N.-F. Broadband Achromatic Dielectric Metalenses. Light Sci. Appl. 2018, 7, 85. [Google Scholar] [CrossRef]
- Zhou, H.-P.; Chen, L.; Shen, F.; Guo, K.; Guo, Z.-Y. Broadband Achromatic Metalens in the Midinfrared Range. Phys. Rev. Appl. 2019, 11, 024066. [Google Scholar] [CrossRef]
- Hu, S.; Wei, L.; Long, Y.; Huang, S.; Dai, B.; Qiu, L.; Zhuang, S.; Zhang, D. Longitudinal Polarization Manipulation Based on All-Dielectric Terahertz Metasurfaces. Opt. Express 2024, 32, 6963–6976. [Google Scholar] [CrossRef]
- Wang, B.; Dong, F.; Feng, H.; Yang, D.; Song, Z.; Xu, L.; Chu, W.; Gong, Q.; Li, Y. Rochon-Prism-Like Planar Circularly Polarized Beam Splitters Based on Dielectric Metasurfaces. ACS Photonics 2018, 5, 1660–1664. [Google Scholar] [CrossRef]
- Zhang, F.; Yu, H.; Fang, J.; Zhang, M.; Chen, S.; Wang, J.; He, A.; Chen, J. Efficient Generation and Tight Focusing of Radially Polarized Beam from Linearly Polarized Beam with All-Dielectric Metasurface. Opt. Express 2016, 24, 6656–6664. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, Z.; Wang, J.; Wu, J.; Tian, S. Creating Perfect Composite Vortex Beams with a Single All-Dielectric Geometric Metasurface. Opt. Express 2022, 30, 40231–40242. [Google Scholar] [CrossRef]
- Zang, H.; Zhou, X.; Yang, Z.; Yu, Q.; Zheng, C.; Yao, J. Polarization Multiplexed Multifunctional Metasurface for Generating Longitudinally Evolving Vector Vortex Beams. Phys. Lett. A 2024, 497, 129336. [Google Scholar] [CrossRef]
- Huo, P.; Zhang, C.; Zhu, W.; Liu, M.; Zhang, S.; Zhang, S.; Chen, L.; Lezec, H.J.; Agrawal, A.; Lu, Y.; et al. Photonic Spin-Multiplexing Metasurface for Switchable Spiral Phase Contrast Imaging. Nano Lett. 2020, 20, 2791–2798. [Google Scholar] [CrossRef]
- Wen, D.; Yue, F.; Ardron, M.; Chen, X. Multifunctional Metasurface Lens for Imaging and Fourier Transform. Sci. Rep. 2016, 6, 27628. [Google Scholar] [CrossRef]
- Ge, S.; Li, X.; Liu, Z.; Zhao, J.; Wang, W.; Li, S.; Zhang, W. Polarization-Multiplexed Metasurface Enabled Tri-Functional Imaging. Opt. Lett. 2023, 48, 5683–5686. [Google Scholar] [CrossRef]
- Zheng, C.L.; Ni, P.N.; Xie, Y.Y.; Genevet, P. On-Chip Light Control of Semiconductor Optoelectronic Devices Using Integrated Metasurfaces. Opto-Electron. Adv. 2025, 8, 240159. [Google Scholar] [CrossRef]
- Fu, P.; Ni, P.-N.; Wu, B.; Pei, X.-Z.; Wang, Q.-H.; Chen, P.-P.; Xu, C.; Kan, Q.; Chu, W.-G.; Xie, Y.-Y. Metasurface Enabled On-Chip Generation and Manipulation of Vector Beams from Vertical Cavity Surface-Emitting Lasers. Adv. Mater. 2022, 34, 202204286. [Google Scholar] [CrossRef] [PubMed]
- Chen, W.-T.; Zhu, A.Y.; Sisler, J.; Huang, Y.-W.; Yousef, K.; Lee, E.; Qiu, C.-W.; Capasso, F. Broadband Achromatic Metasurface-Refractive Optics. Nano Lett. 2018, 18, 7801–7808. [Google Scholar] [CrossRef] [PubMed]
- Hu, T.; Wang, S.; Wei, Y.; Wen, L.; Feng, X.; Yang, Z.; Zheng, J.; Zhao, M. Design of a Centimeter-Scale Achromatic Hybrid Metalens with Polarization Insensitivity in the Visible. Opt. Lett. 2023, 48, 1898–1901. [Google Scholar] [CrossRef]
- Sawant, R.; Andrén, D.; Martins, R.J.; Khadir, S.; Verre, R.; Käll, M.; Genevet, P. Aberration-Corrected Large-Scale Hybrid Metalenses. Optica 2021, 8, 1405–1411. [Google Scholar] [CrossRef]
- Chu, Y.; Xiao, X.; Ye, X.; Chen, C.; Zhu, S.; Li, T. Design of Achromatic Hybrid Metalens with Secondary Spectrum Correction. Opt. Express 2023, 31, 21399–21406. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, W.; Wang, Y.; Huo, P.; Zhang, H.; Lu, Y.-Q.; Xu, T. Achromatic and Coma-Corrected Hybrid Meta-Optics for High-Performance Thermal Imaging. Nano Lett. 2024, 24, 7609–7615. [Google Scholar] [CrossRef]
- Thomas, S.; George, J.G.; Ferranti, F.; Bhattacharya, S. Metaoptics for Aberration Correction in Microendoscopy. Opt. Express 2024, 32, 9686–9698. [Google Scholar] [CrossRef]
- Cuillerier, A.C.; Borne, J.; Thibault, S. Fast Metasurface Hybrid Lens Design Using a Semi-Analytical Model. J. Opt. Soc. Am. B 2023, 40, 72–78. [Google Scholar] [CrossRef]
- Chen, W.; Shih, K.-H.; Renshaw, C.K. Dispersive Sweatt Model for Broadband Lens Design with Metasurfaces. Photonics 2025, 12, 43. [Google Scholar] [CrossRef]
- Ding, Y.; Stone, B.D.; Bahl, M.; Heller, E.; Scarmozzino, R. Hybrid Refractive-Metalens Design for Imaging Applications. In Proceedings of the SPIE 12666, Current Developments in Lens Design and Optical Engineering XXIV, San Diego, CA, USA, 20–25 August 2023. [Google Scholar] [CrossRef]
- Shih, K.-H.; Renshaw, C.K. Hybrid Meta/Refractive Lens Design with an Inverse Design Using Physical Optics. Appl. Opt. 2024, 63, 4032–4043. [Google Scholar] [CrossRef] [PubMed]
- Wyrowski, F.; Kuhn, M. Introduction to Field Tracing. J. Modern Opt. 2010, 58, 449–466. [Google Scholar] [CrossRef]
- Ashcraft, J.N.; Douglas, E.S.; Kim, D.; Riggs, A.J.E. Hybrid Propagation Physics for the Design and Modeling of Astronomical Observatories: A Coronagraphic Example. J. Astron. Telesc. Instrum. Syst. 2023, 9, 048003. [Google Scholar] [CrossRef]
- Worku, N.G.; Hambach, R.; Gross, H. Decomposition of a Field with Smooth Wavefront into a Set of Gaussian Beams with Non-Zero Curvatures. J. Opt. Soc. Am. A 2018, 35, 1091–1102. [Google Scholar] [CrossRef]
- Harvey, J.E.; Irvin, R.G.; Pfisterer, R.N. Modeling Physical Optics Phenomena by Complex Ray Tracing. Opt. Eng. 2015, 54, 035105. [Google Scholar] [CrossRef]
- Bergbauer, S.; Pollard, D.D. How to Calculate Normal Curvatures of Sampled Geological Surfaces. J. Struct. Geol. 2003, 25, 277–289. [Google Scholar] [CrossRef]
- McCartin, B.J. A Matrix Analytic Approach to Conjugate Diameters of an Ellipse. Appl. Math. Sci. 2013, 7, 1797–1810. [Google Scholar] [CrossRef]
- Yun, G.; Crabtree, K.; Chipman, R.A. Three-Dimensional Polarization Ray-Tracing Calculus I: Definition and Diattenuation. Appl. Opt. 2011, 50, 2855–2865. [Google Scholar] [CrossRef]
- Worku, N.G.; Gross, H. Propagation of Truncated Gaussian Beams and Their Application in Modeling Sharp-Edge Diffraction. J. Opt. Soc. Am. A 2019, 36, 859–868. [Google Scholar] [CrossRef]
- Luce, A.; Mahdavi, A.; Marquardt, F.; Wankerl, H. TMM-Fast, a Transfer Matrix Computation Package for Multilayer Thin-Film Optimization: Tutorial. J. Opt. Soc. Am. A 2022, 39, 1007–1013. [Google Scholar] [CrossRef] [PubMed]
- Shalaginov, M.Y.; An, S.-S.; Yang, F.; Su, P.; Lyzwa, D.; Agarwal, A.M.; Zhang, H.-L.; Hu, J.-J.; Gu, T. Single-Element Diffraction-Limited Fisheye Metalens. Nano Lett. 2020, 20, 7429–7437. [Google Scholar] [CrossRef]
- Fan, C.-Y.; Lin, C.-P.; Su, G.-D.J. Ultrawide-Angle and High-Efficiency Metalens in Hexagonal Arrangement. Sci. Rep. 2020, 10, 15677. [Google Scholar] [CrossRef] [PubMed]
- Arbabi, A.; Arbabi, E.; Kamali, S.M.; Horie, Y.; Han, S.; Faraon, A. Miniature Optical Planar Camera Based on a Wide-Angle Metasurface Doublet Corrected for Monochromatic Aberrations. Nat. Commun. 2016, 7, 13682. [Google Scholar] [CrossRef] [PubMed]
- Groever, B.; Chen, W.-T.; Capasso, F. Meta-Lens Doublet in the Visible Region. Nano Lett. 2017, 17, 4902–4907. [Google Scholar] [CrossRef]
- Pestourie, R.; Pérez-Arancibia, C.; Lin, Z.; Shin, W.; Capasso, F.; Johnson, S.G. Inverse Design of Large-Area Metasurfaces. Opt. Express 2018, 26, 33732–33747. [Google Scholar] [CrossRef]
- An, S.; Zheng, B.; Shalaginov, M.Y.; Tang, H.; Li, H.; Zhou, L.; Dong, Y.; Haerinia, M.; Agarwal, A.M.; Rivero-Baleine, C.; et al. Deep Convolutional Neural Networks to Predict Mutual Coupling Effects in Metasurfaces. Adv. Opt. Mater. 2022, 10, 2102113. [Google Scholar] [CrossRef]
- Torfeh, M.; Arbabi, A. Modeling Metasurfaces Using Discrete-Space Impulse Response Technique. ACS Photonics 2020, 7, 941–950. [Google Scholar] [CrossRef]
- Lin, Z.; Johnson, S.G. Overlapping Domains for Topology Optimization of Large-Area Metasurfaces. Opt. Express 2019, 27, 32445–32453. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, X.; Yu, N.; Yu, Z. Inverse Design of a Dielectric Metasurface by the Spatial Coupled Mode Theory. ACS Photonics 2024, 11, 3019–3025. [Google Scholar] [CrossRef]
- Rumpf, R.C. Improved Formulation of Scattering Matrices for Semi-Analytical Methods That Is Consistent with Convention. Prog. Electromagn. Res. B 2011, 35, 241–261. [Google Scholar] [CrossRef]
- Zhan, Q.; Leger, J.R. Focus Shaping Using Cylindrical Vector Beams. Opt. Express 2002, 10, 324–331. [Google Scholar] [CrossRef] [PubMed]
- Backer, A.S. Computational Inverse Design for Cascaded Systems of Metasurface Optics. Opt. Express 2019, 27, 30308–30331. [Google Scholar] [CrossRef]
- Wang, Z.-Q.; Li, F.-J.; Deng, Q.-M.; Wan, Z.; Li, X.; Deng, Z.-L. Inverse-Designed Jones Matrix Metasurfaces for High-Performance Meta-Polarizers. Chin. Opt. Lett. 2024, 22, 023601. Available online: https://opg.optica.org/col/abstract.cfm?URI=col-22-2-023601 (accessed on 17 April 2025). [CrossRef]
- Zheng, H.; He, M.; Zhou, Y.; Kravchenko, I.I.; Caldwell, J.D.; Valentine, J.G. Compound Meta-Optics for Complete and Lossless Field Control. ACS Nano 2022, 16, 15100–15107. [Google Scholar] [CrossRef]
- Soma, G.; Komatsu, K.; Ren, C.; Nakano, Y.; Tanemura, T. Metasurface-Enabled Non-Orthogonal Four-Output Polarization Splitter for Non-Redundant Full-Stokes Imaging. Opt. Express 2024, 32, 34207–34222. [Google Scholar] [CrossRef]
- Hu, Y.; Wang, Z.; Wang, X.; Ji, S.; Zhang, C.; Li, J.; Zhu, W.; Wu, D.; Chu, J. Efficient Full-Path Optical Calculation of Scalar and Vector Diffraction Using the Bluestein Method. Light Sci. Appl. 2020, 9, 119. [Google Scholar] [CrossRef]
- Rosen, J.; Alford, S.; Allan, B.; Anand, V.; Arnon, S.; Arockiaraj, F.G.; Art, J.; Bai, B.; Balasubramaniam, G.M.; Birnbaum, T.; et al. Roadmap on Computational Methods in Optical Imaging and Holography [Invited]. Appl. Phys. B 2024, 130, 166. [Google Scholar] [CrossRef]
- Isnard, E.; Héron, S.; Lanteri, S.; Elsawy, M. Advancing Wavefront Shaping with Resonant Nonlocal Metasurfaces: Beyond the Limitations of Lookup Tables. Sci. Rep. 2024, 14, 1555. [Google Scholar] [CrossRef]
- Chung, H.; Miller, O.D. High-NA Achromatic Metalenses by Inverse Design. Opt. Express 2020, 28, 6945–6965. [Google Scholar] [CrossRef] [PubMed]
- Xia, D.; Ma, L.; Bai, M.; Shao, X. Fast Algorithm of Arbitrary Beam Propagation Based on Adaptive Elliptical Gaussian Beam Decomposition. In Proceedings of the 2019 International Applied Computational Electromagnetics Society Symposium (ACES), Miami, FL, USA, 14–19 April 2019; Available online: https://ieeexplore.ieee.org/document/8712898 (accessed on 15 April 2025).






| Method | Speed | Application Scope | Accuracy | Strengths | Limitations |
|---|---|---|---|---|---|
| ASM | Fast | Free-space | High | Provides full-wave solution for free-space propagation | Limited to homogeneous, non-refractive media |
| GDM | Moderate | Refractive optics and free-space | High | Captures diffraction effects, handles non-paraxial propagation | Slower than RFM; requires careful decomposition strategy |
| RFM | Very fast | Refractive optics and free-space | Moderate | Efficient for large-scale simulations; works well for smooth wavefronts | Cannot handle diffraction effects; inaccurate near foci or caustics |
| RCWA | Moderate | Nanostructured surfaces (e.g., MS) under the LUA | High for slow-varying structures | Efficiently models MS response including polarization and angular dependence | Limited to slow-varying MS; computationally expensive for large surfaces |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shih, K.-H.; Renshaw, C.K. Metasurface-Refractive Hybrid Lens Modeling with Vector Field Physical Optics. Photonics 2025, 12, 401. https://doi.org/10.3390/photonics12040401
Shih K-H, Renshaw CK. Metasurface-Refractive Hybrid Lens Modeling with Vector Field Physical Optics. Photonics. 2025; 12(4):401. https://doi.org/10.3390/photonics12040401
Chicago/Turabian StyleShih, Ko-Han, and C. Kyle Renshaw. 2025. "Metasurface-Refractive Hybrid Lens Modeling with Vector Field Physical Optics" Photonics 12, no. 4: 401. https://doi.org/10.3390/photonics12040401
APA StyleShih, K.-H., & Renshaw, C. K. (2025). Metasurface-Refractive Hybrid Lens Modeling with Vector Field Physical Optics. Photonics, 12(4), 401. https://doi.org/10.3390/photonics12040401





