Application of Deep Learning in the Phase Processing of Digital Holographic Microscopy

Abstract

Digital holographic microscopy (DHM) provides numerous advantages, such as noninvasive sample analysis, real-time dynamic detection, and three-dimensional (3D) reconstruction, making it a valuable tool in fields such as biomedical research, cell mechanics, and environmental monitoring. To achieve more accurate and comprehensive imaging, it is crucial to capture detailed information on the microstructure and 3D morphology of samples. Phase processing of holograms is essential for recovering phase information, thus making it a core component of DHM. Traditional phase processing techniques often face challenges, such as low accuracy, limited robustness, and poor generalization. Recently, with the ongoing advancements in deep learning, addressing phase processing challenges in DHM has become a key research focus. This paper provides an overview of the principles behind DHM and the characteristics of each phase processing step. It offers a thorough analysis of the progress and challenges of deep learning methods in areas such as phase retrieval, filtering, phase unwrapping, and distortion compensation. The paper concludes by exploring trends, such as ultrafast 3D holographic reconstruction, high-throughput holographic data analysis, multimodal data fusion, and precise quantitative phase analysis.

1. Introduction

The concept of digital holography was first introduced by Professor Goodman in 1967, marking the beginning of holographic technology development [1]. However, in the 1970s and 1980s, digital holography faced significant challenges in realizing its full potential due to constraints in imaging hardware and computational power. In the 1990s, the development of high-resolution charge-coupled devices (CCDs) allowed CCDs to replace traditional photosensitive media, such as photographic and laser plates, for recording holograms. This shift enabled the use of digital methods to simulate optical diffraction, facilitating the full digitalization of both hologram recording and reconstruction.

Digital holographic microscopy (DHM) is a technology that combines traditional optical microscopy with holographic phase imaging techniques [2]. It provides benefits, such as noninvasive sample analysis, real-time dynamic detection, and three-dimensional (3D) reconstruction [3]. Furthermore, DHM allows for the quantitative measurement of a sample’s 3D morphological characteristics. This technology has found widespread use in fields such as biomedical research [4,5], cell mechanics studies [6], and environmental monitoring [7].

The goal of phase processing is to recover the complete phase information of an object from incomplete data, thereby obtaining its 3D shape and characteristics. However, traditional phase processing methods in DHM face several challenges, such as high computational complexity, poor resistance to noise, phase ambiguity, and limited real-time performance. Additionally, as the demand for higher resolution, increased imaging precision, and 3D imaging grows, issues such as larger data volumes, more complex scenes, and diverse equipment have become more prominent.

As noted by Rivenson et al., recent advancements in deep learning have led to significant progress in holography and coherent imaging by effectively addressing their inherent challenges while preserving their fundamental benefits [8]. Unlike traditional methods, deep learning-based phase processing techniques do not require prior knowledge and can automatically manage complex, nonlinear relationships. These methods have been progressively applied to various steps, such as phase retrieval [9], phase filtering [10], phase unwrapping [11], and phase distortion compensation [12]. Recently, the use of deep learning in solving phase processing challenges in DHM has become a major research focus in the field.

Deep learning, inspired by the structure and function of the human brain, utilizes deep neural networks composed of multiple layers of interconnected neurons through which information is propagated [13].

This paper provides a brief overview of the fundamental principles of DHM and emphasizes its potential advantages in addressing the challenges faced by traditional methods. It also examines the application of current deep learning methods in phase retrieval, phase filtering, phase unwrapping, and phase distortion compensation, while comparing the performance of various deep learning approaches. Furthermore, the paper highlights the limitations of existing methods and offers perspectives on future developments in the field, such as ultrafast 3D holographic reconstruction, high-throughput holographic data analysis, precise quantitative phase analysis, and multimodal data fusion. The aim is to offer valuable insights for advancing phase processing techniques in DHM.

2. Principles of Digital Holographic Microscopy

2.1. Theoretical Foundations of Digital Holographic Microscopy

The evolution of quantitative phase imaging (QPI) technology began with the introduction of phase contrast microscopy in 1942, followed by a major breakthrough in holography in 1962, and the further development of digital holography in 1999. Over time, QPI has become a highly accurate imaging technique that is now widely applied in various fields, such as biomedical research and materials science.

QPI addresses the challenge of phase information loss in optical imaging by quantitatively measuring the changes in diffraction patterns or interference fringes caused by variations in the refractive index, thus extracting the phase information of the object [14].

Holographic microscopy (HM), a prominent technique within the QPI framework, works by combining a reference wave with an object wave to create interference, converting phase information into intensity, which is then captured in a hologram. When a reconstruction wave is used to illuminate the hologram, the phase and amplitude distribution of the object can be restored. With the development of CCDs and complementary metal-oxide-semiconductor (CMOS) sensors, hologram recording shifted from photographic plates to digital methods. The interference pattern is projected onto a high-resolution CCD or CMOS sensor for capture, and digital signal processing techniques are applied for decoding and reconstruction, allowing for the recording and reproduction of 3D object images [15].

2.1.1. Digital Holographic Microscopy Recording

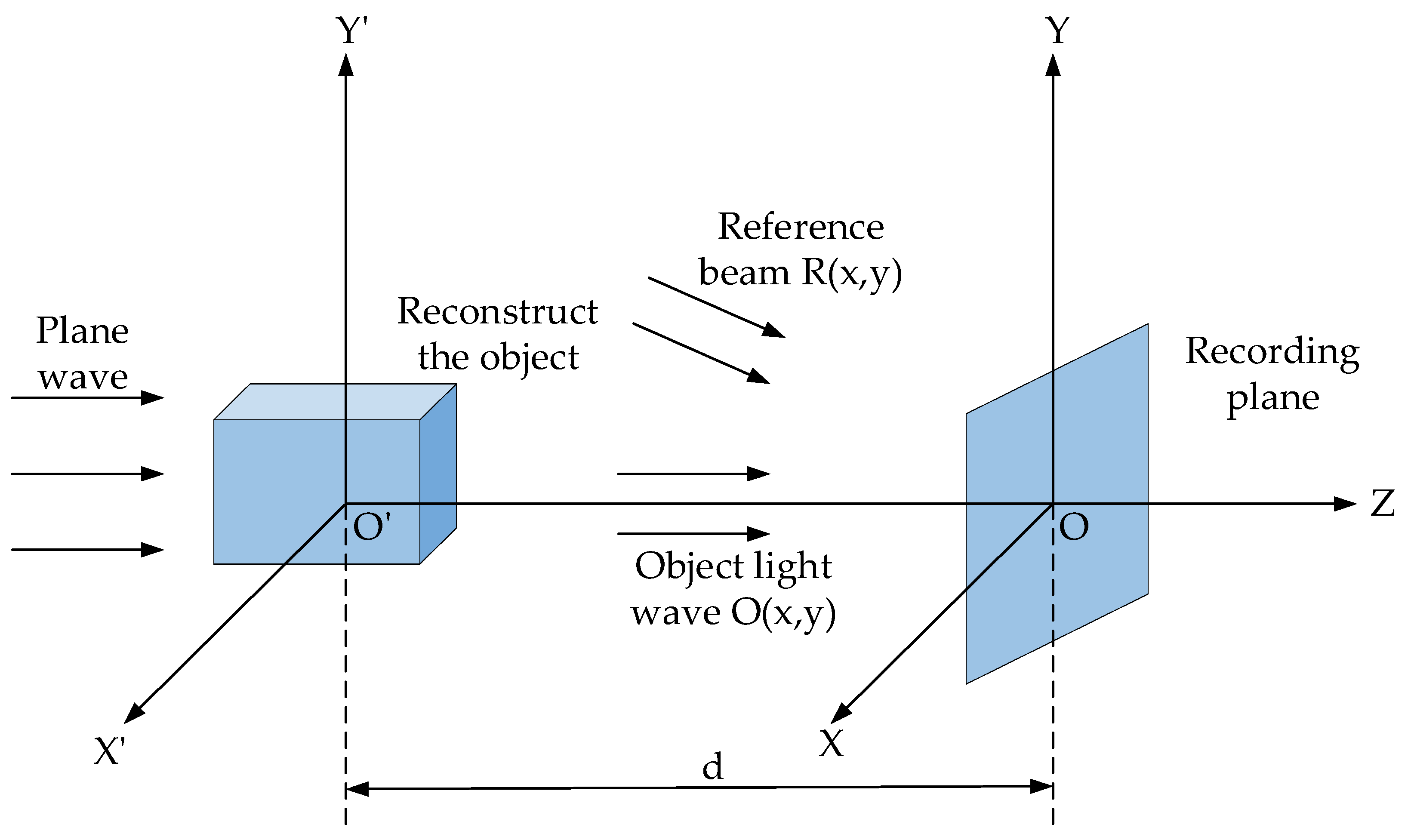
The measurement principle of digital holography follows the same basic concept as traditional optical holography, with the key difference being that digital holography utilizes an electronic imaging sensor instead of a traditional holographic plate to record a digital hologram. Figure 1 illustrates the optical path for recording a digital hologram. In this setup, X’0’Y’ represents the object plane, X0Y signifies the recording plane where the CCD photosensitive surface is located, and d indicates the recording distance of the digital holography system. When the object wave and reference wave are illuminated simultaneously, the hologram is captured by the CCD based on the principle of light interference, thereby achieving the digitalization of the hologram.

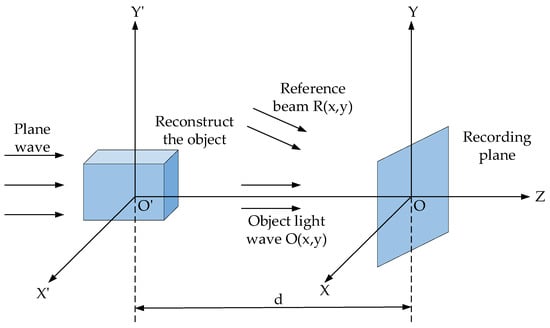
Figure 1. Schematic of the digital holography recording process.

Let the object wave $O\left(x,y\right)$, generated on the object plane by the illumination of the observed object, and the reference wave $R\left(x,y\right)$, be represented by the following mathematical expressions:

$$O\left(x,y\right)=A_0\left(x,y\right)\mathit{exp}\left[-i{\phi }_0\left(x,y\right)\right]$$

(1)

$$R\left(x,y\right)=A_R\left(x,y\right)\mathit{exp}\left[-ik \mathit{sin} \theta y\right]$$

(2)

where $A_0$ and $A_R$ denote the amplitudes of the object wave and reference wave, respectively; $k=2\pi /\lambda$, where $\lambda$ is the light’s wavelength; and θ is the angle between the reference wave and the z-axis.

The intensity distribution of the interference pattern created by the two waves at the recording plane is expressed as

$$I\left(x,y\right)={\left|O\left(x,y\right)\right|}^2+{\left|R\left(x,y\right)\right|}^2+O\left(x,y\right)R^{*}\left(x,y\right)+O^{*}\left(x,y\right)R\left(x,y\right)$$

(3)

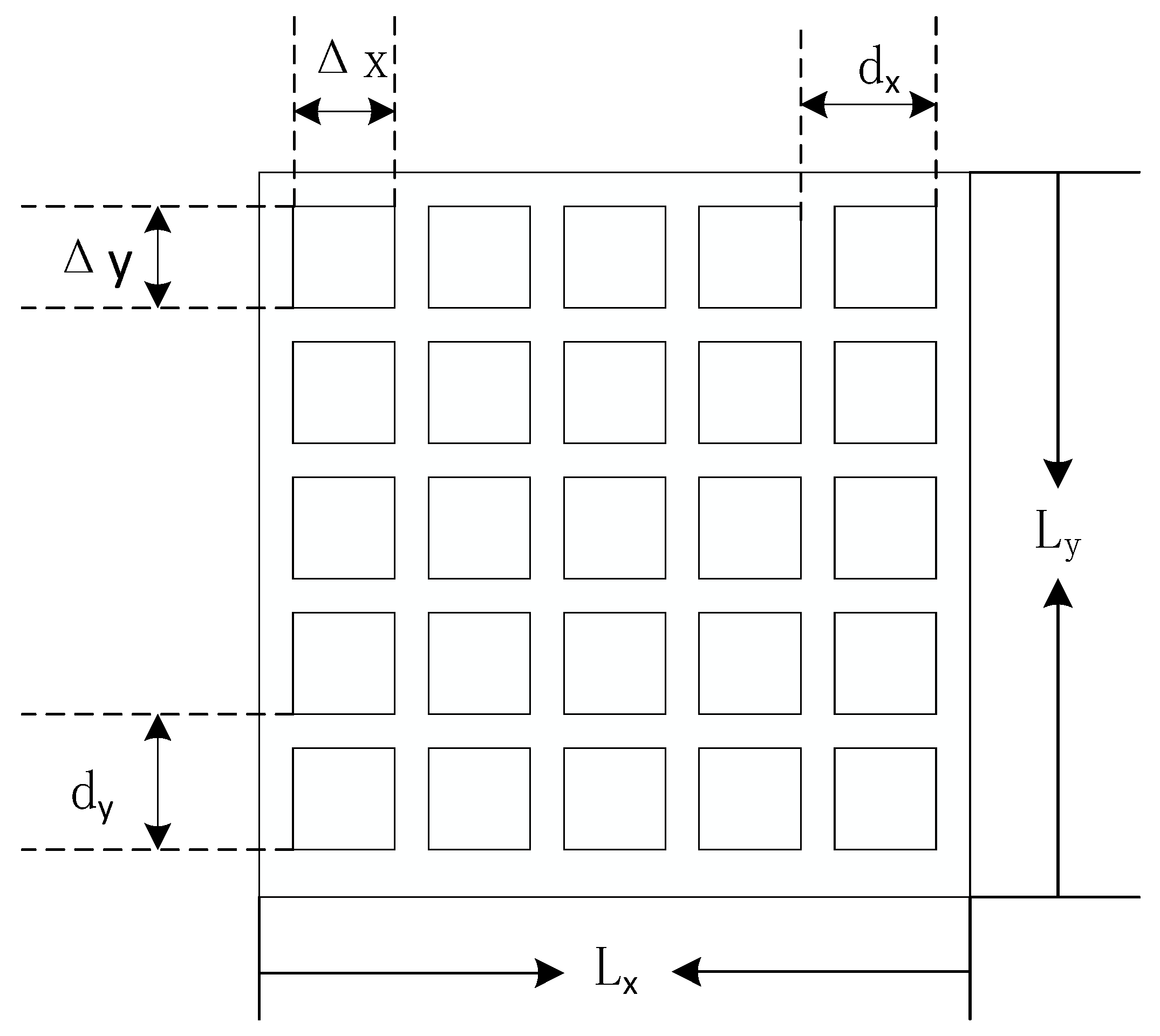
where $O^{\mathrm{*}}\left(x,y\right)$ and $R^{\mathrm{*}}\left(x,y\right)$ are the complex conjugates of the object wave and reference wave, respectively. The CCD captures the interference light intensity and converts it into an electrical signal. The structural schematic of the CCD is presented in Figure 2. Let the dimensions of the CCD’s photosensitive surface be $L_x$ and $L_y$, the pixel size be $∆x\times ∆y$, the number of pixels be $M_x\times M_y$, and the pixel interval be $d_x\times d_y$, where $M_x=L_x/∆x$ and $M_y=L_y/∆y$. The discretized interference intensity recorded by the CCD can then be expressed as

$$I\left(p,q\right)=I_H\left(x,y\right)\mathrm{rect}\left({\displaystyle \frac{x}{L_x}},{\displaystyle \frac{y}{L_y}}\right)\sum _{p=-{\displaystyle \frac{M_x}{2}}}^{{\displaystyle \frac{M_x}{2}}-1}\sum _{q=-{\displaystyle \frac{M_y}{2}}}^{{\displaystyle \frac{M_y}{2}}-1}\delta \left(x-p\mathsf{\Delta }x,y-q\mathsf{\Delta }y\right)$$

(4)

$$rect(t)=\{\begin{array}{cc}1,& \mathit{if}\left|t\right|\le 0.5\\ 0,& \mathit{if}\left|t\right|>0.5\end{array}$$

(5)

where p and q refer to integers within specified ranges $-M_x/2\le p\le M_x/2-1$ and $-M_y/2\le q\le M_y/2-1$, and $\delta (x,y)$ signifies a two-dimensional Dirac delta function, which is an extension of the one-dimensional Dirac delta function, $\delta \left(x\right)$. The one-dimensional Dirac delta function, $\delta \left(x\right)$, is defined as $\delta (x)=\{\begin{array}{cc}\mathrm{\infty },& \mathrm{if} x=0\\ 0,& \mathrm{if} x\ne 0\end{array}$. The two-dimensional Dirac delta function, $\delta (x,y)$, can be formulated as the product of two one-dimensional delta functions: $\delta (x,y)=\delta \left(x\right)\delta \left(y\right)$. Finally, the hologram recorded by the CCD is stored as a numerical matrix in the computer.

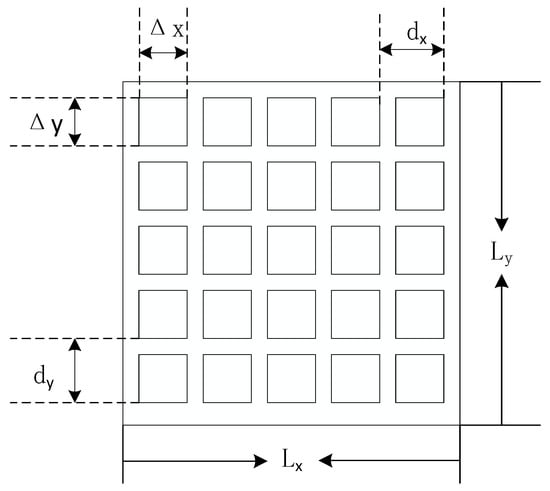
Figure 2. Schematic of the CCD image sensor structure.

2.1.2. Digital Holographic Microscopy Reconstruction

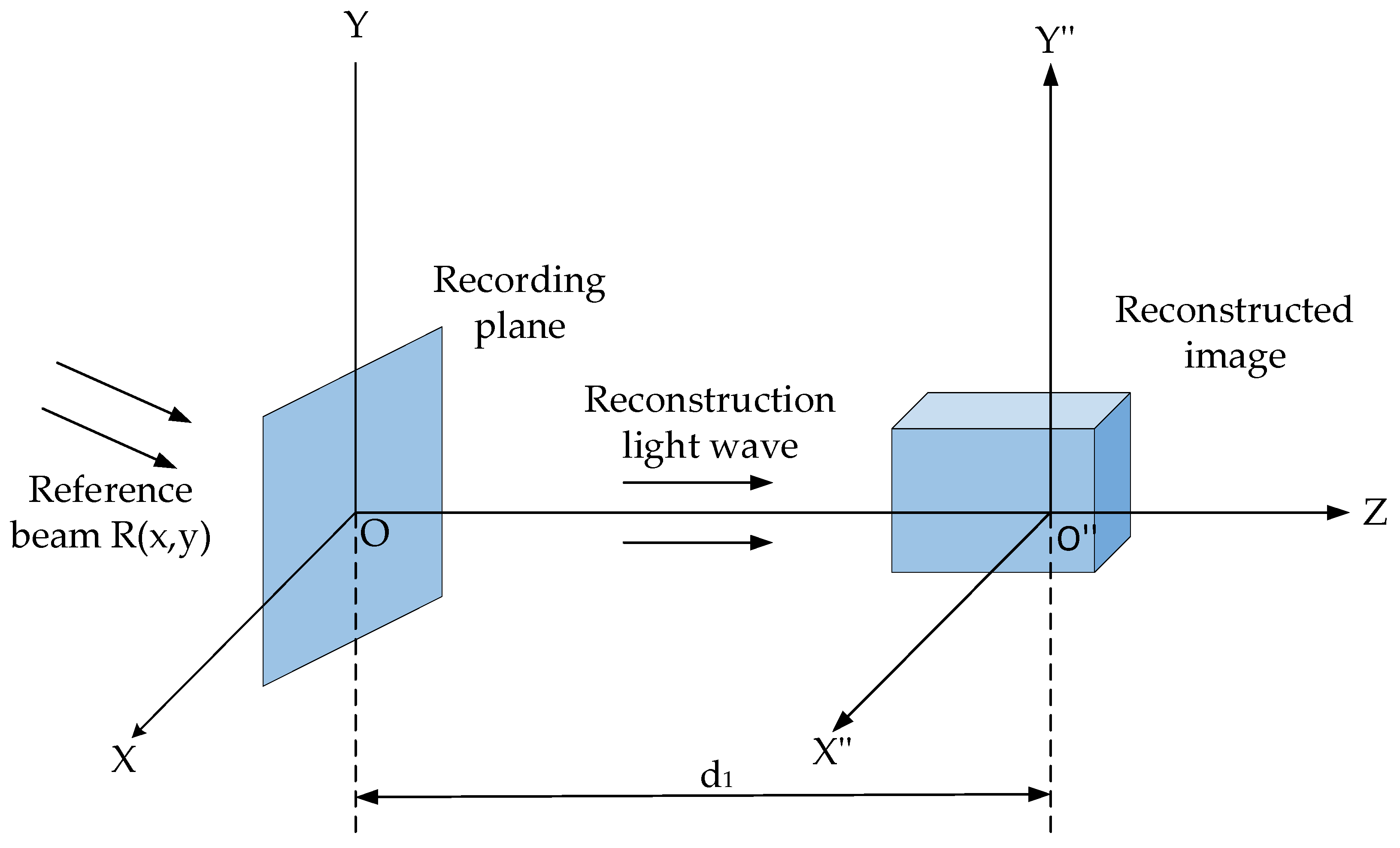
The digital holography reconstruction process involves digitizing the recorded interference image and inputting it into a computer system. The computer then simulates the illumination of the hologram by light waves and the diffraction of emitted light reaching the observation plane. This allows for the calculation of both the intensity and phase information of the object being measured. Figure 3 illustrates the hologram reconstruction process, where the hologram is positioned in the XOY plane, and the reconstructed image is in the X″O″Y″ plane. The distance d₁ represents the reconstruction distance.

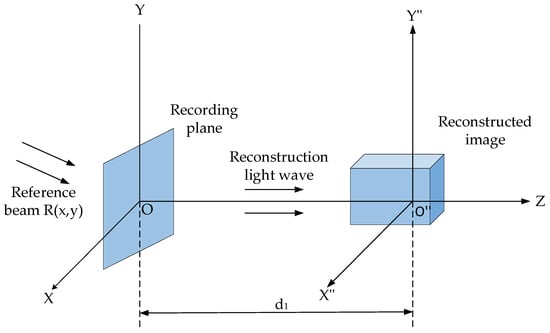
Figure 3. Schematic of the digital holographic reconstruction process.

Let the complex amplitude of the light wave after illuminating the hologram be denoted as $U(x,y)$. During the reconstruction process, a numerical reconstruction algorithm is employed to obtain the complex amplitude of the object wave at the image plane, denoted as $U_1(x_1,y_1)$. From the complex amplitude distribution, the intensity $I_1\left(x_1,y_1\right)$ and phase ${\Phi }_1\left(x_1,y_1\right)$ of the reconstructed image can then be calculated as follows:

$$I_1\left(x_1,y_1\right)=U_1\left(x_1,y_1\right)U_1^{*}\left(x_1,y_1\right)$$

(6)

$${\Phi }_1\left(x_1,y_1\right)=\mathit{arctan}{\displaystyle \frac{\mathit{Im}\left[U_1\left(x_1,y_1\right)\right]}{\mathit{Re}\left[U_1\left(x_1,y_1\right)\right]}}$$

(7)

where $\mathit{Im}\left[U_1\left(x_1,y_1\right)\right]$ and $\mathit{Re}\left[U_1\left(x_1,y_1\right)\right]$ denote the imaginary and real parts of $U_1\left(x_1,y_1\right)$, respectively. Since the phase calculated using the arctangent function is wrapped within the range [$-\pi ,\pi$], phase unwrapping is necessary to recover the true phase of the object.

2.2. Signal Changes in Phase Processing

Phase processing is a critical aspect of DHM, encompassing several key steps, such as phase recovery, filtering, phase unwrapping, and distortion compensation. These processes together guarantee the quality and precision of the imaging results.

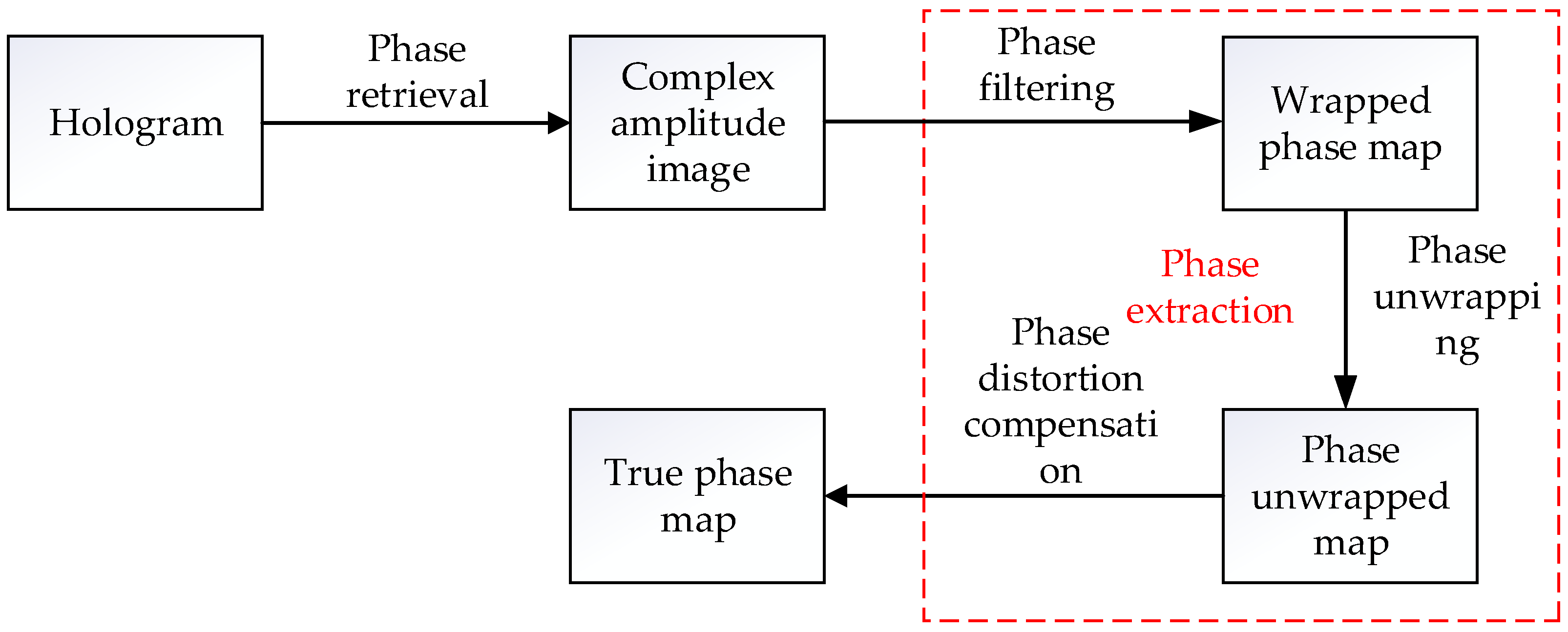
As illustrated in Figure 4, which presents a flowchart for phase processing steps in DHM, the red dashed section is designed as phase extraction. This phase extraction process involves three main steps: phase filtering, phase unwrapping, and phase distortion compensation.

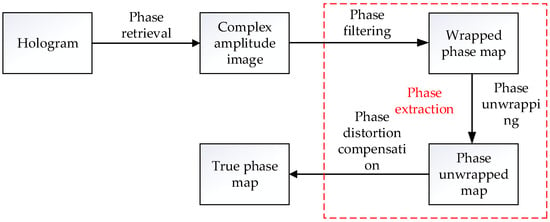
Figure 4. Flowchart of phase processing.

In the phase recovery step, the intensity $I_H(x,y)$ of the recorded interference light field is extracted using Equation (3). DHM algorithms, Fourier transform, or deep learning techniques are then applied to recover the phase information, allowing the complex amplitude $U(x,y)$ to be computed, which encompasses both intensity and phase. The phase that needs to be recovered is denoted as $\phi (x,y)$.

$$U\left(x,y\right)=\left|O\left(x,y\right)\right|e^{i\phi \left(x,y\right)}$$

(8)

In the phase filtering step, the process involves applying a Fourier transform to convert the complex amplitude $U(x,y)$ into the frequency domain, performing the filtering operation, and subsequently transforming it back to the spatial domain. Suppose the complex amplitude $U(x,y)$ is processed with the frequency domain filter $H(f_x,f_y)$, resulting in $U_2\left(x,y\right)$.

$$U_2\left(x,y\right)={\mathcal{F}}^{-1}\left[\mathcal{F}\left(U\left(x,y\right)\right)\cdot H\left(f_x,f_y\right)\right]$$

(9)

where $\mathcal{F}\left(U\left(x,y\right)\right)$ implies the frequency domain representation of $U\left(x,y\right)$ and $H\left(f_x,f_y\right)$ implies the frequency domain filter. ${\mathcal{F}}^{-1}$ denotes the inverse Fourier transform.

After phase filtering, the updated phase information ${\phi }^{\prime }(x,y)$ can be extracted from $U_2\left(x,y\right)$, and its expression is denoted as

$$U_2\left(x,y\right)=\left|O^{\prime }\left(x,y\right)\right|e^{i{\phi }^{\prime }\left(x,y\right)}$$

(10)

where $\left|O^{\prime }\left(x,y\right)\right|$ represents the intensity information of the object wave after filtering, and ${\phi }^{\prime }(x,y)$ denotes the phase information after filtering.

During phase unwrapping, the unwrapped phase information is given by

$${\Phi }^{\prime }\left(x,y\right)={\phi }^{\prime }\left(x,y\right)+2\pi \cdot N\left(x,y\right)$$

(11)

where $N\left(x,y\right)$ signifies an integer function, indicating the integer multiple of 2π that should be added during the phase unwrapping process. The complex amplitude following phase unwrapping is expressed as

$${ U}_3\left(x,y\right)=\left|O^{\prime }\left(x,y\right)\right|e^{i{\Phi }^{\prime }\left(x,y\right)}$$

(12)

In the phase distortion compensation step, assuming that the unwrapped phase ${\Phi }^{\prime }\left(x,y\right)$ contains a certain known phase distortion $\mathsf{\Delta }\phi (x,y)$, the phase information after distortion compensation, ${\Phi }^{″}\left(x,y\right)$, can be expressed as

$${\Phi }^{″}\left(x,y\right)={\Phi }^{\prime }\left(x,y\right)-\mathsf{\Delta }\phi \left(x,y\right)$$

(13)

The complex amplitude after distortion compensation can be expressed as

$$U_4\left(x,y\right)=\left|O^{\prime }\left(x,y\right)\right|e^{i{(\Phi }^{\prime }\left(x,y\right)-\mathsf{\Delta }\phi \left(x,y\right)+\mathsf{\Delta }\omega \left(x,y\right))}$$

(14)

where $\mathsf{\Delta }\omega \left(x,y\right)$ denotes the estimated aberration.

Following the above steps, the phase complex amplitude can be represented as

$$U\left(x,y\right)=\left|O^{\prime }\left(x,y\right)\right|e^{i\left({\Phi }^{\prime }\left(x,y\right)-\mathsf{\Delta }\phi \left(x,y\right)+\mathsf{\Delta }\omega \left(x,y\right)+\mathsf{\Delta }\Phi \left(x,y\right)\right)}$$

(15)

where $\mathsf{\Delta }\Phi (x,y)$ indicates the phase information derived from the difference between the phase after distortion compensation and the original signal during the phase processing. Finally, the real phase $\Phi \left(x,y\right)$ obtained through phase processing is

$$\Phi \left(x,y\right)={\Phi }^{\prime }\left(x,y\right)-\mathsf{\Delta }\phi \left(x,y\right)+\mathsf{\Delta }\omega \left(x,y\right)+\mathsf{\Delta }\Phi \left(x,y\right)={\Phi }_1\left(x_1,y_1\right)$$

(16)

2.3. Theoretical Framework for Phase Processing in Deep Learning

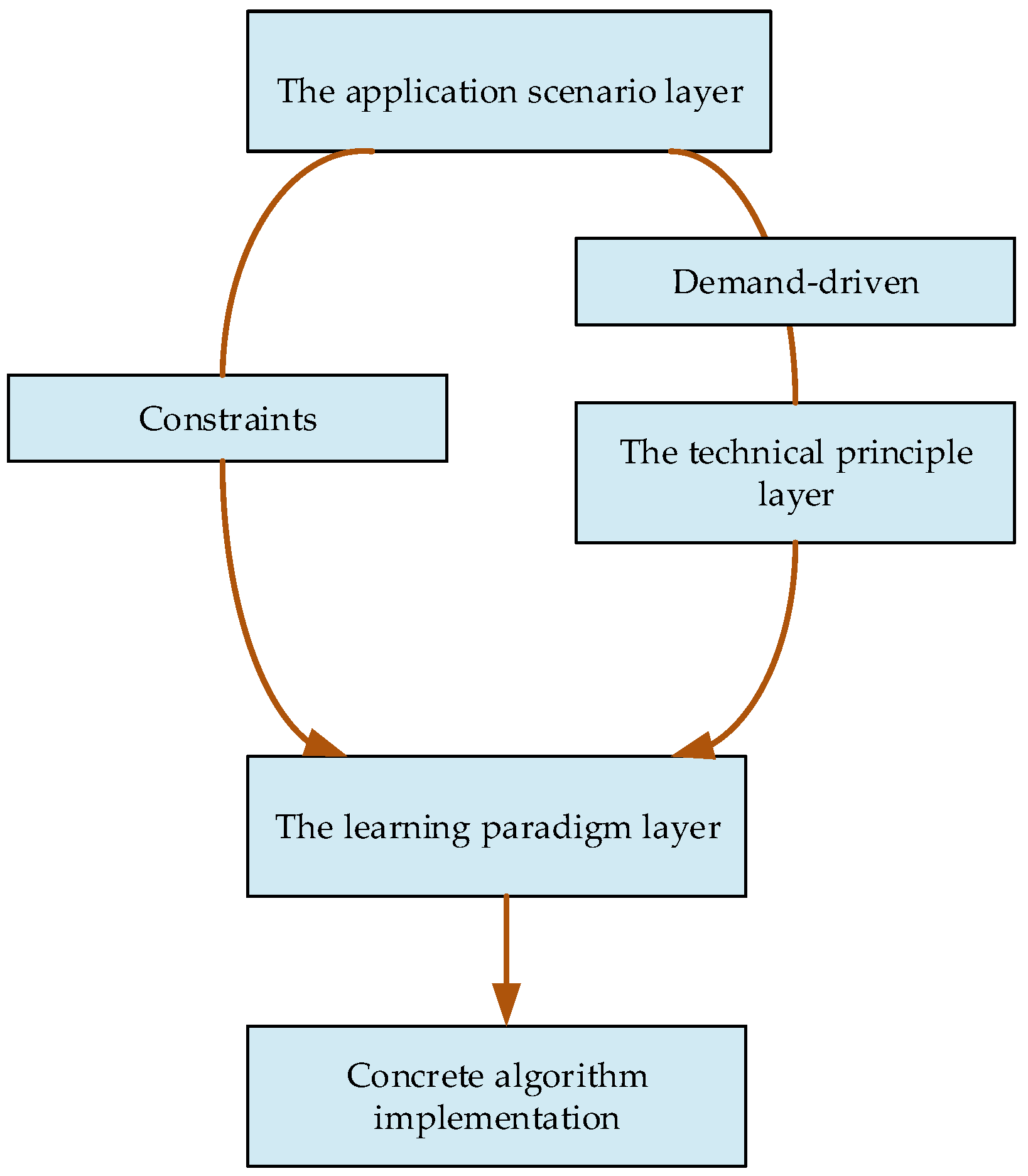
Figure 5 introduces a structured, three-layer classification framework designed to clarify how deep learning techniques are applied to DHM phase processing across three dimensions: the application scenario layer (e.g., biomedical, materials science), the technical principle layer (data-driven, model-driven, hybrid), and the learning paradigm layer (supervised, unsupervised, self-supervised learning).

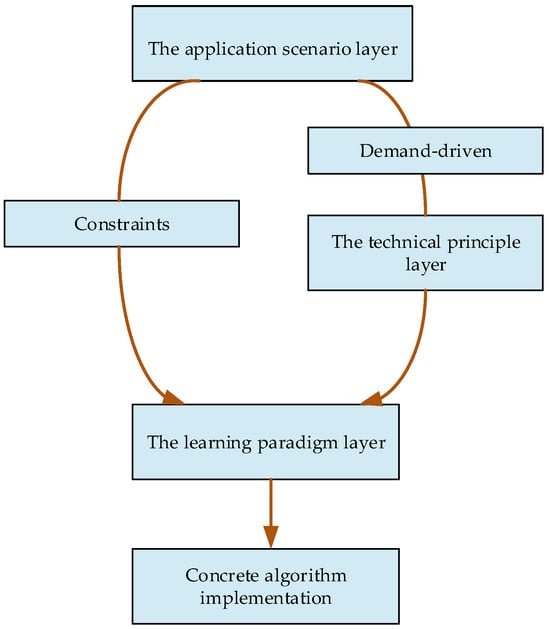
Figure 5. Theoretical framework for phase processing in digital holographic microscopy.

Additionally, the theoretical framework for deep learning-based phase processing is structured into four hierarchical layers: the application scenario, technical principle, learning paradigm, and algorithm implementation.

2.3.1. Application Scenario Dimension

From the perspective of application scenarios, deep learning-based phase processing in DHM serves distinct roles across fields. In biomedical research, it enables label-free, dynamic analysis of biological samples by suppressing phase noise and reconstructing 3D structures for high-resolution, long-term live-cell tracking.

In materials science, deep learning-based phase processing facilitates the extraction of microstructural features, such as crystal orientations and interfacial defects, supporting process optimization and performance prediction for advanced materials.

While both fields rely on precise phase analysis at the microscale, biomedical applications emphasize non-destructive monitoring of dynamic processes, whereas materials science focuses on high-throughput analysis of static structure–property relationships.

2.3.2. Technical Principle Dimension

From the perspective of technical principles, three paradigms have been adopted in DHM phase processing using deep learning. In the data-driven paradigm, models are trained on large annotated datasets to automatically learn phase reconstruction mapping relationships from raw holograms. This approach, reliant on data volume and model capacity, is suited for data-rich scenarios involving complex, non-explicit physical mechanisms.

In the physics model-driven paradigm, optical priors, such as light wave propagation and diffraction theory, are embedded into model structures or loss functions. By incorporating physical constraints or differentiable simulation modules, model outputs are aligned with underlying physical laws. This paradigm offers greater interpretability and generalization, particularly in data-limited cases with well-defined physics.

The hybrid paradigm combines both strategies. Deep learning is used to model nonlinearities and noise, while physical constraints are introduced—e.g., via wave equation regularization terms based on wave equations to neural networks. This method enhances phase reconstruction accuracy while preserving physical consistency, making it well-suited for biomedical and materials science applications demanding both high precision and interpretability.

2.3.3. Learning Paradigm Dimension

The characteristics of the three learning paradigms are discussed in what follows.

Supervised learning involves training models on large volumes of annotated data to directly learn the mapping between inputs and corresponding outputs. The accuracy of such models is highly dependent on both the quality and quantity of the annotations provided. In applications requiring phase continuity constraints, loss functions are employed to enforce consistency between the model’s output and the continuous phase of the target labels.

Unsupervised learning performs phase unwrapping by harnessing the intrinsic structure of the data, thereby eliminating the need for annotated datasets. This approach is particularly suitable for scenarios where annotation is costly or prior domain knowledge is scarce. Phase continuity constraints are implemented by designing prior constraints or leveraging the intrinsic structure of the data.

Self-supervised learning automatically circumvents manual annotation by constructing supervisory signals through proxy tasks designed directly from unlabeled data. Incorporating physical priors improves the model’s generalization to unseen samples. Phase continuity constraints are enforced either through transformations—such as rotation or occlusion—that require consistent phase predictions, or by leveraging phase correlation across multi-frame images or data from different sensors.

3. Application of Deep Learning in Phase Recovery of Digital Holographic Microscopy

Phase information is essential for reconstructing the 3D structure and complex details of an object. However, direct measurement of phase information from a hologram is not possible. Phase retrieval techniques reconstruct the object’s phase from the recorded holographic intensity, forming the foundation for subsequent phase reconstruction and 3D imaging from indirect or incomplete data. This process enhances image quality and contrast while enabling the analysis of internal structures and dynamic changes in the object. Traditional phase retrieval methods, such as the Gerchberg–Saxton algorithm [16] and the Fienup algorithm [17], have robust anti-interference capabilities. However, they face the following limitations:

(1)

They rely on iterative calculations, which are time-consuming and inefficient.

(2)

The complex operational processes lead to lower-quality reconstructed images.

(3)

They require that the intensity and phase be processed separately in sequential steps, as they lack an integrated framework for efficient joint reconstruction.

To address the issue (1), Zhang et al. from Tsinghua University proposed a model in 2018 based on a U-shaped (U-Net) convolutional neural network (CNN) [18]. This model incorporates the U-Net structure, enabling faster recovery of the original phase of the sample and replacing traditional iterative methods, thus reducing computation time. However, this study did not provide specific evaluation metrics.

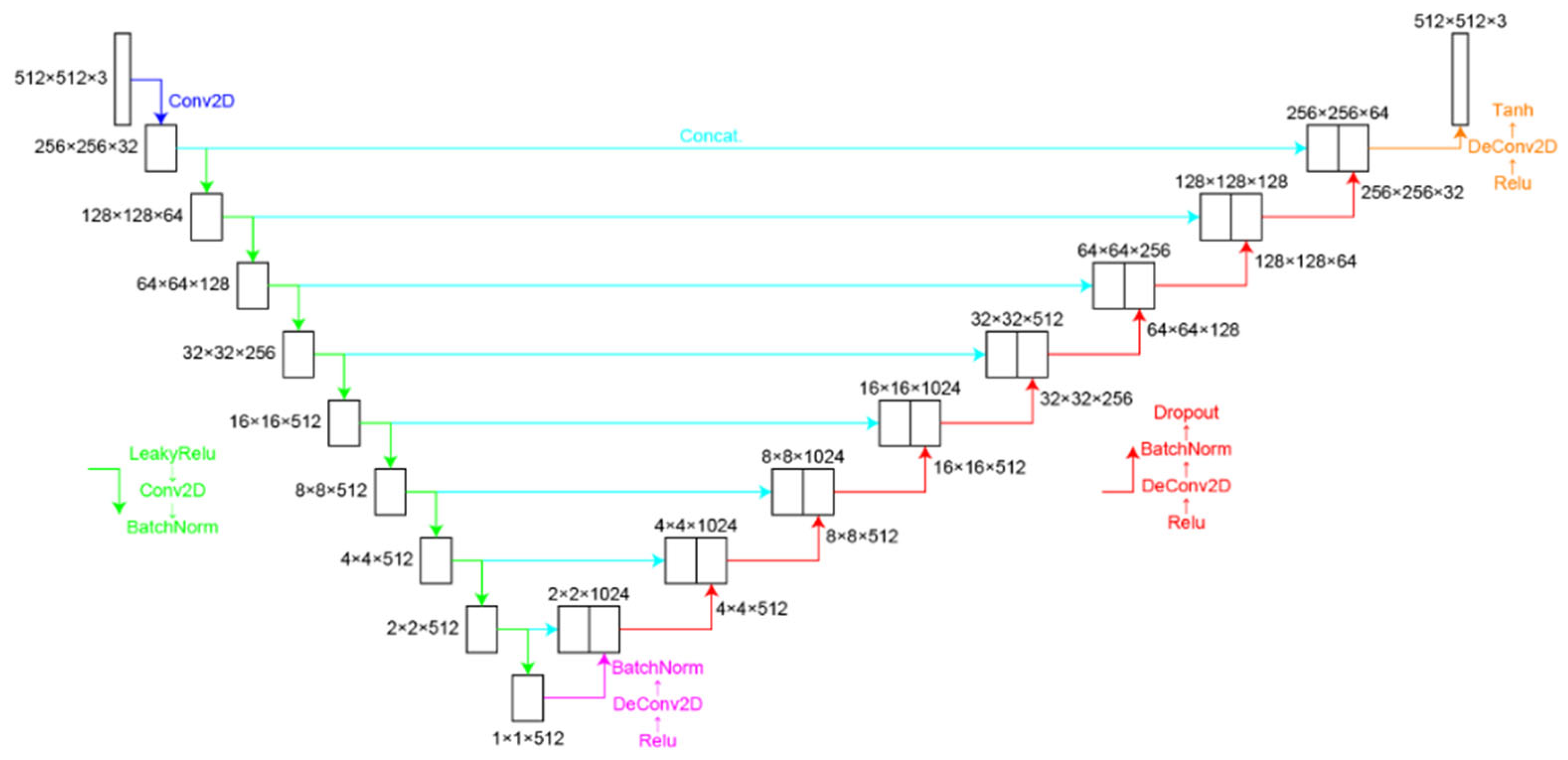
To address the issue (2), Yuki Nagahama from the Tokyo University of Agriculture and Technology introduced a phase retrieval method using a U-Net network model in 2022 [19]. Figure 6 depicts the U-Net CNN model. This approach can process a single hologram, significantly simplifying the process, effectively removing overlapping conjugate images, and enhancing the quality of reconstructed images. In terms of the evaluation metric mean absolute error (MAE), this method reduces the error by 0.058–0.069 π compared to traditional methods. However, comparisons of this method to other deep learning models were not provided.

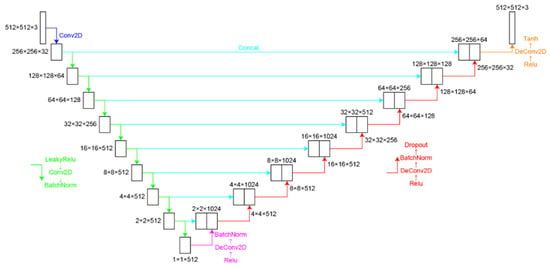
Figure 6. U-Net CNN model [19], where green line represents the combination of LeakyRelu + Conv2D + BatchNorm, pink line represents the combination of Relu + DeConv2D + BatchNorm, red line represents the combination of Relu + DeConv2D + BatchNorm + Dropout, and orange line represents the combination of Relu + DeConv2D + Tanh.

To address the issue (3), Wang et al. from Northwestern Polytechnic University proposed the one-to-two Y-Net network in 2019 [20]. This network was developed to simultaneously reconstruct both intensity (light intensity distribution) and phase information from a single digital hologram. However, the Y-Net network requires three rounds of training, which affects its training efficiency and necessitates further optimization.

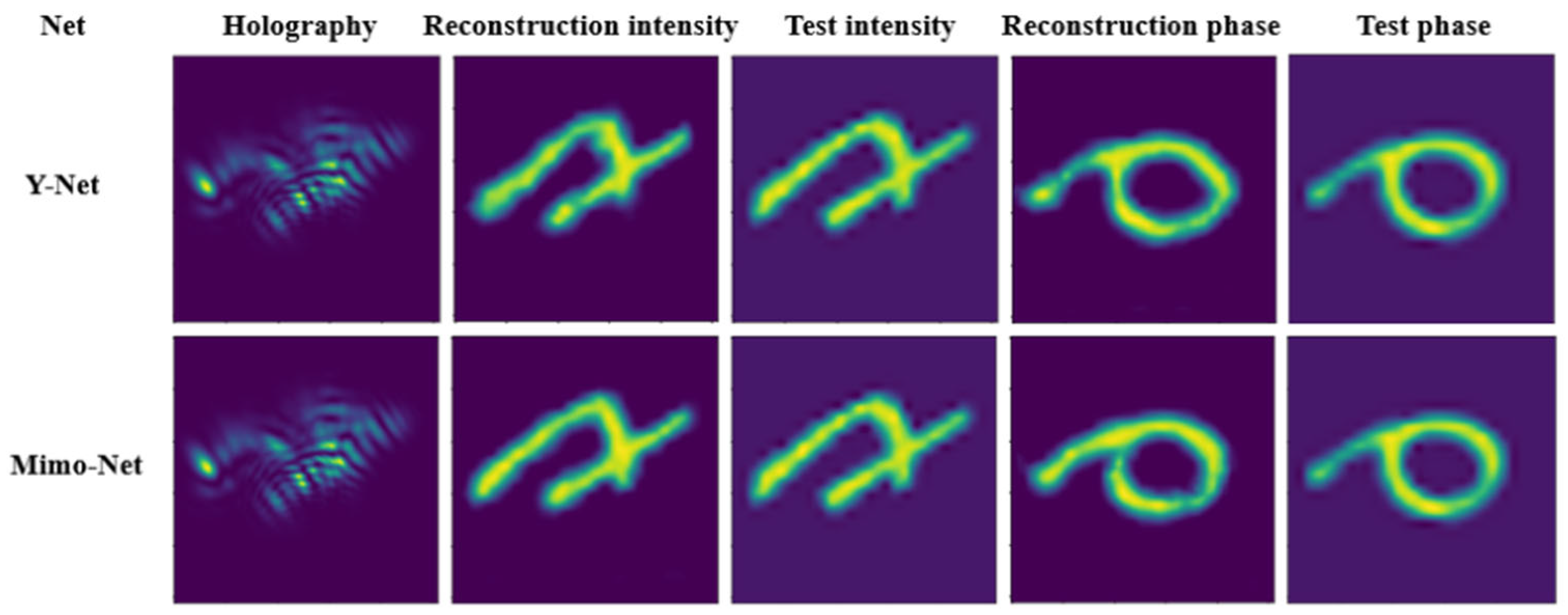
In 2023, Chen et al. from the North China University of Science and Technology proposed the Mimo-Net network [21], which requires only a single training session to simultaneously reconstruct intensity and phase information at three different scales. Compared to Y-Net [20], Mimo-Net offers superior reconstruction performance in terms of image quality. Figure 7 compares the reconstruction results of Mimo-Net and Y-Net at the same scale of 256 × 256.

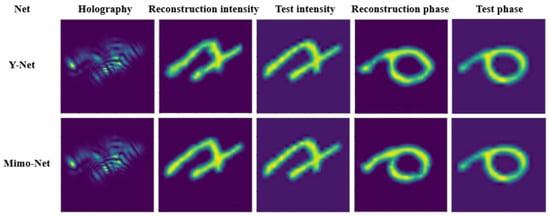
Figure 7. Comparison of network reconstruction results between Mimo-Net and Y-Net at a 256 × 256 scale [21].

To provide a structured overview of phase processing research, the subsequent analysis is organized across multiple dimensions. Table 1 classifies existing phase recovery networks, highlighting structural design principles that impact phase recovery performance. Table 2 compares the core mechanisms, advantages, and disadvantages of phase recovery algorithms, distilling key insights to validate algorithmic applicability across diverse scenarios.

Table 1. Classification of phase recovery networks across key dimensions.

Method	Application Scenario Dimension	Technical Principle Dimension	Learning Paradigm Dimension
U-Net [18]	Biomedicine (off-axis DHM).	Data-driven (end-to-end mapping from defocused holograms to focused phases using U-Net).	Supervised learning (L2 Loss + high-frequency weighting for phase reconstruction accuracy).
U-Net [19]	Biomedicine/materials science (in-line DHM).	Data-driven (multi-scale feature fusion via U-Net for separating object waves and conjugate images in single holograms).	Supervised learning (using MAE loss function for optimizing the mapping relationship between complex amplitude and light intensity).
Y-Net [20]	Real-time biomedical imaging; simultaneous intensity and phase reconstruction (off-axis DHM).	Dual-branch U-Net with single/double/triple convolutional kernels for multi-scale feature extraction.	Supervised learning.
Mimo-Net [21]	Multi-scale holographic reconstruction (off-axis DHM).	Multi-branch input with multi-scale feature extraction modules and cross-layer fusion.	Supervised learning.

Table 2. Comparison of advantages, disadvantages, and mechanisms analysis of phase recovery algorithms.

Method	Core Mechanism	Advantages	Limitations	Conclusion
Gerchberg–Saxton iterative algorithm [16], Fienup iterative algorithm [17]	Alternating projections between spatial and frequency domains to iteratively approximate the true phase using known amplitude.	High interpretability and low data dependency.	Low computational efficiency, sub-optimal noise resistance, and limited adaptability to complex scenes.	Traditional algorithms offer strong physical interpretability in simple and low-noise settings but are constrained by limited real-time performance and scalability in complex scenarios.
U-Net [18]	Extracts multi-level features from defocused holograms via multi-layer convolutions, retains structural details through skip connections, and directly outputs the focused phase.	High real-time performance, strong noise resistance, detail preservation, and good adaptability to complex scenarios.	Dependent on simulated data and sensitive to parameter tuning.	Well-suited for real-time dynamic applications, such as rapid phase monitoring of living cells in biomedical imaging.
U-Net [19]	The U-Net encoder captures noise patterns from holograms, while the decoder separates object waves and conjugates images via a nonlinear transformation to output pure phases.	High efficiency in single-image processing, targeted noise reduction, and a simplified workflow.	Limited generalization to diverse noise types and high computational resource demands.	Optimized for single-image noise reduction, making it suitable for high-throughput hologram analysis in materials science.
Y-Net [20]	Utilizes a dual-branch U-Net to integrate multi-scale convolutional features for concurrent intensity and phase reconstruction from digital holograms.	Symmetrical structure with 30% fewer parameters than U-Net; achieves SSIM > 0.96 for simultaneous intensity and phase reconstruction.	Limited generalization to complex noise environments and multi-scale scenarios.	Well-suited for real-time biomedical imaging with a reduced parameter count; generalization to complex and multi-scale conditions requires enhancement.
Mimo-Net [21]	Applies a multi-branch network to extract global and local features at multiple scales, enabling phase reconstruction through cross-layer fusion.	Supports three scales within a single model; delivers 62% faster reconstruction with superior PSNR and SSIM compared to Y-Net.	Higher computational overhead for multi-scale training; slightly reduced phase reconstruction accuracy.	Effective for high-throughput tasks via multi-branch, multi-scale feature extraction; however, phase accuracy lags behind intensity reconstruction.

4. Application of Deep Learning in Phase Extraction for Digital Holographic Microscopy

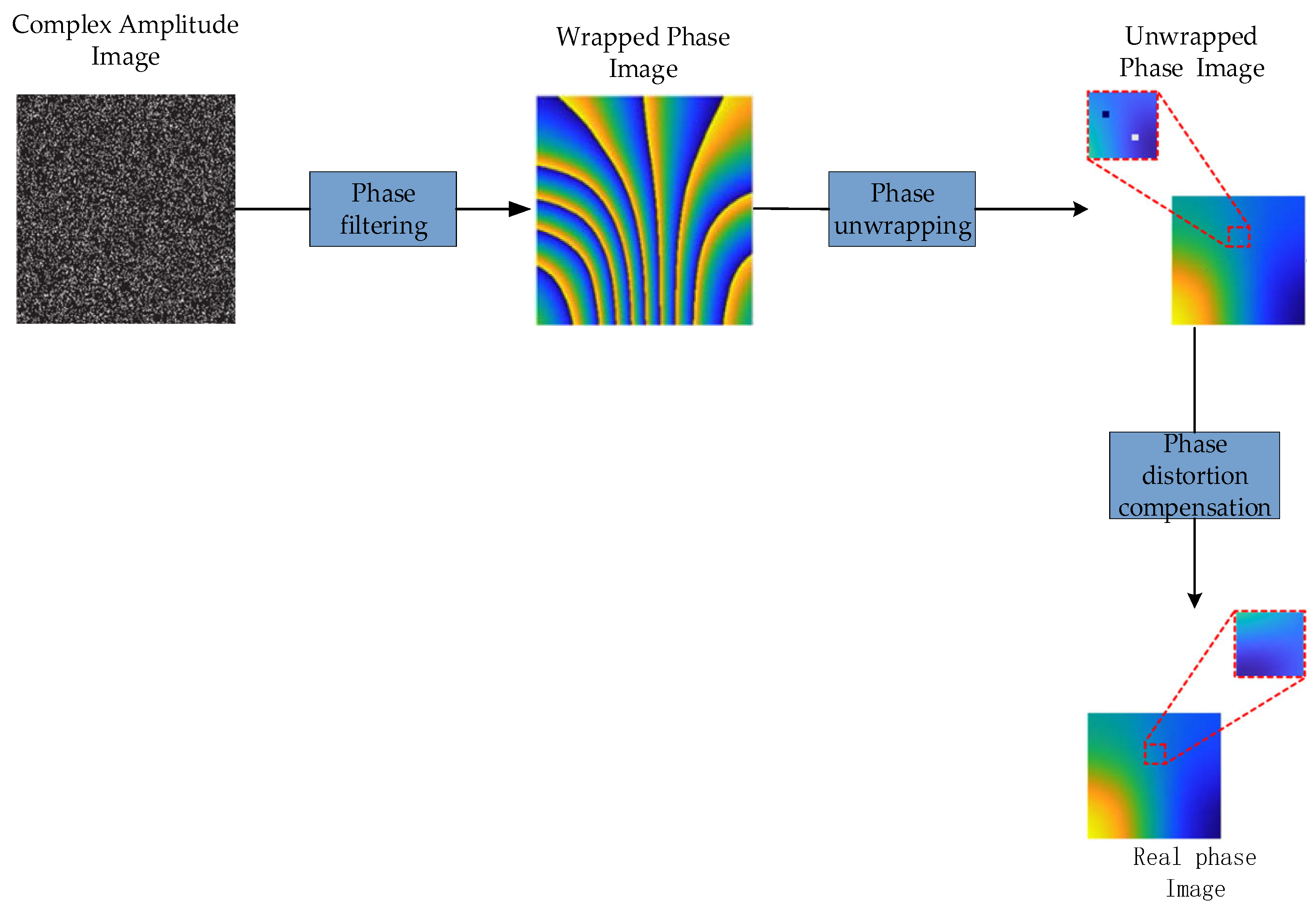
Figure 8 illustrates the process of phase extraction in DHM, which involves three key steps: phase filtering, phase unwrapping, and phase distortion compensation. The phase extraction process begins with phase retrieval to acquire the complex amplitude image. This image is then subjected to phase filtering to produce the wrapped phase map. Subsequently, phase unwrapping is performed on the wrapped phase map to generate the phase unwrapping map. Finally, phase distortion compensation is applied to the unwrapped phase map to obtain the final real phase information.

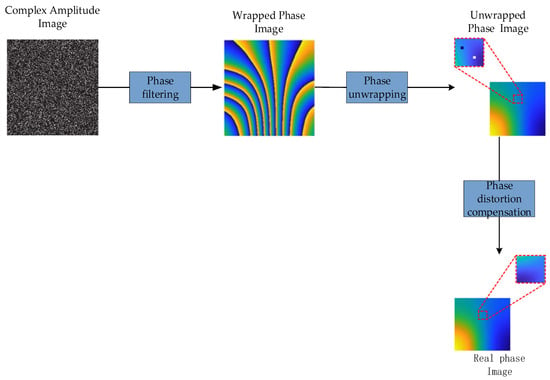
Figure 8. Flowchart of phase extraction, where the red dashed box represents local magnification.

4.1. Application of Deep Learning in Phase Filtering

Phase information obtained through phase retrieval can be affected by high-frequency noise or artifacts due to environmental noise, optical system limitations, or computational errors. These noises can cause the phase images to become unstable or distorted. Phase filtering helps remove such unwanted noise, smooth the phase map, and optimize its spatial distribution, effectively reducing artifacts and minimizing imaging errors caused by noise.

Traditional speckle noise filtering methods are divided into spatial domain, transform domain, and deep learning-based techniques, based on their theoretical foundations and processing stages. Spatial domain filtering methods include median filtering [22], mean filtering [23], blind convolution filtering [24], block matching [25], and 3D filtering [26], while transform domain methods include Wiener filtering [27], windowed Fourier transform [28], and wavelet filtering [29]. Although these methods classify and process objects, several challenges remain in practice:

(1)

Difficulty in obtaining noise-free phase maps for labeling.

(2)

Unclear feature representation.

(3)

Inefficient in denoising.

Recent studies have shown that deep learning approaches enable robust single-image super-resolution without iterative processing, greatly enhancing the speed of high-resolution hologram acquisition and reconstruction.

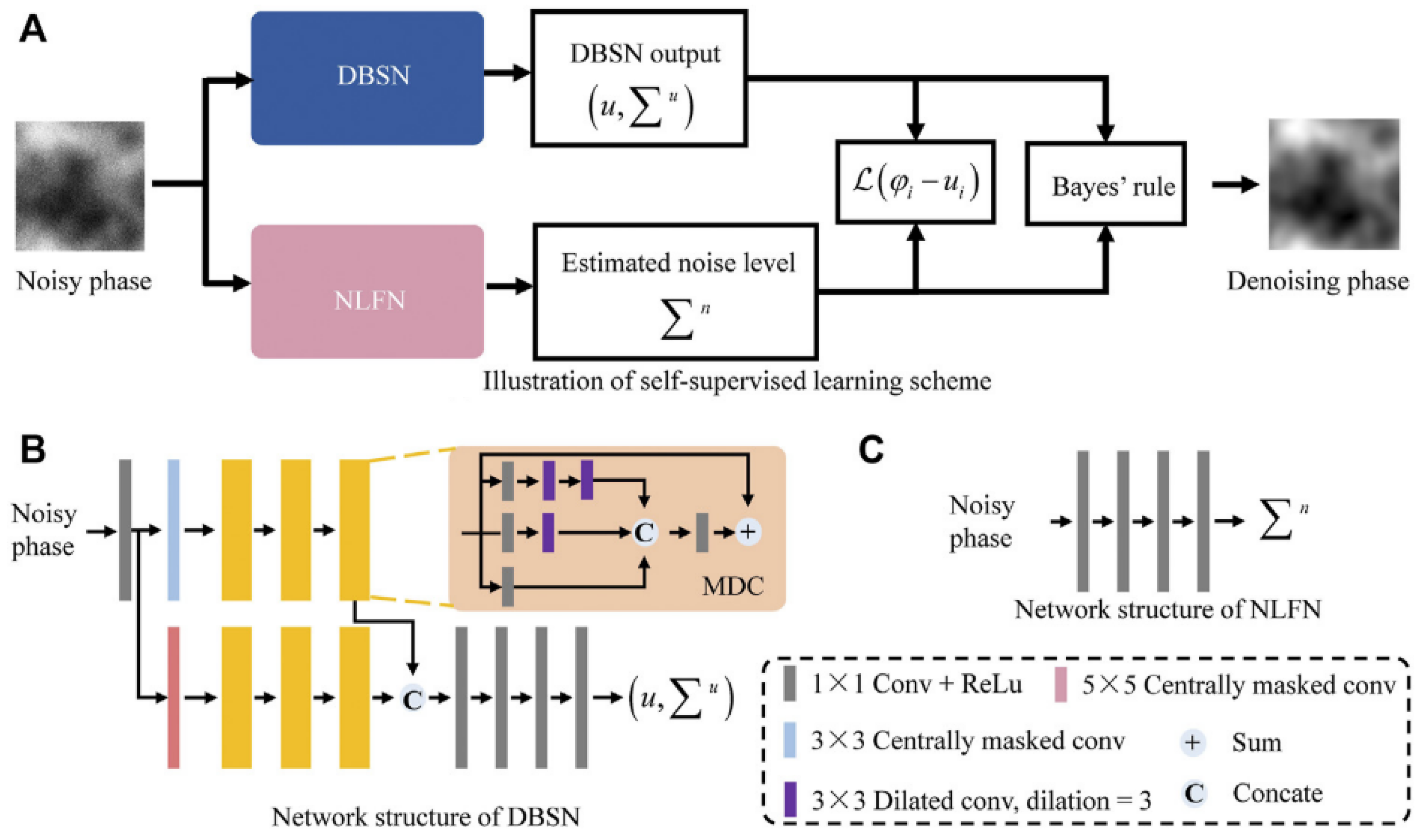
To address the issue (1), Wu et al. from Guangdong University of Technology proposed a network comprising a deep bilateral network (DBSN) and a non-local feature network (NLFN) in 2022 [30]. The framework of the DBSN and NLFN network is shown in Figure 9. The network is trained using a self-supervised loss function and outperforms traditional median filtering, block-matching, and 3D filtering in noise removal, providing superior noise suppression and generating noise-free phase maps.

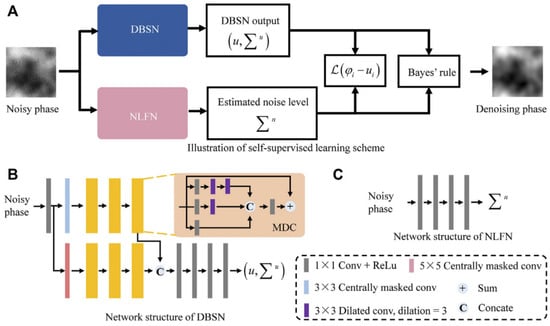
Figure 9. Network framework diagrams of DBSN and NLFN [30], where (A) represent the self-supervised learning scheme, (B) represent the DBSN network model, and (C) represent the NLFN network model.

To address the issue (2), Tang et al. from Zhejiang University of Science and Technology (2024) identified the high similarity between digital holographic mixed phase noise (DHHPN) and Perlin noise and proposed a deep learning-based continuous phase denoising method utilizing this similarity [31]. This approach not only resolved challenges associated with experimental data collection and labeling but also improved the generalizability of the trained CNN model across different DHM systems, effectively addressing unclear feature representation.

In 2025, Awais et al. proposed a lightweight wrapped-phase denoising network, WPD-Net [32], that enhances feature selection capability in noisy regions through residual dense attention blocks (RDABs), thereby providing an efficient solution for real-time biomedical imaging.

The Table 3 below presents an analysis and comparative summary of the mechanisms of deep learning and traditional methods for phase filtering, focusing on the challenges in acquiring noise-free phase labels and unclear feature representations.

Table 3. Mechanism analysis and comparison of traditional methods and deep learning algorithms for phase filtering, focusing on the challenges in acquiring noise-free phase labels and unclear feature representations.

Method	Core Mechanism	Advantages	Limitations	Conclusion
References [22,23,24,25,26,27,28,29]	Signal processing based on prior models, including spatial filtering, frequency-domain filtering, and statistical models.	Strong physical interpretability and low dependency on training data.	Poor adaptability to complex or structured noise, sensitivity to parameters, and potential for structural distortion.	Traditional algorithms retain advantages in physical interpretability for simple and low-noise scenarios, but they are limited in real-time performance and effectiveness under complex scenarios.
DBSN and NLFN [30]	Joint training of a denoising network (DBSN) and a noise level estimation network (NLFN) using Bayesian rules and negative log-likelihood loss, eliminating the need for clean labels.	No requirement for labels and dynamic noise estimation capability of noise levels.	Model assumption limitations, high computational complexity.	Designed for biomedical scenarios where label acquisition is difficult; however, generalizability is limited when noise deviates from Gaussian distributions.
DHHPN [31]	Observes that holographic noise resembles Perlin noise, which is then used to simulate and generate training data.	Accurate noise simulation and low labeling cost.	Simulation bias and absence of frequency-domain feature representation.	Enhances denoising accuracy through physically inspired noise modeling, but its effectiveness depends on how closely simulated noise matches real noise and the absence of frequency-domain feature representation.
WPD-Net [32]	Residual dense attention blocks (RDABs) + dense feature fusion (DFF) with a dynamic hybrid loss function	Lightweight model with strong mixed noise suppression and excellent real-time performance	Performance degrades under extreme noise conditions (SNR < 0 dB)	Suitable for high-noise scenarios in biomedicine and materials science imaging

To tackle the issue (3), Fang et al. from the Kunming University of Science and Technology (2022) introduced a deep learning-based speckle denoising algorithm using conditional generative adversarial networks (cGANs) [33], which enhanced feature extraction and denoising performance. In 2023, they integrated the Fourier neural operator into the CNN model [34], proposing the Fourier-UNet network. This architecture boosted denoising accuracy while reducing the number of training parameters. In 2024, they further enhanced their model by incorporating a 4-f optical speckle simulation module into the CycleGAN network [35]. This approach eliminated the need for pre-labeled paired data, improving both training accuracy and speed, and resulting in a 6.9% performance improvement over traditional methods when applied to simulated data. Figure 10 compares various methods with those reported in [24] for speckle noise denoising performance.

Figure 10. Comparison of speckle noise image denoising using different methods [35].

The Table 4 below presents an analysis and comparative summary of the mechanisms of deep learning and traditional methods for phase filtering, focusing on denoising inefficiencies.

Table 4. Mechanism-level analysis and comparison of deep learning algorithms for phase filtering, focusing on denoising inefficiencies.

Method	Core Mechanism	Advantages	Limitations	Conclusion
cGAN [33]	The generator (U-Net+DenseNet) maps holograms to clean phases, and the discriminator enforces the generated images to match optical physical characteristics by combining PSNR loss.	High-fidelity reconstruction and strong generalizability.	High data dependency and unstable training.	Enables high-fidelity reconstruction of phase images under strong speckle noise, but requires high-quality labels and is susceptible to generative adversarial network (GAN) mode collapse.
Fourier-Unet [34]	Combines CNN for local spatial feature extraction with a Fourier neural operator to capture global frequency information.	Multi-domain complementarity and physically informed design.	High computational cost and complex architecture.	Enhances denoising accuracy and subsequent phase unwrapping effects through joint spatial-frequency processing, but demands significant computational complexity and careful architectural parameters.
4-fCycleGAN [35]	Integrates a 4-f optical system to simulate a speckle noise generator (F) and employs CycleGAN with cyclic consistency loss (Lcyc) to ensure phase reversibility before and after denoising.	Fully unsupervised; accommodates diverse noise patterns.	Limited by fixed simulation parameters; potential performance bottlenecks.	Designed for label-free industrial optical inspection with fixed simulation parameters and tasks, but its generalizability to complex real-world noise is lower than that of supervised methods.

The Table 5 below presents a classification and comparative summary of deep learning and traditional methods for phase filtering.

Table 5. Classification of phase filtering network dimensions.

Method	Application Scenario Dimension	Technical Principle Dimension	Learning Paradigm Dimension
DBSN and NLFN [30]	Biomedicine, materials science (Off-axis DHM).	Physical noise modeling with self-supervised learning structure.	Unsupervised learning (trained solely on noisy data).
DHHPN [31]	Precision measurement, biomedicine (in-line DHM).	Supervised learning with physical noise simulation based on the Perlin noise model.	Supervised learning (paired training with simulated datasets).
WPD-Net [32]	Biomedicine, materials science (in-line DHM).	Data-driven (RDAB + DFF) + attention mechanisms	Supervised learning (dynamic hybrid loss)
cGAN [33]	Industrial inspection, optical metrology (in-line DHM).	Generative adversarial networks (GANs) with optical simulation datasets.	Supervised learning with noise-clean image pairing.
Fourier-Unet [34]	Phase denoising in holographic interferometry, 3D topography measurement (in-line DHM).	Hybrid approach: CNN for spatial features combined with Fourier frequency-domain features.	Supervised learning (using both simulated and experimental data).
4-fCycleGAN [35]	Industrial optical inspection, holographic metrology (in-line DHM).	Unsupervised learning combined with speckle noise simulation via 4-f optical system.	Unsupervised learning (trained on unpaired data).

The Table 6 below presents a comparative analysis of deep learning methods for improving phase filtering denoising effects.

$$MAE={\displaystyle \frac{1}{m}}\sum _{i=1}^m\left|y_i-y_i^{\prime }\right|$$

(17)

$$MSE={\displaystyle \frac{1}{m}}\sum _{i=1}^m{\left(y_i-y_i^{\prime }\right)}^2$$

(18)

$$PSNR=10 {\mathit{log}}_{10}{\displaystyle \frac{{\left(MA{X}_I\right)}^2}{MSE}}=20 {\mathit{log}}_{10}{\displaystyle \frac{MA{X}_I}{\sqrt{MSE}}}$$

(19)

$$SSIM={\displaystyle \frac{\left(2{\mu }_x{\mu }_y+c_1\right)\left({\sigma }_{xy}+c_2\right)}{\left({\mu }_x^2+{\mu }_y^2+c_1\right)\left({\sigma }_x^2+{\sigma }_y^2+c_2\right)}}$$

(20)

$$RF=\sqrt{{\displaystyle \frac{{\sum }_{t=1}^M{\sum }_{j=1}^N\left(d\left(i,j\right)-d\left(i,j-1\right)\right)}{\left(MN\right)}}}$$

(21)

$$CF=\sqrt{{\displaystyle \frac{{\sum }_{i=2}^M{\sum }_{j=1}^N\left(d\left(i,j\right)-d\left(i-1,j\right)\right)}{\left(MN\right)}}}$$

(22)

$$SF=\sqrt{R{F}^2+{CF}^2}$$

(23)

where $y_i \mathrm{a}\mathrm{n}\mathrm{d} y_i^{\prime }$ denote the true and predicted values of the $i$ sample, respectively. ${MAX}_I$ represents the maximum value of the image point color, which is 255 when each sample point is represented by 8 bits. $u_x$ and $u_y$ represent the mean values of images X and Y, respectively. ${\sigma }_x$ and ${\sigma }_y$ are the variances of images X and Y, respectively. ${\sigma }_{xy}$ indicates the covariance between images X and Y, and $c_1$ and $c_2$ are constants.

Table 6. Comparative analysis of deep learning methods for enhancing denoising performance in phase filtering.

Year	Method	MAE	PSNR	SSIM	SF	Suggestions for Improvement
2025	WPD-Net [32]	0.0068	26.586	0.987	/	Enhance WPD-Net’s performance under extreme noise conditions (SNR < 0 dB) by integrating temporal dynamics into the training process
2022	cGAN [33]	0.0055	25.25	0.9974	1.3567	Improve adaptability to dynamic scenes and enhance overall denoising performance.
2023	Fourier-Unet [34]	0.0039	43.28	0.9999	/	Strengthen denoising capabilities under complex backgrounds and improve phase unwrapping accuracy.
2024	4-fCycleGAN [35]	0.09549	16.1647	/	0.03614	Improve generalization to non-Gaussian noise and enhance real-time processing efficiency.

Note: The data presented above are the experimental results obtained from their respective datasets. Evaluation metrics: The calculation formulas for MAE, peak signal-to-noise ratio (PSNR), structural similarity index (SSIM), and signal fidelity (SF) are provided as follows.

In phase filtering, spatial frequency serves as a key metric for assessing the effectiveness of denoising. Equations (21) and (22) define the row frequency and column frequency, which quantify the frequency variations along the row and column directions of an image, respectively. Equation (23) combines row frequency and column frequency to compute the overall spatial frequencies, providing a comprehensive measure of the image’s frequency distribution.

Currently, deep learning-based denoising techniques are confronted with challenges, such as limited accuracy, high reliance on data, poor generalization, substantial computational demands, and model complexity. Future research is expected to focus on enhancing adaptability, improving accuracy, and simplifying model architectures to address these limitations.

4.2. Application of Deep Learning in Phase Unwrapping

After phase filtering, phase values are often confined within the 2π periodic range, resulting in jumps or discontinuities in the phase signal $[-\mathsf{\pi }$, $\mathsf{\pi }]$. The goal of phase unwrapping is to remove these periodic jumps, enabling the phase variation to represent a continuous and physically plausible process. This process involves sequentially correcting the phase data to eliminate errors introduced by periodic constraints, thereby ensuring an accurate representation of the object’s surface morphology and subtle phase variations.

Traditional phase unwrapping techniques are generally categorized into time phase unwrapping (TPU) and spatial phase unwrapping (SPU) methods. TPU methods address phase unwrapping by acquiring multiple phase maps at different frequencies over time, with multi-frequency approaches [36] being commonly used to resolve phase surface discontinuities. SPU methods, which focus on phase unwrapping the phase in a single two-dimensional wrapped phase image, include path-following and minimum norm methods. The path-following approach recovers the continuous phase by defining integration paths, with common techniques, such as branch cut [37], quality-guided [38], and region growth [39]. The minimum norm method transforms phase unwrapping into a global optimization problem, aiming to minimize the difference between the phase gradient and the true phase gradient, with least squares being a typical representative technique.

Traditional phase unwrapping methods take into account the image features of the phase map and the algorithm’s stability, but they still encounter several challenges, including

(1)

Prolonged phase unwrapping time;

(2)

Limited robustness;

(3)

Poor generalization;

(4)

Low accuracy.

Deep learning approaches to phase unwrapping are typically categorized into two main types: regression-based methods and segmentation-based methods. Regression-based methods approach phase unwrapping as an image recovery problem, whereas segmentation-based methods treat it as an image segmentation issue.

To address the issue (1), Seonghwan Park et al. from South Korea introduced a deep learning model called “UnwrapGAN” in 2021 [40]. This model uses phase unwrapping as an image recovery task, effectively overcoming the challenges posed by phase discontinuities. Compared to traditional phase unwrapping methods, UnwrapGAN is able to perform phase unwrapping at twice the speed.

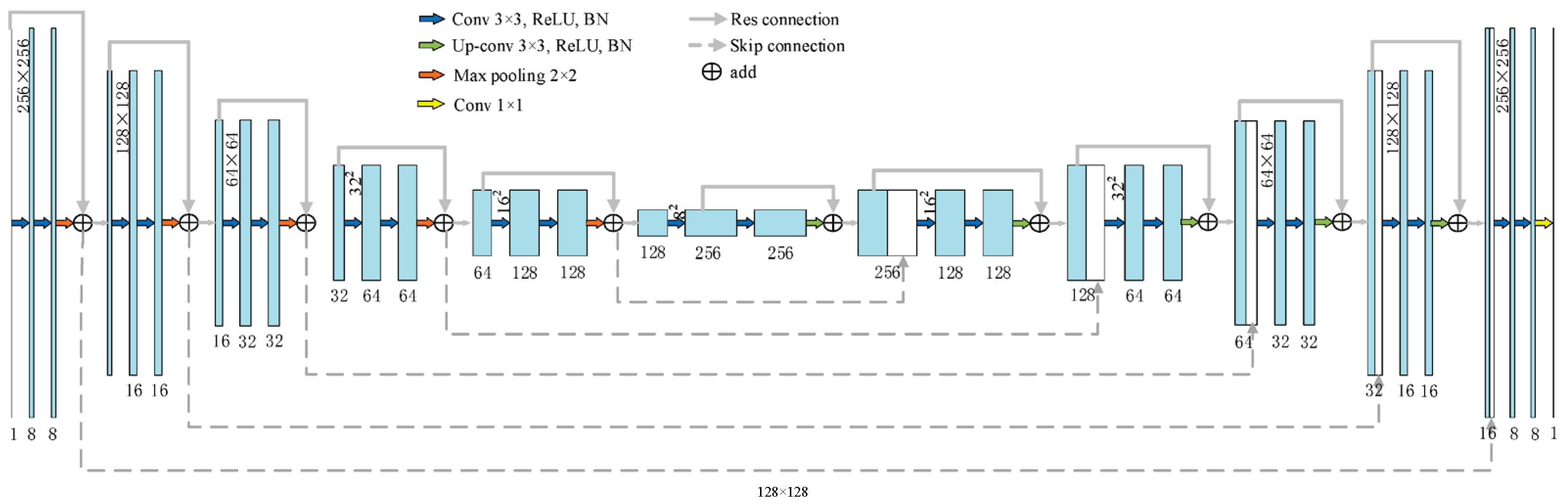
In 2024, Wang et al. from Hefei University of Technology introduced the Res-UNet network [41], as depicted in the detailed schematic in Figure 11. This network leverages the correlation between residual networks and U-Net networks. Compared to the “UnwrapGAN” model [40], the Res-UNet network achieves phase unwrapping in approximately 1 s, even for larger images. Additionally, in comparison to path-based algorithms, this network not only demonstrates superior noise suppression capabilities but also delivers better performance across varying image sizes.

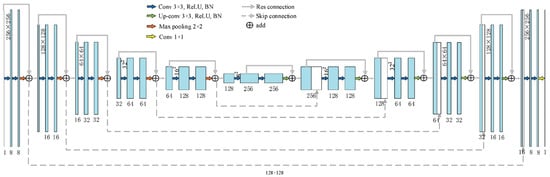
Figure 11. Detailed schematic of the neural network structure [41].

The Table 7 below presents an analysis and comparative summary of the mechanisms of deep learning and traditional methods for phase unwrapping, focusing on mitigating the phase unwrapping time problem.

Table 7. Comparative analysis of traditional and deep learning methods in mitigating the phase unwrapping time problem.

Method	Core Mechanism	Advantages	Limitations	Conclusion
References [36,37,38,39]	The path tracking method utilizes a phase quality map to guide integration paths. The minimum norm method performs global optimization to minimize phase gradient errors.	High physical interpretability; low dependence on training data.	Sensitive to noise; low computational efficiency; fails in complex phase scenarios.	These traditional methods offer clarity in physical principles and require no training data; however, they are sensitive to noise and phase mutations and are best suited for simple scenarios with low noise and continuous-phase settings.
UnwrapGAN [40]	Generative adversarial learning (GAN) improves the authenticity of phase structures through discriminators.	Good real-time performance and strong generalization ability.	Requires high-quality paired data; unstable training.	Enables automatic focusing and phase unwrapping, at over twice the speed of traditional algorithms, but depends heavily on high-quality paired data and is vulnerable to mode collapse during training.
Res-Unet [41]	Incorporates residual blocks and attention mechanisms to enhance edge feature extraction and structural detail.	Strong noise resistance; robust in the presence of phase discontinuities.	High model complexity; large parameter count; significant computational demands.	Demonstrates strong robustness to complex noise and undersampling conditions. However, its practical deployment is constrained by high computing resources.

The Table 8 below presents a comparative analysis of the impact of deep learning methods on reducing phase unwrapping time.

Table 8. Comparative analysis of deep learning methods for reducing phase unwrapping time.

Year	Method	SSIM	Time (Seconds)	Suggestions for Improvement
2021	UnwrapGAN [40]	0.9000	0.5021	Enhance generalization by expanding the training dataset to cover more diverse cell types and complex phase structures; explore lightweight network designs to reduce computational latency in real-time applications.
2024	Res-Unet [41]	0.9936	1.087	Incorporate physics-based constraints into the loss function to improve handling of phase discontinuities under extreme noise scenarios; implement a multi-scale network architecture to enhance performance on high-resolution images without image stitching.

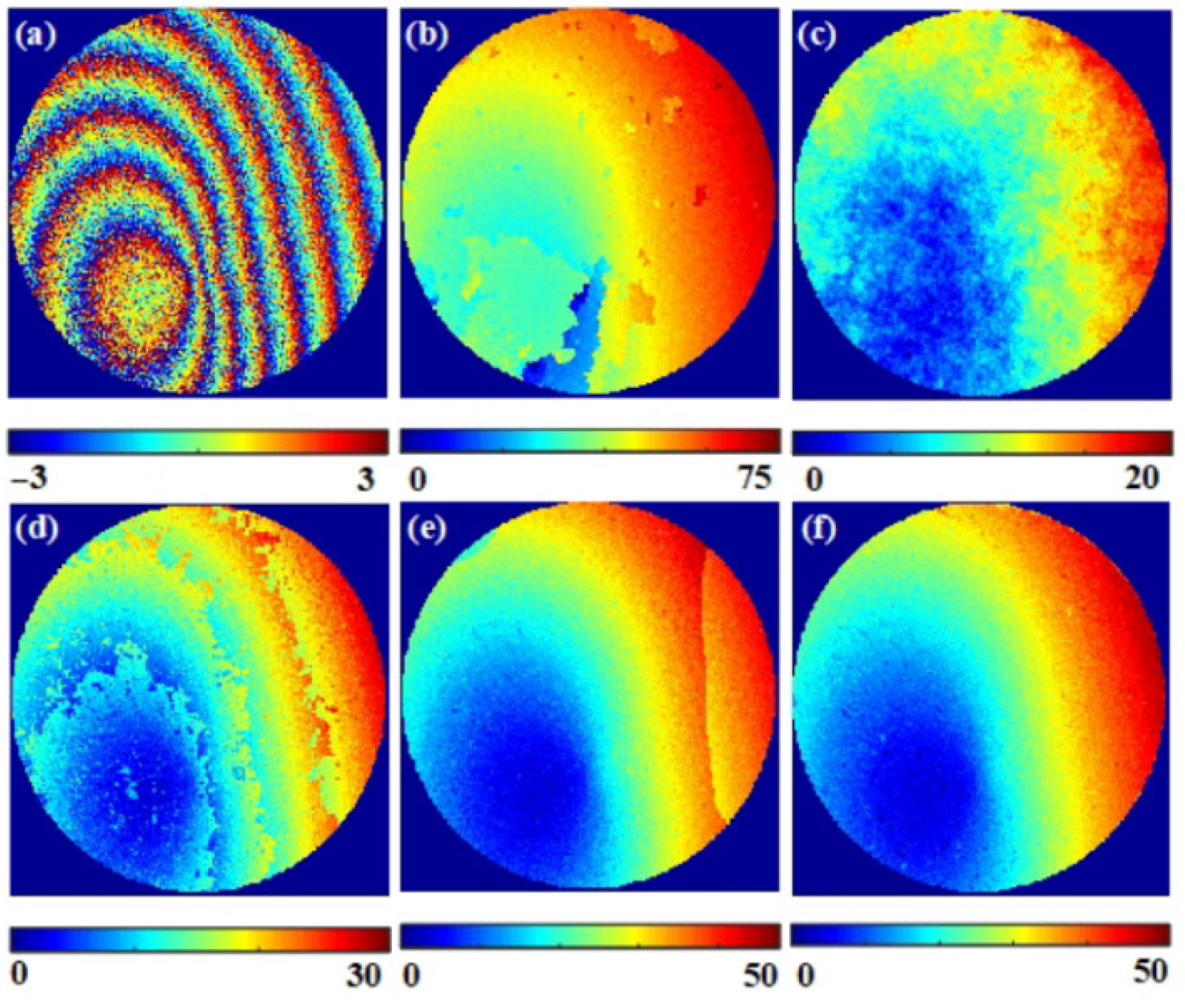
To address the issue (2), the following methods frame the problem as an image segmentation task. In 2019, Zhang et al. from Hangzhou Dianzi University introduced the DeepLabV3+ network [42], based on deep CNNs. Compared to conventional phase unwrapping techniques, this network delivers satisfactory phase unwrapping results, even in highly noisy conditions. Figure 12 in their study illustrates the phase unwrapping of real circular data of the methods in reference [42] and the traditional methods sorting by reliability following a noncontinuous path (SRFNP), transport of intensity equation (TIE), iterative transport of intensity equation (ITIE), and robust transport of intensity equation (RTIE) under significant noise.

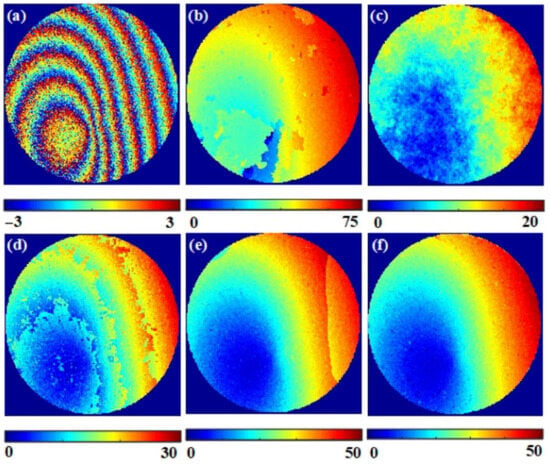
Figure 12. Phase unwrapping of real circular data under strong noise ((a–f) represent the wrapped phase map, SRFNP, TIE, ITIE, RTIE, and the unwrapped phase map generated by the method in reference [42], respectively).

In 2020, Spoorthi et al. from the Indian Institute of Technology introduced a new phase unwrapping learning framework called PhaseNet2.0 [43]. Unlike the previously proposed PhaseNet method [44], this framework incorporates a novel loss function (such as L1 and residual loss) and uses L1 loss to address class imbalance. Moreover, it eliminates the need for post-processing.

In 2024, Zhang et al. from Northwestern Polytechnical University, drawing inspiration from SegFormer [45], introduced a new phase unwrapping approach based on SFNet. This method outperforms traditional phase unwrapping approaches and the DeepLabV3+ network [42] in terms of noise resistance, accuracy, and generalization, especially in cases involving mixed noise and discontinuities.

In 2025, Awais et al. proposed the DenSFA-PU [46] network to address issues of poor robustness, error accumulation, and low computational efficiency in phase unwrapping under strong noise conditions.

The Table 9 below presents an analysis and comparative summary of the mechanisms of deep learning and traditional methods for phase unwrapping, focusing on addressing limited robustness.

Table 9. Comparative mechanism analysis of deep learning methods addressing limited robustness in phase unwrapping.

Method	Core Mechanism	Advantages	Limitations	Conclusion
DeepLabV3+ [42]	Utilizes the encoder-decoder architecture for semantic segmentation. Multi-scale features are extracted through atrous spatial pyramid pooling (ASPP), and high- and low-level features are fused through skip connections to predict wrap counts in phase unwrapping.	Enables multi-scale feature fusion, suitable for unwrapping complex phase structures.	Limited performance on small-target details; requires additional post-processing optimization.	Effectively addresses accuracy and efficiency issues in low-noise, regular-structure scenarios. However, performance on large-sized images requires downsampling, and training depends on high-quality paired datasets.
PhaseNet2.0 [43]	Utilizes a fully convolutional DenseNet architecture, framing phase unwrapping as a dense classification problem. A novel loss function combining gradient difference minimization and L1 loss is employed to mitigate class imbalance, directly and predict wrap counts.	Strong resistance to noise; supports high-dynamic range phase recovery; end-to-end training reduces manual intervention.	High reliance on simulated data; limited generalization to unseen noise types.	Effectively addresses the insufficient robustness against complex noise and high-dynamic-range phase conditions. However, it exhibits a large parameter volume and limited generalization to highly complex or geometric structures.
SFNet [45]	Builds on a lightweight variant of SegFormer using a hierarchical transformer encoder without positional encoding to capture global phase dependencies, combines an MLP decoder to fuse multi-scale features, and enhances phase unwrapping accuracy in complex noise and discontinuous scenarios via self-attention mechanisms.	Demonstrates strong global feature modeling capability with low parameter count; facilitates real-time inference.	Limited handling of fine local details; relying on the Transformer structure results in slightly higher computational complexity.	This approach addresses the limitations of traditional methods in global feature modeling and real-time performance. However, tile-based processing is needed for extremely high-resolution images, with edge detail accuracy left to be improved.
DenSFA-PU [46]	Densely connected encoder + SFA module (Bi-LSTM + BAM)	High robustness to strong noise; fast unwrapping speed	Requires optimization of initial conditions under extreme noise	Suitable for real-time holographic imaging and unwrapping

The Table 10 below presents a comparative analysis of the impact of deep learning methods on improving robustness.

Table 10. Comparative analysis of the effects of deep learning methods in addressing limited robustness in phase unwrapping.

Year	Method	SSIM	RMSE	PSNR	Suggestions for Improvement
2019	DeepLabV3+ [42]	/	1.2325	/	Explore multi-scale training strategies to improve performance on high-resolution images, and integrate physics-informed constraints into the network to enhance noise suppression in extreme scenarios.
2020	PhaseNet2.0 [43]	0.9200	0.035	40.5	Develop an adaptive loss function capable of handling diverse noise types, and explore lightweight network architectures to improve real-time processing efficiency.
2024	SFNet [45]	0.9963	0.5268	101.22	Include dynamic attention mechanisms to better capture local phase discontinuities, and expand the training dataset to include more complex real-world noise patterns.
2025	DenSFA-PU [46]	0.999	/	/	Improve stability under extreme noise conditions (e.g., SNR < 0 dB) and enhance the network’s ability to capture long-range dependencies.

To address the problem (3), the following networks treat the phase unwrapping algorithm as an image restoration task. In 2022, Zhao et al. from the University of Electronic Science and Technology of China introduced the VDE-Net network [47], building upon the VUR-Net network [48]. This network incorporated a weighted skip-edge attention mechanism for the first time, and, compared to VUR-Net, the VDE-Net demonstrated improved performance in undersampled wrapped phase maps.

In 2023, Chen et al. from the University of Shanghai for Science and Technology developed the U2-Net network [49]. This model enhances generalization by incorporating deeper nested U-structures and residual modules, allowing it to maintain strong performance across various noise conditions and diverse datasets.

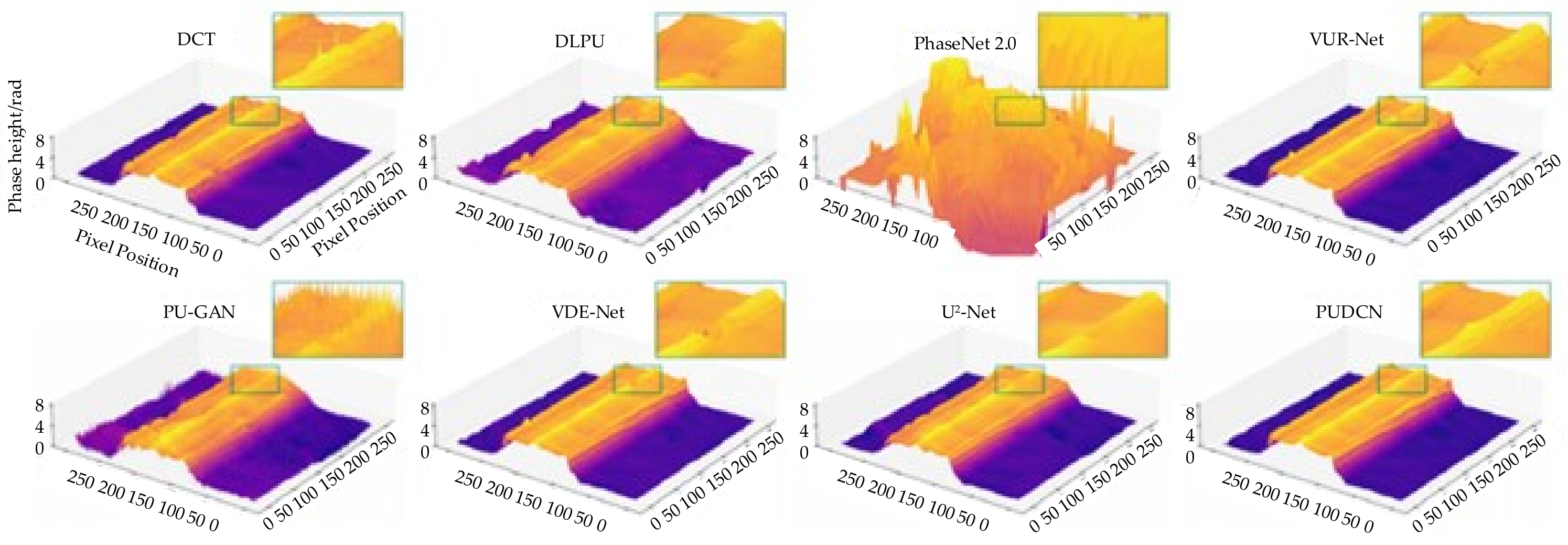
In 2024, Li et al. from Harbin Engineering University proposed the phase unwrapping deep convolutional network (PUDCN) for phase unwrapping in the presence of mixed noise and discontinuous regions [50]. The PUDCN was applied to phase unwrapping of optical fibers in interferometric measurements, demonstrating fewer fluctuations, outliers, and distortions, which indicates its robust generalization ability. Figure 13 presents a 3D visualization of the phase height of coaxial dual-waveguide fiber side projections, calculated using different methods.

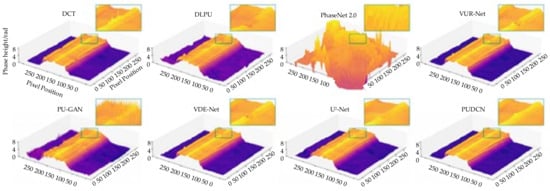
Figure 13. Three-dimensional visualization of the side projection phase height of coaxial dual-waveguide fibers calculated using different methods [50].

The Table 11 below presents an analysis and comparative summary of the mechanisms of deep learning and traditional methods for phase unwrapping, focusing on addressing poor generalization.

Table 11. Mechanism comparison of deep learning methods addressing poor generalization in phase unwrapping.

Method	Core Mechanism	Advantages	Limitations	Conclusion
VDE-Net [47]	Utilizes a two-stage architecture that emphasizes phase jump regions through a weighted jump-edge attention mechanism; applies dilated convolutions to expand the receptive field and achieves robust phase unwrapping to noise and undersampling.	Enhances edge feature enhancement; robust to noise and undersampling; incorporates physical priors in the preprocessing stage to improve interpretability.	Increased computational complexity due to attention modules; reduced stability under extreme noise environments.	Effectively addresses the shortcomings of traditional methods in edge detail processing and noise robustness.
U2-Net [49]	Constructs an encoder–decoder architecture using nested U-shaped residual blocks, enabling multi-scale feature fusion and deep supervision to improve phase unwrapping accuracy and structural stability in complex noise environments.	Provides strong multi-resolution feature extraction capability, superior noise robustness over traditional U-Net, and supports wide dynamic range.	High parameter count and extended training time; performance degrades in extremely low signal-to-noise ratio.	Strikes a balance between parameter scale and noise resilience than traditional deep learning models.
PUDCN [50]	Incorporates deformable convolutions to dynamically capture irregular phase edges, combining a pyramid feature dynamic selection module and fusion feature dynamic selection module for multi-scale feature extraction and detail-optimized phase unwrapping via a coarse-to-fine strategy.	Deformable convolutions adapt to phase jumps of arbitrary shapes; lightweight design with only 1.16 M parameters, suitable for deployment on edge devices.	The two-stage training process is complex; inference speed decreases significantly for extremely high-resolution images.	Effectively addresses the limitations of traditional CNNs in handling irregular edges.

The Table 12 below presents a comparative analysis of the impact of deep learning methods in addressing poor generalization.

Table 12. Comparative analysis of the effects of deep learning methods in addressing poor generalization.

Year	Method	SSIM	RMSE	PSNR	Suggestions for Improvement
2022	VDE-Net [47]	0.9984	/	/	Dynamically adjust the weighted factors in the jump-edge attention mechanism to improve the adaptability to various noise distributions and phase discontinuities.
2023	U2-Net [49]	0.9989	/	63.6289	Incorporate lightweight attention modules into U2-Net to reduce computational overhead while preserving its multi-scale feature extraction capability for real-time applications.
2024	PUDCN [50]	0.9986	0.2625	/	Employ self-adaptive deformable convolution kernels to effectively extract irregular phase edges and enhance generalization under extreme noise conditions.

To address the problem (4), Li et al. from Guangxi University of Science and Technology proposed a deep learning-based center difference information filtering PU (DLCDIFPU) algorithm in 2023 [51]. This algorithm approaches the phase unwrapping problem as an image restoration task and introduces a novel, efficient, and robust filter (CDIF) combined with efficient local phase gradient estimation and a path-tracking strategy based on heap sorting. This approach improved the accuracy of phase unwrapping by approximately 15%.

In 2024, Zhao et al. from Guilin University of Electronic Technology introduced the C-HRNet network [52], which framed the phase unwrapping problem as an image segmentation challenge. By incorporating a high-resolution network and an object context representation module, the C-HRNet network significantly enhanced phase unwrapping accuracy. Notably, when compared to the DeeplabV3+ network, it exhibited lower root mean square error (RMSE) and higher PSNR.

The Table 13 below presents an analysis and comparative summary of the mechanisms of deep learning and traditional methods for phase unwrapping, focusing on addressing low accuracy.

Table 13. Mechanism analysis of deep learning mechanisms addressing low accuracy in phase unwrapping.

Method	Core Mechanism	Advantages	Limitations	Conclusion
DLCDIFPU [51]	Utilizes a deep learning-based region segmentation model to divide wrapped phase maps into irregular regions along fringe edges; integrates CDIF with a heap-sort path-tracking strategy to unwrap each region independently, merging the results via phase consistency and achieving noise-resistant, and localized phase unwrapping.	Integrates data-driven learning with physical models; achieves an RMSE of only 0.24π under strong noise. Regional segmentation effectively suppresses cross-edge error propagation.	Depends on a dual-network architecture and necessitates high-precision annotated data, increasing implementation complexity.	Enhances phase unwrapping accuracy and efficiency by leveraging regional processing and physical prior, such as fringe edge detection, to guide localized unwrapping.
C-HRNet [52]	Extends HRNet by adding a fifth stage for enhanced multi-resolution feature fusion and incorporates the OCR module to aggregate pixel-object relationships. Treats phase unwrapping as a semantic segmentation task, predicting fringe order maps directly from single-frame wrapped phases, thereby improving unwrapping accuracy in complex noise and isolated regions.	Supports multi-scale feature fusion and contextual mechanisms; enables attention, and end-to-end learning for improved phase unwrapping accuracy.	Relies heavily on large-scale, data; lacks clear physical interpretability; incurs high computational cost.	Enhances the robustness of phase unwrapping in complex scenarios through multi-scale feature extraction and contextual semantic modeling.

The following Table 14 presents a comparative analysis of deep learning-based methods for enhancing accuracy.

$$RMSE=\sqrt{{\displaystyle \frac{1}{N}}{\sum }_{i=1}^N{\left(y_i-\widehat{y_i}\right)}^2}$$

(24)

$$AU={\displaystyle \frac{1}{XY}}\sum _{x=1}^X\sum _{y=1}^Y\mathit{BEM}\left(x,y\right)\times 1$$

(25)

where N represents the number of observations, $y_i$ denotes the actual value of the i-th observation, and ${\hat{y}}_i$ indicates the predicted value of the i-th observation. X and Y signify the number of rows and columns of the unwrapped phase image, respectively. BEM(x, y) is the pixel value on the binary error map, where the pixel is 1 if the phase is correctly unwrapped, and 0 otherwise.

Table 14. Comparative analysis of deep learning methods for addressing low accuracy in phase unwrapping.

Year	Method	RMSE	Suggestions for Improvement
2023	DLCDIFPU [51]	/	Incorporate adaptive noise suppression mechanisms into the central difference information filter to enhance the robustness of complex fringe structures and under severe noise variations.
2024	C-HRNet [52]	1.76	Establish a dynamic context aggregation mechanism in the object contextual representation module to effectively extract diverse phase discontinuities in isolated regions.

Note: The data presented above are the experimental results obtained from their respective datasets.

In phase unpacking, the absolute error graph map serves as a critical metric for evaluating unwrapping accuracy. Equation (25) quantifies the error of understanding by computing the difference between the unwrapped and the ground truth phase images.

The Table 15 below presents a classification and comparative summary of deep learning and traditional methods for phase unwrapping.

Table 15. Classification of phase unwrapping network dimensions.

Method	Application Domain	Technical Principle Dimension	Learning Paradigm
UnwrapGAN [40]	Biomedicine (off-axis DHM).	Pix2Pix-based GAN with an encoder-decoder structure; incorporates adversarial and L1 loss functions.	Supervised learning (paired data).
Res-Unet [41]	Digital holographic interferometry; industrial inspection (off-axis DHM).	Residual U-Net architecture enhanced with weighted skip-edge attention mechanisms.	Supervised learning (training on simulated data).
DeepLabV3+ [42]	Optical metrology under complex noise conditions (off-axis DHM).	Semantic segmentation framework using dilated convolutions and spatial pyramid pooling.	Supervised learning (augmented noisy data).
PhaseNet2.0 [43]	Optical metrology; SAR interferometry (off-axis DHM).	Fully convolutional DenseNet architecture; utilizes composite loss functions (cross-entropy, L1, and residual loss).	Supervised learning (multimodal noisy data).
SFNet [45]	Industrial optical inspection; 3D shape reconstruction (off-axis DHM).	Transformer-based encoder with MLP decoder and self-attention mechanism.	Supervised learning (combined simulated and real data).
DenSFA-PU [46]	Digital holographic interferometry (off-axis DHM).	Densely connected network + spatial feature aggregator (SFA)	Supervised learning (composite loss function)
VDE-Net [47]	Biomedical imaging (off-axis DHM).	Two-stage deep architecture incorporating dilated convolutions and weighted edge attention mechanism.	Supervised learning (attention-guided learning strategy).
U2-Net [49]	Dynamic flame imaging; complex surface structure measurement (in-line DHM).	Nested U-shaped residual blocks with deep supervision loss for multi-scale feature extraction.	Supervised learning (multi-scale fusion).
PUDCN [50]	Fiber optic interferometry, industrial defect detection (off-axis DHM).	Deformable convolution layers with a pyramid feature selection module for dynamic representation.	Supervised learning (coarse-to-fine two-stage training).
DLCDIFPU [51]	Industrial inspection (in-line DHM).	Deep region segmentation combined with central difference information filtering (CDIF) and path tracking.	Supervised learning (simulated phase maps with real phase labels).
C-HRNet [52]	Precision metrology, biomedical imaging, industrial inspection (off-axis DHM).	High-resolution network (HRNet) with object-contextual representation (OCR) module for semantic segmentation.	Supervised learning (mixed simulated dataset and real data using cross-entropy loss).

4.3. Application of Deep Learning in Phase Distortion Compensation

Phase distortion can arise due to factors such as aberrations in the optical system, uneven illumination, tilt between the recording surface and the object, and the surface morphology of the object. These distortions can introduce unwanted low-frequency backgrounds, nonlinear errors, or high-frequency noise during the holographic reconstruction process, ultimately affecting the accuracy of the reconstructed image and the true optical characteristics of the sample.

Phase distortion compensation is a crucial process for eliminating these artifacts caused by imperfect systems or environments, correcting non-physical backgrounds, and restoring the true phase distribution of the target. This process improves the quality of holographic image reconstruction and enhances the accuracy of quantitative analysis. Traditional phase distortion compensation methods can generally be categorized into physical and numerical approaches. Physical methods typically involve electronically adjustable lenses, co-located DHM configurations, telecentric setups, and the use of identical objective lenses. Numerical methods rely on post-processing techniques and do not require additional holograms or optical components. These include fitting calculations, principal component analysis, spectral analysis, geometric transformations, and nonlinear optimization, typically implemented using traditional software.

While these traditional methods are grounded in mature physical and mathematical theories, they still face several limitations:

(1)

They require extensive preprocessing.

(2)

They are constrained by perturbation assumptions.

(3)

They often require manual intervention.

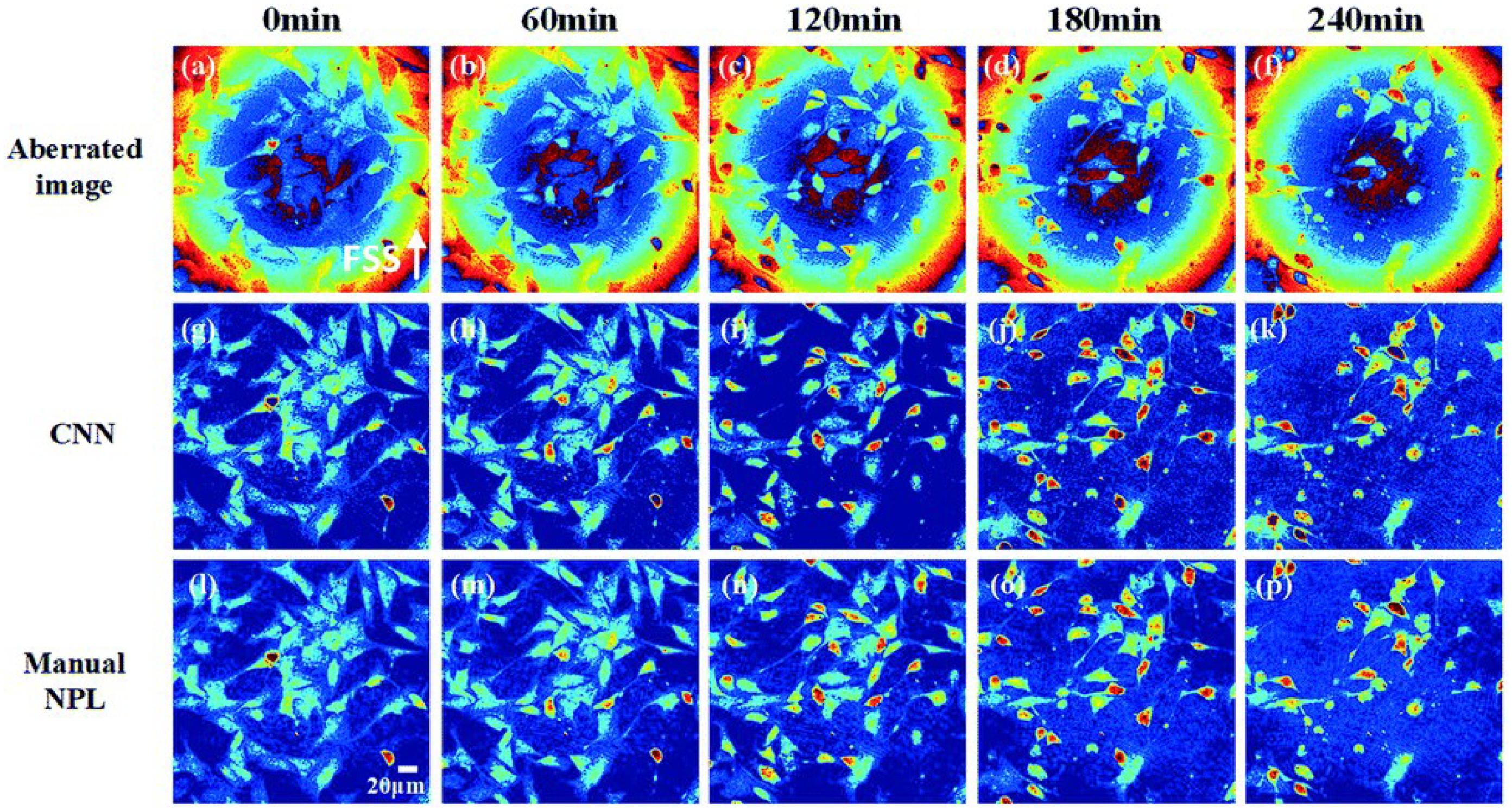
To address the issue (1), Xiao et al. from Beihang University proposed a CNN-based multi-variable regression distortion compensation method in 2021 [53]. This method predicts the optimal compensation coefficients and automatically compensates for phase distortions without needing to detect background areas or any physical parameters. Figure 14 compares the compensation results of this method with those of manual nonlinear programming-based phase compensation (NPL) methods across multiple time periods.

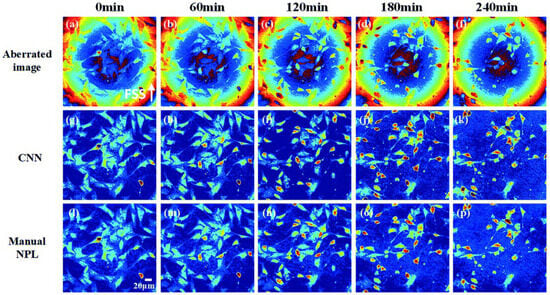
Figure 14. Comparison of compensation results between the method in reference [53] and manual NPL over multiple time periods, where (a–d,f) represent distorted images at different time periods, (g–k) represent distorted images after distortion compensation by CNN at different time periods, and (l–p) represent distorted images after distortion compensation by Manual NPL at different time periods.

In 2023, Li et al. from Xi’an University of Technology introduced a digitally-driven phase distortion compensation network (PACUnet3+) [54]. This network directly generates a reference hologram from sample holograms, eliminating the need for any preprocessing techniques. PACUnet3+ outperforms the original Unet3+ network [55] in eliminating phase distortion and also surpasses traditional methods, such as phase aberration compensation (PAC) and fitting.

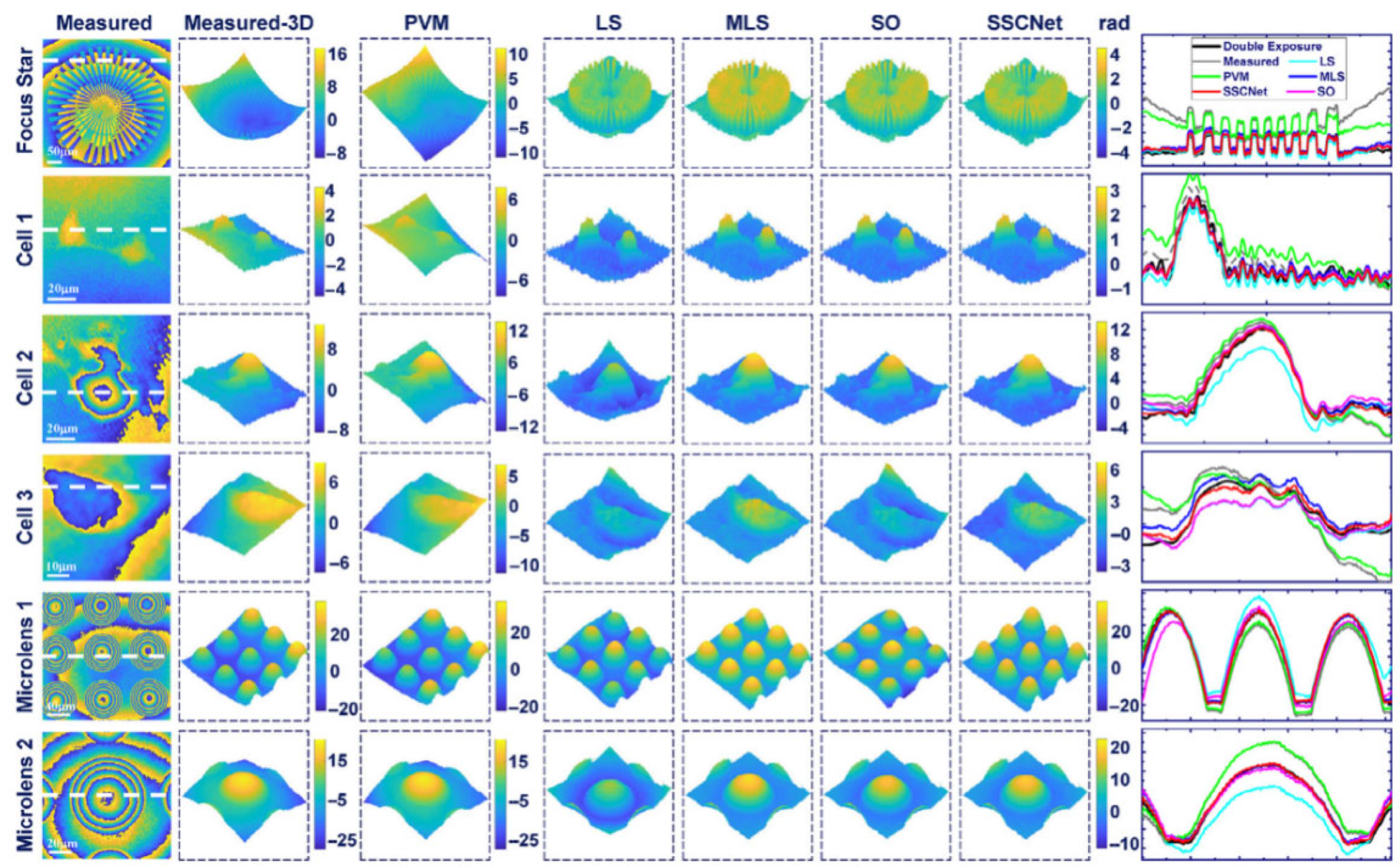
To address the issue (2), Tang et al. from Northwestern Polytechnical University introduced a self-supervised sparse constraint network (SSCNet) in 2023 [56]. The SSCNet combines sparse constraints with Zernike model enhancement and requires only a single measured phase for self-supervision. This network achieves high accuracy and stability in PAC, without the need for target masks or perturbation assumptions. When it comes to adaptive compensation for dynamic distortions, SSCNet outperforms the double exposure technique. Figure 15 compares the compensation results of SSCNet with those of various algorithms.

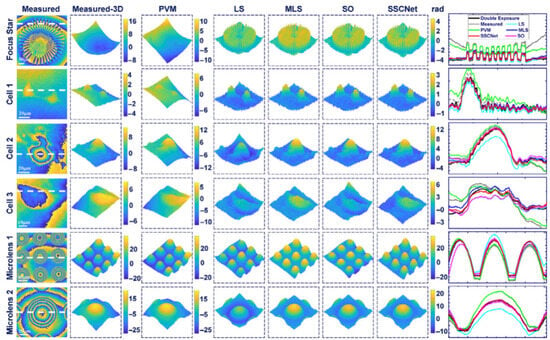
Figure 15. Compensation effects of SSCNet and various algorithms [56].

The Table 16 below presents an analysis and comparative summary of the mechanisms of deep learning and traditional methods for phase distortion compensation, focusing on extensive preprocessing and perturbation assumption constraints.

Table 16. Comparative analysis of deep learning mechanisms in extensive preprocessing and perturbation assumption constraints.

Method	Core Mechanism	Advantages	Limitations	Conclusion
CNN+ZPF [53]	Employs a CNN to automatically identify background regions in DHM, fitting phase aberrations via Zernike polynomial expression.	High-accuracy background detection with automated compensation.	Limited generalizability and dependency on annotated datasets.	Enables long-term phase distortion correction without manual intervention by integrating automatic segmentation with model-based phase fitting.
PACUnet3+ [54]	Constructs an encoder-decoder architecture based on Unet3+ to learn the mapping between object holograms and sample-free references, enabling data-driven background subtraction for phase correction.	Eliminates reliance on physical modeling while maintaining high accuracy.	Computationally intensive and requires large-scale training data.	Achieves accurate PAC using data-driven hologram reconstruction, bypassing explicit physical model assumptions.
SSCNet [56]	Combines a Zernike polynomial-constrained phase model with self-supervised learning and sparse optimization to estimate phase aberration coefficients using a single hologram input.	Capable of compensating for dynamic phase distortions without reference data.	Sensitive to initial conditions and exhibits slow convergence.	Enables adaptive correction of phase errors in dynamically varying systems through self-supervised optimization aligned with physical constraints.

To address the issue (3), Thanh Nguyen et al. from the Catholic University of America proposed a fully automated technique in 2017 that combined deep learning-based CNNs and Zernike polynomial fitting (ZPF) [57]. This method’s advantage lies in its ability to automatically monitor the background region and compensate for higher-order aberrations, enhancing the accuracy of real-time measurements and enabling dynamic process monitoring.

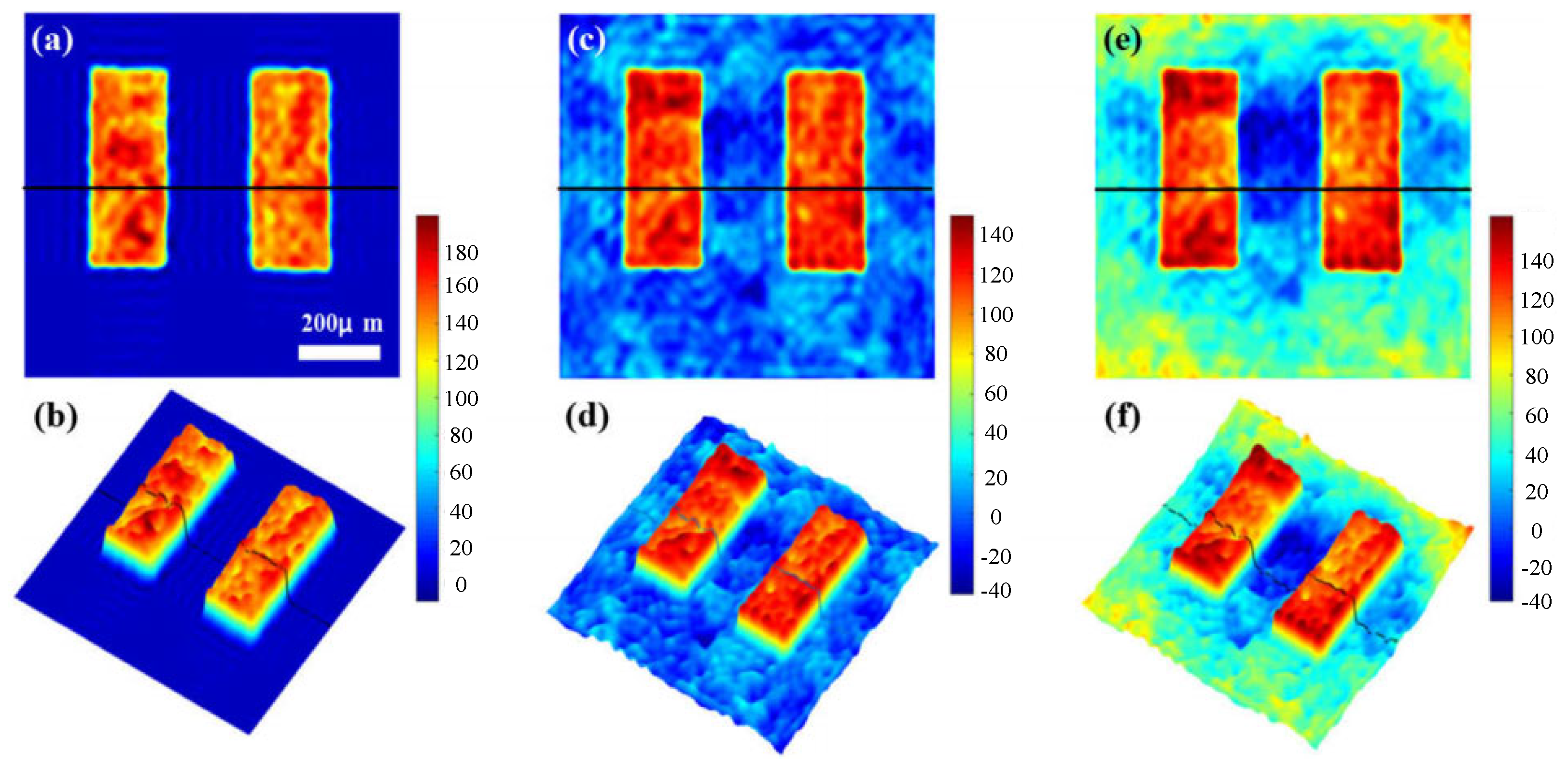
In 2021, MA et al. from Northeastern University [58] introduced a phase distortion compensation method for DHM based on a two-stage generative adversarial network (GAN). This method eliminates the need for a complex spectral centering process or prior knowledge, significantly simplifying the operational workflow while improving both precision and efficiency. It successfully automates the compensation process without requiring manual intervention. Figure 16 compares the distortion compensation results of this method with those of traditional approaches.

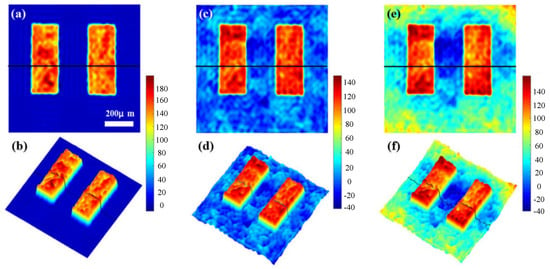
Figure 16. (a) Result obtained by the proposed method; (b) 3D rendering of (a). (c) Result obtained by BS+ZPF; (d) 3D rendering of (c). (e) Result obtained by ZPF; (f) 3D rendering of (e) [58].

The Table 17 below presents an analysis and comparative summary of the mechanisms of deep learning and traditional methods for phase distortion compensation, focusing on addressing the manual intervention issue.

Table 17. Comparative analysis of deep learning mechanisms addressing the manual intervention issue.

Method	Core Mechanism	Advantages	Limitations	Conclusion
CNN+ZPF [57]	Utilizes a CNN to segment background regions in the phase image, followed by Zernike polynomial fitting to decouple sample-induced phase from system aberrations, enabling fully automated compensation.	Enables high-throughput processing with simple operation.	Limited robustness under complex background textures or high noise.	Facilitates rapid and automated background identification, making it particularly effective for high-throughput applications, such as cell morphology analysis.
Two-stage GAN [58]	Implements a two-step generative adversarial network: the first network reconstructs structural edges of occluded regions, while the second completes the missing content, thereby generating sample-independent reference holograms for phase correction.	Strong capability for large-area restoration with realistic details.	Training is unstable; performance degrades when occlusion exceeds 40%.	Applies unsupervised adversarial learning to restore phase data in highly occluded conditions, outperforming traditional methods in challenging scenarios.

In summary, traditional phase distortion compensation methods offer advantages in terms of theoretical framework and algorithmic simplicity, while deep learning methods stand out for their adaptability and ability to manage complex relationships. However, there is still considerable potential for improving the effectiveness of phase distortion compensation using deep learning techniques in the future.

The Table 18 below presents a classification and comparative summary of deep learning and traditional methods for phase distortion compensation.

Table 18. Classification table of phase distortion compensation network dimensions.

Method	Application Scenario Dimension	Technical Principle Dimension	Learning Paradigm Dimension
CNN+ZPF [53]	Biomedical applications and real-time phase analysis (off-axis DHM).	Data-driven + physical model fitting.	Supervised learning.
PACUnet3+ [54]	High-precision reconstruction of microstructures (off-axis DHM).	Data-driven (end-to-end hologram generation).	Supervised learning.
SSCNet [56]	Adaptive phase correction in dynamic environments (off-axis DHM).	Physical model + self-supervised sparse constraints.	Self-supervised learning.
CNN+ZPF [57]	Restoration in complex and large-field-of-view samples. (off-axis DHM).	Data-driven (GAN-generated restoration) + edge priors.	Unsupervised learning.
Two-stage GAN [58]	Single-frame unwrapping in noise-intensive conditions (off-axis DHM).	Multi-scale feature fusion + contextual semantic enhancement.	Supervised learning.

The Table 19 below presents a comparative analysis of deep learning-based phase distortion compensation methods.

Table 19. Summary of deep learning-based methods for phase distortion compensation.

Year	Method	SSIM	MAE	RMSE	PV	Suggestions for Improvement
2021	CNN+ZPF [53]	0.943	0.021	/	/	Enhance generalization capabilities to accommodate complex cell morphologies or dynamic noise environments.
2023	PACUnet3+ [54]	0.93	/	0.0963	0.6308	Optimize the network architectures to minimize computational complexity and enhance real-time performance.
2023	SSCNet [56]	0.9924	0.012	0.441	5.490	Investigate more robust sparsity-constrained optimization strategies to accelerate convergence and improve stability.
2017	CNN+ZPF [57]	0.927	0.028	/	/	Enhance the precision of background segmentation in scenarios for complex backgrounds or low-contrast sample features.
2021	Two-stage GAN [58]	0.9885	0.0029	/	/	Optimize GAN training strategies to ensure repair consistency and detail fidelity for high-occlusion-rate samples.

Note: The data presented above are the experimental results obtained from their respective datasets. Evaluation Metric: The formula for calculating PV is as follows.

$$PV={\varphi }_{max}-{\varphi }_{min}$$

(26)

where ${\varphi }_{max}$ represents the maximum phase value in the phase distribution, and ${\varphi }_{min}$ denotes the minimum phase value in the phase distribution.

4.4. Evaluation Metrics for Phase Processing Results

In DHM, the quality of phase processing is essential, as it directly impacts the accuracy, fidelity, and applicability of the results. These results influence subsequent analyses and applications. Both qualitative and quantitative evaluations are commonly used to assess phase processing.

Qualitative evaluation generally focuses on three key factors: visual quality, detail preservation, and background smoothness. Quantitative evaluation involves numerical metrics to objectively assess the reconstruction from several perspectives, including phase accuracy, image quality, and noise suppression. Accuracy is often evaluated using metrics, such as the mean squared error (MSE) and MAE. Image quality is assessed with the PSNR and SSIM. Noise suppression is evaluated using the RMSE.

5. Summary and Outlook

Deep learning approaches in DHM have shown improvements in accuracy, processing speed, and generalization compared to traditional phase processing methods. However, research in this field is still in its early stages. Key areas for further exploration include the following:

(1)

Ultrafast 3D Holographic Reconstruction: Current 3D reconstruction in DHM relies on time-consuming iterative algorithms. Future work could focus on deep learning-based fast inversion algorithms, such as Bayesian–physical joint modeling [59] or a 3D reconstruction method based on unpaired data learning [60]. By training on a large dataset of paired holographic interference patterns and their 3D reconstructions, these models can be trained to learn the direct mapping. This pattern enables the rapid conversion of interference patterns into 3D reconstructions, significantly improving real-time imaging—particularly for capturing dynamic processes, such as cell movement.

(2)

High-Throughput Holographic Data Analysis: DHM generates vast amounts of data in high-throughput experiments (such as drug screening). Automating data analysis using deep learning pipelines, such as few-shot learning and transfer learning, could improve classification, segmentation, and feature extraction. In practice, the model can first be pre-trained on a large-scale general holographic dataset to learn a broad feature representation of the data. Subsequently, few-shot learning can be applied to quickly adapt the model to specific high-throughput experimental data, enabling accurate analysis and enhancing the efficiency and automation of these experiments.

(3)

Precise Quantification of Phase Analysis: In biomedical applications, accurate phase analysis is crucial for the non-destructive measurement of optical thickness and refractive index in cells and tissues. Deep learning could help develop more precise phase recovery algorithms. A CNN-based architecture can be tailored to effectively extract phase information from holograms. By introducing an attention mechanism, the network can prioritize key regions with significant phase features, enabling automatic extraction of quantitative data for complex biological analysis.

(4)

Multimodal Data Fusion: Combining DHM with other imaging techniques (e.g., electron or fluorescence microscopy) could significantly enhance the information gathered from images. Deep learning could integrate these modalities. A multimodal fusion network is specifically designed to extract features from each modality separately. These features are then combined through the fusion layer to reveal deeper structural and biological information, enhancing resolution, contrasts, and the diversity of biological markers in biomedical research.