Formation of Inverse Energy Flux in the Case of Diffraction of Linearly Polarized Radiation by Conventional and Generalized Spiral Phase Plates
Abstract
:1. Introduction
2. Methods
3. Results
3.1. Theoretical Analysis Based on the Stationary Phase Method
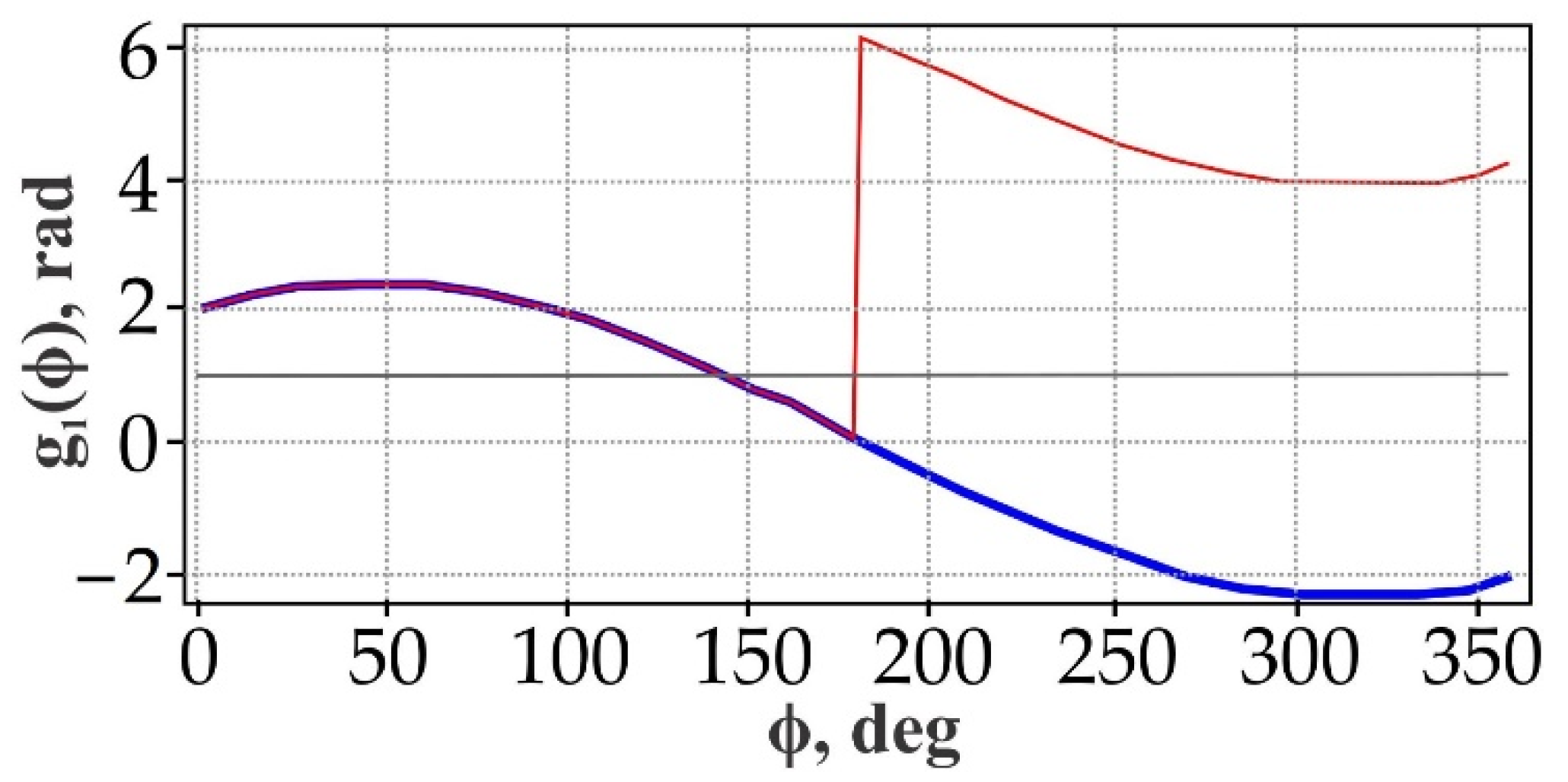
3.2. Determination of Conditions for Inverse Energy Flow on the Optical Axis
3.3. Determination of Conditions for Off-Axis Inverse Energy Flow
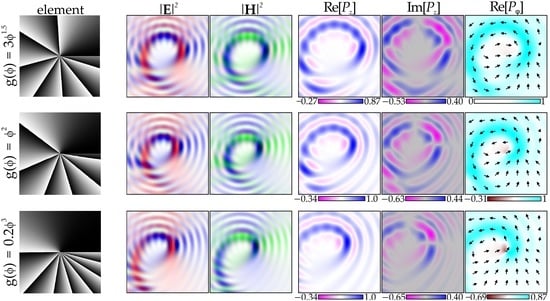
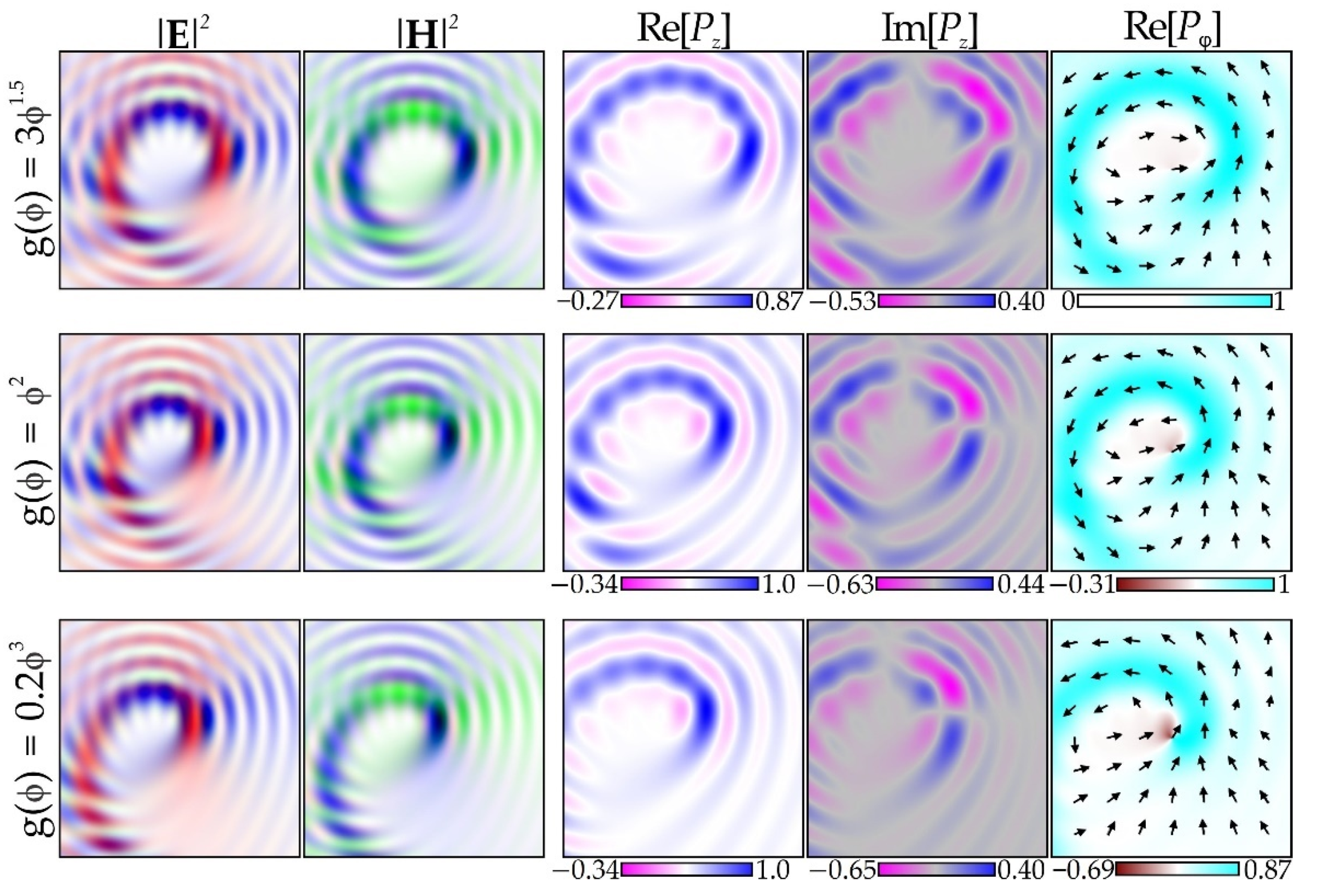
3.4. Analysis of Special Cases and Simulation Results
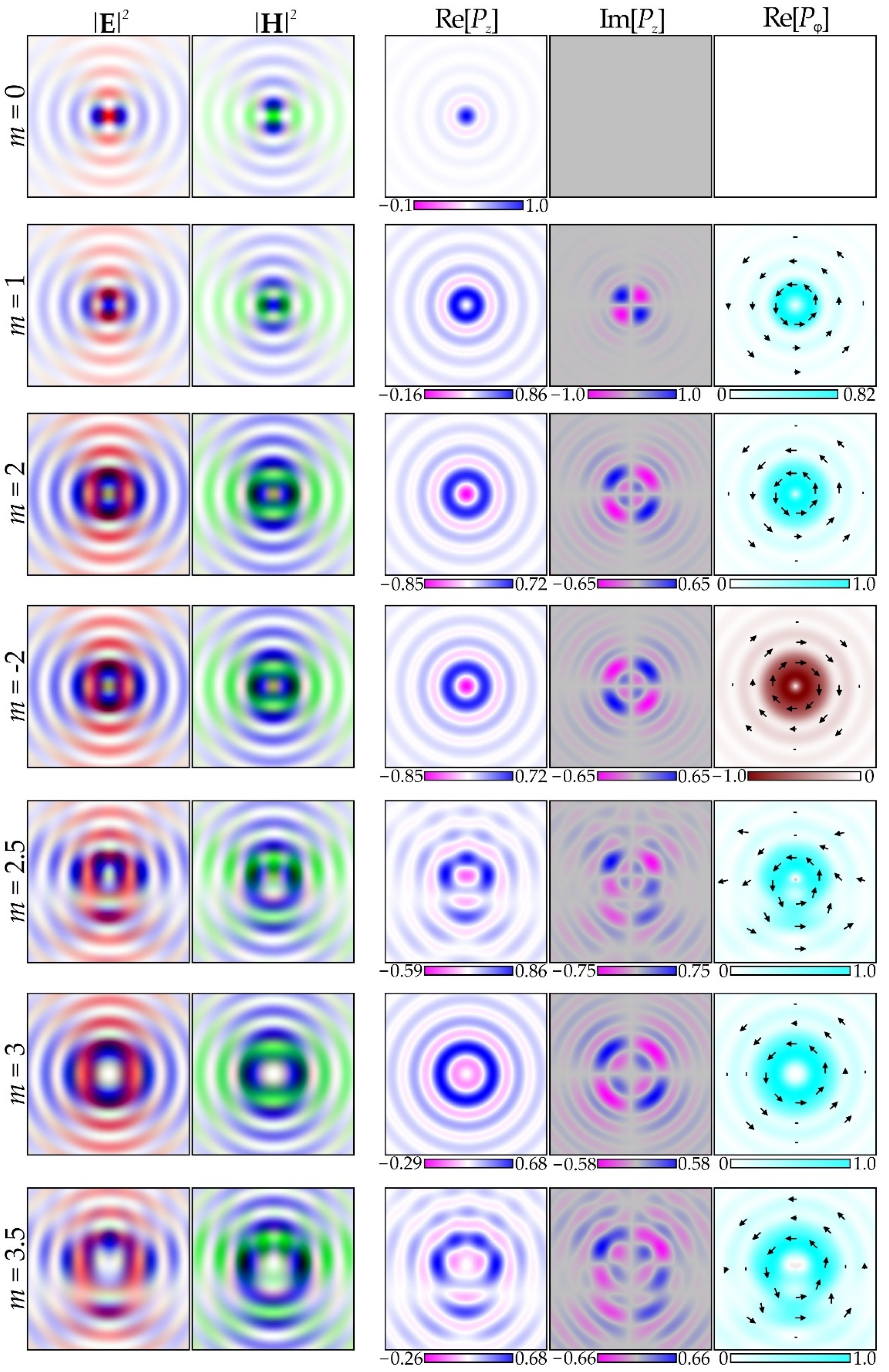
3.4.1. Example 1: Classic SPP
3.4.2. Example 2: Amplitude Spiral Plate with a Phase Shift
3.4.3. Example 3: Power-Exponent Phase Plate
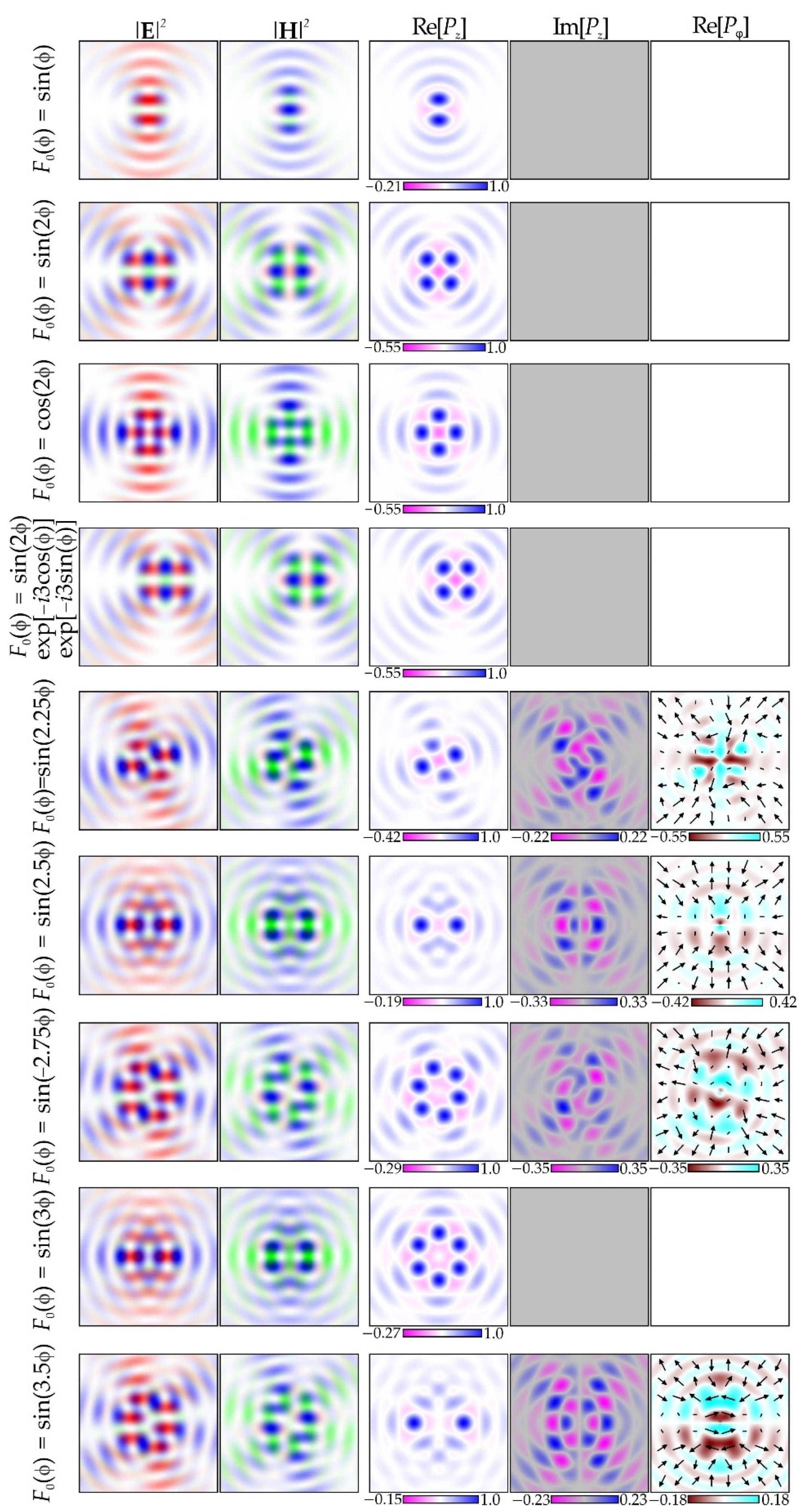
3.4.4. Example 4: Light Fields Resulting from the Stationary Phase Method
3.4.5. Example 5: Binary Phase
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Higgins, T.V. Spiral waveplate design produces radially polarized laser light. Laser Focus World 1992, 28, 18–20. [Google Scholar]
- Beijersbergen, M.W.; Coerwinkel, R.C.; Kristensen, M.; Woerdman, J.P. Helical-wavefront laser beams produced with a spiral phase plate. Opt. Commun. 1994, 112, 321–327. [Google Scholar] [CrossRef]
- Moh, K.J.; Yuan, X.-C.; Tang, D.Y.; Cheong, W.C.; Zhang, L.S.; Low, D.K.Y.; Peng, X.; Niu, H.B.; Lin, Z.Y. Generation of femtosecond optical vortices using a single refractive optical element. Appl. Phys. Lett. 2006, 88, 091103. [Google Scholar] [CrossRef]
- Berry, M.V. Optical vortices evolving from helicoidal integer and fractional phase steps. J. Opt. A Pure Appl. Opt. 2004, 6, 259–268. [Google Scholar] [CrossRef]
- Luo, M.; Wang, Z. Fractional vortex ultrashort pulsed beams with modulating vortex strength. Opt. Express 2019, 27, 36259–36268. [Google Scholar] [CrossRef]
- Khonina, S.; Karpeev, S.; Butt, M. Spatial-Light-Modulator-Based Multichannel Data Transmission by Vortex Beams of Various Orders. Sensors 2021, 21, 2988. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Liu, S.; Peng, T.; Xie, G.; Gan, X.; Zhao, J. Spiral autofocusing Airy beams carrying power-exponent-phase vortices. Opt. Express 2014, 22, 7598–7606. [Google Scholar] [CrossRef]
- Lao, G.; Zhang, Z.; Zhao, D. Propagation of the power-exponent-phase vortex beam in paraxial ABCD system. Opt. Express 2016, 24, 18082–18094. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Logachev, V.I.; Porfirev, A.P. Properties of vortex light fields generated by generalized spiral phase plates. Phys. Rev. A 2020, 101, 043829. [Google Scholar] [CrossRef]
- Ustinov, A.V.; Khonina, S.N.; Khorin, P.A.; Porifrev, A.P. Control of the intensity distribution along the light spiral generated by a generalized spiral phase plate. J. Opt. Soc. Am. B 2021, 38, 420. [Google Scholar] [CrossRef]
- Shanblatt, E.R.; Grier, D.G. Extended and knotted optical traps in three dimensions. Opt. Express 2011, 19, 5833–5838. [Google Scholar] [CrossRef]
- Rodrigo, J.A.; Alieva, T.; Abramochkin, E.; Castro, I. Shaping of light beams along curves in three dimensions. Opt. Express 2013, 21, 20544–20555. [Google Scholar] [CrossRef] [Green Version]
- Woerdemann, M.; Alpmann, C.; Esseling, M.; Denz, C. Advanced optical trapping by complex beam shaping. Laser Photon- Rev. 2013, 7, 839–854. [Google Scholar] [CrossRef]
- Bekshaev, A.; Soskin, M. Transverse energy flows in vectorial fields of paraxial beams with singularities. Opt. Commun. 2007, 271, 332–348. [Google Scholar] [CrossRef]
- Bekshaev, A.Y. Internal energy flows and instantaneous field of a monochromatic paraxial light beam. Appl. Opt. 2012, 51, C13–C16. [Google Scholar] [CrossRef] [PubMed]
- Novitsky, A.; Novitsky, D. Negative propagation of vector Bessel beams. J. Opt. Soc. Am. A 2007, 24, 2844–2849. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V.; Degtyarev, S. Inverse energy flux of focused radially polarized optical beams. Phys. Rev. A 2018, 98, 043823. [Google Scholar] [CrossRef]
- Khonina, S.N.; Ustinov, A.V. Increased reverse energy flux area when focusing a linearly polarized annular beam with binary plates. Opt. Lett. 2019, 44, 2008–2011. [Google Scholar] [CrossRef]
- Kotlyar, V.V.; Stafeev, S.S.; Nalimov, A.G.; Kovalev, A.A.; Porfirev, A.P. Mechanism of formation of an inverse energy flow in a sharp focus. Phys. Rev. A 2020, 101, 033811. [Google Scholar] [CrossRef]
- Zemánek, P.; Volpe, G.; Jonáš, A.; Brzobohatý, O. Perspective on light-induced transport of particles: From optical forces to phoretic motion. Adv. Opt. Photon. 2019, 11, 577–678. [Google Scholar] [CrossRef]
- Saenz, J.J. Laser tractor beams. Nat. Photon. 2011, 5, 514–515. [Google Scholar] [CrossRef]
- Sukhov, S.; Dogariu, A. On the concept of ‘tractor beams’. Opt. Lett. 2010, 35, 3847–3849. [Google Scholar] [CrossRef]
- Novitsky, A.; Ding, W.; Wang, M.; Gao, D.; Lavrinenko, A.; Qiu, C.-W. Pulling cylindrical particles using a soft-nonparaxial tractor beam. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [Green Version]
- Lan, C.; Yang, Y.; Geng, Z.; Li, B.; Zhou, J. Electrostatic Field Invisibility Cloak. Sci. Rep. 2015, 5, 16416. [Google Scholar] [CrossRef] [Green Version]
- Novitsky, A.; Qiu, C.-W.; Wang, H. Single Gradientless Light Beam Drags Particles as Tractor Beams. Phys. Rev. Lett. 2011, 107, 203601. [Google Scholar] [CrossRef] [Green Version]
- Qiu, C.-W.; Palima, D.; Novitsky, A.; Gao, D.; Ding, W.; Zhukovsky, S.; Gluckstad, J. Engineering light-matter interaction for emerging optical manipulation applications. Nanophotonics 2014, 3, 181–201. [Google Scholar] [CrossRef]
- Wong, V.; Ratner, M.A. Explicit computation of gradient and nongradient contributions to optical forces in the discrete-dipole approximation. J. Opt. Soc. Am. B 2006, 23, 1801–1814. [Google Scholar] [CrossRef]
- Novitsky, A.; Qiu, C.-W. Pulling extremely anisotropic lossy particles using light without intensity gradient. Phys. Rev. A 2014, 90, 053815. [Google Scholar] [CrossRef] [Green Version]
- Bliokh, K.; Bekshaev, A.Y.; Nori, F. Extraordinary momentum and spin in evanescent waves. Nat. Commun. 2014, 5, 3300. [Google Scholar] [CrossRef]
- Bekshaev, A.Y.; Bliokh, K.; Nori, F. Transverse Spin and Momentum in Two-Wave Interference. Phys. Rev. X 2015, 5, 011039. [Google Scholar] [CrossRef]
- Xu, X.; Nieto-Vesperinas, M. Azimuthal Imaginary Poynting Momentum Density. Phys. Rev. Lett. 2019, 123, 233902. [Google Scholar] [CrossRef]
- Khonina, S.N.; Degtyarev, S.A.; Ustinov, A.V.; Porfirev, A.P. Metalenses for the generation of vector Lissajous beams with a complex Poynting vector density. Opt. Express 2021, 29, 18634–18645. [Google Scholar] [CrossRef]
- Richards, B.; Wolf, E. Electromagnetic diffraction in optical systems, II. Structure of the image field in an aplanatic system. Proc. R. Soc. London. Ser. A Math. Phys. Sci. 1959, 253, 358–379. [Google Scholar] [CrossRef]
- Pereira, S.; van de Nes, A. Superresolution by means of polarisation, phase and amplitude pupil masks. Opt. Commun. 2004, 234, 119–124. [Google Scholar] [CrossRef]
- Khonina, S.; Ustinov, A.V.; Volotovsky, S.G. Shaping of spherical light intensity based on the interference of tightly focused beams with different polarizations. Opt. Laser Technol. 2014, 60, 99–106. [Google Scholar] [CrossRef]
- Jackson, J.D.; Levitt, L.C. Classical Electrodynamics. Phys. Today 1962, 15, 62. [Google Scholar] [CrossRef] [Green Version]
- Cameron, R.P.; Speirits, F.C.; Gilson, C.R.; Allen, L.; Barnett, S.M. The azimuthal component of Poynting’s vector and the angular momentum of light. J. Opt. 2015, 17, 125610. [Google Scholar] [CrossRef] [Green Version]
- Ustinov, A.V.; Niziev, V.G.; Khonina, S.N.; Karpeev, S.V. Local characteristics of paraxial Laguerre–Gaussian vortex beams with a zero total angular momentum. J. Mod. Opt. 2019, 66, 1961–1972. [Google Scholar] [CrossRef]
- Sheppard, C.J.R.; Choudhury, A. Annular pupils, radial polarization, and superresolution. Appl. Opt. 2004, 43, 4322–4327. [Google Scholar] [CrossRef] [PubMed]
- Khonina, S.N. Vortex beams with high-order cylindrical polarization: Features of focal distributions. Appl. Phys. A 2019, 125, 100. [Google Scholar] [CrossRef]
- Fedoruk, M.V. Asymptotics Integral and Series; Nauka: Moscow, Russia, 1987. [Google Scholar]
- Friberg, A.T. Stationary-phase analysis of generalized axicons. J. Opt. Soc. Am. A 1996, 13, 743–750. [Google Scholar] [CrossRef]
- Prudnikov, A.; Brychkov, Y.A.; Marichev, O. Integrals and Series; Informa UK Limited: London, UK, 2018; Volume 1. [Google Scholar]
- Khonina, S.N.; Ustinov, A.V.; Porfirev, A.P. Fractional two-parameter parabolic diffraction-free beams. Opt. Commun. 2019, 450, 103–111. [Google Scholar] [CrossRef]



Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ustinov, A.V.; Khonina, S.N.; Porfirev, A.P. Formation of Inverse Energy Flux in the Case of Diffraction of Linearly Polarized Radiation by Conventional and Generalized Spiral Phase Plates. Photonics 2021, 8, 283. https://doi.org/10.3390/photonics8070283
Ustinov AV, Khonina SN, Porfirev AP. Formation of Inverse Energy Flux in the Case of Diffraction of Linearly Polarized Radiation by Conventional and Generalized Spiral Phase Plates. Photonics. 2021; 8(7):283. https://doi.org/10.3390/photonics8070283
Chicago/Turabian StyleUstinov, Andrey V., Svetlana N. Khonina, and Alexey P. Porfirev. 2021. "Formation of Inverse Energy Flux in the Case of Diffraction of Linearly Polarized Radiation by Conventional and Generalized Spiral Phase Plates" Photonics 8, no. 7: 283. https://doi.org/10.3390/photonics8070283
APA StyleUstinov, A. V., Khonina, S. N., & Porfirev, A. P. (2021). Formation of Inverse Energy Flux in the Case of Diffraction of Linearly Polarized Radiation by Conventional and Generalized Spiral Phase Plates. Photonics, 8(7), 283. https://doi.org/10.3390/photonics8070283