Composition-Dependent Phonon and Thermodynamic Characteristics of C-Based XxY1−xC (X, Y ≡ Si, Ge, Sn) Alloys
Abstract
:1. Introduction
2. Computational Details
2.1. Phonons in XC Materials
2.1.1. Rigid-Ion Model
2.2. Lattice Dynamics of Ternary XxY1−xC Alloys
2.3. Thermodynamic Properties
2.4. Interaction of Photons with Solids
2.4.1. Born’s Effective Charge
2.4.2. Fröhlich Coefficients
3. Numerical Computations and Results
3.1. Lattice Dynamics of Binary XC Materials
3.1.1. Phonon Characteristics
3.1.2. Thermodynamic Characteristics
3.2. Phonon and Thermodynamic Properties of XxY1−xC Ternary Alloys
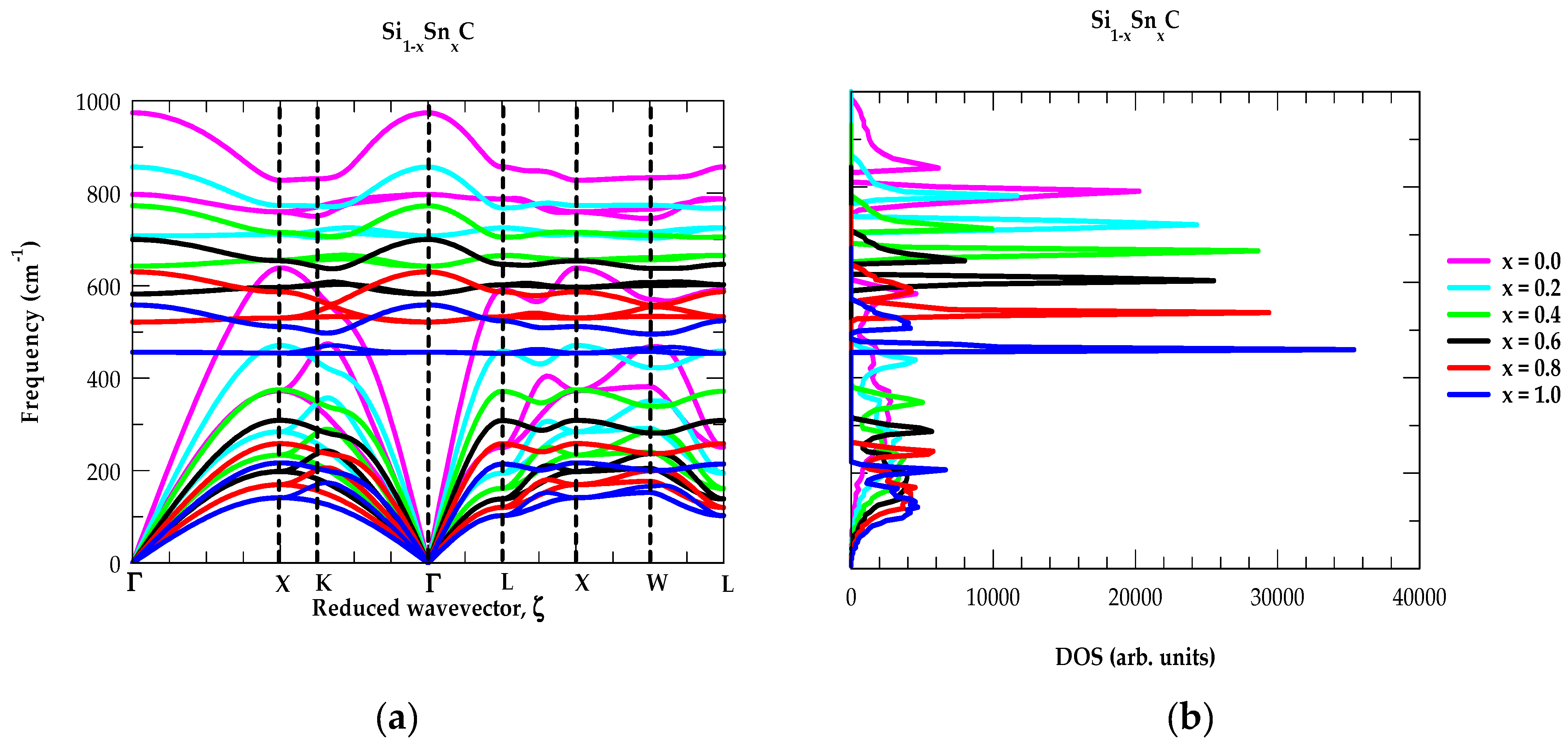
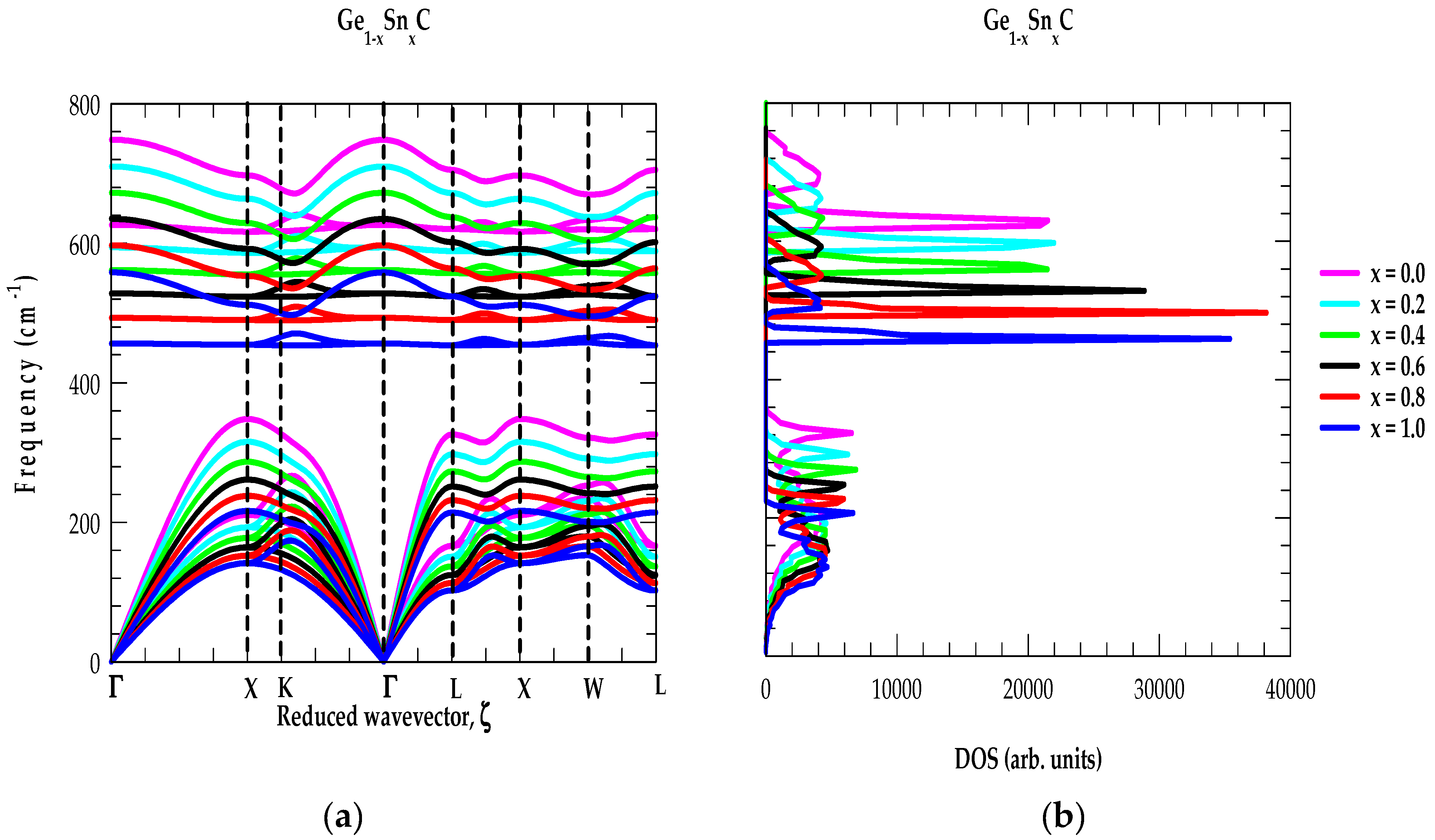
3.2.1. Phonon Characteristics of X1−xYxC Alloys
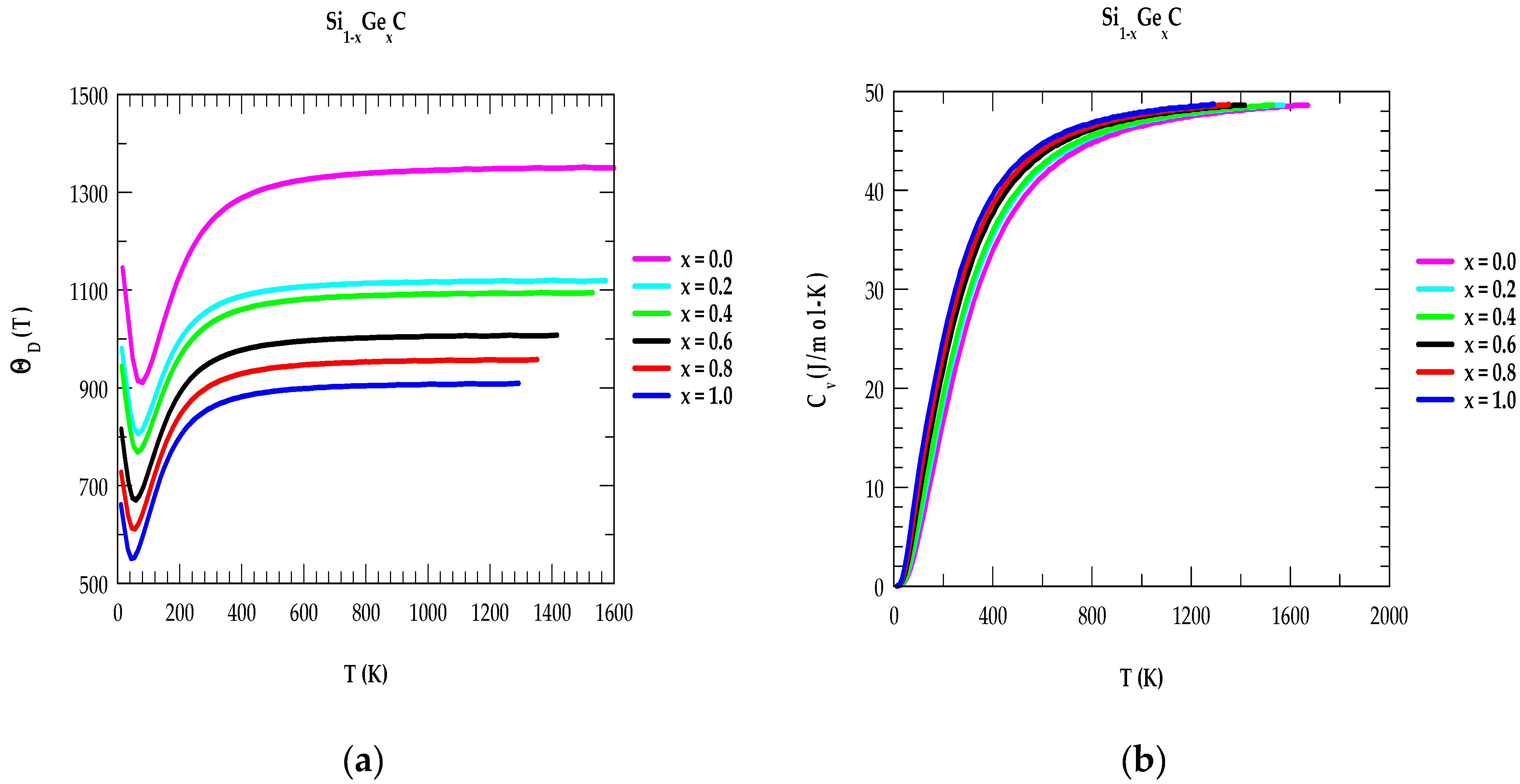
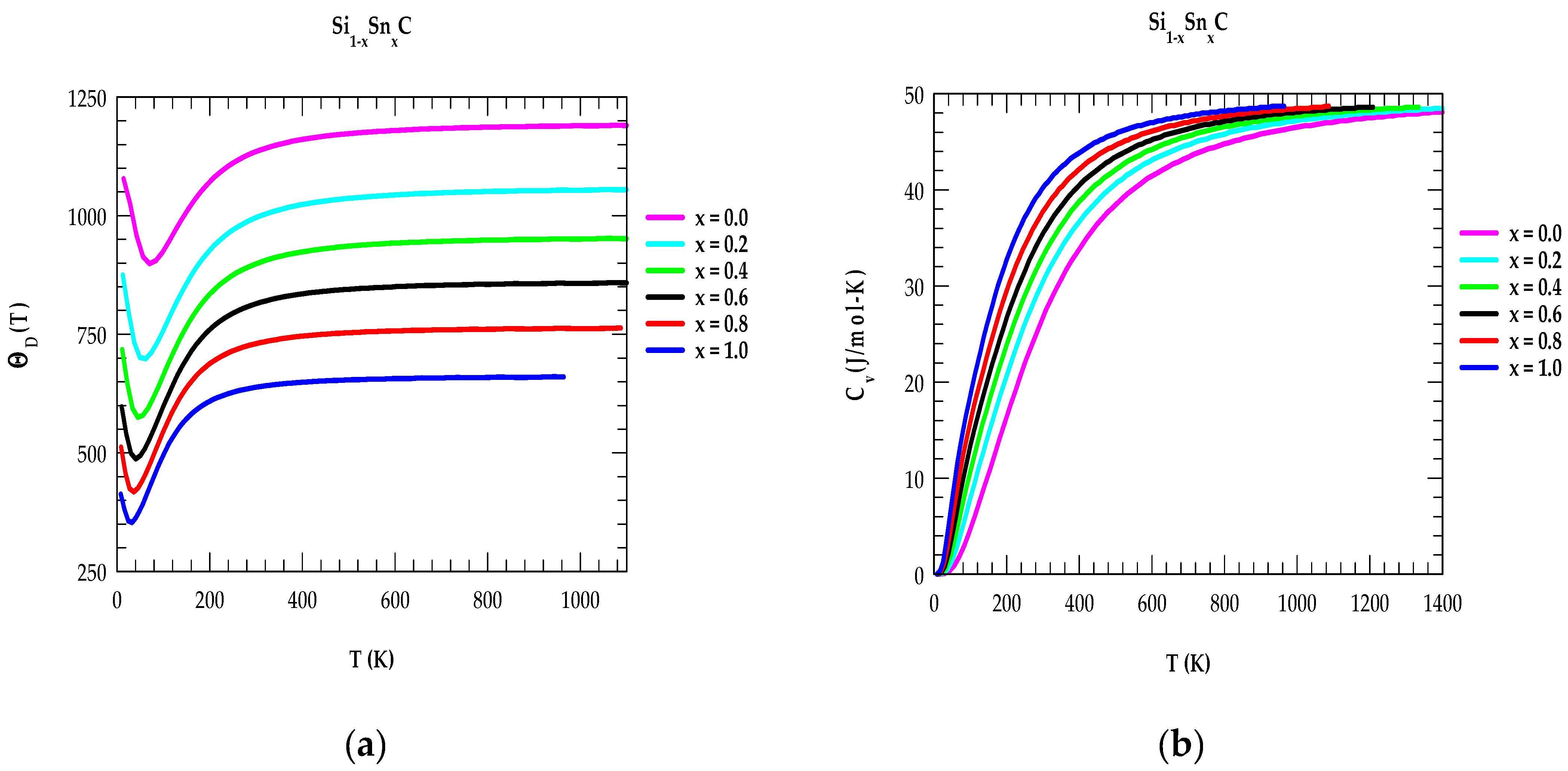
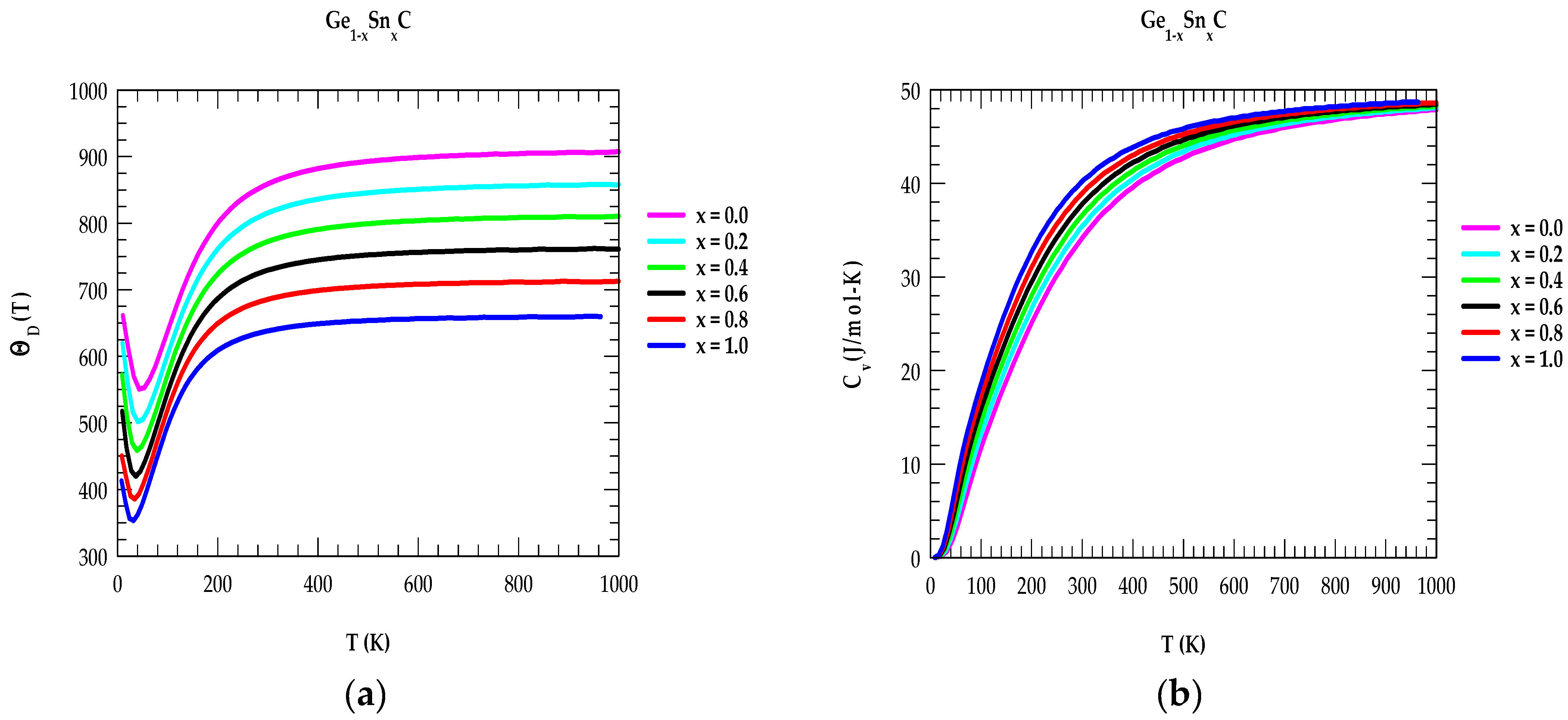
3.2.2. Thermodynamic Characteristics of X1−xYxC Alloys
3.2.3. Born Effective Charge for X1−xYxC Alloys
3.2.4. Fröhlich Coefficients
4. Discussions and Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bell Telephone Laboratories, Inc. The Transistor: Selected Reference Material on Characteristics and Applications; Western Electric Co., Inc.: New York, NY, USA, 1951. [Google Scholar]
- Maram, R.; Kaushal, S.; Azaña, J.; Chen, L.R. Recent Trends and Advances of Silicon-Based Integrated Microwave Photonics. Photonics 2019, 6, 13. [Google Scholar] [CrossRef]
- Bennett, H.S.; Brederlow, R.; Costa, J.C.; Cottrell, P.E.; Huang, W.M.; Immorlica, A.A., Jr.; Mueller, J.-E.; Racanelli, M.; Shichijo, H.; Weitzel, C.E.; et al. Device and Technology Evolution for Si-Based RF Integrated Circuits. IEEE Trans. Electron Dev. 2005, 52, 1235. [Google Scholar] [CrossRef]
- Gutmann, R.J. Advanced Silicon IC Interconnect Technology and Design: Present Trends and RF Wireless Implications. IEEE Trans. Microwave Theory Tech. 1999, 47, 667–674. [Google Scholar] [CrossRef]
- Burghartz, J.N. Silicon RF technology—The two generic approaches. In Proceedings of the 27th European Solid-State Device Research Conference, Stuttgart, Germany, 22–24 September 1997; pp. 143–153. [Google Scholar]
- Razavi, B. CMOS technology characterization for analog and RF design. IEEE J. Solid-State Circuits 1999, 34, 268–276. [Google Scholar]
- Harame, D.; Comfort, J.; Cressler, J.; Crabbé, E.; Sun, J.; Meyerson, B.; Tice, T. Si/SiGe epitaxial base transistors, Parts I and II. IEEE Trans. Electron Dev. 1995, 42, 455–482. [Google Scholar] [CrossRef]
- Chen, D.; Li, R.; Xu, J.; Li, D.; Fei, C.; Yang, Y. Recent progress and development of radio frequency energy harvesting devices and circuits. Nano Energy 2023, 117, 108845. [Google Scholar] [CrossRef]
- Raut, P.; Nanda, U.; Panda, D.K. Review—Recent Trends on Junction-Less Field Effect Transistors in Terms of Device Topology, Modeling, and Application. ECS J. Solid Stat. Sci. Technol. 2023, 12, 031010. [Google Scholar] [CrossRef]
- Fu, Q.; Zhang, W.R.; Jin, D.Y.; Ding, C.B.; Zhao, Y.X.; Lu, D. Collector optimization for tradeoff between breakdown voltage and cut-off frequency in SiGe HBT. Chin. Phys. B 2014, 23, 114402. [Google Scholar] [CrossRef]
- Shahbaz, M.; Butt, M.A.; Piramidowicz, R. Breakthrough in Silicon Photonics Technology in Telecommunications, Biosensing, and Gas Sensing. Micromachines 2023, 14, 1637. [Google Scholar] [CrossRef]
- Kadri, E.; Messaoudi, O.; Krichen, M.; Dhahri, K.; Rasheed, M.; Dhahri, E.; Zouari, A.; Khirouni, K.; Barille, R. Optical and electrical properties of SiGe/Si solar cell heterostructures: Ellipsometric study. J. Alloys Compd. 2017, 721, 779–783. [Google Scholar] [CrossRef]
- Sun, Z.; Wang, L.; Luo, H.; Hamer, P.; Ye, H.; Hallam, B. Study of the Hydrogen Passivation Effect of Low-Temperature Deposited Amorphous Silicon Layers on SiGe Solar Cells Grown on a Silicon Substrate. ACS Appl. Energy Mater. 2023, 6, 12064–12071. [Google Scholar] [CrossRef]
- Ringel, S.A.; Carlin, J.; Andre, C.; Hudait, M.; Gonzalez, M.; Wilt, D.; Clark, E.; Jenkins, P.; Scheiman, D.; Allerman, A.; et al. Single-junction InGaP/GaAs solar cells grown on Si substrates with SiGe buffer layers. Prog. Photovolt. Res. Appl. 2002, 10, 417–426. [Google Scholar] [CrossRef]
- Erdtmann, M.; Carroll, M.; Vineis, C.; Badawi, H.; Bulsara, M.; Ringel, S. Growth and characterization of high-Ge content SiGe virtual substrates. Proc. Electrochem. Soc. 2003, 11, 106–117. [Google Scholar]
- Wang, L.; Conrad, B.; Soeriyadi, A.; Zhao, X.; Li, D.; Diaz, M.; Lochtefeld, A.; Gerger, A.; Perez-Wurfl, I.; Barnett, A. Current matched three-terminal dual junction GaAsP/SiGe tandem solar cell on Si. Sol. Energy Mater. Sol. Cells 2016, 146, 80–86. [Google Scholar] [CrossRef]
- Sankarasubramaniam, Y.; Akyildiz, I.E.; Mchughlin, S.W. Energy Efficiency based Packet Size Optimization in Wireless Sensor Networks. In Proceedings of the First IEEE International Workshop on Sensor Network Protocols and Applications, Anchorage, AK, USA, 11 May 2003. [Google Scholar] [CrossRef]
- Ojeda, F.; Mendez, D.; Fajardo, A.; Ellinger, F. On Wireless Sensor Network Models: A Cross-Layer Systematic Review. J. Sens. Actuator Netw. 2023, 12, 50. [Google Scholar] [CrossRef]
- Xing, J.; Sun, C.; Xiong, B.; Wang, J.; Hao, Z.; Wang, L.; Han, Y.; Li, H.; Luo, Y. Membrane multiple quantum-well electro-optical modulator employing low loss high-k radio-frequency slot waveguides. Opt. Express 2022, 30, 23260. [Google Scholar] [CrossRef] [PubMed]
- Zhao, X.; Xiong, B.; Sun, C.; Luo, Y. Low drive voltage optical phase modulator with novel InGaAlAs/InAlAs multiple-quantum-barrier based n-i-n heterostructure. Opt. Express 2013, 21, 24894–24903. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.; Xiong, B.; Sun, C.; Wang, J.; Hao, Z.; Wang, L.; Han, Y.; Li, H.; Yu, J.; Luo, Y. Wideband thin-film lithium niobate modulator with low half-wave-voltage length product. Chin. Opt. Lett. 2021, 19, 060016. [Google Scholar] [CrossRef]
- Xing, J.; Sun, C.; Xiong, B.; Wang, J.; Hao, Z.; Wang, L.; Han, Y.; Li, H.; Yu, J.; Luo, Y. Low loss hybrid plasmon polariton Mach-Zehnder modulators. OSA Contin. 2021, 4, 2721–2733. [Google Scholar] [CrossRef]
- Fujii, T.; Hiraki, T.; Aihara, T.; Nishi, H.; Takeda, K.; Sato, T.; Kakitsuka, T.; Tsuchizawa, T.; Matsuo, S. Development of an Epitaxial Growth Technique Using III-V on a Si Platform for Heterogeneous Integration of Membrane Photonic Devices on Si. Appl. Sci. 2021, 11, 1801. [Google Scholar] [CrossRef]
- Rickman, A. The commercialization of silicon photonics. Nat. Photonics 2014, 8, 579–582. [Google Scholar] [CrossRef]
- Nagarajan, R.; Joyner, C.H.; Schneider, R.P.; Bostak, J.S.; Butrie, T.; Dentai, A.G.; Dominic, V.G.; Evans, P.W.; Kato, M.; Kauffman, M.; et al. Large-scale photonic integrated circuits. IEEE J. Sel. Top. Quantum Electron. 2005, 11, 50–65. [Google Scholar] [CrossRef]
- Komljenovic, T.; Davenport, M.; Hulme, J.; Liu, A.Y.; Santis, C.T.; Spott, A.; Srinivasan, S.; Stanton, E.J.; Zhang, C.; Bowers, J.E. Heterogeneous Silicon Photonic Integrated Circuits. J. Light. Technol. 2016, 34, 20–35. [Google Scholar] [CrossRef]
- Dong, P.; Liu, X.; Chandrasekhar, S.; Buhl, L.L.; Aroca, R.; Chen, Y.-K. Monolithic Silicon Photonic Integrated Circuits for Compact 100+Gb/s Coherent Optical Receivers and Transmitters. IEEE J. Sel. Top. Quantum Electron. 2014, 20, 150–157. [Google Scholar] [CrossRef]
- Horikawa, T.; Shimura, D.; Okayama, H.; Jeong, S.-H.; Takahashi, H.; Ushida, J.; Sobu, Y.; Shiina, A.; Tokushima, M.; Kinoshita, K.; et al. A 300-mm Silicon Photonics Platform for Large-Scale Device Integration. IEEE J. Sel. Top. Quantum Electron. 2018, 24, 1–15. [Google Scholar] [CrossRef]
- Kukushkin, S.; Osipov, A.; Redkov, A. SiC/Si as a New Platform for Growth of Wide-Bandgap Semiconductors. In Mechanics and Control of Solids and Structures; Polyanskiy, V.A., Belyaev, A.K., Eds.; Advanced Structured Materials; Springer Nature: Cham, Switzerland, 2022; Chapter 18; p. 164. [Google Scholar]
- Nguyen, T.-K.; Yadav, S.; Truong, T.-A.; Han, M.; Barton, M.; Leitch, M.; Guzman, P.; Dinh, T.; Ashok, A.; Vu, H.; et al. Integrated, Transparent Silicon Carbide Electronics and Sensors for Radio Frequency Biomedical Therapy. ACS Nano 2022, 16, 10890–10903. [Google Scholar] [CrossRef] [PubMed]
- Pham, T.A.; Nguyen, T.K.; Vadivelu, R.K.; Dinh, T.; Qamar, A.; Yadav, S.; Yamauchi, Y.; Rogers, J.A.; Nguyen, N.T.; Phan, H.P. Stretchable Bioelectronics: A Versatile Sacrificial Layer for Transfer Printing of Wide Bandgap Materials for Implantable and Stretchable Bioelectronics. Adv. Funct. Mater. 2020, 30, 2070287. [Google Scholar] [CrossRef]
- Nguyen, T.K.; Phan, H.P.; Kamble, H.; Vadivelu, R.; Dinh, T.; Iacopi, A.; Walker, G.; Hold, L.; Nguyen, N.T.; Dao, D.V. Superior Robust Ultrathin Single-Crystalline Silicon Carbide Membrane as a Versatile Platform for Biological Applications. ACS Appl. Mater. Interfaces 2017, 9, 41641–41647. [Google Scholar] [CrossRef] [PubMed]
- Yang, H.; Ma, Y.; Da, Y. Progress of structural and electronic properties of diamond: A mini review. Funct. Diam. 2021, 1, 150–159. [Google Scholar] [CrossRef]
- Yue, Y.; Gao, Y.; Hu, W.; Xu, B.; Wang, J.; Zhang, X.; Zhang, Q.; Wang, Y.; Ge, B.; Yang, Z.; et al. Hierarchically structured diamond composite with exceptional Toughness. Nature 2020, 582, 370–374. [Google Scholar] [CrossRef]
- Huang, Q.; Yu, D.; Xu, B.; Hu, W.; Ma, Y.; Wang, Y.; Zhao, Z.; Wen, B.; He, J.; Liu, Z.; et al. Nanotwinned diamond with unprecedented hardness and stability. Nature 2014, 510, 250–253. [Google Scholar] [CrossRef]
- Ekimov, E.A.; Sidorov, V.A.; Bauer, E.D.; Mel’Nik, N.N.; Curro, N.J.; Thompson, J.D.; Stishov, S.M. Superconductivity in diamond. Nature 2004, 428, 542–545. [Google Scholar] [CrossRef] [PubMed]
- Bauer, M.R.; Tolle, J.; Bungay, C.; Chizmeshya, A.V.G.; Smith, D.J.; Menéndez, J.; Kouvetakis, J. Tunable band structure in diamond–cubic tin–germanium alloys grown on silicon substrates. Solid State Commun. 2003, 127, 355–359. [Google Scholar] [CrossRef]
- Islam, M.S.; Mojumder, R.H.; Hassan, A.; Sohag, M.U.; Park, J. High-Efficiency Multi Quantum Well Blue LED Using 2D-SiC as an Active Material. In Proceedings of the 2021 5th International Conference on Electrical Engineering and Information & Communication Technology (ICEEICT), Dhaka, Bangladesh, 18–20 November 2021. [Google Scholar]
- Zhang, L.; Cui, Z. Theoretical Study on Electronic, Magnetic and Optical Properties of Non-Metal Atoms Adsorbed onto Germanium Carbide. Nanomaterials 2022, 12, 1712. [Google Scholar] [CrossRef] [PubMed]
- Mélinon, P.; Masenelli, B.; Tournus, F.; Perez, A. Playing with carbon and silicon at the nanoscale. Nat. Mater. 2007, 6, 479–490. [Google Scholar] [CrossRef] [PubMed]
- Polyanskiy, V.A.; Belyaev, A.K. (Eds.) Mechanics and Control of Solids and Structures, Advanced Structured Materials; Springer Nature: Cham, Switzerland, 2022; p. 164. Available online: https://link.springer.com/bookseries/8611 (accessed on 27 February 2024).
- Ikoma, Y.; Endo, T.; Watanabe, F.; Motooka, T. Growth of Ultrathin Epitaxial 3C-SiC Films on Si(100) by Pulsed Supersonic Free Jets of CH3SiH3. Jpn. J. Appl. Phys. 1999, 38, L301. [Google Scholar] [CrossRef]
- Ikoma, Y.; Endo, T.; Watanabe, F.; Motooka, T. Growth of Si/3C–SiC/Si(100) heterostructures by pulsed supersonic free jets. Appl. Phys. Lett. 1999, 75, 3977–3979. [Google Scholar] [CrossRef]
- Ohtani, R.; Ikoma, Y.; Motooka, T. Formation of Si/SiC heterostructures for silicon-based quantum devices using single CH3SiH3-gas source free jet. Mater. Res. Soc. Symp. Proc. 2004, 815, J5.11.1. [Google Scholar] [CrossRef]
- Yoshimura, S.; Sugimoto, S.; Takeuchi, T.; Murai, K.; Kiuchi, M. Low energy Si+, SiCH5+, or C+ beam injections to silicon substrates during chemical vapor deposition with dimethyl silane. Heliyon 2023, 9, e19002. [Google Scholar] [CrossRef] [PubMed]
- Gallagher, J.D.; Senaratne, C.L.; Kouvetakis, J.; Menéndez, J. Compositional dependence of the bowing parameter for the direct and indirect band gaps in Ge 1-y Sn y alloys. Appl. Phys. Lett. 2014, 105, 142102. [Google Scholar] [CrossRef]
- Ghetmiri, S.A.; Du, W.; Margetis, J.; Mosleh, A.; Cousar, L.; Conley, B.R.; Domulevicz, L.; Nazzal, A.; Sun, G.; Soref, R.A.; et al. Direct-bandgap GeSn grown on silicon with 2230 nm photoluminescence. Appl. Phys. Lett. 2014, 105, 151109. [Google Scholar] [CrossRef]
- Wirths, S.; Geiger, R.; von den Driesch, N.; Mussler, G.; Stoica, T.; Mantl, S.; Ikonic, Z.; Luysberg, M.; Chiussi, S.; Hartmann, J.M.; et al. Lasing in direct-bandgap GeSn alloy grown on Si. Nat. Photonics 2015, 9, 88–92. [Google Scholar] [CrossRef]
- Xu, Z.; Li, Y.; Liu, Z. Controlling electronic and optical properties of layered SiC and GeC sheets by strain engineering. Mater. Des. 2016, 108, 333–342. [Google Scholar] [CrossRef]
- Xua, Q.; Cai, W.; Li, W.; Sreeprasad, T.S.; He, Z.; Ong, W.-J.; Li, N. Two-dimensional quantum dots: Fundamentals, photoluminescence mechanism and their energy and environmental applications. Mater. Today Energy 2018, 10, 222–240. [Google Scholar] [CrossRef]
- Schulte-Braucks, C.; Glass, S.; Hofmann, E.; Stange, D.; von den Driesch, N.; Hartmann, J.M.; Ikonic, Z.; Zhao, Q.T.; Buca, D.; Mantl, S. Process modules for GeSn nanoelectronics with high Sn-contents. Solid-State Electron. 2017, 128, 54–59. [Google Scholar] [CrossRef]
- Shen, Z.; Chen, J.; Li, B.; Li, G.; Zheng, H.; Men, J.; Hou, X. Tunable fabrication and photoluminescence property of SiC nano wires with different microstructures. Appl. Surf. Sci. 2020, 506, 144979. [Google Scholar] [CrossRef]
- Dey, T.; Reza, M.S.; Arbogast, A.W.; Holtz, M.; Droopad, R.; Bank, S.R.; Wistey, M.A. Molecular beam epitaxy of highly crystalline GeSnC using CBr4 at low temperatures. Appl. Phys. Lett. 2022, 121, 122104. [Google Scholar] [CrossRef]
- Dey, T.; Arbogast, A.W.; Meng, Q.; Reza, M.S.; Muhowski, A.J.; Cooper, J.P.; Ozdemir, E.; Naab, F.U.; Borrely, T.; Anderson, J.; et al. Influence of H on Sn incorporation in GeSnC alloys grown using molecular beam epitaxy. J. Appl. Phys. 2023, 134, 193102. [Google Scholar] [CrossRef]
- Giunto, A.; Morral, A.F.I. The GeSn Alloy and its Optoelectronic Properties: A Critical Review of the Current Understanding. arXiv 2023, arXiv:2309.10584. [Google Scholar] [CrossRef]
- Cardoux, C.; Casiez, L.; Pauc, N.; Calvo, V.; Coudurier, N.; Rodriguez, P.; Richy, J.; Barritault, P.; Lartigue, O.; Constancias, C.; et al. Room temperature spectral characterization of direct band gap Ge0.85Sn0.15 LEDs and photodiodes. In Proceedings of the 2022 Proceedings SPIE OPTO, Silicon Photonics XVII, San Francisco, CA, USA, 22–27 January 2022; p. 120060A. [Google Scholar] [CrossRef]
- Moutanabbir, O.; Assali, S.; Gong, X.; O’Reilly, E.; Broderick, C.A.; Marzban, B.; Witzens, J.; Du, W.; Yu, S.-Q.; Chelnokov, A.; et al. Monolithic infrared silicon photonics: The rise of (Si)GeSn semiconductors. Appl. Phys. Lett. 2021, 118, 110502. [Google Scholar] [CrossRef]
- Atalla, M.R.M.; Assali, S.; Koelling, S.; Attiaoui, A.; Moutanabbir, O. High-Bandwidth Extended-SWIR GeSn Photodetectors on Silicon Achieving Ultrafast Broadband Spectroscopic Response. ACS Photonics 2022, 9, 1425–1433. [Google Scholar] [CrossRef]
- Simola, E.T.; Kiyek, V.; Ballabio, A.; Schlykow, V.; Frigerio, J.; Zucchetti, C.; De Iacovo, A.; Colace, L.; Yamamoto, Y.; Capellini, G.; et al. CMOS-Compatible Bias-Tunable Dual-Band Detector Based on GeSn/Ge/Si Coupled Photodiodes. ACS Photonics 2021, 8, 2166–2173. [Google Scholar] [CrossRef]
- Tran, H.; Pham, T.; Margetis, J.; Zhou, Y.; Dou, W.; Grant, P.C.; Grant, J.M.; Al-Kabi, S.; Sun, G.; Soref, R.A.; et al. Si-Based GeSn Photodetectors toward MidInfrared Imaging Applications. ACS Photonics 2019, 6, 2807–2815. [Google Scholar] [CrossRef]
- Zhang, D.; Hu, X.; Liu, D.; Lin, X.; Wang, W.; Ding, Z.; Wang, Z.; Cheng, B.; Xue, C. GeSn on Si avalanche photodiodes for short wave infrared detection. In Optical Sensing and Imaging Technologies and Applications; Liu, D., Gong, H., Guina, M., Lu, J., Eds.; SPIE: Bellingham, WA, USA, 2018; p. 54. [Google Scholar]
- Kim, Y.; Assali, S.; Burt, D.; Jung, Y.; Joo, H.-J.; Chen, M.; Ikonic, Z.; Moutanabbir, O.; Nam, D. Improved GeSn microdisk lasers directly sitting on Si. In Silicon Photonics XVII; Reed, G.T., Knights, A.P., Eds.; SPIE: Bellingham, WA, USA, 2022; p. 21. [Google Scholar]
- Ojo, S.; Zhou, Y.; Acharya, S.; Saunders, N.; Amoah, S.; Jheng, Y.-T.; Tran, H.; Du, W.; Chang, G.-E.; Li, B.; et al. Silicon-based electrically injected GeSn lasers. In Physics and Simulation of Optoelectronic Devices XXX; Osinski, M., Arakawa, Y., Witzigmann, B., Eds.; SPIE: Bellingham, WA, USA, 2022; p. 15. [Google Scholar]
- Marzban, B.; Seidel, L.; Liu, T.; Wu, K.; Kiyek, V.; Zoellner, M.H.; Ikonic, Z.; Schulze, J.; Grutzmacher, D.; Capellini, G.; et al. Strain Engineered Electrically Pumped SiGeSn Microring Lasers on Si. ACS Photonics 2023, 10, 217–224. [Google Scholar] [CrossRef]
- Kasper, E.; Herzog, H.J.; Kibbel, H. A one-dimensional SiGe superlattice grown by UHV epitaxy. Appl. Phys. 1975, 8, 199–205. [Google Scholar] [CrossRef]
- Iyer, S.S.; Patton, G.L.; Delage, S.S.; Tiwari, S.; Stork, J.M.C. Silicon-germanium base heterojunction bipolar transistors by molecular beam epitaxy. In Proceedings of the International Electron Devices Meeting, IEDM Technical Digest, Washington, DC, USA, 6–9 December 1987; p. 874. [Google Scholar]
- Okinaka, M.; Hamana, Y.; Tokuda, T.; Ohta, J.; Nunoshita, M. MBE growth mode and C incorporation of GeC epilayers on Si(0 0 1) substrates using an arc plasma gun as a novel C source. J. Cryst. Growth 2003, 249, 78–86. [Google Scholar] [CrossRef]
- Lu, H.; Liu, W.; Wang, H.; Liu, X.; Zhang, Y.; Yang, D.; Pi, X. Molecular beam epitaxy growth and scanning tunneling microscopy study of 2D layered materials on epitaxial graphene/silicon carbide. Nanotechnology 2023, 34, 132001. [Google Scholar] [CrossRef] [PubMed]
- Islam, M.R.; Islam, M.S.; Mitul, A.F.; Mojumder, M.R.H.; Jannatul, A.S.M.; Islam, C.S.; Park, J. Superior tunable photocatalytic properties for water splitting in two dimensional GeC/SiC van der Waals hetero bilayers. Sci. Rep. 2021, 11, 17739. [Google Scholar] [CrossRef] [PubMed]
- Tayaba, S.; Sethi, H.; Shahid, H.; Malik, R.; Ikram, M.; Ali, S.; Khaliq, S.; Khan, Q.; Maqbool, M. Silicon-Germanium and carbon-based superconductors for electronic, industrial, and medical applications. Mater. Sci. Eng. B 2023, 290, 116332. [Google Scholar] [CrossRef]
- Bean, J.C. Silicon based semiconductor heterostructures: Column IV bandgap engineering. Proc. IEEE 1992, 80, 571–587. [Google Scholar] [CrossRef]
- Li, X.; Jacobson, H.; Boulle, A.; Chaussende, D.; Henry, A. Double-Position-Boundaries Free 3C-SiC Epitaxial Layers Grown on On-Axis 4H-SiC. ECS J. Solid State Sci. Technol. 2014, 3, P75. [Google Scholar] [CrossRef]
- Xin, B.; Jia, R.X.; Hu, J.C.; Tsai, C.Y.; Lin, H.H.; Zhang, Y.M. A step-by-step experiment of 3C-SiC hetero-epitaxial growth on 4H-SiC by CVD. Appl. Surf. Sci. 2015, 357, 985–993. [Google Scholar] [CrossRef]
- Wu, J.; Qian, S.T.; Huo, T.G.; Zheng, J.X.; Zhang, P.L.; Dai, Y.; Geng, D.S. Effect of PyC Inner Coating on Preparation of 3C-SiC Coating on Quartz Glass by Chemical Vapor Reaction. Front. Mater. 2022, 9, 897900. [Google Scholar] [CrossRef]
- Kaloyeros, A.E.; Arkles, B. Silicon Carbide Thin Film Technologies: Recent Advances in Processing, Properties, and Applications—Part I Thermal and Plasma CVD. ECS J. Solid State Sci. Technol. 2023, 12, 103001. [Google Scholar] [CrossRef]
- Hartmanna, J.M.; Abbadiea, A.; Vineta, M.; Claveliera, L.; Holligera, P.; Lafonda, D.; Semeria, M.N.; Gentile, P. Growth kinetics of Si on fullsheet, patterned and silicon-on-insulator substrates. J. Cryst. Growth 2003, 257, 19–30. [Google Scholar] [CrossRef]
- Lukin, D.M.; Guidry, M.A.; Vučković, J. Silicon Carbide: From Abrasives to Quantum Photonics. Opt. Photonics News 2021, 32, 34–41. [Google Scholar] [CrossRef]
- La Via, F.; Camarda, M.; La Magna, A. Mechanisms of growth and defect properties of epitaxial SiC. Appl. Phys. Rev. 2014, 1, 031301. [Google Scholar] [CrossRef]
- Fraga, M.A.; Bosi, M.; Negri, N. Silicon carbide in microsystem technology—Thin film vs bulk material. In Advanced Silicon Carbide Devices and Processing; Saddow, S.E., La Via, F., Eds.; IntechOpen: London, UK, 2015; Chapter 1; p. 3. [Google Scholar]
- Ou, H.; Shi, X.; Lu, Y.; Kollmuss, M.; Steiner, J.; Tabouret, V.; Syväjärvi, M.; Wellmann, P.; Chaussende, D. Novel photonic applications of silicon carbide. Materials 2023, 16, 1014. [Google Scholar] [CrossRef]
- Kaloyeros, A.E.; Jové, F.A.; Goff, J.; Arkles, B. Silicon nitride and silicon nitride-rich thin film technologies: Trends in deposition techniques and related applications. ECS J. Solid State Sci. Technol. 2017, 6, P691. [Google Scholar] [CrossRef]
- Kaloyeros, A.E.; Pan, Y.; Goff, J.; Arkles, B. Review—Silicon nitride and silicon nitride-rich thin film technologies: State-of-the-art processing technologies, properties, and applications. ECS J. Solid State Sci. Technol. 2020, 9, 062006. [Google Scholar] [CrossRef]
- Marsi, N.; Majlis, B.Y.; Hamzah, A.; Mohd-Yasin, F. High reliability of MEMS packaged capacitive pressure sensor employing 3C-SiC for high temperature. Energy Procedia 2015, 68, 471–479. [Google Scholar] [CrossRef]
- Feller, T.; Rosenfeldt, S.; Retsch, M. Carbothermal synthesis of micron-sized, uniform, spherical silicon carbide (SiC) particles. Z. Anorg. Allg. Chem. 2021, 647, 2172–2180. [Google Scholar] [CrossRef]
- Kawanishi, S.; Daikoku, H.; Shibata, H.; Yoshikawa, T. Suppressing solvent compositional change during solution growth of SiC using SiC/C gradient crucible. J. Cryst. Growth 2021, 576, 126382. [Google Scholar] [CrossRef]
- Sannodo, N.; Osumi, A.; Kaminaga, K.; Maruyama, S.; Matsumoto, Y. Vapor-liquid-solid-like growth of high-quality and uniform 3C-SiC heteroepitaxial films on alpha-Al2O3 (0001) substrates. CrystEngComm 2021, 23, 1709–1717. [Google Scholar] [CrossRef]
- Kukushkin, S.A.; Osipov, A.V. Epitaxial silicon carbide on silicon. method of coordinated substitution of atoms (a review). Russ. J. Gen. Chem. 2022, 92, 584–610. [Google Scholar] [CrossRef]
- Majid, A. A perspective on non-stoichiometry in silicon carbide (review article). Ceram. Int. 2018, 44, 1277–1283. [Google Scholar] [CrossRef]
- Spera, M.; Greco, G.; Lo Nigro, R.; Bongiorno, C.; Giannazzo, F.; Zielinski, M.; La Via, F.; Roccaforte, F. Ohmic contacts on n-type and p-type cubic silicon carbide (3C-SiC) grown on silicon. Mater. Sci. Semicond. Process. 2019, 93, 295–298. [Google Scholar] [CrossRef]
- Galashev, A.Y.; Abramova, K.A. Computer simulation of obtaining thin films of silicon carbide. Phys. Chem. Chem. Phys. 2023, 25, 3834–3847. [Google Scholar] [CrossRef] [PubMed]
- Smith, D.J.; Todd, M.; McMurran, J.; Kouvetakis, J. Structural properties of heteroepitaxial germanium carbon alloys grown on (100) Si. Philos. Mag. A 2001, 81, 1613–1624. [Google Scholar] [CrossRef]
- Schuh, P.; Scholer, M.; Wilhelm, M.; Syvajarvi, M.; Litrico, G.; La Via, F.; Mauceri, M.; Wellmann, P.J. Sublimation growth of bulk 3C-SiC using 3C-SiC-on-Si (100) seeding layers. J. Cryst. Growth 2017, 478, 159–162. [Google Scholar] [CrossRef]
- Ha, C.V.; Ha, L.T.; Hue, D.T.; Nguyen, D.K.; Anh, D.T.; Sanchezd, J.G.; Hoat, D.M. First-principles study of SiC and GeC monolayers with adsorbed non-metal atoms. RSC Adv. 2023, 13, 14879–14886. [Google Scholar] [CrossRef]
- Werninghaus, T.; Friedrich, M.; Cimalla, V.; Scheiner, J.; Goldhahn, R.; Zahn, D.R.T.; Pezold, J. Optical characterization of MBE grown cubic and hexagonal SiC films on Si(111). Diam. Relat. Mater. 1998, 7, 1385–1389. [Google Scholar]
- Yasui, K.; Narita, Y.; Inubushi, T.; Akahane, T. In situ observation of reflection high-energy electron diffraction during the initial growth of SiC on Si using dimethylsilane. J. Cryst. Growth 2002, 237–239, 1254–1259. [Google Scholar] [CrossRef]
- Kosiba, R.; Liday, J.; Ecke, G.; Ambacher, O.; Breza, J.; Vogrincic, P. Quantitative Auger electron spectroscopy of SiC. Vacuum 2006, 80, 990–995. [Google Scholar] [CrossRef]
- Zhao, S.; Chen, J.; Yang, S.; Yan, G.; Shen, Z.; Zhao, W.; Wang, L.; Liu, X.; Sun, G.; Zeng, Y. Effect of temperature on growth of epitaxial layer on semi-insulating 4H-SiC substrate. J. Cryst. Growth 2023, 603, 127008. [Google Scholar] [CrossRef]
- Tang, Z.; Gu, L.; Ma, H.; Dai, K.; Luo, Q.; Zhang, N.; Huang, J.; Fan, J. Study on the Surface Structure of N-Doped 4H-SiC Homoepitaxial Layer Dependence on the Growth Temperature and C/Si Ratio Deposited by CVD. Crystals 2023, 13, 193. [Google Scholar] [CrossRef]
- Sreelakshmi, N.; Umapathy, G.R.; Abhaya, S.; David, C.; Ojha, S.; Amirthapandian, S. Ionization-induced annealing of defects in 3C–SiC: Ion channeling and positron annihilation spectroscopy investigations. J. Mater. Res. 2023, 38, 1349–1362. [Google Scholar] [CrossRef]
- Bayu Aji, L.B.; Stavrou, E.; Wallace, J.B.; Boulle, A.; Debelle, A.; Kucheyev, S.O. Comparative study of radiation defect dynamics in 3C-SiC by X-ray diffraction, Raman scattering, and ion channeling. Appl. Phys. A 2019, 125, 28. [Google Scholar] [CrossRef]
- Boulle, A.; Debelle, A.; Wallace, J.B.; Aji, L.B.; Kucheyev, S.O. The amorphization of 3C-SiC irradiated at moderately elevated temperatures as revealed by X-ray diffraction. Acta Mater. 2017, 140, 250–257. [Google Scholar] [CrossRef]
- Zhang, L.; Jiang, W.; Pan, C.; Fadanelli, R.C.; Ai, W.; Chen, L.; Wang, T. Raman study of amorphization in nanocrystalline 3C–SiC irradiated with C+ and He+ ions. J. Raman Spectrosc. 2019, 50, 1197–1204. [Google Scholar] [CrossRef]
- Lindner, J.K.N.; Tsang, W.M.; Wong, S.P.; Xu, J.B.; Wilson, I.H. XTEM characterization of tungsten implanted SiC thin films on silicon for field emission devices. Thin Solid Films 2003, 427, 417–421. [Google Scholar] [CrossRef]
- Scuderi, V.; Calabretta, C.; Anzalone, R.; Mauceri, M.; La Via, F. Characterization of 4H- and 6H-Like Stacking Faults in Cross Section of 3C-SiC Epitaxial Layer by Room-Temperature µ-Photoluminescence and µ-Raman Analysis. Materials 2020, 13, 1837. [Google Scholar] [CrossRef]
- Feldman, D.W.; Parker, J.H., Jr.; Choyke, W.J.; Patrick, L. Phonon Dispersion Curves by Raman Scattering in SiC, Polytypes 3C, 4H, 6H, 15R, and 21R. Phys. Rev. 1968, 173, 787. [Google Scholar] [CrossRef]
- Yoshida, M.; Onodera, A.; Ueno, M.; Takemura, K.; Shimomura, O. Pressure-induced phase transition in SiC. Phys. Rev. B 1993, 48, 10587. [Google Scholar] [CrossRef] [PubMed]
- Olego, D.; Cardona, M.; Vogl, P. Pressure dependence of the optical phonons and transverse effective charge in 3C-SiC. Phys. Rev. B 1982, 25, 3878. [Google Scholar] [CrossRef]
- Talwar, D.N. Spectroscopic Investigations for the Dynamical Properties of Defects in Bulk and Epitaxially Grown 3C-SiC/Si (100). In Handbook of Silicon Carbide Materials and Devices; Feng, Z.C., Ed.; CRC Press: Boca Raton, FL, USA, 2023; Chapter 3. [Google Scholar]
- Sahin, H.; Cahangirov, S.; Topsakal, M.; Bekaroglu, E.; Akturk, E.; Senge, R.T.; Ciraci, S. Monolayer honeycomb structures of group-IV elements and III-V binary compounds: First-principles calculations. Phys. Rev. B 2009, 80, 155453. [Google Scholar] [CrossRef]
- Lin, S.S. Light-emitting two-dimensional ultrathin silicon carbide. J. Phys. C 2012, 116, 3951–3955. [Google Scholar] [CrossRef]
- Jankousky, M.; Garrity, E.M.; Stevanovic, V. Polymorphism of group-IV carbides: Structures, (meta)stability, electronic, and transport properties. Phys. Rev. Mater. 2023, 7, 053606. [Google Scholar] [CrossRef]
- Karch, K.; Bechstedt, F.; Pavone, P.; Strauch, D. Pressure-dependent properties of SiC polytypes. Phys. Rev. B 1996, 53, 13400. [Google Scholar] [CrossRef]
- Miao, M.S.; Prikhodko, M.; Lambrecht, W.R.L. Changes of the geometry and band structure of SiC along the orthorhombic high-pressure transition path between the zinc-blende and rocksalt structures. Phys. Rev. B 2002, 66, 064107. [Google Scholar] [CrossRef]
- Jiang, J.; Zheng, W.; Xiao, H.Y.; Liu, Z.J.; Zu, X.T. A comparative study of the mechanical and thermal properties of defective ZrC, TiC and SiC. Sci. Rep. 2017, 7, 9344. [Google Scholar] [CrossRef]
- Lu, Y.P.; Wei, H.D.; Zhu, J.; Yang, X.D. First-principles study of pressure-induced phase transition in silicon carbide. Physica B 2008, 403, 3543–3546. [Google Scholar] [CrossRef]
- Hao, A.; Yang, X.C.; Wang, X.M.; Zhu, Y.; Liu, X.; Liu, R.P. First-principles investigations on electronic, elastic, and optical properties of XC (X = Si, Ge, and Sn) under high pressure. J. Appl. Phys. 2010, 108, 063531. [Google Scholar] [CrossRef]
- Pandey, R.; Rérat, M.; Darrigan, C.; Causà, M. A theoretical study of stability, electronic, and optical properties of GeC and SnC. J. Appl. Phys. 2000, 88, 6462–6466. [Google Scholar] [CrossRef]
- Khenata, R.; Baltache, H.; Sahnoun, M.; Driz, M.; Rérat, M.; Abbar, B. Full potential linearized augmented plane wave calculations of structural and electronic properties of GeC, SnC and GeSn. Physica B 2003, 336, 321–328. [Google Scholar] [CrossRef]
- Sekkal, W.; Zaoui, A. Predictive study of thermodynamic properties of GeC. New J. Phys. 2002, 4, 9. [Google Scholar] [CrossRef]
- Varshney, D.; Shriya, S.; Varshney, M.; Singh, N.; Khenata, R. Elastic and thermo-dynamical properties of cubic (3C) silicon carbide under high pressure and high temperature. J. Theor. Appl. Phys. 2015, 9, 221–249. [Google Scholar] [CrossRef]
- Karch, K.; Bechstedt, F.; Pavone, P.; Strauch, D. Pressure-dependent dynamical and dielectric properties of cubic SiC. J. Phys. Condens. Matter 1996, 8, 2945. [Google Scholar] [CrossRef]
- Karch, K.; Pavone, P.; Windl, W.; Schütt, O.; Strauch, D. Ab initio calculation of structural and lattice-dynamical properties of silicon carbide. Phys. Rev. B 1994, 50, 17054. [Google Scholar] [CrossRef]
- Wang, C.Z.; Yu, R.C.; Krakauer, H. Pressure dependence of Born effective charges, dielectric constant, and lattice dynamics in SiC. Phys. Rev. B 1996, 53, 5430. [Google Scholar] [CrossRef] [PubMed]
- Souadkia, M.; Bennecer, B.; Kalarasse, F. Elastic, vibrational and thermodynamic properties of α-Sn based group IV semiconductors and GeC under pressure. J. Phys. Chem. Solids 2013, 74, 1615–1625. [Google Scholar] [CrossRef]
- Zhang, X.; Quan, S.; Ying, C.; Li, Z. Theoretical investigations on the structural, lattice dynamical and thermodynamic properties of XC (X = Si, Ge, Sn). Solid State Commun. 2011, 151, 1545–1549. [Google Scholar] [CrossRef]
- Zhang, P.; Crespi, V.H.; Chang, E.; Louie, S.G.; Cohen, M.L. Theory of metastable group-IV alloys formed from CVD precursors. Phys. Rev. B 2001, 64, 235201. [Google Scholar] [CrossRef]
- Kunc, K. Dynamique de réseau de composés ANB8-N présentant la structure de la blende. Ann. Phys. 1973, 8, 319–401. [Google Scholar]
- Plumelle, P.; Vandevyver, M. Lattice dynamics of ZnTe and CdTe. Phys. Stat. Sol. 1976, 73, 271–281. [Google Scholar] [CrossRef]
- Serrano, J.; Strempfer, J.; Cardona, M.; Schwoerer-Böhning, M.; Requardt, H.; Lorenzen, M.; Stojetz, B.; Pavone, P.; Choyke, W.J. Determination of the phonon dispersion of zinc blende (3C) silicon carbide by inelastic X-ray scattering. Appl. Phys. Lett. 2002, 80, 4360–4362. [Google Scholar] [CrossRef]
- Adachi, S. Properties of Semiconductor Alloys: Group-IV, III–V and II–VI, Semiconductors; Wiley: Hoboken, NJ, USA, 2009. [Google Scholar]
- Kutty, A.P.G. Phonons in mixed crystals. Solid State Commun. 1974, 14, 213–215. [Google Scholar] [CrossRef]
- Talwar, D.N. On the pressure-dependent phonon characteristics and anomalous thermal expansion coefficient of 3C-SiC. Mater. Sci. Eng. B 2017, 226, 1–9. [Google Scholar] [CrossRef]
- Talwar, D.N.; Vandevyver, M. Pressure-dependent phonon properties of III-V compound semiconductors. Phys. Rev. B 1990, 41, 12129–12139. [Google Scholar] [CrossRef]
- Talwar, D.N.; Vandevyver, M.; Kunc, K.; Zigone, M. Lattice dynamics of zinc chalcogenides under compression: Phonon dispersion, mode Grüneisen, and thermal expansion. Phys. Rev. B 1981, 24, 741. [Google Scholar] [CrossRef]
- Talwar, D.N.; Feng, Z.C.; Becla, P. Impurity-induced phonon disordering in Cd1−xZnxTe ternary alloys. Phys. Rev. B 1993, 48, 17064. [Google Scholar] [CrossRef]
- Talwar, D.N.; Roughani, B.; Pellegrino, J.G.; Amirtharaj, P.; Qadri, S.B. Study of phonons in semiconductor superlattices by Raman scattering spectroscopy and microscopic model calculation. Mater. Sci. Eng. B 1997, 44, 143–146. [Google Scholar] [CrossRef]
- Talwar, D.N. Dilute III–V Nitride Semiconductors and Material Systems—Physics and Technology; Erol, A., Ed.; Springer Series in Materials Science; Springer: Berlin/Heidelberg, Germany, 2008; Volume 105, Chapter 9; p. 222. [Google Scholar]
- Boer, K.W.; Pohl, U.W. Phonon-induced thermal properties. In Semiconductor Physics; Springer International Publishing: Cham, Switzerland, 2014. [Google Scholar]
- Grimm, A.; Maradudin, A.A.; Ipatova, I.P.; Subashiev, A.V. Impurity vibrations of copper defect complexes in gallium arsenide crystals. J. Phys. Chem. Solids 1972, 33, 775–796. [Google Scholar] [CrossRef]
- Grimm, A. Infrared absorption by point defects in gallium arsenide. J. Phys. C 1972, 5, 1883. [Google Scholar] [CrossRef]
- Vetelino, J.F.; Mitra, S.S. Lattice dynamics of cubic SiC. Phys. Rev. 1969, 178, 1349. [Google Scholar] [CrossRef]
- Vetelino, J.F.; Mitra, S.S.; Namjoshi, K.V. Lattice Dynamics of ZnTe: Phonon Dispersion, Multi-phonon Infrared Spectrum, Mode Grüneisen Parameters, and Thermal Expansion. Phys. Rev. B 1970, 2, 967. [Google Scholar] [CrossRef]
- Banerjee, R.; Varshni, Y.P. Lattice dynamics of III-V compounds. Can. J. Phys. 1969, 47, 451–462. [Google Scholar] [CrossRef]
- Banerjee, R.; Varshni, Y.P. Lattice Dynamics and Thermodynamic Properties of β-ZnS, GaP and β-SiC. J. Phys. Soc. Jpn. 1971, 30, 1015–1021. [Google Scholar] [CrossRef]
- Kellermann, E.W. Theory of the vibrations of the sodium chloride lattice. Philos. Trans. R. Soc. Lond. A 1944, 238, 513–548. [Google Scholar]
- Cochran, W. Crystal stability and the theory of ferroelectricity. Adv. Phys. 1960, 9, 387–423. [Google Scholar] [CrossRef]
- Merten, L. Zur Ultrarot-Dispersion zweiachsiger und einachsiger Kristalle II. Das außerordentliche Ultrarot-Spektrum von a-Quarz. Z. Naturforsch A 1958, 13, 662–679. [Google Scholar] [CrossRef]
- Reparaz, J.S.; Muniz, L.R.; Wagner, M.R.; Goñi, A.R.; Alonso, M.I.; Hoffmann, A.; Meyer, B.K. Reduction of the transverse effective charge of optical phonons in ZnO under pressure. Appl. Phys. Lett. 2010, 96, 231906-03. [Google Scholar] [CrossRef]
- Goldberg, Y.; Levinshtein, M.E.; Rumyantsev, S.L.; Levinshtein, M.E.; Rumyantsev, S.L.; Shur, M.S. (Eds.) Properties of Advanced Semiconductor Materials GaN, AlN, SiC, BN, SiC, SiGe; John Wiley & Sons, Inc.: New York, NY, USA, 2001; pp. 93–148. [Google Scholar]
- Barin, I. Thermochemical Data of Pure Substances Part II; VCH: New York, NY, USA, 1989. [Google Scholar]
- Hu, Y.-F.; Kong, F.-J.; Zhou, C. Structures and Thermodynamic Properties of 3C-SiC Compound. Acta Phys. Chim. Sin. 2008, 24, 1845–1849. [Google Scholar]
- Pässler, R. Limiting Debye temperature behavior following from cryogenic heat capacity data for group-IV, III–V, and II–VI materials. Phys. Status Solidi B 2010, 247, 77–92. [Google Scholar] [CrossRef]
- Pässler, R. Basic moments of phonon density of states spectra and characteristic phonon temperatures of group IV, III–V, and II–VI materials. J. Appl. Phys. 2007, 101, 093513-12. [Google Scholar] [CrossRef]
- Persson, C.; Lindefelt, U. Relativistic band structure calculation of cubic and hexagonal SiC polytypes. J. Appl. Phys. 1997, 82, 5496–5508. [Google Scholar] [CrossRef]
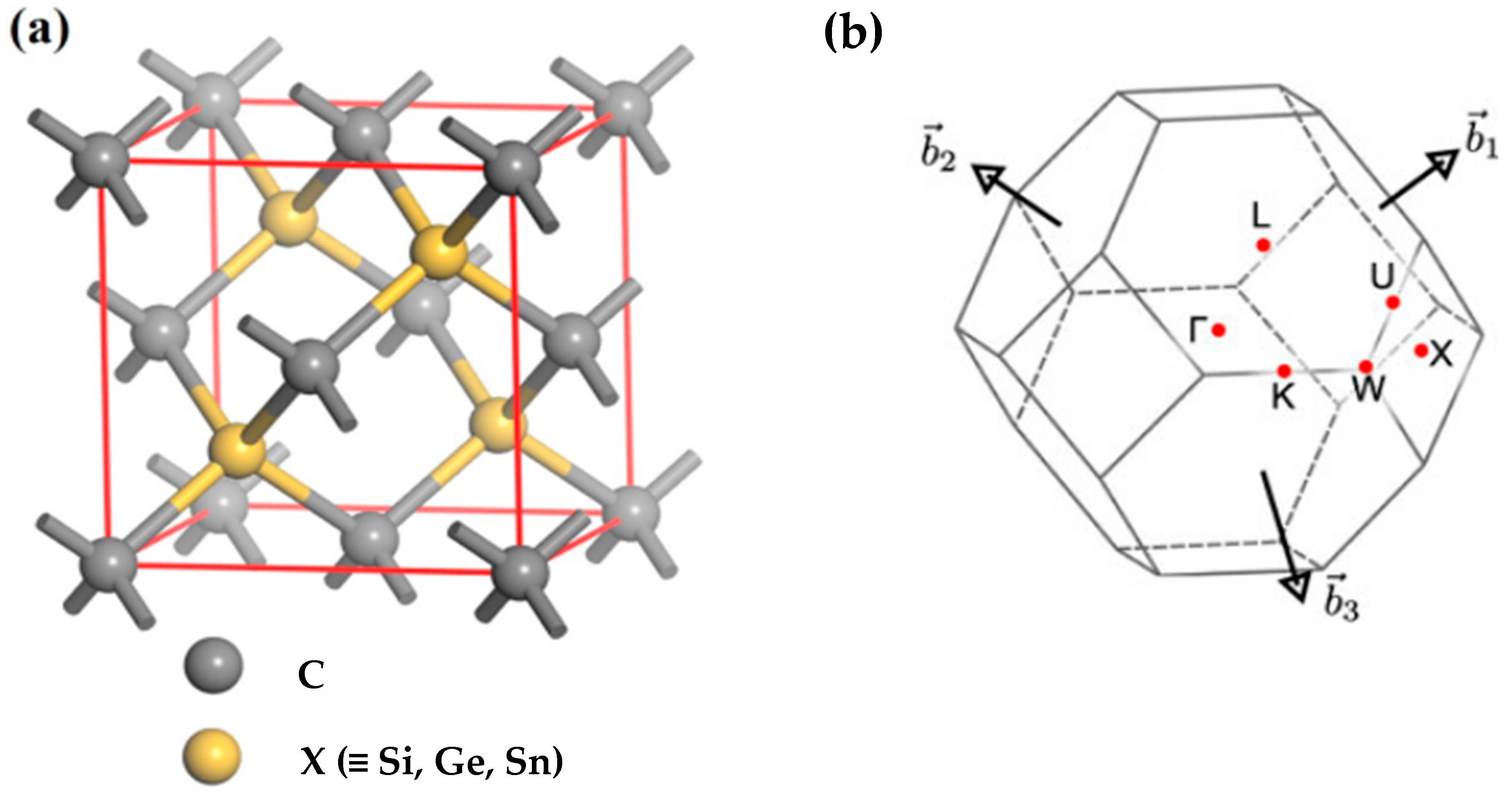
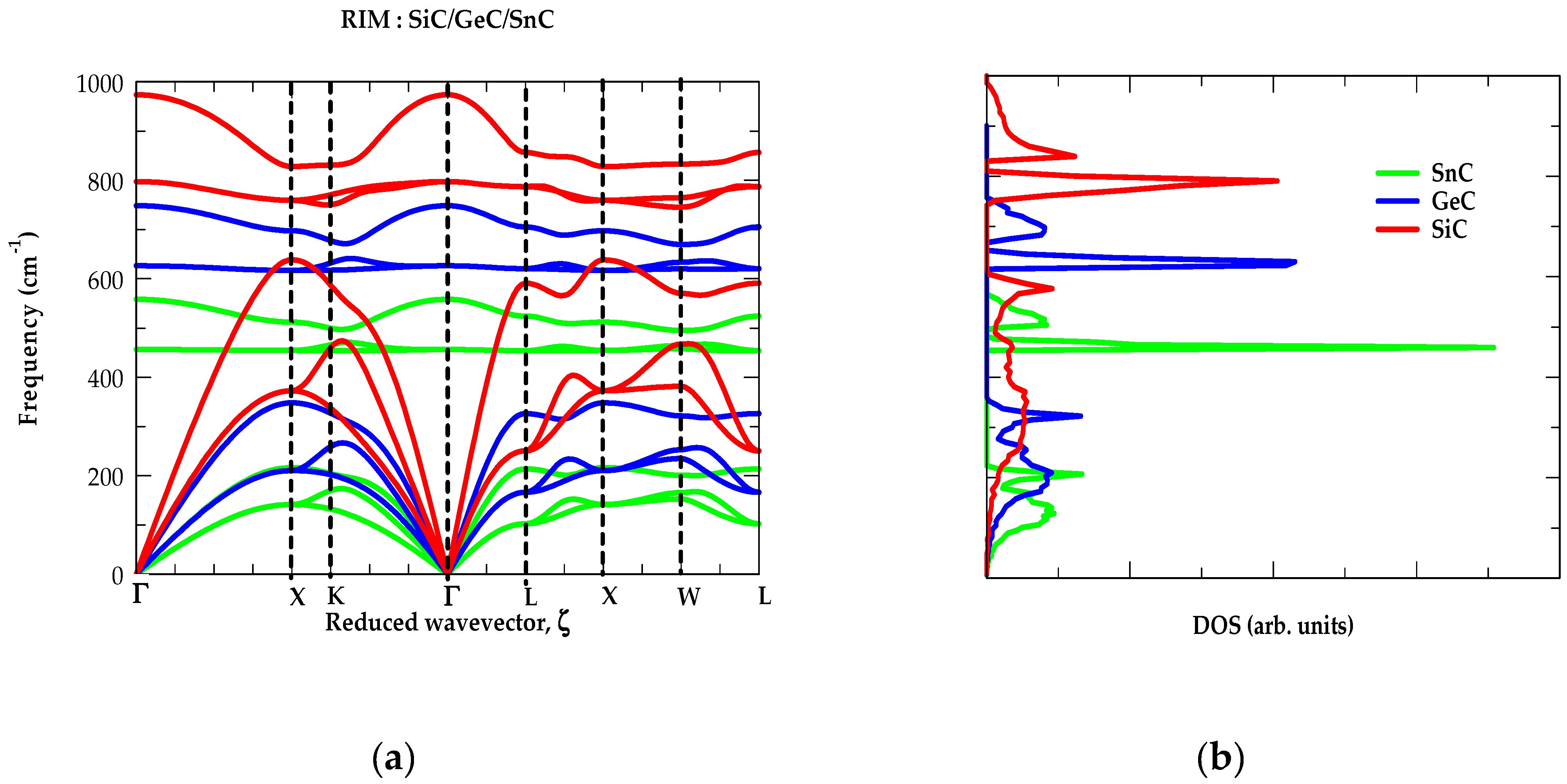
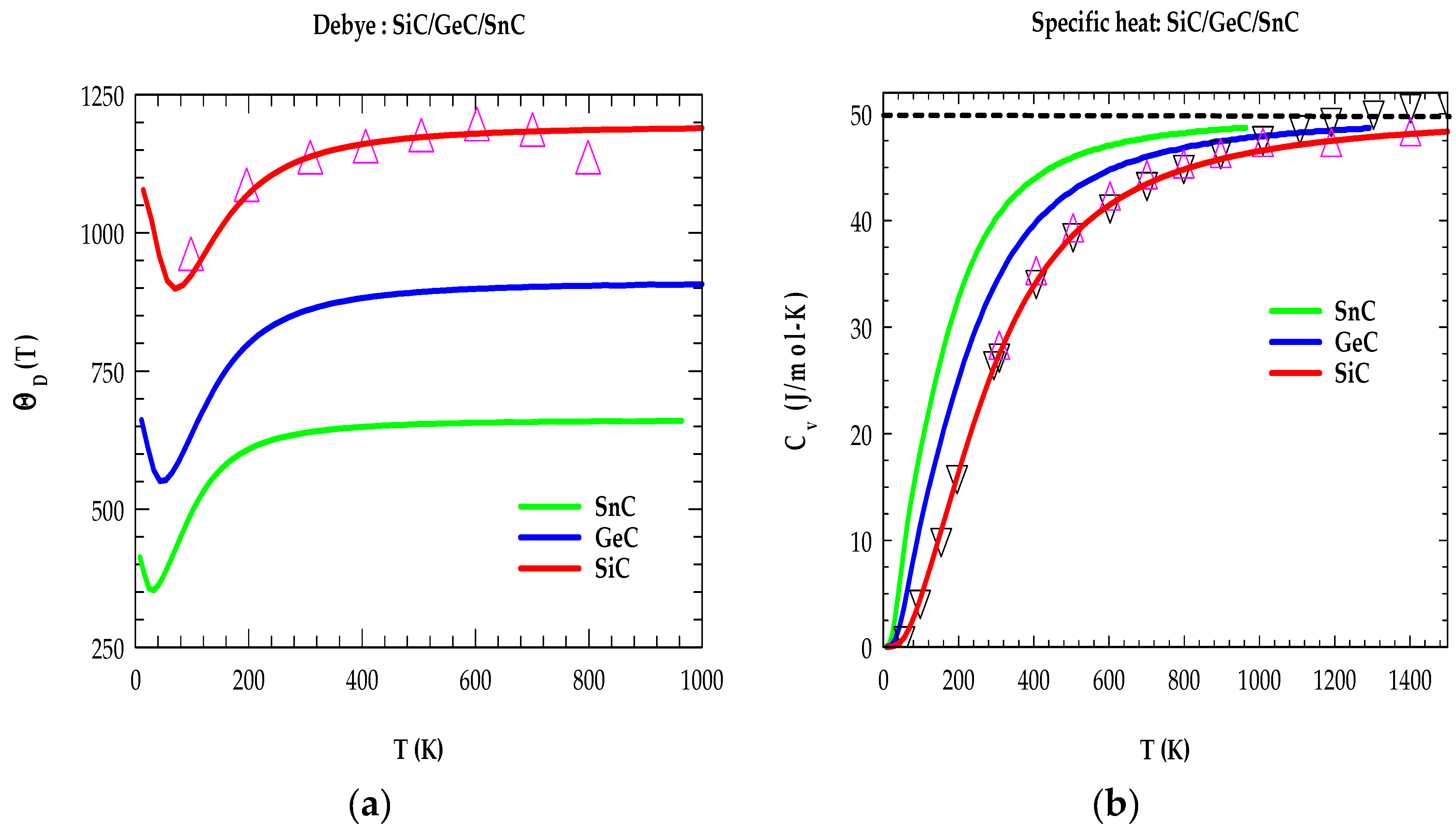
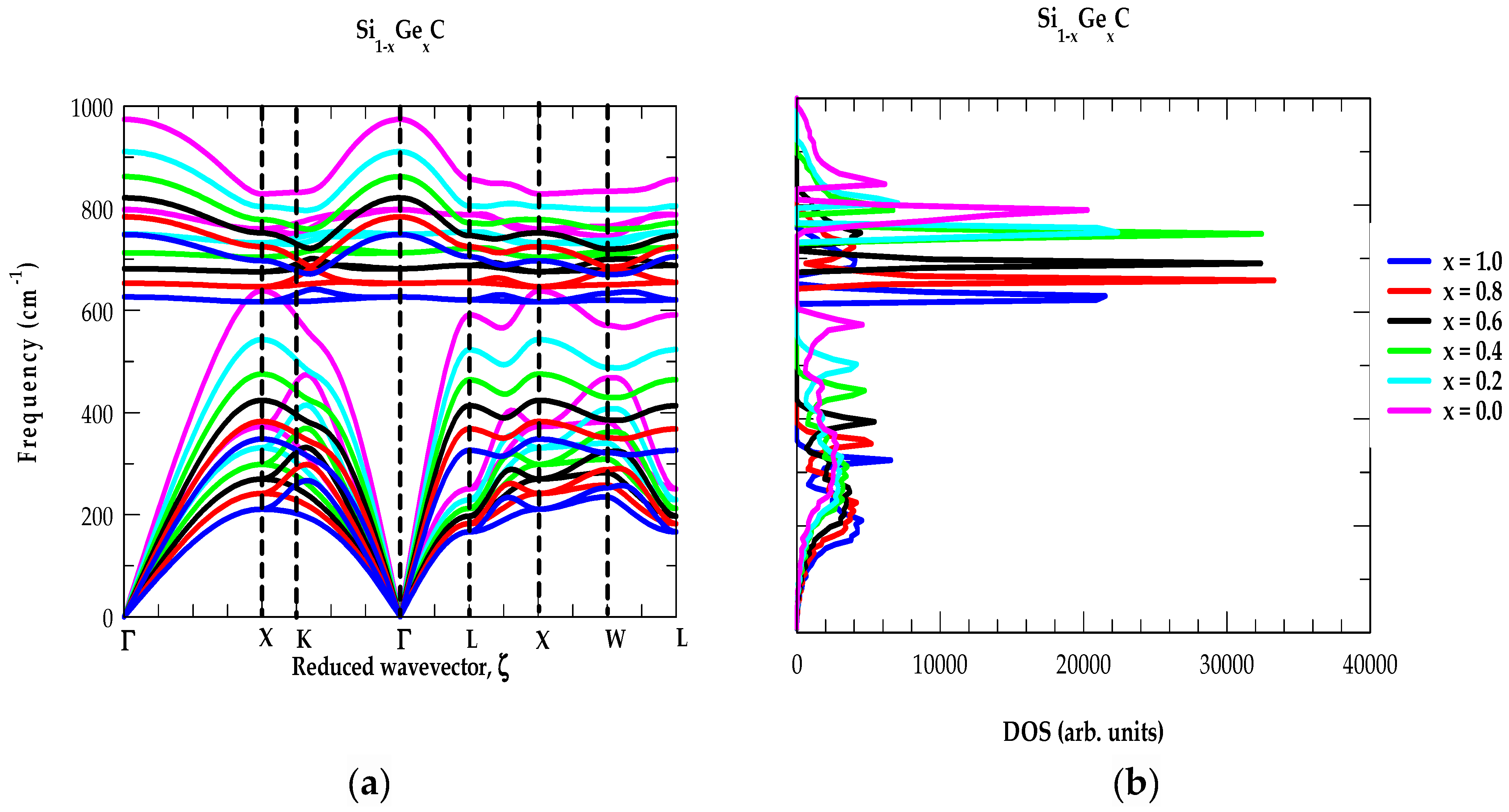
| Parameters | 3C-SiC | zb-GeC | zb-SnC |
|---|---|---|---|
| () | 4.360 (a), 4.40 (b), 4.374 (c) | 4.610 (d), 4.590 (e) | 5.130 (f), 5.170 (h) |
| 38.0 (a), 38.3 (b), 38.5 (c) | 29.7 (f), 35.8 (g) | 24.6 (g) | |
| 14.2 (a), 12.5 (b), 12.2 (c) | 12.4 (f), 12.2 (g) | 11.3 (g) | |
| 25.6 (a), 24.0 (b), 24.3 (c) | 14.1 (f), 21.4 (g) | 14.3 (g) | |
| 974 (b) 793 (b) | 748 (h) 626 (h) | 558 (h) 456 (h) | |
| 830 (b) 759 (b) 644 (b) 373 (b) | 697 (h) 617 (h) 348 (h) 214 (h) | 503 (h) 450 (h) 216 (h) 134 (h) | |
| 850 (b) 770 (b) 605 (b) 260 (b) | 705 (h) 612 (h) 331 (h) 162 (h) | 516 (h) 440 (h) 199 (h) 109 (h) |
| Parameters (a) | 3C-SiC | GeC | SnC |
|---|---|---|---|
| A | −0.91723 | −0.68066 | −0.39000 |
| B | −0.44500 | −0.66000 | −0.37000 |
| C1 | −0.04050 | −0.02300 | −0.00400 |
| C2 | −0.15900 | −0.13200 | −0.09300 |
| D1 | 0.06440 | −0.02097 | −0.00135 |
| D2 | −0.33088 | −0.38000 | −0.07200 |
| E1 | 0.06200 | −0.01000 | −0.01000 |
| E2 | 0.10850 | 0.02000 | 0.02000 |
| F1 | −0.04100 | 0.03550 | 0.01050 |
| F2 | 0.28800 | 0.02780 | 0.01480 |
| Zeff | 1.05300 | 0.92200 | 0.88030 |
| (A) | |||||||||||
| 3C-SiC | |||||||||||
| Our (a) | 974 | 797 | 828 | 760 | 639 | 373 | 857 | 787 | 591 | 250 | 177 |
| Expt. (b) | 974 | 793 | 830 | 759 | 644 | 373 | 850 | 770 | 605 | 260 | 181 |
| Expt. (c) | 972 | 796 | 829 | 761 | 640 | 373 | 838 | 766 | 610 | 266 | 176 |
| Calc. (d) | 953 | 783 | 811 | 749 | 623 | 364 | 832 | 755 | 608 | 260 | 170 |
| Calc. (e) | 956 | 783 | 829 | 755 | 629 | 366 | 838 | 766 | 610 | 261 | 173 |
| Calc. (f) | 945 | 774 | 807 | 741 | 622 | 361 | 817 | 747 | 601 | 257 | 171 |
| (a) Our; (b) Ref. [105]; (c) Ref. [129]; (d) Ref. [125]; (e) Ref. [122]; (f) Ref. [123]. | |||||||||||
| (B) | |||||||||||
| GeC | |||||||||||
| Our (a) | 749 | 626 | 697 | 617 | 348 | 211 | 705 | 621 | 326 | 166 | 123 |
| Calc. (b) | 812 | 682 | 785 | 695 | 378 | 222 | 789 | 683 | 366 | 161 | 130 |
| Calc. (c) | 748 | 626 | 697 | 617 | 348 | 214 | 705 | 612 | 331 | 162 | 122 |
| (a) Our; (b) Ref. [124], (c) Ref. [125]. | |||||||||||
| (C) | |||||||||||
| SnC | |||||||||||
| Our (a) | 558 | 456 | 512 | 454 | 216 | 141 | 524 | 454 | 214 | 102 | 102 |
| Calc. (b) | 711 | 590 | 689 | 621 | 268 | 150 | 694 | 600 | 262 | 106 | 121 |
| Calc. (c) | 558 | 456 | 503 | 450 | 216 | 134 | 516 | 440 | 199 | 109 | 102 |
| (a) Our; (b) Ref. [124], (c) Ref. [125]. | |||||||||||
| (A) | ||||||
| (T) | ||||||
| T | 3C-SiC RIM (a) | Others | GeC RIM (a) | Others | SnC RIM (a) | Others |
| 0 | 1090 (a) | 673 (a) | 419 (a) | |||
| 100 | 923 (a) | 635 (a) | 490 (a) | |||
| 300 | 1134 (a) | 960.61 (b), 1130 (c), 611.6 (d), 1151 (e), 1080 (f) | 857 (a) | 759.6 (g), 616 (e), 831 (f) | 619 (a) | 506.7 (g), 472 (e) |
| 600 | 1180 (a) | 951.54 (b) | 899 (a) | 651 (a) | ||
| 900 | 1188 (a) | 942.52 (b) | 906 (a) | 657 (a) | ||
| 1200 | 1192 (a) | 934.94 (b) | 908 (a) | 659 (a) | ||
| 1500 | 1194 (a) | 930.02 (b) | 910 (a) | 660 (a) | ||
| (a) Our; (b) Refs. [149,150]; (c) Ref. [152]; (d) Ref. [120]; (e) Ref. [118]; (f) Ref. [119]; (g) Ref. [123]. | ||||||
| (B) | ||||||
| (T) | ||||||
| T | 3C-SiC RIM (a) | Others | GeC RIM (a) | Others | SnC RIM (a) | Others |
| 300 | 26.24 | 27.09 (b), 31.39 (c), 26.8 (d) | 34.31 | 32.35 (e) | 40.01 | 35.70 (e) |
| 600 | 41.49 | 42.09 (b), 44.14 (c), 41.3 (d) | 44.58 | 44.6 (e*) | 46.96 | 46.10 (e*) |
| 900 | 45.77 | 47.60 (b), 47.26 (c), 46.7 (d) | 47.41 | 47.1 (e*) | 48.56 | 48.32 (e*) |
| 1200 | 47.51 | 50.19 (b), 48.41 (c), 49.6 (d) | 48.46 | 48.2 (e*) | - | - |
| 1500 | 48.34 | 51,77 (b), 48.94 (c), 51.2 (d) | - | - | - | - |
| (a) Our; (b) Refs. [149,150]; (c) Ref. [152]; (d) Ref. [120]; (e) Ref. [125] (e*) estimated from the graph. | ||||||
| (A) | |||||
| Si1−xGexC | |||||
| x | (a) | others | |||
| 0.0 | 974 | 797 | 177 | 2.683 | 2.697 (b), 2.72 (c) |
| 0.2 | 911 | 750 | 161 | 2.675 | |
| 0.4 | 862 | 713 | 149 | 2.659 | |
| 0.6 | 821 | 682 | 139 | 2.629 | |
| 0.8 | 783 | 653 | 130 | 2.611 | |
| 1.0 | 749 | 626 | 123 | 2.581 | 2.62 (d) |
| (a) Our; (b) Ref. [107]; (c) Refs. [122,123]; (d) Ref. [124]. | |||||
| (B) | |||||
| Si1−xSnxC | |||||
| x | (a) | others | |||
| 0.0 | 974 | 797 | 177 | 2.683 | 2.697 (b), 2.72 (c) |
| 0.2 | 856 | 707 | 149 | 2.697 | |
| 0.4 | 773 | 642 | 131 | 2.695 | |
| 0.6 | 700 | 582 | 118 | 2.684 | |
| 0.8 | 630 | 522 | 108 | 2.658 | |
| 1.0 | 558 | 456 | 102 | 2.629 | 2.95 (d) |
| (a) Our; (b) Ref. [107]; (c) Refs. [122,123]; (d) Ref. [124]. | |||||
| (C) | |||||
| Ge1−xSnxC | |||||
| x | (a) | others | |||
| 0.0 | 749 | 626 | 177 | 2.581 | 2.62 (d) |
| 0.2 | 710 | 594 | 116 | 2.595 | |
| 0.4 | 673 | 562 | 111 | 2.600 | |
| 0.6 | 635 | 528 | 107 | 2.615 | |
| 0.8 | 597 | 493 | 104 | 2.623 | |
| 1.0 | 558 | 456 | 102 | 2.629 | 2.95 (d) |
| (a) Our; (d) Ref. [124]. | |||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Talwar, D.N. Composition-Dependent Phonon and Thermodynamic Characteristics of C-Based XxY1−xC (X, Y ≡ Si, Ge, Sn) Alloys. Inorganics 2024, 12, 100. https://doi.org/10.3390/inorganics12040100
Talwar DN. Composition-Dependent Phonon and Thermodynamic Characteristics of C-Based XxY1−xC (X, Y ≡ Si, Ge, Sn) Alloys. Inorganics. 2024; 12(4):100. https://doi.org/10.3390/inorganics12040100
Chicago/Turabian StyleTalwar, Devki N. 2024. "Composition-Dependent Phonon and Thermodynamic Characteristics of C-Based XxY1−xC (X, Y ≡ Si, Ge, Sn) Alloys" Inorganics 12, no. 4: 100. https://doi.org/10.3390/inorganics12040100
APA StyleTalwar, D. N. (2024). Composition-Dependent Phonon and Thermodynamic Characteristics of C-Based XxY1−xC (X, Y ≡ Si, Ge, Sn) Alloys. Inorganics, 12(4), 100. https://doi.org/10.3390/inorganics12040100





