Some Aspects of Hot Carrier Photocurrent across GaAs p-n Junction
Abstract
1. Introduction
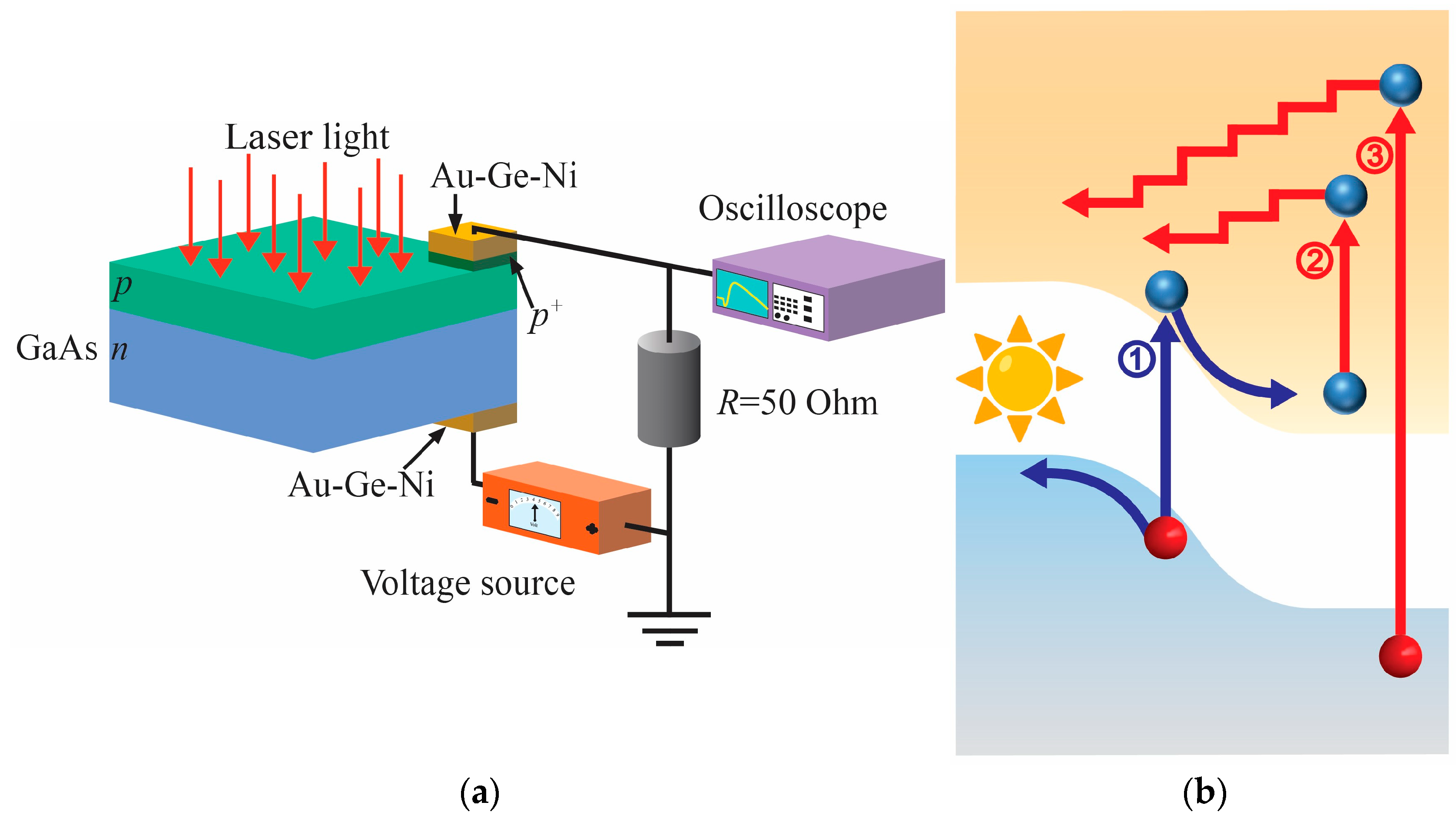
2. Materials and Methods
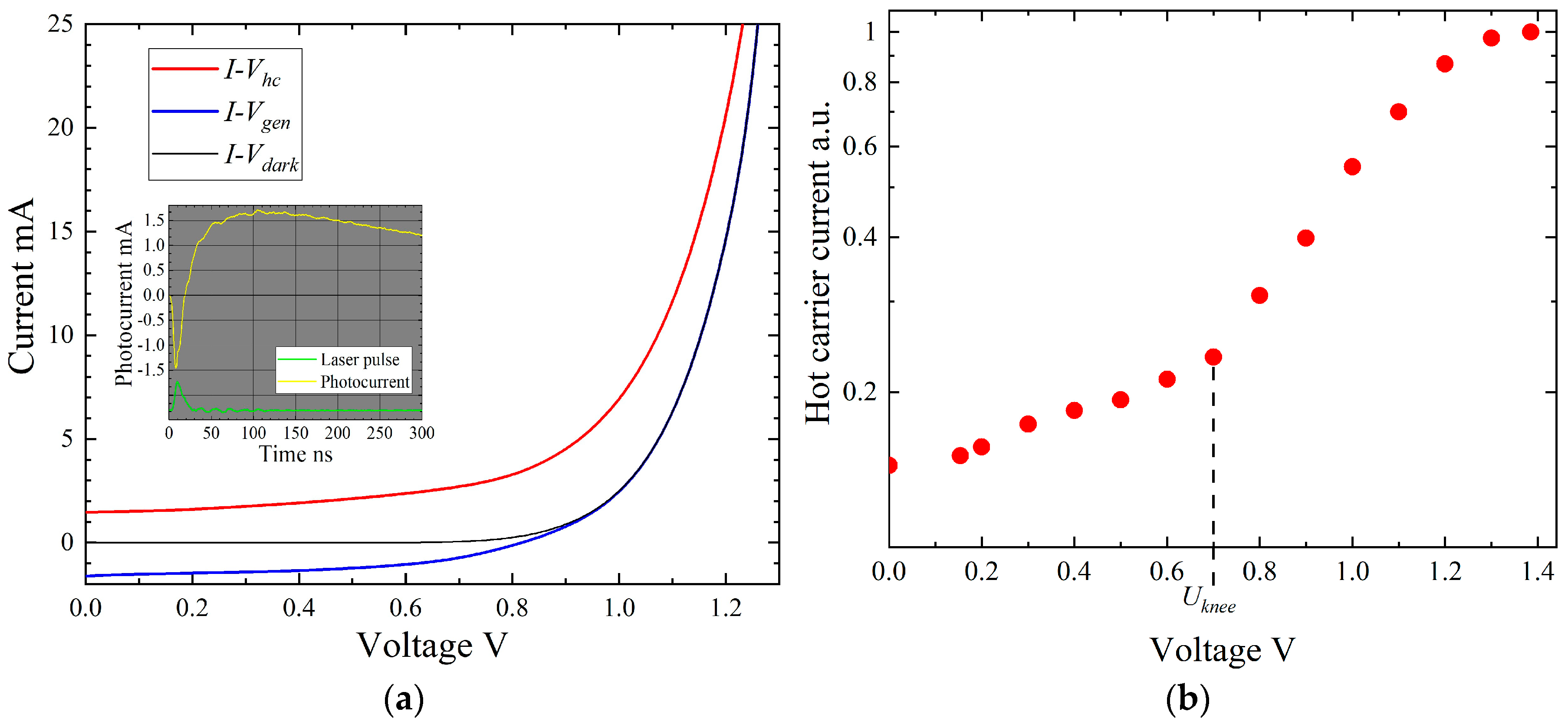
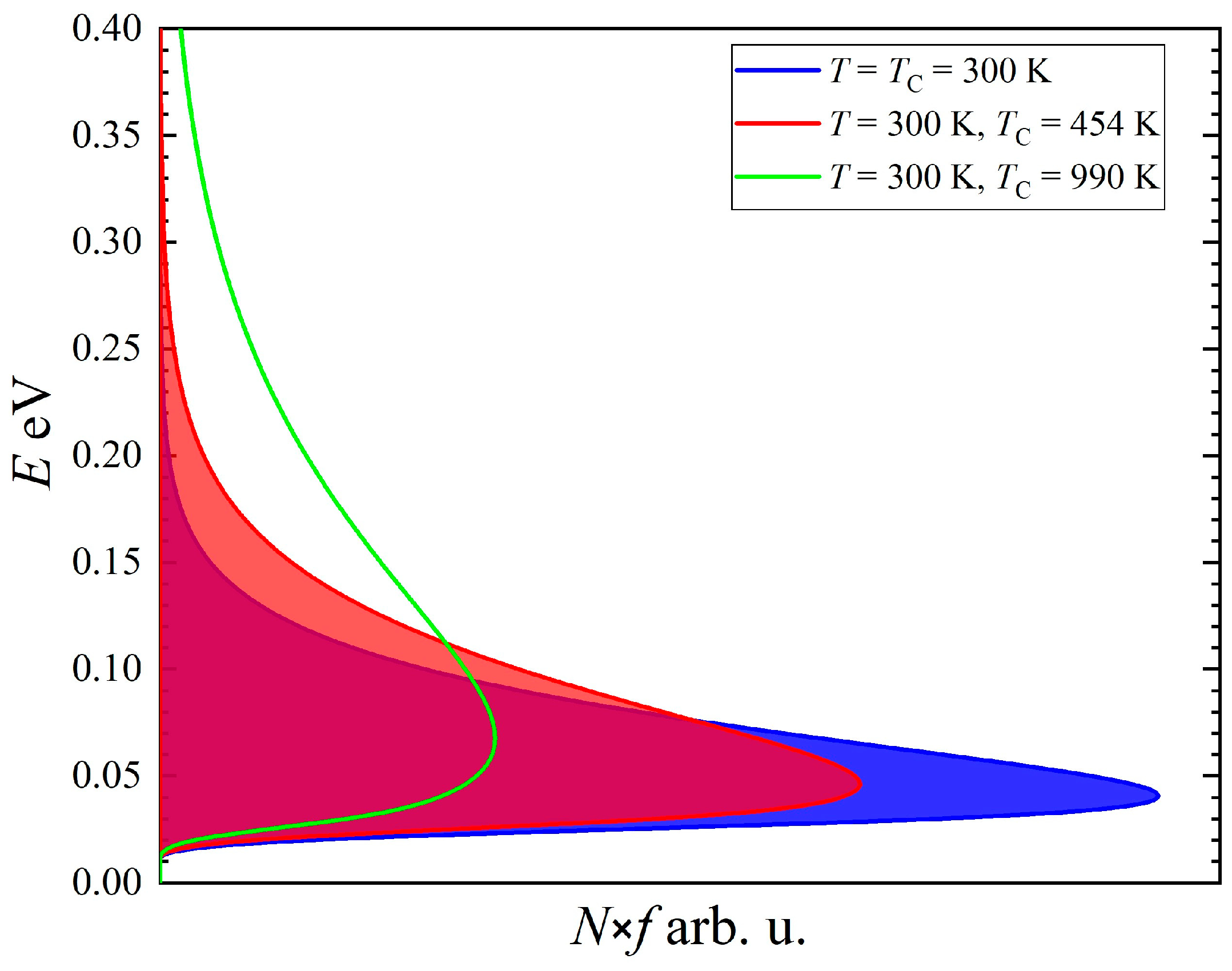
3. Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Murray, R. Infrared Absorption and Energy Levels Due to Impurities. In Properties of Gallium Arsenide, 3rd ed.; Brozel, M.R., Stillman, G.E., Eds.; The Institution of Electrical Engineers INSPEC: London, UK, 1996; pp. 225–256. [Google Scholar]
- Umeno, M.; Sugito, Y.; Jimbo, T.; Hattori, H.; Amenixa, Y. Hot photo-carrier and hot electron effects in p-n junctions. Solid-State Electron. 1978, 21, 191–195. [Google Scholar] [CrossRef]
- Encinas-Sanz, F.; Guerra, J.M. Laser-induced hot carrier photovoltaic effects in semiconductor junctions. Prog. Quantum Electron. 2003, 27, 267–294. [Google Scholar] [CrossRef]
- Ašmontas, S.; Gradauskas, J.; Seliuta, D.; Širmulis, E. Photoelectrical properties of nonuniform semiconductor under infrared laser radiation. In Proceedings of the International Conference on Nonresonant Laser-Matter Interaction, St. Petersburg, Russia, 21–23 August 2000. [Google Scholar]
- Ašmontas, S.; Gradauskas, J.; Seliuta, D.; Šilėnas, A.; Širmulis, E.; Marmur, I.Y. Photoelectrical properties of nonuniform GaAs structures under infrared laser illumination. In Proceedings of the International Conference on SPIE: Nonresonant Laser-Matter Interaction, St. Petersburg, Russia, 1–3 July 1996. [Google Scholar]
- Dargys, A.; Kundrotas, J. Physical data for gallium arsenide. 143–188. In Handbook on the Physical Properties of Ge, Si, GaAs and InP, 1st ed.; Science and Encyclopedia: Vilnius, Lithuania, 1994. [Google Scholar]
- Shockley, W.; Queisser, H. Detailed Balance Limit of Efficiency of p-n Junction Solar Cells. J. Appl. Phys. 1961, 32, 510–519. [Google Scholar] [CrossRef]
- Hirst, L.C.; Ekins-Daukes, N.J. Fundamental losses in solar cells. Prog. Photovolt. Res. Appl. 2011, 19, 286–293. [Google Scholar] [CrossRef]
- Saeed, S.; de Jong, E.M.L.D.; Dohnalova, K.; Gregorkiewicz, T. Efficient optical extraction of hot-carrier energy. Nat. Commun. 2014, 5, 4665. [Google Scholar] [CrossRef] [PubMed]
- Torchynska, T.V.; Vivas Hernandez, A.; Goldstein, Y.; Jedrzejewskii, J.; Jimenez Sandoval, S. Photoluminescence of Si or Ge nanocrystallites embedded in silicon oxide. J. Non-Cryst. Solids 2006, 352, 1152–1155. [Google Scholar] [CrossRef]
- Kolodinski, S.; Werner, J.H.; Wittchen, T.; Queisser, H.J. Quantum efficiencies exceeding unity due to impact ionization in silicon solar cells. Appl. Phys. Lett. 1993, 63, 2405–2407. [Google Scholar] [CrossRef]
- Wurfel, P. Solar energy conversion with hot electrons from impact ionisation. Sol. Energy Mater. Sol. Cells 1997, 46, 43–52. [Google Scholar] [CrossRef]
- Fast, J.; Aeberhard, U.; Bremner, S.P.; Linke, H. Hot-carrier optoelectronic devices based on semiconductor nanowires. Appl. Phys. Rev. 2021, 8, 021309. [Google Scholar] [CrossRef]
- Kempa, K.; Naughton, M.J.; Ren, Z.F.; Herczynski, A.; Kirkpatrick, T.; Rybczynski, J.; Gao, Y. Hot electron effect in nanoscopically thin photovoltaic junctions. Appl. Phys. Lett. 2009, 95, 233121–2331214. [Google Scholar] [CrossRef]
- Shayan, S.; Matloub, S.; Rostami, A. Efficiency enhancement in a single bandgap silicon solar cell considering hot-carrier extraction using selective energy contacts. Opt. Express 2021, 29, 5068–5080. [Google Scholar] [CrossRef] [PubMed]
- Esgandari, M.; Barzinjy, A.A.; Rostami, A.; Rostami, G.; Dolatyari, M. Solar cells efficiency enhancement using multilevel selective energy contacts (SECs). Opt. Quantum Electron. 2022, 54, 1–9. [Google Scholar] [CrossRef]
- Ross, R.T.; Nozik, A.J. Efficiency of hot-carrier solar energy converters. J. Appl. Phys. 1982, 53, 3813–3818. [Google Scholar] [CrossRef]
- Neges, M.; Schwarzburg, K.; Willig, F. Monte Carlo simulation of energy loss and collection of hot charge carriers, first step towards a more realistic hot-carrier solar energy converter. Sol. Energy Mater. Sol. Cells 2006, 90, 2107–2128. [Google Scholar] [CrossRef]
- Conibeer, G.; Ekins-Daukes, N.; Guillemoles, J.-F.; Konig, D.; Cho, E.-C.; Jiang, C.-W.; Shrestha, S.; Green, M.A. Progress on hot carrier cells. Sol. Energy Mater. Sol. Cells 2009, 93, 713–719. [Google Scholar] [CrossRef]
- Le Bris, A.; Guillemoles, J.-F. Hot carrier solar cells: Achievable efficiency accounting for heat losses in the absorber and through contacts. Appl. Phys. Lett. 2010, 97, 113506. [Google Scholar] [CrossRef]
- Kirk, A.P.; Fischetti, M.V. Fundamental limitations of hot-carrier solar cells. Phys. Rev. B Condens. Matter. 2012, 86, 165206. [Google Scholar] [CrossRef]
- Rodiere, J.; Lombez, L.; Le Corre, A.; Durand, O.; Guillemoles, J.-F. Experimental evidence of hot carrier solar cell operation in multi-quantum wells heterostructures. Appl. Phys. Lett. 2015, 106, 183901. [Google Scholar] [CrossRef]
- Conibeer, G.; Shrestha, S.; Huang, S.; Patterson, R.; Xia, H.; Feng, Y.; Zhang, P.; Gupta, N.; Tayebjee, M.; Smyth, S.; et al. Hot carrier solar cell absorber prerequisites and candidate material systems. Sol. Energy Mater. Sol. Cells 2015, 135, 124–129. [Google Scholar] [CrossRef]
- Chung, S.; Wen, X.; Huang, S.; Gupta, N.; Conibeer, G.; Shrestha, S.; Harada, T.; Kee, T.W. Nanosecond long excited state lifetimes observed in hafnium nitride. Sol. Energy Mater. Sol. Cells 2017, 169, 13–18. [Google Scholar] [CrossRef]
- Takeda, Y. Hot-carrier solar cells and improved types using wide-bandgap energy-selective contacts. Prog. Photovolt. Res. Appl. 2022, 30, 65–84. [Google Scholar] [CrossRef]
- Sharma, A.S.; Hanif, M.; Bremner, S.P.; Nielsen, M.P.; Tayebjee, M.J.Y.; Rougieux, F.E.; Ekins-Daukes, N.J.; Pusch, A. Heat Flow through Nonideal Contacts in Hot-Carrier Solar Cells. Phys. Rev. Appl. 2023, 20, 034001. [Google Scholar] [CrossRef]
- Li, M.; Bhaumik, S.; Goh, T.W.; Kumar, M.S.; Yantara, N.; Grätzel, M.; Mhaisalkar, S.; Mathews, N.; Sum, T.C. Slow cooling and highly efficient extraction of hot carriers in colloidal perovskite nanocrystals. Nat. Commun. 2017, 8, 14350. [Google Scholar] [CrossRef] [PubMed]
- Yang, Y.; Ostrowski, D.P.; France, R.M.; Zhu, K.; Van De Lagemaat, J.; Luther, J.M.; Beard, M.C. Observation of a hot-phonon bottleneck in lead-iodide perovskites. Nat. Photonics 2016, 10, 53–59. [Google Scholar] [CrossRef]
- Johannsen, J.C.; Ulstrup, S.; Cilento, F.; Crepaldi, A.; Zacchigna, M.; Cacho, C.; Turcu, I.E.; Springate, E.; Fromm, F.; Raidel, C.; et al. Direct View of Hot Carrier Dynamics in Graphene. Phys. Rev. Lett. 2013, 111, 027403. [Google Scholar] [CrossRef] [PubMed]
- El Fatimy, A.; Myers-Ward, R.L.; Boyd, A.K.; Daniels, K.M.; Gaskill, D.K.; Barbara, P. Epitaxial graphene quantum dots for high-performance terahertz bolometers. Nat. Nanotechnol. 2016, 11, 335–338. [Google Scholar] [CrossRef] [PubMed]
- Esmaielpour, H.; Lombez, L.; Giteau, M.; Delamarre, A.; Ory, D.; Cattoni, A.; Collin, S.; Guillemoles, J.-F.; Suchet, D. Investigation of hot carrier thermalization mechanisms in quantum well structures. In Proceedings of the SPIE, Online, 6–11 March 2021; Volume 11681. Physics, Simulation, and Photonic Engineering of Photovoltaic Devices X. [Google Scholar]
- Gibelli, F.; Lombez, L.; Guillemoles, J.-F. Two carrier temperatures non-equilibrium generalized Planck law for semiconductors. Phys. B Condens. Matter. 2016, 498, 7–16. [Google Scholar] [CrossRef]
- The National Renewable Energy Laboratory. Best Research-Cell Efficiency Chart. Nrel.Gov. Available online: https://www.nrel.gov/pv/cell-efficiency.html (accessed on 10 October 2023).
- Gradauskas, J.; Ašmontas, S.; Sužiedėlis, A.; Šilėnas, A.; Vaičikauskas, V.; Čerškus, A.; Širmulis, E.; Žalys, O.; Masalskyi, O. Influence of Hot Carrier and Thermal Components on Photovoltage Formation across the p–n Junction. Appl. Sci. 2020, 10, 7483. [Google Scholar] [CrossRef]
- Ašmontas, S.; Gradauskas, J.; Sužiedėlis, A.; Šilėnas, A.; Širmulis, E.; Švedas, V.; Vaičikauskas, V.; Žalys, O. Hot carrier impact on photovoltage formation in solar cells. Appl. Phys. Lett. 2018, 113, 071103. [Google Scholar] [CrossRef]
- Sze, S.M. Physics of Semiconductor Devices, 1st ed.; John Wiley & Sons, Inc.: New York, NY, USA, 1969; pp. 25–38. [Google Scholar]
- Ašmontas, S.; Širmulis, E.; Stonys, S. Investigation of the photovoltage across germanium p-n-junction under pulsed CO2 laser irradiation. Lith. J. Phys. 1984, 24, 75–82. [Google Scholar]
- Ašmontas, S.; Gradauskas, J.; Seliuta, D.; Suziedelis, A.; Silenas, A.; Valusis, G. GaAs/AlGaAs heterojunction: A promising detector for infrared radiation. In Proceedings of the 5th European Gallium Arsenide and related III–V compounds Applications Symposium, Bolonga, Italy, 3–5 September 1997. [Google Scholar]
- Gradauskas, J.; Ašmontas, S. Hot Carrier Photocurrent through MOS Structure. Appl. Sci. 2021, 11, 7211. [Google Scholar] [CrossRef]
- Green, M.A.; Emery, K.; Blakers, A.W. Silicon solar cells with reduced temperature sensitivity. Electron. Lett. 1982, 18, 97–98. [Google Scholar] [CrossRef]
- Schaffner, J.S.; Shea, R.F. The Variation of the Forward Characteristics of Junction Diodes with Temperature. Proc. IRE 1955, 43, 101. [Google Scholar]
- Singh, P.; Ravindra, N.M. Temperature dependence of solar cell performance—An analysis. Sol. Energy Mater. Sol. Cells 2012, 101, 36–45. [Google Scholar] [CrossRef]
- Nootan, C.P. Voltage-Current Characteristics of GaAs Diodes as a Function of Temperature. Master’s Thesis, Lehigh University, Bethlehem, PA, USA, 1964. [Google Scholar]
- Cavassilas, N.; Makhfudz, I.; Daré, A.-M.; Lannoo, M.; Dangoisse, G.; Bescond, M.; Michelini, F. Theoretical Demonstration of Hot-Carrier Operation in an Ultrathin Solar Cell. Phys. Rev. Appl. 2022, 17, 064001. [Google Scholar] [CrossRef]
- Pelouch, W.S.; Ellingson, R.J.; Powers, P.E.; Tang, C.L.; Szmyd, D.M.; Nozik, A.J. Comparison of hot-carrier relaxation in quantum wells and bulk GaAs at high carrier densities. Phys. Rev. B 1992, 45, 1450–1453. [Google Scholar] [CrossRef]
- Nguyen, D.-T.; Lombez, L.; Gibelli, F.; Boyer-Richard, S.; Le Corre, A.; Durand, O.; Guillemoles, J.-F. Quantitative experimental assessment of hot carrier-enhanced solar cells at room temperature. Nat. Energy 2018, 3, 236–242. [Google Scholar] [CrossRef]

| Absorber | K | Method | Excitation Details | Reference |
|---|---|---|---|---|
| GaAs | 454 | Temperature coefficient | 700 kW/cm2 | This work |
| (In,Ga)As | 430 | Theoretical simulation | 1 kW/cm2 | [44] |
| Bulk GaAs | 300–680 | Time-resolved luminescence | 12.5 mW (at corresponding 100 ps to 1 ps time delay) | [45] |
| QW InGaAsP | 400–1200 | Photoluminescence | 1.7–25 kW/cm2 | [46] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ašmontas, S.; Masalskyi, O.; Zharchenko, I.; Sužiedėlis, A.; Gradauskas, J. Some Aspects of Hot Carrier Photocurrent across GaAs p-n Junction. Inorganics 2024, 12, 174. https://doi.org/10.3390/inorganics12060174
Ašmontas S, Masalskyi O, Zharchenko I, Sužiedėlis A, Gradauskas J. Some Aspects of Hot Carrier Photocurrent across GaAs p-n Junction. Inorganics. 2024; 12(6):174. https://doi.org/10.3390/inorganics12060174
Chicago/Turabian StyleAšmontas, Steponas, Oleksandr Masalskyi, Ihor Zharchenko, Algirdas Sužiedėlis, and Jonas Gradauskas. 2024. "Some Aspects of Hot Carrier Photocurrent across GaAs p-n Junction" Inorganics 12, no. 6: 174. https://doi.org/10.3390/inorganics12060174
APA StyleAšmontas, S., Masalskyi, O., Zharchenko, I., Sužiedėlis, A., & Gradauskas, J. (2024). Some Aspects of Hot Carrier Photocurrent across GaAs p-n Junction. Inorganics, 12(6), 174. https://doi.org/10.3390/inorganics12060174







