Metalloborospherene Analogs to Metallofullerene
Abstract
:1. Introduction
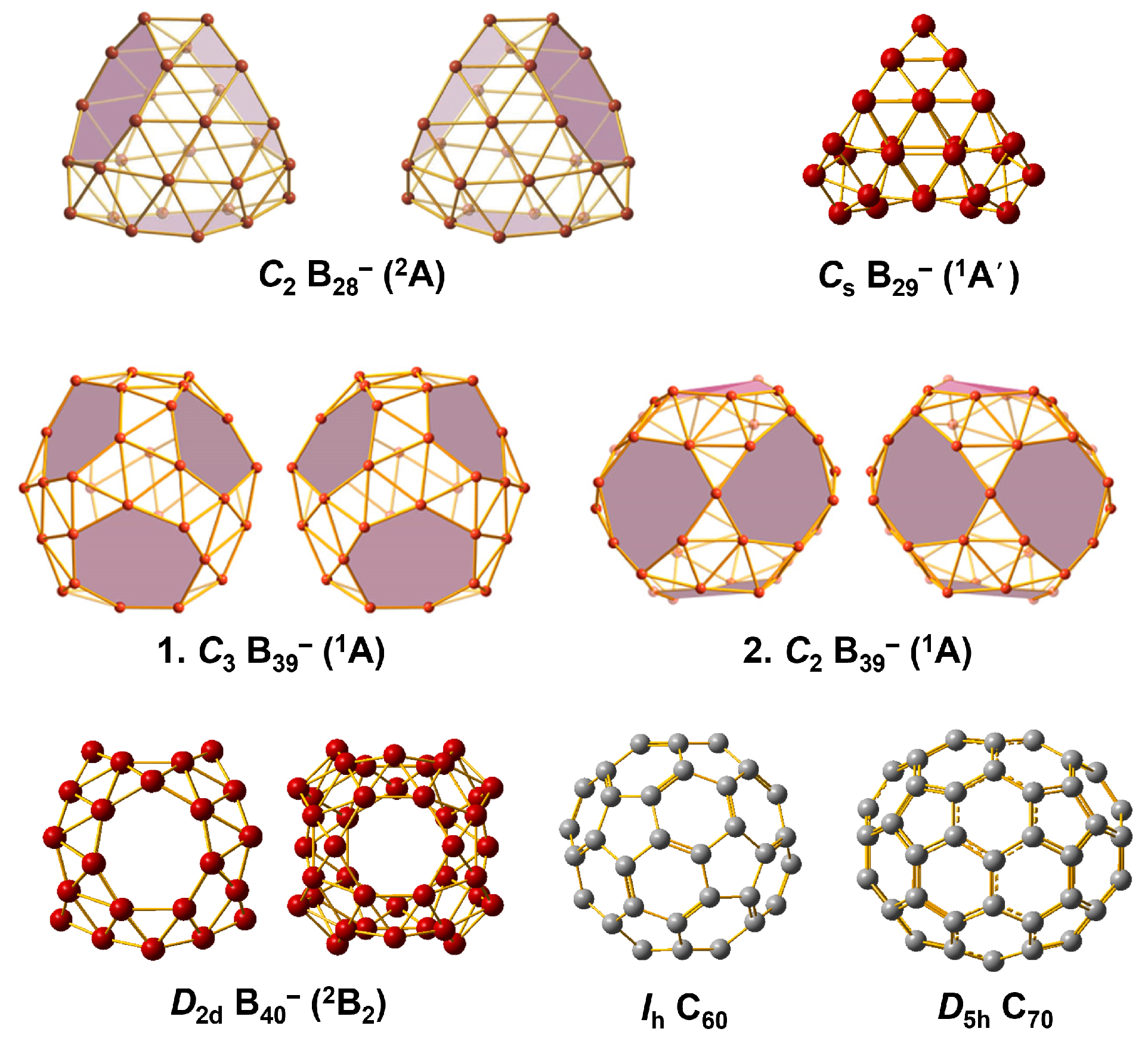
2. Structures of Fullerene and Borospherene
3. Metallofullerene and Metalloborospherene
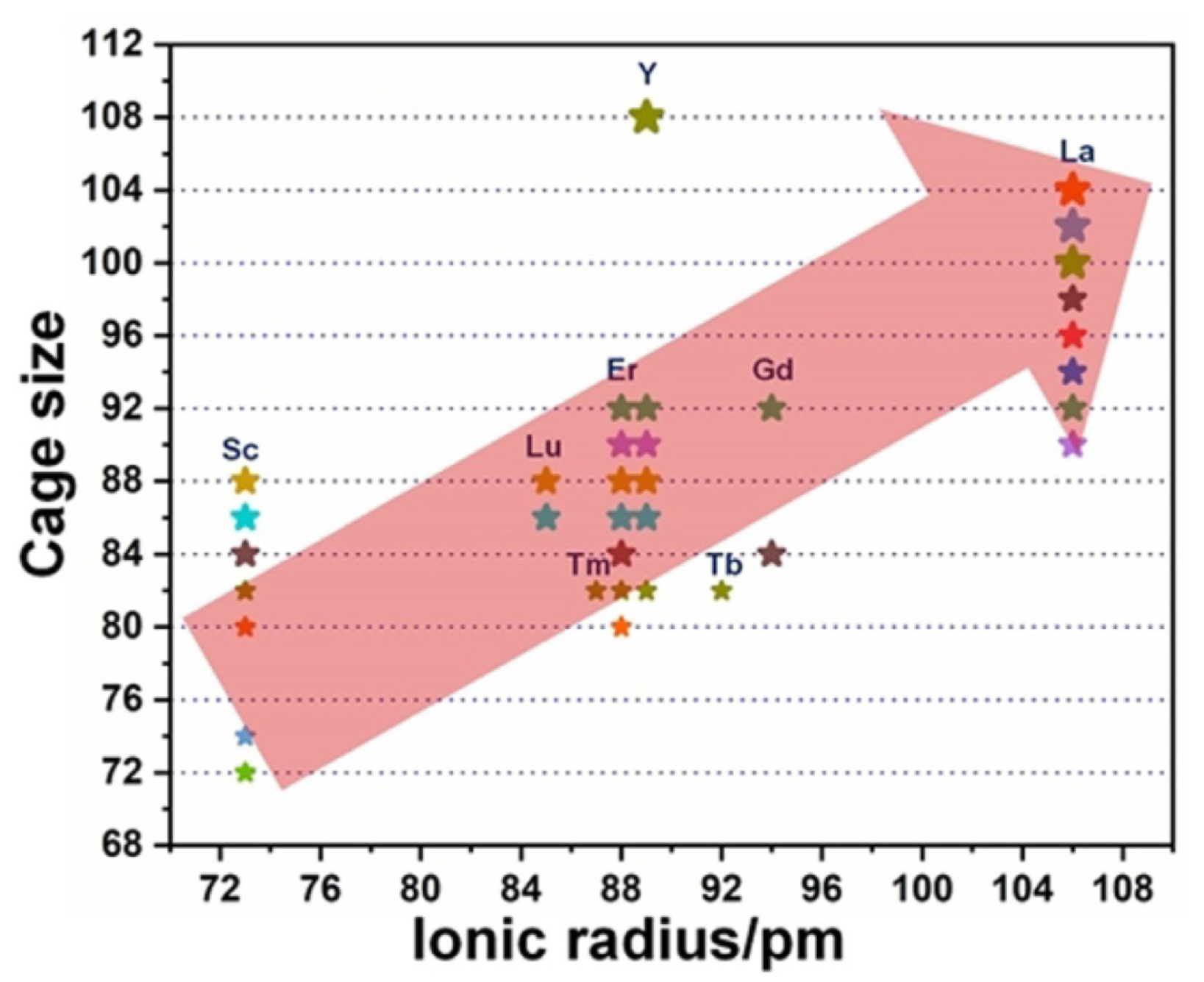
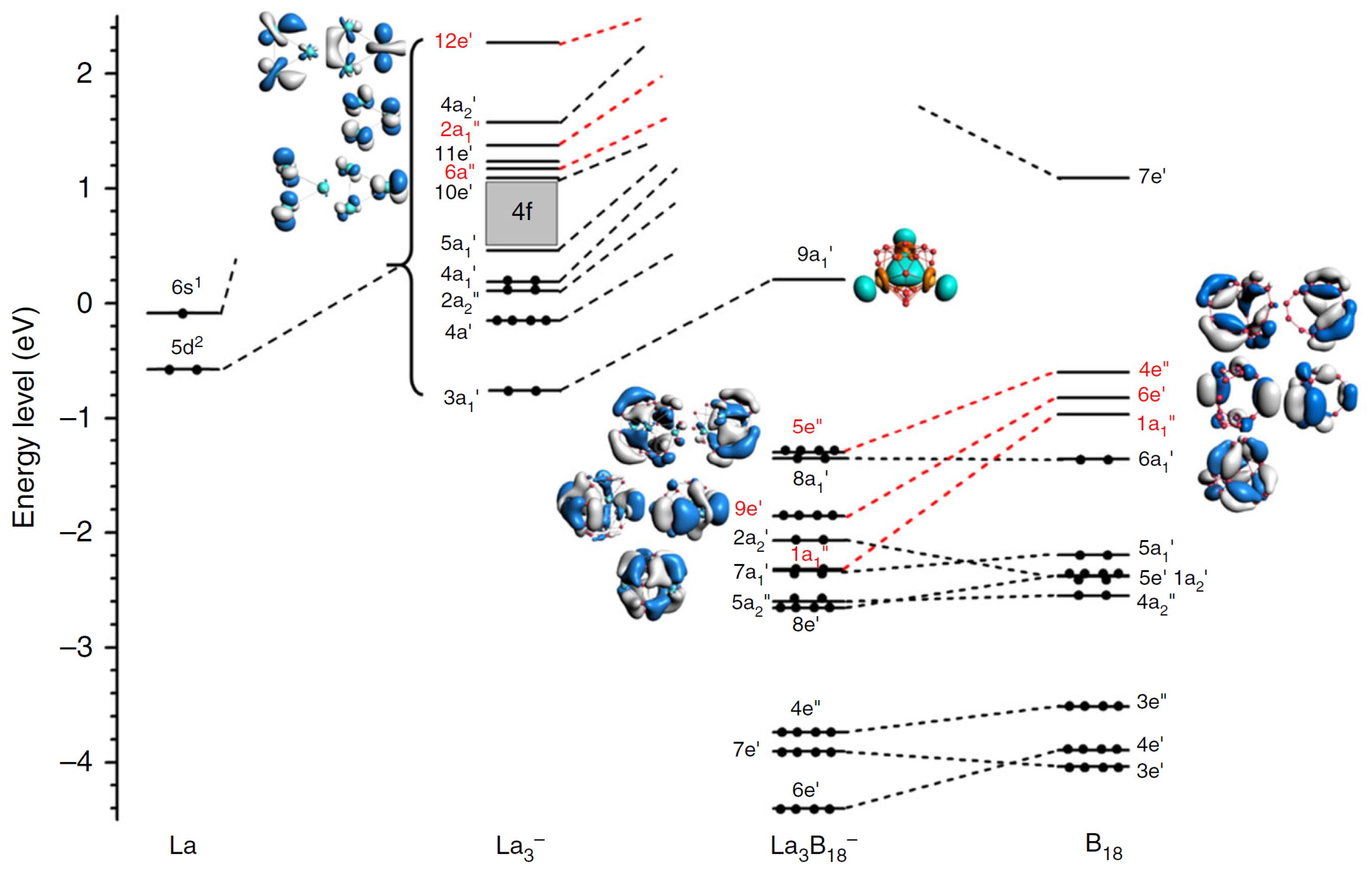
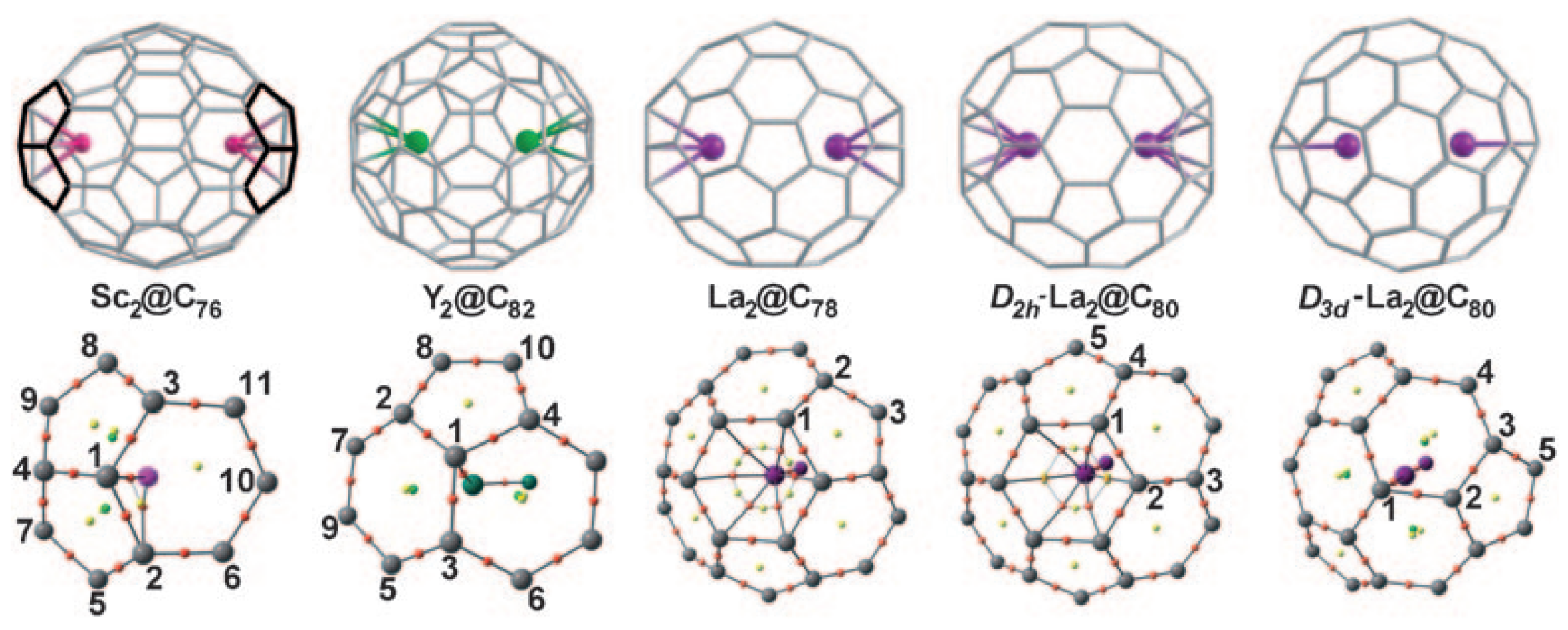
3.1. Lanthanide-Doped Fullerene and Borospherene Clusters
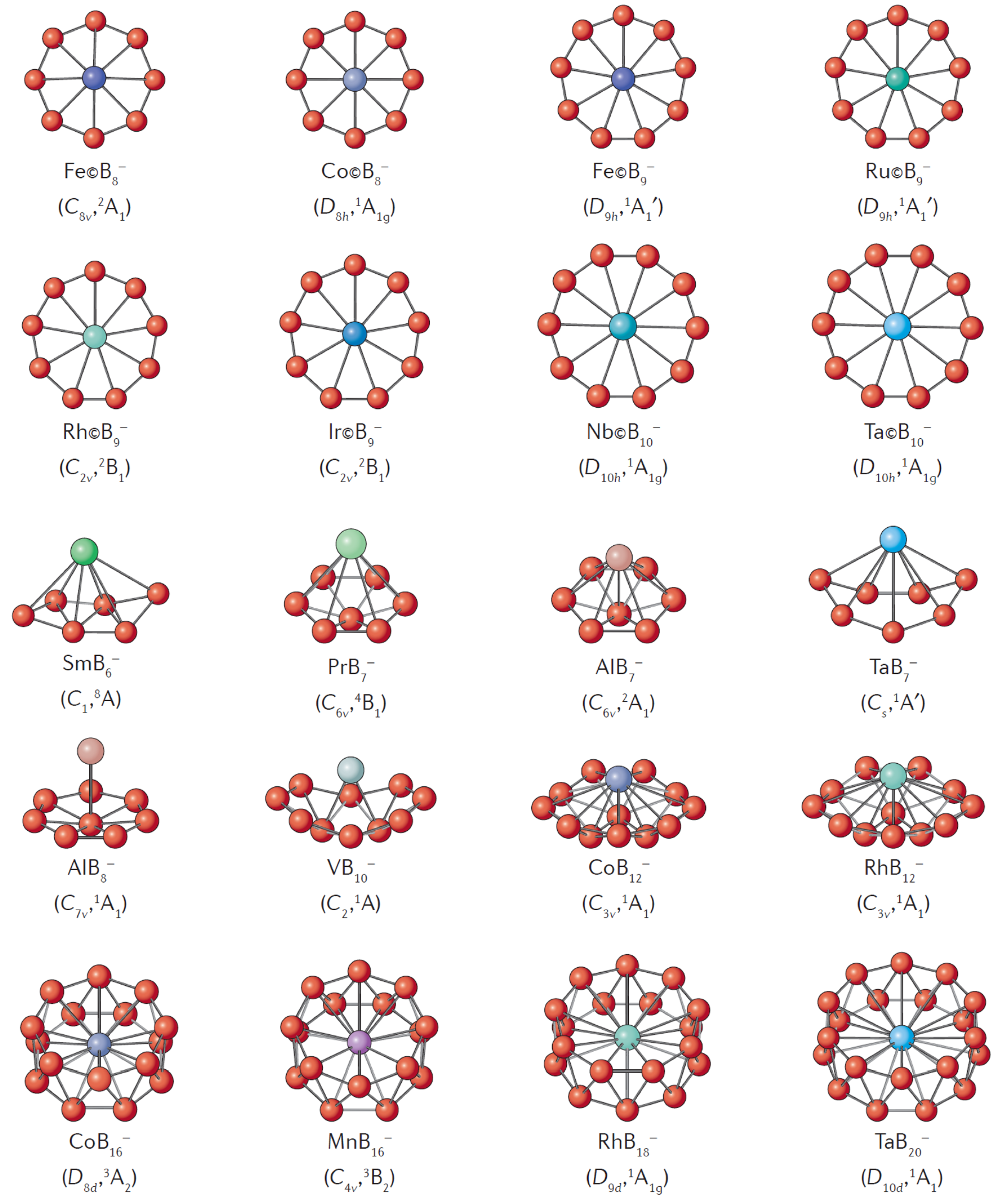
3.2. Transition Metal-Containing Fullerene and Borospherene
3.3. Actinide-Containing Fullerene and Borospherene
4. Theoretical and Computational Methods
4.1. Global Minimum Search
4.2. Photoelectron Spectroscopy Simulation
4.3. Molecular Orbitals and Chemical Bonding Analysis
5. Conclusions and Perspectives
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kroto, H. The stability of the fullerenes Cn, with n = 24, 28, 32, 36, 50, 60 and 70. Nature 1987, 329, 529–531. [Google Scholar] [CrossRef]
- Lu, X.; Chen, Z. Curved pi-conjugation, aromaticity, and the related chemistry of small fullerenes (<C60) and single-walled carbon nanotubes. Chem. Rev. 2005, 105, 3643–3696. [Google Scholar] [PubMed]
- Hebard, A. Buckminsterfullerene. Annu. Rev. Mater. Sci. 1993, 23, 159–191. [Google Scholar] [CrossRef]
- Kroto, H.W.; Heath, J.R.; O’Brien, S.C.; Curl, R.F.; Smalley, R.E. C60: Buckminsterfullerene. Nature 1985, 318, 162–163. [Google Scholar] [CrossRef]
- Yadav, B.; Kumar, R. Structure, properties and applications of fullerenes. Int. J. Nanotechnol. 2008, 2, 15–24. [Google Scholar]
- Zhai, H.J.; Zhao, Y.F.; Li, W.L.; Chen, Q.; Bai, H.; Hu, H.S.; Piazza, Z.A.; Tian, W.J.; Lu, H.G.; Wu, Y.B.; et al. Observation of an all-boron fullerene. Nat. Chem. 2014, 6, 727–731. [Google Scholar] [CrossRef] [PubMed]
- Li, W.L.; Chen, X.; Jian, T.; Chen, T.T.; Li, J.; Wang, L.S. From planar boron clusters to borophenes and metalloborophenes. Nat. Rev. Chem. 2017, 1, 71. [Google Scholar] [CrossRef]
- Sergeeva, A.P.; Popov, I.A.; Piazza, Z.A.; Li, W.L.; Romanescu, C.; Wang, L.S.; Boldyrev, A.I. Understanding boron through size-selected clusters: Structure, chemical bonding, and fluxionality. Acc. Chem. Res. 2014, 47, 1349–1358. [Google Scholar] [CrossRef] [PubMed]
- Popov, I.A.; Piazza, Z.A.; Li, W.L.; Wang, L.S.; Boldyrev, A.I. A combined photoelectron spectroscopy and ab initio study of the quasi-planar B24− cluster. J. Chem. Phys. 2013, 139, 144307. [Google Scholar] [CrossRef]
- Zhai, H.J.; Kiran, B.; Li, J.; Wang, L.S. Hydrocarbon analogues of boron clusters—Planarity, aromaticity and antiaromaticity. Nat. Mater. 2003, 2, 827–833. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, X.; Shi, R.; Liu, H.; Su, Y.; King, R.B. B28: The smallest all-boron cage from an ab initio global search. Nanoscale 2015, 7, 15086–15090. [Google Scholar] [CrossRef] [PubMed]
- Popov, A.A.; Yang, S.; Dunsch, L. Endohedral fullerenes. Chem. Rev. 2013, 113, 5989–6113. [Google Scholar] [CrossRef] [PubMed]
- Lu, X.; Akasaka, T.; Nagase, S. Chemistry of endohedral metallofullerenes: The role of metals. Chem. Commun. 2011, 47, 5942–5957. [Google Scholar] [CrossRef] [PubMed]
- Shinohara, H. Endohedral metallofullerenes. Rep. Prog. Phys. 2000, 63, 843. [Google Scholar] [CrossRef]
- Wilson, L.J.; Cagle, D.W.; Thrash, T.P.; Kennel, S.J.; Mirzadeh, S.; Alford, J.M.; Ehrhardt, G.J. Metallofullerene drug design. Coord. Chem. Rev. 1999, 190–192, 199–207. [Google Scholar] [CrossRef]
- Xu, J.; Li, Y.K.; Janssens, E.; Hou, G.L. Multifacets of fullerene–metal clusters: From fundamental to application. Acc. Chem. Res. 2024, 57, 1670–1683. [Google Scholar] [CrossRef] [PubMed]
- Barroso, J.; Pan, S.; Merino, G. Structural transformations in boron clusters induced by metal doping. Chem. Soc. Rev. 2022, 51, 1098–1123. [Google Scholar] [CrossRef] [PubMed]
- Chen, T.T.; Li, W.L.; Chen, W.J.; Yu, X.H.; Dong, X.R.; Li, J.; Wang, L.S. Spherical trihedral metallo-borospherenes. Nat. Commun. 2020, 11, 2766. [Google Scholar] [CrossRef]
- Jian, T.; Chen, X.; Li, S.D.; Boldyrev, A.I.; Li, J.; Wang, L.S. Probing the structures and bonding of size-selected boron and doped-boron clusters. Chem. Soc. Rev. 2019, 48, 3550–3591. [Google Scholar] [CrossRef]
- Li, W.L.; Chen, T.T.; Xing, D.H.; Chen, X.; Li, J.; Wang, L.S. Observation of highly stable and symmetric lanthanide octa-boron inverse sandwich complexes. Proc. Natl. Acad. Sci. USA 2018, 115, E6972–E6977. [Google Scholar] [CrossRef]
- Chen, T.T.; Li, W.L.; Li, J.; Wang, L.S. [La(ηx-Bx)La]− (x = 7–9): A new class of inverse sandwich complexes. Chem. Sci. 2019, 10, 2534–2542. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Chen, C.H.; Chen, N.; Echegoyen, L. Fullerenes as nanocontainers that stabilize unique actinide species inside: Structures, formation, and reactivity. Acc. Chem. Res. 2019, 52, 1824–1833. [Google Scholar] [CrossRef] [PubMed]
- Cai, W.; Zhang, M.; Echegoyen, L.; Lu, X. Recent advances in endohedral metallofullerenes. Fundam. Res. 2023; in press. [Google Scholar] [CrossRef]
- Wang, L.S. Photoelectron spectroscopy of size-selected boron clusters: From planar structures to borophenes and borospherenes. Int. Rev. Phys. 2016, 35, 69–142. [Google Scholar] [CrossRef]
- Hirsch, A.; Chen, Z.; Jiao, H. Spherical aromaticity in Ih symmetrical fullerenes: The 2(N+1)2 rule. Angew. Chem. Int. Ed. 2000, 39, 3915–3917. [Google Scholar] [CrossRef]
- Pei, L.; Li, H.R.; Yan, M.; Chen, Q.; Mu, Y.W.; Lu, H.G.; Wu, Y.B.; Li, S.D. Charge-induced structural transition between seashell-like and in 18 π-electron configurations. Phys. Chem. Chem. Phys. 2018, 20, 15330–15334. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.J.; Zhao, Y.F.; Li, W.L.; Jian, T.; Chen, Q.; You, X.R.; Ou, T.; Zhao, X.Y.; Zhai, H.J.; Li, S.D.; et al. Observation and characterization of the smallest borospherene, and B28. J. Chem. Phys. 2016, 144, 064307. [Google Scholar] [CrossRef] [PubMed]
- Li, H.R.; Jian, T.; Li, W.L.; Miao, C.Q.; Wang, Y.J.; Chen, Q.; Luo, X.M.; Wang, K.; Zhai, H.J.; Li, S.D.; et al. Competition between quasi-planar and cage-like structures in the B29− cluster: Photoelectron spectroscopy and ab initio calculations. Phys. Chem. Chem. Phys. 2016, 18, 29147–29155. [Google Scholar] [CrossRef]
- Chen, Q.; Li, W.L.; Zhao, Y.F.; Zhang, S.Y.; Hu, H.S.; Bai, H.; Li, H.R.; Tian, W.J.; Lu, H.G.; Zhai, H.J.; et al. Experimental and theoretical evidence of an axially chiral borospherene. ACS Nano 2015, 9, 754–760. [Google Scholar] [CrossRef]
- Chen, Q.; Zhang, S.Y.; Bai, H.; Tian, W.J.; Gao, T.; Li, H.R.; Miao, C.Q.; Mu, Y.W.; Lu, H.G.; Zhai, H.J.; et al. Cage-like and : New chiral members of the borospherene family. Angew. Chem. Int. Ed. 2015, 54, 8160–8164. [Google Scholar] [CrossRef]
- Pei, L.; Yan, M.; Zhao, X.Y.; Mu, Y.W.; Lu, H.G.; Wu, Y.B.; Li, S.D. Sea-shell-like and B32: Two new axially chiral members of the borospherene family. RSC Adv. 2020, 10, 10129–10133. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Chen, Q.; Li, H.R.; Zhao, X.Y.; Tian, X.X.; Mu, Y.W.; Lu, H.G.; Li, S.D. Aromatic cage-like B34 and : New axially chiral members of the borospherene family. Phys. Chem. Chem. Phys. 2018, 20, 15344–15349. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Mu, Y.W.; Li, S.D. Axially Chiral Cage-like and : New aromatic members of the borospherene family. J. Clust. Sci. 2022, 33, 81–87. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Chen, Q.; Li, H.R.; Mu, Y.W.; Lu, H.G.; Li, S.D. Cage-like clusters with the bonding pattern of σ + π double delocalization: New members of the borospherene family. Phys. Chem. Chem. Phys. 2017, 19, 10998–11003. [Google Scholar] [CrossRef] [PubMed]
- Li, H.R.; Chen, Q.; Tian, X.X.; Lu, H.G.; Zhai, H.J.; Li, S.D. Cage-like : A perfect borospherene monocation. J. Mol. Model. 2016, 22, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Lu, H.G.; Li, S.D. B111, B112, B113, and B114: The most stable core-shell borospherenes with an icosahedral B12 core at the center exhibiting superatomic behaviors. Nano Res. 2021, 14, 4719–4724. [Google Scholar] [CrossRef]
- Pei, L.; Yan, Q.Q.; Li, S.D. Predicting the structural transition in medium-sized boron nanoclusters: From bilayer B64, B66, B68, B70, and B72 to core-shell B74. Eur. J. Inorg. Chem. 2021, 2021, 2618–2624. [Google Scholar] [CrossRef]
- Gonzalez Szwacki, N.; Sadrzadeh, A.; Yakobson, B.I. B80 fullerene: An ab initio prediction of geometry, stability, and electronic structure. Phys. Rev. Lett. 2007, 98, 166804. [Google Scholar] [CrossRef] [PubMed]
- Mukhopadhyay, S.; He, H.; Pandey, R.; Yap, Y.K.; Boustani, I. Novel spherical boron clusters and structural transition from 2D quasi-planar structures to 3D double-rings. J. Phys. Conf. Ser. 2009, 176, 012028. [Google Scholar] [CrossRef]
- Shen, W.; Hu, S.; Lu, X. Endohedral metallofullerenes: New structures and unseen phenomena. Chem. Eur. J. 2020, 26, 5748–5757. [Google Scholar] [CrossRef]
- Lu, X.; Feng, L.; Akasaka, T.; Nagase, S. Current status and future developments of endohedral metallofullerenes. Chem. Soc. Rev. 2012, 41, 7723–7760. [Google Scholar] [CrossRef]
- Liu, F.; Spree, L.; Krylov, D.S.; Velkos, G.; Avdoshenko, S.M.; Popov, A.A. Single-electron lanthanide-lanthanide bonds inside fullerenes toward robust redox-active molecular magnets. Acc. Chem. Res. 2019, 52, 2981–2993. [Google Scholar] [CrossRef] [PubMed]
- Hu, Z.; Yang, S. Endohedral metallofullerene molecular nanomagnets. Chem. Soc. Rev. 2024, 53, 2863–2897. [Google Scholar] [CrossRef] [PubMed]
- Shannon, R.D. Revised effective ionic radii and systematic studies of interatomic distances in halides and chalcogenides. Acta Crystallogr. A 1976, 32, 751–767. [Google Scholar] [CrossRef]
- Chen, T.T.; Li, W.L.; Chen, W.J.; Li, J.; Wang, L.S. La3: An inverse triple-decker lanthanide boron cluster. Chem. Commun. 2019, 55, 7864–7867. [Google Scholar] [CrossRef]
- Zhao, X.Y.; Yan, M.; Wei, Z.; Li, S.D. Donor–acceptor duality of the transition-metal-like B2 core in core–shell-like metallo-borospherenes La3&[B2@B17]− and La3&[B2@B18]−. RSC Adv. 2020, 10, 34225–34230. [Google Scholar]
- Jiang, Y.; Li, Z.; Wu, Y.; Wang, Z. Ln3@C80+ (Ln = lanthanide): A new class of stable metallofullerene cations with multicenter metal–metal bonding in the sub-nanometer confined space. Inorg. Chem. Front. 2022, 9, 2173–2181. [Google Scholar] [CrossRef]
- Lu, X.Q.; Gao, C.Y.; Wei, Z.; Li, S.D. Cage-like La4B24 and Core-Shell La4: Perfect spherically aromatic tetrahedral metallo-borospherenes. J. Mol. Model. 2021, 27, 1–7. [Google Scholar] [CrossRef]
- Guo, T.; Diener, M.D.; Chai, Y.; Alford, M.J.; Haufler, R.E.; McClure, S.M.; Ohno, T.; Weaver, J.H.; Scuseria, G.E.; Smalley, R.E. Uranium stabilization of C28: A tetravalent fullerene. Science 1992, 257, 1661–1664. [Google Scholar] [CrossRef]
- Xi, C.; Yang, L.; Liu, C.; You, P.; Li, L.; Jin, P. Lanthanide metals in the boron cages: Computational prediction of M@Bn (M = Eu, Gd; n = 38, 40). Int. J. Quantum Chem. 2018, 118, e25576. [Google Scholar] [CrossRef]
- Dunlap, B.I.; Haeberlen, O.D.; Roesch, N. Asymmetric localization of titanium in carbon molecule (C28). J. Phys. Chem. 1992, 96, 9095–9097. [Google Scholar] [CrossRef]
- Cao, B.; Hasegawa, M.; Okada, K.; Tomiyama, T.; Okazaki, T.; Suenaga, K.; Shinohara, H. EELS and 13C NMR characterization of pure Ti2@C80 metallofullerene. J. Am. Chem. Soc. 2001, 123, 9679–9680. [Google Scholar] [CrossRef] [PubMed]
- Cao, B.; Suenaga, K.; Okazaki, T.; Shinohara, H. Production, Isolation, and EELS Characterization of Ti2@C84 Dititanium Metallofullerenes. J. Phys. Chem. B 2002, 106, 9295–9298. [Google Scholar] [CrossRef]
- Li, F.F.; Chen, N.; Mulet-Gas, M.; Triana, V.; Murillo, J.; Rodríguez-Fortea, A.; Poblet, J.M.; Echegoyen, L. Ti2S@D3h(24109)-C78: A sulfide cluster metallofullerene containing only transition metals inside the cage. Chem. Sci. 2013, 4, 3404–3410. [Google Scholar] [CrossRef]
- Yu, P.; Shen, W.; Bao, L.; Pan, C.; Slanina, Z.; Lu, X. Trapping an unprecedented Ti3C3 unit inside the icosahedral C80 fullerene: A crystallographic survey. Chem. Sci. 2019, 10, 10925–10930. [Google Scholar] [CrossRef] [PubMed]
- Yu, P.; Bao, L.; Yang, L.; Hao, D.; Jin, P.; Shen, W.; Fang, H.; Akasaka, T.; Lu, X. Crystallographic characterization of Ti2C2@D3h(5)-C78, Ti2C2@C3v(8)-C82, and Ti2C2@Cs(6)-C82: Identification of unsupported Ti2C2 cluster with cage-dependent configurations. Inorg. Chem. 2020, 59, 9416–9423. [Google Scholar] [CrossRef] [PubMed]
- Guan, R.; Chen, Z.C.; Huang, J.; Tian, H.R.; Xin, J.; Ying, S.W.; Chen, M.; Zhang, Q.; Li, Q.; Xie, S.Y.; et al. Self-driven carbon atom implantation into fullerene embedding metal–carbon cluster. Proc. Natl. Acad. Sci. USA 2022, 119, e2202563119. [Google Scholar] [CrossRef] [PubMed]
- Johnson, R.D.; De Vries, M.S.; Salem, J.; Bethune, D.S.; Yannoni, C.S. Electron paramagnetic resonance studies of lanthanum-containing C82. Nature 1992, 355, 239–240. [Google Scholar] [CrossRef]
- Alvarez, L.; Pichler, T.; Georgi, P.; Schwieger, T.; Peisert, H.; Dunsch, L.; Hu, Z.; Knupfer, M.; Fink, J.; Bressler, P.; et al. Electronic structure of pristine and intercalated Sc3N@C80 metallofullerene. Phys. Rev. B 2002, 66, 035107. [Google Scholar] [CrossRef]
- Campanera, J.M.; Bo, C.; Olmstead, M.M.; Balch, A.L.; Poblet, J.M. Bonding within the endohedral fullerenes Sc3N@C78 and Sc3N@C80 as determined by density functional calculations and reexamination of the crystal structure of Sc3N@C78Co(OEP) 1.5(C6H6)0.3(CHCl3). J. Phys. Chem. A 2002, 106, 12356–12364. [Google Scholar] [CrossRef]
- Macchi, P.; Sironi, A. Chemical bonding in transition metal carbonyl clusters: Complementary analysis of theoretical and experimental electron densities. Coord. Chem. Rev. 2003, 238–239, 383–412. [Google Scholar] [CrossRef]
- Popov, A.A.; Dunsch, L. Bonding in endohedral metallofullerenes as studied by quantum theory of atoms in molecules. Chem. Eur. J. 2009, 15, 9707–9729. [Google Scholar] [CrossRef] [PubMed]
- Romanescu, C.; Galeev, T.R.; Li, W.L.; Boldyrev, A.I.; Wang, L.S. Aromatic metal-centered monocyclic boron rings: Co©− and Ru©−. Angew. Chem. Int. Ed. 2011, 50, 9334–9337. [Google Scholar] [CrossRef]
- Chen, T.T.; Li, W.L.; Bai, H.; Chen, W.J.; Dong, X.R.; Li, J.; Wang, L.S. Re©− and Re©−: New members of the transition-metal-centered borometallic molecular wheel family. J. Phys. Chem. A 2019, 123, 5317–5324. [Google Scholar] [CrossRef] [PubMed]
- Romanescu, C.; Galeev, T.R.; Li, W.L.; Boldyrev, A.I.; Wang, L.S. Transition-metal-centered monocyclic boron wheel clusters (M©Bn): A new class of aromatic borometallic compounds. Acc. Chem. Res. 2013, 46, 350–358. [Google Scholar] [CrossRef]
- Popov, I.A.; Li, W.L.; Piazza, Z.A.; Boldyrev, A.I.; Wang, L.S. Complexes between planar boron clusters and transition metals: A photoelectron spectroscopy and ab initio study of and . J. Phys. Chem. A 2014, 118, 8098–8105. [Google Scholar] [CrossRef]
- Popov, I.A.; Jian, T.; Lopez, G.V.; Boldyrev, A.I.; Wang, L.S. Cobalt-centred boron molecular drums with the highest coordination number in the CoB16− cluster. Nat. Commun. 2015, 6, 8654. [Google Scholar] [CrossRef]
- Jian, T.; Li, W.L.; Popov, I.A.; Lopez, G.V.; Chen, X.; Boldyrev, A.I.; Li, J.; Wang, L.S. Manganese-centered tubular boron cluster–MnB16−: A new class of transition-metal molecules. J. Chem. Phys. 2016, 144, 154310. [Google Scholar] [CrossRef] [PubMed]
- Jian, T.; Li, W.L.; Chen, X.; Chen, T.T.; Lopez, G.V.; Li, J.; Wang, L.S. Competition between drum and quasi-planar structures in RhB18−: Motifs for metallo-boronanotubes and metallo-borophenes. Chem. Sci. 2016, 7, 7020–7027. [Google Scholar] [CrossRef]
- Li, W.L.; Jian, T.; Chen, X.; Li, H.R.; Chen, T.T.; Luo, X.M.; Li, S.D.; Li, J.; Wang, L.S. Observation of a metal-centered B2-Ta@B18− tubular molecular rotor and a perfect Ta@B20− boron drum with the record coordination number of twenty. Chem. Commun. 2017, 53, 1587–1590. [Google Scholar] [CrossRef]
- Yan, L. Large B7 triangles in hollow spherical trihedral metallo-borospherenes and their endohedral complexes of B20TMn (TM = Sc, Y; n = 3, 4): A theoretical characterization. Inorg. Chem. 2022, 61, 10652–10660. [Google Scholar] [CrossRef] [PubMed]
- Li, H.R.; Liu, H.; Lu, X.Q.; Zan, W.Y.; Tian, X.X.; Lu, H.G.; Wu, Y.B.; Mu, Y.W.; Li, S.D. Cage-like Ta@Bnq complexes (n = 23–28, q = −1 − +3) in 18-electron configurations with the highest coordination number of twenty-eight. Nanoscale 2018, 10, 7451–7456. [Google Scholar] [CrossRef] [PubMed]
- Li, H.R.; Liu, H.; Tian, X.X.; Zan, W.Y.; Mu, Y.W.; Lu, H.G.; Li, J.; Wang, Y.K.; Li, S.D. Structural transition in metal-centered boron clusters: From tubular molecular rotors Ta@B21 and Ta@B22+ to cage-like endohedral metalloborospherene Ta@B22−. Phys. Chem. Chem. Phys. 2017, 19, 27025–27030. [Google Scholar] [CrossRef] [PubMed]
- Li, H.R.; Tian, X.X.; Luo, X.M.; Yan, M.; Mu, Y.W.; Lu, H.G.; Li, S.D. Heteroborospherene clusters Nin∈B40 (n = 1–4) and heteroborophene monolayers Ni2∈B14 with planar heptacoordinate transition-metal centers in η7-B7 heptagons. Sci. Rep. 2017, 7, 5701. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhao, X.Y.; Yan, M.; Li, S.D. From inverse sandwich Ta2 and Ta2B8 to spherical trihedral Ta3: Prediction of the smallest metallo-borospherene. RSC Adv. 2020, 10, 29320–29325. [Google Scholar] [CrossRef] [PubMed]
- Bai, H.; Chen, Q.; Zhai, H.J.; Li, S.D. Endohedral and exohedral metalloborospherenes: M@B40 (M = Ca, Sr) and M&B40 (M = Be, Mg). Angew. Chem. Int. Ed. 2015, 54, 941–945. [Google Scholar]
- Yan, L. Expanded spherical trihedral metallo-borospherenes of transition-metal doped boron clusters: TM3B15q (TM = Zr, Hf; q = −1, 0, +1). Results Phys. 2022, 33, 105214. [Google Scholar] [CrossRef]
- Li, C.G.; Shen, Z.G.; Zhang, J.; Cui, Y.Q.; Li, J.J.; Xue, H.Y.; Li, H.F.; Ren, B.Z.; Hu, Y.F. Analysis of the structures, stabilities and electronic properties of MTa@B16− (M = V, Cr, Mn, Fe, Co, Ni) clusters and assemblies. New J. Chem. 2020, 44, 5109–5119. [Google Scholar] [CrossRef]
- Zhang, Y.; Lu, X.Q.; Yan, M.; Li, S.D. Perfect spherical tetrahedral metallo-borospherene Ta4B18 as a superatom following the 18-electron rule. ACS Omega 2021, 6, 10991–10996. [Google Scholar] [CrossRef] [PubMed]
- Li, S.X.; Yang, Y.J.; Chen, D.L.; Long, Z.W. Structures, and electronic and spectral properties of single-atom transition metal-doped boron clusters (M = Sc, Ti, V, Cr, Mn, Fe, Co, and Ni). RSC Adv. 2022, 12, 16706–16716. [Google Scholar] [CrossRef]
- An, Y.; Zhang, M.; Wu, D.; Fu, Z.; Wang, T.; Xia, C. Electronic transport properties of the first all-boron fullerene B40 and its metallofullerene Sr@ B40. Phys. Chem. Chem. Phys. 2016, 18, 12024–12028. [Google Scholar] [CrossRef]
- Fa, W.; Chen, S.; Pande, S.; Zeng, X.C. Stability of metal-encapsulating boron fullerene B40. J. Phys. Chem. A 2015, 119, 11208–11214. [Google Scholar] [CrossRef]
- Jin, P.; Yang, L.; Liu, C.; Hou, Q.; Li, L. Computational prediction of the endohedral metalloborofullerenes Tin@B40 (n = 1, 2). Theor. Chem. Acc. 2017, 136, 1–12. [Google Scholar] [CrossRef]
- Mikheev, N. Lower oxidation states of lanthanides and actinides. Inorg. Chim. Acta. 1984, 94, 241–248. [Google Scholar] [CrossRef]
- MacDonald, M.R.; Fieser, M.E.; Bates, J.E.; Ziller, J.W.; Furche, F.; Evans, W.J. Identification of the +2 oxidation state for uranium in a crystalline molecular complex, [K(2.2.2-Cryptand)][(C5H4SiMe3)3U]. J. Am. Chem. Soc. 2013, 135, 13310–13313. [Google Scholar] [CrossRef] [PubMed]
- La Pierre, H.S.; Scheurer, A.; Heinemann, F.W.; Hieringer, W.; Meyer, K. Synthesis and characterization of a uranium(II) monoarene complex supported by δ backbonding. Angew. Chem. Int. Ed. 2014, 53, 7158–7162. [Google Scholar] [CrossRef] [PubMed]
- Hayton, T.W. Recent developments in actinide–ligand multiple bonding. Chem. Commun. 2013, 49, 2956–2973. [Google Scholar] [CrossRef] [PubMed]
- Akiyama, K.; Zhao, Y.; Sueki, K.; Tsukada, K.; Haba, H.; Nagame, Y.; Kodama, T.; Suzuki, S.; Ohtsuki, T.; Sakaguchi, M.; et al. Isolation and characterization of light actinide metallofullerenes. J. Am. Chem. Soc. 2001, 123, 181–182. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, W.; Feng, L.; Chen, X.; Hansen, A.; Grimme, S.; Fortier, S.; Sergentu, D.C.; Duignan, T.J.; Autschbach, J.; et al. A diuranium carbide cluster stabilized inside a C80 fullerene cage. Nat. Commun. 2018, 9, 2753. [Google Scholar] [CrossRef]
- Zhuang, J.; Abella, L.; Sergentu, D.C.; Yao, Y.R.; Jin, M.; Yang, W.; Zhang, X.; Li, X.; Zhang, D.; Zhao, Y.; et al. Diuranium(IV) carbide cluster U2C2 stabilized inside fullerene cages. J. Am. Chem. Soc. 2019, 141, 20249–20260. [Google Scholar] [CrossRef]
- Yao, Y.R.; Qiu, J.; Zheng, L.; Jiang, H.; Xia, Y.; Chen, N. Endohedral Fullerenes. In Atomically Precise Nanochemistry; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2023; Chapter 11; pp. 331–371. [Google Scholar]
- Meng, Q.; Abella, L.; Yang, W.; Yao, Y.R.; Liu, X.; Zhuang, J.; Li, X.; Echegoyen, L.; Autschbach, J.; Chen, N. UCN@Cs(6)-C82: An encapsulated triangular UCN Cluster with ambiguous U oxidation state [U(III) versus U(I)]. J. Am. Chem. Soc. 2021, 143, 16226–16234. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.X.; Chen, M.; Ao, B. Theoretical studies on the oxidation states and electronic structures of actinide-borides: AnB12 (An = Th–Cm) clusters. Phys. Chem. Chem. Phys. 2018, 20, 23856–23863. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Zhang, N.X.; Wang, C.Z.; Wu, Q.Y.; Lan, J.H.; Chai, Z.F.; Nie, C.M.; Shi, W.Q. Theoretical probing of twenty-coordinate actinide-centered boron molecular drums. Phys. Chem. Chem. Phys. 2021, 23, 26967–26973. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Wang, C.Z.; Wu, Q.Y.; Lan, J.H.; Chai, Z.F.; Nie, C.M.; Shi, W.Q. Construction of the largest metal-centered double-ring tubular boron clusters based on actinide metal doping. J. Phys. Chem. A 2022, 126, 3445–3451. [Google Scholar] [CrossRef] [PubMed]
- Hu, S.X.; Zhang, P.; Zou, W.; Zhang, P. New theoretical insights into high-coordination-number complexes in actinides-centered borane. Nanoscale 2020, 12, 15054–15065. [Google Scholar] [CrossRef]
- Li, W.L.; Chen, T.T.; Chen, W.J.; Li, J.; Wang, L.S. Monovalent lanthanide (I) in borozene complexes. Nat. Commun. 2021, 12, 6467. [Google Scholar] [CrossRef]
- Wang, B.; Li, W.L. Revisiting the quasi-aromaticity in polynuclear metal chalcogenide clusters and their derivative “cluster-assembly” crystalline structures. Phys. Chem. Chem. Phys. 2024, 26, 17370–17382. [Google Scholar] [CrossRef] [PubMed]
- Wang, C.Z.; Bo, T.; Lan, J.H.; Wu, Q.Y.; Chai, Z.F.; Gibson, J.K.; Shi, W.Q. Ultrastable actinide endohedral borospherenes. Chem. Commun. 2018, 54, 2248–2251. [Google Scholar] [CrossRef] [PubMed]
- Yu, T.; Gao, Y.; Xu, D.; Wang, Z. Actinide endohedral boron clusters: A closed-shell electronic structure of U@B40. Nano Res. 2018, 11, 354–359. [Google Scholar] [CrossRef]
- Zhang, N.; Li, A.; Wang, C.; Wu, Q.; Lan, J.; Chai, Z.; Zhao, Y.; Shi, W. Theoretical prediction of chiral actinide endohedral borospherenes. New J. Chem. 2021, 45, 6803–6810. [Google Scholar] [CrossRef]
- Zhang, N.X.; Wang, C.Z.; Lan, J.H.; Wu, Q.Y.; Chai, Z.F.; Shi, W.Q. Actinide-doped boron clusters: From borophenes to borospherenes. Phys. Chem. Chem. Phys. 2022, 24, 29705–29711. [Google Scholar] [CrossRef] [PubMed]
- Wales, D.J.; Doye, J.P.K. Global optimization by basin-hopping and the lowest energy structures of Lennard-Jones clusters containing up to 110 atoms. J. Phys. Chem. A 1997, 101, 5111–5116. [Google Scholar] [CrossRef]
- Zhao, Y.; Chen, X.; Li, J. TGMin: A global-minimum structure search program based on a constrained basin-hopping algorithm. Nano Res. 2017, 10, 3407–3420. [Google Scholar] [CrossRef]
- White, R.P.; Mayne, H.R. An investigation of two approaches to basin hopping minimization for atomic and molecular clusters. Chem. Phys. Lett. 1998, 289, 463–468. [Google Scholar] [CrossRef]
- Liberti, L.; Maculan, N. Global Optimization: From Theory to Implementation; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006; Volume 84. [Google Scholar]
- Chen, X.; Zhao, Y.F.; Zhang, Y.Y.; Li, J. TGMin: An efficient global minimum searching program for free and surface-supported clusters. J. Comput. Chem. 2019, 40, 1105–1112. [Google Scholar] [CrossRef] [PubMed]
- Shang, C.; Liu, Z.P. Constrained Broyden minimization combined with the dimer method for locating transition state of complex reactions. J. Chem. Theory Comput. 2010, 6, 1136–1144. [Google Scholar] [CrossRef]
- Shang, C.; Liu, Z.P. Constrained Broyden dimer method with bias potential for exploring potential energy surface of multistep reaction process. J. Chem. Theory Comput. 2012, 8, 2215–2222. [Google Scholar] [CrossRef] [PubMed]
- Shang, C.; Liu, Z.P. Stochastic surface walking method for structure prediction and pathway searching. J. Chem. Theory Comput. 2013, 9, 1838–1845. [Google Scholar] [CrossRef] [PubMed]
- Averkiev, B. Geometry and Electronic Structure of Doped Clusters via the Coalescence Kick Method; Utah State University: Logan, UT, USA, 2009. [Google Scholar]
- Saunders, M. Stochastic search for isomers on a quantum mechanical surface. J. Comput. Chem. 2004, 25, 621–626. [Google Scholar] [CrossRef]
- Bera, P.P.; Sattelmeyer, K.W.; Saunders, M.; Schaefer, H.F.; Schleyer, P.v.R. Mindless chemistry. J. Phys. Chem. A 2006, 110, 4287–4290. [Google Scholar] [CrossRef]
- Wang, Y.; Lv, J.; Zhu, L.; Ma, Y. Crystal structure prediction via particle-swarm optimization. Phys. Rev. B 2010, 82, 094116. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95-International Conference on Neural Networks, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Yen, G.; Lu, H. Dynamic population strategy assisted particle swarm optimization. In Proceedings of the 2003 IEEE International Symposium on Intelligent Control, Houston, TX, USA, 8 October 2003; pp. 697–702. [Google Scholar]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16 Revision C.01; Gaussian Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- ADF 2024.1, SCM. Vrije Universiteit, Amsterdam, The Netherlands. Available online: http://www.scm.com (accessed on 25 June 2024).
- te Velde, G.; Bickelhaupt, F.M.; Baerends, E.J.; Fonseca Guerra, C.; van Gisbergen, S.J.A.; Snijders, J.G.; Ziegler, T. Chemistry with ADF. J. Comput. Chem. 2001, 22, 931–967. [Google Scholar] [CrossRef]
- Behler, J.; Parrinello, M. Generalized neural-network representation of high-dimensional potential-energy surfaces. Phys. Rev. Lett. 2007, 98, 146401. [Google Scholar] [CrossRef]
- Rupp, M.; Tkatchenko, A.; Müller, K.R.; von Lilienfeld, O.A. Fast and accurate modeling of molecular atomization energies with machine learning. Phys. Rev. Lett. 2012, 108, 058301. [Google Scholar] [CrossRef] [PubMed]
- Schütt, K.T.; Arbabzadah, F.; Chmiela, S.; Müller, K.R.; Tkatchenko, A. Quantum-chemical insights from deep tensor neural networks. Nat. Commun. 2017, 8, 13890. [Google Scholar] [CrossRef] [PubMed]
- Smith, J.S.; Isayev, O.; Roitberg, A.E. ANI-1: An extensible neural network potential with DFT accuracy at force field computational cost. Chem. Sci. 2017, 8, 3192–3203. [Google Scholar] [CrossRef]
- Bartók, A.P.; Payne, M.C.; Kondor, R.; Csányi, G. Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons. Phys. Rev. Lett. 2010, 104, 136403. [Google Scholar] [CrossRef] [PubMed]
- Chmiela, S.; Tkatchenko, A.; Sauceda, H.E.; Poltavsky, I.; Schütt, K.T.; Müller, K.R. Machine learning of accurate energy-conserving molecular force fields. Sci. Adv. 2017, 3, e1603015. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Han, J.; Wang, H.; Car, R.; E, W. Deep potential molecular dynamics: A scalable Model with the accuracy of quantum mechanics. Phys. Rev. Lett. 2018, 120, 143001. [Google Scholar] [CrossRef]
- Deringer, V.L.; Caro, M.A.; Csányi, G. Machine learning interatomic potentials as emerging tools for materials science. Adv. Mat. 2019, 31, 1902765. [Google Scholar]
- Li, J.; Li, X.; Zhai, H.J.; Wang, L.S. Au20: A tetrahedral cluster. Science 2003, 299, 864–867. [Google Scholar] [CrossRef]
- Bauernschmitt, R.; Ahlrichs, R. Treatment of electronic excitations within the adiabatic approximation of time dependent density functional theory. Chem. Phys. Lett. 1996, 256, 454–464. [Google Scholar] [CrossRef]
- Li, W.L.; Liu, H.T.; Jian, T.; Lopez, G.V.; Piazza, Z.A.; Huang, D.L.; Chen, T.T.; Su, J.; Yang, P.; Chen, X.; et al. Bond-bending isomerism of Au2: Competition between covalent bonding and aurophilicity. Chem. Sci. 2016, 7, 475–481. [Google Scholar] [CrossRef]
- Gritsenko, O.; Schipper, P.; Baerends, E. Approximation of the exchange-correlation Kohn–Sham potential with a statistical average of different orbital model potentials. Chem. Phys. Lett. 1999, 302, 199–207. [Google Scholar] [CrossRef]
- Stowasser, R.; Hoffmann, R. What do the Kohn- Sham orbitals and eigenvalues mean? J. Am. Chem. Soc. 1999, 121, 3414–3420. [Google Scholar] [CrossRef]
- Mitoraj, M.P.; Michalak, A.; Ziegler, T. A combined charge and energy decomposition scheme for bond analysis. J. Chem. Theory Comput. 2009, 5, 962–975. [Google Scholar] [CrossRef]
- Frenking, G.; Matthias Bickelhaupt, F. The EDA Perspective of Chemical Bonding. In The Chemical Bond; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2014; Chapter 4; pp. 121–157. [Google Scholar]
- Zhao, L.; Hermann, M.; Schwarz, W.E.; Frenking, G. The Lewis electron-pair bonding model: Modern energy decomposition analysis. Nat. Rev. Chem. 2019, 3, 48–63. [Google Scholar] [CrossRef]
- Dong, X.; Liu, Y.Q.; Tiznado, W.; Cabellos-Quiroz, J.L.; Zhao, J.; Pan, S.; Cui, Z.H. Designing a Four-Ring Tubular Boron Motif through Metal Doping. Inorg. Chem. 2022, 61, 14553–14559. [Google Scholar] [CrossRef]
- Poater, J.; Duran, M.; Sola, M.; Silvi, B. Theoretical evaluation of electron delocalization in aromatic molecules by means of atoms in molecules (AIM) and electron localization function (ELF) topological approaches. Chem. Rev. 2005, 105, 3911–3947. [Google Scholar] [CrossRef]
- Kobayashi, K.; Nagase, S. Bonding features in endohedral metallofullerenes. Topological analysis of the electron density distribution. Chem. Phys. Lett. 1999, 302, 312–316. [Google Scholar] [CrossRef]
- Kobayashi, K.; Nagase, S. A stable unconventional structure of Sc2@C66 found by density functional calculations. Chem. Phys. Lett. 2002, 362, 373–379. [Google Scholar] [CrossRef]
- Du, J.; Jiang, G. Theoretical characterization of the endohedral metalloborospherenes M@B36 (M = Ti, Zr, Hf, Ce, Th, Pa+, U2+, Np3+, and Pu4+). J. Mol. Liq. 2020, 319, 114088. [Google Scholar] [CrossRef]
- Zubarev, D.Y.; Boldyrev, A.I. Developing paradigms of chemical bonding: Adaptive natural density partitioning. Phys. Chem. Chem. Phys. 2008, 10, 5207–5217. [Google Scholar] [CrossRef]
- Tian, J.; Xu, Z.; Shen, C.; Liu, F.; Xu, N.; Gao, H.J. One-dimensional boron nanostructures: Prediction, synthesis, characterizations, and applications. Nanoscale 2010, 2, 1375–1389. [Google Scholar] [CrossRef]
- Yin, J.; Li, J.; Hang, Y.; Yu, J.; Tai, G.; Li, X.; Zhang, Z.; Guo, W. Boron Nitride Nanostructures: Fabrication, Functionalization and Applications. Small 2016, 12, 2942–2968. [Google Scholar] [CrossRef]
- Yang, M.; Jin, H.; Sun, Z.; Gui, R. Experimental synthesis, functionalized modifications and potential applications of monoelemental zero-dimensional boron nanomaterials. J. Mater. Chem. A 2022, 10, 5111–5146. [Google Scholar] [CrossRef]
- Tan, C.; Cao, X.; Wu, X.J.; He, Q.; Yang, J.; Zhang, X.; Chen, J.; Zhao, W.; Han, S.; Nam, G.H.; et al. Recent Advances in Ultrathin Two-Dimensional Nanomaterials. Chem. Rev. 2017, 117, 6225–6331. [Google Scholar] [CrossRef]
- Rycenga, M.; Camargo, P.H.C.; Xia, Y. Template-assisted self-assembly: A versatile approach to complex micro- and nanostructures. Soft Matter 2009, 5, 1129–1136. [Google Scholar]




| Species | Symmetry | Doping Mechanism |
|---|---|---|
| [75] | exohedral | |
| [77] | exohedral | |
| [77] | exohedral | |
| [77] | exohedral | |
| [77] | exohedral | |
| [77] | exohedral | |
| [77] | exohedral | |
| [78] | endohedral | |
| [78] | endohedral | |
| [78] | endohedral | |
| [78] | endohedral | |
| [78] | endohedral | |
| [78] | endohedral | |
| [79] | exohedral | |
| [79] | exohedral | |
| [71] | exohedral | |
| [71] | exohedral | |
| [71] | exohedral | |
| [71] | exohedral | |
| [71] | exohedral | |
| [71] | exohedral | |
| [71] | exohedral | |
| [71] | exohedral | |
| [71] | exohedral | |
| [80] | endohedral | |
| [80] | endohedral | |
| [80] | endohedral | |
| [80] | endohedral | |
| [80] | endohedral | |
| [80] | endohedral | |
| [80] | endohedral | |
| [76,81] | endohedral | |
| [76,81] | endohedral | |
| [76,81] | exohedral | |
| [76,81] | exohedral | |
| [82] | exohedral | |
| [82] | endohedral | |
| [82] | exohedral | |
| [82] | endohedral | |
| [82] | exohedral | |
| [83] | endohedral | |
| [83] | endohedral |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Burkhardt, J.; Prescott, H.; Li, W.-L. Metalloborospherene Analogs to Metallofullerene. Inorganics 2024, 12, 193. https://doi.org/10.3390/inorganics12070193
Burkhardt J, Prescott H, Li W-L. Metalloborospherene Analogs to Metallofullerene. Inorganics. 2024; 12(7):193. https://doi.org/10.3390/inorganics12070193
Chicago/Turabian StyleBurkhardt, Jordan, Hayden Prescott, and Wan-Lu Li. 2024. "Metalloborospherene Analogs to Metallofullerene" Inorganics 12, no. 7: 193. https://doi.org/10.3390/inorganics12070193
APA StyleBurkhardt, J., Prescott, H., & Li, W.-L. (2024). Metalloborospherene Analogs to Metallofullerene. Inorganics, 12(7), 193. https://doi.org/10.3390/inorganics12070193










