Heteroleptic β-Diketonate Fe3+ Complex: Spin-Crossover and Optical Characteristics
Abstract
1. Introduction
2. Results and Discussion
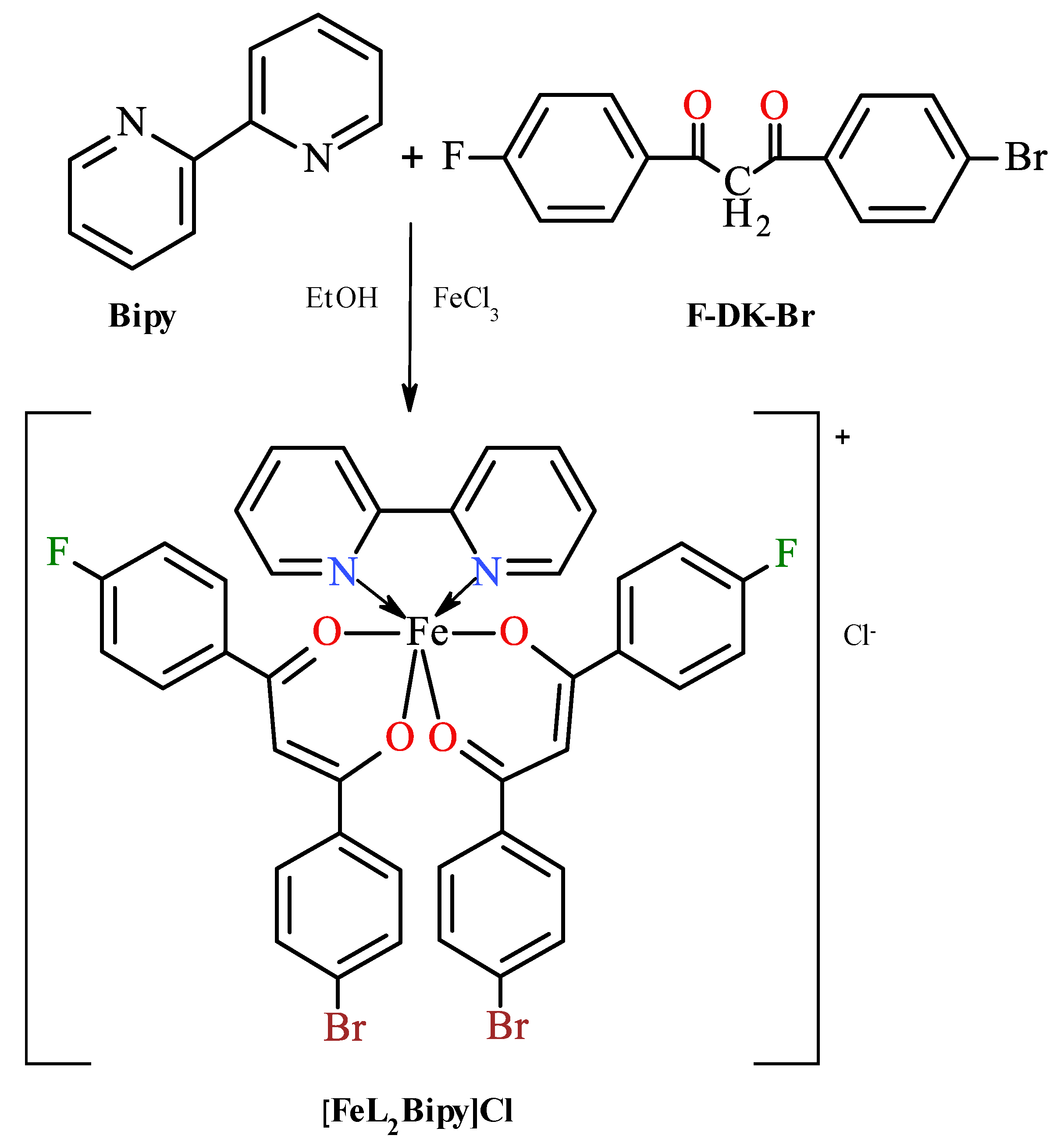
2.1. Synthesis of Compounds
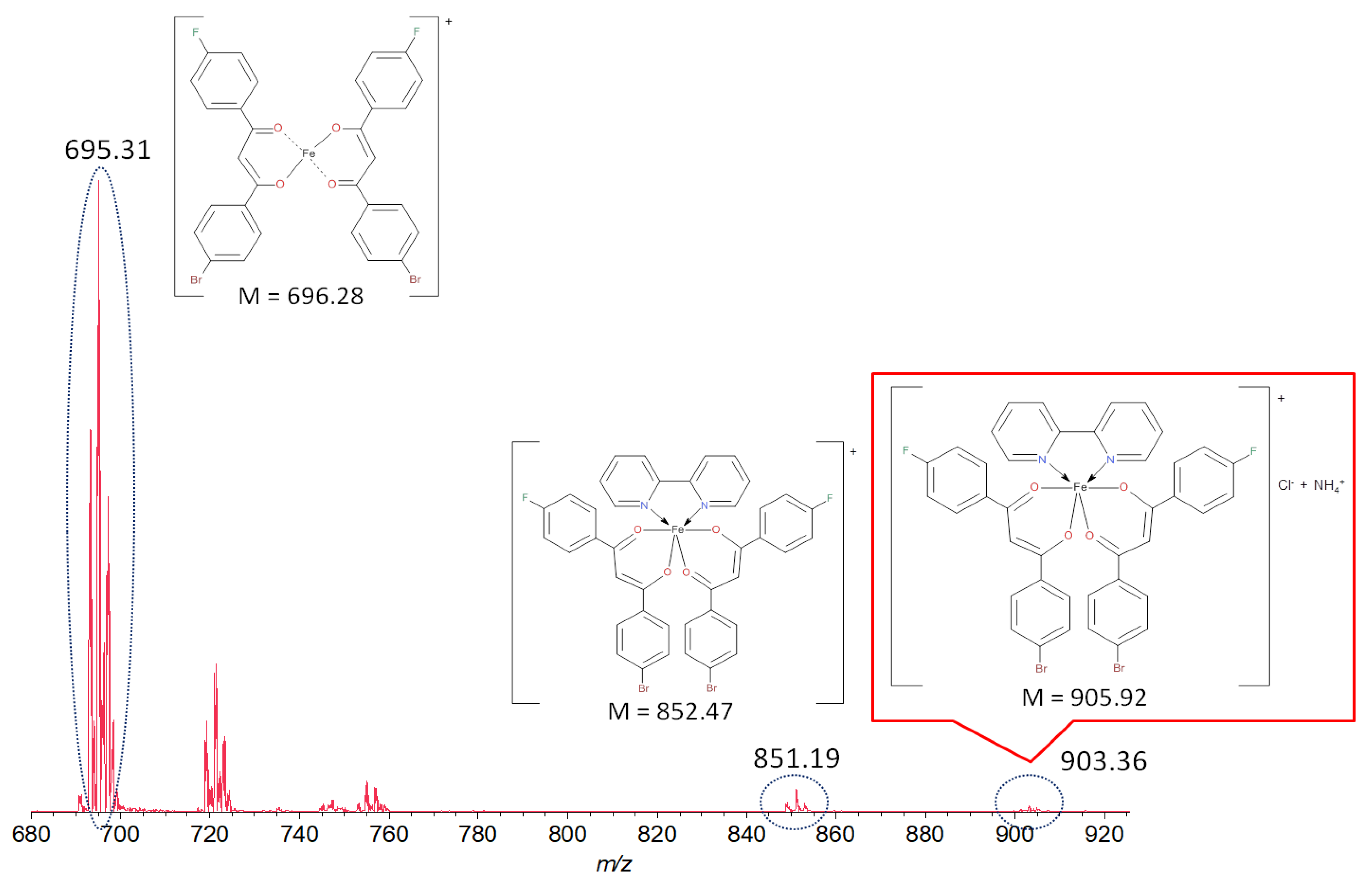
2.2. Spectral Characteristics
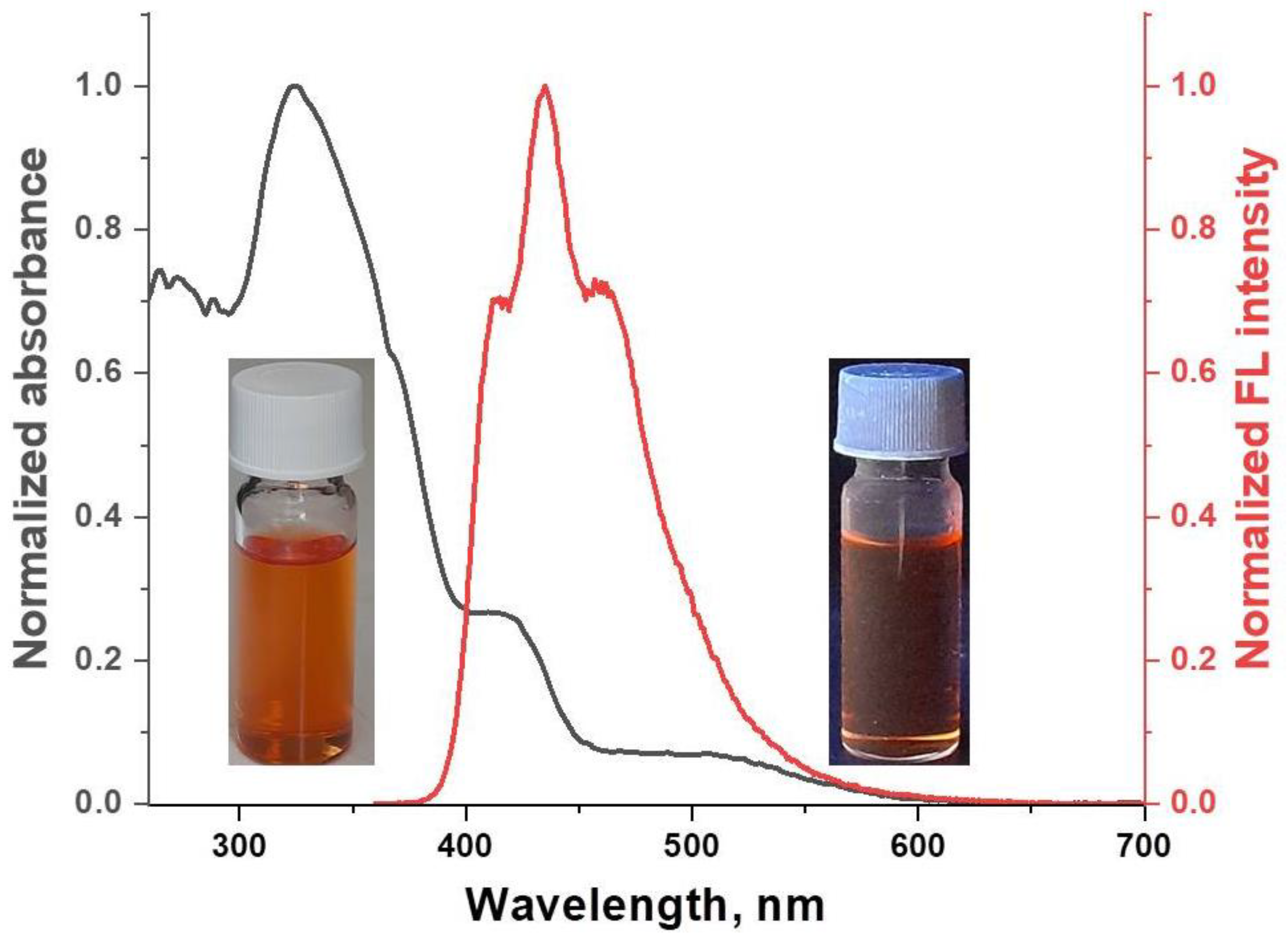
2.3. Optical Properties
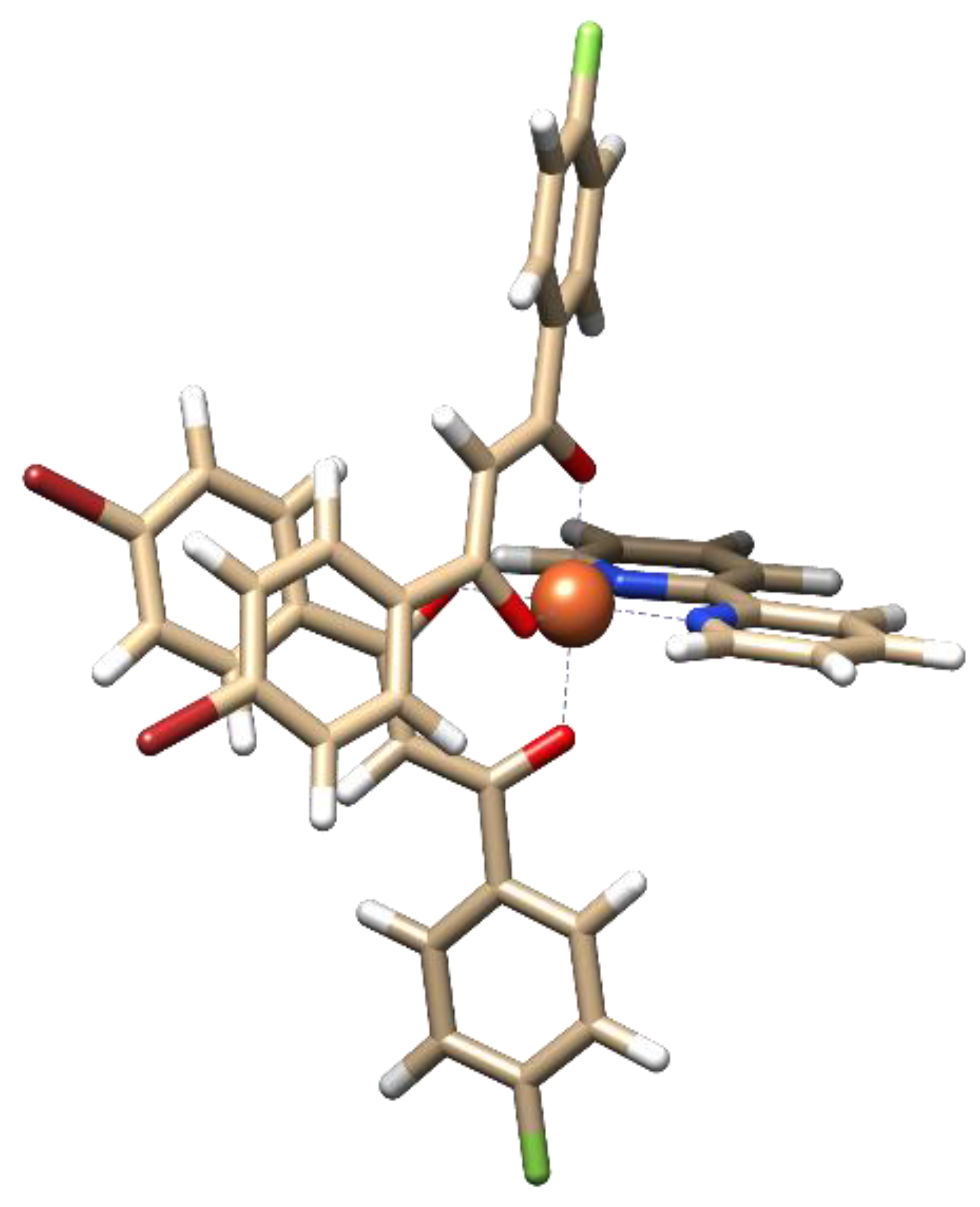
2.4. DFT Calculations
2.5. Magnetic and Resonance Properties
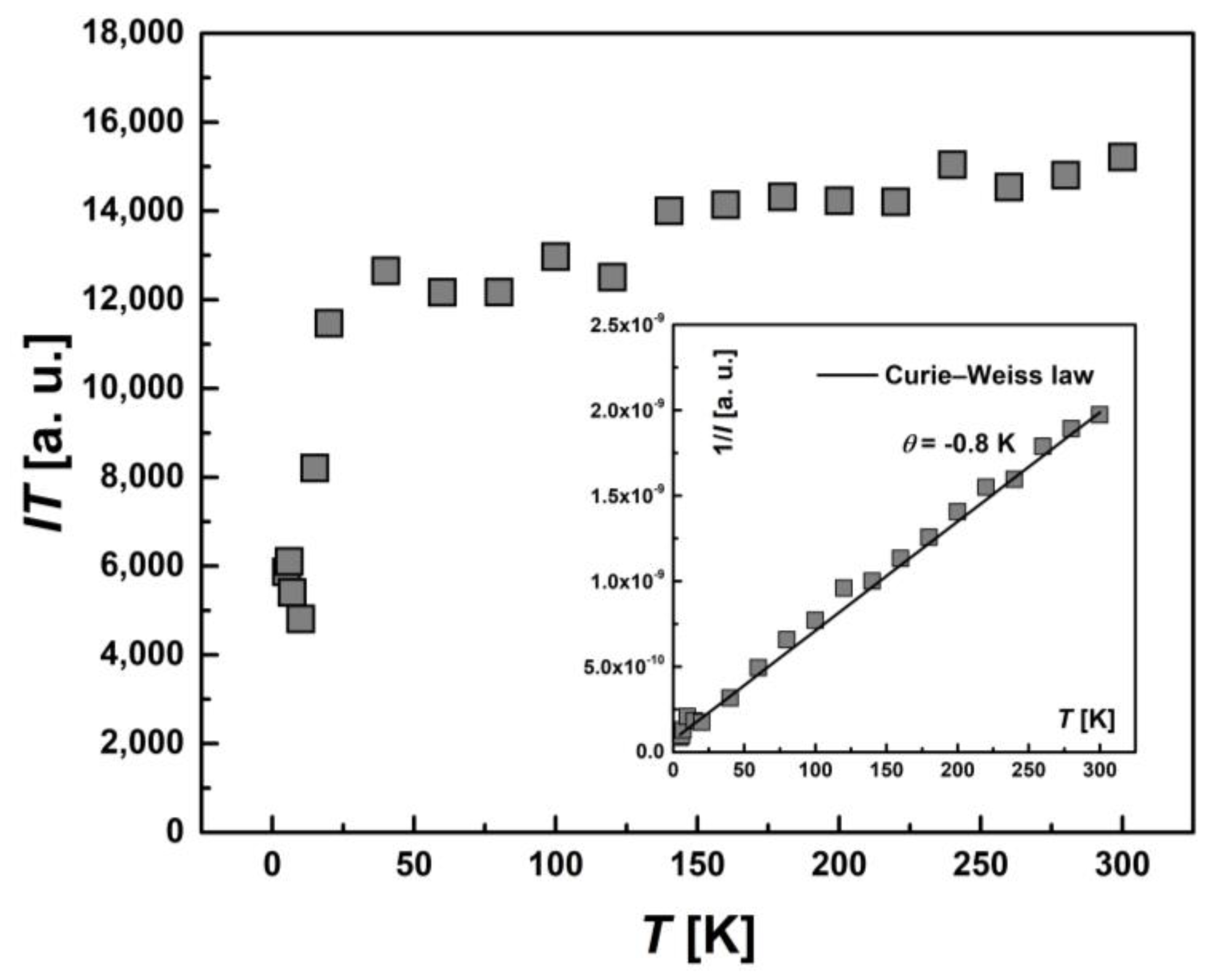
2.5.1. SQUID Magnetometry
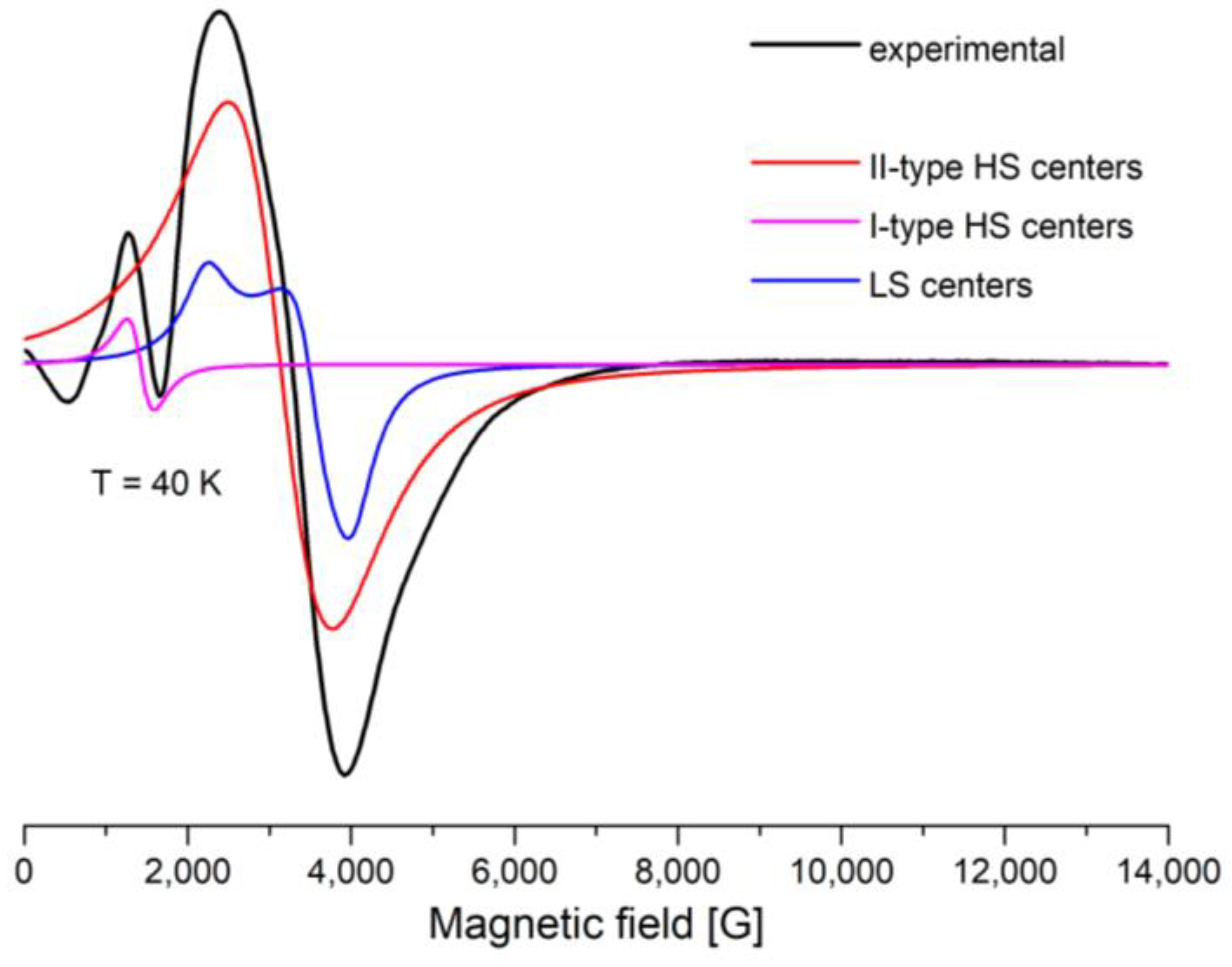
2.5.2. EPR Spectroscopy
3. Experimental Section
3.1. Materials
3.2. Methods
3.3. Chemical Synthesis
3.3.1. Synthesis of 1-(4-Fluoro-phenyl)-3-(4-bromo-phenyl)-propane-1,3-dione, F-DK-Br (Ligand) [41]
3.3.2. Synthesis of Iron(III) Bis[1-(4-fluoro-phenyl)-3-(4-bromo-phenyl)propane-1,3-dionate](2,2′-bipyridine) chloride,[FeL2Bipy]Cl
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Vigato, P.A.; Peruzzo, V.; Tamburini, S. The evolution of β-diketone or β-diketophenol ligands and related complexes. Coord. Chem. Rev. 2009, 253, 1099–1201. [Google Scholar] [CrossRef]
- Gaspar, R.D.L.; Fortes, P.R.; Mazali, I.O.; Sigoli, F.A.; Raimundo, I.M., Jr. Optical Temperature Sensors Based on Europium(III) Beta-Diketonate Complexes Chemically Bonded to Functionalized Polydimethylsiloxane. Chem. Sel. 2018, 3, 10491–10501. [Google Scholar] [CrossRef]
- Bezzubov, S.I.; Zharinova, I.S.; Khusyainova, A.A.; Kiselev, Y.M.; Taydakov, I.V.; Varaksina, E.A.; Metlin, M.T.; Tobohova, A.S.; Korshunov, V.M.; Kozyukhin, S.A.; et al. Aromatic β-Diketone as a Novel Anchoring Ligand in Iridium(III) Complexes for Dye-Sensitized Solar Cells. Eur. J. Inorg. Chem. 2020, 2020, 3277–3286. [Google Scholar] [CrossRef]
- Pousaneh, E.; Korb, M.; Assim, K.; Rüffer, T.; Dzhagan, V.; Noll, J.; Zahn, D.R.T.; Schulz, S.E.; Lang, H. Iron(III) β-diketonates: CVD precursors for iron oxide film formation. Inorg. Chim. Acta 2019, 487, 1–8. [Google Scholar] [CrossRef]
- Martins, J.P.; Martín-Ramos, P.; Coya, C.; Ramos Silva, M.; Eusebio, M.E.S.; de Andrés, A.; Álvarez, Á.L.; Martín-Gil, J. Highly luminescent pure-red-emitting fluorinated β-diketonate europium(III) complex for full solution-processed OLEDs. J. Lumin. 2015, 159, 17–25. [Google Scholar] [CrossRef]
- Wang, R.; Gao, H.; Yu, R.; Jia, H.; Ma, Z.; He, Z.; Zhang, Y.; Yang, J.; Zhang, L.; Tan, Z. β-Diketone Coordination Strategy for Highly Efficient and Stable Pb–Sn Mixed Perovskite Solar Cells. J. Phys. Chem. Lett. 2021, 12, 11772–11778. [Google Scholar] [CrossRef]
- Nehra, K.; Dalal, A.; Hooda, A.; Bhagwan, S.; Saini, R.K.; Mari, B.; Kumar, S.; Singh, D. Lanthanides β-diketonate complexes as energy-efficient emissive materials: A review. J. Mol. Struct. 2022, 1249, 131531. [Google Scholar] [CrossRef]
- Schwieger, S.; Herzog, R.; Wagner, C.; Steinborn, D. Platina-β-diketones as catalysts for hydrosilylation and their reactivity towards hydrosilanes. J. Organomet. Chem. 2009, 694, 3548–3558. [Google Scholar] [CrossRef]
- Wolf, L.; Butter, E.; Weinelt, H. Über die Darstellung höherer β-Diketonkomplexe des Eisens, Rutheniums und Rhodiums. Z. Anorg. Und allgemeine Chemie 1960, 306, 87–93. [Google Scholar] [CrossRef]
- Eng, S.J.; Motekaitis, R.J.; Martell, A.E. The effect of end-group substitutions and use of a mixed solvent system on β-diketones and their iron complexes. Inorg. Chim. Acta 1998, 278, 170–177. [Google Scholar] [CrossRef]
- Twigg, M.V.; Burgess, J. Iron. In Comprehensive Coordination Chemistry II. From Biology to Nanotechnology, Volume 5 (Transition Metal Groups 7 and 8); McCleverty, J.A., Meyer, T.J., Eds.; Elsevier: Amsterdam, The Netherlands, 2003; p. 500. [Google Scholar]
- Matsushita, M.M.; Yasuda, T.; Kawano, R.; Kawai, T.; Iyoda, T. Intramolecular Magnetic Interaction of Phenylene-Linked Bis-β-diketone Metal Complexes. Chem. Lett. 2000, 29, 812–813. [Google Scholar] [CrossRef]
- Guedes, G.P.; Florencio, A.S.; Carneiro, J.W.d.M.; Vaz, M.G.F. Mononuclear and dinuclear iron(III) compounds with β-diketonate ligands: Synthesis, magnetic behavior and DFT calculations. Solid State Sci. 2013, 18, 10–16. [Google Scholar] [CrossRef]
- Nihei, M.; Shiga, T.; Maeda, Y.; Oshio, H. Spin crossover iron(III) complexes. Coord. Chem. Rev. 2007, 251, 2606–2621. [Google Scholar] [CrossRef]
- Dey, B.; Mondal, A.; Konar, S. Effect of ligand field strength on the spin crossover behavior in 5-X-SalEen (X=Me, Br and OMe) based Fe(III) complexes. Chem. Asian J. 2020, 15, 1709–1721. [Google Scholar] [CrossRef]
- Kumar, K.S.; Bayeh, Y.; Gebretsadik, Y.; Elemo, F.; Gebrezgiabher, M.; Thomas, M.; Ruben, M. Spin-crossover in iron(II)-Schiff base complexes. Dalton Trans. 2019, 48, 15321–15337. [Google Scholar] [CrossRef]
- Gruzdev, M.S.; Domracheva, N.E.; Chervonova, U.V.; Kolker, A.M.; Golubeva, A.S. Bis-chelate Fe(III) complex of an azomethine at the focal point of a branched ester functionalized with cyclohexylbenzoic acid. J. Coord. Chem. 2012, 65, 1812–1820. [Google Scholar] [CrossRef]
- Muraškova, V.; Eigner, V.; Dušek, M.; Sedmidubsky, D. Iron(III) and cobalt(III) complexes with pentadentate pyridoxal Schiff base ligand—Structure, spectral, electrochemical, magnetic properties and DFT calculations. Polyhedron 2021, 197, 115019. [Google Scholar] [CrossRef]
- Gentili, D.; Cavallini, M. Wet-lithographic processing of coordination compounds. Coord. Chem. Rev. 2013, 257, 2456–2467. [Google Scholar] [CrossRef]
- Juráková, J.; Midlíková, J.D.; Hrubý, J.; Kliuikov, A.; Santana, V.T.; Pavlik, J.; Moncoľ, J.; Čižmár, E.; Orlita, M.; Mohelský, I.; et al. Pentacoordinate cobalt(II) single ion magnets with pendant alkyl chains: Shall we go for chloride or bromide? Inorg. Chem. Front. 2022, 9, 1179–1194. [Google Scholar] [CrossRef]
- Cavallini, M.; Gentili, D.; Greco, P.; Valle, F.; Biscarini, F. Micro- and nanopatterning by lithographically controlled wetting. Nat. Protoc. 2012, 7, 1668–1676. [Google Scholar] [CrossRef]
- Mallah, T.; Cavallini, M. Surfaces, thin films and patterning of spin crossover compounds. C. R. Chimie 2018, 21, 1270–1286. [Google Scholar] [CrossRef]
- Claisen, L. Uber die Einführung von Säureradicalen in Ketone. Ber. Dtsch. Chem. Ges. 1887, 20, 655–657. [Google Scholar] [CrossRef]
- Kaes, C.; Katz, A.; Hosseini, M.W. Bipyridine: The most widely used ligand. A review of molecules comprising at least two 2,2′-bipyridine units. Chem. Rev. 2000, 100, 3553–3590. [Google Scholar] [CrossRef] [PubMed]
- Starnovskaya, E.S.; Kopchuk, D.S.; Khasanov, A.F.; Tanya, O.S.; Santra, S.; Giri, K.; Rahman, M.; Kovalev, I.S.; Zyryanov, G.V.; Majee, A.; et al. Synthesis and photophysics of new unsymmetrically substituted 5,5′-diaryl-2,2′-bypiridine-based “push-pull” fluorophores. Dye. Pigment. 2019, 162, 324–330. [Google Scholar] [CrossRef]
- Chervonova, U.V.; Bichan, N.G.; Ksenofontov, A.A.; Gruzdev, M.S. Heterofunctional β-diketones incorporating ester linkages: Mesomorphism and solvatochromic effect. J. Mol. Liq. 2025, 417, 126572. [Google Scholar] [CrossRef]
- Nakamoto, K. Infrared and Raman Spectra of Inorganic and Coordination Compounds, Part B: Applications in Coordination, Organometallic, and Bioinorganic Chemistry, 6th ed; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2009; 424p. [Google Scholar]
- Halcrow, M.A. Spin-Crossover Materials: Properties and Applications; John Wiley & Sons, Ltd.: Chicheser, UK, 2013. [Google Scholar]
- Domracheva, N.; Vorobeva, V.; Pyataev, A.; Ivanova, A. Magnetic properties of novel dendrimeric iron(III) complexes of the first generation: EPR and Mössbauer study. Appl. Magn. Reson. 2016, 47, 903–913. [Google Scholar] [CrossRef]
- Kahn, O. Molecular Magnetism; Wiley-VCH: New York, NY, USA, 1993. [Google Scholar]
- Shvachko, Y.N.; Starichenko, D.V.; Korolyov, A.V.; Yagubskii, E.B.; Kotov, A.I.; Buravov, L.I.; Lyssenko, K.A.; Zverev, V.N.; Simonov, S.V.; Zorina, L.V. The Conducting Spin-Crossover Compound Combining Fe(II) Cation Complex with TCNQ in a Fractional Reduction State. Inorg. Chem. 2016, 55, 9121–9130. [Google Scholar] [CrossRef]
- Stoll, S.; Schweiger, A. EasySpin, a comprehensive software package for spectral simulation and analysis in EPR. J. Magn. Reson. 2006, 178, 42–55. [Google Scholar] [CrossRef]
- Stoll, S. Chapter Six—CW-EPR Spectral Simulations: Solid State. Methods Enzymol. 2015, 563, 121–142. [Google Scholar] [CrossRef]
- Poole, C.P., Jr. Electron Spin Resonance: A Comprehensive Treatise on Experimental Techniques; John Wiley & Sons, Ltd.: New York, NY, USA, 1983. [Google Scholar]
- Bannwarth, C.; Ehlert, S.; Grimme, S. GFN2-xTB—An Accurate and Broadly Parametrized Self-Consistent Tight-Binding Quantum Chemical Method with Multipole Electrostatics and Density-Dependent Dispersion Contributions. J. Chem. Theory Comput. 2019, 15, 1652–1671. [Google Scholar] [CrossRef]
- Schäfer, A.; Horn, H.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets for atoms Li to Kr. J. Chem. Phys. 1992, 97, 2571–2577. [Google Scholar] [CrossRef]
- Chai, J.-D.; Head-Gordon, M. Long-range corrected hybrid density functionals with damped atom–atom dispersion corrections. Phys. Chem. Chem. Phys. 2008, 10, 6615–6620. [Google Scholar] [CrossRef] [PubMed]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Petersson, G.A.; Nakatsuji, H.; et al. Gaussian 16, Revision C.01; Gaussian, Inc.: Wallingford, CT, USA, 2016. [Google Scholar]
- Pettersen, E.F.; Goddard, T.D.; Huang, C.C.; Couch, G.S.; Greenblatt, D.M.; Meng, E.C.; Ferrin, T.E. UCSF Chimera—A visualization system for exploratory research and analysis. Comput. Chem. 2008, 25, 1605–1612. [Google Scholar] [CrossRef] [PubMed]
- Zhurko, G.A. Chemcraft—Graphical Program for Visualization of Quantum Chemistry Computations 2005, Version 1.8, Build 648. Available online: https://chemcraftprog.com (accessed on 21 April 2025).
- Chervonova, U.V.; Ksenofontov, A.A.; Gruzdev, M.S. Synthesis, Thermal, and Spectroscopic Properties of High-Temperature Photoactive Halogen-Substituted β-Boron Difluoride Diketonate. Russ. J. Phys. Chem. A 2024, 98, 3474–3480. [Google Scholar] [CrossRef]

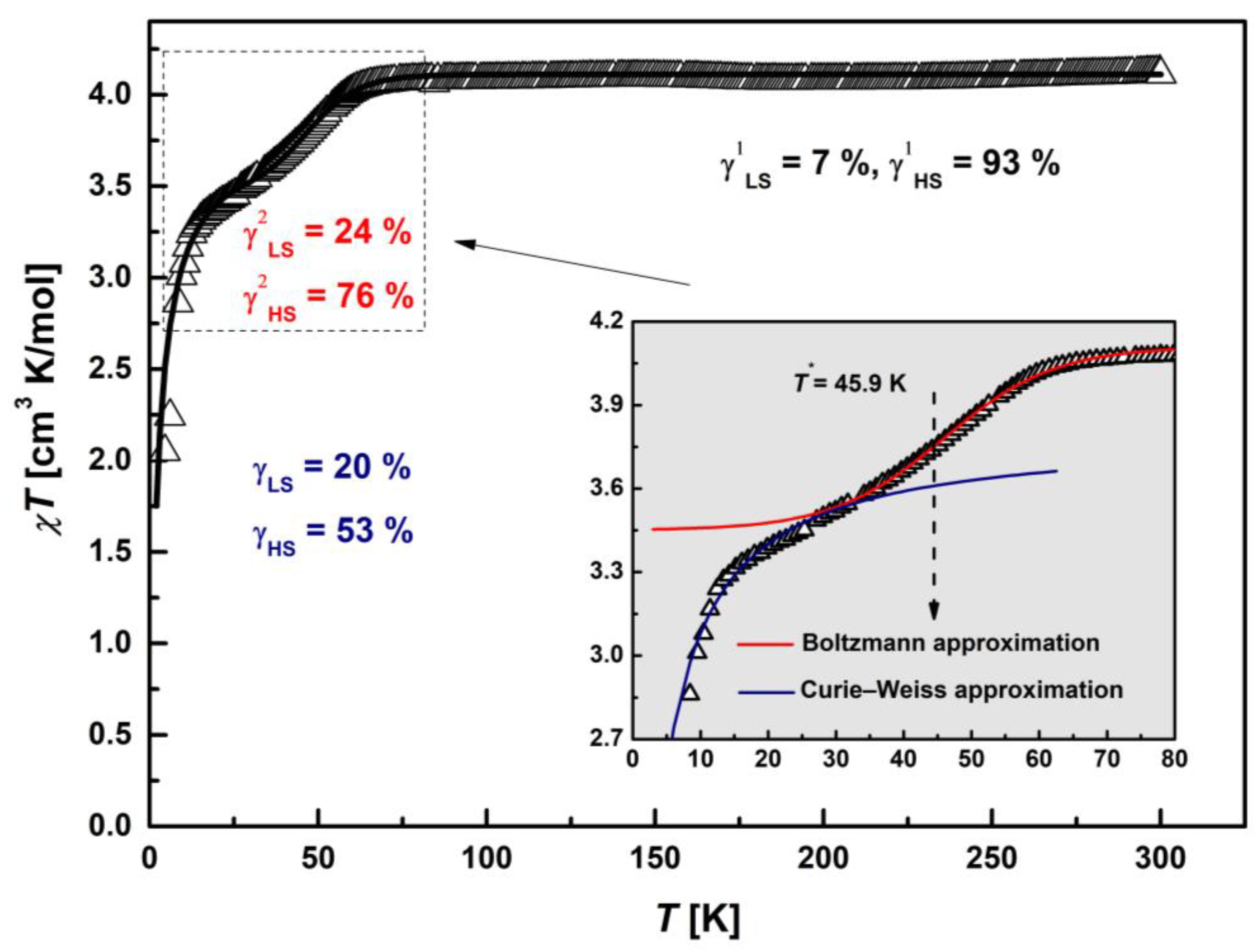

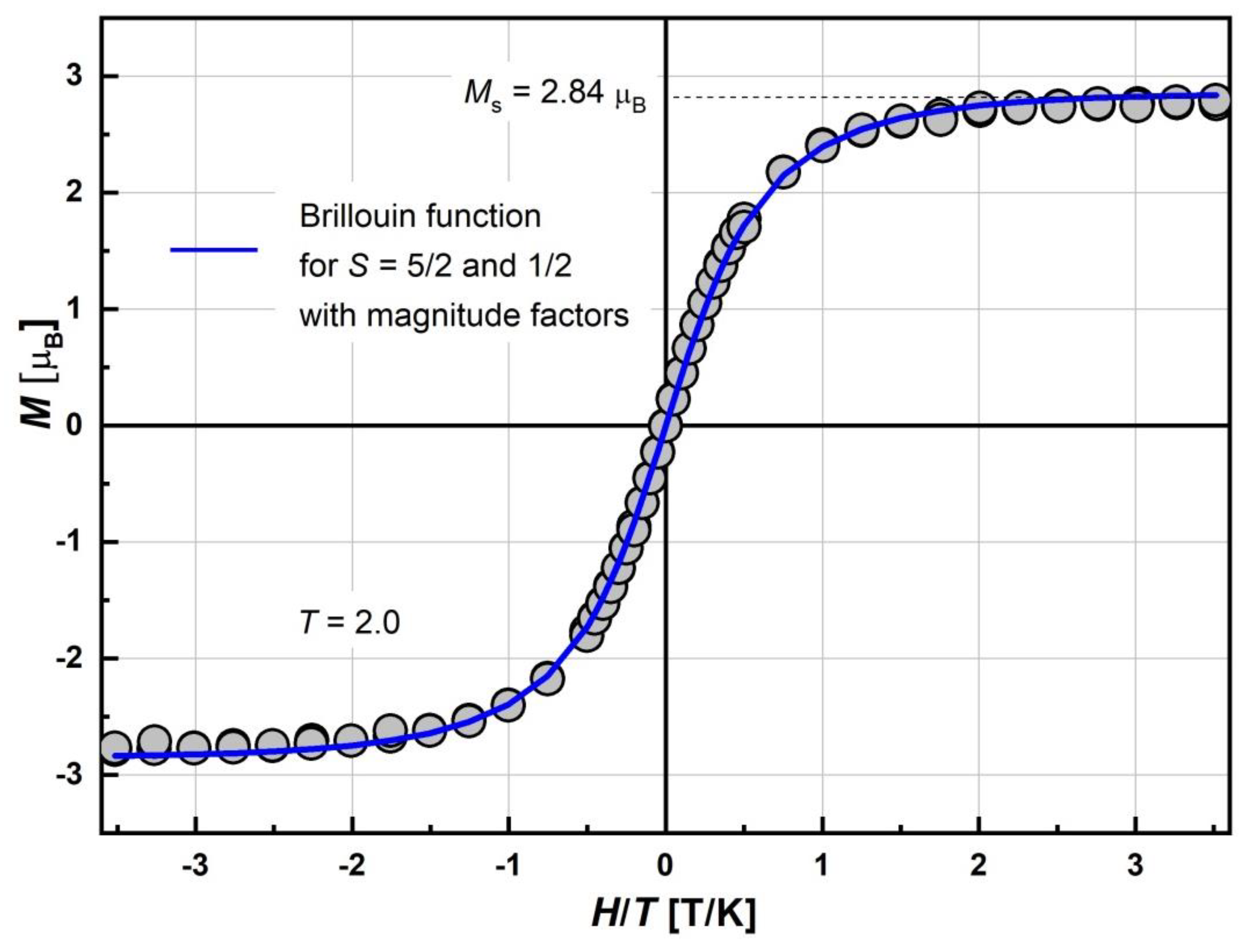

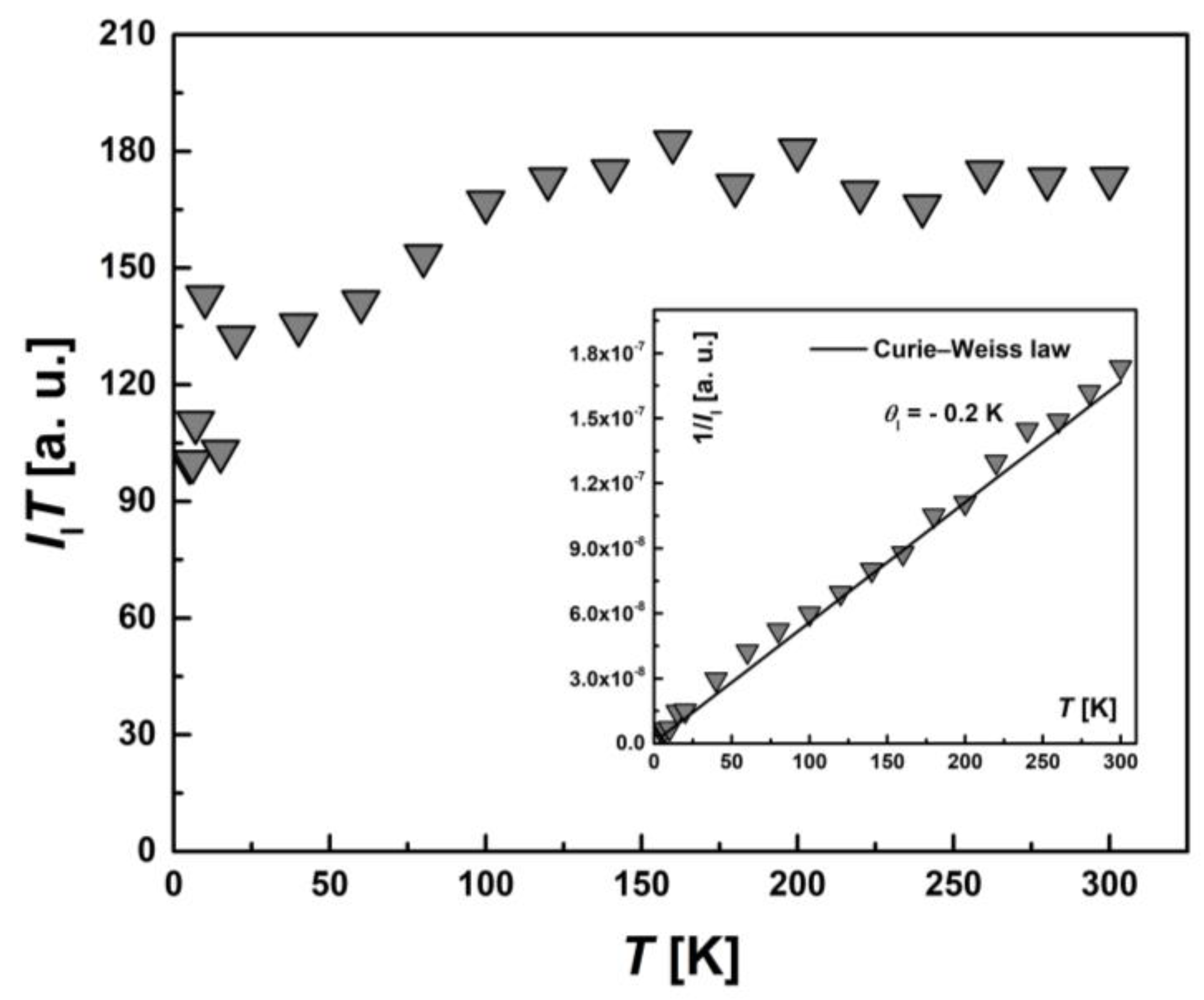


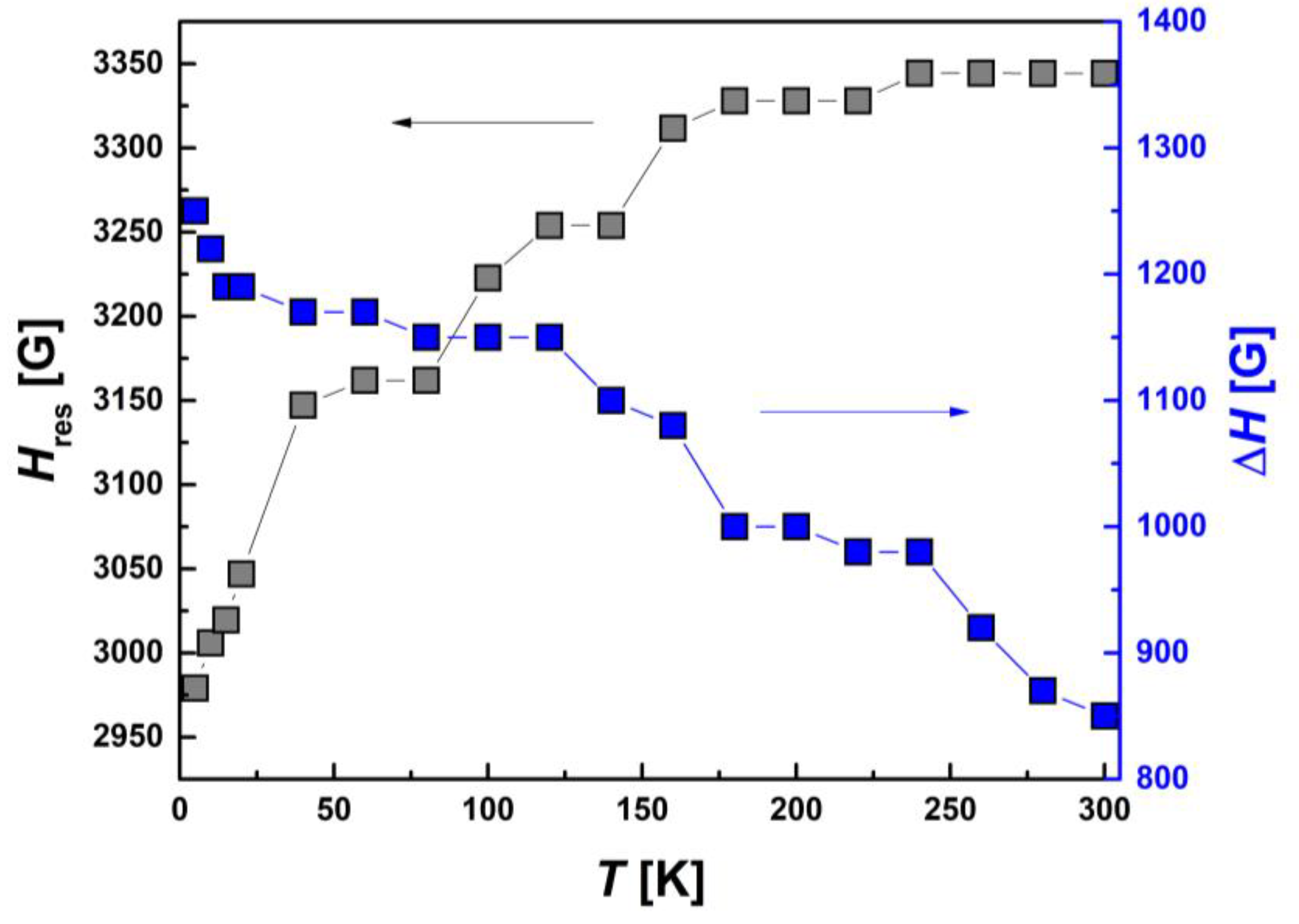
| Compound | Ms, μB | Magnitude Factor γLS (Brillouin Function for S = 1/2) | Magnitude Factor γHS (Brillouin Function for S = 5/2) |
|---|---|---|---|
| [FeL2Bipy]Cl | 2.84 | 0.2 | 0.53 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Starichenko, D.V.; Vorobeva, V.E.; Gruzdev, M.S.; Chervonova, U.V.; Ksenofontov, A.A.; Volegov, A.S.; Yatsyk, I.V. Heteroleptic β-Diketonate Fe3+ Complex: Spin-Crossover and Optical Characteristics. Inorganics 2025, 13, 134. https://doi.org/10.3390/inorganics13050134
Starichenko DV, Vorobeva VE, Gruzdev MS, Chervonova UV, Ksenofontov AA, Volegov AS, Yatsyk IV. Heteroleptic β-Diketonate Fe3+ Complex: Spin-Crossover and Optical Characteristics. Inorganics. 2025; 13(5):134. https://doi.org/10.3390/inorganics13050134
Chicago/Turabian StyleStarichenko, Denis V., Valerya E. Vorobeva, Matvey S. Gruzdev, Ulyana V. Chervonova, Alexander A. Ksenofontov, Aleksey S. Volegov, and Ivan V. Yatsyk. 2025. "Heteroleptic β-Diketonate Fe3+ Complex: Spin-Crossover and Optical Characteristics" Inorganics 13, no. 5: 134. https://doi.org/10.3390/inorganics13050134
APA StyleStarichenko, D. V., Vorobeva, V. E., Gruzdev, M. S., Chervonova, U. V., Ksenofontov, A. A., Volegov, A. S., & Yatsyk, I. V. (2025). Heteroleptic β-Diketonate Fe3+ Complex: Spin-Crossover and Optical Characteristics. Inorganics, 13(5), 134. https://doi.org/10.3390/inorganics13050134









