Porphyrins for Second Order Nonlinear Optics (NLO): An Intriguing History §
Abstract
:1. Introduction
2. The Role of the Metal
3. The Effect of the Nature and the Position of the Substituents on the Porphyrin Core: The Ambivalent Donor or Acceptor Role of the Porphyrin Ring in a Push–Pull System
4. The Effect of Coordination in the Axial Position
5. The Effect of Aggregation
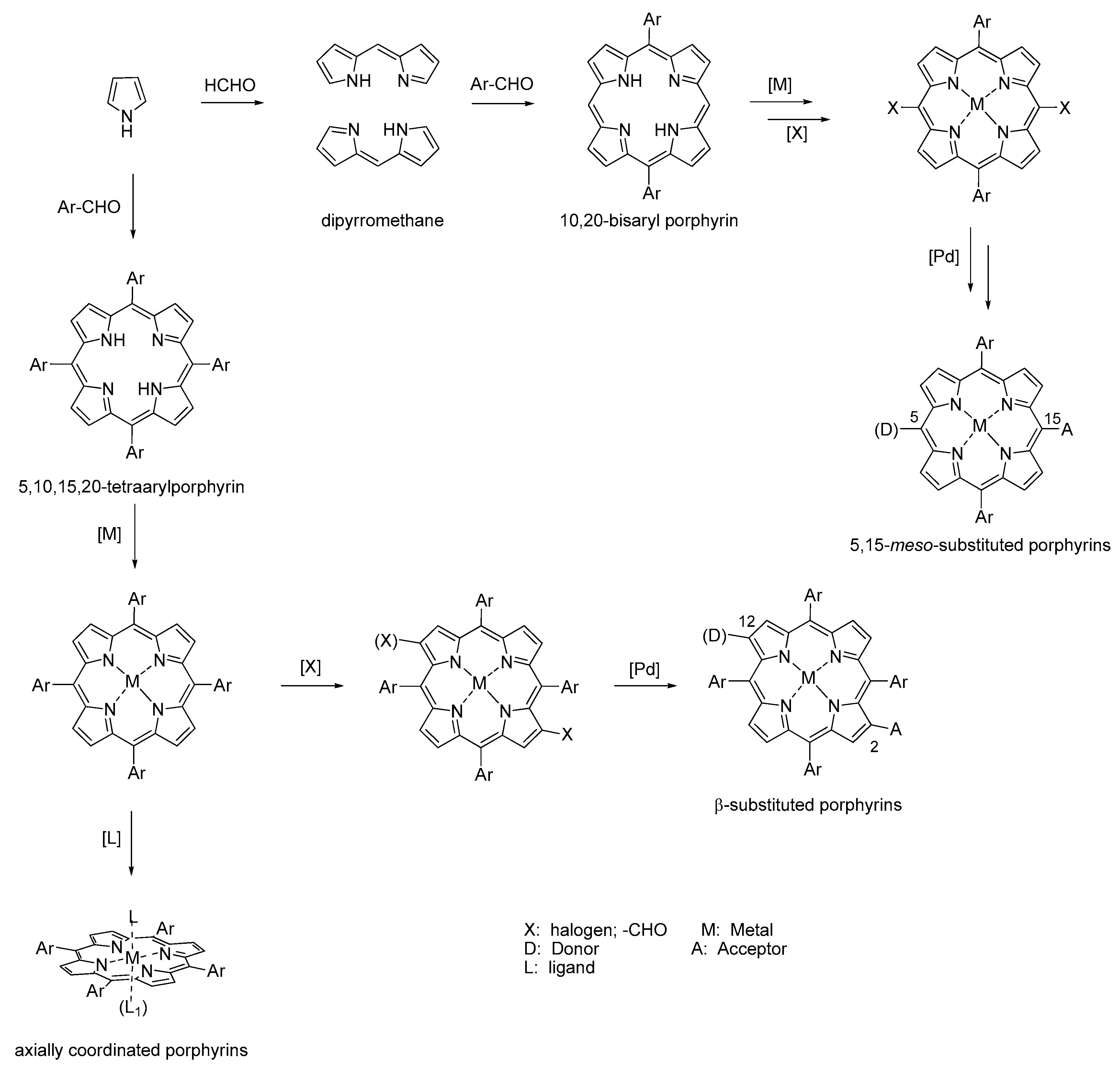
6. About the Synthesis
7. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Oudar, J.L.; Chemla, D.S. Hyperpolarizabilities of the nitroanilines and their relations to the excited state dipole moment. J. Chem. Phys. 1977, 66, 2664–2668. [Google Scholar] [CrossRef]
- Oudar, J.L. Optical nonlinearities of conjugated molecule. Stilbene derivatives and highly polar aromatic compounds. J. Chem. Phys. 1977, 67, 446–457. [Google Scholar] [CrossRef]
- Long, N.J. Organometallic Compounds for Nonlinear Optics-The Search for En-light-enment. Angew. Chem. Int. Ed. Engl. 1995, 34, 21–38. [Google Scholar] [CrossRef]
- Whittal, I.R.; McDonagh, A.M.; Humphrey, M.G. Organometallic complexes in nonlinear optics I: Second-order nonlinearities. Adv. Organomet. Chem. 1998, 42, 291–362. [Google Scholar]
- Di Bella, S. Second-order nonlinear optical properties of transition metal complexes. Chem. Soc. Rev. 2001, 30, 355–366. [Google Scholar] [CrossRef]
- Cariati, E.; Pizzotti, M.; Roberto, D.; Tessore, F.; Ugo, R. Coordination and organometallic compounds and inorganic–organic hybrid cristalline materials for second-order non-linear optics. Coord. Chem. Rev. 2006, 250, 1210–1233. [Google Scholar] [CrossRef]
- Di Bella, S.; Dragonetti, C.; Pizzotti, M.; Roberto, D.; Tessore, F.; Ugo, R. Coordination and organometallic complexes as second-order nonlinear optical materials. In Molecular Organometallic Material for Optics; Bozec, H., Guerchais, V., Eds.; Springer: Heidelberg, Germenay, 2010; pp. 1–55. [Google Scholar]
- Suslick, K.S.; Chen, C.T.; Meredith, G.R.; Cheng, L.T. Push–pull porphyrins as nonlinear optical materials. J. Am. Chem. Soc. 1992, 114, 6928–6930. [Google Scholar] [CrossRef]
- Pizzotti, M.; Ugo, R.; Annoni, E.; Quici, S.; Ledoux-Rak, I.; Zerbi, G.; Del Zoppo, M.; Fantucci, P.; Invernizzi, I. A critical evaluation of EFISH and THG non-linear optical responses of asymmetrically substituted meso-tetraphenyl porphyrins and their metal complexes. Inorg. Chim. Acta 2002, 340, 70–80. [Google Scholar] [CrossRef]
- LeCours, S.M.; Guan, H.W.; Di Magno, S.G.; Wang, C.H.; Therien, M.J. Push–pull Arylethynyl Porphyrins: New Chromophores That Exhibit Large Molecular First-Order Hyperpolarizabilities. J. Am. Chem. Soc. 1996, 118, 1497–1503. [Google Scholar] [CrossRef]
- Karki, L.; Vance, F.W.; Hupp, J.T.; LeCours, S.M.; Therien, M.J. Electronic Stark Effect Studies of a Porphyrin-Based Push–pull Chromophore Displaying a Large First Hyperpolarizability: State-Specific Contributions to β. J. Am. Chem. Soc. 1998, 120, 2606–2611. [Google Scholar] [CrossRef]
- Yeung, M.; Ng, A.C.H.; Drew, M.G.E.; Vorpagel, E.; Breitung, E.M.; McMahon, R.J.; Ng, D.K. Facile Synthesis and Nonlinear Optical Properties of Push–pull 5,15-Diphenylporphyrins. J. Org. Chem. 1998, 63, 7143–7150. [Google Scholar] [CrossRef] [PubMed]
- Pizzotti, M.; Annoni, E.; Ugo, R.; Bruni, S.; Quici, S.; Fantucci, P.; Zerbi, G.; Del Zoppo, M. A multitechnique investigation of the second order NLO response of a 10,20-diphenylporphyrinato nickel(II) complex carrying a phenylethynyl based push–pull system in the 5- and 15- positions. J. Porphyrines Phtalocyanines 2004, 8, 1311–1324. [Google Scholar] [CrossRef]
- Offord, D.A.; Sachs, S.B.; Ennis, M.S.; Eberspacher, T.A.; Griffin, J.H.; Chidsey, C.E.D.; Collman, J.P. Synthesis and Properties of Metalloporphyrin Monolayers and Stacked Multilayers Bound to an Electrode via Site Specific Axial Ligation to a Self-Assembled Monolayer. J. Am. Chem. Soc. 1998, 120, 4478–4487. [Google Scholar] [CrossRef]
- Chemla, D.S.; Zyss, J. Nonlinear Optical Properties of Organic Molecules and Crystals; Academic Press: New York, NY, USA, 1987; pp. 23–187. ISBN 978-0-12-170611-1. [Google Scholar]
- Annoni, E.; Pizzotti, M.; Ugo, R.; Quici, S.; Morotti, T.; Bruschi, M.; Mussini, P. Synthesis, Electronic Characterization and Significant Second Order Non Linear Optical Responses of meso Tetraphenylporphyrins and their Zn(II) Complexes Carrying a Push or Pull Group in β Pyrrolic Position. Eur. J. Inorg. Chem. 2005, 3857–3874. [Google Scholar] [CrossRef]
- Annoni, E.; Pizzotti, M.; Ugo, R.; Quici, S.; Morotti, T.; Casati, N.; Macchi, P. The effect on E-stilbazoles second order NLO response by axial interaction with M(II) 5,10,15,20-tetraphenyl porphyrinates (M = Zn, Ru, Os); a new crystalline packing with very large holes. Inorg. Chim. Acta 2006, 359, 3029–3041. [Google Scholar] [CrossRef]
- Albert, I.D.L.; Marks, T.J.; Ratner, M.A. Large Molecular Hyperpolarizabilities in “Push–pull” Porphyrins. Molecular Planarity and Auxiliary Donor-Acceptor Effects. Chem. Mater. 1998, 10, 753–762. [Google Scholar] [CrossRef]
- Bruni, S.; Cariati, F.; Cariati, E.; Porta, F.A.; Quici, S.; Roberto, D. Determination of the quadratic hyperpolarizability of trans-4-[4-(dimethylamino)styryl]pyridine and 5-dimethylamino-1,10-phenanthroline from solvatochromism of absorption and fluorescence spectra: A comparison with the electric-field-induced second-harmonic generation technique. Spectrochim. Acta Part. A 2001, 57, 1417–1426. [Google Scholar]
- Ledoux, I.; Zyss, J. Influence of the molecular environment in solution measurements of the Second-order optical susceptibility for urea and derivatives. J. Chem. Phys. 1982, 73, 203–213. [Google Scholar] [CrossRef]
- Williams, D.J. Organic polymeric and non-polymeric materials with large optical nonlinearities. Angew. Chem. Int. Ed. Engl. 1984, 23, 690–703. [Google Scholar] [CrossRef]
- Rojo, G.; de la Torre, G.; Garcia-Ruiz, J.; Ledoux, I.; Torres, T.; Zyss, G.; Agullo-Lopez, F. Novel unsymmetrically substituted push–pull phthalocyanines for second-order nonlinear optics. Chem. Phys. 1999, 245, 27–34. [Google Scholar] [CrossRef]
- Chou, H.; Chen, C.T.; Stork, K.F.; Bohn, P.W.; Suslik, K.S. Langmuir-Blodgett films of Amphiphilic Push–pull Porphyrins. J. Phys. Chem 1994, 98, 383–385. [Google Scholar] [CrossRef]
- Castiglioni, C.; Gussoni, M.; Del Zoppo, M.; Zerbi, G. Relaxation contribution to hyperpolarizability. A semiclassical model. Solid State Commun. 1992, 82, 13–17. [Google Scholar] [CrossRef]
- Del Zoppo, M.; Castiglioni, C.; Zerbi, G. A novel approach to estimate NLO response in organic conjugated molecules from vibrational spectra: Molecules with large β values. Nonlinear Opt. 1995, 9, 73–86. [Google Scholar]
- De Angelis, F.; Fantacci, S.; Sgamellotti, A.; Pizzotti, M.; Tessore, F.; Orbelli Biroli, A. Time-dependent and coupled-perturbed DFT and HF investigations on the absorption spectrum and nonlinear optical properties of push–pull M(II)-porphyrin complexes (M=Zn, Cu, Ni). Chem. Phys. Lett. 2007, 447, 10–15. [Google Scholar] [CrossRef]
- Pizzotti, M.; Tessore, F.; Orbelli Biroli, A.; Ugo, R.; De Angelis, F.; Fantacci, S.; Sgamellotti, A.; Zuccaccia, D.; Macchioni, A. An EFISH, Theoretical, and PGSE NMR investigation on the Relevant Role of Aggregation on the Second Order Response in CHCl3 of the Push–pull Chromophores [5-[[4’-(Dimethylamino)phenyl]ethynyl]-15-[(4”-nitrophenyl)ethynyl]-10,20-diphenylporphyrinate]M(II) (M=Zn, Ni). J. Phys. Chem. C 2009, 113, 11131–11141. [Google Scholar]
- Morotti, T.; Pizzotti, M.; Ugo, R.; Quici, S.; Bruschi, M.; Mussini, P.; Righetto, S. Electronic Characterisation and Significant Second Order NLO response of 10,20-Diphenylporphyrins and their ZnII Complexes Substituted in the meso position with π-Delocalised Linkers Carrying Push or Pull Groups. Eur. J. Inorg. Chem. 2006, 1743–1757. [Google Scholar] [CrossRef]
- Becks, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef]
- Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef]
- Schafer, A.; Huber, C.; Ahlrichs, R. Fully optimized contracted Gaussian basis sets of triple zeta valence quality for atoms Li to Kr. J. Chem. Phys. 1994, 100, 5829–5835. [Google Scholar] [CrossRef]
- Roberto, D.; Ugo, R.; Bruni, S.; Cariati, E.; Cariati, F.; Fantucci, P.C.; Invernizzi, I.; Quici, S.; Ledoux, I.; Zyss, J. Quadratic Hyperpolarizability Enhancement of para-Substituted Pyridines upon Coordination to Organometallic Moieties: The Ambivalent Donor or Acceptor Role of the Metal. Organometallics 2000, 19, 1775–1788. [Google Scholar] [CrossRef]
- Kanis, D.R.; Lacroix, P.G.; Ratner, M.A.; Marks, T.J. Electronic structure and quadratic hyperpolarizabilities in organotransition-metal chromophores having weakly coupled π-networks. Unusual mechanisms for second-order response. J. Am. Chem. Soc. 1994, 116, 10089–10102. [Google Scholar] [CrossRef]
- Cheng, L.T.; Tam, W.; Stevenson, S.H.; Meredith, G.R.; Rikken, G.; Marder, S.R. Experimental investigations of organic molecular nonlinear optical polarizabilities. 1. Methods and results on benzene and stilbene derivatives. J. Phys. Chem. 1991, 95, 10631–10643. [Google Scholar] [CrossRef]
- Roberto, D.; Ugo, R.; Tessore, F.; Lucenti, E.; Quici, S.; Vezza, S.; Fantucci, P.C.; Invernizzi, I.; Bruni, S.; Ledoux, I.; et al. Effect of the coordination to to M(II) Metal Centers (M = Zn, Cd, Pt) on the Quadratic Hyperpolarizability of Various Substituted 5-X-1,10-phenanthrolines (X = Donor Group) and of trans-4-(Dimethylamino)-4‘-stilbazole. Organometallics 2002, 21, 161–170. [Google Scholar] [CrossRef]
- Lucenti, E.; Cariati, E.; Dragonetti, C.; Manassero, L.; Tessore, F. Effect of the Coordination to the “Os3(CO)11” Cluster Core on the Quadratic Hyperpolarizability of trans-4-(4‘-X-styryl)pyridines (X = NMe2, t-Bu, CF3) and trans,trans-4-(4‘-NMe2-phenyl-1,3-butadienyl)pyridine. Organometallics 2004, 23, 687–692. [Google Scholar] [CrossRef]
- Orbelli Biroli, A.; Tessore, F.; Righetto, S.; Forni, A.; Macchioni, A.; Rocchigiani, L.; Pizzotti, M.; Di Carlo, G. Intriguing Influence of –COOH-Driven Intermolecular Aggregation and Acid–Base Interactions with N,N-Dimethylformamide on the Second-Order Nonlinear-Optical Response of 5,15 Push–Pull Diarylzinc(II) Porphyrinates. Inorg. Chem. 2017, 56, 6438–6450. [Google Scholar] [CrossRef] [PubMed]
- Orbelli Biroli, A.; Tessore, F.; Pizzotti, M.; Biaggi, C.; Ugo, R.; Caramori, S.; Aliprandi, A.; Bignozzi, C.A.; De Angelis, F.; Giorgi, G.; et al. A Multitechnique Physicochemical Investigation of Various Factors Controlling the photoaction Spectra and of Some Aspects of the Electron Transfer for a Series of Push_Pull Zn(II) Porphyrins Acting as Dyes in DSSCs. J. Phys. Chem. C 2011, 115, 23170–23182. [Google Scholar] [CrossRef]
- Di Carlo, G.; Orbelli Biroli, A.; Pizzotti, M.; Tessore, F.; Trifiletti, V.; Ruffo, R.; Abbotto, A.; Amat, A.; De Angelis, F.; Mussini, P.R. Tetraaryl ZnII Porphyrinates Substituted at β-Pyrrolic Positions as Sensitizers in Dye-Sensitized Solar Cells: A Comparison with meso-Disubstituted Push–Pull ZnII Porphyrinates. Chem. Eur. J. 2013, 19, 10723–10740. [Google Scholar] [CrossRef] [PubMed]
- Dale, S.H.; Elsegood, M.R.J. Hydrogen bonding adducts of benzene polycarboxylic acids with N,N-dimethylformamide: Benzene-1,4-dicarbixylic acid N,N-dimethylformamide disolvate, benzene-1,2,4,5-tetracarboxylic acid N,N-dimethylformamide disolvate monohydrate. Acta Crystallogr. C 2004, 60, 444–448. [Google Scholar] [CrossRef] [PubMed]
- Etter, M.C. Encoding and Decoding hydrogen-bond patterns of organic compounds. Acc. Chem. Res. 1990, 23, 120–126. [Google Scholar] [CrossRef]
- Kang, H.; Facchetti, A.; Jiang, H.; Cariati, E.; Righetto, S.; Ugo, R.; Zuccaccia, C.; Macchioni, A.; Stern, C.; Liu, Z.; et al. Ultralarge hyperpolarizability twisted π-electronsystem electro-optic chromophores: Synthesis, solid state and solution-phase structural characteristics, electronic structures, linear and nonlinear optical properties, and computational studies. J. Am. Chem. Soc. 2007, 129, 3267–3286. [Google Scholar] [CrossRef] [PubMed]
- Tessore, F.; Locatelli, D.; Righetto, S.; Roberto, D.; Ugo, R.; Mussini, P. An investigation on the role of the nature of sulfonated ancillary ligands on the strength and concentration dependence of the second-order NLO responses in CHCl3 of Zn(II) complexes with 4,4′-trans-NC5H4CH=CHC6H4NMe2 and 4,4′-trans,trans-NC5H4(CH=CH)2C6H4NMe2. Inorg. Chem. 2005, 44, 2437–2442. [Google Scholar] [PubMed]
- Di Carlo, G.; Orbelli Biroli, A.; Tessore, F.; Caramori, S.; Pizzotti, M. β-Substituted ZnII porphyrins as dyes for DSSC: A possible approach to photovoltaic windows. Coord. Chem. Rev. 2018, 358, 153–177. [Google Scholar] [CrossRef]
- Mussini, P.R.; Orbelli Biroli, A.; Tessore, F.; Pizzotti, M.; Biaggi, C.; Di Carlo, G.; Lobello, M.G.; De Angelis, F. Modulating the electronic properties of asymettric push–pull and symmetric Zn(II)-diarylporphyrinates with para substituted phenylethynyl moieities in 5,15 meso positions: A combined electrochemical and spectroscopic investigation. Electrochim. Acta 2012, 85, 509–523. [Google Scholar] [CrossRef]
- Di Carlo, G.; Caramori, S.; Trifiletti, V.; Giannuzzi, R.; De Marco, L.; Pizzotti, M.; Orbelli Biroli, A.; Tessore, F.; Argazzi, R.; Bignozzi, C.A. Influence of porphyrinic structure on electron transfer processes at the electrolyte/dye/TiO2 interface in PSSCs: A comparison between meso push–pull and β-pyrrolic architectures. ACS Appl. Mater. Interfaces 2014, 6, 15841–15852. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, G.; Caramori, S.; Casarin, L.; Orbelli Biroli, A.; Tessore, F.; Argazzi, R.; Oriana, A.; Cerullo, G.; Bignozzi, C.A.; Pizzotti, M. Charge transfer dynamics in β- and meso-substituted dithienylethylene porphyrins. J. Phys. Chem. C 2017, 121, 18385–18400. [Google Scholar] [CrossRef]
- Cerqueira, A.F.R.; Moura, N.M.M.; Serra, V.V.; Faustino, M.A.F.; Tomé, A.C.; Cavaleiro, J.A.S.; Neves, M.G.P.M.S. β-Formyl- and β-Vinylporphyrins: Magic Building Blocks for Novel Porphyrin Derivatives. Molecules 2017, 22, 1269. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, G.; Orbelli Biroli, A.; Tessore, F.; Rizzato, S.; Forni, A.; Magnano, G.; Pizzotti, M. Light-induced regiospecific bromination of meso-tetra(3,5-di-tert-butylphenyl)porphyrin on 2,12 β-pyrrolic position. J. Org. Chem. 2015, 80, 4973–4980. [Google Scholar] [CrossRef] [PubMed]
- Di Carlo, G.; Orbelli Biroli, A.; Tessore, F.; Pizzotti, M.; Mussini, P.R.; Amat, A.; De Angelis, F.; Abbotto, A.; Trifiletti, V.; Ruffo, R. Physicochemical investigation of the panchromatic effect on β-substituted ZnII porphyrinates for DSSCs: The role of the π bridge between a dithienylethylene unit and the porphyrinic ring. J. Phys. Chem. C 2014, 118, 7307–7320. [Google Scholar] [CrossRef]
- Orbelli Biroli, A.; Tessore, F.; Vece, V.; Di Carlo, G.; Mussini, P.R.; Trifiletti, V.; De Marco, L.; Giannuzzi, R.; Manca, M.; Pizzotti, M. Highly improved performance of ZnII tetraarylporphyrinates in DSSCs by the presence of octyloxy chains in the aryl rings. J. Mater. Chem. A 2015, 3, 2954–2959. [Google Scholar] [CrossRef]
- Covezzi, A.; Orbelli Biroli, A.; Tessore, F.; Forni, A.; Marinotto, D.; Biagini, P.; Di Carlo, G.; Pizzotti, M. 4D–π–1A type β-substituted ZnII-porphyrins: Ideal green sensitizers for building-integrated photovoltaics. Chem. Commun. 2016, 52, 12642–12645. [Google Scholar] [CrossRef] [PubMed]
- Magnano, G.; Marinotto, D.; Cipolla, M.P.; Trifiletti, V.; Listorti, A.; Mussini, P.R.; Di Carlo, G.; Tessore, F.; Manca, M.; Orbelli Biroli, A.; et al. Influence of alkoxy chain envelopes on the interfacial photoinduced processes in tetraarylporphyrin-sensitized solar cells. Phys. Chem. Chem. Phys. 2016, 18, 9577–9585. [Google Scholar] [CrossRef] [PubMed]







| Compound | μ (theor) (D) a | β1907 (10−30 esu) b |
|---|---|---|
| 4 | 8.55 | 30.1 |
| 5 | 8.82 | 20.4 |
| 6 | 8.31 | 39.3 |
| 7 | 8.69 | 29.7 |
| 8 | 5.33 | 75.7 |
| 9 | 5.16 | 127.5 |
| 10 | 8.54 | 64 |
| 11 | 8.48 | n.d. c |
| 12 | 7.70 | 67 |
| 13 | 7.73 | −94 |
| 14 | 6.07 | 64 |
| 15 | 5.89 | 87.5 |
| 16 | 5.77 | 99 |
| 17 | 5.65 | 112 |
| Compound | μ (D) | Δμeg (D) | βCT (10−30 esu) | β1907 (10−30 esu) |
|---|---|---|---|---|
| L1 | 3.9 a | n.d. c | n.d. | 35 |
| L2 | 4.5 a | n.d. | n.d. | 69 |
| L3 | 2.0 b | n.d. | n.d. | 36 |
| [Zn(TPP)L1] 18 | 4.8 | −3.31 −3.55 | –78.2 –11 | 40 |
| –89.2 | ||||
| [Zn(TPP)L2] 19 | 4.8 | –2.31 –3.08 | –56.9 –9.9 | 82 |
| –66.8 | ||||
| [Zn(TPP)L3] 20 | 3.9 | –3.78 –4.57 | –76.1 –14.4 | 35 |
| –90.5 | ||||
| [Ru(TPP)(CO)L1] 21 | 4.2 | 2.94 2.30 | 94.6 6.3 | 100 |
| 101 | ||||
| [Ru(TPP)(CO)L2] 22 | 5.7 | 2.77 0.17 | 64.8 4.0 | 75 |
| 68.8 | ||||
| [Ru(TPP)(CO)L3] 23 | 7.2 | 1.46 0.16 | 34.2 3.8 | 46 |
| 38.0 | ||||
| [Os(TPP)(CO)L1] 24 | 7.4 | 1.15 2.26 | 21.4 8.4 | 28 |
| 29.8 | ||||
| [Os(TPP)(CO)L2] 25 | 5.1 | 4.74 1.74 | 75.3 5.3 | 73 |
| 80.6 | ||||
| [Os(TPP)(CO)L3] 26 | 4.7 | 1.17 –1.52 | 13.4 –4 | 95 |
| 9.4 |
| Concentration (mol L−1) | Μβ1907 (× 10−48 esu) | β1907 (× 10−30 esu) |
|---|---|---|
| 5 × 10−5 | 6093 a | 438 d |
| 10−5 | 5438 a | 391 d |
| 5 × 10−6 | 6412 a | 461 d |
| 5 × 10−5 | 2921 b | 208 e |
| 5 × 10−5 | 2600 c | 188 e |
| Concentration (mol L−1) | μβ1907 (× 10−48 esu) | β1907d (× 10−30 esu) |
|---|---|---|
| 7.5 × 10−4 | 676 a | 50 |
| 2 × 10−4 | 1200 a | 90 |
| 5 × 10−5 | 3076 a | 230 |
| 5 × 10−5 | 2627 b | 196 |
| 5 × 10−5 | 2864 c | 214 |
| Chromophores | μβ1907 (×10−48 esu) DMF | μβ1907 (×10−48 esu) CHCl3 |
|---|---|---|
| 27 | −1600 a | |
| −3055 b | −215 b | |
| −3320 c | ||
| 28 | −1720 a | |
| −2520 b | −670 b | |
| −3010 c | −970 c | |
| 29 | −1080 a | |
| −1096 b | −357 b | |
| 30 | −4180 a | |
| −7470 b | −830 b | |
| −7940 c | ||
| 31 | −490 a | −457 b |
| 32 | −1240 a | |
| −1490 b | +586 b | |
| 33 | +1030 a | +2978 d |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tessore, F.; Orbelli Biroli, A.; Di Carlo, G.; Pizzotti, M. Porphyrins for Second Order Nonlinear Optics (NLO): An Intriguing History §. Inorganics 2018, 6, 81. https://doi.org/10.3390/inorganics6030081
Tessore F, Orbelli Biroli A, Di Carlo G, Pizzotti M. Porphyrins for Second Order Nonlinear Optics (NLO): An Intriguing History §. Inorganics. 2018; 6(3):81. https://doi.org/10.3390/inorganics6030081
Chicago/Turabian StyleTessore, Francesca, Alessio Orbelli Biroli, Gabriele Di Carlo, and Maddalena Pizzotti. 2018. "Porphyrins for Second Order Nonlinear Optics (NLO): An Intriguing History §" Inorganics 6, no. 3: 81. https://doi.org/10.3390/inorganics6030081
APA StyleTessore, F., Orbelli Biroli, A., Di Carlo, G., & Pizzotti, M. (2018). Porphyrins for Second Order Nonlinear Optics (NLO): An Intriguing History §. Inorganics, 6(3), 81. https://doi.org/10.3390/inorganics6030081