σ-Holes vs. Buildups of Electronic Density on the Extensions of Bonds to Halogen Atoms
Abstract
:1. σ-Hole Interactions
2. The Molecular Electrostatic Potential
3. Electrostatic Potentials Associated with σ-Holes
4. Electrostatic Potentials on Extensions of Bonds to Halogen Atoms
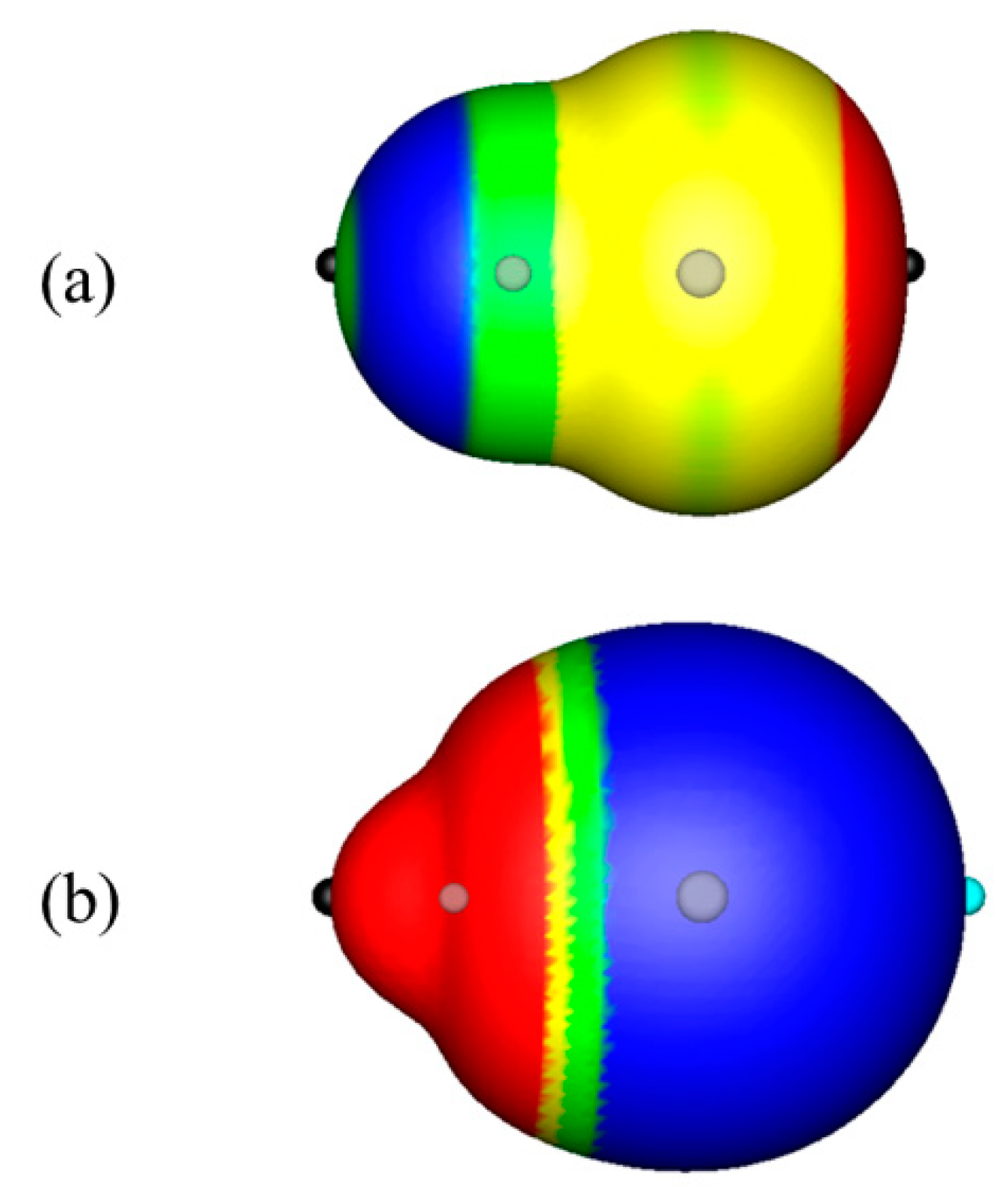
4.1. Diatomic Molecules
4.2. Substituted Hydrides, HnA–X
5. Discussion and Summary
- (1)
- A lower electronic density (a σ-hole) accompanied by a positive electrostatic potential with a VS,max.
- (2)
- A lower electronic density (a σ-hole) accompanied by a negative electrostatic potential with a VS,max.
- (3)
- A buildup of electronic density (no σ-hole), usually accompanied by a negative electrostatic potential with a VS,min.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Clark, T.; Hennemann, M.; Murray, J.S.; Politzer, P. Halogen bonding: The σ-hole. J. Mol. Model. 2007, 13, 291–296. [Google Scholar] [CrossRef] [PubMed]
- Brinck, T.; Murray, J.S.; Politzer, P. Surface electrostatic potentials of halogenated methanes as indicators of directional intermolecular interactions. Int. J. Quantum Chem. 1992, 44 (Suppl. 19), 57–64. [Google Scholar] [CrossRef]
- Brinck, T.; Murray, J.S.; Politzer, P. Molecular electrostatic potentials and local ionization energies of Group V-VII hydrides and their anions. Relationships for aqueous and gas-phase acidities. Int. J. Quantum Chem. 1993, 48 (Suppl. 20), 73–88. [Google Scholar] [CrossRef]
- Hennemann, M.; Murray, J.S.; Riley, K.E.; Politzer, P.; Clark, T. Polarization-induced σ-holes and hydrogen bonding. J. Mol. Model. 2012, 18, 2461–2469. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T. Mathematical modeling and physical reality in noncovalent interactions. J. Mol. Model. 2015, 21, 52. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Clark, T.; Politzer, P. σ-Hole bonding: Molecules containing Group VI atoms. J. Mol. Model. 2007, 13, 1033–1038. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Lane, P.; Politzer, P. A predicted new type of directional noncovalent interaction. Int. J. Quantum Chem. 2007, 107, 2286–2292. [Google Scholar] [CrossRef]
- Murray, J.S.; Lane, P.; Politzer, P. Expansion of the σ-hole concept. J. Mol. Model. 2009, 15, 723–729. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Clark, T. Halogen bonding and other σ-hole interactions: A perspective. Phys. Chem. Chem. Phys. 2013, 15, 11178–11189. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Janjić, G.V.; Zarić, S.D. σ-Hole interactions of covalently-bonded nitrogen, phosphorus and arsenic: A survey of crystal structures. Crystals 2014, 4, 12–31. [Google Scholar] [CrossRef]
- Scilabra, P.; Terraneo, G.; Resnati, G. The chalcogen bond in crystalline solids: A world parallel to hydrogen bond. Acc. Chem. Res. 2019, 52, 1314–1324. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. Halogen bonding: An interim discussion. ChemPhysChem 2013, 14, 278–294. [Google Scholar] [CrossRef] [PubMed]
- Bauzá, A.; Mooibroek, T.J.; Frontera, A. The bright future of unconventional σ/π-hole interactions. ChemPhysChem 2015, 16, 2496–2517. [Google Scholar] [CrossRef] [PubMed]
- Kolář, M.H.; Hobza, P. Computer modeling of halogen bonds and other σ-hole interactions. Chem. Rev. 2016, 116, 5155–5187. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Wang, W.; Jin, W.J. σ-Hole bond vs. π-hole bond: A comparison based on halogen bond. Chem. Rev. 2016, 116, 5072–5104. [Google Scholar] [CrossRef] [PubMed]
- Nyburg, S.C.; Faerman, C.H. A revision of van der Waals atomic radii for molecular crystals: N, O, F, S, Cl, Se, Br and I bonded to carbon. Acta Cryst. B 1985, 41, 274–279. [Google Scholar] [CrossRef]
- Ikuta, S. Anisotropy of electron density distribution around atoms in molecules: N, P, O and S atoms. J. Mol. Struct. 1990, 205, 191–201. [Google Scholar] [CrossRef]
- Eramian, H.; Tian, Y.-H.; Fox, Z.; Beneberu, H.Z.; Kertesz, M. On the anisotropy of van der Waals atomic radii of O, S, Se, F, Cl, Br and I. J. Phys. Chem. A 2013, 117, 14184–14190. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S.; Clark, T.; Resnati, G. The σ-hole revisited. Phys. Chem. Chem. Phys. 2017, 19, 32166–32178. [Google Scholar] [CrossRef]
- Rosenfeld, R.E., Jr.; Parthasarathy, R.; Dunitz, J.D. Directional preferences of nonbonded atomic contacts with divalent sulfur. 1. Electrophiles and nucleophiles. J. Am. Chem. Soc. 1977, 99, 4860–4862. [Google Scholar] [CrossRef]
- Ramasubbu, N.; Parthasarathy, R.; Murray-Rust, P. Angular preferences of intermolecular forces around halogen centers: Preferred directions of approach of electrophiles and nucleophiles around carbon-halogen bond. J. Am. Chem. Soc. 1986, 108, 4308–4314. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Concha, M.C. σ-Hole bonding between like atoms: A fallacy of atomic charges. J. Mol. Model. 2008, 14, 659–665. [Google Scholar] [CrossRef] [PubMed]
- Stewart, R.F. On the mapping of electrostatic properties from Bragg diffraction data. Chem. Phys. Lett. 1979, 65, 335–342. [Google Scholar] [CrossRef]
- Politzer, P.; Truhlar, D.G. (Eds.) Chemical Applications of Atomic and Molecular Electrostatic Potentials; Plenum Press: New York, NY, USA, 1981. [Google Scholar]
- Klein, C.L.; Stevens, E.D. Charge density studies of drug molecules. In Structure and Reactivity; Liebman, J.F., Goldberg, A., Eds.; VCH Publishers: New York, NY, USA, 1988; pp. 26–64. [Google Scholar]
- Politzer, P.; Murray, J.S. Molecular electrostatic potentials and chemical reactivity. In Reviews in Computational Chemistry; Lipkowitz, K.B., Boyd, D.B., Eds.; VCH Publishers: New York, NY, USA, 1991; Volume 2, pp. 273–312. [Google Scholar]
- Wheeler, S.E.; Houk, K.N. Through-space effects of substituents dominate molecular electrostatic potentials of substituted arenes. J. Chem. Theory Comput. 2009, 5, 2301–2312. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.S.; Shields, Z.P.-I.; Seybold, P.G.; Politzer, P. Intuitive and counterintuitive noncovalent interactions of aromatic π-regions with the hydrogen and the nitrogen of HCN. J. Comput. Sci. 2015, 10, 209–216. [Google Scholar] [CrossRef]
- Murray, J.S.; Politzer, P. Molecular electrostatic potentials and noncovalent interactions. WIREs Comput. Mol. Sci. 2017, 7, e1236. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S. σ-Holes and π-holes: Similarities and differences. J. Comput. Chem. 2018, 39, 464–471. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S. σ-Hole interactions: Perspectives and misconceptions. Crystals 2017, 7, 212. [Google Scholar] [CrossRef]
- Murray, J.S.; Resnati, G.; Politzer, P. Close contacts and noncovalent interactions in crystals. Faraday Discuss. 2017, 203, 113–130. [Google Scholar] [CrossRef]
- Bader, R.F.W.; Carroll, M.T.; Cheeseman, J.R.; Chang, C. Properties of atoms in molecules: Atomic volumes. J. Am. Chem. Soc. 1987, 109, 7968–7979. [Google Scholar] [CrossRef]
- Frisch, M.J.; Trucks, G.W.; Schlegel, H.B.; Scuseria, G.E.; Robb, M.A.; Cheeseman, J.R.; Scalmani, G.; Barone, V.; Mennucci, B.; Petersson, G.A. Gaussian 09; Revision A.1; Gaussian, Inc.: Wallingford, CT, USA, 2009. [Google Scholar]
- Bulat, F.A.; Toro-Labbé, A.; Brinck, T.; Murray, J.S.; Politzer, P. Quantitative analysis of molecular surface properties. J. Mol. Model. 2010, 16, 1679–1691. [Google Scholar] [CrossRef] [PubMed]
- Zhao, Y.; Truhlar, D.G. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states and transition elements: Two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor. Chem. Acc. 2008, 120, 215–241. [Google Scholar]
- Zhao, Y.; Truhlar, D.G. Density functionals with broad applicability in chemistry. Acc. Chem. Res. 2008, 41, 157–167. [Google Scholar] [CrossRef] [PubMed]
- Paykatov, G.; Dinadayalane, T.; Leszczynski, J. Towards selection of efficient density functionals for van der Waals molecular complexes: Comparative study of C–H···π and N–H···π interactions. J Phys. Chem. A 2015, 119, 1190–1200. [Google Scholar]
- Riley, K.E.; Tran, K.; Lane, P.; Murray, J.S.; Politzer, P. Comparative analysis of electrostatic potential maxima and minima on molecular surfaces, as determined by three methods and a variety of basis sets. J. Comput. Sci. 2016, 17, 273–284. [Google Scholar] [CrossRef]
- Politzer, P.; Murray, J.S.; Concha, M.C. Halogen bonding and the design of new materials: Organic bromides, chlorides and perhaps even fluorides as donors. J. Mol. Model. 2007, 13, 643–650. [Google Scholar] [CrossRef]
- Chopra, D.; Row, T.N.G. Role of organic fluorine in crystal engineering. CrystEngComm 2011, 13, 2175–2186. [Google Scholar] [CrossRef]
- Metrangolo, P.; Murray, J.S.; Pilati, T.; Politzer, P.; Resnati, G.; Terraneo, G. Fluorine-centered halogen bonding: A factor in recognition phenomena and reactivity. Cryst. Growth Des. 2011, 11, 4238–4246. [Google Scholar] [CrossRef]
- Bundhun, A.; Ramasami, P.; Murray, J.S.; Politzer, P. Trends in σ-hole strengths and interactions of F3MX molecules (M = C, Si, Ge and X = F, Cl, Br, I). J. Mol. Model. 2013, 19, 2739–2746. [Google Scholar] [CrossRef]
- Murray, J.S.; Macaveiu, L.; Politzer, P. Factors affecting the strengths of σ-hole electrostatic potentials. J. Comput. Sci. 2014, 5, 590–596. [Google Scholar] [CrossRef]
- Politzer, P.; Shields, Z.P.-I.; Bulat, F.A.; Murray, J.S. Average Local Ionization Energies as a Route to Intrinsic Atomic Electronegativities. J. Chem. Theory Comput. 2011, 7, 377–384. [Google Scholar] [CrossRef] [PubMed]
- Politzer, P.; Murray, J.S. Electronegativity—A perspective. J. Mol. Model. 2018, 24, 214. [Google Scholar] [CrossRef] [PubMed]
- Allen, L.C. Electronegativity Is the Average One-Electron Energy of the Valence-Shell Electrons in Ground-State Free Atoms. J. Am. Chem. Soc. 1989, 111, 9003–9014. [Google Scholar] [CrossRef]
- Allen, L.C. Encyclopedia of Computational Chemistry; Schleyer, P.V.R., Ed.; Wiley: New York, NY, USA, 1998; Volume 2, pp. 835–852. [Google Scholar]
- Lide, D.R. Handbook of Chemistry and Physics, 87th ed.; CRC Press: Boca Raton, FL, USA, 2006. [Google Scholar]
- NCSS 11 Statistical Software (2016). NCSS, LLC.: Kaysville, UT, USA. Available online: Ncss.com/software/ncss (accessed on 12 May 2019).


| AX | VS(X) | χA − χX | R1 | R2 |
|---|---|---|---|---|
| HF | −28.1 | −1.60 | 1.58 | 1.61 |
| LiF | −67.6 (min) | −3.00 | 1.67 | 1.63 |
| BeF | −27.1 (min) | −2.27 | 1.63 | 1.49 |
| BF | 1.1 (min) | −1.80 | 1.59 | 1.43 |
| CF | 3.5 | −1.32 | 1.57 | 1.61 |
| NF | −1.2 | −0.80 | 1.57 | 1.61 |
| OF | 3.1 | −0.48 | 1.56 | 1.63 |
| FF | 11.2 | 0.00 | 1.52 | 1.63 |
| HCl | 5.5 | −0.57 | 1.94 | 2.16 |
| LiCl | −43.1 (min) | −1.97 | 2.15 | 2.05 |
| BeCl | −4.4 | −1.24 | 2.02 | 2.12 |
| BCl | 10.8 | −0.77 | 2.02 | 2.10 |
| CCl | 18.5 | −0.29 | 1.96 | 2.12 |
| NCl | 25.0 | 0.23 | 1.90 | 2.11 |
| OCl | 36.0 | 0.55 | 1.85 | 2.13 |
| FCl | 45.0 | 1.03 | 1.81 | 2.12 |
| HBr | 13.4 | −0.31 | 2.04 | 2.27 |
| LiBr | −36.8 (min) | −1.71 | 2.26 | 2.11 |
| BeBr | −0.2 | −0.98 | 2.14 | 2.24 |
| BBr | 10.8 | −0.51 | 2.15 | 2.22 |
| CBr | 20.4 | −0.03 | 2.08 | 2.24 |
| NBr | 28.1 | 0.49 | 2.02 | 2.23 |
| OBr | 40.7 | 0.81 | 1.97 | 2.24 |
| FBr | 53.0 | 1.29 | 1.91 | 2.23 |
| ClF | −8.2 | −1.03 | 1.57 | 1.62 |
| BrF | −13.4 | −1.29 | 1.58 | 1.62 |
| ClCl | 25.5 | 0.00 | 1.88 | 2.14 |
| ClBr | 35.6 | 0.26 | 1.97 | 2.26 |
| BrCl | 19.2 | −0.26 | 1.91 | 2.15 |
| BrBr | 29.2 | 0.00 | 2.00 | 2.26 |
| Atom | χ b | α c |
|---|---|---|
| H | 2.40 | 0.667 |
| Li | 1.00 | 24.33 |
| Be | 1.73 | 5.60 |
| B | 2.20 | 3.03 |
| C | 2.68 | 1.76 |
| N | 3.20 | 1.10 |
| O | 3.52 | 0.802 |
| F | 4.00 | 0.557 |
| Na | 0.99 | 24.11 |
| Mg | 1.46 | 10.6 |
| Al | 1.67 | 6.8 |
| Si | 1.93 | 5.38 |
| P | 2.34 | 3.63 |
| S | 2.63 | 2.90 |
| Cl | 2.97 | 2.18 |
| K | 1.01 | 43.4 |
| Ca | 1.17 | 22.8 |
| Ga | 1.79 | 8.12 |
| Ge | 1.90 | 6.07 |
| As | 2.17 | 4.31 |
| Se | 2.40 | 3.77 |
| Br | 2.71 | 3.05 |
| A | X = F | X = Cl | X = Br | |||
|---|---|---|---|---|---|---|
| VS(F) | χA − χF | VS(Cl) | χA − χCl | VS(Br) | χA − χBr | |
| H | −28.1 | −1.60 | 5.5 | −0.57 | 13.4 | −0.31 |
| Li | −67.6 (min) | −3.00 | −43.1 (min) | −1.97 | −36.8 (min) | −1.71 |
| Be | −26.0 (min) | −2.27 | −3.4 | −1.24 | 1.0 | −0.98 |
| B | −15.8 (min) | −1.80 | 1.1 | −0.77 | 5.6 | −0.51 |
| C | −24.7 | −1.32 | −0.9 | −0.29 | 5.7 | −0.03 |
| N | b | −0.80 | 11.0 | 0.23 | 17.8 | 0.49 |
| O | −6.7 | −0.48 | 25.3 | 0.55 | 32.7 | 0.81 |
| F | 11.2 | 0.00 | 45.0 | 1.03 | 53.0 | 1.29 |
| Na | −80.4 (min) | −3.01 | −52.4 (min) | −1.98 | −45.2 (min) | −1.72 |
| Mg | −46.4 (min) | −2.54 | −19.7 | −1.51 | −12.9 | −1.25 |
| Al | −32.5 (min) | −2.33 | −10.4 | −1.30 | −4.2 | −1.04 |
| Si | −26.2 (min) | −2.07 | −5.9 | −1.04 | 0.5 | −0.78 |
| P | b | −1.66 | −3.4 | −0.63 | 3.5 | −0.37 |
| S | b | −1.37 | 8.7 | −0.34 | 17.3 | −0.08 |
| Cl | −8.2 | −1.03 | 25.5 | 0.00 | 35.6 | 0.26 |
| K | −84.4 (min) | −2.99 | −61.1 (min) | −1.96 | −54.4 (min) | −1.70 |
| Ca | −50.5 (min) | −2.83 | −33.7 (min) | −1.80 | −27.5 (min) | −1.54 |
| Ga | −37.9 (min) | −2.21 | −11.9 | −1.18 | −5.3 | −0.92 |
| Ge | −33.1 (min) | −2.10 | −8.3 | −1.07 | −1.6 | −0.81 |
| As | −29.8 (min) | −1.83 | −5.8 | −0.8 | 1.3 | −0.54 |
| Se | −22.6 | −1.60 | 5.4 | −0.57 | 13.8 | −0.31 |
| Br | −13.4 | −1.29 | 19.2 | −0.26 | 29.2 | 0.00 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Politzer, P.; Murray, J.S. σ-Holes vs. Buildups of Electronic Density on the Extensions of Bonds to Halogen Atoms. Inorganics 2019, 7, 71. https://doi.org/10.3390/inorganics7060071
Politzer P, Murray JS. σ-Holes vs. Buildups of Electronic Density on the Extensions of Bonds to Halogen Atoms. Inorganics. 2019; 7(6):71. https://doi.org/10.3390/inorganics7060071
Chicago/Turabian StylePolitzer, Peter, and Jane S. Murray. 2019. "σ-Holes vs. Buildups of Electronic Density on the Extensions of Bonds to Halogen Atoms" Inorganics 7, no. 6: 71. https://doi.org/10.3390/inorganics7060071
APA StylePolitzer, P., & Murray, J. S. (2019). σ-Holes vs. Buildups of Electronic Density on the Extensions of Bonds to Halogen Atoms. Inorganics, 7(6), 71. https://doi.org/10.3390/inorganics7060071





