Abstract
The crystal structure of the Zintl phase hydride CaSiH≈4/3 was discussed controversially, especially with respect to the nature of the silicon-hydrogen interaction. We have applied X-ray and neutron powder diffraction as well as total neutron scattering on a deuterated sample, CaSiD1.1. Rietveld refinement (CaSiD1.1, Pnma, a = 14.579(4) Å, b = 3.8119(4) Å, c = 11.209(2) Å) and an analysis of the neutron pair distribution function show a silicon-deuterium bond length of 1.53 Å. The Si–H bond may thus be categorized as covalent and the main structural features described by a limiting ionic formula Ca2+H−(Si−)2/3(SiH−)1/3. Hydrogen atoms decorating the ribbon-like silicon polyanion made of three connected zigzag chains are under-occupied, resulting in a composition CaSiH1.1. Hydrogen-poor Zintl phase hydrides CaSiH<1 with hydride ions in Ca4 tetrahedra only were found in an in situ neutron diffraction experiment at elevated temperature. Hydrogen (deuterium) uptake and release in CaSiDx (0.05 ≤ x ≤ 0.17) is a very fast process and takes less than 1 min to complete, which is of importance for possible hydrogen storage applications.
1. Introduction
During the last twenty years, a new class of compounds has been developed: Hydrides of Zintl phases exhibiting hydrogen atoms coordinated to a polyanion. The first examples were Ae(TrH)2 and Ae(TrH)Tt, Ae = Ca–Ba, Tr = Al–In, Tt = Si–Sn [,,,,,,,]. These phases show a puckered honeycomb-like structure of Tr or Tr and Tt atoms. Hydrogen is bound to the group 13 element. The interaction is clearly covalent, as indicated by a short bond length and neutron vibrational spectroscopy [,,,]. Such pseudo-molecular moieties are referred to as polyanionic hydrides []. In contrast, there are LnGaH1+x (Ln = Nd [,], Gd [], x < 1) phases that show a pronounced homogeneity range for the hydrogen incorporation []. One hydrogen per formula unit occupies a tetrahedral Ln4 void (interstitial hydride). The remaining hydrogen atoms are located in trigonal-bipyramidal Ln3Ga2 voids. The Ga–H distance is rather long (≈2 Å). The same structure motif was recently found for LaGa2H0.71(2) [] as well. The bonding situation is comparable to classical metallic hydrides like PdH0.7 rather than to covalent ones.
The existence of polyanionic hydrides with a covalent element-hydrogen bond (next to an element–element bond) of group 14 elements was long unclear. The Zintl phase hydride CaSiH≈4/3 was the first example of this type of compound with a silicon-backbone and a silicon-hydrogen contact [,,,]. The system CaSi–H2 also gathered interest as a potential hydrogen storage material with 1.9 wt % hydrogen capacity and good reversibility at mild conditions (473–573 K) [,].
Considering the idealized chemical formula CaSiH4/3, the material can be understood according to the rules of hydrogen incorporation in Zintl phases []. There are two types of hydrogen atoms present. One is incorporated as hydride ion in sheets of edge sharing calcium tetrahedra, (HCa4/4)+. The silicon atoms thus get a negative formal charge, Si−. According to the Zintl-concept, a three-binding behavior is expected. This is realized by forming rows of six-membered rings in a boat configuration running in crystallographic b direction. Two of these rows are condensed in c direction. One third of the silicon atoms thus has only two silicon neighbors. The remaining bond is saturated by hydrogen atoms. The chemical formula can be reordered as Ca2+H−[Si−]2/3[(SiH)−]1/3. The polyanion is a one-dimensional row of
[(HSi4H)4−]-units (Figure 1).
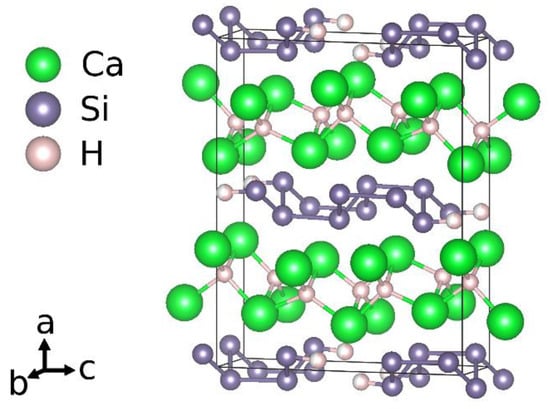
Figure 1.
Crystal structure according to an idealized chemical formula CaSiH4/3.
In addition to CaSiH≈4/3, there are the isotypic compounds SrGeH1.19, BaSnH1.28 [], and the structurally closely related to compounds BaSiH1.87 [] as well as SrSiH1.49 and BaGeH1.56 [,], all of them showing a group 14 element-hydrogen contact. An intrinsic feature of these compounds is a pronounced under-occupation of the polyanion binding hydrogen site. For the title compound, this led to a controversy about the character of the bond.
Originally, a compound CaSiH1.3 was described showing a short, covalent Si–H bond of 1.58 Å []. The structure was determined from X-ray powder diffraction and DFT calculations. All the silicon atoms are three binding (except for the non-stoichiometry of hydrogen) with almost equal Si–Si distances. A neutron diffraction and spectroscopy study were done on a deuterated compound CaSiD1.2 []. This work describes a much longer Si–D distance of 1.82 Å. Further hydrogenation studies propose the composition CaSiH1.06 []. The Rietveld analysis of the corresponding powder X-ray diffraction pattern confirms the heavy metal structure that was originally described. From 2H solid state nuclear magnetic resonance spectroscopy we recently could estimate the Si–D bond length as 1.56(1) Å [].
To end the controversy about chemical bonding in this compound, we combined a Rietveld analysis of X-ray and neutron powder diffraction patterns with small box pair distribution function (PDF) modelling of neutron total scattering data. Furthermore, we could identify new, hydrogen poor phases CaSiH<1 by an in situ neutron diffraction study.
2. Results
The crystal structure of CaSiH≈4/3 was reevaluated by a Rietveld analysis based on X-ray and neutron powder diffraction and a pair distribution function (PDF) analysis based on neutron total scattering data. The study considers a deuterated sample with a refined composition of CaSiD1.1. Furthermore, the deuteration process was monitored in situ by neutron diffraction of a CaSi sample under a deuterium gas atmosphere up to 5.5 MPa and elevated temperatures. At high temperatures (>520 K), hydrogen-poor phases CaSiDx<1 occur while the hydrogen-rich phase is formed upon cooling. Crystallographic information (CIF) for all phases can be found in the Supplementary Materials.
2.1. The Crystal Structure of CaSiD1.1
The structural study of CaSiD1.1 is based on a Zintl phase precursor that is almost phase pure (Figure 2). There is an impurity phase of CaO (2%) which is most probably introduced by the used calcium metal. There is a second impurity phase present that can hardly be seen in X-ray diffraction data (marked as * in Figure 2). Thus, the phases content appears neglectable. Both impurity phases do not change upon hydrogenation. Since the reflections of CaSiD1.1 are strongly broadened, these two phases appear more pronounced in the diffraction pattern. We want to emphasize that the integrated intensity of the impurity phases is still negligible and does not influence the Rietveld or the PDF analysis.
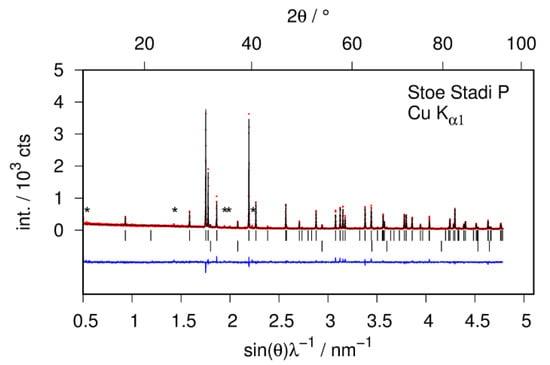
Figure 2.
Quantitative phase analysis of the hydrogen-free sample CaSi by Rietveld analysis of X-ray powder diffraction data. Bragg marker: Top row CaSi (98 wt %); bottom row CaO (2 wt %). (*) marks minute intensities of an unidentified impurity phase; red points: observed intensity; black line: calculated intensity; blue line: difference plot.
2.1.1. Total Scattering and PDF Analysis
Fourier transforming properly corrected total scattering data leads to the pair distribution function (PDF; or, more general, the pair correlation function) of the atomic structure. Since it is a real-space representation of the structure, peaks can be directly interpreted as interatomic distances. A qualitative inspection of the neutron PDF data shows a first distance correlation at 1.53 Å. According to chemical reasoning, it can be directly assigned to the Si–D bond (Figure 3). The remaining atomic distance correlations need to be larger than 2 Å according to the crystal structure model which fits the PDF data.
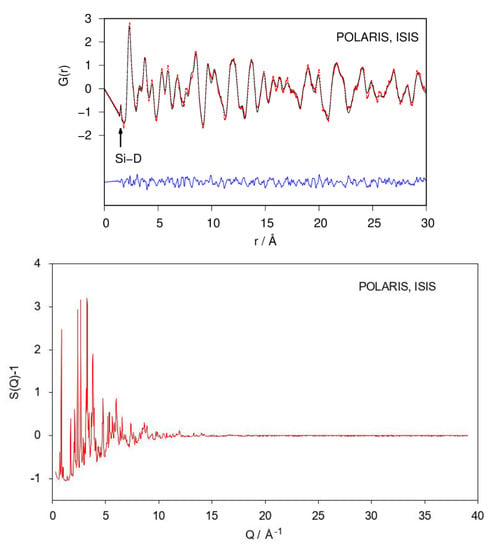
Figure 3.
Refinement of the crystal structure of CaSiD1.1 (space group Pnma) using neutron pair distribution function (PDF)-data (top) and corresponding S(Q) (bottom). The Si–D correlation is marked. Rwp = 0.165. Red points, observed intensity; black line, calculated intensity; blue line, difference plot.
Neutron PDF data were fitted using the crystallographic model in space group type Pnma as shown in Figure 1. Atomic fractional coordinates were constrained according to the given symmetry. Modelling PDF data up to 30 Å results in a proper description of experimental data (Rwp = 0.165; Figure 3). The refined Si1–D4 distance is 1.53 Å with an occupancy (SOF) of the D4 site of 0.35. Two of tetrahedral Ca4 void are fully occupied. The corresponding SOF parameters were fixed during the last cycles. The D3 site is under-occupied as well (Table 1), giving a chemical formula CaSiD1.08.

Table 1.
Crystallographic data of CaSiD1.1, according to a Rietveld refinement with a bond length restraint (a = 14.579(4) Å, b = 3.8119(4) Å, c = 11.209(2) Å) and PDF small-box modelling (a = 14.594 Å, b = 3.8200 Å, c = 11.230 Å). Lattice parameters of the corresponding hydride CaSiH≈1.1 are a = 14.6356(10) Å, b = 3.81207(15) Å, c = 11.2115(7) Å, based on laboratory X-ray diffraction.
According to the refined model, Si–Si distances within the zigzag chain (crystallographic b direction) are 2.31 Å. The chain-connection bond (crystallographic c direction) is 2.55 Å long. The Ca–D distances within the Ca4D-tetrahedra reach from 2.15 Å to 2.54 Å.
2.1.2. Bragg Diffraction and Rietveld Analysis
The structural model of CaSiD1.1 was refined using X-ray and neutron diffraction data simultaneously (Figure 4, Table 1). Furthermore, the structure of the hydride CaSiH≈1.1 was refined using laboratory X-ray data (hydrogen positions fixed according to CaSiD1.1; data not shown). All crystallographic data are available in the Supplementary Materials.
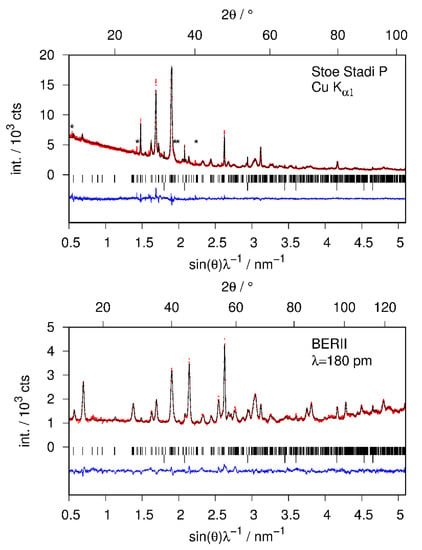
Figure 4.
Rietveld of the crystal structure of CaSiD1.1 (Pnma) using X-ray (top) and neutron diffraction data (bottom) simultaneously; Rwp = 4.20%, Rp = 3.20%, GoF = 1.90; Bragg marker are: top row CaSiD1.1, bottom row CaO (2 wt %); (*) marks an unidentified impurity phase already present in the pristine Zintl phase (see text); red points, observed intensity; black line, calculated intensity; blue line, difference plot.
The crystal structure refinements suffer from various complications. The reflection profiles are strongly broadened compared to the pristine Zintl phase. These effects are furthermore anisotropic. Reflections with a large k-component are much narrower than the remaining ones. This effect was treated by the empirical Stephens model [] in Rietveld refinements, as implemented in TOPAS []. The anisotropic broadening effect can be sufficiently described by the two parameters S400 and S004 with a fixed profile mixing parameter of 1.0 (pure Lorentzian type) and might arise from anisotropic crystallite size broadening. A previous report states that the compound tends to delaminate perpendicular to the crystallographic a axis as determined from SEM images []. Since the polyanions run along the crystallographic b direction, it appears reasonable that (0k0) reflections are the sharpest ones.
The atomic parameters were refined with one Debye–Waller factor per atom type. Two of the tetrahedral Ca4 voids are filled (SOF(D1) = 1 (fixed during the last cycle), SOF(D2) = 0.95(3)), which is in agreement with the PDF-model. The D3 site shows a lower occupancy of about 80%. A free refinement of the silicon-bound deuterium position leads to a short Si1–D4 bond smaller than 1.40 Å, which is chemically unreasonable and contradicts total scattering data. The overall contribution of the D4 site to the diffraction pattern is quite small. Thus, a soft restraint was used to force the Si–D bond length to fit the PDF-derived value of 1.53 Å. The effect of different restraint distances on the goodness of fit (GoF) is small, i.e., well below 1% (Figure 5). Since the effect on the overall profile fitting is small, and considering the PDF analysis, the usage of a bond-length restraint is justified.
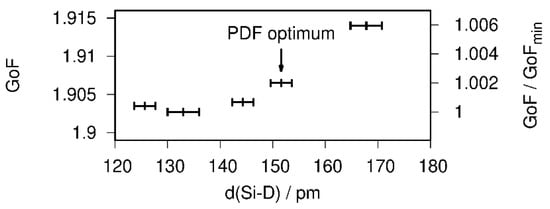
Figure 5.
Influence of the Si–D bond length on the goodness of fit (GoF) of the Rietveld refinement of the crystal structure of CaSiD1.1 (space group Pnma) based on neutron diffraction data.
The restraint crystallographic model gives a Si–D bond length of 1.52(3) Å in a Rietveld refinement (Figure 4). The occupancy of the D4 site is 0.468(15). The Si–Si distance within the chain is 2.382(6) Å long, while the chain connecting bond is 2.621(9) Å. Within the Ca4D-tetraheda the Ca–D distances reach from 2.104(16) to 2.479(15) Å.
2.2. In Situ Diffraction of the Hydrogenation Reaction and Hydrogen-Poor Phases
The hydrogenation of CaSi was monitored by in situ neutron powder diffraction. Heating the pristine Zintl phase to 520 K before pressurizing the in situ cell suppresses the formation of CaSiD1.1. Instead, deuterium-poor phases CaSiD<1 are formed. Fast heating under deuterium pressure leads to the same result. Deuterium uptake starting from the pristine phase takes about 10 min to finish. Subsequent dedeuteration (vacuum) and redeuteration (about 5 MPa D2) cycles are very fast with less than 1 min until completion.
In a first step, CaSi reacted at 524 K and 5.5 MPa D2 pressure (Table 2, (a)). Deuterium was released from the sample, reducing the gas pressure to 0.2 MPa (Table 2, (d)). In a second step, the sample was redeuterated at 3 MPa D2 (Table 2, (b)), again dedeuterated at 0.2 MPa (Table 2, (e)), and finally under applied vacuum (≈1 Pa, Table 2, (f)). In the end, the gas pressure was increased to 5.5 MPa again (Table 2, (c)), leading to the largest hydrogen incorporation.

The hydrogen-poor phases CaSiD<1 keep the structure of the pristine Zintl phase (Figure 6). Tetrahedral Ca4 voids get partially filled. The occupation of the voids SOF = x corresponds to the chemical formula CaSiDx. Experimental conditions, compositions, and selected structural parameters can be found in Table 2. Rietveld profiles are given in Figure 7.
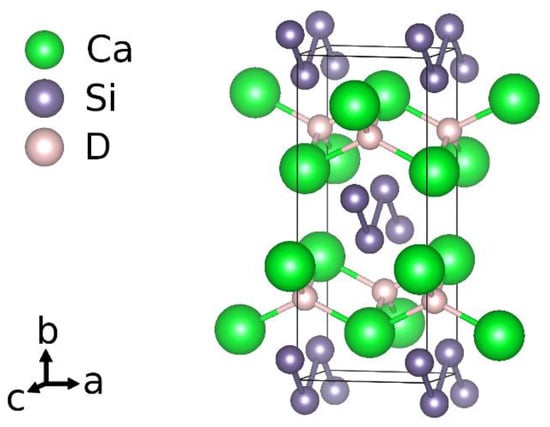
Figure 6.
Crystal structure of the deuterium-poor phase CaSiDx. The tetrahedral Ca4 voids are partially filled. The SOF(D) corresponds to x in the chemical formula.
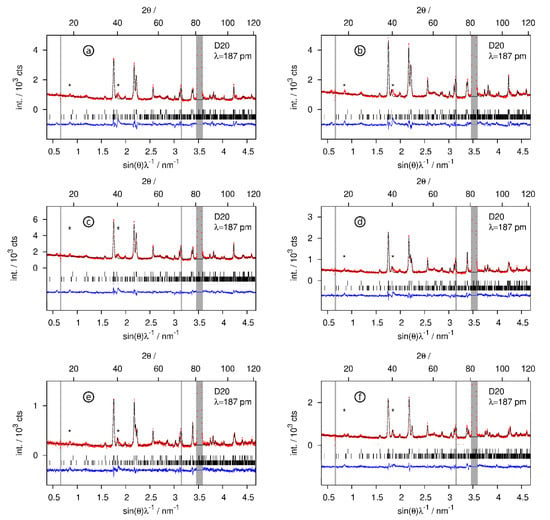
Figure 7.
Rietveld refinements of the crystal structures of the deuterium-poor CaSiDx<1 phases. Neutron diffraction data were collected in situ according to the conditions given in Table 2. The grey regions correspond to contributions of the sapphire cell. (*) marks unidentified peaks already present in the pristine Zintl phase. Bragg markers: CaSiDx (top) and Ca14Si17 (bottom). (a) CaSiD0.126(6) (first deuteration cycle), (b) CaSiD0.137(5), (c) CaSiD0.168(6), (d) CaSiD0.092(5), (e) CaSiD0.096(6), (f) CaSiD0.047(5). Red points, observed intensity; black line, calculated intensity; blue line, difference plot.
3. Discussion
3.1. The Crystal Structure of CaSiD1.1
The crystal structure of CaSiD1.1 was determined by complementary techniques, i.e., a Rietveld and a PDF analysis. Both evaluations give a conclusive picture. The structural model originally described by Ohba et al. [] can be confirmed. On the other hand, we do not find any indication of the presence of a phase that corresponds to the structure or the composition as described by Wu et al. []. The compound CaSiD1.1 exhibits a polyanionic hydride moiety with a short Si–D distance of 1.53 Å. This is clearly in a covalent range and agrees well with a recent nuclear magnetic resonance study that estimates the bond length as 1.56(1) Å []. The silicon bound deuterium position is heavily under-occupied with only 35% ≤ SOF ≤ 46%. There is a discrepancy between PDF and Rietveld analysis. The collection of total scattering data was done about one year after the Bragg diffraction study. The deuterium content of CaSiD1.1 might be variable in a small range. We found such an indication also for a similar compound, SrGeD1.2 []. Except for the SOF, the overall agreement between PDF and Rietveld analysis is considerable, as shown for the polyanion (Figure 8).

Figure 8.
Comparison of the polyanionic structures as determined by the PDF and the Rietveld model (with constrained Si–D distance). The overlay of both models is shown in the middle.
While tetrahedral voids are usually considered to be fully occupied by hydrogen atoms, we find a significant under-occupation of the D3 site. This position shows the shortest distance to the also under-occupied silicon bound D4 position. The SOF of the D2 and D1 site are not significantly different from unity (SOF(D1) was actually fixed during the last refinement cycles).
3.2. Deuterium-Poor Phases
Hydrogen-poor phases CaSiDx<1 were identified in in situ experiments. These phases keep the structure of the pristine Zintl phase without any indication of deuterium ordering in the tetrahedral Ca4 voids. They therefore can be compared to α-BaGeDx, α-BaSnDx [], and α-SrGeDx [], which all show a deuterium content x < 0.5. It was argued before that the formation of hydride/deuteride anions leads to a partial oxidation of the Si2− zigzag chains. Since π* bands get depopulated, the Si–Si bond length should decrease. Such a trend can indeed be seen (Table 2), but the effect is smaller than the estimated error.
Deuterium incorporation leads to an anisotropic expansion of the unit cell (Figure 9). The effect on lattice parameters is strongly anisotropic; a decreases, b expands, and c, which is the direction of the Si zigzag chains, is hardly affected. This is quite typical for the deuterium-poor phases [,].
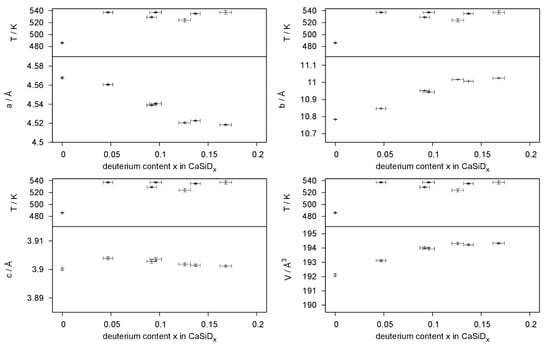
Figure 9.
Change of lattice parameters and unit cell volume with respect to the deuterium incorporation.
The first deuterium uptake is a slow process. After an initial deuteration, compositional changes are very fast in regard to deuterium pressure changes. It is not possible to remove all of the deuterium from the structure. Similar results were found when desorption isotherms were determined [].
4. Conclusions
The crystal structure of the Zintl phase hydride CaSiH≈4/3 was controversial with regard to the nature of the interaction between silicon and hydrogen atoms. A combined neutron powder and total scattering study on the deuteride CaSiD1.1 clearly shows a Si–D distance of 1.53 Å, which is in the range of typical covalent bonds. Therefore, a description with a limiting ionic formula Ca2+H(Si−)2/3(SiH−)1/3 gives an appropriate description. It is emphasizing the main structural features, hydride anions in Ca4 tetrahedra and silicon-hydrogen polyanions consisting of a ribbon-like polyanion made of three zigzag chains decorated by covalently bound hydrogen atoms. The latter position is under-occupied, thus resulting in a composition CaSiH1.1. The crystal structure is isotypic to those of SrGeH≈4/3 and BaSnH≈4/3, and closely related to those of SrSiH≈5/3, BaGeH≈5/3, and BaSiH≈2, which also show hydrogen decorated group 14 element polyanions.
In situ neutron powder diffraction showed that at 520 K deuterium-poor phases CaSiD<1 form upon increasing the deuterium pressure instead of CaSiD1.1. While the initial deuterium uptake starting from the pristine phase takes about 10 min to finish, subsequent cycles complete in less than 1 min. Such fast kinetics is beneficial for the potential use as hydrogen storage material. The crystal structure is that of the Zintl phase with hydride ions residing in tetrahedral Ca4 voids with occupation 0.05 ≤ x ≤ 0.17 in CaSiDx, depending on temperature and deuterium pressure.
This study underlines the rich structural chemistry of Zintl phase hydrides. It further shows the limits of powder diffraction methods in cases where complications like pseudo-symmetry, anisotropic reflection broadening, high defect concentration, and the presence of light elements diminish the information content of diffraction data and the averaging character of diffraction methods blurs certain structural features. In such cases, methods like total scattering, nuclear magnetic resonance, and quantum-mechanical, calculations are indispensable for a complete picture of the crystal structure.
5. Materials and Methods
All educts and samples were handled in an argon filled glove box. Moisture and oxygen content were each kept below 1 ppm. Indeed, CaSiD1.1/CaSiH1.1 is stable in air over months and decomposes only slowly in water.
The Zintl phase CaSi was prepared from stoichiometric mixtures of the elements (Si: abcr, (Karlsruhe, Germany), 99.9999%; Ca: Alfa Aesar, (Kandel, Germany), 99.5%) using tantalum metal jackets which were subsequently sealed and fused into silica ampoules at reduced pressure. They were heated with 2.2 K·min−1 to 1573 K and kept there for one hour. The samples then were annealed at 1473 K for 12 h. According to the literature, the CaSi containing ampoules need to be fast-quenched in cold water to obtain samples reactive towards hydrogen [,,]. We want to emphasize that this step is a crucial one.
The deuterides were prepared in a Nicrofer 5219Nb-alloy 718 autoclave (home built) at deuterium gas pressures of 15 MPa and 523 K. The samples were annealed for 72 h.
X-ray diffraction was done on a laboratory Stadi P diffractometer (STOE & Cie, Darmstadt, Germany). The instrument is equipped with a sealed copper X-ray tube and a germanium monochromator (Cu Kα1 radiation). Data were collected with a position sensitive Mythen 1K silicon-strip detector. Measurements were done in Debye-Scherrer geometry using 0.2 mm glass capillaries.
Neutron powder diffraction was performed at the E9 FIREPOD diffractometer [] at the reactor source BERII of the Helmholtz-Zentrum Berlin (HZB), Germany on samples enclosed in 6 mm vanadium cans at a constant wave length of 1.7982 Å.
In situ neutron diffraction of the deuteration process was performed at the D20 instrument [] at the reactor source of the Institut-Laue-Langevin (ILL), Grenoble, France. The experiments were done in home-build sapphire single-crystal cells attached to a gas supply system. Heating was realised by two infrared laser beams. Details of the setup were already described elsewhere [,]. Measurements were done at a constant wavelength of 1.86829 Å.
Powder diffraction data were treated by the Rietveld method [,] as implemented in the program Topas [].
Neutron total scattering experiments were done at the time-of-flight (TOF) instrument POLARIS [,] of ISIS spallation source, Didcot, UK, on samples enclosed in 8 mm vanadium cans. Data and Proposal information can be accessed under reference []. Data reduction was done using the GunrunN package []. Data were corrected for background using measurements of an empty vanadium can and the empty instrument. To get an absolute data scale, intensities were normalized to the measurement of a vanadium rod with 5 mm diameter. The maximum of reciprocal space data used for the Fourier transformation was set to 39 Å−1. The minimum real space radius for the Fourier transform was set to 1.15 Å.
The obtained real space pair distribution function was evaluated using small box modelling. A crystallographic model (full symmetry) was fitted to the data using pdfGUI [].
All graphs were prepared using the program Gnuplot []. Molecular and crystal structures were prepared using VESTA [,].
Supplementary Materials
The following are available online at https://www.mdpi.com/2304-6740/7/9/106/s1; CIF and checkCIF output files for the following compounds with file names compound datasource (COD-number; CSD-number). CaSiHx_stoe.cif (3000246; 1918684), CaSiD0.047_ILL.cif (3000247; 1918677), CaSiD0.092_ILL.cif (3000248; 1918678), CaSiD0.096_ILL.cif (3000249; 1918679), CaSiD0.126_ILL.cif (3000250; 1918680), CaSiD0.137_ILL.cif (3000251; 1918681), CaSiD0.168_ILL.cif (3000252; 1918682), CaSiD1.2_BERII.cif (3000253; 1918683). CIFs may also be obtained from the Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (Fax: +49-7247-808-666; E-Mail: crysdata@fiz-karlsruhe.de, http://www.fiz-karlsruhe.de/request for deposited data.html) on quoting the depository numbers CSD-1918677 (CaSiD0.047), CSD-1918678 (CaSiD0.092), CSD-1918679 (CaSiD0.096), CSD-1918680 (CaSiD0.126), CSD-1918681 (CaSiD0.137), CSD-1918682 (CaSiD0.168), CSD-1918683 (CaSiD1.1) and CSD-1918684 (CaSiH1.1); The crystallographic data are also available free of charge at the Crystallographic Open Database (COD) under the following deposition numbers: 3000247 (CaSiD0.047), 3000248 (CaSiD0.092), 3000249 (CaSiD0.096), 3000250 (CaSiD0.126), 3000251 (CaSiD0.137), 3000252 (CaSiD0.168), 3000253 (CaSiD1.1) and 3000246 (CaSiH1.1).
Author Contributions
Conceptualization, H.A. and H.K.; methodology, H.A.; validation, H.A. and F.Y.; formal analysis, H.A.; investigation, H.A., F.Y., H.Y.P., A.F. and T.C.H.; writing—original draft preparation, H.A and F.Y.; writing—review and editing, all authors; visualization, H.A.; supervision, H.K.; funding acquisition, H.K. and H.A.
Funding
This research was funded by DEUTSCHE FORSCHUNGSGEMEINSCHAFT (DFG), grant number KO1803/7 and FONDS DER CHEMISCHEN INDUSTRIE, grant number 194371.
Acknowledgments
We thank Helmholtz-Zentrum Berlin (Berlin, Germany), Institut Laue-Langevin (Grenoble, France) and The ISIS Facility (Didcot, UK) for the allocation of neutron radiation beamtime.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- Gingl, F.; Vogt, T.; Akiba, E. Trigonal SrAl2H2: the first Zintl phase hydride. J. Alloys Compd. 2000, 306, 127–132. [Google Scholar] [CrossRef]
- Björling, T.; Noréus, D.; Häussermann, U. Polyanionic Hydrides from Polar Intermetallics AeE2 (Ae = Ca, Sr, Ba; E = Al, Ga, In). J. Am. Chem. Soc. 2006, 128, 817–824. [Google Scholar] [CrossRef]
- Lee, M.H.; Björling, T.; Hauback, B.C.; Utsumi, T.; Moser, D.; Bull, D.; Noréus, D.; Sankey, O.F.; Häussermann, U. Crystal structure, electronic structure, and vibrational properties of MAlSiH (M = Ca, Sr, Ba): Hydrogenation-induced semiconductors from the AlB2-type alloys MAlSi. Phys. Rev. B 2008, 78, 195209. [Google Scholar] [CrossRef]
- Lee, M.H.; Evans, M.J.; Daemen, L.L.; Sankey, O.F.; Häussermann, U. Vibrational Property Study of SrGa2H2 and BaGa2H2 by Inelastic Neutron Scattering and First Principles Calculations. Inorg. Chem. 2008, 47, 1496–1501. [Google Scholar] [CrossRef]
- Evans, M.J.; Holland, G.P.; Garcia-Garcia, F.J.; Häussermann, U. Polyanionic Gallium Hydrides from AlB2-Type Precursors AeGaE (Ae = Ca, Sr, Ba; E = Si, Ge, Sn). J. Am. Chem. Soc. 2008, 130, 12139–12147. [Google Scholar] [CrossRef] [PubMed]
- Kranak, V.F.; Evans, M.J.; Daemen, L.L.; Proffen, T.; Lee, M.H.; Sankey, O.F.; Häussermann, U. Structural and dynamic properties of the polyanionic hydrides SrAlGeH and BaAlGeH. Solid State Sci. 2009, 11, 1847–1853. [Google Scholar] [CrossRef]
- Evans, M.J.; Kranak, V.F.; Garcia-Garcia, F.J.; Holland, G.P.; Daemen, L.L.; Proffen, T.; Lee, M.H.; Sankey, O.F.; Häussermann, U. Structural and Dynamic Properties of BaInGeH: A Rare Solid-State Indium Hydride. Inorg. Chem. 2009, 48, 5602–5604. [Google Scholar] [CrossRef]
- Evans, M.J.; Lee, M.H.; Holland, G.P.; Daemen, L.L.; Sankey, O.F.; Häussermann, U. Vibrational properties of the gallium monohydrides SrGaGeH, BaGaSiH, BaGaGeH, and BaGaSnH. J. Solid State Chem. 2009, 182, 2068–2073. [Google Scholar] [CrossRef]
- Häussermann, U.; Kranak, V.F.; Puhakainen, K. Hydrogenous Zintl Phases: Interstitial Versus Polyanionic Hydrides. Struct. Bond. 2010, 139, 143–161. [Google Scholar] [CrossRef]
- Ångström, J.; Johansson, R.; Sarkar, T.; Sørby, M.H.; Zlotea, C.; Andersson, M.S.; Nordblad, P.; Scheicher, R.H.; Häussermann, U.; Sahlberg, M. Hydrogenation-Induced Structure and Property Changes in the Rare-Earth Metal Gallide NdGa: Evolution of a [GaH]2− Polyanion Containing Peierls-like Ga–H Chains. Inorg. Chem. 2016, 55, 345–352. [Google Scholar] [CrossRef]
- Auer, H.; Nedumkandathil, R.; Häussermann, U.; Kohlmann, H. The Hydrogenation of the Zintl Phase NdGa Studied by in situ Neutron Diffraction. Z. Anorg. Allg. Chem. 2019, 645, 175–181. [Google Scholar] [CrossRef]
- Nedumkandathil, R.; Kranak, V.F.; Johansson, R.; Ångström, J.; Balmes, O.; Andersson, M.S.; Nordblad, P.; Scheicher, R.H.; Sahlberg, M.; Häussermann, U. Hydrogenation Induced Structure and Property Changes in GdGa. J. Solid State Chem. 2016, 239, 184–191. [Google Scholar] [CrossRef]
- Werwein, A.; Benndorf, C.; Bertmer, M.; Franz, A.; Oeckler, O.; Kohlmann, H. Hydrogenation Properties of LnAl2 (Ln = La, Eu, Yb), LaGa2, LaSi2 and the Crystal Structure of LaGa2H0.71(2). Crystals 2019, 9, 193. [Google Scholar] [CrossRef]
- Aoki, M.; Ohba, N.; Noritake, T.; Towata, S. Reversible hydriding and dehydriding properties of CaSi: Potential of metal silicides for hydrogen storage. Appl. Phys. Lett. 2004, 85, 387–388. [Google Scholar] [CrossRef]
- Ohba, N.; Aoki, M.; Noritake, T.; Miwa, K.; Towata, S.-i. Development of New Hydrogen Storage Material CaSi Theoretical Prediction and Experiment. RD Rev. Toyota CRDL 2004, 39, 40–45. [Google Scholar]
- Aoki, M.; Ohba, N.; Noritake, T.; Towata, S.-i. Hydriding and dehydriding properties of CaSi. J. Alloys Compd. 2005, 404, 402–404. [Google Scholar] [CrossRef]
- Ohba, N.; Aoki, M.; Noritake, T.; Miwa, K.; Towata, S.-i. First-principles study of a hydrogen storage material CaSi. Phys. Rev. B 2005, 72, 075104. [Google Scholar] [CrossRef]
- Auer, H.; Guehne, R.; Bertmer, M.; Weber, S.; Wenderoth, P.; Hansen, T.C.; Haase, J.; Kohlmann, H. Hydrides of Alkaline Earth-Tetrel (AeTt) Zintl Phases: Covalent Tt–H Bonds from Silicon to Tin. Inorg. Chem. 2017, 56, 1061–1071. [Google Scholar] [CrossRef]
- Auer, H.; Schlegel, R.; Oeckler, O.; Kohlmann, H. Structural and Electronic Flexibility in Hydrides of Zintl Phases with Tetrel-Hydrogen and Tetrel-Tetrel Bonds. Angew. Chem. Int. Ed. 2017, 56, 12344–12347. [Google Scholar] [CrossRef]
- Auer, H.; Schlegel, R.; Oeckler, O.; Kohlmann, H. Strukturelle und elektronische Flexibilität in Hydriden von Zintl-Phasen mit Tetrel-Wasserstoff- und Tetrel-Tetrel-Bindung. Angew. Chem. 2017, 129, 12515–12518. [Google Scholar] [CrossRef]
- Wu, H.; Zhou, W.; Udovic, T.J.; Rush, J.J.; Yildirim, T. Structure and hydrogen bonding in CaSiD1+x Issues about covalent bonding. Phys. Rev. B 2006, 74, 224101. [Google Scholar] [CrossRef]
- Armbruster, M.; Wörle, M.; Krumeich, F.; Nesper, R. Structure and Properties of Hydrogenated Ca, Sr, Ba, and Eu Silicides. Z. Anorg. Allg. Chem. 2009, 635, 1758–1766. [Google Scholar] [CrossRef]
- Guehne, R.; Auer, H.; Kohlmann, H.; Haase, J.; Bertmer, M. Determination of element-deuterium bond lengths in Zintl phase deuterides by 2H-NMR. Phys. Chem. Chem. Phys. 2019, 21, 10594–10602. [Google Scholar] [CrossRef] [PubMed]
- Stephens, P.W. Phenomenological model of anisotropic peak broadening in powder diffraction. J. Appl. Crystallogr. 1999, 32, 281–289. [Google Scholar] [CrossRef]
- Bruker AXS. TOPAS Version 5. Available online: www.bruker-axs.com (accessed on 25 June 2019).
- Auer, H.; Weber, S.; Hansen, T.C.; Többens, D.M.; Kohlmann, H. Reversible hydrogenation of the Zintl phases BaGe and BaSn studied by in situ diffraction. Z. Kristallogr. Cryst. Mater. 2018, 233, 399–409. [Google Scholar] [CrossRef]
- Auer, H.; Wallacher, D.; Hansen, T.C.; Kohlmann, H. In Situ Hydrogenation of the Zintl Phase SrGe. Inorg. Chem. 2017, 56, 1072–1079. [Google Scholar] [CrossRef] [PubMed]
- Anikina, E.Y.; Verbetsky, V.N. Investigation of hydrogen desorption from CaSiH by means of calorimetric method. J. Therm. Anal. Calorim. 2014, 118, 801–805. [Google Scholar] [CrossRef]
- Wenderoth, P. Untersuchungen zur Hydridbildung von Zintl-Phasen der Erdalkalimetalle mit Aluminium, Gallium und Silicium. Ph.D. Thesis, Universität des Saarlandes, Saarbrücken, Germany, 2014. [Google Scholar]
- Franz, A.; Hoser, A. E9: The Fine Resolution Powder Diffractometer (FIREPOD) at BER II. J. Large-Scale Res. Facil. 2017, 3, A103. [Google Scholar] [CrossRef]
- Hansen, T.C.; Henry, P.F.; Fischer, H.E.; Torregrossa, J.; Convert, P. The D20 instrument at the ILL: A versatile high-intensity two-axis neutron diffractometer. Meas. Sci. Technol. 2008, 19, 034001. [Google Scholar] [CrossRef]
- Kohlmann, H.; Kurtzemann, N.; Weihrich, R.; Hansen, T. In situ Neutron Powder Diffraction on Intermediate Hydrides of MgPd3 in a Novel Sapphire Gas Pressure Cell. Z. Anorg. Allg. Chem. 2009, 635, 2399–2405. [Google Scholar] [CrossRef]
- Götze, A.; Auer, H.; Finger, R.; Hansen, T.; Kohlmann, H. A sapphire single-crystal cell for in situ neutron powder diffraction of solid-gas reactions. Phys. B 2018, 551, 395–400. [Google Scholar] [CrossRef]
- Rietveld, H.M. Line profiles of neutron powder-diffraction peaks for structure refinement. Acta Crystallogr. 1967, 22, 151–152. [Google Scholar] [CrossRef]
- Rietveld, H.M. A profile refinement method for nuclear and magnetic structures. J. Appl. Crystallogr. 1969, 2, 65–71. [Google Scholar] [CrossRef]
- Hull, S.; Smith, R.I.; David, W.I.F.; Hannon, A.C.; Mayers, J.; Cywinski, R. The Polaris powder diffractometer at ISIS. Phys. B 1992, 180, 1000–1002. [Google Scholar] [CrossRef]
- Smith, R.I.; Hull, S.; Tucker, M.; Playford, H.Y.; McPhail, D.; Waller, S.; Norberg, S. The Upgraded Polaris Powder Diffractometer at ISIS. Rev. Sci. Inst. 2019. submitted for publication. [Google Scholar]
- Kohlmann, H.; Auer, H.; Playford, H.Y. Total scattering of Zintl phase deuterides CaSiD1.3, BaSiD1.9 and SrGeD1.3. STFC ISIS Neutron Muon Source 2018. [Google Scholar] [CrossRef]
- Soper, A.K. GudrunN and GudrunX programs for correcting raw neutron and X-ray diffraction data to differential scattering cross section, RAL Technical Report; Science and Technology Facilities Council: Oxforf, UK, 2011. [Google Scholar]
- Farrow, C.L.; Juhas, P.; Liu, J.W.; Bryndin, D.; Bozin, E.S.; Bloch, J.; Proffen, T.; Billinge, S.J.L. PDFfit2 and PDFgui: computer programs for studying nanostructure in crystals. J. Phys. Condens. Matter 2007, 19, 335219. [Google Scholar] [CrossRef] [PubMed]
- GNUPLOT Version 5.0, Patchlevel 7. Available online: http://www.gnuplot.info (accessed on 25 June 2019).
- VESTA—Visualisation for Electronic and Structural Analysis. Version 3.3.1. Koichi Momma and Fujio Izumi: Ibaraki, Japan, 2018.
- Momma, K.; Izumi, F. VESTA3 for three-dimensional visualization of crystal, volumetric and morphology data. J. Appl. Crystallogr. 2011, 44, 1272–1276. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).