Next Article in Journal
Controlling the Lifetime of the Triplet MLCT State in Fe(II) Polypyridyl Complexes through Ligand Modification
Next Article in Special Issue
Photophysical and Electrocatalytic Properties of Rhenium(I) Triazole-Based Complexes
Previous Article in Journal / Special Issue
Excited-State Relaxation in Luminescent Molybdenum(0) Complexes with Isocyanide Chelate Ligands
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Inorganics
Volume 8
Issue 2
10.3390/inorganics8020015
inorganics-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Communication

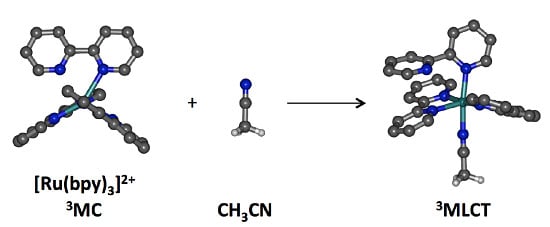
On the Possible Coordination on a 3MC State Itself? Mechanistic Investigation Using DFT-Based Methods

by
Adrien Soupart
,
Fabienne Alary
,
Jean-Louis Heully
and
Isabelle M. Dixon
*
Laboratoire de Chimie et Physique Quantiques, UMR 5626 CNRS/Université Toulouse 3-Paul Sabatier, Université de Toulouse, 118 route de Narbonne, 31062 Toulouse, France
*
Author to whom correspondence should be addressed.
Inorganics 2020, 8(2), 15; https://doi.org/10.3390/inorganics8020015
Submission received: 30 January 2020 / Revised: 14 February 2020 / Accepted: 16 February 2020 / Published: 19 February 2020
(This article belongs to the Special Issue Photochemistry & Photophysics of Transition Metal Complexes)
Browse Figures
Versions Notes

Abstract

:
Understanding light-induced ligand exchange processes is key to the design of efficient light-releasing prodrugs or photochemically driven functional molecules. Previous mechanistic investigations had highlighted the pivotal role of metal-centered (MC) excited states in the initial ligand loss step. The question remains whether they are equally important in the subsequent ligand capture step. This article reports the mechanistic study of direct acetonitrile coordination onto a 3MC state of [Ru(bpy)3]2+, leading to [Ru(bpy)2(κ1-bpy)(NCMe)]2+ in a 3MLCT (metal-to-ligand charge transfer) state. Coordination of MeCN is indeed accompanied by the decoordination of one pyridine ring of a bpy ligand. As estimated from Nudged Elastic Band calculations, the energy barrier along the minimum energy path is 20 kcal/mol. Interestingly, the orbital analysis conducted along the reaction path has shown that creation of the metallic vacancy can be achieved by reverting the energetic ordering of key dσ* and bpy-based π* orbitals, resulting in the change of electronic configuration from 3MC to 3MLCT. The approach of the NCMe lone pair contributes to destabilizing the dσ* orbital by electrostatic repulsion.

Graphical Abstract

1. Introduction

The photophysics of ruthenium polypyridine compounds is governed by the subtle balance between the population of two types of triplet excited states of similar energies: metal-to-ligand charge transfer states (MLCT) and metal-centered states (MC) [1]. 3MLCT states are photoluminescent, contrary to 3MC states, which quench the luminescence and may lead to ligand loss [2]. Forty years of spectroscopic studies on this family of compounds have provided a wealth of robust experimental data, but MC states are spectroscopically “dark” and therefore their theoretical characterization is essential in the rationalization and the anticipation of photophysical properties. For more than a decade, we have been able to optimize 3MC excited states [3] and to explore the topology of the lowest triplet potential energy surface using DFT-based methods [4,5,6,7,8,9]. Spectacular bond elongations and angular distortions have been characterized in numerous Ru(II) 3MC states [10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28] and for other metals, e.g., Ir(III) [29,30,31]. Our contribution to the field covers photoisomerization mechanisms [32,33,34] and photoluminescence quenching mechanisms [35,36], as well as exploratory ruthenium(II) [37,38] and iron(II) [39,40,41,42] photophysics, in a constant dialogue with experimental chemists.
In the course of our theoretical investigations of photosubstitution mechanisms, we have identified some key 3MC states along the pathways for ligand photorelease, particularly pentacoordinate or pseudopentacoordinate species [7,8]. In that work, these 3MC states have been considered to be involved in such mechanisms via intersystem crossing (ISC) through a neighboring minimum energy crossing point (MECP), allowing the system to populate an electrophilic, coordinatively unsaturated, and closed-shell species. The final coordination of a molecule of incoming ligand is thought to be an efficient process [43,44,45,46,47] and yields a κ1-bound intermediate product that requires the absorption of a second photon to fully release the departing bidentate ligand [48,49]. However an alternative pathway can also be envisaged, overall requiring only one photon, namely the direct reaction between the incoming ligand and the complex in its distorted 3MC state, to form a new complex with triplet spin multiplicity according to Wigner rules. The aim of this work was therefore to investigate this type of reactivity through DFT-based methods, computing minimum energy paths using Nudged Elastic Band calculations and undertaking a thorough orbital analysis along this path. The model reaction we chose is the approach of an acetonitrile molecule on the previously reported 3MCcis state of Ru(bpy)32+ [50]. This state, repelling the two pyridine fragments of a single bpy ligand, is thought to be prone to bpy loss, or at least more prone than the classical 3MCtrans state that repels two pyridines from two different ligands (Figure 1).
Acetonitrile was selected for its charge neutrality, for being a reactant that bears only one lone pair, and for being an aprotic and weakly self-associating solvent, that allows us to consider the approach of a single NCMe molecule as a reasonable model. The aim of this work was to envisage direct NCMe coordination on the 3MCcis state of Ru(bpy)32+ in order to form an intermediate triplet state bearing one monodentate bpy and one bound acetonitrile ligand (Scheme 1). This process was found to have an energy barrier of 20 kcal/mol. Analysis of the coordination process from an orbital perspective has shown that MeCN approach and change in electronic configuration from 3MC to 3MLCT were intimately related.

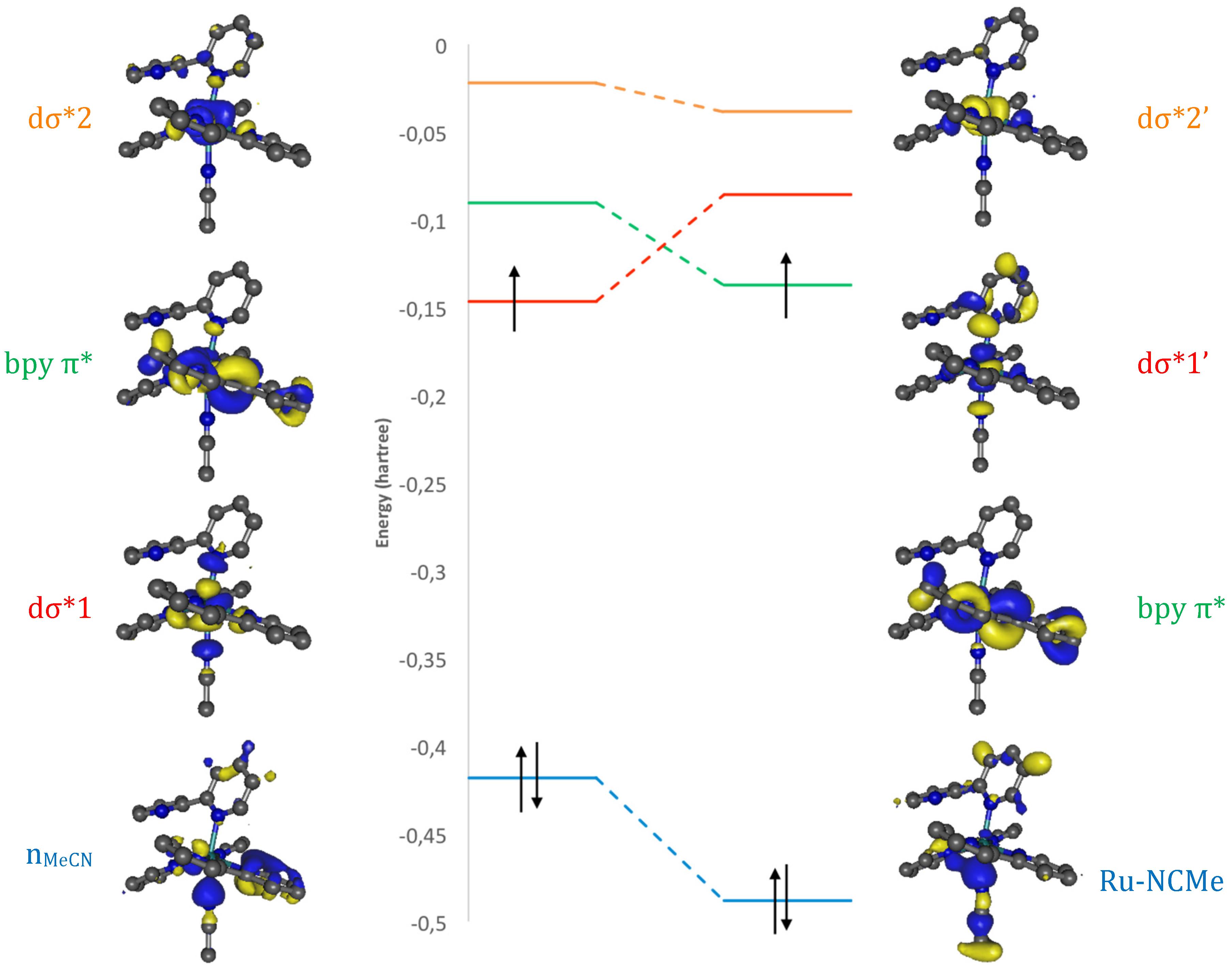
2. Results and Discussion

Working on the photoinduced loss of bidentate ligands, Elliott et al. reported the crystallographic characterization of intermediate photoproducts of the type trans-[Ru(bpy)(κ2-btz)(κ1-btz)(NCMe)]2+ bearing a singly-bound bitriazolyl (btz) ligand [48,49]. By analogy we have built and optimized trans-[Ru(bpy)2(κ1-bpy)(NCMe)]2+ in a singlet state, from which an excited state with triplet spin multiplicity was subsequently optimized by unrestricted DFT. This state is unambiguously of MLCT electronic nature and was used as endpoint for a minimum energy path calculation. This state contains a bpy ligand that is a monodentate, κ1-bpy ligand. The exploration of the envisaged chemical reaction was undertaken starting from the 3MCcis state having an acetonitrile molecule 5 Å away with its lone pair oriented towards the metal, in the most open quadrant of the complex. Note that NCMe is not interacting with the [Ru(bpy)3]2+ moiety in this structure, as estimated from its total energy that is equal to the sum of the fragments’ energies.
At the starting point of the reaction path the complex is in the 3MCcis state. The rationale for this choice lies in its presumed higher propensity for ligand loss than the 3MCtrans state. This is due to its peculiar geometry repelling a single bpy ligand and opening a quadrant, allowing a potentially entering ligand to approach the metal [50]. In the 3MCcis state, two major elongations are found towards the same bpy ligand (Ru–N5 and Ru–N6, Table 1), the opposite quadrant opens up to 121° (Figure 1), and the Mulliken spin population on ruthenium is 1.7. At the end point, the complex contains one monodentate bpy ligand (the pyridine ring containing N5 is rotated out of plane and Ru–N5 = 3.59 Å); the Ru–N6 distance is standard and the two bonds towards the formally anionic bpy ligand are the shortest (Ru–N3 and Ru–N4). The 3MLCT nature of this state is illustrated by its Mulliken spin population on ruthenium, which is 0.9 (the other spin residing on a bpy ligand).
Minimum energy paths (MEPs) can be efficiently computed using the Nudged Elastic Band method [51,52], which discretizes the reaction path into a series of points, called beads. The initial path consists in a series of single point energy calculations along a geometry interpolation, which we perform using the image dependent pair potential (IDPP) method [53]. Subsequently each intermediate bead is minimized using path gradient and tangent information, until convergence to the MEP. The energy gap between the two endpoints is 17 kcal/mol, and a first estimate of the energy barrier for the reaction is 18 kcal/mol, as shown on Figure 2. The energy profile for this reaction appears as having a very moderate slope up to bead 15 (Ru–NCMe distance of 2.77 Å), after which the energy suddenly rises by about 14 kcal/mol at bead 18.
A sudden drop in the Mulliken spin population on ruthenium is apparent between bead 17 and bead 18, signifying a change between MC and MLCT character. Thus, a second nudged elastic band (NEB) calculation was performed to refine this region. For simplicity the beads in this second calculation have been numbered with intermediate values 17.25, 17.50, and 17.75 (Figure 3).
The switch between MC and MLCT states here occurs between beads 17.50 and 17.75, providing a refined energy barrier of 20 kcal/mol. Wiberg bond indices (WBIs) have been computed at all geometries along the reaction path, and have been used to quantify the Ru–N interactions. In the starting 3MC structure, two Ru–N bonds are significantly elongated as a result of the population of an antibonding dσ* orbital, namely Ru–N5 (2.53 Å) and Ru–N6 (2.38 Å). The corresponding WBIs are consequently the lowest, 0.19 and 0.26 respectively (Figure 4). Bonds trans to these, Ru–N4 and Ru–N1, are slightly elongated with WBIs of 0.36 and 0.41. The two remaining bonds, Ru–N2 and Ru–N3, display WBIs that are similar to the ones found in the ground state, i.e., 0.44. Notably the gradual drop in the Ru–N5 WBI along the reaction path is paralleled by a gradual increase in the Ru–NCMe WBI, until bead 17.50 where this latter WBI doubles to reach 0.45 in the 3MLCT state. At the endpoint, the highest two WBIs are the ones to the nitrogen atoms of the formally anionic bpy ligand, N3 (0.51) and N4 (0.54), Ru–N3, and Ru–N4 being the shortest bonds (Table 1). The intermediate zone (between beads 7–14), where WBIs towards departing and incoming ligands are both low, illustrates the fact that the complex gets pentacoordinated and is stabilized by two successive weak Ru–N interactions along this path.
In order to allow the Ru–NCMe bond to form, a low-lying vacancy should be identified on the metal with appropriate symmetry and orientation to enable significant overlap with the incoming nitrogen lone pair. The crucial orbitals in this process are thus: (i) the metallic dσ* orbitals, (ii) the NCMe lone pair that eventually evolves to a Ru–NCMe dative bond, and (iii) the bpy-based π* orbital that will be singly occupied in the final 3MLCT state. The eigenvalues of these four molecular orbitals (MOs) are plotted against bead number on Figure 5. All lines are broken between beads 17.50 and 17.75 to signify the rupture in the correlation diagram, e.g., when the NCMe lone pair is replaced by a bonding Ru–NCMe interaction. At this very point along the path, we propose that the electrostatic repulsion between the NCMe lone pair and the singly occupied dσ*1 orbital (as illustrated by the gradual destabilization of dσ*1 from bead 12 onwards) is such that the dσ*1 is destabilized to a point where its energy is higher than that of the bpy π* orbital. As a result, the electron that was in dσ*1 in the MC state is transferred to the bpy π* orbital, thus producing an MLCT state. This change in electronic configuration is what allows the total energy of the system to decrease towards the endpoint of the path. In addition, the quasi invariance in the energy of dσ*2 confirms that it is always nonbonding towards the incoming ligand.
A close inspection of these crucial orbitals, at beads 17.50 and 17.75 (Figure 6), reveals that the formation of the Ru–NCMe bond is accompanied by a repolarization of both dσ* orbitals, as seen for instance in the disappearance of the Ru–N6 antibonding interaction in dσ*2’. The interaction of dσ*1 with the NCMe lone pair produces two new orbitals: the Ru–NCMe bond and the dσ*1’ antibond (Figure S1). In this system, coordination of the incoming ligand is accompanied by the change of electronic state nature, from 3MC to 3MLCT, which has a vacant dσ*1’ (as stated in the introduction, an alternative to create a metallic vacancy is spin crossing to a closed-shell pentacoordinate singlet state [8,54], which would also vacate the required dσ* orbital).

3. Computational Details and Methods

Geometry optimizations were performed without symmetry with Orca [55] using the B3LYP functional [56,57], a relativistic small core pseudopotential on Ru (SD28) [58], the def2-TZVP(-f) basis set [59], and the empirical D3 dispersion correction [60,61]. Solvent effects were modelled as the SMD polarizable continuum [62]. The restricted Kohn–Sham formalism was used for ground states, while its unrestricted analogue was used for triplet states. SCF convergence was achieved using the DIIS algorithm followed by a semi-quadratic SOSCF converger. Frequency calculations were run at the same level of theory and the absence of imaginary frequencies ascertained the nature of these points as minima. Molecular orbitals were viewed using Gabedit [63]. Mulliken spin densities on Ru were used as a straightforward descriptor of the electronic nature of the triplet excited state (~0.9 for a 3MLCT state, ~1.8 for a 3MC state). Orbital analysis was systematically undertaken to view the localization of the unpaired electrons.
The 3MLCT–3MC minimum energy paths were optimized with the nudged elastic band (NEB) method [51,52] using a python module developed in the Clancy group [64] that is interfaced with Orca. The convergence criterion was set to 0.03 eV/Å. A 20-frame initial path was prepared by interpolating start and end geometries using the IDPP method [53]. The geometries were previously processed using lab-developed programs to minimize the discrepancy between start and end geometries. These calculations were performed at the same level of theory as all the geometry optimizations. Convergence of the MEP was achieved using a combination of FIRE and BFGS algorithms.

4. Conclusions

In this work, we have envisaged the direct addition of an acetonitrile molecule on the 3MCcis state of [Ru(bpy)3]2+, a state that we had proposed to consider as potentially photoreactive [50]. Nudged elastic band calculations have provided an energy barrier of 20 kcal/mol for this model reaction, significantly higher than the energy barrier involved in the spin crossing process towards a pentacoordinate ground state species [54] (note that the former pathway requires a single photon excitation, whereas the latter requires a second photon to fully release the departing bidentate ligand). The orbital analysis we have conducted along the reaction path has enabled us to describe the chemical reaction and the MC–MLCT transition. The change in electronic nature, from 3MC to 3MLCT, is concomitant to the approach of the NCMe lone pair and triggers the interaction between the newly formed metallic vacancy and the NCMe lone pair. In this view, the 3MC state itself can be seen as unable to bind MeCN. It is noteworthy that the approach of an incoming nucleophile is able to perturbate the metal complex so as to modify the electronic nature of its excited state. These results offer an interesting glimpse of processes that could be involved in excited state reaction mechanisms under specific experimental conditions such as pulsed irradiation. We are currently extending this work to the mechanistic study of the subsequent steps, i.e., κ1-bpy ligand loss.

Supplementary Materials

The following are available online at https://www.mdpi.com/2304-6740/8/2/15/s1, Figure S1: MO diagram schematizing the interaction between the metallic fragment in the 3MC state and the approaching acetonitrile ligand; Figure S2: MO diagram at selected points along the reaction path; Cartesian coordinates of the 20 beads along the minimum energy path.

Author Contributions

A.S. performed the research and analyzed the data. I.M.D., F.A. and J.-L.H. conceived and supervised the work, and analyzed the data. I.M.D. wrote the original draft, which F.A. and J.-L.H. reviewed. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Acknowledgments

HPC resources from LCPQ and from CALMIP (p1112 project) are kindly acknowledged.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Juris, A.; Balzani, V.; Barigelletti, F.; Campagna, S.; Belser, P.; von Zelewsky, A. Ru(II) Polypyridine Complexes: Photophysics, Photochemistry, Electrochemistry, and Chemiluminescence. Coord. Chem. Rev. 1988, 84, 85–277. [Google Scholar] [CrossRef]
  2. Van Houten, J.; Watts, R.J. Photochemistry of Tris(2,2’-bipyridyl)ruthenium(II) in Aqueous Solution. Inorg. Chem. 1978, 17, 3381–3385. [Google Scholar] [CrossRef]
  3. Alary, F.; Heully, J.-L.; Bijeire, L.; Vicendo, P. Is the 3MLCT the Only Photoreactive State of Polypyridyl Complexes? Inorg. Chem. 2007, 46, 3154–3165. [Google Scholar] [CrossRef]
  4. Alary, F.; Boggio-Pasqua, M.; Heully, J.-L.; Marsden, C.J.; Vicendo, P. Theoretical Characterization of the Lowest Triplet Excited States of the Tris-(1,4,5,8-tetraazaphenanthrene)Ruthenium Dication Complex. Inorg. Chem. 2008, 47, 5259–5266. [Google Scholar] [CrossRef]
  5. Heully, J.-L.; Alary, F.; Boggio-Pasqua, M. Spin-orbit effects on the photophysical properties of Ru(bpy)32+. J. Chem. Phys. 2009, 131, 184308. [Google Scholar] [CrossRef]
  6. Sanz García, J.; Alary, F.; Boggio-Pasqua, M.; Dixon, I.M.; Heully, J.-L. Is Photoisomerization Required for NO Photorelease in Ruthenium Nitrosyl Complexes? J. Mol. Model. 2016, 22, 284. [Google Scholar] [CrossRef]
  7. Göttle, A.J.; Alary, F.; Boggio-Pasqua, M.; Dixon, I.M.; Heully, J.-L.; Bahreman, A.; Askes, S.H.C.; Bonnet, S. Pivotal Role of a Pentacoordinate 3MC State on the Photocleavage Efficiency of a Thioether Ligand in Ruthenium(II) Complexes: A Theoretical Mechanistic Study. Inorg. Chem. 2016, 55, 4448–4456. [Google Scholar] [CrossRef] [Green Version]
  8. Dixon, I.M.; Heully, J.-L.; Alary, F.; Elliott, P.I.P. Theoretical illumination of highly original photoreactive 3MC states and the mechanism of the photochemistry of Ru(II) tris(bidentate) complexes. Phys. Chem. Chem. Phys. 2017, 19, 27765–27778. [Google Scholar] [CrossRef]
  9. Daniel, C.; Gourlaouen, C. Chemical bonding alteration upon electronic excitation in transition metal complexes. Coord. Chem. Rev. 2017, 344, 131–149. [Google Scholar] [CrossRef]
  10. Abrahamsson, M.; Lundqvist, M.J.; Wolpher, H.; Johansson, O.; Eriksson, L.; Bergquist, J.; Rasmussen, T.; Becker, H.-C.; Hammarström, L.; Norrby, P.-O.; et al. Steric Influence on the Excited-State Lifetimes of Ruthenium Complexes with Bipyridyl–Alkanylene–Pyridyl Ligands. Inorg. Chem. 2008, 47, 3540–3548. [Google Scholar] [CrossRef]
  11. Borg, O.A.; Godinho, S.S.M.C.; Lundqvist, M.J.; Lunell, S.; Persson, P. Computational Study of the Lowest Triplet State of Ruthenium Polypyridyl Complexes Used in Artificial Photosynthesis. J. Phys. Chem. A 2008, 112, 4470–4476. [Google Scholar] [CrossRef]
  12. Österman, T.; Abrahamsson, M.; Becker, H.-C.; Hammarström, L.; Persson, P. Influence of Triplet State Multidimensionality on Excited State Lifetimes of Bis-tridentate Ru(II) Complexes: A Computational Study. J. Phys. Chem. A 2012, 116, 1041–1050. [Google Scholar] [CrossRef]
  13. Fredin, L.A.; Wallenstein, J.; Sundin, E.; Jarenmark, M.; Barbosa de Mattos, D.F.; Persson, P.; Abrahamsson, M. Excited State Dynamics of Bistridentate and Trisbidentate Ru(II) Complexes of Quinoline-Pyrazole Ligands. Inorg. Chem. 2019, 58, 16354–16363. [Google Scholar] [CrossRef] [Green Version]
  14. Salassa, L.; Garino, C.; Salassa, G.; Gobetto, R.; Nervi, C. Mechanism of Ligand Photodissociation in Photoactivable [Ru(bpy)2L2]2+ Complexes: A Density Functional Theory Study. J. Am. Chem. Soc. 2008, 130, 9590–9597. [Google Scholar] [CrossRef]
  15. Salassa, L.; Garino, C.; Salassa, G.; Nervi, C.; Gobetto, R.; Lamberti, C.; Gianolio, D.; Bizzarri, R.; Sadler, P.J. Ligand-Selective Photodissociation from [Ru(bpy)(4AP)4]2+: A Spectroscopic and Computational Study. Inorg. Chem. 2009, 48, 1469–1481. [Google Scholar] [CrossRef]
  16. Borfecchia, E.; Garino, C.; Gianolio, D.; Salassa, L.; Gobetto, R.; Lamberti, C. Monitoring excited state dynamics in cis-[Ru(bpy)2(py)2]2+ by ultrafast synchrotron techniques. Catal. Today 2014, 229, 34–45. [Google Scholar] [CrossRef]
  17. Breivogel, A.; Meister, M.; Förster, C.; Laquai, F.; Heinze, K. Excited State Tuning of Bis(tridentate) Ruthenium(II) Polypyridine Chromophores by Push-Pull Effects and Bite Angle Optimization: A Comprehensive Experimental and Theoretical Study. Chem. Eur. J. 2013, 19, 13745–13760. [Google Scholar] [CrossRef]
  18. Kreitner, C.; Heinze, K. Excited state decay of cyclometalated polypyridine ruthenium complexes: Insight from theory and experiment. Dalton Trans. 2016, 45, 13631–13647. [Google Scholar] [CrossRef] [Green Version]
  19. Sun, Q.; Mosquera-Vazquez, S.; Lawson Daku, L.M.; Guénée, L.; Goodwin, H.A.; Vauthey, E.; Hauser, A. Experimental Evidence of Ultrafast Quenching of the 3MLCT Luminescence in Ruthenium(II) Tris-bipyridyl Complexes via a 3dd State. J. Am. Chem. Soc. 2013, 135, 13660–13663. [Google Scholar] [CrossRef]
  20. Sun, Q.; Dereka, B.; Vauthey, E.; Lawson Daku, L.M.; Hauser, A. Ultrafast Transient IR Spectroscopy and DFT Calculations of Ruthenium(II) Polypyridyl Complexes. Chem. Sci. 2017, 8, 223–230. [Google Scholar] [CrossRef] [Green Version]
  21. Ding, L.; Chung, L.W.; Morokuma, K. Excited-State Proton Transfer Controls Irreversibility of Photoisomerization in Mononuclear Ruthenium(II) Monoaquo Complexes: A DFT Study. J. Chem. Theory Comput. 2014, 10, 668–675. [Google Scholar] [CrossRef]
  22. Greenough, S.E.; Roberts, G.M.; Smith, N.A.; Horbury, M.D.; McKinlay, R.G.; Żurek, J.M.; Paterson, M.J.; Sadler, P.J.; Stavros, V.G. Ultrafast photo-induced ligand solvolysis of cis-[Ru(bipyridine)2(nicotinamide)2]2+: Experimental and theoretical insight into its photoactivation mechanism. Phys. Chem. Chem. Phys. 2014, 16, 19141–19155. [Google Scholar] [CrossRef] [Green Version]
  23. Camilo, M.R.; Cardoso, C.R.; Carlos, R.M.; Lever, A.B.P. Photosolvolysis of cis-[Ru(α-diimine)2(4-aminopyridine)2]2+ Complexes: Photophysical, Spectroscopic, and Density Functional Theory Analysis. Inorg. Chem. 2014, 53, 3694–3708. [Google Scholar] [CrossRef]
  24. Tu, Y.-J.; Mazumder, S.; Endicott, J.F.; Turro, C.; Kodanko, J.J.; Schlegel, H.B. Selective Photodissociation of Acetonitrile Ligands in Ruthenium Polypyridyl Complexes Studied by Density Functional Theory. Inorg. Chem. 2015, 54, 8003–8011. [Google Scholar] [CrossRef] [Green Version]
  25. Nisbett, K.; Tu, Y.-J.; Turro, C.; Kodanko, J.J.; Schlegel, H.B. DFT Investigation of Ligand Photodissociation in [Ru(II)(tpy)(bpy)(py)]2+ and [Ru(II)(tpy)(Me2bpy)(py)]2+ Complexes. Inorg. Chem. 2018, 57, 231–240. [Google Scholar] [CrossRef] [Green Version]
  26. Petroni, A.; Slep, L.D.; Etchenique, R. Ruthenium(II) 2,2’-Bipyridyl Tetrakis Acetonitrile Undergoes Selective Axial Photocleavage. Inorg. Chem. 2008, 47, 951–956. [Google Scholar] [CrossRef]
  27. Rojas Pérez, Y.; Slep, L.D.; Etchenique, R. Cis–Trans Interconversion in Ruthenium(II) Bipyridine Complexes. Inorg. Chem. 2019, 58, 11606–11613. [Google Scholar] [CrossRef]
  28. Feng, L.; Wang, Y.; Jia, J. Triplet Ground-State-Bridged Photochemical Process: Understanding the Photoinduced Chiral Inversion at the Metal Center of [Ru(phen)2(l-ser)]+ and Its Bipy Analogues. Inorg. Chem. 2017, 56, 14467–14476. [Google Scholar] [CrossRef]
  29. Jacquemin, D.; Escudero, D. The Short Device Lifetimes of Blue PhOLEDs: Insights into the Photostability of Blue Ir(III) Complexes. Chem. Sci. 2017, 8, 7844–7850. [Google Scholar] [CrossRef] [Green Version]
  30. Arroliga-Rocha, S.; Escudero, D. Facial and Meridional Isomers of Tris(bidentate) Ir(III) Complexes: Unravelling Their Different Excited State Reactivity. Inorg. Chem. 2018, 57, 12106–12112. [Google Scholar] [CrossRef] [Green Version]
  31. Escudero, D. Mer-Ir(ppy)3 to Fac-Ir(ppy)3 Photoisomerization. ChemPhotoChem 2019, 3, 697–701. [Google Scholar] [CrossRef]
  32. Göttle, A.J.; Dixon, I.M.; Alary, F.; Heully, J.-L.; Boggio-Pasqua, M. Adiabatic Versus Nonadiabatic Photoisomerization in Photochromic Ruthenium Sulfoxide Complexes: A Mechanistic Picture from Density Functional Theory Calculations. J. Am. Chem. Soc. 2011, 133, 9172–9174. [Google Scholar] [CrossRef]
  33. Göttle, A.J.; Alary, F.; Dixon, I.M.; Heully, J.-L.; Boggio-Pasqua, M. Unravelling the S→O Linkage Photoisomerization Mechanisms in cis- and trans-[Ru(bpy)2(DMSO)2]2+ Using Density Functional Theory. Inorg. Chem. 2014, 53, 6752–6760. [Google Scholar] [CrossRef]
  34. Sanz García, J.; Alary, F.; Boggio-Pasqua, M.; Dixon, I.M.; Malfant, I.; Heully, J.-L. Establishing the Two-Photon Linkage Isomerization Mechanism in the Nitrosyl Complex trans-[RuCl(NO)(py)4]2+ by DFT and TDDFT. Inorg. Chem. 2015, 54, 8310–8318. [Google Scholar] [CrossRef]
  35. Lebon, E.; Bastin, S.; Sutra, P.; Vendier, L.; Piau, R.E.; Dixon, I.M.; Boggio-Pasqua, M.; Alary, F.; Heully, J.-L.; Igau, A.; et al. Can a Functionalized Phosphine Ligand Promote Room Temperature Luminescence of the [Ru(bpy)(tpy)]2+ Core? Chem. Commun. 2012, 48, 741–743. [Google Scholar] [CrossRef]
  36. Triadon, A.; Grelaud, G.; Richy, N.; Mongin, O.; Moxey, G.J.; Dixon, I.M.; Yang, X.; Wang, G.; Barlow, A.; Rault-Berthelot, J.; et al. Linear and Third-Order Nonlinear Optical Properties of Fe(η5-C5Me5)(κ2-dppe)- and trans-Ru(κ2-dppe)2-Alkynyl Complexes Containing 2-Fluorenyl End Groups. Organometallics 2018, 37, 2245–2262. [Google Scholar] [CrossRef]
  37. Guillon, T.; Boggio-Pasqua, M.; Alary, F.; Heully, J.-L.; Lebon, E.; Sutra, P.; Igau, A. Theoretical Investigation on the Photophysical Properties of Model Ruthenium Complexes with Diazabutadiene Ligands [Ru(bpy)3−x(dab)x]2+ (x = 1–3). Inorg. Chem. 2010, 49, 8862–8872. [Google Scholar] [CrossRef]
  38. Vieuxmaire, O.P.J.; Piau, R.E.; Alary, F.; Heully, J.-L.; Sutra, P.; Igau, A.; Boggio-Pasqua, M. Theoretical Investigation of Phosphinidene Oxide Polypyridine Ruthenium(II) Complexes: Toward the Design of a New Class of Photochromic Compounds. J. Phys. Chem. A 2013, 117, 12821–12830. [Google Scholar] [CrossRef]
  39. Dixon, I.M.; Alary, F.; Boggio-Pasqua, M.; Heully, J.-L. The (N4C2)2− Donor Set as Promising Motif for Bis(tridentate) Iron(II) Photoactive Compounds. Inorg. Chem. 2013, 52, 13369–13374. [Google Scholar] [CrossRef]
  40. Dixon, I.M.; Khan, S.; Alary, F.; Boggio-Pasqua, M.; Heully, J.-L. Probing the photophysical capability of mono and bis(cyclometallated) Fe(II) polypyridine complexes using inexpensive ground state DFT. Dalton Trans. 2014, 43, 15898–15905. [Google Scholar] [CrossRef]
  41. Dixon, I.M.; Alary, F.; Boggio-Pasqua, M.; Heully, J.-L. Reversing the relative 3MLCT-3MC order in Fe(II) complexes using cyclometallating ligands: A computational study aiming at luminescent Fe(II) complexes. Dalton Trans. 2015, 44, 13498–13503. [Google Scholar] [CrossRef]
  42. Dixon, I.M.; Boissard, G.; Whyte, H.; Alary, F.; Heully, J.-L. Computational Estimate of the Photophysical Capabilities of Four Series of Organometallic Iron(II) Complexes. Inorg. Chem. 2016, 55, 5089–5091. [Google Scholar] [CrossRef] [Green Version]
  43. Durham, B.; Caspar, J.V.; Nagle, J.K.; Meyer, T.J. Photochemistry of Ru(bpy)32+. J. Am. Chem. Soc. 1982, 104, 4803–4810. [Google Scholar] [CrossRef]
  44. Kirchhoff, J.R.; McMillin, D.R.; Marnot, P.A.; Sauvage, J.-P. Photochemistry and Photophysics of Bis(terpyridyl) Complexes of Ru(II) in Fluid Solution. Evidence for the Formation of an η2-Diphenylterpyridine Complex. J. Am. Chem. Soc. 1985, 107, 1138–1141. [Google Scholar] [CrossRef]
  45. Thompson, D.W.; Wishart, J.F.; Brunschwig, B.S.; Sutin, N. Efficient Generation of the Ligand Field Excited State of Tris-(2,2’-bipyridine)–ruthenium(II) through Sequential Two-Photon Capture by [Ru(bpy)3]2+ or Electron Capture by [Ru(bpy)3]3+. J. Phys. Chem. A 2001, 105, 8117–8122. [Google Scholar] [CrossRef]
  46. Kunnus, K.; Josefsson, I.; Rajkovic, I.; Schreck, S.; Quevedo, W.; Beye, M.; Weniger, C.; Grübel, S.; Scholz, M.; Nordlund, D.; et al. Identification of the dominant photochemical pathways and mechanistic insights to the ultrafast ligand exchange of Fe(CO)5 to Fe(CO)4EtOH. Struct. Dyn. 2016, 3, 043204. [Google Scholar] [CrossRef] [Green Version]
  47. Reinhard, M.; Auböck, G.; Besley, N.A.; Clark, I.P.; Greetham, G.M.; Hanson-Heine, M.W.D.; Horvath, R.; Murphy, T.S.; Penfold, T.J.; Towrie, M.; et al. Photoaquation Mechanism of Hexacyanoferrate(II) Ions: Ultrafast 2D UV and Transient Visible and IR Spectroscopies. J. Am. Chem. Soc. 2017, 139, 7335–7347. [Google Scholar] [CrossRef]
  48. Welby, C.E.; Rice, C.R.; Elliott, P.I.P. Unambiguous Characterization of a Photoreactive Ligand-Loss Intermediate. Angew. Chem. Int. Ed. 2013, 52, 10826–10829. [Google Scholar] [CrossRef]
  49. Welby, C.E.; Armitage, G.K.; Bartley, H.; Wilkinson, A.; Sinopoli, A.; Uppal, B.S.; Rice, C.R.; Elliott, P.I.P. Photochemistry of Ru(II) 4,4′-Bi-1,2,3-triazolyl (btz) Complexes: Crystallographic Characterization of the Photoreactive Ligand-Loss Intermediate trans-[Ru(bpy)(κ2-btz)(κ1-btz)(NCMe)]2+. Chem. Eur. J. 2014, 20, 8467–8476. [Google Scholar] [CrossRef] [Green Version]
  50. Soupart, A.; Alary, F.; Heully, J.-L.; Elliott, P.I.P.; Dixon, I.M. Exploration of Uncharted 3PES Territory for [Ru(bpy)3]2+: A New 3MC Minimum Prone to Ligand Loss Photochemistry. Inorg. Chem. 2018, 57, 3192–3196. [Google Scholar] [CrossRef] [Green Version]
  51. Jónsson, H.; Mills, G.; Jacobsen, K.W. Nudged elastic band method for finding minimum energy paths of transitions. In Classical and Quantum Dynamics in Condensed Phase Simulations; Berne, B.J., Cicotti, G., Coker, D.F., Eds.; World Scientific: Singapore, 1998; pp. 385–404. [Google Scholar]
  52. Henkelman, G.; Johannesson, G.; Jónsson, H. Methods for Finding Saddle Points and Minimum Energy Paths. In Progress on Theoretical Chemistry and Physics; Schwartz, S.D., Ed.; Kluwer Academic: Dordrecht, The Netherlands, 2000; pp. 269–302. [Google Scholar]
  53. Smidstrup, S.; Pedersen, A.; Stokbro, K.; Jónsson, H. Improved initial guess for minimum energy path calculations. J. Chem. Phys. 2014, 140, 214106. [Google Scholar] [CrossRef] [Green Version]
  54. Soupart, A.; Alary, F.; Heully, J.-L.; Elliott, P.I.P.; Dixon, I.M. Recent Progress in Ligand Photorelease Reaction Mechanisms: Theoretical Insights Focusing on Ru(II) 3MC States. Coord. Chem. Rev. 2020, 408, 213184. [Google Scholar] [CrossRef] [Green Version]
  55. Neese, F. The ORCA Program System. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2012, 2, 73–78. [Google Scholar] [CrossRef]
  56. Lee, C.; Yang, W.; Parr, R.G. Development of the Colle-Salvetti Correlation-Energy Formula into a Functional of the Electron Density. Phys. Rev. B 1988, 37, 785–789. [Google Scholar] [CrossRef] [Green Version]
  57. Becke, A.D. Density-functional thermochemistry. III. The role of exact exchange. J. Chem. Phys. 1993, 98, 5648–5652. [Google Scholar] [CrossRef] [Green Version]
  58. Andrae, D.; Haeussermann, U.; Dolg, M.; Stoll, H.; Preuss, H. Energy-adjusted ab initio Pseudopotentials for the Second and Third Row Transition Elements. Theor. Chim. Acta 1990, 77, 123–141. [Google Scholar] [CrossRef]
  59. Weigend, F.; Ahlrichs, R. Balanced Basis Sets of Split Valence, Triple Zeta Valence and Quadruple Zeta Valence Quality for H to Rn: Design and Assessment of Accuracy. Phys. Chem. Chem. Phys. 2005, 7, 3297–3305. [Google Scholar] [CrossRef]
  60. Grimme, S.; Antony, J.; Ehrlich, S.; Krieg, H. A Consistent and Accurate ab initio Parametrization of Density Functional Dispersion Correction (DFT-D) for the 94 Elements H-Pu. J. Chem. Phys. 2010, 132, 154104. [Google Scholar] [CrossRef] [Green Version]
  61. Grimme, S.; Ehrlich, S.; Goerigk, L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. [Google Scholar] [CrossRef]
  62. Marenich, A.V.; Cramer, C.J.; Truhlar, D.G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. [Google Scholar] [CrossRef]
  63. Allouche, A.-R. Gabedit-A Graphical User Interface for Computational Chemistry Softwares. J. Comput. Chem. 2011, 32, 174–182. [Google Scholar] [CrossRef]
  64. Herbol, H.C.; Stevenson, J.; Clancy, P. Computational Implementation of Nudged Elastic Band, Rigid Rotation, and Corresponding Force Optimization. J. Chem. Theory Comput. 2017, 13, 3250–3259. [Google Scholar] [CrossRef]
Inorganics 08 00015 g001 550
Figure 1. Structures of 3MCtrans and 3MCcis in Ru(bpy)32+ (H atoms not shown).
Figure 1. Structures of 3MCtrans and 3MCcis in Ru(bpy)32+ (H atoms not shown).
Inorganics 08 00015 g001
Inorganics 08 00015 sch001 550
Scheme 1. Coordination of one acetonitrile molecule onto the 3MCcis state of Ru(bpy)32+.
Scheme 1. Coordination of one acetonitrile molecule onto the 3MCcis state of Ru(bpy)32+.
Inorganics 08 00015 sch001
Inorganics 08 00015 g002 550
Figure 2. Minimum energy path (blue) and Mulliken spin population on Ru (red) for the coordination of acetonitrile on the 3MC state from Nudged Elastic Band calculations.
Figure 2. Minimum energy path (blue) and Mulliken spin population on Ru (red) for the coordination of acetonitrile on the 3MC state from Nudged Elastic Band calculations.
Inorganics 08 00015 g002
Inorganics 08 00015 g003 550
Figure 3. Minimum energy path (blue) and Mulliken spin population on Ru (red) between beads 17 and 18 of the reaction path.
Figure 3. Minimum energy path (blue) and Mulliken spin population on Ru (red) between beads 17 and 18 of the reaction path.
Inorganics 08 00015 g003
Inorganics 08 00015 g004 550
Figure 4. Evolution of WBIs along the reaction path. The MC–MLCT transition region is highlighted in yellow.
Figure 4. Evolution of WBIs along the reaction path. The MC–MLCT transition region is highlighted in yellow.
Inorganics 08 00015 g004
Inorganics 08 00015 g005 550
Figure 5. Selected orbital eigenvalues along the reaction path. The MC–MLCT transition region is highlighted in yellow.
Figure 5. Selected orbital eigenvalues along the reaction path. The MC–MLCT transition region is highlighted in yellow.
Inorganics 08 00015 g005
Inorganics 08 00015 g006 550
Figure 6. Partial MO correlation diagram between beads 17.50 and 17.75 (Kohn–Sham orbitals), showing NCMe coordination at bead 17.75 (a more complete MO diagram is given as Figure S2).
Figure 6. Partial MO correlation diagram between beads 17.50 and 17.75 (Kohn–Sham orbitals), showing NCMe coordination at bead 17.75 (a more complete MO diagram is given as Figure S2).
Inorganics 08 00015 g006
Table
Table 1. Atom numbering and Ru–N distances (Å) at the start (3MC + MeCN) and end (3MLCT) points of the computed reaction path.
Table 1. Atom numbering and Ru–N distances (Å) at the start (3MC + MeCN) and end (3MLCT) points of the computed reaction path.
Ru–N3MC + MeCN3MLCT
Inorganics 08 00015 i001Ru–N12.1352.118
Ru–N22.0802.110
Ru–N32.0782.049
Ru–N42.1772.057
Ru–N52.5303.593
Ru–N62.3842.132
Ru–NCMe5.0002.055

Share and Cite

MDPI and ACS Style

Soupart, A.; Alary, F.; Heully, J.-L.; Dixon, I.M. On the Possible Coordination on a 3MC State Itself? Mechanistic Investigation Using DFT-Based Methods. Inorganics 2020, 8, 15. https://doi.org/10.3390/inorganics8020015

AMA Style

Soupart A, Alary F, Heully J-L, Dixon IM. On the Possible Coordination on a 3MC State Itself? Mechanistic Investigation Using DFT-Based Methods. Inorganics. 2020; 8(2):15. https://doi.org/10.3390/inorganics8020015

Chicago/Turabian Style

Soupart, Adrien, Fabienne Alary, Jean-Louis Heully, and Isabelle M. Dixon. 2020. "On the Possible Coordination on a 3MC State Itself? Mechanistic Investigation Using DFT-Based Methods" Inorganics 8, no. 2: 15. https://doi.org/10.3390/inorganics8020015

APA Style

Soupart, A., Alary, F., Heully, J. -L., & Dixon, I. M. (2020). On the Possible Coordination on a 3MC State Itself? Mechanistic Investigation Using DFT-Based Methods. Inorganics, 8(2), 15. https://doi.org/10.3390/inorganics8020015

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop