Volumetrics of Hydrogen Storage by Physical Adsorption
Abstract
1. Introduction
2. Adsorption Fundamentals
2.1. Adsorption Measurements
2.2. Adsorption Analysis
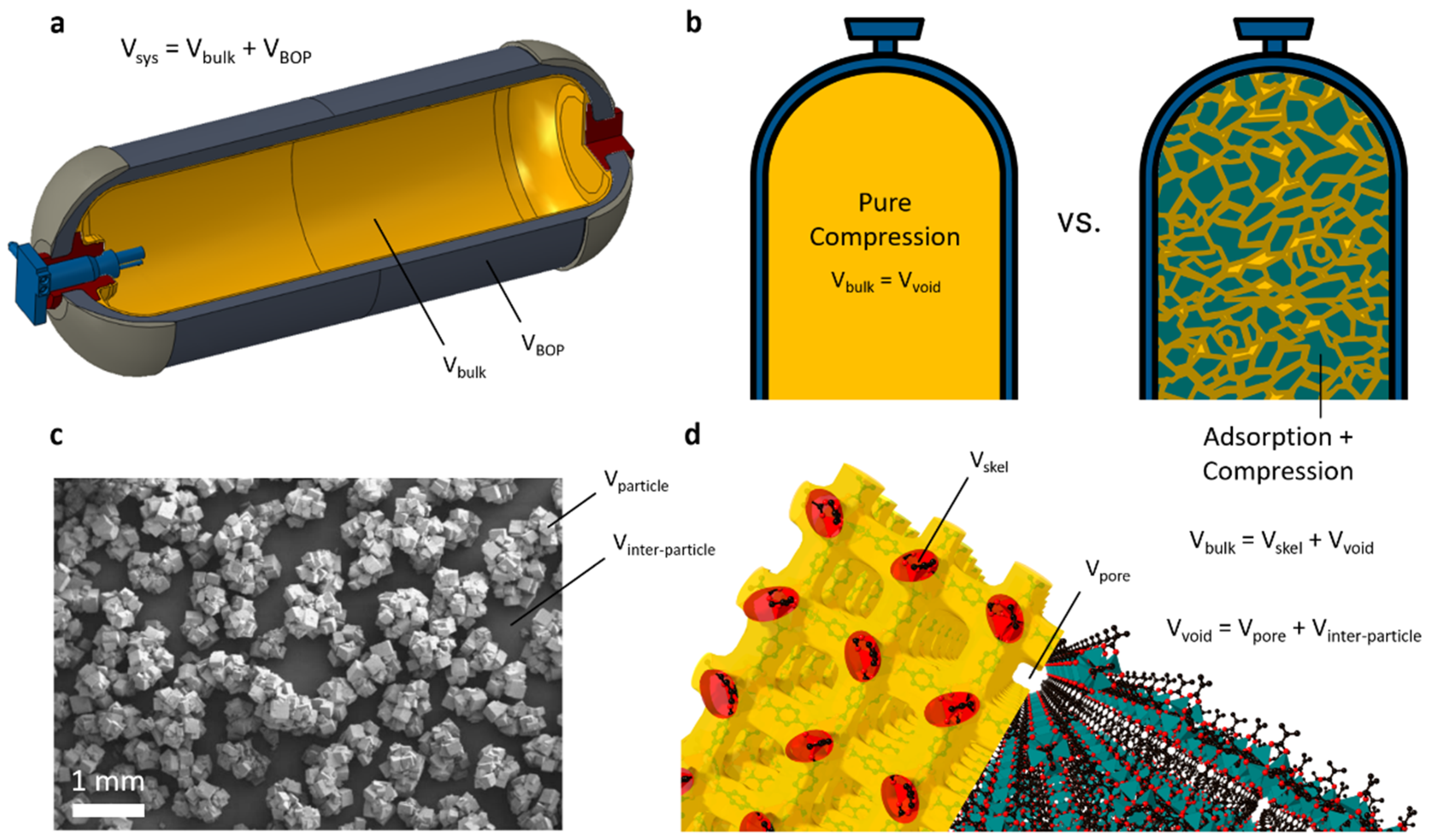
2.3. Assessments of System, Skeletal, and Void Volumes
2.4. System Performance Metrics
3. Density and Densification
3.1. Tapping and Jolting
3.2. Mechanical Compaction
3.3. Binders/Pelletization
3.4. Direct Monolith Synthesis
4. Volumetric Hydrogen Storage
4.1. Zeolites
4.2. Porous Carbons

| Model | Spacing (Å) | Pore Width (Å) | (g L−1) | Ref | ||
|---|---|---|---|---|---|---|
| 5 bar | 50 bar | 100 bar | ||||
| SLG9Å | 9.0 | 5.8 2 | 47.1 | 56.9 | 57.6 | [87] |
| SLG12Å | 12 | 8.7 2 | 32.5 | 53.0 | 53.8 | [87] |
| SLG15Å | 15 | 11.7 2 | 23.5 | 48.4 | 51.9 | [87] |
| SLG18Å | 18 | 14.7 2 | 19.1 | 43.6 | 49.8 | [87] |
| SLG20Å | 20 | 16.7 2 | 16.8 | 40.9 | 48.2 | [87] |
| ZTC [86] | 13.9 1 | 11.3 2 | 20.1 | 40.6 | 48.5 | [98] |
| ZTC+ | 14.2 1 | 12.3 2 | 18.9 | 39.0 | 47.4 | 3 |
| ZTC- | 13.6 1 | 11.7 2 | 21.4 | 42.3 | 49.8 | 3 |
| ZTC-- | 12.2 1 | 10.3 2 | 29.2 | 52.3 | 56.7 | 3 |
4.3. Metal-Organic Frameworks
5. Guiding Principles
6. Conclusions
- i.
- researchers should accurately measure and report the skeletal density of all adsorbents investigated,
- ii.
- researchers should accurately measure and report the apparent density of all adsorbents investigated, prior to performing adsorption measurements,
- iii.
- automated tapping (jolting) is a key strategy to increasing H2 PS delivery at any temperature,
- iv.
- light mechanical compaction (e.g., as performed for SNU-70 [32]) can result in very high volumetric capacity and delivery gains over a loose powder,
- v.
- volumetric H2 storage and delivery should be reported based on the “skeletal approximation” (Equation (9)), especially but not only for powders, and
- vi.
- novel adsorbents should be designed with large void volume, high gravimetric surface area, and a dense, well-organized skeletal framework with a primary focus on improving H2 delivery at cryogenic conditions, where current system-level energy densities clearly outperform commercial batteries.
Supplementary Materials
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bowman, R.C., Jr.; (Frankin, OH, USA). Private Communication, 2021.
- Rivard, E.; Trudeau, M.; Zaghib, K. Hydrogen storage for mobility: A review. Materials 2019, 12, 1973. [Google Scholar] [CrossRef]
- Adams, J.; Houchins, C.; Ahluwalia, R. Onboard Type IV Compressed Hydrogen Storage System Cost and Performance Status. In DOE Hydrogen and Fuel Cells Program Record 19008; US Department of Energy, 2019. Available online: https://www.hydrogen.energy.gov/pdfs/19008_onboard_storage_cost_performance_status.pdf (accessed on 16 May 2021).
- DOE Technical Targets for Onboard Hydrogen Storage for Light-Duty Vehicles; Hydrogen and Fuel Cell Technologies Office, 2020. Available online: https://www.energy.gov/eere/fuelcells/doe-technical-targets-onboard-hydrogen-storage-light-duty-vehicles (accessed on 16 May 2021).
- Hirscher, M.; Yartys, V.A.; Baricco, M.; von Colbe, J.B.; Blanchard, D.; Bowman, R.C., Jr.; Broom, D.P.; Buckley, C.E.; Chang, F.; Chen, P. Materials for hydrogen-based energy storage–past, recent progress and future outlook. J. Alloys Compd. 2020, 827, 153548. [Google Scholar] [CrossRef]
- Paggiaro, R.; Bénard, P.; Polifke, W. Cryo-adsorptive hydrogen storage on activated carbon. I: Thermodynamic analysis of adsorption vessels and comparison with liquid and compressed gas hydrogen storage. Int. J. Hydroen Energy 2010, 35, 638–647. [Google Scholar] [CrossRef]
- Liu, Y.; Kabbour, H.; Brown, C.M.; Neumann, D.A.; Ahn, C.C. Increasing the density of adsorbed hydrogen with coordinatively unsaturated metal centers in metal-organic frameworks. Langmuir 2008, 24, 4772–4777. [Google Scholar] [CrossRef] [PubMed]
- Gallego, N.C.; He, L.; Saha, D.; Contescu, C.I.; Melnichenko, Y.B. Hydrogen confinement in carbon nanopores: Extreme densification at ambient temperature. J. Am. Chem. Soc. 2011, 133, 13794–13797. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, A.; Liu, Y.; Purewal, J.; Tran, L.D.; Wong-Foy, A.G.; Veenstra, M.; Matzger, A.J.; Siegel, D.J. Balancing gravimetric and volumetric hydrogen density in MOFs. Energy Environ. Sci. 2017, 10, 2459–2471. [Google Scholar] [CrossRef]
- Balderas-Xicohténcatl, R.; Schlichtenmayer, M.; Hirscher, M. Volumetric hydrogen storage capacity in metal–organic frameworks. Energy Technol. 2018, 6, 578–582. [Google Scholar] [CrossRef]
- Allendorf, M.D.; Hulvey, Z.; Gennett, T.; Ahmed, A.; Autrey, T.; Camp, J.; Cho, E.S.; Furukawa, H.; Haranczy, M.; Head-Gordon, M.; et al. An assessment of strategies for the development of solid-state adsorbents for vehicular hydrogen storage. Energy Environ. Sci. 2018, 11, 2784–2812. [Google Scholar] [CrossRef]
- Hurst, K.E.; Gennett, T.; Adams, J.; Allendorf, M.D.; Balderas-Xicohténcatl, R.; Bielewski, M.; Edwards, B.; Espinal, L.; Fultz, B.; Hirscher, M. An international laboratory comparison study of volumetric and gravimetric hydrogen adsorption measurements. ChemPhysChem 2019, 20, 1997–2009. [Google Scholar] [CrossRef]
- Gómez-Gualdrón, D.A.; Wang, T.C.; García-Holley, P.; Sawelewa, R.M.; Argueta, E.; Snurr, R.Q.; Hupp, J.T.; Yildirim, T.; Farha, O.K. Understanding volumetric and gravimetric hydrogen adsorption trade-off in metal–organic frameworks. ACS Appl. Mater. Inter. 2017, 9, 33419–33428. [Google Scholar] [CrossRef] [PubMed]
- Chahine, R.; Bose, T.K. Characterization and optimization of adsorbents for hydrogen storage. Hydrog. Energy Prog. XI 1996, 2, 1259–1264. [Google Scholar]
- Ahmed, A.; Seth, S.; Purewal, J.; Wong-Foy, A.G.; Veenstra, M.; Matzger, A.J.; Siegel, D.J. Exceptional hydrogen storage achieved by screening nearly half a million metal-organic frameworks. Nat. Commun. 2019, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Goldsmith, J.; Wong-Foy, A.G.; Cafarella, M.J.; Siegel, D.J. Theoretical limits of hydrogen storage in metal–organic frameworks: Opportunities and trade-offs. Chem. Mater. 2013, 25, 3373–3382. [Google Scholar] [CrossRef]
- Colón, Y.J.; Fairen-Jimenez, D.; Wilmer, C.E.; Snurr, R.Q. High-throughput screening of porous crystalline materials for hydrogen storage capacity near room temperature. J. Phys. Chem. C 2014, 118, 5383–5389. [Google Scholar] [CrossRef]
- Thornton, A.W.; Simon, C.M.; Kim, J.; Kwon, O.; Deeg, K.S.; Konstas, K.; Pas, S.J.; Hill, M.R.; Winkler, D.A.; Haranczyk, M. Materials genome in action: Identifying the performance limits of physical hydrogen storage. Chem. Mater. 2017, 29, 2844–2854. [Google Scholar] [CrossRef]
- Zhou, H.-C.; Long, J.R.; Yaghi, O.M. Introduction to metal–organic frameworks. Chem. Rev. 2012, 112, 673–674. [Google Scholar] [CrossRef]
- Purewal, J.; Liu, D.; Yang, J.; Sudik, A.; Siegel, D.; Maurer, S.; Müller, U. Increased volumetric hydrogen uptake of MOF-5 by powder densification. Int. J. Hydroen Energy 2012, 37, 2723–2727. [Google Scholar] [CrossRef]
- Hou, J.; Sapnik, A.F.; Bennett, T.D. Metal–organic framework gels and monoliths. Chem. Sci. 2020, 11, 310–323. [Google Scholar] [CrossRef] [PubMed]
- Nishihara, H.; Kyotani, T. Zeolite-templated carbons—Three-dimensional microporous graphene frameworks. Chem. Commun. 2018, 54, 5648–5673. [Google Scholar] [CrossRef]
- Taylor, E.E.; Garman, K.; Stadie, N.P. Atomistic Structures of Zeolite-Templated Carbon. Chem. Mater. 2020, 32, 2742–2752. [Google Scholar] [CrossRef]
- Broom, D.P.; Hirscher, M. Irreproducibility in hydrogen storage material research. Energy Environ. Sci. 2016, 9, 3368–3380. [Google Scholar] [CrossRef]
- Broom, D.; Webb, C. Pitfalls in the characterisation of the hydrogen sorption properties of materials. Int. J. Hydroen Energy 2017, 42, 29320–29343. [Google Scholar] [CrossRef]
- Blach, T.P.; Gray, E.M. Sieverts apparatus and methodology for accurate determination of hydrogen uptake by light-atom hosts. J. Alloys Compd. 2007, 446–447, 692–697. [Google Scholar] [CrossRef]
- Sircar, S. Role of helium void measurement in estimation of Gibbsian surface excess. Proc. Fundam. Adsorpt. 2002, 7, 656–663. [Google Scholar]
- Malbrunot, P.; Vidal, D.; Vermesse, J.; Chahine, R.; Bose, T. Adsorbent helium density measurement and its effect on adsorption isotherms at high pressure. Langmuir 1997, 13, 539–544. [Google Scholar] [CrossRef]
- Talu, O. Net Adsorption of Gas/Vapor Mixtures in Microporous Solids. J. Phys. Chem. C 2013, 117, 13059–13071. [Google Scholar] [CrossRef]
- Stadie, N.P. Synthesis and Thermodynamic Studies of Physisorptive Energy Storage Materials. Ph.D. Thesis, California Institute of Technology, Pasadena, CA, USA, 2013. [Google Scholar]
- Parilla, P.A.; Gross, K.; Hurst, K.; Gennett, T. Recommended volumetric capacity definitions and protocols for accurate, standardized and unambiguous metrics for hydrogen storage materials. Appl. Phys. A 2016, 122, 201. [Google Scholar] [CrossRef]
- Purewal, J.; Veenstra, M.; Tamburello, D.; Ahmed, A.; Matzger, A.J.; Wong-Foy, A.G.; Seth, S.; Liu, Y.; Siegel, D.J. Estimation of system-level hydrogen storage for metal-organic frameworks with high volumetric storage density. Int. J. Hydrogen Energy 2019, 44, 15135–15145. [Google Scholar] [CrossRef]
- Hydrogen Storage. DOE Fact Sheet DOE/EE-1552; Hydrogen and Fuel Cell Technologies Office, 2017. Available online: https://www.energy.gov/sites/prod/files/2017/03/f34/fcto-h2-storage-fact-sheet.pdf (accessed on 16 May 2021).
- Mueller, U.; Schubert, M.; Teich, F.; Puetter, H.; Schierle-Arndt, K.; Pastré, J. Metal–organic frameworks—prospective industrial applications. J. Mater. Chem. 2006, 16, 626–636. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. NIST Standard Reference Database 23: Reference Fluid Thermodynamic and Transport Properties—REFPROP; National Institute of Standards and Technology: Gaithersburg, MD, USA, 2007; Number Version 8.0 in Standard Reference Data Program.
- Ming, Y.; Purewal, J.; Sudik, A.; Xu, C.; Yang, J.; Veenstra, M.; Rhodes, K.; Soltis, R.; Warner, J.; Gaab, M. Thermophysical properties of MOF-5 powders. Microporous Mesoporous Mater. 2014, 185, 235–244. [Google Scholar] [CrossRef]
- Purewal, J.; Liu, D.; Sudik, A.; Veenstra, M.; Yang, J.; Maurer, S.; Müller, U.; Siegel, D.J. Improved hydrogen storage and thermal conductivity in high-density MOF-5 composites. J. Phys. Chem. C 2012, 116, 20199–20212. [Google Scholar] [CrossRef]
- Yang, J.; Sudik, A.; Wolverton, C.; Siegel, D.J. High capacity hydrogen storage materials: Attributes for automotive applications and techniques for materials discovery. Chem. Soc. Rev. 2010, 39, 656–675. [Google Scholar] [CrossRef]
- Tamburello, D.; Hardy, B.; Corgnale, C.; Sulic, M.; Anton, D. Cryo-Adsorbent Hydrogen Storage Systems For Fuel Cell Vehicles. In Proceedings of the ASME 2017 Fluids Engineering Division Summer Meeting, Waikoloa, HI, USA, 30 July–3 August 2017. [Google Scholar] [CrossRef]
- Chahine, R.; (Rio Tinto, London, UK). Private Communication, 2021.
- Wilmer, C.E.; Leaf, M.; Lee, C.Y.; Farha, O.K.; Hauser, B.G.; Hupp, J.T.; Snurr, R.Q. Large-scale screening of hypothetical metal–organic frameworks. Nat. Chem. 2012, 4, 83. [Google Scholar] [CrossRef]
- Hausner, H.H. Friction Conditions in a Mass of Metal Powder; Polytechnic Institute of Brooklyn; University of California, Los Angeles: Los Angeles, CA, USA, 1967. [Google Scholar]
- Santomaso, A.; Lazzaro, P.; Canu, P. Powder flowability and density ratios: The impact of granules packing. Chem. Eng. Sci. 2003, 58, 2857–2874. [Google Scholar] [CrossRef]
- Peng, Y.; Krungleviciute, V.; Eryazici, I.; Hupp, J.T.; Farha, O.K.; Yildirim, T. Methane Storage in Metal−Organic Frameworks: Current Records, Surprise Findings, and Challenges. J. Am. Chem. Soc. 2013, 135, 11887–11894. [Google Scholar] [CrossRef]
- Cooper, A., Jr.; Eaton, L. Compaction behavior of several ceramic powders. J. Am. Ceram. Soc. 1962, 45, 97–101. [Google Scholar] [CrossRef]
- Alcaniz-Monge, J.; Trautwein, G.; Pérez-Cadenas, M.; Roman-Martinez, M. Effects of compression on the textural properties of porous solids. Microporous Mesoporous Mater. 2009, 126, 291–301. [Google Scholar] [CrossRef]
- Vezzalini, G.; Arletti, R.; Quartieri, S. High-pressure-induced structural changes, amorphization and molecule penetration in MFI microporous materials: A review. Acta Cryst. B 2014, 70, 444–451. [Google Scholar] [CrossRef]
- Bazer-Bachi, D.; Assié, L.; Lecocq, V.; Harbuzaru, B.; Falk, V. Towards industrial use of metal-organic framework: Impact of shaping on the MOF properties. Powder Technol. 2014, 255, 52–59. [Google Scholar] [CrossRef]
- Dhainaut, J.; Avci-Camur, C.; Troyano, J.; Legrand, A.; Canivet, J.; Imaz, I.; Maspoch, D.; Reinsch, H.; Farrusseng, D. Systematic study of the impact of MOF densification into tablets on textural and mechanical properties. CrystEngComm 2017, 19, 4211–4218. [Google Scholar] [CrossRef]
- Ardelean, O.; Blanita, G.; Borodi, G.; Lazar, M.D.; Misan, I.; Coldea, I.; Lupu, D. Volumetric hydrogen adsorption capacity of densified MIL-101 monoliths. Int. J. Hydroen Energy 2013, 38, 7046–7055. [Google Scholar] [CrossRef]
- Nandasiri, M.I.; Jambovane, S.R.; McGrail, B.P.; Schaef, H.T.; Nune, S.K. Adsorption, separation, and catalytic properties of densified metal-organic frameworks. Coord. Chem. Rev. 2016, 311, 38–52. [Google Scholar] [CrossRef]
- Wang, T.C.; White, J.L.; Bie, B.; Deng, H.; Edgington, J.; Sugar, J.D.; Stavila, V.; Allendorf, M.D. Design Rules for Metal-Organic Framework Stability in High-Pressure Hydrogen Environments. ChemPhysChem 2019, 20, 1305–1310. [Google Scholar] [CrossRef]
- Zacharia, R.; Cossement, D.; Lafi, L.; Chahine, R. Volumetric hydrogen sorption capacity of monoliths prepared by mechanical densification of MOF-177. J. Mater. Chem. 2010, 20, 2145. [Google Scholar] [CrossRef]
- Hou, P.-X.; Orikasa, H.; Itoi, H.; Nishihara, H.; Kyotani, T. Densification of ordered microporous carbons and controlling their micropore size by hot-pressing. Carbon 2007, 45, 2011–2016. [Google Scholar] [CrossRef]
- Balahmar, N.; Lowbridge, A.M.; Mokaya, R. Templating of carbon in zeolites under pressure: Synthesis of pelletized zeolite templated carbons with improved porosity and packing density for superior gas (CO2 and H2) uptake properties. J. Mater. Chem. A 2016, 4, 14254–14266. [Google Scholar] [CrossRef]
- Adeniran, B.; Mokaya, R. Compactivation: A mechanochemical approach to carbons with superior porosity and exceptional performance for hydrogen and CO2 storage. Nano Energy 2015, 16, 173–185. [Google Scholar] [CrossRef]
- Gabe, A.; Ouzzine, M.; Taylor, E.E.; Stadie, N.P.; Uchiyama, N.; Kanai, T.; Nishina, Y.; Tanaka, H.; Pan, Z.-Z.; Kyotani, T.; et al. High-density monolithic pellets of double-sided graphene fragments based on zeolite-templated carbon. J. Mater. Chem. A 2021, 9, 7503–7507. [Google Scholar] [CrossRef]
- Juan-Juan, J.; Marco-Lozar, J.; Suarez-Garcia, F.; Cazorla-Amorós, D.; Linares-Solano, A. A comparison of hydrogen storage in activated carbons and a metal–organic framework (MOF-5). Carbon 2010, 48, 2906–2909. [Google Scholar] [CrossRef]
- Masika, E.; Mokaya, R. Exceptional gravimetric and volumetric hydrogen storage for densified zeolite templated carbons with high mechanical stability. Energy Environ. Sci. 2013, 7, 427–434. [Google Scholar] [CrossRef]
- Blankenship, T.S.; Mokaya, R. Cigarette butt-derived carbons have ultra-high surface area and unprecedented hydrogen storage capacity. Energy Environ. Sci. 2017, 10, 2552–2562. [Google Scholar] [CrossRef]
- Singer, J.; Mayergoyz, A.; Portet, C.; Schneider, E.; Gogotsi, Y.; Fischer, J. Enhanced volumetric hydrogen storage capacity of porous carbon powders by forming peels or pellets. Microporous Mesoporous Mater. 2008, 116, 469–472. [Google Scholar] [CrossRef]
- Biloe, S.; Goetz, V.; Mauran, S. Characterization of adsorbent composite blocks for methane storage. Carbon 2001, 39, 1653–1662. [Google Scholar] [CrossRef]
- Lozano-Castelló, D.; Cazorla-Amorós, D.; Linares-Solano, A.; Quinn, D. Activated carbon monoliths for methane storage: Influence of binder. Carbon 2002, 40, 2817–2825. [Google Scholar] [CrossRef]
- Balathanigaimani, M.; Shim, W.-G.; Lee, J.-W.; Moon, H. Adsorption of methane on novel corn grain-based carbon monoliths. Microporous Mesoporous Mater. 2009, 119, 47–52. [Google Scholar] [CrossRef]
- Machnikowski, J.; Kierzek, K.; Torchała, K. Adsorption capacity enhancement by activation with CO2 of monolithic adsorbents made of KOH-activated carbon and polymer-derived binder. Energy Fuels 2012, 26, 3697–3702. [Google Scholar] [CrossRef]
- Valekar, A.H.; Cho, K.-H.; Lee, U.-H.; Lee, J.S.; Yoon, J.W.; Hwang, Y.K.; Lee, S.G.; Cho, S.J.; Chang, J.-S. Shaping of porous metal–organic framework granules using mesoporous ρ-alumina as a binder. RSC Adv. 2017, 7, 55767–55777. [Google Scholar] [CrossRef]
- Mallick, A.; Mouchaham, G.; Bhatt, P.M.; Liang, W.; Belmabkhout, Y.; Adil, K.; Jamal, A.; Eddaoudi, M. Advances in Shaping of Metal–Organic Frameworks for CO2 Capture: Understanding the Effect of Rubbery and Glassy Polymeric Binders. Ind. Eng. Chem. Res. 2018, 57, 16897–16902. [Google Scholar] [CrossRef]
- Hastürk, E.; Höfert, S.-P.; Topalli, B.; Schlüsener, C.; Janiak, C. Shaping of MOFs via freeze-casting method with hydrophilic polymers and their effect on textural properties. Microporous Mesoporous Mater. 2020, 295, 109907. [Google Scholar] [CrossRef]
- Liu, X.-M.; Xie, L.-H.; Wu, Y. Recent advances in the shaping of metal–organic frameworks. Inorg. Chem. Front. 2020, 7, 2840–2866. [Google Scholar] [CrossRef]
- Ren, J.; Musyoka, N.M.; Langmi, H.W.; Swartbooi, A.; North, B.C.; Mathe, M. A more efficient way to shape metal-organic framework (MOF) powder materials for hydrogen storage applications. Int. J. Hydrogen Energy 2015, 40, 4617–4622. [Google Scholar] [CrossRef]
- Bye, K.; White, E. Hydrothermal growth of sodalite single crystals. J. Cryst. Growth 1970, 6, 355–356. [Google Scholar] [CrossRef]
- Lethbridge, Z.A.; Williams, J.J.; Walton, R.I.; Evans, K.E.; Smith, C.W. Methods for the synthesis of large crystals of silicate zeolites. Microporous Mesoporous Mater. 2005, 79, 339–352. [Google Scholar] [CrossRef]
- Sorrenti, A.; Jones, L.; Sevim, S.; Cao, X.; DeMello, A.J.; Martí-Gastaldo, C.; Puigmartí-Luis, J. Growing and Shaping Metal–Organic Framework Single Crystals at the Millimeter Scale. J. Am. Chem. Soc. 2020, 142, 9372–9381. [Google Scholar] [CrossRef]
- Tovar, T.M.; Zhao, J.; Nunn, W.T.; Barton, H.F.; Peterson, G.W.; Parsons, G.N.; LeVan, M.D. Diffusion of CO2 in large crystals of Cu-BTC MOF. J. Am. Chem. Soc. 2016, 138, 11449–11452. [Google Scholar] [CrossRef]
- Moitra, N.; Fukumoto, S.; Reboul, J.; Sumida, K.; Zhu, Y.; Nakanishi, K.; Furukawa, S.; Kitagawa, S.; Kanamori, K. Mechanically stable, hierarchically porous Cu 3 (btc) 2 (HKUST-1) monoliths via direct conversion of copper (ii) hydroxide-based monoliths. Chem. Commun. 2015, 51, 3511–3514. [Google Scholar] [CrossRef] [PubMed]
- Connolly, B.M.; Madden, D.G.; Wheatley, A.E.; Fairen-Jimenez, D. Shaping the future of fuel: Monolithic metal–organic frameworks for high-density gas storage. J. Am. Chem. Soc. 2020, 142, 8541–8549. [Google Scholar] [CrossRef]
- Tian, T.; Zeng, Z.; Vulpe, D.; Casco, M.E.; Divitini, G.; Midgley, P.A.; Silvestre-Albero, J.; Tan, J.-C.; Moghadam, P.Z.; Fairen-Jimenez, D. A sol–gel monolithic metal–organic framework with enhanced methane uptake. Nat. Mater. 2018, 17, 174. [Google Scholar] [CrossRef]
- Connolly, B.M.; Aragones-Anglada, M.; Gandara-Loe, J.; Danaf, N.A.; Lamb, D.C.; Mehta, J.P.; Vulpe, D.; Wuttke, S.; Silvestre-Albero, J.; Moghadam, P.Z. Tuning porosity in macroscopic monolithic metal-organic frameworks for exceptional natural gas storage. Nat. Commun. 2019, 10, 1–11. [Google Scholar] [CrossRef]
- Hunter-Sellars, E.; Saenz-Cavazos, P.A.; Houghton, A.R.; McIntyre, S.R.; Parkin, I.P.; Williams, D.R. Sol–Gel Synthesis of High-Density Zeolitic Imidazolate Framework Monoliths via Ligand Assisted Methods: Exceptional Porosity, Hydrophobicity, and Applications in Vapor Adsorption. Adv. Funct. Mater. 2021, 31, 2008357. [Google Scholar] [CrossRef]
- Baerlocher, C.; McCusker, L.B. Database of Zeolite Structures. Available online: http://www.iza-structure.org/databases/ (accessed on 16 May 2021).
- Lopes, F.V.; Grande, C.A.; Ribeiro, A.M.; Loureiro, J.M.; Evaggelos, O.; Nikolakis, V.; Rodrigues, A.E. Adsorption of H2, CO2, CH4, CO, N2 and H2O in activated carbon and zeolite for hydrogen production. Sep. Sci. Technol. 2009, 44, 1045–1073. [Google Scholar] [CrossRef]
- Langmi, H.; Walton, A.; Al-Mamouri, M.; Johnson, S.; Book, D.; Speight, J.; Edwards, P.; Gameson, I.; Anderson, P.; Harris, I. Hydrogen adsorption in zeolites A, X, Y and RHO. J. Alloys Compd. 2003, 356, 710–715. [Google Scholar] [CrossRef]
- Chahine, R.; Bose, T. Low-pressure adsorption storage of hydrogen. Int. J. Hydroen Energy 1994, 19, 161–164. [Google Scholar] [CrossRef]
- Streb, A.; Mazzotti, M. Adsorption for efficient low carbon hydrogen production: Part 1—adsorption equilibrium and breakthrough studies for H2/CO2/CH4 on zeolite 13X. Adsorption 2021, 1–18. [Google Scholar] [CrossRef]
- Nishihara, H.; Fujimoto, H.; Itoi, H.; Nomura, K.; Tanaka, H.; Miyahara, M.T.; Bonnaud, P.A.; Miura, R.; Suzuki, A.; Miyamoto, N. Graphene-based ordered framework with a diverse range of carbon polygons formed in zeolite nanochannels. Carbon 2018, 129, 854–862. [Google Scholar] [CrossRef]
- Nomura, K.; Nishihara, H.; Yamamoto, M.; Gabe, A.; Ito, M.; Uchimura, M.; Nishina, Y.; Tanaka, H.; Miyahara, M.T.; Kyotani, T. Force-driven reversible liquid–gas phase transition mediated by elastic nanosponges. Nat. Commun. 2019, 10, 2559. [Google Scholar] [CrossRef] [PubMed]
- Bénard, P.; Chahine, R.; Chandonia, P.; Cossement, D.; Dorval-Douville, G.; Lafi, L.; Lachance, P.; Paggiaro, R.; Poirier, E. Comparison of hydrogen adsorption on nanoporous materials. J. Alloys Compd. 2007, 446, 380–384. [Google Scholar] [CrossRef]
- Gómez-Gualdrón, D.A.; Wilmer, C.E.; Farha, O.K.; Hupp, J.T.; Snurr, R.Q. Exploring the limits of methane storage and delivery in nanoporous materials. J. Phys. Chem. C 2014, 118, 6941–6951. [Google Scholar] [CrossRef]
- Martínez-Mesa, A.; Zhechkov, L.; Yurchenko, S.; Heine, T.; Seifert, G.; Rubayo-Soneira, J. Hydrogen physisorption on carbon foams upon inclusion of many-body and quantum delocalization effects. J. Phys. Chem. C 2012, 116, 19543–19553. [Google Scholar] [CrossRef]
- Dimitrakakis, G.K.; Tylianakis, E.; Froudakis, G.E. Pillared graphene: A new 3-D network nanostructure for enhanced hydrogen storage. Nano Lett. 2008, 8, 3166–3170. [Google Scholar] [CrossRef] [PubMed]
- Krasnov, P.O.; Shkaberina, G.S.; Kuzubov, A.A.; Kovaleva, E.A. Molecular hydrogen sorption capacity of D-shwarzites. Appl. Surf. Sci. 2017, 416, 766–771. [Google Scholar] [CrossRef]
- Casco, M.E.; Martínez-Escandell, M.; Gadea-Ramos, E.; Kaneko, K.; Silvestre-Albero, J.; Rodriguez-Reinoso, F. High-Pressure Methane Storage in Porous Materials: Are Carbon Materials in the Pole Position? Chem. Mater. 2015. [Google Scholar] [CrossRef]
- Voskuilen, T.; Pourpoint, T.; Dailly, A. Hydrogen adsorption on microporous materials at ambient temperatures and pressures up to 50 MPa. Adsorption 2012, 18, 239–249. [Google Scholar] [CrossRef]
- Stadie, N.P.; Purewal, J.J.; Ahn, C.C.; Fultz, B. Measurements of hydrogen spillover in platinum doped superactivated carbon. Langmuir 2010, 26, 15481–15485. [Google Scholar] [CrossRef]
- Stadie, N.P.; Vajo, J.J.; Cumberland, R.W.; Wilson, A.A.; Ahn, C.C.; Fultz, B. Zeolite-templated carbon materials for high-pressure hydrogen storage. Langmuir 2012, 28, 10057–10063. [Google Scholar] [CrossRef]
- Nishihara, H.; Hou, P.X.; Li, L.X.; Ito, M.; Uchiyama, M.; Kaburagi, T.; Ikura, A.; Katamura, J.; Kawarada, T.; Mizuuchi, K.; et al. High-pressure hydrogen storage in zeolite-templated carbon. J. Phys. Chem. C 2009, 113, 3189–3196. [Google Scholar] [CrossRef]
- Ramirez-Vidal, P.; Canevesi, R.L.; Sdanghi, G.; Schaefer, S.; Maranzana, G.; Celzard, A.; Fierro, V. A Step Forward in Understanding the Hydrogen Adsorption and Compression on Activated Carbons. ACS Appl. Mater. Inter. 2021, 13, 12562–12574. [Google Scholar] [CrossRef]
- Geng, Z.; Zhang, C.; Wang, D.; Zhou, X.; Cai, M. Pore size effects of nanoporous carbons with ultra-high surface area on high-pressure hydrogen storage. J. Energy Chem. 2015, 24, 1–8. [Google Scholar] [CrossRef]
- García-Holley, P.; Schweitzer, B.; Islamoglu, T.; Liu, Y.; Lin, L.; Rodriguez, S.; Weston, M.H.; Hupp, J.T.; Gómez-Gualdrón, D.A.; Yildirim, T. Benchmark study of hydrogen storage in metal–organic frameworks under temperature and pressure swing conditions. ACS Energy Lett. 2018, 3, 748–754. [Google Scholar] [CrossRef]
- Kaye, S.S.; Dailly, A.; Yaghi, O.M.; Long, J.R. Impact of preparation and handling on the hydrogen storage properties of Zn4O (1, 4-benzenedicarboxylate) 3 (MOF-5). J. Am. Chem. Soc. 2007, 129, 14176–14177. [Google Scholar] [CrossRef] [PubMed]
- Bambalaza, S.E.; Langmi, H.W.; Mokaya, R.; Musyoka, N.M.; Ren, J.; Khotseng, L.E. Compaction of a zirconium metal–organic framework (UiO-66) for high density hydrogen storage applications. J. Mater. Chem. A 2018, 6, 23569–23577. [Google Scholar] [CrossRef]
- Kapelewski, M.T.; Runčevski, T.e.; Tarver, J.D.; Jiang, H.Z.; Hurst, K.E.; Parilla, P.A.; Ayala, A.; Gennett, T.; FitzGerald, S.A.; Brown, C.M. Record High Hydrogen Storage Capacity in the Metal–Organic Framework Ni2 (m-dobdc) at Near-Ambient Temperatures. Chem. Mater. 2018, 30, 8179–8189. [Google Scholar] [CrossRef]
- Blanita, G.; Mihet, M.; Borodi, G.; Misan, I.; Coldea, I.; Lupu, D. Ball milling and compression effects on hydrogen adsorption by MOF:Pt/carbon mixtures. Microporous Mesoporous Mater. 2015, 203, 195–201. [Google Scholar] [CrossRef]
- Beckner, M.; Dailly, A. Adsorption enthalpy calculations of hydrogen adsorption at ambient temperature and pressures exceeding 300 bar. Am. J. Anal. Chem. 2013, 4, 8–16. [Google Scholar] [CrossRef]





| Material | Form | Calculation | (g L−1) | Ref | ||
|---|---|---|---|---|---|---|
| 5 bar | 50 bar | 100 bar | ||||
| MOF-5 | Powder 2,5 | (Equation (8)) | 8.3 | 17.8 | 20.5 | [36] |
| Powder 2,4 | (Equation (9)) | 9.3 | 27.9 | 39.7 | [36] | |
| Powder 4,5 | (Equation (10)) | 21.4 | 46.0 | 52.9 | [36] | |
| Powder 6 | (Equation (11)) | 22.6 | 48.9 | 56.5 | [36] | |
| MOF-5 | Powder 1 | (Equation (9)) | 6.1 | 23.3 | 36.3 | [36] |
| Powder 2 | (Equation (9)) | 9.3 | 27.9 | 39.7 | [36] | |
| Pellet 3 | (Equation (9)) | 16.7 | 38.0 | 45.2 | [37] | |
| MOF-5/ENG | Pellet 3 | (Equation (9)) | 13.2 | 33.9 | 41.5 | [37] |
| Material | Form | (g mL−1) | (g mL−1) | (mL g−1) | SA 5 (m2 g−1) | SA (m2 mL−1) | (%) |
|---|---|---|---|---|---|---|---|
| MOF-5 | powder | 0.13 1 | 2.03 | 1.27 | 2763 | 359 | 94% |
| MOF-5 | powder | 0.22 2 | 2.03 | 1.27 | 2763 | 608 | 89% |
| MOF-5 | pellet | 0.52 3 | 2.03 | 1.12 | 2263 | 1177 | 74% |
| MOF-5/ENG | pellet | 0.47 3 | 2.03 | 1.14 | 2623 | 1233 | 77% |
| MOF-177 | powder | 0.21 1 | 1.56 | 1.74 | 4143 | 858 | 87% |
| MOF-177 | pellet | 0.39 3 | 1.56 | 1.62 | 4029 | 1551 | 75% |
| SNU-70 | powder | 0.20 1 | 1.95 | 2.03 | 4944 | 989 | 90% |
| SNU-70 | pellet | 0.243 | 1.95 | NR | NR | NR | 88% |
| ZTC | powder | 0.19 1 | 1.75 | 1.70 | 3792 | 720 | 89% |
| ZTC/rGO | pellet | 0.67 3 | 1.69 | 1.35 | 2585 | 1732 | 60% |
| Zeolite 13X | powder | 0.595 1 | 2.36 4 | NR | NR | NR | 75% |
| T (K) | Material | Form | Calculation | (g L−1) | Ref | ||
|---|---|---|---|---|---|---|---|
| 5 bar | 50 bar | 100 bar | |||||
| 77 | MOF-5 | crystal | 1 | 22.6 | 48.9 | 56.5 | [36] |
| MOF-5 | pellet | 2,3 | 16.5 | 37.9 | 45.7 | [37] | |
| MOF-5/ENG | pellet | 2,3 | 12.9 | 33.7 | 42.0 | [37] | |
| MOF-177 | crystal | 1 | 15.9 | 41.7 | 50.2 | [53] | |
| MOF-177 | pellet | 2,3 | 13.1 | 35.9 | 44.4 | [53] | |
| SNU-70 | crystal | 1 | 14.5 | 41.4 | 50.0 | [32] | |
| SNU-70 | compact | 2,3 | 9.0 | 30.7 | 41.8 | [32] | |
| ZTC | “crystal” | 1 | 20.1 | 40.6 | 48.5 | [37] | |
| ZTC/rGO | pellet | 2,3 | 22.4 | 37.8 | 42.8 | SI | |
| Zeolite 13X | crystal | 1 | 15.0 | 22.7 | 27.9 | [87] | |
| 298 | MOF-5 | crystal | 1 | 0.5 | 4.8 | 8.9 | [36] |
| IRMOF-20 | crystal | 1 | 0.6 | 5.0 | 9.2 | [32] | |
| HKUST-1 | crystal | 1 | 0.7 | 5.9 | 10.2 | [99] | |
| HKUST-1 | pellet | 2,3 | 0.5 | 4.6 | 7.8 | [103] | |
| Ni2(m-dobdc) | crystal | 1 | 0.8 | 6.9 | 11.8 | [102] | |
| ZTC | “crystal” | 1 | 0.6 | 5.1 | 9.2 | [57] | |
| ZTC/rGO | pellet | 2,3 | 0.5 | 4.9 | 8.4 | [57] | |
| Zeolite 13X | crystal | 1 | 0.5 | 4.3 | 7.7 | [84] | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Samantaray, S.S.; Putnam, S.T.; Stadie, N.P. Volumetrics of Hydrogen Storage by Physical Adsorption. Inorganics 2021, 9, 45. https://doi.org/10.3390/inorganics9060045
Samantaray SS, Putnam ST, Stadie NP. Volumetrics of Hydrogen Storage by Physical Adsorption. Inorganics. 2021; 9(6):45. https://doi.org/10.3390/inorganics9060045
Chicago/Turabian StyleSamantaray, Sai Smruti, Seth T. Putnam, and Nicholas P. Stadie. 2021. "Volumetrics of Hydrogen Storage by Physical Adsorption" Inorganics 9, no. 6: 45. https://doi.org/10.3390/inorganics9060045
APA StyleSamantaray, S. S., Putnam, S. T., & Stadie, N. P. (2021). Volumetrics of Hydrogen Storage by Physical Adsorption. Inorganics, 9(6), 45. https://doi.org/10.3390/inorganics9060045







