Trabecular Bone Component Assessment under Orthodontic Loads and Movements during Periodontal Breakdown—A Finite Elements Analysis
Abstract
1. Introduction
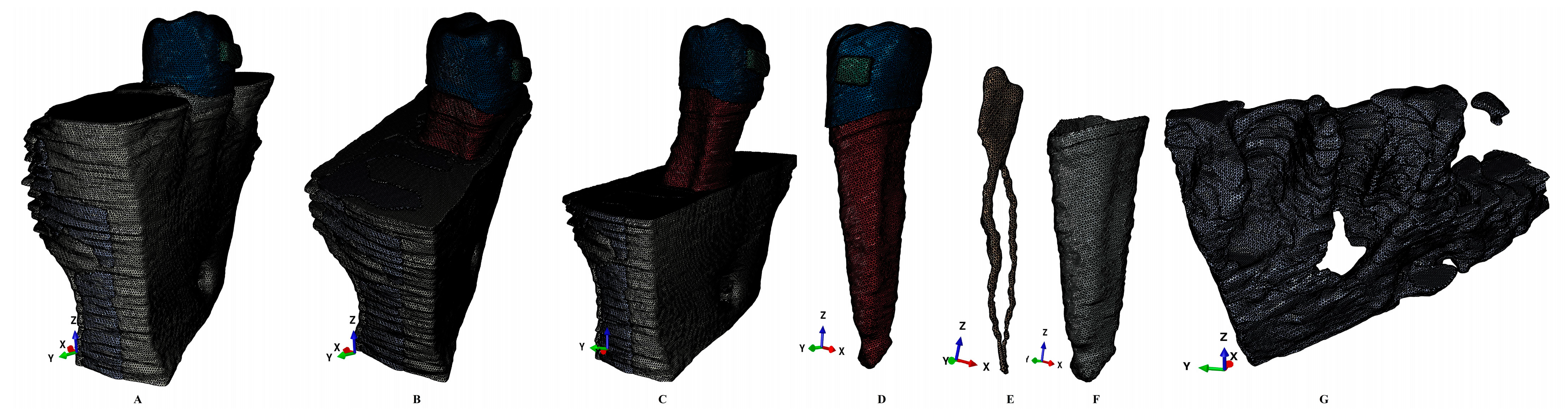
2. Materials and Methods
3. Results
4. Discussion
5. Conclusions
- Both failure criteria showed similar qualitative results, while the quantitative results were 1.09–1.21 higher for T when compared with VM. There were no qualitative differences between the stress resulting from the three orthodontic loads. Quantitatively, a doubling was seen for 1.2 N and quadrupling for 2.4 N when compared to 0.6 N.
- Rotation and translation followed by tipping seemed to be the most stressful movements especially for a reduced periodontium, prone to higher ischemic and resorptive risks.
- If, in an intact periodontium with up to 1.2 N, there seemed to be no major ischemic and resorptive risks, in a reduced periodontium, 1.2 N could be used only for extrusion and intrusion. For the other three movements, more than 0.6 N is prone to increasing ischemic and resorptive risks.
- Biomechanically, in an intact periodontium, the stress is spread in the alveolar socket and entire trabecular structure. In a reduced periodontium, a visible concentration and increase in stress around the cervical third of the remaining alveolar socket after 4 mm of loss is visible, for all orthodontic movements and loads.
- Biomechanically, it seems that 4 mm of loss is a marker for the change in stress distribution during periodontal breakdown. A visible correlation between bone loss progress, changes in stress distribution (especially concentrations around the alveolar socket after 4 mm), and quantitative stress increase was seen.
Practical Implications
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Moga, R.A.; Olteanu, C.D.; Buru, S.M.; Botez, M.D.; Delean, A.G. Cortical and Trabecular Bone Stress Assessment during Periodontal Breakdown—A Comparative Finite Element Analysis of Multiple Failure Criteria. Medicina 2023, 59, 1462. [Google Scholar] [CrossRef] [PubMed]
- Moga, R.A.; Olteanu, C.D.; Botez, M.D.; Buru, S.M. Assessment of the Orthodontic External Resorption in Periodontal Breakdown-A Finite Elements Analysis (Part I). Healthcare 2023, 11, 1447. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; You, X.; Zhang, L.; Zhang, C.; Zou, W. Mechanical regulation of bone remodeling. Bone Res. 2022, 10, 16. [Google Scholar] [CrossRef]
- Prados-Privado, M.; Martínez-Martínez, C.; Gehrke, S.A.; Prados-Frutos, J.C. Influence of Bone Definition and Finite Element Parameters in Bone and Dental Implants Stress: A Literature Review. Biology 2020, 9, 224. [Google Scholar] [CrossRef]
- Yamanishi, Y.; Yamaguchi, S.; Imazato, S.; Nakano, T.; Yatani, H. Effects of the implant design on peri-implant bone stress and abutment micromovement: Three-dimensional finite element analysis of original computer-aided design models. J. Periodontol. 2014, 85, e333–e338. [Google Scholar] [CrossRef] [PubMed]
- Pérez-Pevida, E.; Brizuela-Velasco, A.; Chávarri-Prado, D.; Jiménez-Garrudo, A.; Sánchez-Lasheras, F.; Solaberrieta-Méndez, E.; Diéguez-Pereira, M.; Fernández-González, F.J.; Dehesa-Ibarra, B.; Monticelli, F. Biomechanical Consequences of the Elastic Properties of Dental Implant Alloys on the Supporting Bone: Finite Element Analysis. BioMed Res. Int. 2016, 2016, 1850401. [Google Scholar] [CrossRef] [PubMed]
- Shash, Y.H.; El-Wakad, M.T.; Eldosoky, M.A.A.; Dohiem, M.M. Evaluation of stress and strain on mandible caused using “All-on-Four” system from PEEK in hybrid prosthesis: Finite-element analysis. Odontology 2022, 111, 618–629. [Google Scholar] [CrossRef] [PubMed]
- Park, J.M.; Kim, H.J.; Park, E.J.; Kim, M.R.; Kim, S.J. Three dimensional finite element analysis of the stress distribution around the mandibular posterior implant during non-working movement according to the amount of cantilever. J. Adv. Prosthodont. 2014, 6, 361–371. [Google Scholar] [CrossRef] [PubMed]
- Cicciù, M.; Cervino, G.; Milone, D.; Risitano, G. FEM Investigation of the Stress Distribution over Mandibular Bone Due to Screwed Overdenture Positioned on Dental Implants. Materials 2018, 11, 1512. [Google Scholar] [CrossRef]
- Tawara, D.; Nagura, K. Predicting changes in mechanical properties of trabecular bone by adaptive remodeling. Comput. Methods Biomech. Biomed. Eng. 2017, 20, 415–425. [Google Scholar] [CrossRef]
- Aunmeungtong, W.; Khongkhunthian, P.; Rungsiyakull, P. Stress and strain distribution in three different mini dental implant designs using in implant retained overdenture: A finite element analysis study. ORAL Implantol. 2016, 9, 202–212. [Google Scholar]
- Merdji, A.; Bachir Bouiadjra, B.; Achour, T.; Serier, B.; Ould Chikh, B.; Feng, Z.O. Stress analysis in dental prosthesis. Comput. Mater. Sci. 2010, 49, 126–133. [Google Scholar] [CrossRef]
- Shaw, A.M.; Sameshima, G.T.; Vu, H.V. Mechanical stress generated by orthodontic forces on apical root cementum: A finite element model. Orthod. Craniofacial Res. 2004, 7, 98–107. [Google Scholar] [CrossRef] [PubMed]
- Field, C.; Ichim, I.; Swain, M.V.; Chan, E.; Darendeliler, M.A.; Li, W.; Li, Q. Mechanical responses to orthodontic loading: A 3-dimensional finite element multi-tooth model. Am. J. Orthod. Dentofac. Orthop. 2009, 135, 174–181. [Google Scholar] [CrossRef] [PubMed]
- Merdji, A.; Mootanah, R.; Bachir Bouiadjra, B.A.; Benaissa, A.; Aminallah, L.; Ould Chikh El, B.; Mukdadi, S. Stress analysis in single molar tooth. Mater. Sci. Eng. C Mater. Biol. Appl. 2013, 33, 691–698. [Google Scholar] [CrossRef] [PubMed]
- Shetty, B.; Fazal, I.; Khan, S.F. FEA analysis of Normofunctional forces on periodontal elements in different angulations. Bioinformation 2022, 18, 245–250. [Google Scholar] [CrossRef] [PubMed]
- Moga, R.-A.; Olteanu, C.D.; Delean, A.G. Investigating the Ability of the Tooth and Surrounding Support Tissues to Absorb and Dissipate Orthodontic Loads during Periodontal Breakdown—Finite Elements Analysis. Appl. Sci. 2024, 14, 1041. [Google Scholar] [CrossRef]
- Wu, V.; Schulten, E.; Helder, M.N.; Ten Bruggenkate, C.M.; Bravenboer, N.; Klein-Nulend, J. Bone vitality and vascularization of mandibular and maxillary bone grafts in maxillary sinus floor elevation: A retrospective cohort study. Clin. Implant Dent. Relat. Res. 2023, 25, 141–151. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Liu, Y.; Wang, D.; Zhang, J.; Dong, X.; Jiang, X.; Xu, X. Investigation of effective intrusion and extrusion force for maxillary canine using finite element analysis. Comput. Methods Biomech. Biomed. Eng. 2019, 22, 1294–1302. [Google Scholar] [CrossRef]
- Moga, R.A.; Buru, S.M.; Olteanu, C.D. Assessment of the Best FEA Failure Criteria (Part I): Investigation of the Biomechanical Behavior of PDL in Intact and Reduced Periodontium. Int. J. Environ. Res. Public Health 2022, 19, 12424. [Google Scholar] [CrossRef]
- Perez-Gonzalez, A.; Iserte-Vilar, J.L.; Gonzalez-Lluch, C. Interpreting finite element results for brittle materials in endodontic restorations. Biomed. Eng. Online 2011, 10, 44. [Google Scholar] [CrossRef] [PubMed]
- Moga, R.A.; Olteanu, C.D.; Botez, M.; Buru, S.M. Assessment of the Maximum Amount of Orthodontic Force for Dental Pulp and Apical Neuro-Vascular Bundle in Intact and Reduced Periodontium on Bicuspids (Part II). Int. J. Environ. Res. Public Health 2023, 20, 1179. [Google Scholar] [CrossRef] [PubMed]
- Moga, R.A.; Buru, S.M.; Chiorean, C.G. Overall stress in periodontal ligament under orthodontic movement during a periodontal breakdown. Am. J. Orthod. Dentofac. Orthop. 2022, 161, e127–e135. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Liu, Y.; Li, B.; Wang, D.; Dong, X.; Sun, Q.; Chen, G. Numerical simulation of optimal range of rotational moment for the mandibular lateral incisor, canine and first premolar based on biomechanical responses of periodontal ligaments: A case study. Clin. Oral Investig. 2021, 25, 1569–1577. [Google Scholar] [CrossRef] [PubMed]
- Burr, D.B. Why bones bend but don’t break. J. Musculoskelet. Neuronal Interact. 2011, 11, 270–285. [Google Scholar] [PubMed]
- Hart, N.H.; Nimphius, S.; Rantalainen, T.; Ireland, A.; Siafarikas, A.; Newton, R.U. Mechanical basis of bone strength: Influence of bone material, bone structure and muscle action. J. Musculoskelet. Neuronal Interact. 2017, 17, 114–139. [Google Scholar] [PubMed]
- Hemanth, M.; Deoli, S.; Raghuveer, H.P.; Rani, M.S.; Hegde, C.; Vedavathi, B. Stress Induced in the Periodontal Ligament under Orthodontic Loading (Part I): A Finite Element Method Study Using Linear Analysis. J. Int. Oral Health JIOH 2015, 7, 129–133. [Google Scholar] [PubMed]
- Hemanth, M.; Deoli, S.; Raghuveer, H.P.; Rani, M.S.; Hegde, C.; Vedavathi, B. Stress Induced in Periodontal Ligament under Orthodontic Loading (Part II): A Comparison of Linear Versus Non-Linear Fem Study. J. Int. Oral Health JIOH 2015, 7, 114–118. [Google Scholar] [PubMed]
- Toms, S.R.; Eberhardt, A.W. A nonlinear finite element analysis of the periodontal ligament under orthodontic tooth loading. Am. J. Orthod. Dentofac. Orthop. 2003, 123, 657–665. [Google Scholar] [CrossRef]
- Proffit, W.R.; Fields, H.; Sarver, D.M.; Ackerman, J.L. Contemporary Orthodontics, 5th ed.; Elsevier: St. Louis, MO, USA, 2012. [Google Scholar]
- Villaman-Santacruz, H.; Torres-Rosas, R.; Acevedo-Mascarúa, A.E.; Argueta-Figueroa, L. Root resorption factors associated with orthodontic treatment with fixed appliances: A systematic review and meta-analysis. Dent. Med. Probl. 2022, 59, 437–450. [Google Scholar] [CrossRef]
- Laskowska, J.; Paradowska-Stolarz, A.; Miralles-Jordá, L.; Schutty, D.; Mikulewicz, M. Complication of Orthodontic Treatment: A Case Report on Severe Apical Root Resorption (ARR) in a Patient with Turner Syndrome. Children 2024, 11, 358. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Zhou, H.; Liao, X.; Liu, Y. The influence of bracket torque on external apical root resorption in bimaxillary protrusion patients: A retrospective study. BMC Oral Health 2022, 22, 7. [Google Scholar] [CrossRef] [PubMed]
- Cheng, L.L.; Turk, T.; Elekdag-Turk, S.; Jones, A.S.; Petocz, P.; Darendeliler, M.A. Physical properties of root cementum: Part 13. Repair of root resorption 4 and 8 weeks after the application of continuous light and heavy forces for 4 weeks: A microcomputed-tomography study. Am. J. Orthod. Dentofac. Orthop. 2009, 136, 320.e1–320.e10, Discussion 320–321. [Google Scholar] [CrossRef]
- Zhong, J.; Chen, J.; Weinkamer, R.; Darendeliler, M.A.; Swain, M.V.; Sue, A.; Zheng, K.; Li, Q. In vivo effects of different orthodontic loading on root resorption and correlation with mechanobiological stimulus in periodontal ligament. J. R. Soc. Interface 2019, 16, 20190108. [Google Scholar] [CrossRef] [PubMed]
- Zhang, X.; Li, M.Q.; Guo, J.; Yang, H.W.; Yu, J.; Li, G.J. An analysis of the optimal intrusion force of the maxillary central incisor with root horizontal resorption using the finite element method and curve fitting. Comput. Methods Biomech. Biomed. Eng. 2022, 25, 1471–1486. [Google Scholar] [CrossRef] [PubMed]
- Patel, S.; Saberi, N.; Pimental, T.; Teng, P.H. Present status and future directions: Root resorption. Int. Endod. J. 2022, 55 (Suppl. S4), 892–921. [Google Scholar] [CrossRef] [PubMed]
- Deng, Y.; Sun, Y.; Xu, T. Evaluation of root resorption after comprehensive orthodontic treatment using cone beam computed tomography (CBCT): A meta-analysis. BMC Oral Health 2018, 18, 116. [Google Scholar] [CrossRef] [PubMed]
- Chan, E.; Darendeliler, M.A. Physical properties of root cementum: Part 5. Volumetric analysis of root resorption craters after application of light and heavy orthodontic forces. Am. J. Orthod. Dentofac. Orthop. 2005, 127, 186–195. [Google Scholar] [CrossRef] [PubMed]
- Lee, Y.J.; Lee, T.Y. External root resorption during orthodontic treatment in root-filled teeth and contralateral teeth with vital pulp: A clinical study of contributing factors. Am. J. Orthod. Dentofac. Orthop. 2016, 149, 84–91. [Google Scholar] [CrossRef]
- Moga, R.A.; Delean, A.G.; Buru, S.M.; Botez, M.D.; Olteanu, C.D. Orthodontic Internal Resorption Assessment in Periodontal Breakdown-A Finite Elements Analysis (Part II). Healthcare 2023, 11, 2622. [Google Scholar] [CrossRef]
- Rey, D.; Smit, R.M.; Gamboa, L. Orthodontic treatment in patient with idiopathic root resorption: A case report. Dent. Press J. Orthod. 2015, 20, 108–117. [Google Scholar] [CrossRef] [PubMed][Green Version]
- Iglesias-Linares, A.; Yañez-Vico, R.M.; Ballesta, S.; Ortiz-Ariza, E.; Mendoza-Mendoza, A.; Perea, E.; Solano-Reina, E. Interleukin 1 gene cluster SNPs (rs1800587, rs1143634) influences post-orthodontic root resorption in endodontic and their contralateral vital control teeth differently. Int. Endod. J. 2012, 45, 1018–1026. [Google Scholar] [CrossRef] [PubMed]
- Iglesias-Linares, A.; Yañez-Vico, R.M.; Ortiz-Ariza, E.; Ballesta, S.; Mendoza-Mendoza, A.; Perea, E.; Solano-Reina, E. Postorthodontic external root resorption in root-filled teeth is influenced by interleukin-1β polymorphism. J. Endod. 2012, 38, 283–287. [Google Scholar] [CrossRef] [PubMed]
- Iglesias-Linares, A.; Yañez-Vico, R.M.; Ballesta-Mudarra, S.; Ortiz-Ariza, E.; Mendoza-Mendoza, A.; Perea-Pérez, E.; Moreno-Fernández, A.M.; Solano-Reina, E. Interleukin 1 receptor antagonist (IL1RN) genetic variations condition post-orthodontic external root resorption in endodontically-treated teeth. Histol. Histopathol. 2013, 28, 767–773. [Google Scholar] [PubMed]
- Iglesias-Linares, A.; Yañez-Vico, R.; Ballesta-Mudarra, S.; Ortiz-Ariza, E.; Ortega-Rivera, H.; Mendoza-Mendoza, A.; Solano-Reina, E.; Perea-Pérez, E. Postorthodontic external root resorption is associated with IL1 receptor antagonist gene variations. Oral Dis. 2012, 18, 198–205. [Google Scholar] [CrossRef] [PubMed]
- Pereira, S.A.; Melo, A.; Resende, E.; Regateiro, F.; Coimbra Silva, H. Antagonistic effect of IL1 variants in periodontitis and external apical root resorption: Evidence from a literature review. Arch. Oral Biol. 2018, 95, 195–201. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.L.; Liu, Y.F.; Peng, W.; Dong, H.Y.; Zhang, J.X. A biomechanical case study on the optimal orthodontic force on the maxillary canine tooth based on finite element analysis. J. Zhejiang Univ. Sci. B 2018, 7, 535–546. [Google Scholar] [CrossRef] [PubMed]
- Alhadainy, H.A.; Flores-Mir, C.; Abdel-Karim, A.H.; Crossman, J.; El-Bialy, T. Orthodontic-induced External Root Resorption of Endodontically Treated Teeth: A Meta-analysis. J. Endod. 2019, 45, 483–489. [Google Scholar] [CrossRef] [PubMed]
- Moga, R.A.; Olteanu, C.D.; Buru, S.M.; Botez, M.D.; Delean, A.G. Finite Elements Analysis of Biomechanical Behavior of the Bracket in a Gradual Horizontal Periodontal Breakdown—A Comparative Analysis of Multiple Failure Criteria. Appl. Sci. 2023, 13, 9480. [Google Scholar] [CrossRef]
- Kochar, G.D.; Jayan, B.; Chopra, S.S.; Mechery, R.; Goel, M.; Verma, M. Interdisciplinary Management of Patient with Advanced Periodontal Disease. Int. J. Orthod. 2016, 27, 51–56. [Google Scholar]
- Sivakumar, A.; Raju, M.A.; Sunny, J.; Cyriac, R.; Bhat, S.; Mohandas, A.A.; Divya, B. Collaborative management of a young patient with generalized aggressive periodontitis. Int. J. Orthod. 2014, 25, 27–31. [Google Scholar]
- Pamukçu, H.; Polat-Özsoy, Ö.; Gülşahi, A.; Özemre, M. External apical root resorption after nonextraction orthodontic treatment with labial vs. lingual fixed appliances. J. Orofac. Orthop. 2020, 81, 41–51. [Google Scholar] [CrossRef] [PubMed]
- Yi, J.; Li, M.; Li, Y.; Li, X.; Zhao, Z. Root resorption during orthodontic treatment with self-ligating or conventional brackets: A systematic review and meta-analysis. BMC Oral Health 2016, 16, 125. [Google Scholar] [CrossRef] [PubMed]
- Alves Otelakoski, B.; Magno Gonçalves, F.; Marques de Mattos de Araujo, B.; Zeigelboim, B.S.; Veríssimo Meira Taveira, K.; Sampaio Santos, R.; Guariza-Filho, O.; Stechman-Neto, J.; Miranda de Araujo, C. Comparison of orthodontic root resorption of root-filled and vital teeth: A meta-analysis. J. Am. Dent. Assoc. 2022, 153, 532–541.e7. [Google Scholar] [CrossRef] [PubMed]
- Ioannidou-Marathiotou, I.; Zafeiriadis, A.A.; Papadopoulos, M.A. Root resorption of endodontically treated teeth following orthodontic treatment: A meta-analysis. Clin. Oral Investig. 2013, 17, 1733–1744. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D.; Xue, K.; Meng, J.; Hu, M.; Bi, F.; Tan, X. Orthodontically induced external apical root resorption considerations of root-filled teeth vs vital pulp teeth: A systematic review and meta-analysis. BMC Oral Health 2023, 23, 241. [Google Scholar] [CrossRef] [PubMed]
- Gravholt, C.H.; Viuff, M.H.; Brun, S.; Stochholm, K.; Andersen, N.H. Turner syndrome: Mechanisms and management. Nat. Rev. Endocrinol. 2019, 15, 601–614. [Google Scholar] [CrossRef]
- Leone, P.E.; Yumiceba, V.; Jijón-Vergara, A.; Pérez-Villa, A.; Armendáriz-Castillo, I.; García-Cárdenas, J.M.; Guerrero, S.; Guevara-Ramírez, P.; López-Cortés, A.; Zambrano, A.K.; et al. Cytogenetic and genomic analysis of a patient with turner syndrome and t(2;12): A case report. Mol. Cytogenet. 2020, 13, 46. [Google Scholar] [CrossRef]


| Material | Young’s Modulus, E (GPa) | Poisson Ratio, ʋ | Refs. |
|---|---|---|---|
| Enamel | 80 | 0.33 | [1,2,17,20,22,23] |
| Dentin/Cementum | 18.6 | 0.31 | [1,2,17,20,22,23] |
| Pulp | 0.0021 | 0.45 | [1,2,17,20,22,23] |
| PDL | 0.0667 | 0.49 | [1,2,17,20,22,23] |
| Cortical bone | 14.5 | 0.323 | [1,2,17,20,22,23] |
| Trabecular bone | 1.37 | 0.3 | [1,2,17,20,22,23] |
| Stainless Steel | 190 | 0.265 | [1,2,17,20,22,23] |
| Resorption (mm) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Intrusion | Tresca | a | 4.13 | 4.20 | 4.27 | 4.34 | 4.42 | 5.16 | 5.90 | 6.64 | 7.38 |
| 0.6 N/60 gf | m | 8.31 | 8.97 | 9.64 | 10.30 | 10.97 | 12.86 | 14.75 | 16.64 | 18.43 | |
| c | 11.07 | 13.23 | 15.39 | 17.55 | 19.72 | 23.07 | 26.43 | 29.78 | 33.14 | ||
| VM | a | 2.97 | 3.19 | 3.41 | 3.64 | 3.86 | 4.51 | 5.15 | 5.80 | 6.44 | |
| m | 7.28 | 7.87 | 8.44 | 9.02 | 9.61 | 11.22 | 12.84 | 14.46 | 16.08 | ||
| c | 10.18 | 11.95 | 13.72 | 15.49 | 17.26 | 20.17 | 23.09 | 26.00 | 28.92 | ||
| 1.2 N/120 gf | Tresca | a | 8.26 | 8.40 | 8.54 | 8.68 | 8.83 | 10.32 | 11.80 | 13.28 | 14.77 |
| m | 16.63 | 17.94 | 19.28 | 20.60 | 21.95 | 25.72 | 29.50 | 33.28 | 36.86 | ||
| c | 22.14 | 26.46 | 30.78 | 35.10 | 39.45 | 46.14 | 52.86 | 59.56 | 66.28 | ||
| VM | a | 5.94 | 6.38 | 6.83 | 7.27 | 7.73 | 9.01 | 10.30 | 11.59 | 12.89 | |
| m | 14.56 | 15.73 | 16.88 | 18.04 | 19.21 | 22.44 | 25.68 | 28.92 | 32.17 | ||
| c | 20.36 | 23.90 | 27.44 | 30.98 | 34.52 | 40.34 | 46.18 | 52.00 | 57.85 | ||
| 2.4 N/240 gf | Tresca | a | 16.52 | 16.80 | 17.08 | 17.36 | 17.66 | 20.64 | 23.60 | 26.56 | 29.53 |
| m | 33.25 | 35.88 | 38.56 | 41.20 | 43.89 | 51.44 | 59.00 | 66.56 | 73.72 | ||
| c | 44.29 | 52.92 | 61.56 | 70.20 | 78.89 | 92.28 | 105.72 | 119.12 | 132.57 | ||
| VM | a | 11.88 | 12.77 | 13.66 | 14.55 | 15.46 | 18.02 | 20.60 | 23.18 | 25.77 | |
| m | 29.12 | 31.46 | 33.76 | 36.08 | 38.43 | 44.88 | 51.36 | 57.84 | 64.34 | ||
| c | 40.73 | 47.80 | 54.88 | 61.96 | 69.05 | 80.68 | 92.36 | 104.00 | 115.69 | ||
| Extrusion | Tresca | a | 4.13 | 4.20 | 4.27 | 4.34 | 4.42 | 5.16 | 5.90 | 6.64 | 7.38 |
| 0.6 N/60 gf | m | 8.31 | 8.97 | 9.64 | 10.30 | 10.97 | 12.86 | 14.75 | 16.64 | 18.43 | |
| c | 11.07 | 13.23 | 15.39 | 17.55 | 19.72 | 23.07 | 26.43 | 29.78 | 33.14 | ||
| VM | a | 2.97 | 3.19 | 3.41 | 3.64 | 3.86 | 4.51 | 5.15 | 5.80 | 6.44 | |
| m | 7.28 | 7.87 | 8.44 | 9.02 | 9.61 | 11.22 | 12.84 | 14.46 | 16.08 | ||
| c | 10.18 | 11.95 | 13.72 | 15.49 | 17.26 | 20.17 | 23.09 | 26.00 | 28.92 | ||
| 1.2 N/120 gf | Tresca | a | 8.26 | 8.40 | 8.54 | 8.68 | 8.83 | 10.32 | 11.80 | 13.28 | 14.77 |
| m | 16.63 | 17.94 | 19.28 | 20.60 | 21.95 | 25.72 | 29.50 | 33.28 | 36.86 | ||
| c | 22.14 | 26.46 | 30.78 | 35.10 | 39.45 | 46.14 | 52.86 | 59.56 | 66.28 | ||
| VM | a | 5.94 | 6.38 | 6.83 | 7.27 | 7.73 | 9.01 | 10.30 | 11.59 | 12.89 | |
| m | 14.56 | 15.73 | 16.88 | 18.04 | 19.21 | 22.44 | 25.68 | 28.92 | 32.17 | ||
| c | 20.36 | 23.90 | 27.44 | 30.98 | 34.52 | 40.34 | 46.18 | 52.00 | 57.85 | ||
| 2.4 N/240 gf | Tresca | a | 16.52 | 16.80 | 17.08 | 17.36 | 17.66 | 20.64 | 23.60 | 26.56 | 29.53 |
| m | 33.25 | 35.88 | 38.56 | 41.20 | 43.89 | 51.44 | 59.00 | 66.56 | 73.72 | ||
| c | 44.29 | 52.92 | 61.56 | 70.20 | 78.89 | 92.28 | 105.72 | 119.12 | 132.57 | ||
| VM | a | 11.88 | 12.77 | 13.66 | 14.55 | 15.46 | 18.02 | 20.60 | 23.18 | 25.77 | |
| m | 29.12 | 31.46 | 33.76 | 36.08 | 38.43 | 44.88 | 51.36 | 57.84 | 64.34 | ||
| c | 40.73 | 47.80 | 54.88 | 61.96 | 69.05 | 80.68 | 92.36 | 104.00 | 115.69 | ||
| Translation | Tresca | a | 8.06 | 8.26 | 8.46 | 8.66 | 8.87 | 9.88 | 10.90 | 11.92 | 12.94 |
| 0.6 N/60 gf | m | 17.08 | 19.14 | 21.20 | 23.26 | 25.32 | 35.08 | 44.85 | 54.61 | 64.38 | |
| c | 22.74 | 28.65 | 34.56 | 40.47 | 46.38 | 63.75 | 81.12 | 98.49 | 115.87 | ||
| VM | a | 7.05 | 7.24 | 7.43 | 7.62 | 7.81 | 8.68 | 9.55 | 10.42 | 11.30 | |
| m | 14.88 | 16.91 | 18.95 | 20.98 | 23.02 | 31.31 | 39.60 | 47.89 | 56.18 | ||
| c | 19.81 | 25.39 | 30.98 | 36.56 | 42.15 | 56.89 | 71.63 | 86.37 | 101.12 | ||
| 1.2 N/120 gf | Tresca | a | 16.12 | 16.52 | 16.92 | 17.32 | 17.75 | 19.76 | 21.80 | 23.84 | 25.89 |
| m | 34.17 | 38.28 | 42.40 | 46.52 | 50.64 | 70.16 | 89.70 | 109.22 | 128.76 | ||
| c | 45.48 | 57.30 | 69.12 | 80.94 | 92.75 | 127.50 | 162.24 | 196.98 | 231.74 | ||
| VM | a | 14.10 | 14.48 | 14.86 | 15.24 | 15.61 | 17.36 | 19.10 | 20.84 | 22.60 | |
| m | 29.76 | 33.82 | 37.90 | 41.96 | 46.04 | 62.62 | 79.20 | 95.78 | 112.36 | ||
| c | 39.63 | 50.78 | 61.96 | 73.12 | 84.31 | 113.78 | 143.26 | 172.74 | 202.25 | ||
| 2.4 N/240 gf | Tresca | a | 32.23 | 33.04 | 33.84 | 34.64 | 35.50 | 39.52 | 43.60 | 47.68 | 51.77 |
| m | 68.34 | 76.56 | 84.80 | 93.04 | 101.28 | 140.32 | 179.40 | 218.44 | 257.53 | ||
| c | 90.97 | 114.60 | 138.24 | 161.88 | 185.50 | 255.00 | 324.48 | 393.96 | 463.48 | ||
| VM | a | 28.19 | 28.96 | 29.72 | 30.48 | 31.23 | 34.72 | 38.20 | 41.68 | 45.21 | |
| m | 59.53 | 67.64 | 75.80 | 83.92 | 92.08 | 125.24 | 158.40 | 191.56 | 224.72 | ||
| c | 79.25 | 101.56 | 123.92 | 146.24 | 168.62 | 227.56 | 286.52 | 345.48 | 404.50 | ||
| Rotation | Tresca | a | 11.56 | 13.78 | 16.00 | 18.22 | 20.45 | 20.87 | 21.30 | 21.72 | 22.15 |
| 0.6 N/60 gf | m | 22.86 | 24.79 | 26.72 | 28.65 | 30.59 | 39.39 | 48.20 | 57.01 | 65.82 | |
| c | 22.86 | 37.47 | 52.00 | 66.71 | 81.33 | 91.12 | 100.91 | 110.70 | 120.50 | ||
| VM | a | 10.51 | 12.34 | 14.17 | 16.00 | 17.84 | 18.18 | 18.52 | 18.86 | 19.21 | |
| m | 20.76 | 22.23 | 23.70 | 25.17 | 26.65 | 34.26 | 41.88 | 49.50 | 57.12 | ||
| c | 20.76 | 33.27 | 45.78 | 58.29 | 70.81 | 79.24 | 87.67 | 96.10 | 104.53 | ||
| 1.2 N/120 gf | Tresca | a | 23.13 | 27.56 | 32.00 | 36.44 | 40.91 | 41.74 | 42.60 | 43.44 | 44.29 |
| m | 45.71 | 49.58 | 53.44 | 57.30 | 61.19 | 78.78 | 96.40 | 114.02 | 131.64 | ||
| c | 45.71 | 74.94 | 104.00 | 133.42 | 162.65 | 182.24 | 201.82 | 221.40 | 240.99 | ||
| VM | a | 21.01 | 24.68 | 28.34 | 32.00 | 35.69 | 36.36 | 37.04 | 37.72 | 38.42 | |
| m | 41.52 | 44.46 | 47.40 | 50.34 | 53.30 | 68.52 | 83.76 | 99.00 | 114.24 | ||
| c | 41.52 | 66.54 | 91.56 | 116.58 | 141.62 | 158.48 | 175.34 | 192.20 | 209.06 | ||
| 2.4 N/240 gf | Tresca | a | 46.26 | 55.12 | 64.00 | 72.88 | 81.81 | 83.48 | 85.20 | 86.88 | 88.58 |
| m | 91.42 | 99.16 | 106.88 | 114.60 | 122.37 | 157.56 | 192.80 | 228.04 | 263.28 | ||
| c | 91.42 | 149.88 | 208.00 | 266.84 | 325.31 | 364.48 | 403.64 | 442.80 | 481.98 | ||
| VM | a | 42.02 | 49.36 | 56.68 | 64.00 | 71.37 | 72.72 | 74.08 | 75.44 | 76.84 | |
| m | 83.05 | 88.92 | 94.80 | 100.68 | 106.59 | 137.04 | 167.52 | 198.00 | 228.48 | ||
| c | 83.05 | 133.08 | 183.12 | 233.16 | 283.24 | 316.96 | 350.68 | 384.40 | 418.12 | ||
| Tipping | Tresca | a | 6.20 | 6.54 | 6.88 | 7.22 | 7.57 | 9.39 | 11.21 | 13.03 | 14.86 |
| 0.6 N/60 gf | m | 15.15 | 16.92 | 18.70 | 20.48 | 22.26 | 31.45 | 40.65 | 49.84 | 59.04 | |
| c | 15.15 | 22.44 | 29.73 | 37.02 | 44.31 | 59.05 | 73.79 | 88.53 | 103.28 | ||
| VM | a | 5.95 | 6.11 | 6.27 | 6.43 | 6.60 | 8.19 | 9.79 | 11.38 | 12.98 | |
| m | 14.54 | 15.75 | 16.96 | 18.17 | 19.39 | 2.44 | 35.50 | 43.56 | 51.62 | ||
| c | 14.54 | 20.54 | 26.55 | 32.56 | 38.57 | 51.48 | 64.40 | 77.31 | 90.23 | ||
| 1.2 N/120 gf | Tresca | a | 12.40 | 13.08 | 13.76 | 14.44 | 15.14 | 18.78 | 22.42 | 26.06 | 29.71 |
| m | 30.31 | 33.84 | 37.40 | 40.96 | 44.52 | 62.90 | 81.30 | 99.68 | 118.09 | ||
| c | 30.31 | 44.88 | 59.46 | 74.04 | 88.61 | 118.10 | 147.58 | 177.06 | 206.56 | ||
| VM | a | 11.90 | 12.22 | 12.54 | 12.86 | 13.20 | 16.38 | 19.58 | 22.76 | 25.96 | |
| m | 29.08 | 31.50 | 33.92 | 36.34 | 38.77 | 4.88 | 71.00 | 87.12 | 103.24 | ||
| c | 29.08 | 41.08 | 53.10 | 65.12 | 77.13 | 102.96 | 128.80 | 154.62 | 180.46 | ||
| 2.4 N/240 gf | Tresca | a | 24.80 | 26.16 | 27.52 | 28.88 | 30.29 | 37.56 | 44.84 | 52.12 | 59.42 |
| m | 60.62 | 67.68 | 74.80 | 81.92 | 89.05 | 125.80 | 162.60 | 199.36 | 236.17 | ||
| c | 60.62 | 89.76 | 118.92 | 148.08 | 177.23 | 236.20 | 295.16 | 354.12 | 413.11 | ||
| VM | a | 23.80 | 24.44 | 25.08 | 25.72 | 26.39 | 32.76 | 39.16 | 45.52 | 51.92 | |
| m | 58.17 | 63.00 | 67.84 | 72.68 | 77.55 | 9.76 | 142.00 | 174.24 | 206.47 | ||
| c | 58.17 | 82.16 | 106.20 | 130.24 | 154.27 | 205.92 | 257.60 | 309.24 | 360.93 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moga, R.-A.; Olteanu, C.D.; Delean, A.G. Trabecular Bone Component Assessment under Orthodontic Loads and Movements during Periodontal Breakdown—A Finite Elements Analysis. Dent. J. 2024, 12, 190. https://doi.org/10.3390/dj12060190
Moga R-A, Olteanu CD, Delean AG. Trabecular Bone Component Assessment under Orthodontic Loads and Movements during Periodontal Breakdown—A Finite Elements Analysis. Dentistry Journal. 2024; 12(6):190. https://doi.org/10.3390/dj12060190
Chicago/Turabian StyleMoga, Radu-Andrei, Cristian Doru Olteanu, and Ada Gabriela Delean. 2024. "Trabecular Bone Component Assessment under Orthodontic Loads and Movements during Periodontal Breakdown—A Finite Elements Analysis" Dentistry Journal 12, no. 6: 190. https://doi.org/10.3390/dj12060190
APA StyleMoga, R.-A., Olteanu, C. D., & Delean, A. G. (2024). Trabecular Bone Component Assessment under Orthodontic Loads and Movements during Periodontal Breakdown—A Finite Elements Analysis. Dentistry Journal, 12(6), 190. https://doi.org/10.3390/dj12060190








