Spatial Fingerprinting: Horizontal Fusion of Multi-Dimensional Bio-Tracers as Solution to Global Food Provenance Problems
Abstract
:1. Introduction
2. Materials and Methods
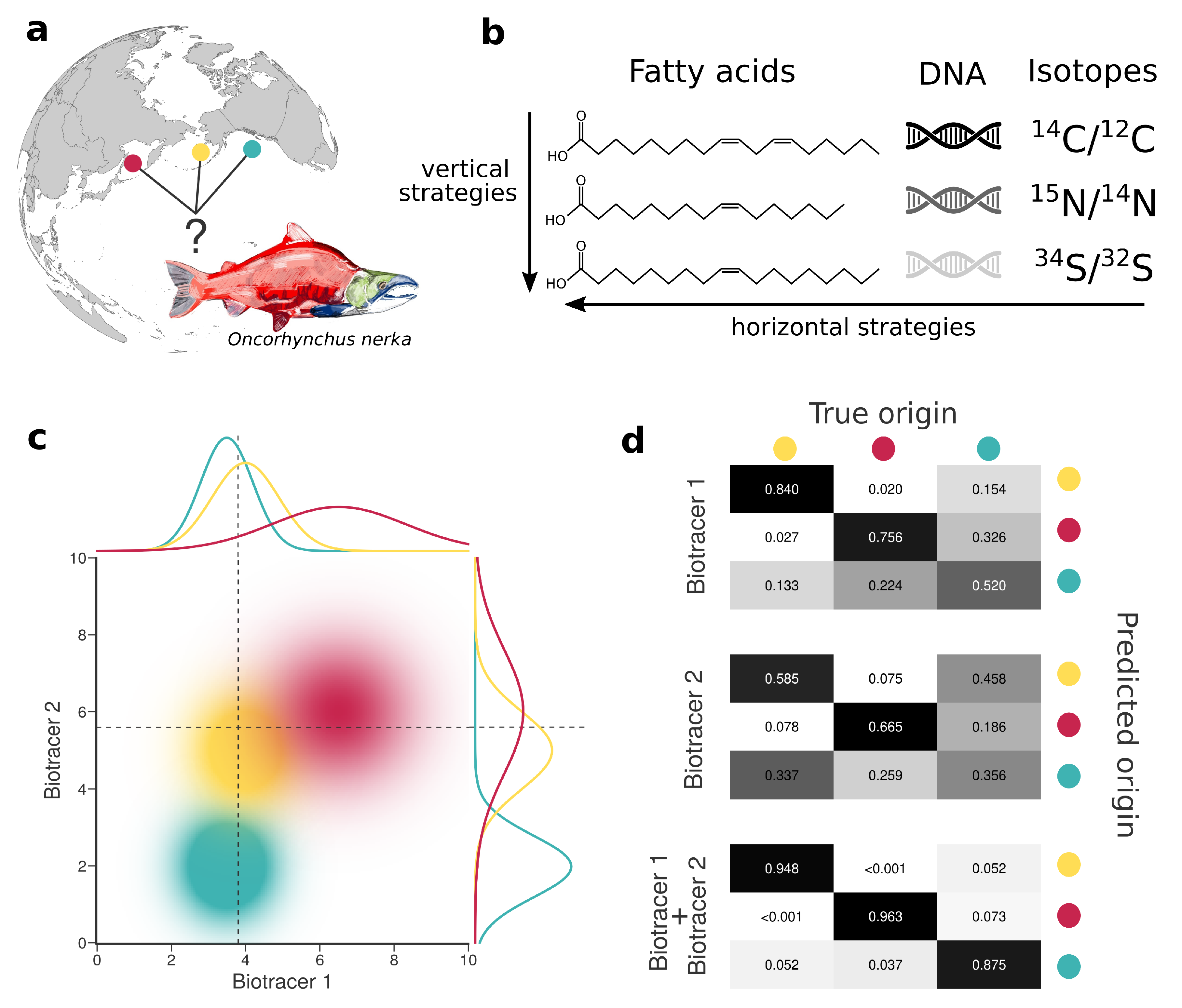
2.1. Data
2.2. Numerical Simulations
2.2.1. Statistical Models
2.2.2. Simulations Design
2.3. Mathematical Proof
Numerical Implementation
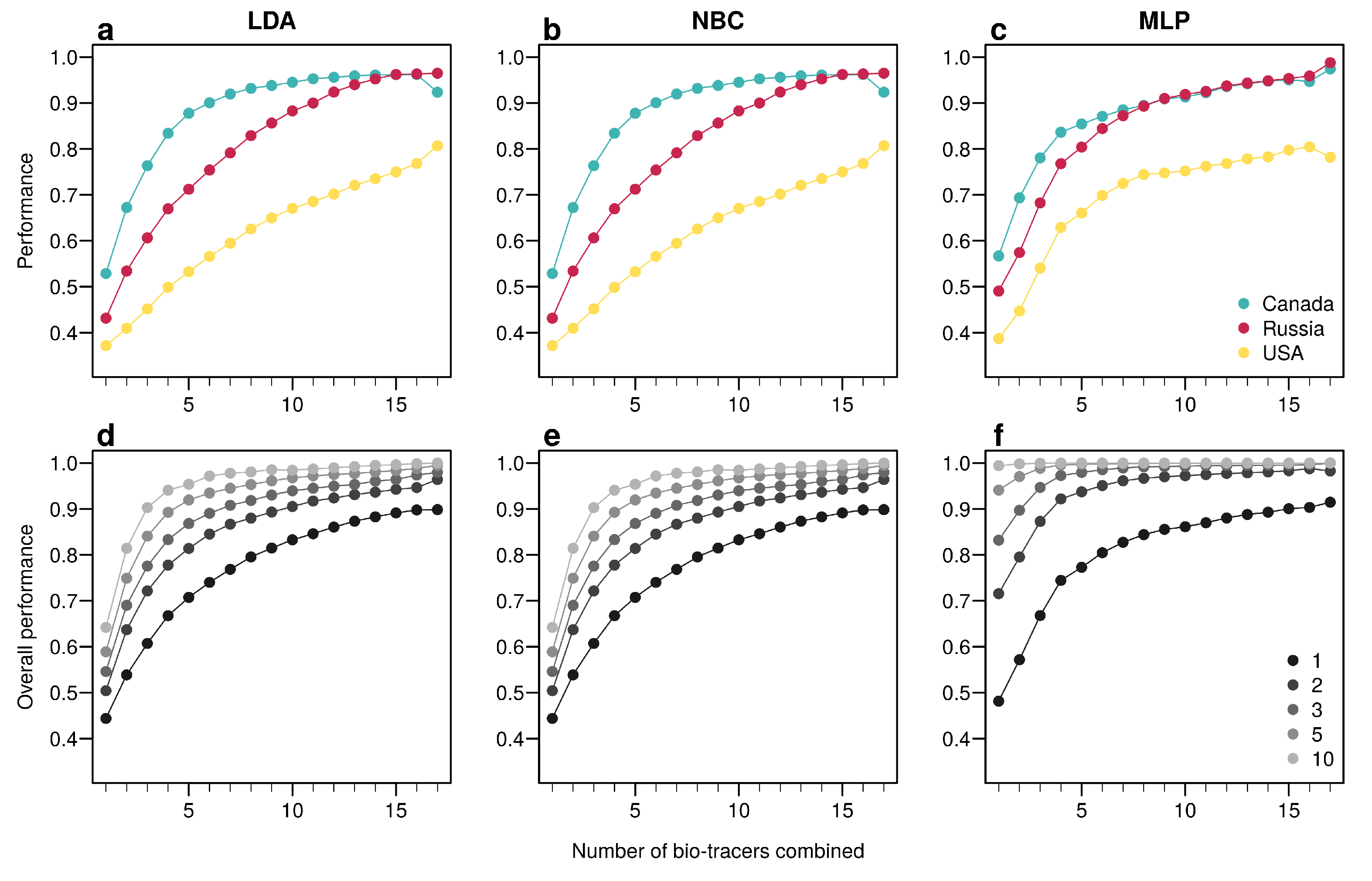
3. Results
3.1. The More Bio-Tracers the Better
3.2. An Examination of the Performances
4. Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Mathematical Proofs
Appendix A.1. Objectives
Appendix A.2. Notations and Definitions
- n, p and q are three natural numbers other than zero;
- is the set of natural numbers ranging from 0 to n, where ;
- denotes the probability of the event X (X being an event, or a realization of a random variable), and probability of X given Y;
- denotes a Gaussian distribution of parameter ;
- denotes the expected value of the random variable X.
Appendix A.3. Bayesian Approach
Appendix A.4. Effect of Dissimilarity between 2 Distributions
Appendix A.4.1. General Considerations
- Improving the a priori knowledge (which we do not consider here);
- Considering a larger quantity and/or higher quality of observations;
- Using more reliable inference techniques.
- where the dissimilarity will be quantified as ;
- where the dissimilarity will be quantified as .
Appendix A.4.2. Identical Variances

Appendix A.4.3. Identical Means

Appendix A.5. Effect of Dimensionality
Appendix A.5.1. General Considerations
Appendix A.5.2. Simplification

Appendix A.6. The Role of Correlation


Appendix A.7. Conclusions
- Increase the size of the sample,
- Use bio-tracers that maximize the dissimilarity of distributions,
- Increase the number of bio-tracers used (preferably as less correlated as possible),
- Use a combination of the factors aforementioned.
Appendix B. Additional Figures and Tables
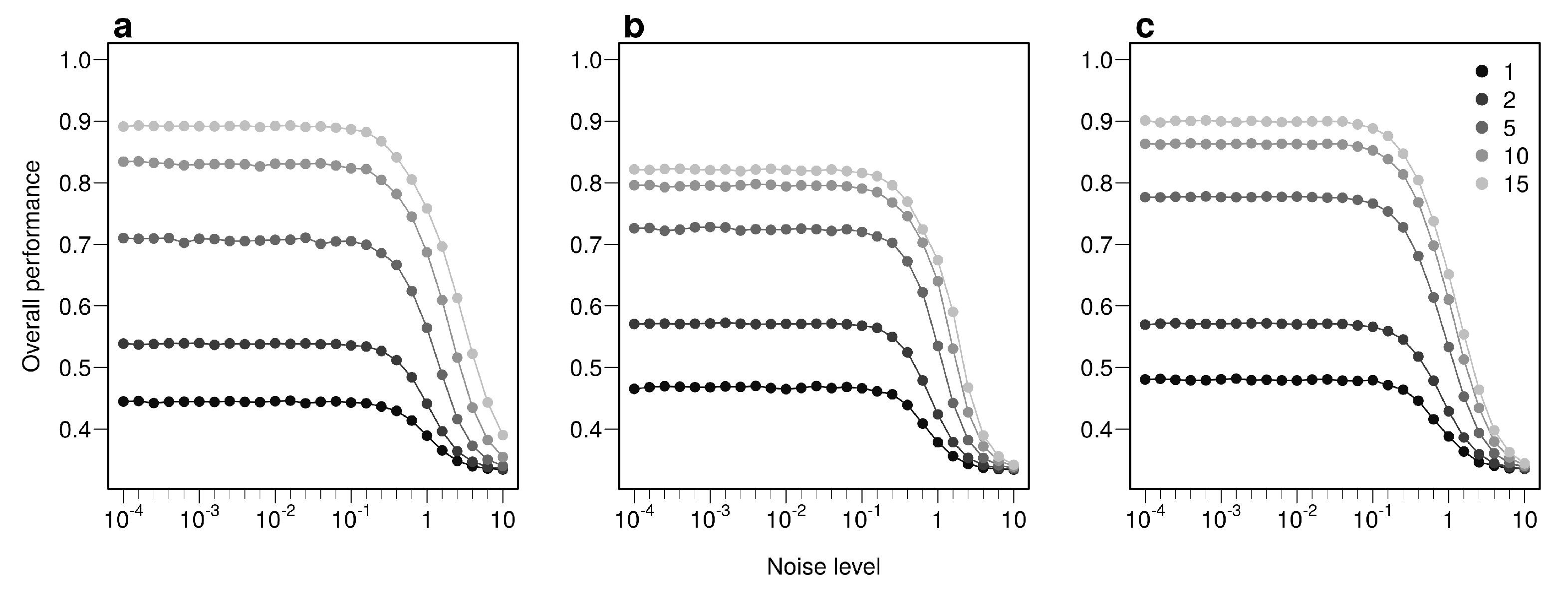
Appendix B.1. Influence of Data Augmentation and Noise Addition for Multi-Layer Perceptron (MLP)

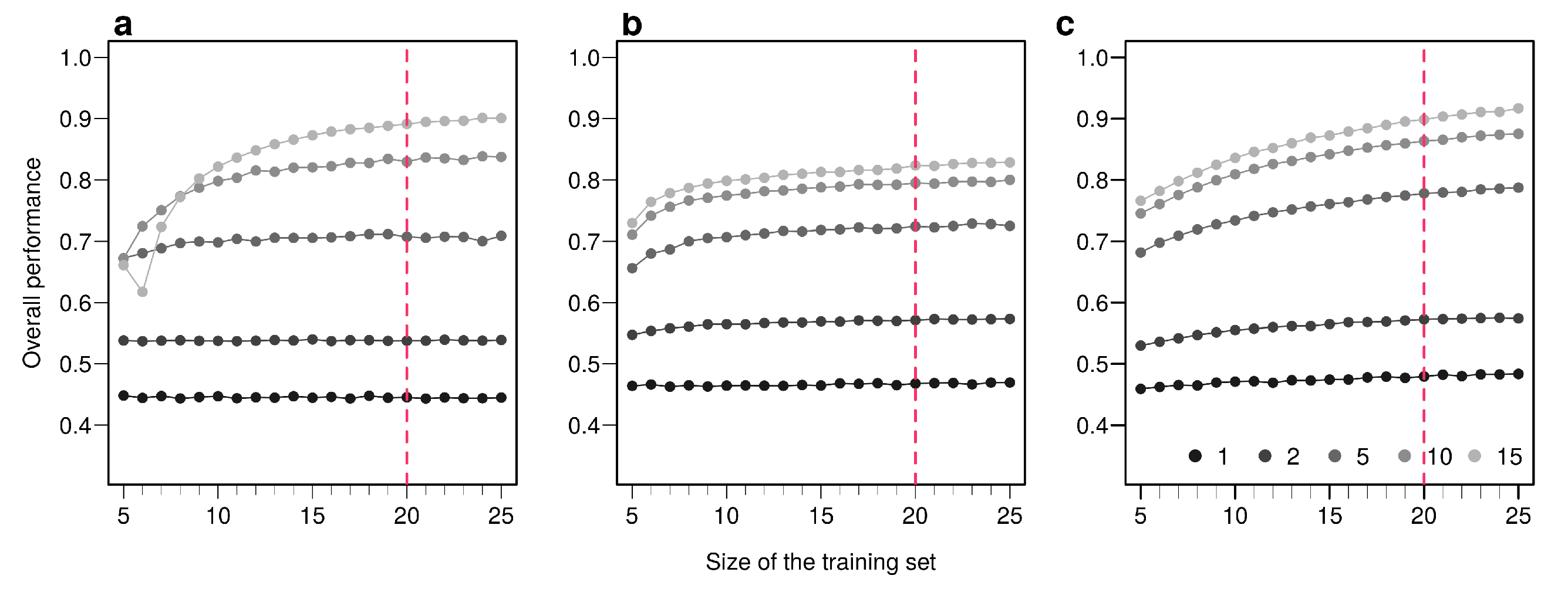
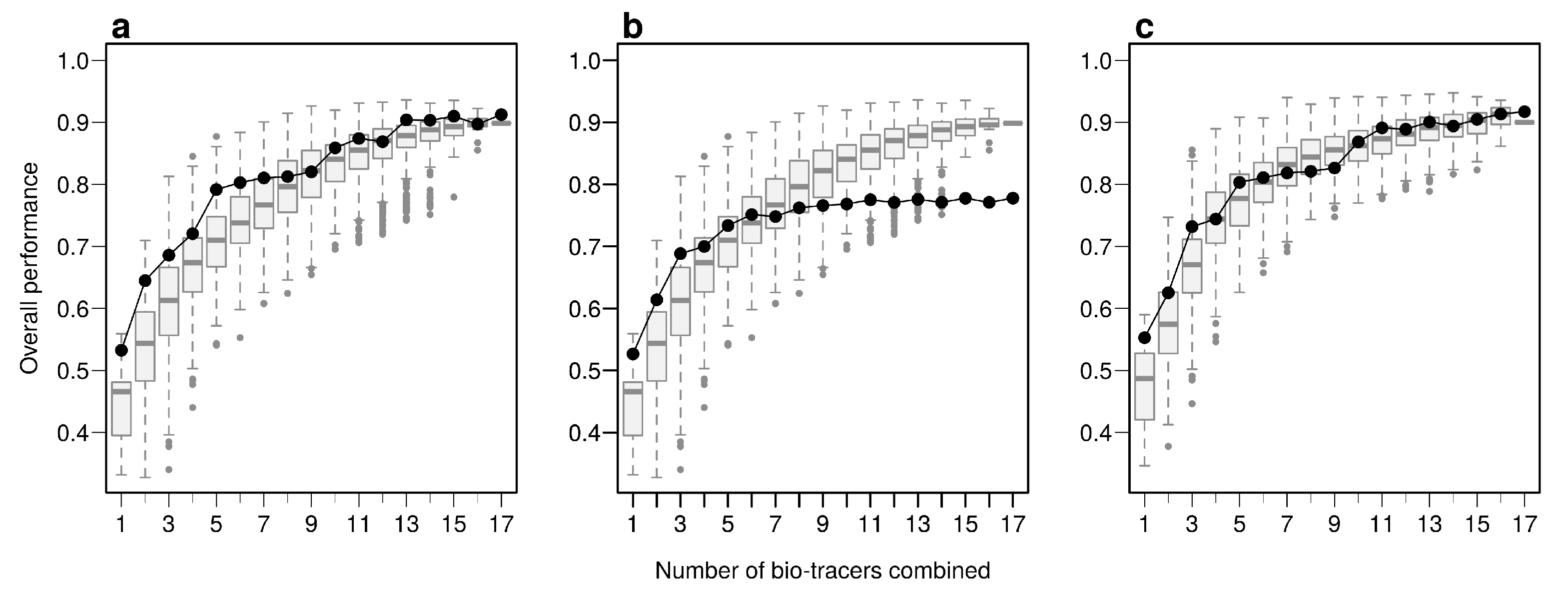
Appendix B.2. Influence of the Training Set Size for the Three Methods
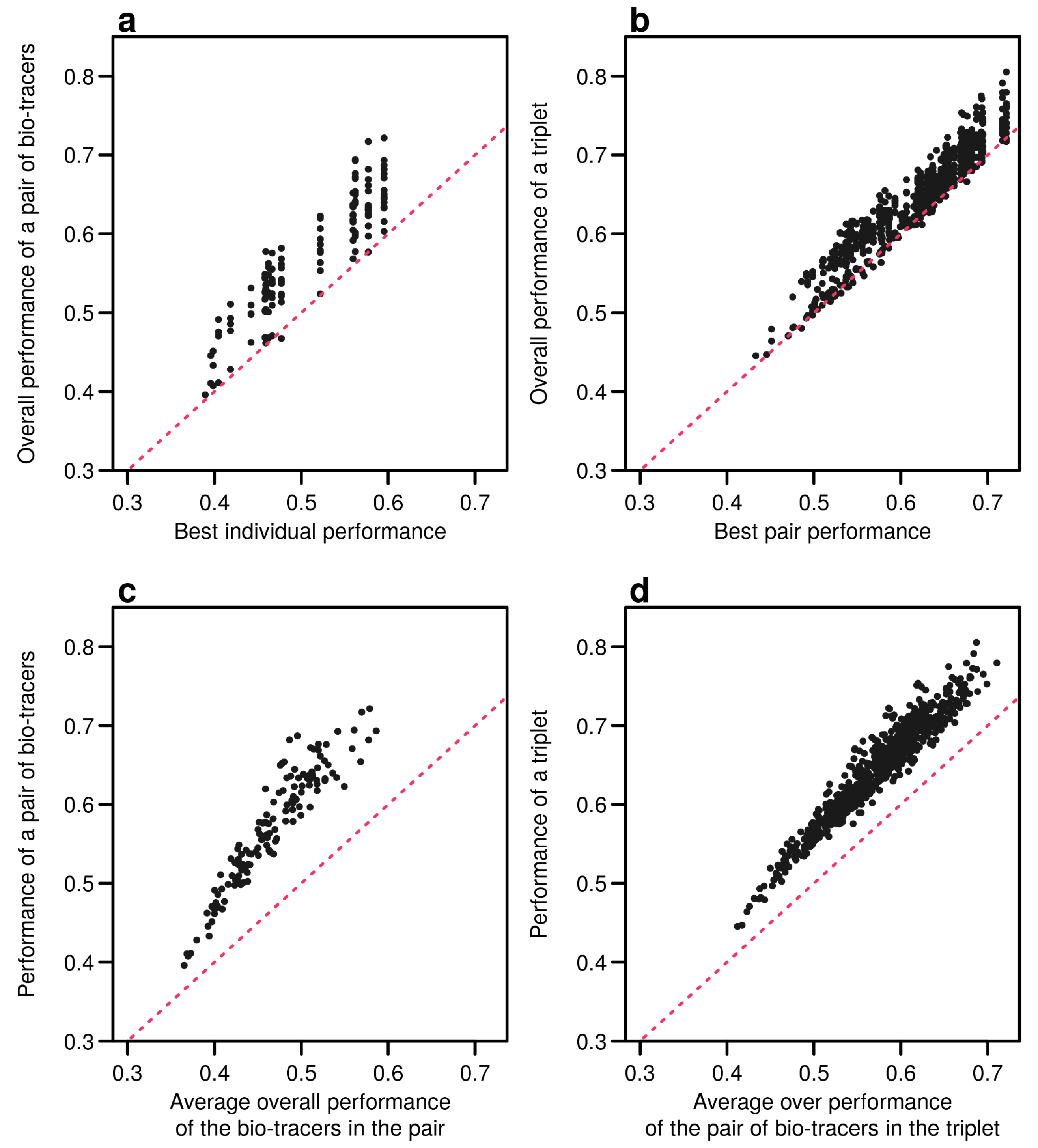
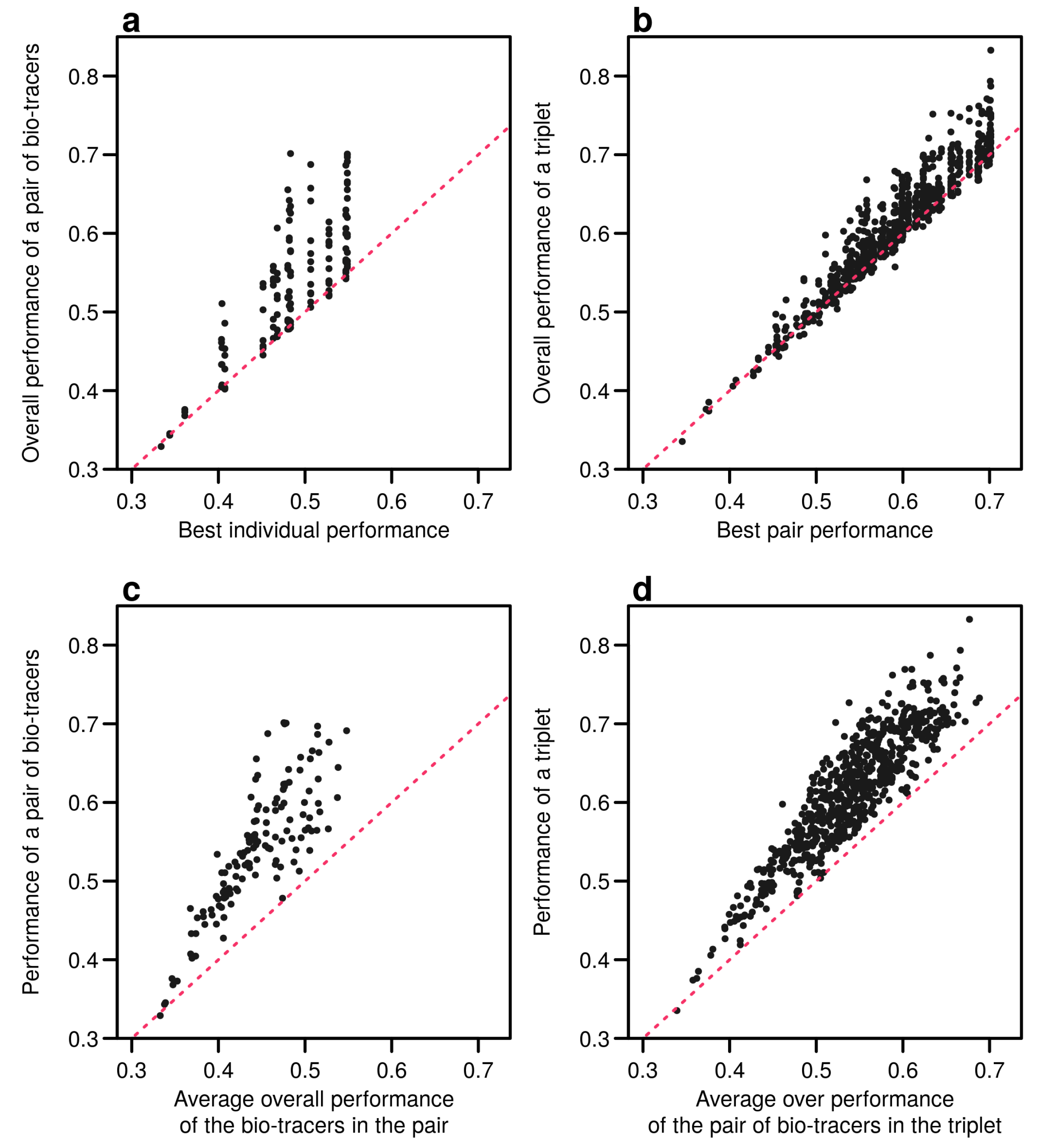
Appendix B.3. Results for Pairs and Triplets
Appendix B.3.1. Equivalent of Figures 5–7 for the Naive Bayesian Classifier (NBC)


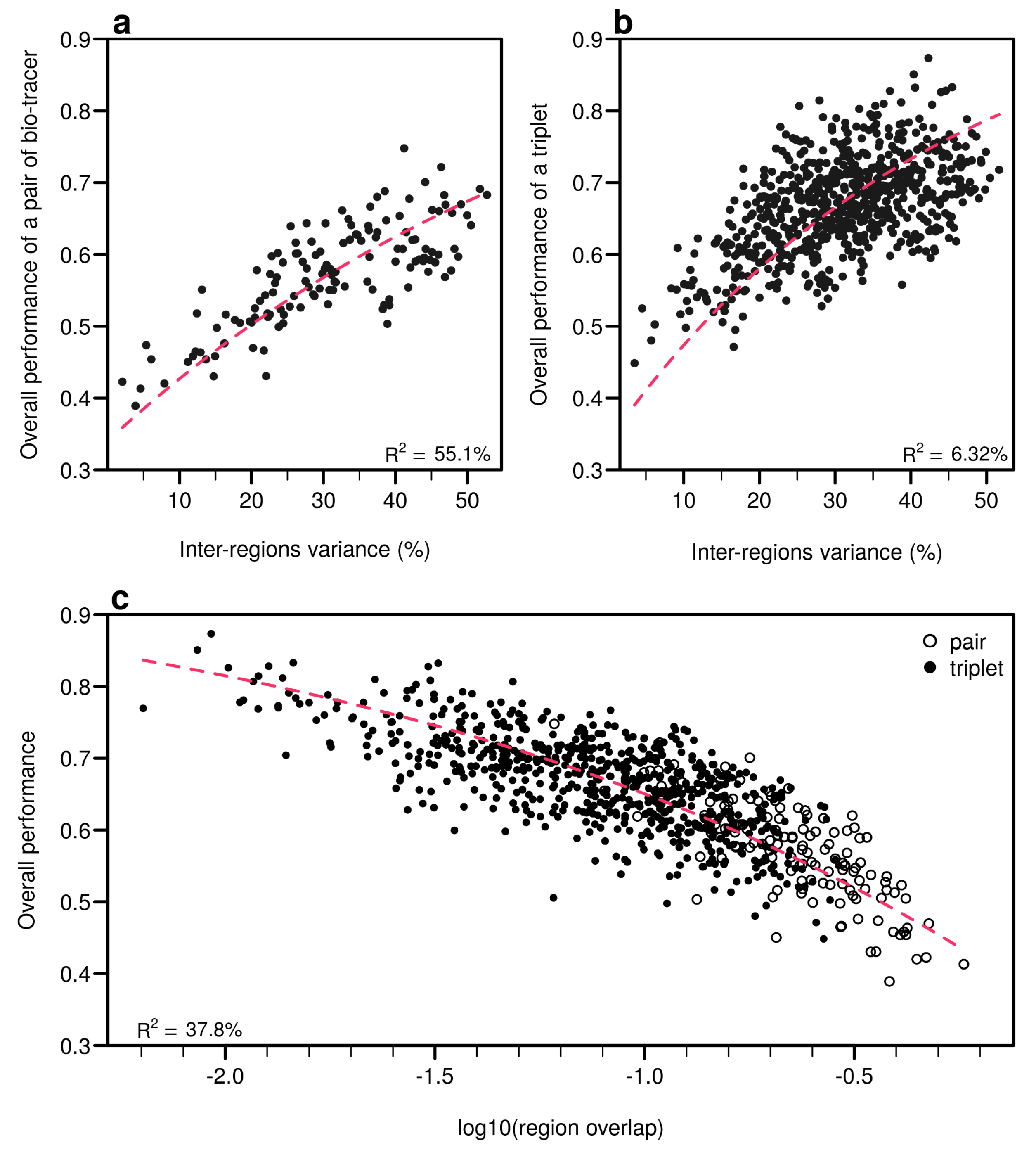
Appendix B.3.2. Equivalent of Figures 5–7 for Mutiple-Layer Perceptron (MLP, a Class of Neural Network)


Appendix B.4. Best Pairs and Triplets of Bio-Tracers
| Rank | LDA | NBC | MLP | ||||||
|---|---|---|---|---|---|---|---|---|---|
| bt 1 | bt 2 | op | bt 1 | bt 2 | op | bt 1 | bt 2 | op | |
| 1 | C20:5n-3 | C22:1 | 0.701 | C18:1 | 0.721 | C20:5n-3 | C22:1 | 0.748 | |
| 2 | C18:1 | C22:6n-3 | 0.701 | C18:1 | C22:5n-3 | 0.717 | C18:1 | C18:3n-3 | 0.722 |
| 3 | C18:0 | C18:1 | 0.700 | C18:1 | C20:1 | 0.694 | C18:3n-3 | C22:5n-3 | 0.701 |
| 4 | C16:0 | C18:1 | 0.697 | C22:5n-3 | 0.693 | C18:1 | C22:5n-3 | 0.691 | |
| 5 | C18:1 | 0.691 | C18:1 | C20:5n-3 | 0.693 | C18:0 | C18:1 | 0.688 | |
| 6 | C20:1 | C22:6n-3 | 0.688 | C18:4n-3 | 0.687 | C18:1 | 0.683 | ||
| 7 | C16:1 | 0.687 | C18:4n-3 | C22:5n-3 | 0.682 | C16:0 | C18:1 | 0.683 | |
| 8 | C18:1 | C20:1 | 0.677 | C20:1 | 0.682 | C18:1 | C22:6n-3 | 0.680 | |
| 9 | C18:1 | C22:1 | 0.666 | C16:0 | C18:1 | 0.677 | C16:0 | C20:5n-3 | 0.678 |
| 10 | C18:1 | C20:5n-3 | 0.663 | C20:4n-3 | 0.676 | C18:1 | C20:5n-3 | 0.670 | |
| LDA | NBC | MLP | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| bt 1 | bt 2 | bt 3 | op | bt 1 | bt 2 | bt 3 | op | bt 1 | bt 2 | bt 3 | op | |
| 1 | C18:1 | C20:5n-3 | C22:1 | 0.833 | C18:1 | C18:4n-3 | 0.805 | C18:1 | C20:4n-3 | C22:5n-3 | 0.873 | |
| 2 | C18:1 | C20:5n-3 | C22:6n-3 | 0.793 | C18:1 | C18:4n-3 | C22:5n-3 | 0.791 | C18:3n-3 | C20:5n-3 | C22:1 | 0.851 |
| 3 | C20:5n-3 | C22:1 | 0.787 | C18:1 | C22:5n-3 | 0.779 | C18:1 | C20:5n-3 | C22:1 | 0.833 | ||
| 4 | C16:0 | C18:1 | C20:5n-3 | 0.771 | C18:1 | C20:4n-3 | C22:5n-3 | 0.779 | C18:1 | C20:4n-3 | C20:5n-3 | 0.832 |
| 5 | C18:0 | C18:1 | C20:4n-3 | 0.769 | C18:1 | C18:4n-3 | C20:5n-3 | 0.775 | C20:5n-3 | C22:1 | 0.828 | |
| 6 | C18:1 | C20:4n-3 | C22:6n-3 | 0.769 | C18:1 | C18:3n-3 | C22:5n-3 | 0.773 | C18:3n-3 | C20:4n-3 | C22:5n-3 | 0.828 |
| 7 | C20:1 | C20:4n-3 | C22:6n-3 | 0.762 | C18:4n-3 | C22:5n-3 | 0.771 | C20:5n-3 | C22:1 | C22:5n-3 | 0.826 | |
| 8 | C18:1 | C20:1 | C20:5n-3 | 0.759 | C18:1 | C20:5n-3 | 0.765 | C18:4n-3 | C20:5n-3 | C22:1 | 0.814 | |
| 9 | C18:0 | C18:1 | C20:5n-3 | 0.758 | C18:1 | C20:4n-3 | 0.762 | C18:1 | C18:3n-3 | C20:4n-3 | 0.812 | |
| 10 | C18:1 | C20:4n-3 | 0.755 | C18:1 | C18:3n-3 | 0.761 | C18:3n-3 | C22:5n-3 | C22:6n-3 | 0.810 | ||
Appendix B.5. DNA Barcodes

References
- Kneen, B. From Land to Mouth: Understanding the Food System; NC Press: Toronto, Japan, 1993. [Google Scholar]
- Godfray, H.C.J.; Crute, I.R.; Haddad, L.; Lawrence, D.; Muir, J.F.; Nisbett, N.; Pretty, J.; Robinson, S.; Toulmin, C.; Whiteley, R. The Future of the Global Food System. Philos. Trans. R. Soc. Biol. Sci. 2010, 365, 2769–2777. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ingram, J. A Food Systems Approach to Researching Food Security and Its Interactions with Global Environmental Change. Food Secur. 2011, 3, 417–431. [Google Scholar] [CrossRef]
- Clapp, J. Distant Agricultural Landscapes. Sustain. Sci. 2015, 10, 305–316. [Google Scholar] [CrossRef] [Green Version]
- FAO. The Future of Food and Agriculture—Alternative Pathways to 2050; Food & Agriculture Org: Rome, Italy, 2018. [Google Scholar]
- Béné, C.; Oosterveer, P.; Lamotte, L.; Brouwer, I.D.; de Haan, S.; Prager, S.D.; Talsma, E.F.; Khoury, C.K. When Food Systems Meet Sustainability—Current Narratives and Implications for Actions. World Dev. 2019, 113, 116–130. [Google Scholar] [CrossRef]
- Weber, C.L.; Matthews, H.S. Food-Miles and the Relative Climate Impacts of Food Choices in the United States. Environ. Sci. Technol. 2008, 42, 3508–3513. [Google Scholar] [CrossRef] [Green Version]
- Roebuck, K.; Turlo, C.; Fuller, S.D. Canadians Eating in the Dark: A Report Card of International Seafood Labelling Requirements; SeaChoice: Pompano Beach, FL, USA, 2017; 24p. [Google Scholar]
- Aung, M.M.; Chang, Y.S. Traceability in a Food Supply Chain: Safety and Quality Perspectives. Food Control 2014, 39, 172–184. [Google Scholar] [CrossRef]
- Galvez, J.F.; Mejuto, J.; Simal-Gandara, J. Future Challenges on the Use of Blockchain for Food Traceability Analysis. TrAC Trends Anal. Chem. 2018, 107, 222–232. [Google Scholar] [CrossRef]
- Badia-Melis, R.; Mishra, P.; Ruiz-García, L. Food Traceability: New Trends and Recent Advances. A Review. Food Control 2015, 57, 393–401. [Google Scholar] [CrossRef]
- Danezis, G.P.; Tsagkaris, A.S.; Brusic, V.; Georgiou, C.A. Food Authentication: State of the Art and Prospects. Curr. Opin. Food Sci. 2016, 10, 22–31. [Google Scholar] [CrossRef]
- Luykx, D.M.; van Ruth, S.M. An Overview of Analytical Methods for Determining the Geographical Origin of Food Products. Food Chem. 2008, 107, 897–911. [Google Scholar] [CrossRef]
- Danezis, G.P.; Tsagkaris, A.S.; Camin, F.; Brusic, V.; Georgiou, C.A. Food Authentication: Techniques, Trends & Emerging Approaches. TrAC Trends Anal. Chem. 2016, 85, 123–132. [Google Scholar] [CrossRef] [Green Version]
- Wong, E.H.K.; Hanner, R.H. DNA Barcoding Detects Market Substitution in North American Seafood. Food Res. Int. 2008, 41, 828–837. [Google Scholar] [CrossRef]
- Baker, C.S. A Truer Measure of the Market: The Molecular Ecology of Fisheries and Wildlife Trade. Mol. Ecol. 2008, 17, 3985–3998. [Google Scholar] [CrossRef] [PubMed]
- Galimberti, A.; De Mattia, F.; Losa, A.; Bruni, I.; Federici, S.; Casiraghi, M.; Martellos, S.; Labra, M. DNA Barcoding as a New Tool for Food Traceability. Food Res. Int. 2013, 50, 55–63. [Google Scholar] [CrossRef]
- Shehata, H.R.; Bourque, D.; Steinke, D.; Chen, S.; Hanner, R. Survey of Mislabelling across Finfish Supply Chain Reveals Mislabelling Both Outside and within Canada. Food Res. Int. 2018, 121, 723–729. [Google Scholar] [CrossRef] [PubMed]
- Shehata, H.R.; Naaum, A.M.; Garduño, R.A.; Hanner, R. DNA Barcoding as a Regulatory Tool for Seafood Authentication in Canada. Food Control 2018, 92, 147–153. [Google Scholar] [CrossRef]
- Louppis, A.P.; Karabagias, I.K.; Papastephanou, C.; Badeka, A. Two-Way Characterization of Beekeepers’ Honey According to Botanical Origin on the Basis of Mineral Content Analysis Using ICP-OES Implemented with Multiple Chemometric Tools. Foods 2019, 8, 210. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Camin, F.; Bontempo, L.; Perini, M.; Piasentier, E. Stable Isotope Ratio Analysis for Assessing the Authenticity of Food of Animal Origin: Authenticity of Animal Origin Food. Compr. Rev. Food Sci. Food Saf. 2016, 15, 868–877. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Bontempo, L.; Paolini, M.; Franceschi, P.; Ziller, L.; García-González, D.L.; Camin, F. Characterisation and Attempted Differentiation of European and Extra-European Olive Oils Using Stable Isotope Ratio Analysis. Food Chem. 2019, 276, 782–789. [Google Scholar] [CrossRef] [PubMed]
- Shin, W.J.; Choi, S.H.; Ryu, J.S.; Song, B.Y.; Song, J.H.; Park, S.; Min, J.S. Discrimination of the Geographic Origin of Pork Using Multi-Isotopes and Statistical Analysis. Rapid Commun. Mass Spectrom. 2018, 32, 1843–1850. [Google Scholar] [CrossRef]
- Chung, I.M.; Kim, J.K.; Lee, K.J.; Park, S.K.; Lee, J.H.; Son, N.Y.; Jin, Y.I.; Kim, S.H. Geographic Authentication of Asian Rice (Oryza Sativa L.) Using Multi-Elemental and Stable Isotopic Data Combined with Multivariate Analysis. Food Chem. 2018, 240, 840–849. [Google Scholar] [CrossRef] [PubMed]
- Karabagias, I.K. Seeking of Reliable Markers Related to Greek Nectar Honey Geographical and Botanical Origin Identification Based on Sugar Profile by HPLC-RI and Electro-Chemical Parameters Using Multivariate Statistics. Eur. Food Res. Technol. 2019, 245, 805–816. [Google Scholar] [CrossRef]
- Zhao, Y.; Tu, T.; Tang, X.; Zhao, S.; Qie, M.; Chen, A.; Yang, S. Authentication of Organic Pork and Identification of Geographical Origins of Pork in Four Regions of China by Combined Analysis of Stable Isotopes and Multi-Elements. Meat Sci. 2020, 165, 108129. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Tian, L.; Chen, B.; Jin, B.; Tian, B.; Xie, L.; Rogers, K.M.; Lin, G. Verification of Imported Red Wine Origin into China Using Multi Isotope and Elemental Analyses. Food Chem. 2019, 301, 125137. [Google Scholar] [CrossRef] [PubMed]
- Fiorillo, J. Canadian Wild Salmon Fisheries Quitting MSC Program. Available online: https://www.intrafish.com/fisheries/canadian-wild-salmon-fisheries-quitting-msc-program/2-1-683519 (accessed on 10 April 2014).
- Centre, T.W.S. A Review of IUU Salmon Fishing and Potential Conservation Strategies in the Russian Far East; Technical Report; The Wild Salmon Center: Portland, OR, USA, 2009. [Google Scholar]
- Clarke, S. Trading Tails: Russian Salmon Fisheries and East Asian Markets; Technical Report; TRAFFIC East Asia: Hong Kong, China, 2007. [Google Scholar]
- Clarke, S.C.; McAllister, M.K.; Kirkpatrick, R.C. Estimating Legal and Illegal Catches of Russian Sockeye Salmon from Trade and Market Data. ICES J. Mar. Sci. 2009, 66, 532–545. [Google Scholar] [CrossRef]
- Bligh, E.G.; Dyer, W.J. A Rapid Method of Total Lipid Extraction and Purification. Can. J. Biochem. Physiol. 1959, 37, 911–917. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Morrison, W.R.; Smith, M. Preparation of Fatty Acid Methyl Esters and Dimethylacetals from Lipids with Boron Fluoride-Methanol. J. Lipid Res. 1964, 5, 600–608. [Google Scholar] [CrossRef]
- Hastie, T.; Tibshirani, R.; Friedman, J. The Elements of Statistical Learning; Springer Series in Statistics; Springer: New York, NY, USA, 2009. [Google Scholar] [CrossRef]
- Sun, S.; Guo, B.; Wei, Y. Origin Assignment by Multi-Element Stable Isotopes of Lamb Tissues. Food Chem. 2016, 213, 675–681. [Google Scholar] [CrossRef]
- Wunder, M.B. Using Isoscapes to Model Probability Surfaces for Determining Geographic Origins. In Isoscapes; West, J.B., Bowen, G.J., Dawson, T.E., Tu, K.P., Eds.; Springer: Dordrecht, the Netherland, 2010; pp. 251–270. [Google Scholar] [CrossRef]
- Bataille, C.P.; Bowen, G.J. Mapping 87Sr/86Sr Variations in Bedrock and Water for Large Scale Provenance Studies. Chem. Geol. 2012, 304–305, 39–52. [Google Scholar] [CrossRef]
- Scott, D.W. Multivariate Density Estimation: Theory, Practice, and Visualization, 2nd ed.; Wiley: Hoboken, NJ, USA, 2014. [Google Scholar]
- Venables, W.N.; Ripley, B.D.; Venables, W.N. Modern Applied Statistics with S, 4th ed.; Statistics and Computing; Springer: New York, NY, USA, 2002. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2020. [Google Scholar]
- Innes, M. Flux: Elegant Machine Learning with Julia. J. Open Source Softw. 2018, 3, 602. [Google Scholar] [CrossRef] [Green Version]
- Naccarato, A.; Furia, E.; Sindona, G.; Tagarelli, A. Multivariate Class Modeling Techniques Applied to Multielement Analysis for the Verification of the Geographical Origin of Chili Pepper. Food Chem. 2016, 206, 217–222. [Google Scholar] [CrossRef] [PubMed]
- Chen, D.; Cao, X.; Wen, F.; Sun, J. Blessing of Dimensionality: High-Dimensional Feature and Its Efficient Compression for Face Verification. In Proceedings of the 2013 IEEE Conference on Computer Vision and Pattern Recognition, Portland, OR, USA, 23–28 June 2013; pp. 3025–3032. [Google Scholar] [CrossRef]
- Taigman, Y.; Yang, M.; Ranzato, M.; Wolf, L. DeepFace: Closing the Gap to Human-Level Performance in Face Verification. In Proceedings of the 2014 IEEE Conference on Computer Vision and Pattern Recognition, Columbus, OH, USA, 23–28 June 2014; pp. 1701–1708. [Google Scholar] [CrossRef]
- Bartos, I.; Kowalski, M.; Institute of Physics (Gran Bretanya). Multimessenger Astronomy; IOP Publishing: Bristol, UK, 2017. [Google Scholar]
- Pimentel, T.; Marcelino, J.; Ricardo, F.; Soares, A.M.V.M.; Calado, R. Bacterial Communities 16S rDNA Fingerprinting as a Potential Tracing Tool for Cultured Seabass Dicentrarchus Labrax. Sci. Rep. 2017, 7, 11862. [Google Scholar] [CrossRef] [PubMed]
- Zhao, H.; Zhang, S.; Zhang, Z. Relationship between Multi-Element Composition in Tea Leaves and in Provenance Soils for Geographical Traceability. Food Control 2017, 76, 82–87. [Google Scholar] [CrossRef]
- Liu, G.; Liu, Q.; Li, P. Blessing of Dimensionality: Recovering Mixture Data via Dictionary Pursuit. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 47–60. [Google Scholar] [CrossRef]
- Hebert, P.D.N.; Cywinska, A.; Ball, S.L.; de Waard, J.R. Biological Identifications through DNA Barcodes. Proc. R. Soc. Lond. Ser. B Biol. Sci. 2003, 270, 313–321. [Google Scholar] [CrossRef] [Green Version]
- Zemlak, T.S.; Ward, R.D.; Connell, A.D.; Holmes, B.H.; Hebert, P.D.N. DNA Barcoding Reveals Overlooked Marine Fishes. Mol. Ecol. Resour. 2009, 9, 237–242. [Google Scholar] [CrossRef]
- Ehleringer, J.R.; Bowen, G.J.; Chesson, L.A.; West, A.G.; Podlesak, D.W.; Cerling, T.E. Hydrogen and Oxygen Isotope Ratios in Human Hair Are Related to Geography. Proc. Natl. Acad. Sci. USA 2008, 105, 2788–2793. [Google Scholar] [CrossRef] [Green Version]
- Fan, X.; Messenger, C.; Heng, I.S. A Bayesian Approach to Multi-Messenger Astronomy: Identification of Gravitational-Wave Host Galaxies. Astrophys. J. 2014, 795, 43. [Google Scholar] [CrossRef]
- Frederic, P.; Lad, F. Two Moments of the Logitnormal Distribution. Commun. Stat. Simul. Comput. 2008, 37, 1263–1269. [Google Scholar] [CrossRef]
- Wutzler, T. Logitnorm: Functions for the Logitnormal Distribution; 2018. [Google Scholar]
- Ratnasingham, S.; Hebert, P.D.N. BOLD: The Barcode of Life Data System (http://www.barcodinglife.org). Mol. Ecol. Notes 2007, 7, 355–364. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kimura, M. A Simple Method for Estimating Evolutionary Rates of Base Substitutions through Comparative Studies of Nucleotide Sequences. J. Mol. Evol. 1980, 16, 111–120. [Google Scholar] [CrossRef] [PubMed]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cazelles, K.; Zemlak, T.S.; Gutgesell, M.; Myles-Gonzalez, E.; Hanner, R.; Shear McCann, K. Spatial Fingerprinting: Horizontal Fusion of Multi-Dimensional Bio-Tracers as Solution to Global Food Provenance Problems. Foods 2021, 10, 717. https://doi.org/10.3390/foods10040717
Cazelles K, Zemlak TS, Gutgesell M, Myles-Gonzalez E, Hanner R, Shear McCann K. Spatial Fingerprinting: Horizontal Fusion of Multi-Dimensional Bio-Tracers as Solution to Global Food Provenance Problems. Foods. 2021; 10(4):717. https://doi.org/10.3390/foods10040717
Chicago/Turabian StyleCazelles, Kevin, Tyler Stephen Zemlak, Marie Gutgesell, Emelia Myles-Gonzalez, Robert Hanner, and Kevin Shear McCann. 2021. "Spatial Fingerprinting: Horizontal Fusion of Multi-Dimensional Bio-Tracers as Solution to Global Food Provenance Problems" Foods 10, no. 4: 717. https://doi.org/10.3390/foods10040717
APA StyleCazelles, K., Zemlak, T. S., Gutgesell, M., Myles-Gonzalez, E., Hanner, R., & Shear McCann, K. (2021). Spatial Fingerprinting: Horizontal Fusion of Multi-Dimensional Bio-Tracers as Solution to Global Food Provenance Problems. Foods, 10(4), 717. https://doi.org/10.3390/foods10040717






