Vacuum and Infrared-Assisted Hot Air Impingement Drying for Improving the Processing Performance and Quality of Poria cocos (Schw.) Wolf Cubes
Abstract
1. Introduction
2. Materials and Methods
2.1. Raw Material
2.2. Drying Equipment
2.3. Drying Experiments
2.4. Drying Kinetics
2.5. Dincer Drying Model
2.6. Response Surface Methodology
2.7. Broken Ratio
2.8. Firmness
2.9. Water-Soluble Polysaccharide Content
2.10. Specific Energy Consumption
2.11. Statistical Analysis
3. Results and Discussion
3.1. Drying Characteristics of Poria Cubes under Different Drying Methods
3.2. Drying Kinetics
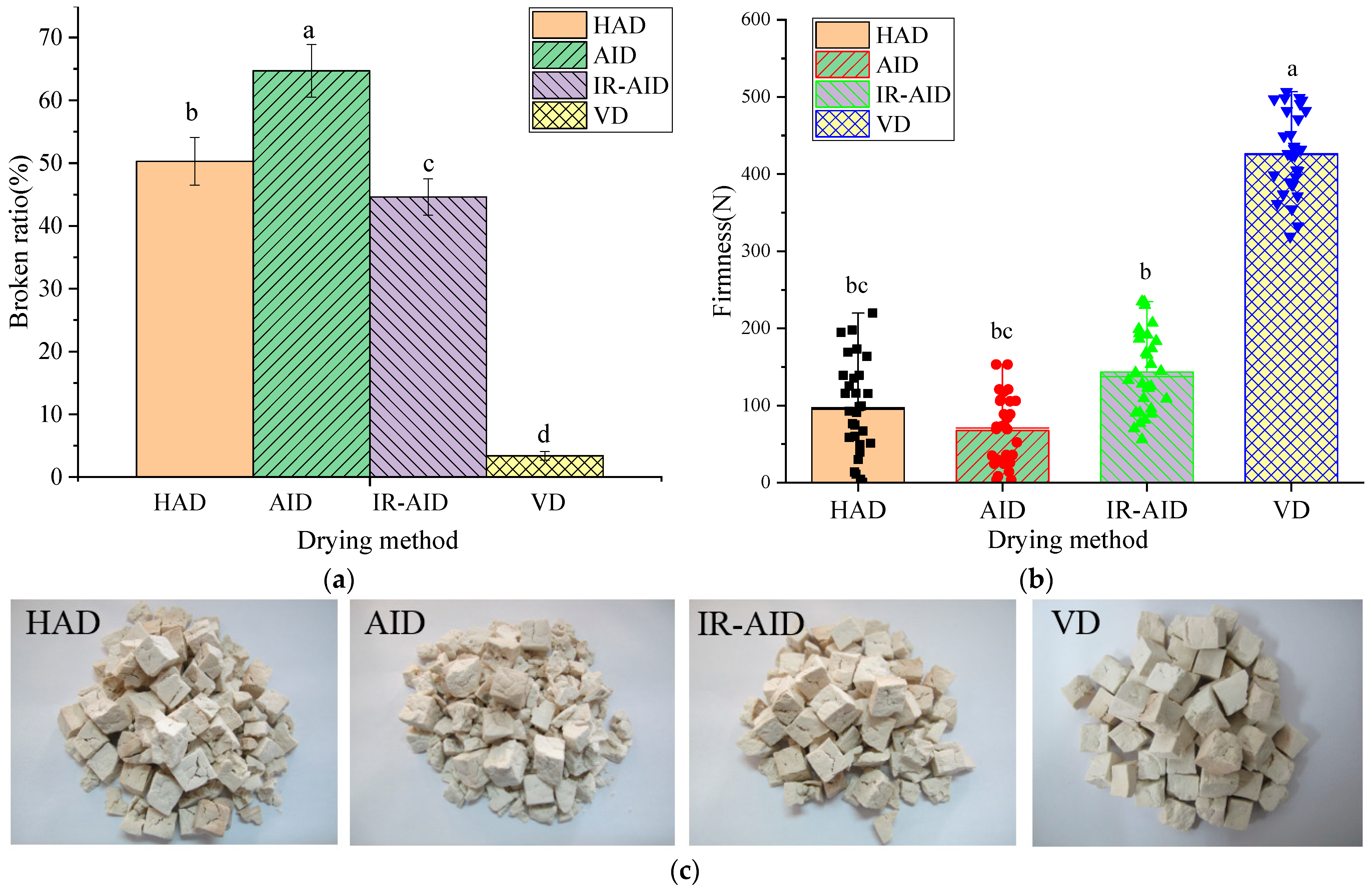
3.3. Broken Ratio and Firmness
3.4. Retention of Water-Soluble Polysaccharide Contents
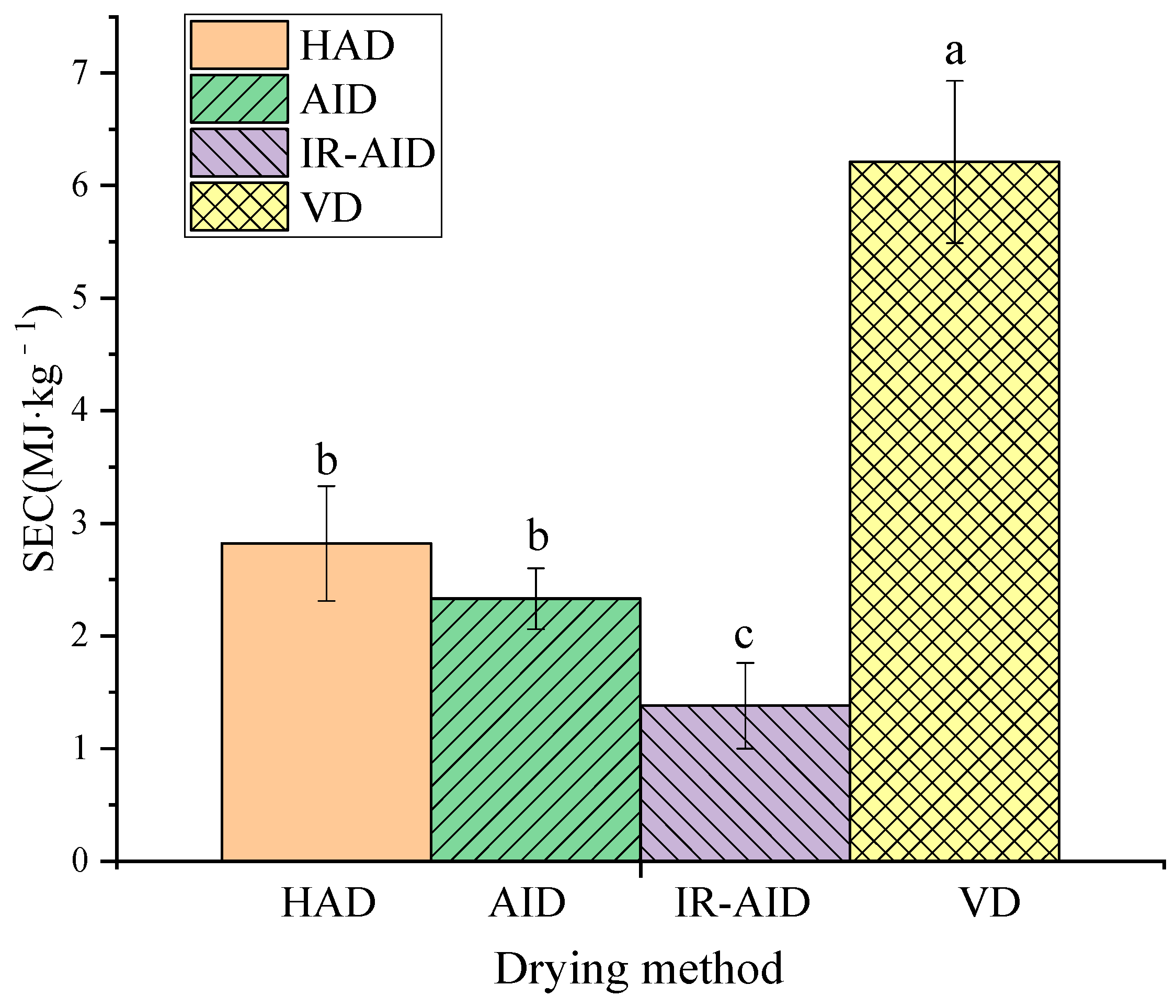
3.5. Specific Energy Consumption
3.6. Two-Stage Vacuum and Infrared-Assisted Hot Air Impingement Drying
3.7. Numerical Optimization and Verification
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wu, K.; Fan, J.; Huang, X.; Wu, X.; Guo, C. Hepatoprotective effects exerted by Poria Cocos polysaccharides against acetaminophen-induced liver injury in mice. Int. J. Biol. Macromol. 2018, 114, 137–142. [Google Scholar] [CrossRef]
- Zou, Y.T.; Zhou, J.; Wu, C.Y.; Zhang, W.; Shen, H.; Xu, J.D.; Zhang, Y.Q.; Long, F.; Li, S.L. Protective effects of Poria cocos and its components against cisplatin-induced intestinal injury. J. Ethnopharmacol. 2021, 269, 113722. [Google Scholar] [CrossRef]
- Zhang, W.; Pan, Z.; Xiao, H.; Zheng, Z.; Chen, C.; Gao, Z. Pulsed vacuum drying (PVD) technology improves drying efficiency and quality of Poria cubes. Dry. Technol. 2017, 36, 908–921. [Google Scholar] [CrossRef]
- Chen, C.; Venkitasamy, C.; Zhang, W.; Deng, L.; Meng, X.; Pan, Z. Effect of step-down temperature drying on energy consumption and product quality of walnuts. J. Food Eng. 2020, 285, 110105. [Google Scholar] [CrossRef]
- Darvishi, H.; Farhudi, Z.; Behroozi-Khazaei, N. Multi-objective optimization of savory leaves drying in continuous infrared-hot air dryer by response surface methodology and desirability function. Comput. Electron. Agric. 2020, 168, 105112. [Google Scholar] [CrossRef]
- Acar, C.; Dincer, I.; Mujumdar, A. A comprehensive review of recent advances in renewable-based drying technologies for a sustainable future. Dry. Technol. 2020, 1–27. [Google Scholar] [CrossRef]
- Deng, L.Z.; Mujumdar, A.S.; Zhang, Q.; Yang, X.H.; Wang, J.; Zheng, Z.A.; Gao, Z.J.; Xiao, H.W. Chemical and physical pretreatments of fruits and vegetables: Effects on drying characteristics and quality attributes—A comprehensive review. Crit. Rev. Food Sci. Nutr. 2019, 59, 1408–1432. [Google Scholar] [CrossRef] [PubMed]
- Xiao, H.-W.; Bai, J.-W.; Xie, L.; Sun, D.-W.; Gao, Z.-J. Thin-layer air impingement drying enhances drying rate of American ginseng (Panax quinquefolium L.) slices with quality attributes considered. Food Bioprod. Process. 2015, 94, 581–591. [Google Scholar] [CrossRef]
- Wang, H.-C.; Zhang, M.; Adhikari, B. Drying of shiitake mushroom by combining freeze-drying and mid-infrared radiation. Food Bioprod. Process. 2015, 94, 507–517. [Google Scholar] [CrossRef]
- Salehi, F. Recent Applications and Potential of Infrared Dryer Systems for Drying Various Agricultural Products: A Review. Int. J. Fruit Sci. 2019, 20, 586–602. [Google Scholar] [CrossRef]
- Lao, Y.; Zhang, M.; Chitrakar, B.; Bhandari, B.; Fan, D. Efficient Plant Foods Processing Based on Infrared Heating. Food Rev. Int. 2019, 35, 640–663. [Google Scholar] [CrossRef]
- Zhang, Y.; Zhu, G.; Li, X.; Zhao, Y.; Lei, D.; Ding, G.; Ambrose, K.; Liu, Y. Combined medium- and short-wave infrared and hot air impingement drying of sponge gourd (Luffa cylindrical) slices. J. Food Eng. 2020, 284. [Google Scholar] [CrossRef]
- Supmoon, N.; Noomhorm, A. Influence of Combined Hot Air Impingement and Infrared Drying on Drying Kinetics and Physical Properties of Potato Chips. Dry. Technol. 2013, 31, 24–31. [Google Scholar] [CrossRef]
- Wan, J.Y.; Fan, Y.; Yu, Q.T.; Ge, Y.Z.; Yan, C.P.; Alolga, R.N.; Li, P.; Ma, Z.H.; Qi, L.W. Integrated evaluation of malonyl ginsenosides, amino acids and polysaccharides in fresh and processed ginseng. J. Pharm. Biomed. Anal. 2015, 107, 89–97. [Google Scholar] [CrossRef] [PubMed]
- Ouakhssase, A.; Ait Addi, E. Mycotoxins in food: A review on liquid chromatographic methods coupled to mass spectrometry and their experimental designs. Crit. Rev. Food Sci. Nutr. 2020, 1–21. [Google Scholar] [CrossRef]
- Šumić, Z.; Tepić, A.; Vidović, S.; Vladić, J.; Pavlić, B. Drying of shiitake mushrooms in a vacuum dryer and optimization of the process by response surface methodology (RSM). J. Food Meas. Charact. 2016, 10, 425–433. [Google Scholar] [CrossRef]
- Thakur, M.; Pant, K.; Naik, R.R.; Nanda, V. Optimization of spray drying operating conditions for production of functional milk powder encapsulating bee pollen. Dry. Technol. 2020, 39, 777–790. [Google Scholar] [CrossRef]
- Onu, C.E.; Igbokwe, P.K.; Nwabanne, J.T.; Nwajinka, C.O.; Ohale, P.E. Evaluation of optimization techniques in predicting optimum moisture content reduction in drying potato slices. Artif. Intell. Agric. 2020, 4, 39–47. [Google Scholar]
- Castro, A.M.; Mayorga, E.Y.; Moreno, F.L. Mathematical modelling of convective drying of fruits: A review. J. Food Eng. 2018, 223, 152–167. [Google Scholar] [CrossRef]
- Dincer, I.; Hussain, M.M. Development of a new Biot number and lag factor correlation for drying applications. Int. J. Heat Mass Transf. 2004, 47, 653–658. [Google Scholar] [CrossRef]
- Ju, H.-Y.; El-Mashad, H.M.; Fang, X.-M.; Pan, Z.; Xiao, H.-W.; Liu, Y.-H.; Gao, Z.-J. Drying characteristics and modeling of yam slices under different relative humidity conditions. Dry. Technol. 2015, 34, 296–306. [Google Scholar] [CrossRef]
- Rajoriya, D.; Shewale, S.R.; Hebbar, H.U. Refractance Window Drying of Apple Slices: Mass Transfer Phenomena and Quality Parameters. Food Bioprocess Technol. 2019, 12, 1646–1658. [Google Scholar] [CrossRef]
- Bezerra, C.V.; Meller da Silva, L.H.; Corrêa, D.F.; Rodrigues, A.M.C. A modeling study for moisture diffusivities and moisture transfer coefficients in drying of passion fruit peel. Int. J. Heat Mass Transf. 2015, 85, 750–755. [Google Scholar] [CrossRef]
- Shi, H.; Zhang, M.; Devahastin, S. New Development of Efficient Processing Techniques on Typical Medicinal Fungi: A Review. Food Rev. Int. 2020, 36, 39–57. [Google Scholar] [CrossRef]
- Mohammadi, I.; Tabatabaekoloor, R.; Motevali, A. Effect of air recirculation and heat pump on mass transfer and energy parameters in drying of kiwifruit slices. Energy 2019, 170, 149–158. [Google Scholar] [CrossRef]
- Onwude, D.I.; Hashim, N.; Abdan, K.; Janius, R.; Chen, G. Modelling the mid-infrared drying of sweet potato: Kinetics, mass and heat transfer parameters, and energy consumption. Heat Mass Transf. 2018, 54, 2917–2933. [Google Scholar] [CrossRef]
- Rahman, M.S.; Al-Shamsi, Q.H.; Bengtsson, G.B.; Sablani, S.S.; Al-Alawi, A. Drying Kinetics and Allicin Potential in Garlic Slices during Different Methods of Drying. Dry. Technol. 2009, 27, 467–477. [Google Scholar] [CrossRef]
- Wang, H.; Liu, Z.L.; Vidyarthi, S.K.; Wang, Q.H.; Gao, L.; Li, B.R.; Wei, Q.; Liu, Y.H.; Xiao, H.W. Effects of different drying methods on drying kinetics, physicochemical properties, microstructure, and energy consumption of potato (Solanum tuberosum L.) cubes. Dry. Technol. 2020, 39, 418–431. [Google Scholar] [CrossRef]
- McMinn, W.A.M. Prediction of moisture transfer parameters for microwave drying of lactose powder using Bi–G drying correlation. Food Res. Int. 2004, 37, 1041–1047. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, C.; Pan, Z.; Xiao, H.-W.; Xie, L.; Gao, Z.-J.; Zheng, Z.-A. Design and performance evaluation of a pilot-vacuum infrared drying (PVID) system for drying of berries. Dry. Technol. 2020, 38, 1340–1355. [Google Scholar] [CrossRef]
- Xiao, H.-W.; Pang, C.-L.; Wang, L.-H.; Bai, J.-W.; Yang, W.-X.; Gao, Z.-J. Drying kinetics and quality of Monukka seedless grapes dried in an air-impingement jet dryer. Biosyst. Eng. 2010, 105, 233–240. [Google Scholar] [CrossRef]
- Seremet Ceclu, L.; Botez, E.; Nistor, O.V.; Andronoiu, D.G.; Mocanu, G.D. Effect of different drying methods on moisture ratio and rehydration of pumpkin slices. Food Chem. 2016, 195, 104–109. [Google Scholar] [CrossRef] [PubMed]
- Joardder, M.U.; Kumar, C.; Karim, M.A. Food structure: Its formation and relationships with other properties. Crit. Rev. Food Sci. Nutr. 2017, 57, 1190–1205. [Google Scholar] [CrossRef] [PubMed]
- Khan, M.I.H.; Nagy, S.A.; Karim, M.A. Transport of cellular water during drying: An understanding of cell rupturing mechanism in apple tissue. Food Res. Int. 2018, 105, 772–781. [Google Scholar] [CrossRef]
- Chen, C.; Upadhyaya, S.; Khir, R.; Pan, Z. Simulation of walnut drying under hot air heating using a nonequilibrium multiphase transfer model. Dry. Technol. 2020, 1–15. [Google Scholar] [CrossRef]
- Chen, L.; Opara, U.L. Texture measurement approaches in fresh and processed foods—A review. Food Res. Int. 2013, 51, 823–835. [Google Scholar] [CrossRef]
- Puente-Diaz, L.; Spolmann, O.; Nocetti, D.; Zura-Bravo, L.; Lemus-Mondaca, R. Effects of Infrared-Assisted Refractance Window Drying on the Drying Kinetics, Microstructure, and Color of Physalis Fruit Puree. Foods 2020, 9, 343. [Google Scholar] [CrossRef] [PubMed]
- Beaudry, C.; Raghavan, G.S.V.; Ratti, C.; Rennie, T.J. Effect of Four Drying Methods on the Quality of Osmotically Dehydrated Cranberries. Dry. Technol. 2004, 22, 521–539. [Google Scholar] [CrossRef]
- Hao, Q.B.; Li, C.S.; Liu, G.Q.; Xu, X.Y.; Jiao, G.F.; Zheng, H.L.; Zhang, S.N.; Bai, L.F. Effect of high-temperature vacuum degassing on microstructure and current-carrying capacity of the Bi-2212 wire. J. Alloys Compd. 2018, 742, 897–902. [Google Scholar] [CrossRef]
- Joardder, M.U.H.; Brown, R.J.; Kumar, C.; Karim, M.A. Effect of Cell Wall Properties on Porosity and Shrinkage of Dried Apple. Int. J. Food Prop. 2015, 18, 2327–2337. [Google Scholar] [CrossRef]
- Souraki, B.A.; Ghavami, M.; Tondro, H. Correction of moisture and sucrose effective diffusivities for shrinkage during osmotic dehydration of apple in sucrose solution. Food Bioprod. Process. 2014, 92, 1–8. [Google Scholar] [CrossRef]
- Goula, A.M.; Chasekioglou, A.N.; Lazarides, H.N. Drying and Shrinkage Kinetics of Solid Waste of Olive Oil Processing. Dry. Technol. 2015, 33, 1728–1738. [Google Scholar] [CrossRef]
- Mancuhan, E.; Özen, S.; Sayan, P.; Sargut, S.T. Experimental investigation of green brick shrinkage behavior with Bigot’s curves. Dry. Technol. 2016, 34, 1535–1545. [Google Scholar] [CrossRef]
- Hentati, F.; Delattre, C.; Ursu, A.V.; Desbrieres, J.; Le Cerf, D.; Gardarin, C.; Abdelkafi, S.; Michaud, P.; Pierre, G. Structural characterization and antioxidant activity of water-soluble polysaccharides from the Tunisian brown seaweed Cystoseira compressa. Carbohydr Polym. 2018, 198, 589–600. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.K.; Wu, L.X.; Qiao, Z.R.; Cai, W.D.; Ma, H. Effect of different drying methods on the product quality and bioactive polysaccharides of bitter gourd (Momordica charantia L.) slices. Food Chem. 2019, 271, 588–596. [Google Scholar] [CrossRef] [PubMed]
- Liu, Y.; Luo, M.; Liu, F.; Feng, X.; Ibrahim, S.A.; Cheng, L.; Huang, W. Effects of freeze drying and hot-air drying on the physicochemical properties and bioactivities of polysaccharides from Lentinula edodes. Int. J. Biol. Macromol. 2020, 145, 476–483. [Google Scholar] [CrossRef] [PubMed]
- Wang, B.; Venkitasamy, C.; Zhang, F.; Zhao, L.; Khir, R.; Pan, Z. Feasibility of jujube peeling using novel infrared radiation heating technology. LWT Food Sci. Technol. 2016, 69, 458–467. [Google Scholar] [CrossRef]
- Chen, J.; Venkitasamy, C.; Shen, Q.; McHugh, T.H.; Zhang, R.; Pan, Z. Development of healthy crispy carrot snacks using sequential infrared blanching and hot air drying method. LWT Food Sci. Technol. 2018, 97, 469–475. [Google Scholar] [CrossRef]





| Drying Parameters | Coded Level of Variables | |||
|---|---|---|---|---|
| −1 | 0 | +1 | ||
| TVD (°C) | X1 | 65 | 75 | 85 |
| MRswitch (%) | X2 | 70 | 80 | 90 |
| TIR-AID (°C) | X3 | 65 | 75 | 85 |
| Drying Methods | Drying Constant | Deff (m2·s−1) | Bi | k (m·s−1) | Adj-R2 | χ2 | RMSE | ||
|---|---|---|---|---|---|---|---|---|---|
| G | S × 10−4 (s−1) | ||||||||
| HAD | 1.089 | 1.036 | 8.148 × 10−9 | 7.531 × 10−9 | 0.5626 | 6.548 × 10−7 | 0.996 | 1.92 × 10−4 | 0.014 |
| AID | 1.023 | 1.688 | 5.768 × 10−8 | 1.310 × 10−8 | 0.1057 | 8.701 × 10−7 | 0.998 | 1.32 × 10−4 | 0.011 |
| IR-AID | 1.022 | 2.197 | 7.901 × 10−8 | 3.767 × 10−8 | 0.1030 | 1.162 × 10−6 | 0.997 | 0.44 × 10−4 | 0.006 |
| VD | 1.087 | 1.044 | 8.401 × 10−9 | 8.335 × 10−9 | 0.5320 | 6.385 × 10−7 | 0.995 | 2.83 × 10−4 | 0.017 |
| No. | Drying Conditions | Response | |||||
|---|---|---|---|---|---|---|---|
| TVD (°C) | MRswitch (%) | TIR-AID (°C) | Total Drying Time (min) | Broken Ratio (%) | Water-Soluble Polysaccharide Content (mg·g−1) | SEC (MJ·kg−1) | |
| 1 | 85 | 90 | 75 | 187 | 43.50 | 6.77 | 1.88 |
| 2 | 75 | 70 | 85 | 287 | 5.23 | 10.69 | 2.97 |
| 3 | 75 | 80 | 75 | 245 | 22.10 | 8.10 | 2.25 |
| 4 | 75 | 90 | 85 | 172 | 44.20 | 4.46 | 1.24 |
| 5 | 65 | 70 | 75 | 325 | 4.35 | 14.54 | 4.04 |
| 6 | 85 | 70 | 75 | 288 | 3.79 | 10.40 | 2.89 |
| 7 | 75 | 90 | 65 | 228 | 43.79 | 5.83 | 1.62 |
| 8 | 75 | 80 | 75 | 245 | 21.10 | 8.17 | 2.27 |
| 9 | 75 | 80 | 75 | 248 | 21.70 | 8.10 | 2.25 |
| 10 | 75 | 70 | 65 | 343 | 4.17 | 12.24 | 3.40 |
| 11 | 85 | 80 | 85 | 212 | 20.90 | 5.36 | 1.49 |
| 12 | 65 | 80 | 85 | 249 | 21.21 | 8.32 | 2.31 |
| 13 | 85 | 80 | 65 | 256 | 20.52 | 6.70 | 1.86 |
| 14 | 75 | 80 | 75 | 242 | 21.06 | 8.93 | 2.48 |
| 15 | 65 | 90 | 75 | 213 | 44.10 | 7.31 | 2.03 |
| 16 | 65 | 80 | 65 | 297 | 20.95 | 9.50 | 2.64 |
| 17 | 75 | 80 | 75 | 251 | 21.37 | 7.70 | 2.14 |
| Source | Total Drying Time (min) | Broken Ratio (%) | Water-Soluble Polysaccharide Content (mg·g−1) | SEC (MJ·kg−1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| DF * | Sum of Squares | p-Value | DF * | Sum of Squares | p-Value | DF * | Sum of Squares | p-Value | DF * | Sum of Squares | p-Value | |
| Model | 9 | 32,556.01 | <0.0001 | 9 | 3160.99 | <0.0001 | 9 | 9.71 | <0.0001 | 9 | 100.69 | <0.001 |
| 1 | 2485.13 | <0.0001 | 1 | 0.45 | 0.1137 | 1 | 2.450 × 10−3 | 0.6237 | 1 | 13.62 | <0.0001 | |
| 1 | 24,531.12 | <0.0001 | 1 | 3122.48 | <0.0001 | 1 | 0.022 | 0.1676 | 1 | 69.08 | <0.0001 | |
| 1 | 5202.00 | <0.0001 | 1 | 0.56 | 0.0848 | 1 | 7.33 | <0.0001 | 1 | 3.69 | <0.0001 | |
| 1 | 30.25 | 0.2892 | 1 | 4.000 × 10−4 | 0.9586 | 1 | 0.12 | 0.0097 | 1 | 3.24 | 0.0033 | |
| 1 | 4.00 | 0.6892 | 1 | 3.600 × 10−3 | 0.8763 | 1 | 0.67 | <0.0001 | 1 | 5.184 × 10−3 | 0.0046 | |
| 1 | 0.000 | 1.0000 | 1 | 0.11 | 0.4110 | 1 | 0.18 | 0.0029 | 1 | 8.100 × 10−3 | 0.8745 | |
| 1 | 9.79 | 0.5350 | 1 | 1.02 | 0.0300 | 1 | 0.30 | 0.0008 | 1 | 0.54 | 0.8435 | |
| 1 | 128.53 | 0.0501 | 1 | 36.91 | <0.0001 | 1 | 0.99 | <0.0001 | 1 | 6.02 | 0.1374 | |
| 1 | 140.42 | 0.0428 | 1 | 0.026 | 0.6750 | 1 | 0.17 | 0.0038 | 1 | 5.00 | 0.0008 | |
| Residual | 7 | 161.05 | - | 7 | 0.97 | 7 | 0.065 | - | 7 | 1.35 | - | |
| Lack of Fit | 3 | 114.25 | 0.1420 | 3 | 0.20 | 0.7903 | 3 | 0.034 | 0.3576 | 3 | 0.55 | 0.5047 |
| Pure Error | 4 | 46.80 | - | 4 | 0.76 | - | 4 | 0.031 | - | 4 | 0.80 | - |
| Total | 16 | 32,717.06 | - | 16 | 3161.96 | - | 16 | 9.78 | - | 16 | 102.04 | - |
| Adj- R2 | - | 0.9887 | - | - | 0.9993 | - | - | 0.9848 | - | - | 0.9697 | - |
| Pre- R2 | - | 0.9419 | - | - | 0.9986 | - | - | 0.9398 | - | - | 0.9009 | - |
| Adeq Precision | - | 43.968 | - | - | 141.174 | - | - | 43.991 | - | - | 30.168 | - |
| C.V.% | - | 1.90 | - | - | 1.65 | - | - | 3.20 | - | - | 5.22 | - |
| PRESS | - | 1901.12 | - | - | 4.44 | - | - | 0.59 | - | - | 10.11 | - |
| Response | Optimized Direction | Lower Limit | Upper Limit | Weight |
|---|---|---|---|---|
| Total Drying time (min) | Minimize | 100 | 400 | 0.25 |
| Broken ratio (%) | Minimize | 2.0 | 50.0 | 0.25 |
| Water-soluble polysaccharide content (mg·g−1) | Maximize | 1.0 | 5.0 | 0.25 |
| SEC (MJ·kg−1) | Minimize | 1.0 | 5.0 | 0.25 |
| Results | Operating Conditions | Response Variables | |||||
|---|---|---|---|---|---|---|---|
| TVD (°C) | MRswitch (%) | TIR-AID (°C) | Total Drying Time (min) | Broken Ratio (%) | Water-Soluble Polysaccharide Content (mg·g−1) | SEC (MJ·kg−1) | |
| Prediction | 82.17 | 81.11 | 69.04 | 245.29 | 23.07 | 3.24 | 2.01 |
| Validation | 82 | 81 | 69 | 255 | 24.88 | 3.32 | 2.04 |
| IR-AID | —— | 100 | 69 | 197 | 53.34 | 3.34 | 1.24 |
| VD | 82 | 9 | —— | 322 | 3.75 | 4.39 | 6.07 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, W.; Chen, C.; Pan, Z.; Zheng, Z. Vacuum and Infrared-Assisted Hot Air Impingement Drying for Improving the Processing Performance and Quality of Poria cocos (Schw.) Wolf Cubes. Foods 2021, 10, 992. https://doi.org/10.3390/foods10050992
Zhang W, Chen C, Pan Z, Zheng Z. Vacuum and Infrared-Assisted Hot Air Impingement Drying for Improving the Processing Performance and Quality of Poria cocos (Schw.) Wolf Cubes. Foods. 2021; 10(5):992. https://doi.org/10.3390/foods10050992
Chicago/Turabian StyleZhang, Weipeng, Chang Chen, Zhongli Pan, and Zhian Zheng. 2021. "Vacuum and Infrared-Assisted Hot Air Impingement Drying for Improving the Processing Performance and Quality of Poria cocos (Schw.) Wolf Cubes" Foods 10, no. 5: 992. https://doi.org/10.3390/foods10050992
APA StyleZhang, W., Chen, C., Pan, Z., & Zheng, Z. (2021). Vacuum and Infrared-Assisted Hot Air Impingement Drying for Improving the Processing Performance and Quality of Poria cocos (Schw.) Wolf Cubes. Foods, 10(5), 992. https://doi.org/10.3390/foods10050992







